the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A simple time-stepping scheme to simulate leaf area index, phenology, and gross primary production across deciduous broadleaf forests in the eastern United States
Yongjiu Dai
Xiaoping Liu
Terrestrial plants play a key role in regulating the exchange of energy and materials between the land surface and the atmosphere. Robust models that simulate both leaf dynamics and canopy photosynthesis are required to understand vegetation–climate interactions. This study proposes a simple time-stepping scheme to simulate leaf area index (LAI), phenology, and gross primary production (GPP) when forced with climate variables. The method establishes a linear function between steady-state LAI and the corresponding GPP. The method applies the established function and the MOD17 algorithm to form simultaneous equations, which can be solved together numerically. To account for the time-lagged responses of plant growth to environmental conditions, a time-stepping scheme is developed to simulate the LAI time series based on the solved steady-state LAI. The simulated LAI time series is then used to derive the timing of key phenophases and simulate canopy GPP with the MOD17 algorithm. The developed method is applied to deciduous broadleaf forests in the eastern United States and is found to perform well for simulating canopy LAI and GPP at the site scale as evaluated using both flux tower and satellite data. The method also captures the spatiotemporal variation of vegetation LAI and phenology across the eastern United States compared with satellite observations. The developed time-stepping scheme provides a simplified and improved version of our previous modeling approach to simulate leaf phenology and can potentially be applied at regional to global scales in future studies.
Terrestrial plants play a key role in regulating the exchange of energy and materials (e.g., radiation, heat and moisture, carbon, and trace gas) between the land surface and the atmosphere (Beer et al., 2010; Zhu et al., 2017). The canopy structure and characteristics govern solar radiation interception and absorption (Ni-Meister et al., 2010; Yuan et al., 2013). Plants control water transpiration and photosynthetic carbon fixation through processes from transient changes in leaf stomatal conductance to seasonal variation in foliage dynamics (Eagleson, 2005). In turn, external environmental conditions, such as sunlight, temperature, and water and nutrient availability, selectively determine plant form and function (Bonan, 2008). Numerical models that integrate multidisciplinary knowledge allow us to understand and predict the interactions between terrestrial ecosystems and the climate.
Developments of terrestrial biosphere models essentially seek accurate solutions to the simulation of energy and material exchanging fluxes between ecosystems and the atmosphere. In terrestrial biosphere models, plant canopies are typically characterized using leaf area index (LAI; leaf area per unit ground area) because plant leaf is the basic organ that intercepts solar radiation for photosynthesis and transpiration (Li et al., 2018; Yuan et al., 2013). The exchanging fluxes of energy and materials over a vegetation canopy can then be modeled as a function of environmental conditions (e.g., sunlight, soil moisture, temperature, and humidity) and vegetation LAI (Ding et al., 2014). The development of satellite remote sensing technology offers large-scale observations for vegetation monitoring and a number of modeling approaches have been developed to quantify and simulate land surface fluxes based on climate variables and satellite-derived LAI. These methods include both light use efficiency models (e.g., the Carnegie–Ames–Stanford approach (CASA) model, Potter et al., 1993; the MOD17 algorithm, Running et al., 2004; the vegetation photosynthesis model (VPM), Xiao et al., 2004; the eddy covariance light use efficiency (EC-LUE) model, Yuan et al., 2010; and the two-leaf light use efficiency (TL-LUE) model, He et al., 2013) and process-based models (e.g., the boreal ecosystem productivity simulator (BEPS; Liu et al., 1997), the Breathing Earth System Simulator (BESS; Ryu et al., 2011), the growing production day model (GPD; Xin, 2016), and the revised Simple Biosphere (SiB2; Sellers et al., 1996b) model). Despite being different from each other in the representation of vegetation processes, these methods have been successfully used for applications from field to global scales. While remotely sensed vegetation data perfectly complement canopy process models, the ability to dynamically simulate vegetation LAI is fundamental to enhancing our abilities to predict terrestrial ecosystem processes.
Modeling vegetation leaf dynamics via climate variables requires in-depth understanding of plant phenological processes. This modeling is still largely empirical to date and contributes considerable uncertainties to current terrestrial biosphere models (Richardson et al., 2012). One common method for simulating vegetation phenology is to predict the timing of key phenophases such as spring onset and autumn senescence in a growing season (Hufkens et al., 2018; Liu et al., 2018). For example, most phenology models originate from the growing degree day (GDD) model, a method first proposed by De Réaumur dating back to 1735 (De Réaumur, 1735). The GDD model assumes that plant leaf onset begins when daily mean temperatures accumulated from a fixed date reach a critical threshold. Studies have identified the fact that various environmental factors other than temperature could affect plant phenology to certain degrees (Polgar and Primack, 2011), and therefore efforts have been made to improve the GDD model by adding different influential factors, such as photoperiod, soil temperature, humidity, and soil moisture (Chuine et al., 1999; Hufkens et al., 2018; Liu et al., 2018; Melaas et al., 2013; Yang et al., 2012). Land surface models like the Community Land Model (Oleson et al., 2013) and the Biome-BGC model (White et al., 2000) use a set of complicated and empirical equations to predict the timing of key phenophases across plant functional types. Arora and Boer (2005) developed a carbon-gain-based scheme that initiates leaf onset when environmental conditions are beneficial for the plant in carbon terms to produce new leaves and initiates leaf offset when environmental conditions are unfavorable with incurred carbon losses for plants. Another method for vegetation phenology modeling is to simulate the entire LAI time series over a growing season. For example, the DeNitrification DeComposition model uses an optimal seasonal growth curve of plant LAI and then calculates environmental stresses of water and nitrogen to limit daily carbon and nitrogen allocation to plant leaves (Yu et al., 2014). The growing season index as proposed by Jolly et al. (2005) is a widely used method that could simulate seasonal phenology curves using photoperiod, air temperature, and vapor pressure deficit. While these studies have greatly benefitted the development of the leaf phenology models, evaluation on 14 land surface models in deciduous forests suggested that almost all models predicted the start of the season earlier or the end of the season later than observations, and the model biases were typically 14 weeks or more. It is therefore necessary to improve the current phenology models.
The physiological processes of leaf phenology and canopy photosynthesis are interrelated. Plants absorb carbon dioxide to accumulate biomass through photosynthesis and then redistribute the photosynthetic gain to organs such as leaves, roots, and stems to optimize carbon gain. Given limited external resources, plants have evolved to effectively allocate photosynthate to organs in response to environmental conditions to maximize photosynthetic carbon gain, the fundamental bioenergy for survival (Givnish, 1986). The strategy of biomass allocation among growth, maintenance, and reproduction in a continuously changing environment directly determines whether plants can persist under natural competition pressure both interspecies and intraspecies (Bonan, 2002). In essence, new leaf phenology models may need to account for the processes of canopy photosynthesis more closely and explicitly than the current leaf phenology models.
Xin (2016) proposed a parameterization scheme to simulate vegetation productivity and phenology simultaneously. The method, named as the growing production day (GPD) model, uses canopy gross primary production (GPP) instead of air temperature as an indicator that synthesizes various environmental factors on plant photosynthesis to track how the environment is suitable for vegetation growth. Analogous to the method that derives reference evapotranspiration, the developed method defines a hypothetic canopy with fixed LAI to model potential GPP under certain environment conditions. Similar to the GDD model, the GPD model predicts vegetation spring onset to occur when the accumulated reference GPP reaches a critical threshold. The method has been successfully applied to the biomes of evergreen needleleaf forest, deciduous broadleaf forest, and grassland. To allow for predicting the entire LAI time series over a growing season, Xin et al. (2018) further improved the GPD model by proposing a linear function between LAI and GPP at the steady state. The proposed function and the canopy GPP model (i.e., modeling GPP as a function of LAI and climate variables) together form a closed system of equations that includes both vegetation GPP and LAI. The improved GPD model uses the numerical approach, a method that gives an initial value and then iterates to the convergence of the solution, to solve the closed system of equations and derive LAI in the steady state. The improved GPD model then applies the simple moving-average method to the steady-state LAI to obtain the modeled LAI time series. The improved method allows for the modeling of LAI time series in addition to the timing of individual phenophases. There remain shortcomings to overcome for broad applications of the GPD model. First, the simple moving-average method, despite being widely used in many studies, is empirical and cannot be used within the framework of models that operate at incremental time steps. Second, the developed GPD model that includes many subtle vegetation processes, such as canopy radiative transfer, leaf stomatal conductance, leaf transpiration, leaf photosynthesis, and soil evaporation, requires various climate input data and is computationally intensive for regional to global applications.
Aiming to solve the abovementioned problems, the objectives of the study are to (1) develop a time-stepping scheme to simulate both leaf dynamics and vegetation productivity and (2) simplify the GPD model to allow for long-term applications at a large scale. Given that the phenology modeling in deciduous broadleaf forest, a biome that has distinct seasonal growing cycles, still has large uncertainties (Melaas et al., 2016), this study chooses to simulate leaf dynamics for the deciduous broadleaf forests across the eastern United States. If successful, such a method can potentially be used for future applications to other biomes.
2.1 Modeling steady-state leaf area index
One difficulty in vegetation phenology modeling is that the timescale associated with leaf allocation far exceeds that of many other vegetation processes. Unlike leaf photosynthesis that approaches equilibrium within 1 min and stomatal functioning that reaches the steady state in minutes (Sellers et al., 1996a), leaf dynamics take days or even months in response to weather variation (Zeng et al., 2013). Xin et al. (2018) first put forward the concept of steady-state leaf area index, i.e., canopy LAI when time approaches infinity while the environmental conditions remain unchanging. An alternative biological explanation to steady-state LAI is the maximum canopy LAI that an environment can sustain infinitely by its own photosynthetic activities. Supposing that the carrying capacity of canopy LAI is proportional to the total canopy photosynthetic rate under a given environment, the steady-state LAI can be modeled as follows:
where LAIs denotes the steady-state leaf area index, and m denotes the constant ratio of steady-state leaf area index to environmental capacity denoted by GPPs, which is the steady-state gross primary production.
The above equation, despite having a simple form, provides a critical function that complements the canopy photosynthesis model. Only parameter m is dependent on plant functional type and can be quantified from field measurements as the average ratio of LAI to GPP at canopy closure (i.e., the time when both canopy LAI and GPP reach equilibrium). Studies have developed various canopy photosynthesis models, such as light use efficiency models and process-based models. Our previous studies (Xin, 2016; Xin et al., 2018) implemented a sophisticated canopy model that assembles the sub-models of canopy radiative transfer, leaf stomatal conductance, leaf transpiration, soil evaporation, and leaf photosynthesis. Although the method has been successfully applied to different biomes, the model structure is complicated for studies at the regional to global scales. To simulate canopy photosynthesis, this study implements the MOD17 algorithm, a big-leaf light use efficiency model that uses routine satellite products (Running et al., 2004). The use of the MOD17 algorithm could greatly simplify the modeling processes and reduce the required climate variables, thereby allowing for broad applications. A brief description of the MOD17 algorithm is provided here and details can be found from the user guide of the MODIS GPP product (Running and Zhao, 2015).
Based on the MOD17 algorithm, vegetation GPP corresponding to the steady-state leaf area index can be modeled as follows:
where GPPs denotes the gross primary production corresponding to the steady-state leaf area index; PAR denotes photosynthetically active radiation; FPARs denotes the fraction of photosynthetically active radiation corresponding to the steady-state leaf area index; εmax denotes maximum light use efficiency; and f(T) and f(VPD) denote the scalar functions that account for the limitation of temperature and vapor pressure deficit, respectively, on canopy photosynthesis.
The fraction of photosynthetically active radiation can be modeled as follows (Turner et al., 2006):
where k denotes the canopy light extinction coefficient and LAIs denotes the steady-state leaf area index.
The environmental scalars can be modeled as follows.
TMIN denotes daily minimum air temperature; TMINmin and TMINmax denote the lower and upper thresholds of daily minimum air temperature for vegetation photosynthetic activities, respectively; VPD denotes daily vapor pressure deficit; and VPDmin and VPDmax denote the lower and upper thresholds of daily vapor pressure deficit for vegetation photosynthetic activities, respectively.
Given the environmental conditions (i.e., given daily values of photosynthetically active radiation, minimum air temperature, and vapor pressure deficit), Eqs. (1) and (2) together form simultaneous equations, meaning that there are two unknown variables (i.e., LAI and GPP at the steady state) and two different general equations. One may derive an analytic solution if both equations have simple forms. But because the dependence of GPP on LAI is nonlinear, deriving the analytic solution is complicated and we could apply the numerical approach to obtain the solutions. Because LAIs increases as a linear function of GPPs in Eq. (1) and GPPs increases as a logarithmic function of LAIs in Eq. (2), the simultaneous equations have one and only one nonzero solution of LAIs. To obtain the nonzero solution, the numerical approach starts with a guess value of LAIs and then iterates to obtain the approximated solution of LAIs until converging. Note that the numerical approach is widely used in land surface models. For example, as the stomatal resistance, CO2 partial pressure at the leaf surface, internal leaf CO2 partial pressure, and leaf net photosynthesis are dependent on each other, the Community Land Model 4.5 uses the numerical approach to solve stomatal resistance and leaf photosynthesis iteratively until the internal leaf CO2 partial pressure converges. For every day, daily photosynthetically active radiation, daily minimum air temperature, and daily vapor pressure deficit are used as forcing data to calculate LAIs for the corresponding day. Because photosynthetically active radiation, minimum air temperature, and vapor pressure deficit vary throughout the year, the calculated LAIs vary from day to day.
2.2 Modeling leaf area index, phenology, and gross primary production
Because the physiological processes through which plants allocate photosynthates to leaves do not respond instantaneously to climate variation, there is a need to simulate vegetation LAI as lagging behind the steady state. One method to account for the time-lagging effect is to apply the simple moving-average method to buffer abrupt changes from individual events in the time series. Our previous study applied the simple moving-average method to model LAI as the unweighted mean of the previous LAIs as follows (Xin et al., 2018):
where LAI(n+1) denotes leaf area index at the n+1 day; n denotes the number of days; i denotes an index starting from 1 to n; and LAIs denotes the steady-state leaf area index.
The simple moving-average method, while useful in vegetation phenology modeling, is suitable for retrospective analysis rather than prediction, and, importantly, it does not match most land surface models that operate at incremental time steps. Analogous to the method used to simulate leaf stomatal conductance in response to environmental variation, this study proposes a time-stepping scheme to simulate LAI realistically as lagging behind the steady state by a simple restricted growth model (Sellers et al., 1996a) as follows:
where t denotes the time; kl denotes a time constant that reflects the fact that photosynthesis does not instantaneously lead to new or big leaves; and LAI(n) and LAIs(n) denote the leaf area index and the steady-state leaf area index at the n time step, respectively.
In the time-stepping scheme, vegetation LAI does not change much during winter or summer as the current LAI is close to LAIs, whereas vegetation LAI increases (or decreases) during spring (or autumn) as the current LAI is less (or greater) than LAIs. For example, when the environment turns favorable for plant growth in spring, LAIs exceeds LAI and dLAI∕dt is positive such that the modeled canopy LAI increases. Note that the method developed here essentially uses the canopy photosynthetic capacity (i.e., the steady-state gross primary production) instead of air temperature as a synthesized indicator to track the suitability of the environment for plant growth in a time series, and therefore the developed method is referred to as the simplified growing production day (SGPD) model following our previous studies (Xin et al., 2018).
Given the modeled LAI time series, both vegetation phenology and canopy GPP can be easily modeled (Xin et al., 2018). Various approaches have already been developed to derive the timing of key phenophases, such as spring onset and autumn senescence, from seasonal LAI trajectories. This study models the phenological transition dates using a simple method that derives the first spring and last autumn dates at which LAI reaches 20 %, 50 %, and 80 % of the seasonal amplitudes (Richardson et al., 2012). The selected relative amplitudes (20 %, 50 %, and 80 %) correspond to different plant growth stages over a growing season. Because the MOD17 algorithm only requires LAI, daily minimum temperature, daily vapor pressure deficit, and daily photosynthetically active radiation as model inputs, the canopy GPP is simply modeled by substituting the modeled LAI time series and the climate variables into the MOD17 algorithm. For the first day of spring when the modeled LAI is zero, the modeled fraction of photosynthetically active radiation is zero and the modeled GPP is zero. As times move forward, the modeled LAI increases and the modeled GPP increases but is still dependent on other climate variables such as solar radiation, temperature, and vapor pressure deficit.
2.3 Comparative studies using the growing season index
The growing season index (GSI), a widely used method in vegetation phenology modeling (Jolly et al., 2005), allows for the modeling of seasonal LAI time series rather than individual phenophases and is implemented to make direct comparisons with the SGPD model. The GSI model performs comparably to or even outperforms other terrestrial biosphere models on predicting the timing of key phenophases for deciduous broadleaf forests (Melaas et al., 2013).
The instantaneous GSI is first derived based on the work of Jolly et al. (2005) as follows:
where iGSI denotes instantaneous growing season index, and iTMIN, iVPD, and iPhoto denote the instantaneous scalar functions that account for the constraints of daily minimum air temperature, vapor pressure deficit, and photoperiod, respectively, on vegetation growth.
The scalar functions for iTMIN, iVPD, and iPhoto have mathematic forms similar to Eqs. (4) and (5) and are obtained the same as defined in Jolly et al. (2005) as follows.
TMIN denotes daily minimum temperature; TMINmin and TMINmax denote the lower and upper thresholds of daily minimum air temperature for vegetation photosynthetic activities, respectively; VPD denotes daily vapor pressure deficit; VPDmin and VPDmax denote the lower and upper thresholds of daily vapor pressure deficit for vegetation photosynthetic activities, respectively; “Photo” denotes daily photoperiod; and Photomax and Photomin denote the lower and upper thresholds of the daily photoperiod for vegetation photosynthetic activities, respectively.
LAI can be modeled as the simple moving average of the instantaneous GSI scaled using maximum LAI as follows:
where GSI denotes growing season index at the n day; nday denotes the number of days; i denotes an index starting from 0 to the previous day; iGSI denotes the instantaneous growing season index; and LAImax denotes the maximum leaf area index at canopy closure.
It is noteworthy that the instantaneous GSI uses the product of the scalars of minimum temperature, vapor pressure deficit, and photoperiod as an indicator to track the potential canopy photosynthetic capacities on a daily basis. Both the GSI model and the SGPD model, despite having different forms, share the same modeling idea. To understand the differences between the simple moving-average method and the time-stepping method, the GSI model is also implemented with the simple restricted growth model as follows:
where iGSI denotes the instantaneous growing season index; LAImax denotes the maximum leaf area index at canopy closure; kl denotes a time constant that accounts for the lagged responses of plant leaf allocation to climate variation; and LAI and LAIs denote the leaf area index and the steady-state leaf area index, respectively.
With the modeled LAI time series, the phenological transition dates are then retrieved based on the seasonal amplitude ratio method, the same way as processing the LAI time series derived from the SGPD model. Vegetation GPP is modeled by substituting the modeled LAI time series into the MOD17 algorithm.
2.4 Model comparison and parameterization
This study compares four different modeling approaches, including the results simulated using both the SGPD model and the simple moving-average method (hereinafter referred to as SGPD-SMA), using both the SGPD model and the time-stepping scheme (hereafter referred to as SGPD-TS), using both the GSI model and the simple moving-average method (hereafter referred to as GSI-SMA), and using both the GSI model and the time-stepping scheme (hereafter referred to as GSI-TS). The commonly used metrics, including the Pearson correlation coefficient (R), the coefficient of determination (R2), the root mean square error (RMSE), and the mean bias error (MBE), are derived for model assessment and comparison.
As the MOD17 algorithm is a well-parameterized model, this study applies model parameters from the literature directly. Following the user guide of the MODIS GPP product (Running and Zhao, 2015), key parameters in the MOD17 algorithm are set as εmax=1.165 g C MJ−1, ∘C, TMINmax=9.94 ∘C, VPDmin=0.65 kPa, and VPDmax=1.65 kPa. The light extinction coefficient of the canopy is 0.5. The parameter that defines the ratio of leaf area index to environmental capacity is set as m=0.58 m2 (leaf area) g C−1 day−1 as quantified using the average ratio of LAI to GPP at canopy closure using flux tower data. The canopy maximum LAI is set as 5.80 based on the maximum 95th percentile of satellite-derived LAI across sites and years (Xin et al., 2018). The parameter nday in the simple moving-average method and the parameter kl in the time-stepping method control the response of plant leaf allocation to environmental variation. The parameter nday is set as 21 days and the parameter kl is calibrated as 0.080 day−1.
2.5 Study materials and preprocessing
We evaluate our approach at the site scale using both flux tower data and remote sensing data and at the regional scale using both climate data and remote sensing data for deciduous broadleaf forests in the eastern United States. For the site-scale studies, all the flux tower sites of deciduous broadleaf forests (Table 1) that are available on the AmeriFlux website (http://ameriflux.lbl.gov/, last access: 13 January 2019) were used for analysis. As the developed SGPD model is a simplified version of our previous modeling approach, the site-scale modeling studies only require daily incoming solar radiation, minimum air temperature, vapor pressure deficit, photoperiod, LAI, and GPP data. Daily incoming solar radiation, vapor pressure deficit, and GPP have already been provided in the level 4 flux tower data, whereas daily minimum air temperature was processed from the half-hourly gap-filled level 2 data, and daily photoperiod as required by the GSI model was computed based on Eq. (17) as a function of geolocation and the day of the year (Allen et al., 1998). As the MODIS LAI has been found to match field measurements well for deciduous broadleaf forests in the eastern United States (Myneni et al., 2002), the 8-day 500 m MODIS LAI version 6 products (MOD15A2H) that are downloaded from the Land Processes Distributed Active Archive Center (https://lpdaac.usgs.gov/, last access: 13 January 2019) were used as the reference data. Canopy LAI at each site was extracted from MOD15A2H for the pixel that contains the corresponding site. The extracted 8-day MODIS LAI, if identified as poor quality in MOD15A2H, was replaced using the three-point median-value moving-window technique. Spikes in the LAI time series were removed using the Hampel filter and then gap-filled using the autoregressive modeling approach (Akaike, 1969). The obtained 8-day LAI time series were further smoothed using the Savitzky–Golay filter and then linearly interpolated to generate daily time series. The phenological transition dates were retrieved from daily LAI time series using the method that derives the first spring and last autumn dates at which LAI reaches 20 %, 50 %, and 80 % of the seasonal amplitudes, respectively (Richardson et al., 2012).
“Pho” denotes daily photoperiod, φ denotes latitude, and DOY denotes the day of the year.
Our regional-scale studies used both climate data and satellite remote sensing data from 1982 to 2016. The daily 1000 m Daymet version 3 dataset (Thornton et al., 2012) was downloaded from the Oak Ridge National Laboratory Distributed Active Archive Center (http://daymet.ornl.gov/, last access: 13 January 2019). The Daymet dataset provided daily incoming solar radiation, minimum temperature, vapor pressure, and photoperiod data, and we derived daily vapor pressure deficit as the difference between average saturated vapor pressure and vapor pressure. Two different satellite LAI products, including the Global Land Surface Satellite (GLASS) dataset (Xiao et al., 2014) spanning from 1982 to 2014 and the MODIS LAI dataset (Myneni et al., 2002) spanning from 2001 to 2016, were used for the regional studies. The 8-day GLASS LAI product was generated at 0.05∘ resolution using AVHRR data for the time period from 1982 to 1999 and at 1000 m resolution using MODIS data for the time period from 2000 to 2012. The 8-day satellite LAI data across the eastern United States were processed the same way as the site-scale data to obtain daily LAI time series. Because seasonal LAI amplitudes for each individual pixel could vary from year to year, the 2001–2010 average seasonal LAI amplitudes were used as a baseline to derive the start of the season (SOS) and the end of the season (EOS) for each pixel for each year as the dates when seasonal LAI reaches 50 % of the multi-year average seasonal LAI amplitude. The growing season length (GSL) was derived as the difference between EOS and SOS. A 500 m MODIS-based land cover map was obtained from the USGS Land Cover Institute (https://landcover.usgs.gov/, last access: 1 December 2018). The land cover map was generated by choosing the land cover classification with the highest overall confidence for each pixel in 10-year (2001–2010) Collection 5.1 MODIS land cover type (MCD12Q1) data (Broxton et al., 2014). The 500 m land cover map was resampled to 1000 m resolution using the majority resampling approach and reprojected to a Lambert conformal conic projection to mask areas that are not covered by deciduous broadleaf forests.
3.1 Site-scale modeling
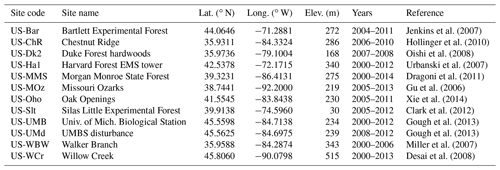
Figure 1 shows an example for the simulated time series of LAI and GPP using data acquired at the US-UMB in 2004. The LAI time series simulated using both the SGPD-SMA and SGPD-TS methods are consistent with that obtained from MODIS. The LAI simulated using both the GSI-SMA and GSI-TS methods also captures the observed seasonal variation, but the modeled phenophases obviously have a leading phase in spring and a lagging phase in autumn compared with observations. For both the SGPD model and the GSI model, the results derived using the time-stepping method are consistent with those derived using the simple moving-average method, indicating that the time-stepping method is an effective way to reflect the lagging responses of plant leaf allocation to environmental conditions. By substituting the time series of LAI derived from different modeling approaches into the MOD17 algorithm, all the simulated GPP time series could match the flux tower measurements. Daily fluctuation in the observed GPP time series is largely due to variation in solar radiation from day to day. The GPP modeled using both the GSI-SMA and GSI-TS methods have slight overestimates in the phenological transition periods, like spring and autumn, and match well with the flux tower observations in summer and winter.
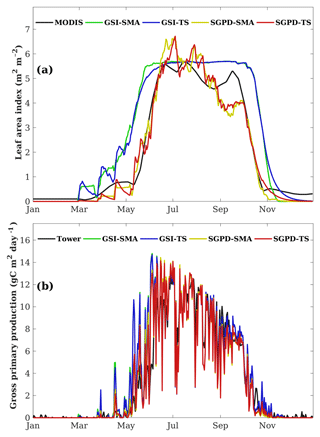
Figure 1The modeled and measured daily time series of (a) leaf area index and (b) gross primary production are shown for the flux tower site of US-UMB in 2004. The reference LAI time series in (a) are derived from the MODIS data and the reference GPP time series in (b) are obtained from flux tower measurements.
Figure 2 shows the regression analysis between the modeled and satellite-derived LAI. Overall, the SGPD model outperforms the GSI model on modeling LAI. When evaluated against the MODIS LAI data, the SGPD-SMA and SGPD-TS models achieved R2 of 0.887 and 0.890, respectively, and RMSE of 0.804 and 0.778 m2 m−2, respectively, whereas the GSI-SMA and GSI-TS models achieved R2 of 0.746 and 0.759, respectively, and RMSE of 1.356 and 1.303 m2 m−2, respectively. Both the GSI-SMA and GSI-TS models simulate LAI reasonably in summer and winter but overestimate LAI in spring and autumn, and therefore the strong correlations between the GSI-modeled and MODIS-derived LAI are largely due to the underlying seasonality of deciduous broadleaf forests. It is noteworthy that the time-stepping method and the simple moving-average method, despite having different mathematical expressions, generate nearly the same simulation results. The R2 values between the SGPD-TS model and the SGPD-SMA model and between the GSI-TS model and the GSI-SMA model are 0.989 and 0.994, respectively, and the regression lines are close to the lines of equity, indicating that the time-stepping method is an alternative representation for the simple moving-average method.
Figure 2Scatter plots are shown for comparisons (a) between the SGPD-SMA LAI and the MODIS LAI, (b) between the SGPD-TS LAI and the MODIS LAI, (c) between the SGPD-TS LAI and the SGPD-SMA LAI, (d) between the GSI-SMA LAI and the MODIS LAI, (e) between the GSI-TS LAI and the MODIS LAI, and (f) between the GSI-TS LAI and the GSI-SMA LAI on a weekly basis. All available site-year flux tower data were included in the analysis. The solid lines denote the 1 : 1 lines and the dashed lines denote the regression lines.
Table 2The performance of the modeled timings of phenophases as evaluated against satellite observations. The timings of phenophases were derived based on the dates at which the leaf area index reaches 20 %, 50 %, and 80 % of seasonal amplitude. Positive mean bias error (MBE) indicates that the modeled spring onsets are earlier than the observed ones and negative MBE indicates the opposite.
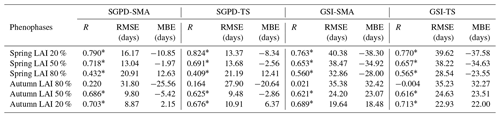
* Correlation is significant at the 0.001 level.
Table 2 lists the statistical metrics that illustrate the model performance on predicting the timing of different phenophases. As evaluated against satellite observations, the SGPD-SMA model retrieves the spring onset dates well when LAI reaches 50 % seasonal amplitude and the obtained correlation coefficient is 0.718 with RMSE of 13.04 days. The SGPD-TS model performs comparably to the SGPD-SMA model and the resulting correlation coefficients are all significant except for the dates on which autumn LAI reaches 80 % seasonal amplitudes. The SGPD-based models generally outperform the GSI-based models as the achieved correlation coefficients are higher and the RMSEs are smaller. Both the GSI-SMA and GSI-TS models predict spring onsets earlier than observations by more than 30 days and predict autumn senescence later than observations by more than 20 days. By comparison, the SGPD-TS model predicts the dates on which spring and autumn LAI reaches 50 % seasonal amplitudes well with MBE of only −2.56 and −2.86 days, respectively.
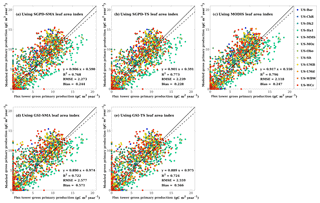
Figure 3Scatter plots are shown for comparisons (a) between the GPP modeled using SGPD-SMA LAI and the flux tower GPP, (b) between the GPP modeled using SGPD-TS LAI and the flux tower GPP, (c) between the GPP modeled using MODIS LAI and the flux tower GPP, (d) between the GPP modeled using GSI-SMA LAI and the flux tower GPP, and (e) between the GPP modeled using GSI-TS LAI and the flux tower GPP on a weekly basis. All available site-year flux tower data were included in the analysis. All modeled GPP values were derived using the MOD17 algorithm. The solid lines denote the 1 : 1 lines and the dashed lines denote the regression lines.
The modeled and measured GPPs are compared in Fig. 3 to understand the performance of GPP modeling. Compared with the flux tower measurements, the results modeled using SGPD-SMA, SGPD-TS, GSI-SMA, and GSI-TS LAI achieved R2 values of 0.768, 0.773, 0.722, and 0.719, respectively, and RMSE values of 2.273, 2.239, 2.577, and 2.535 g C m−2 day−1, respectively. The modeled results using the GSI-based LAI have higher errors, in terms of both RMSE and MBE, than those using SGPD-based LAI. The accuracies of the modeled GPP using SGPD-based LAI are only slightly lower than using the MODIS-based LAI directly. Because GPP is also a function of a range of climate variables, improvements in modeling LAI do not lead to the same amount of improvements in the modeled GPP. The modeling results obtained based on the simple moving-average method are nearly the same as those obtained based on the time-stepping method. Given the high degrees of consistency between the simple moving-average method and the time-stepping method in modeling LAI, phenology, and GPP, only the results obtained using the time-stepping method are shown and discussed in the regional studies as presented in the following section.
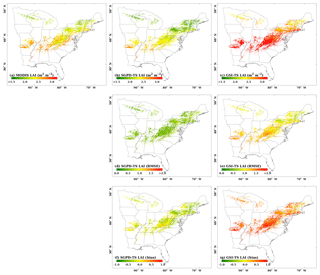
Figure 4The spatial distributions are shown for (a) the 2001–2010 mean MODIS LAI, (b) the 2001–2010 mean SGPD-TS LAI, (c) the 2001–2010 mean GSI-TS LAI, (d) RMSE between SGPD-TS LAI and MODIS LAI, (e) RMSE between GSI-TS LAI and MODIS LAI, (f) MBE between SGPD-TS LAI and MODIS LAI, and (g) MBE between GSI-TS LAI and MODIS LAI across the eastern United States. The units for both RMSE and MBE are m2 (leaf area) per m2 (ground area).
3.2 Regional-scale modeling
Figure 4 shows the spatial distributions of the 10-year (2001–2010) mean LAI and associated errors as derived from remote sensing data and model simulations. The SGPD-TS method captured the spatial pattern of the satellite-derived LAI well, including the decreasing gradients from south to north and the decreases in mountain areas (Fig. 4a and b). The 10-year mean LAI derived from the GSI-TS method (Fig. 4c) also shows a decreasing trend from south to north but the modeled LAI is much larger than the MODIS LAI. Because the GSI-TS method defines the maximum leaf area index for the growing season, the overestimation of the modeled 10-year mean LAI is primarily due to model overestimates in the spring and autumn phenological transitions. Compared with MODIS observations, RMSE and MBE obtained by the SGPD-TS method are much smaller and distributed more evenly than those obtained by the GSI-TS method. RMSE for the GSI-TS LAI exhibit a decreasing north–south gradient, implying that the model accuracies are lower in southern areas than in northern areas. MBEs for the GSI-TS model are greater than 0.5 m2 m−2 for most areas. When comparing SGPD-TS LAI with MODIS LAI, RMSEs are less than 0.5 m2 m−2 and MBEs are minor across the study region. The amplitudes of the error metrics in the regional-scale studies are consistent with those in the site-scale studies. Note that some studies applied the multi-year mean LAI as derived from remote sensing data to simulate land surface processes. The results obtained here indicate that the SGPD-TS method can be used alternatively to provide multi-year mean LAI time series via climate variables for land surface studies.
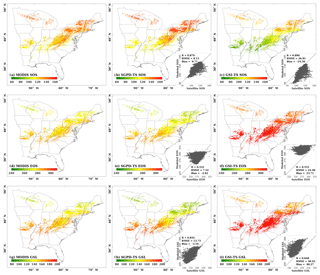
Figure 5The spatial distributions are shown for (a) the start of the season (SOS) derived from MODIS LAI, (b) SOS derived from SGPD-TS LAI, (c) SOS derived from GSI-TS LAI, (d) the end of the season (EOS) derived from MODIS LAI, (e) EOS derived from SGPD-TS LAI, (f) EOS derived from GSI-TS LAI, (g) the growing season length (GSL) derived from MODIS LAI, (h) GSL derived from SGPD-TS LAI, and (i) GSL derived from GSI-TS LAI using 10-year (2001–2010) mean data across the eastern United States. The embedded subplots show comparisons between modeled and MODIS-derived phenological metrics for SOS, EOS, and GSL, respectively.
The spatial distributions for the 10-year mean phenological metrics, including the start of the season (SOS), the end of the season (EOS), and the growing season length (GSL), are shown in Fig. 5. The SGPD-TS method predicts lower SOS (i.e., earlier spring onset), higher EOS (i.e., later autumn senescence), and longer GSL in southern areas than in northern areas. The spatial distributions of all phenological metrics derived using SGPD-TS LAI agree well with those derived using MODIS LAI. From the statistical analysis as shown in the subplots, the phenological metrics derived from the SGPD-TS method achieved correlation coefficient values of 0.879, 0.552, and 0.844, RMSE values of 8.13, 7.54, and 13.73 days, and MBE values of 0.71, −2.82, and −3.54 days, for SOS, EOS, and GSL, respectively, compared to those derived from MODIS data. Although the spatial distributions of the phenological metrics derived from the GSI-TS method match those derived from the satellite observations, the modeled results have considerable biases, with RMSE values of 38.05, 14.37, and 51.58 days and MBE values of −36.33, 12.91, and 49.23 days for SOS, EOS, and GSL, respectively. Consistent with the site-scale studies, the GSI-TS method predicts spring onset much earlier and autumn senescence later than the satellite-derived data, resulting in a large overestimation of the growing season length.
Figure 6 displays the multi-year phenology anomalies that are spatially averaged for deciduous broadleaf forest across the eastern United States. The use of phenology anomalies relative to the 2001–2010 average instead of absolute values makes the results directly comparable. The SGPD-TS method captured the interannual variation of vegetation phenology retrieved from the remote sensing data. When comparing the SGPD-TS method with MODIS (2001–2016) data, the correlation coefficients are 0.896 (p<0.001), 0.650 (p=0.006), and 0.817 (p<0.001) for SOS, EOS, and GSL, respectively. When comparing the SGPD-TS method with GLASS (1982–2014) data, the correlation coefficients are 0.554 (p=0.001), 0.717 (p<0.001), and 0.637 (p<0.001) for SOS, EOS, and GSL, respectively. The SGPD-TS method outperforms the GSI-TS method on capturing the long-term trends of vegetation phenophases, as the correlation coefficients obtained using the GSI-TS method are lower and sometimes insignificant. Yearly fluctuations in EOS derived using the GSI-TS method are smaller than those derived from both the SGPD-TS method and the satellite data. The correlation coefficients between the GLASS data and the MODIS data for SOS, EOS, and GSL from 2001 to 2014 are 0.892, 0.412, and 0.288, respectively. There are only 14 years of overlap between these two different datasets and the correlations are insignificant for both the derived EOS and GSL. The SOS and EOS derived from the GLASS data have much larger variation in 1982–2000 than in 2001–2010. Note that the 8-day GLASS LAI product was generated at 0.05∘ resolution using AVHRR data from 1982 to 1999 and at 1000 m resolution using MODIS from 2000 to 2012. The significantly reduced interannual variability for SOS, EOS, and GSL after 2000 in the GLASS data suggests that the use of AVHRR and MODIS data in the GLASS dataset could contribute uncertainties to the satellite-derived phenological metrics. Both Figs. 5 and 6 indicate that the SGPD-TS method is reliable in capturing the spatiotemporal patterns of regional vegetation phenophases.
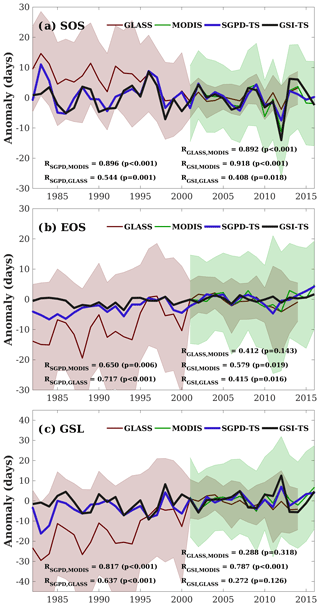
Figure 6The spatially averaged phenology anomalies relative to the 2001–2010 average are shown for (a) the start of the season (SOS), (b) the end of the season (EOS), and (c) the growing season length (GSL). SOS and EOS are derived as the date on which LAI first and last reaches 50 % of the seasonal amplitudes and GSL is derived as the difference between EOS and SOS. The shaded areas denote the standard deviation of the corresponding phenophases across spaces.
Figure 7 compares the simulated GPP using the MOD17 algorithm and LAI derived from different approaches. The 10-year average annual GPP obtained using SGPD-TS LAI has a similar spatial pattern to that obtained using MODIS LAI and has lower values than that obtained using GSI-TS LAI. Taking the GPP simulated using MODIS LAI as a reference, the results simulated using SGPD-TS LAI achieve a correlation coefficient of 0.898 with RMSE of 78.78 g C m−2 year−1 and MBE of 12.22 g C m−2 year−1, whereas the results simulated using GSI-TS LAI achieve a correlation coefficient of 0.898 with RMSE of 173.45 g C m−2 year−1 and MBE of 153.43 g C m−2 year−1. Although the obtained correlation coefficients are close, the SGPD-TS method results in regression lines closer to the 1 : 1 line with smaller bias errors than the GSI-TS method. The zonally average profiles of the 2001–2010 average annual GPP as shown in Fig. 7d suggest that the results obtained from the SGPD-TS method are close to those obtained using MODIS LAI, whereas the results obtained from the GSI-TS method have positive biases of approximately 120–180 g C m−2 year−1 (roughly 10–15 %) across latitudes. Note that the MOD17 algorithm has a positive MBE of 0.247 g C m−2 day−1 and 0.571 g C m−2 day−1 when using SGPD-TS LAI and GSI-TS LAI, respectively, as model input data in the site-scale study. The differences in MBE between the two modeling methods are 0.324 g C m−2 day−1 (or 118.26 g C m−2 year−1 in equivalence) for the site-scale studies, which are consistent with the regional-scale studies.
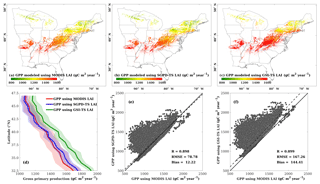
Figure 7Comparisons are shown for (a) the spatial distribution of annual GPP modeled using MODIS LAI, (b) the spatial distribution of annual GPP modeled using SGPD-TS LAI, (c) the spatial distribution of annual GPP modeled using GSI-TS LAI, (d) the zonally averaged profiles of annual gross primary production modeled using LAI derived from different approaches, (e) the regression between GPP modeled using SGPD-TS LAI and MODIS LAI, and (f) the regression between GPP modeled using GSI-TS LAI and MODIS LAI. The simulated daily GPP were first summed for each individual year and were then averaged across years to derive the 2001–2010 average annual GPP as shown in (a–c). The shaded areas in (d) mark the range of the standard deviation. All pixels of deciduous broadleaf forest across the eastern United States are included in the analysis in (e) and (f).
Here we provide a simple time-stepping solution that allows for the simulation of canopy photosynthesis, leaf area index, and leaf phenology simultaneously. The developed method first proposes a linear function between canopy photosynthetic capacity and steady-state LAI to complement the canopy photosynthesis model and then applies a simple restricted growth model to account for the lagged responses of plant leaf allocation to the natural environment. In essence, the developed method, although having a simple form, has synthesized the impacts of various climate factors on leaf dynamics because any climate variable that influences vegetation photosynthesis would affect the process of plant leaf allocation in the models as well. Consistent with field observations, the simulated LAI increases as the environmental conditions turn favorable for photosynthetic activities such as increases in photoperiod and temperature.
Figure 8 further illustrates the relationship between mean LAI and different variables on a monthly basis. All data were averaged to the monthly timescale such that canopy LAI can be considered as nearly steady state. On a monthly basis, mean LAI has a strong near-linear relationship with mean GPP (R2=0.888) and the slope for the regression without intercept is 0.580, the same as we used in the model simulation. On a monthly basis, mean LAI is strongly correlated with mean temperature (R2=0.799), indicating that temperature is the dominate factor that determines vegetation phenology. Factors like vapor pressure deficit and photoperiod also have positive relationships with mean LAI on a monthly basis. Figure 8 suggests that LAI has a stronger correlation with GPP than with temperature on a monthly basis. Our modeling approach that links canopy GPP with LAI reflects the empirically positive relationship found in Figure 8a.
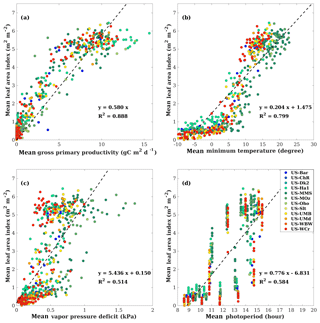
Figure 8Scatter plots are shown for the relationship (a) between mean leaf area index and mean gross primary production, (b) between mean leaf area index and mean temperature, (c) between mean leaf area index and mean vapor pressure deficit, and (d) mean leaf area index and mean photoperiod on a monthly basis. All available site-year flux tower data were included in the analysis. All data were averaged to the monthly timescale for analysis, making the point numbers different from the analysis at the weekly timescale in Fig. 2. The dashed lines denote the regression lines. Panel (a) uses the regression without intercept.
The performance of our developed method is largely dependent on the canopy photosynthesis model used. In our previous studies, we developed a process-based canopy photosynthesis model that synthesizes sub-models such as canopy radiative transfer, leaf transpiration, leaf stomatal conductance, leaf photosynthesis, and soil evaporation and applied it for modeling LAI time series. When applying the simple moving-average method, implementing the process-based model in Xin et al. (2018) achieved higher accuracies than implementing the MOD17 algorithm in modeling canopy GPP and LAI as reflected by higher R2 and lower errors. The MOD17 algorithm only assumes a monotonic relationship between air temperature and photosynthesis and between vapor pressure deficit and photosynthesis. It also does not account for the impacts of CO2 on photosynthesis. The use of the MOD17 algorithm in this study thus has limitations in the model structure. It implies that LAI modeling in our developed method will likely benefit from improvements to the canopy photosynthesis model. This study chooses the MOD17 algorithm instead of the sophisticated process-based model because the MOD17 algorithm is well parameterized across biomes and requires quite limited model inputs of climate variables. Successful implementation with the MOD17 algorithm allows for the extension of the developed method to applications across biomes at regional to global scales.
Land surface models that predict vegetation GPP require either satellite-derived LAI input data or the phenology sub-model. The main idea for this study is to improve phenology modeling by providing time series of LAI simulated using climate variables, hence enabling the simulation of GPP forced only by climate variables. Because we implement the MOD17 algorithm instead of the sophisticated process-based model for the purpose of simplicity, one should not expect the GPP simulated based on model-simulated LAI to be more accurate than GPP simulated based on satellite-derived LAI.
The time-stepping scheme developed here is also an improvement over the simple moving-average method as used in our previous studies. The results obtained using the time-stepping method are consistent with the simple moving-average method at the site scale and are shown to be reasonable at the regional scale. Compared to the simple moving-average method, the time-stepping method could be used in models that operate at incremental time steps. For land surface models that include canopy photosynthesis sub-models, the developed method can be embedded into these models as an alternative phenology model if replacing the MOD17 approach with the canopy photosynthesis sub-model. Compared to simple light use efficiency models like the MOD17 algorithm, implementation of the developed time-stepping scheme in land surface models relies on supercomputing for global applications. To better understand the performance of the developed method, one study is now being undertaken to implement the developed method with the Common Land Model for simulating multi-decadal LAI and GPP for global biomes forced only by climate variables.
Applying the developed method to other biomes and other regions still has issues to be solved appropriately. The time-stepping method uses the parameter kl to account for the time lags of leaf allocation in response to environmental changes. For deciduous broadleaf forests, a biome with strong seasonality, the developed scheme achieved reasonable results with appropriate parameterization. Short vegetation like grasslands tends to respond quickly to abrupt environment changes like precipitation, and tropical ecosystems have strong resilience to short-term environmental variation (Levine et al., 2016; Shen et al., 2011). Another issue is to find the appropriate values of m for different biomes. One way to determine the values of m is to find the regression slope between leaf area index and gross primary production on a monthly basis. Model parameterization, however, requires broad tests. These understandings from observational studies imply that biomes have varied response speeds to the environment, and proper model calibration and assessment are required for the developed method. Using observation data from remote sensing alone is inadequate for model development as satellite-derived LAI could have large uncertainties for some specific biomes other than deciduous broadleaf forests. Fortunately, global flux tower networks and regional phenology observation networks are now established and offer abundant data for comprehensive model assessment.
Numerical models provide a basic tool for understanding the interactions between the land surface and the atmosphere. To provide a complete solution to the simulation of plant leaf dynamics and canopy photosynthesis, this study establishes a linear relationship between the steady-state leaf area index and the corresponding canopy photosynthetic capacity. The proposed leaf allocation function complements the canopy photosynthesis model of the MOD17 algorithm to form simultaneous equations that can be solved using the numerical approach. To account for the time lagging of plant leaf allocation in response to climate variation, a time-stepping scheme based on a simple restricted growth model is applied to the solved steady-state leaf area index to obtain time series of leaf area index. The developed method could perform reasonably well on simulating leaf area index, phenology, and gross primary production for deciduous broadleaf forests across the eastern United States over years, as found in both the site-scale and regional-scale modeling studies. Compared to the simple moving-average method, the time-stepping scheme developed here is consistent with and can potentially be embedded into models that operate at incremental time steps. The developed method allows for the simulation of leaf area index and gross primary production simultaneously and provides a simplified and improved version of our previous model as a basis for global applications in future studies.
The flux tower dataset can be accessed from the AmeriFlux website (http://ameriflux.lbl.gov/data/download-data, last access: 13 January 2019) (AmeriFlux, 2019). The MODIS data can be accessed from the Land Processes Distributed Active Archive Center (https://e4ftl01.cr.usgs.gov/MOLT/,last access: 13 January 2019) (USGS LPDAAC, 2019). The Daymet dataset can be accessed from the Oak Ridge National Laboratory Distributed Active Archive Center (https://daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=132, last access: 13 January 2019) (ORNL DAAC, 2019). The 500 m land cover map used here was accessed from the USGS Land Cover Institute (https://archive.usgs.gov/archive/sites/landcover.usgs.gov/global_climatology.html, last access: 1 December 2018) (USGS LCI, 2018).
QX designed the experiments and performed the simulations. All authors interpreted the results. QX wrote the paper with contributions from all coauthors.
The authors declare that they have no conflict of interest.
We thank the researchers and investigators involved in collecting and
sharing the AmeriFlux dataset. This research is supported by the National Key
R&D Program of China (grant nos. 2017YFA0604302 and 2017YFA0604402) and
the
National Natural Science Foundation of China (grant no. 41875122). We also
thank anonymous reviewers for their constructive comments.
Edited by: Alexey V. Eliseev
Reviewed by: two
anonymous referees
Akaike, H.: Fitting autoregressive models for prediction, Ann. I. Stat. Math., 21, 243–247, 1969.
Allen, R. G., Pereira, L. S., Raes, D., and Smith, M.: Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56, FAO, Rome, 300, 6541, 1998.
AmeriFlux: flux tower data, available at: http://ameriflux.lbl.gov/data/download-data, last access: 13 January 2019.
Arora, V. K. and Boer, G. J.: A parameterization of leaf phenology for the terrestrial ecosystem component of climate models, Glob. Change Biol., 11, 39–59, 2005.
Beer, C., Reichstein, M., Tomelleri, E., Ciais, P., Jung, M., Carvalhais, N., Roedenbeck, C., Arain, M. A., Baldocchi, D., Bonan, G. B., Bondeau, A., Cescatti, A., Lasslop, G., Lindroth, A., Lomas, M., Luyssaert, S., Margolis, H., Oleson, K. W., Roupsard, O., Veenendaal, E., Viovy, N., Williams, C., Woodward, F. I., and Papale, D.: Terrestrial Gross Carbon Dioxide Uptake: Global Distribution and Covariation with Climate, Science, 329, 834–838, 2010.
Bonan, G. B.: Ecological climatology: concepts and applications, Cambridge University Press, 2002.
Bonan, G. B.: Forests and climate change: forcings, feedbacks, and the climate benefits of forests, Science, 320, 1444–1449, 2008.
Broxton, P. D., Zeng, X., Sulla-Menashe, D., and Troch, P. A.: A global land cover climatology using MODIS data, J. Appl. Meteorol. Climatol., 53, 1593–1605, 2014.
Chuine, I., Cour, P., and Rousseau, D. D.: Selecting models to predict the timing of flowering of temperate trees: implications for tree phenology modelling, Plant Cell Environ., 22, 1–13, 1999.
Clark, K. L., Skowronski, N., Gallagher, M., Renninger, H., and Schäfer, K.: Effects of invasive insects and fire on forest energy exchange and evapotranspiration in the New Jersey pinelands, Agr. Forest Meteorol., 166, 50–61, 2012.
De Réaumur, R. A. F.: Observations du thermometer, faites à Paris pendant l'année 1735, comparées avec celles qui ont été faites sous la ligne, à l'Isle de France, à Alger et en quelques-unes de nos isles de l'Amérique, Mémoires de l'Académie des Sciences, 545–584, 1735.
Desai, A. R., Noormets, A., Bolstad, P. V., Chen, J., Cook, B. D., Davis, K. J., Euskirchen, E. S., Gough, C., Martin, J. G., and Ricciuto, D. M.: Influence of vegetation and seasonal forcing on carbon dioxide fluxes across the Upper Midwest, USA: Implications for regional scaling, Agr. Forest Meteorol., 148, 288–308, 2008.
Ding, R., Kang, S., Du, T., Hao, X., and Zhang, Y.: Scaling Up Stomatal Conductance from Leaf to Canopy Using a Dual-Leaf Model for Estimating Crop Evapotranspiration, PloS one, 9, e95584, https://doi.org/10.1371/journal.pone.0095584, 2014.
Dragoni, D., Schmid, H. P., Wayson, C. A., Potter, H., Grimmond, C. S. B., and Randolph, J. C.: Evidence of increased net ecosystem productivity associated with a longer vegetated season in a deciduous forest in south-central Indiana, USA, Glob. Change Biol., 17, 886–897, 2011.
Eagleson, P. S.: Ecohydrology: Darwinian expression of vegetation form and function, Cambridge University Press, 2005.
Givnish, T. J.: On the Economy of Plant Form and Function: Proceedings of the Sixth Maria Moors Cabot Symposium, Evolutionary Constraints on Primary Productivity, Adaptive Patterns of Energy Capture in Plants, Harvard Forest, August 1983, Cambridge University Press, 1986.
Gough, C. M., Hardiman, B. S., Nave, L. E., Bohrer, G., Maurer, K. D., Vogel, C. S., Nadelhoffer, K. J., and Curtis, P. S.: Sustained carbon uptake and storage following moderate disturbance in a Great Lakes forest, Ecol. Appl., 23, 1202–1215, 2013.
Gu, L., Meyers, T., Pallardy, S. G., Hanson, P. J., Yang, B., Heuer, M., Hosman, K. P., Riggs, J. S., Sluss, D., and Wullschleger, S. D.: Direct and indirect effects of atmospheric conditions and soil moisture on surface energy partitioning revealed by a prolonged drought at a temperate forest site, J. Geophys. Res.-Atmos., 111, D16102, https://doi.org/10.1029/2006JD007161, 2006.
He, M., Ju, W., Zhou, Y., Chen, J., He, H., Wang, S., Wang, H., Guan, D., Yan, J., Li, Y., Hao, Y., and Zhao, F.: Development of a two-leaf light use efficiency model for improving the calculation of terrestrial gross primary productivity, Agr. Forest Meteorol., 173, 28–39, 2013.
Hollinger, D. Y., Ollinger, S., Richardson, A., Meyers, T., Dail, D., Martin, M., Scott, N., Arkebauer, T., Baldocchi, D., and Clark, K.: Albedo estimates for land surface models and support for a new paradigm based on foliage nitrogen concentration, Glob. Change Biol., 16, 696–710, 2010.
Hufkens, K., Basler, D., Milliman, T., Melaas, E. K., and Richardson, A. D.: An integrated phenology modelling framework in R, Methods Ecol. Evol., 9, 1276–1285, 2018.
Jenkins, J., Richardson, A. D., Braswell, B., Ollinger, S. V., Hollinger, D. Y., and Smith, M.-L.: Refining light-use efficiency calculations for a deciduous forest canopy using simultaneous tower-based carbon flux and radiometric measurements, Agr. Forest Meteorol., 143, 64–79, 2007.
Jolly, W. M., Nemani, R., and Running, S. W.: A generalized, bioclimatic index to predict foliar phenology in response to climate, Glob. Change Biol., 11, 619–632, 2005.
Levine, N. M., Zhang, K., Longo, M., Baccini, A., Phillips, O. L., Lewis, S. L., Alvarez-Dávila, E., de Andrade, A. C. S., Brienen, R. J., and Erwin, T. L.: Ecosystem heterogeneity determines the ecological resilience of the Amazon to climate change, P. Natl. Acad. Sci. USA, 113, 793–797, 2016.
Li, W., Guo, Q., Tao, S., and Su, Y.: VBRT: A novel voxel-based radiative transfer model for heterogeneous three-dimensional forest scenes, Remote Sens. Environ., 206, 318–335, 2018.
Liu, J., Chen, J., Cihlar, J., and Park, W.: A process-based boreal ecosystem productivity simulator using remote sensing inputs, Remote Sens. Environ., 62, 158–175, 1997.
Liu, Q., Fu, Y. H., Liu, Y., Janssens, I. A., and Piao, S.: Simulating the onset of spring vegetation growth across the Northern Hemisphere, Glob. Change Biol., 24, 1342–1356, 2018.
Melaas, E. K., Richardson, A. D., Friedl, M. A., Dragoni, D., Gough, C. M., Herbst, M., Montagnani, L., and Moors, E.: Using FLUXNET data to improve models of springtime vegetation activity onset in forest ecosystems, Agr. Forest Meteorol., 171, 46–56, 2013.
Melaas, E. K., Friedl, M. A., and Richardson, A. D.: Multiscale modeling of spring phenology across Deciduous Forests in the Eastern United States, Glob. Change Biol., 22, 792–805, 2016.
Miller, G. R., Baldocchi, D. D., Law, B. E., and Meyers, T.: An analysis of soil moisture dynamics using multi-year data from a network of micrometeorological observation sites, Adv. Water Resour., 30, 1065–1081, 2007.
Myneni, R. B., Hoffman, S., Knyazikhin, Y., Privette, J. L., Glassy, J., Tian, Y., Wang, Y., Song, X., Zhang, Y., Smith, G. R., Lotsch, A., Friedl, M., Morisette, J. T., Votava, P., Nemani, R. R., and Running, S. W.: Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data, Remote Sens. Environ., 83, 214–231, 2002.
Ni-Meister, W., Yang, W., and Kiang, N. Y.: A clumped-foliage canopy radiative transfer model for a global dynamic terrestrial ecosystem model. I: Theory, Agr. Forest Meteorol., 150, 881–894, 2010.
Oishi, A. C., Oren, R., and Stoy, P. C.: Estimating components of forest evapotranspiration: a footprint approach for scaling sap flux measurements, Agr. Forest Meteorol., 148, 1719–1732, 2008.
Oleson, K., Lawrence, D., Bonan, G., Drewniak, B., Huang, M., Koven, C., Levis, S., Li, F., Riley, W., and Subin, Z.: Technical Description of version 4.5 of the Community Land Model (CLM), NCAR, National Center for Atmospheric Research (NCAR) Boulder, Colorado, 2013.
ORNL DAAC: Daymet data, available at: https://daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=1328, last access: 13 January 2019.
Polgar, C. A. and Primack, R. B.: Leaf-out phenology of temperate woody plants: from trees to ecosystems, New Phytol., 191, 926–941, 2011.
Potter, C. S., Randerson, J. T., Field, C. B., Matson, P. A., Vitousek, P. M., Mooney, H. A., and Klooster, S. A.: Terrestrial ecosystem production: a process model based on global satellite and surface data, Global Biogeochem. Cy., 7, 811–841, 1993.
Richardson, A. D., Anderson, R. S., Arain, M. A., Barr, A. G., Bohrer, G., Chen, G. S., Chen, J. M., Ciais, P., Davis, K. J., Desai, A. R., Dietze, M. C., Dragoni, D., Garrity, S. R., Gough, C. M., Grant, R., Hollinger, D. Y., Margolis, H. A., McCaughey, H., Migliavacca, M., Monson, R. K., Munger, J. W., Poulter, B., Raczka, B. M., Ricciuto, D. M., Sahoo, A. K., Schaefer, K., Tian, H. Q., Vargas, R., Verbeeck, H., Xiao, J. F., and Xue, Y. K.: Terrestrial biosphere models need better representation of vegetation phenology: results from the North American Carbon Program Site Synthesis, Glob. Change Biol., 18, 566–584, 2012.
Running, S. W. and Zhao, M.: Daily GPP and annual NPP (MOD17A2/A3) products NASA Earth Observing System MODIS land algorithm, MOD17 User's Guide, 2015. 2015.
Running, S. W., Nemani, R. R., Heinsch, F. A., Zhao, M. S., Reeves, M., and Hashimoto, H.: A continuous satellite-derived measure of global terrestrial primary production, Bioscience, 54, 547–560, 2004.
Ryu, Y., Baldocchi, D. D., Kobayashi, H., Ingen, C., Li, J., Black, T. A., Beringer, J., Gorsel, E., Knohl, A., and Law, B. E.: Integration of MODIS land and atmosphere products with a coupled-process model to estimate gross primary productivity and evapotranspiration from 1 km to global scales, Global Biogeochem. Cy., 25, GB4017, https://doi.org/10.1029/2011GB004053, 2011.
Sellers, P., Randall, D., Collatz, G., Berry, J., Field, C., Dazlich, D., Zhang, C., Collelo, G., and Bounoua, L.: A revised land surface parameterization (SiB2) for atmospheric GCMs – Part I: Model formulation, J. Climate, 9, 676–705, 1996a.
Sellers, P. J., Tucker, C. J., Collatz, G. J., Los, S. O., Justice, C. O., Dazlich, D. A., and Randall, D. A.: A revised land surface parameterization (SiB2) for atmospheric GCMs. Part II: The generation of global fields of terrestrial biophysical parameters from satellite data, J. Climate, 9, 706–737, 1996b.
Shen, M., Tang, Y., Chen, J., Zhu, X., and Zheng, Y.: Influences of temperature and precipitation before the growing season on spring phenology in grasslands of the central and eastern Qinghai-Tibetan Plateau, Agr. Forest Meteorol., 151, 1711–1722, 2011.
Thornton, P., Thornton, M., Mayer, B., Wilhelmi, N., Wei, Y., and Cook, R.: Daymet: Daily surface weather on a 1 km grid for North America, 1980–2008, Oak Ridge National Laboratory Distributed Active Archive Center, Oak Ridge, Tennessee, USA, 2012.
Turner, D. P., Ritts, W. D., Cohen, W. B., Gower, S. T., Running, S. W., Zhao, M., Costa, M. H., Kirschbaum, A. A., Ham, J. M., and Saleska, S. R.: Evaluation of MODIS NPP and GPP products across multiple biomes, Remote Sens. Environ., 102, 282–292, 2006.
Urbanski, S., Barford, C., Wofsy, S., Kucharik, C., Pyle, E., Budney, J., McKain, K., Fitzjarrald, D., Czikowsky, M., and Munger, J.: Factors controlling CO2 exchange on timescales from hourly to decadal at Harvard Forest, J. Geophys. Res.-Biogeo., 112, G02020, https://doi.org/10.1029/2006JG000293, 2007.
USGS LCI: land cover data, available at: https://archive.usgs.gov/archive/sites/landcover.usgs.gov/global_climatology.html, last access: 1 December 2018.
USGS LPDAAC: MODIS data, available at: https://e4ftl01.cr.usgs.gov/MOLT/,last access: 13 January 2019.
White, M. A., Thornton, P. E., Running, S. W., and Nemani, R. R.: Parameterization and sensitivity analysis of the BIOME–BGC terrestrial ecosystem model: net primary production controls, Earth Interact., 4, 1–85, 2000.
Xiao, X., Zhang, Q., Braswell, B., Urbanski, S., Boles, S., Wofsy, S., Moore, B., and Ojima, D.: Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data, Remote Sens. Environ., 91, 256–270, 2004.
Xiao, Z., Liang, S., Wang, J., Chen, P., Yin, X., Zhang, L., and Song, J.: Use of General Regression Neural Networks for Generating the GLASS Leaf Area Index Product From Time-Series MODIS Surface Reflectance, IEEE T. Geoscience Remote Sens., 52, 209–223, 2014.
Xie, J., Chen, J., Sun, G., Chu, H., Noormets, A., Ouyang, Z., John, R., Wan, S., and Guan, W.: Long-term variability and environmental control of the carbon cycle in an oak-dominated temperate forest, Forest Ecol. Manage., 313, 319–328, 2014.
Xin, Q.: A risk-benefit model to simulate vegetation spring onset in response to multi-decadal climate variability: Theoretical basis and applications from the field to the Northern Hemisphere, Agr. Forest Meteorol., 228–229, 139–163, 2016.
Xin, Q., Dai, Y., Li, X., Liu, X., Gong, P., and Richardson, A. D.: A steady-state approximation approach to simulate seasonal leaf dynamics of deciduous broadleaf forests via climate variables, Agr. Forest Meteorol., 249, 44–56, 2018.
Yang, X., Mustard, J. F., Tang, J., and Xu, H.: Regional-scale phenology modeling based on meteorological records and remote sensing observations, J. Geophys. Res.-Biogeo., 117, G03029, https://doi.org/10.1029/2012JG001977, 2012.
Yu, C., Li, C., Xin, Q., Chen, H., Zhang, J., Zhang, F., Li, X., Clinton, N., Huang, X., Yue, Y., and Gong, P.: Dynamic assessment of the impact of drought on agricultural yield and scale-dependent return periods over large geographic regions, Environ. Model. Softw., 62, 454–464, 2014.
Yuan, H., Dickinson, R. E., Dai, Y., Shaikh, M. J., Zhou, L., Shangguan, W., and Ji, D.: A 3D Canopy Radiative Transfer Model for Global Climate Modeling: Description, Validation, and Application, J. Climate, 27, 1168–1192, 2013.
Yuan, W., Liu, S., Yu, G., Bonnefond, J.-M., Chen, J., Davis, K., Desai, A. R., Goldstein, A. H., Gianelle, D., and Rossi, F.: Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data, Remote Sens. Environ., 114, 1416–1431, 2010.
Zeng, F., Collatz, G. J., Pinzon, J. E., and Ivanoff, A.: Evaluating and quantifying the climate-driven interannual variability in Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) at global scales, Remote Sens., 5, 3918–3950, 2013.
Zhu, P., Zhuang, Q., Ciais, P., Welp, L., Li, W., and Xin, Q.: Elevated atmospheric CO2 negatively impacts photosynthesis through radiative forcing and physiology-mediated climate feedback, Geophys. Res. Lett., 44, 1956–1963, 2017.