the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Spring net community production and its coupling with the CO2 dynamics in the surface water of the northern Gulf of Mexico
Zong-Pei Jiang
Wei-Jun Cai
John Lehrter
Baoshan Chen
Zhangxian Ouyang
Chengfeng Le
Brian J. Roberts
Najid Hussain
Michael K. Scaboo
Junxiao Zhang
Yuanyuan Xu
Net community production (NCP) in the surface water of the northern Gulf of Mexico (nGOM) and its coupling with the CO2 system were examined during the productive spring season. NCP was estimated using multiple approaches: (1) underway O2 and Ar ratio, (2) oxygen changes during light/dark bottle oxygen incubations, and (3) non-conservative changes in dissolved inorganic carbon or nutrients. These methods all showed high spatial variability of NCP and displayed similar patterns along the river–ocean mixing gradient, showing high production rates in plume regions. NCP estimated from high-resolution O2 and Ar underway measurement indicated heterotrophic conditions at the high-nutrient and high-turbidity Mississippi River end ( mmol C m−2 d−1 when salinity < 2) resulting from the influence of terrestrial carbon input and light limitation on photosynthesis. High NCP rates (105.0±59.2 mmol C m−2 d−1, up to 235.4 mmol C m−2 d−1) were observed in the Mississippi and Atchafalaya plumes at intermediate salinities between 15 and 30 where light and nutrients were both favorable for phytoplankton production. NCP rates observed in the high-salinity, oligotrophic offshore waters (salinity > 35.5) were close to zero due to nutrient limitation. Air–sea CO2 fluxes generally showed corresponding changes, from being a strong CO2 source in the river channel (55.5±7.6 mmol C m−2 d−1), to a CO2 sink in the plume ( mmol C m−2 d−1), and to being nearly in equilibrium with the atmosphere in offshore waters. Overall, the surface water of the nGOM was net autotrophic during spring 2017, with an area-weighted mean NCP of 21.2 mmol C m−2 d−1, and was a CO2 sink of −6.7 mmol C m−2 d−1. A temporal mismatch between in situ biological production and gas exchange of O2 and CO2 was shown through a box model to result in decoupling between NCP and CO2 flux (e.g., autotrophic water as a CO2 source outside the Mississippi River mouth and heterotopic water as a CO2 sink in the Atchafalaya coastal water). This decoupling was a result of in situ biological production superimposed on the lingering background pCO2 from the source water because of the slow air–sea CO2 exchange rate and the buffering effect of the carbonate system.
- Article
(4276 KB) -
Supplement
(1041 KB) - BibTeX
- EndNote
The continental shelf is among the most biologically active areas of the biosphere and plays a significant role in global biogeochemical cycles (Chen and Borges, 2009; Chen and Swaney, 2012; Gattuso et al., 1998; Muller-Karger et al., 2005). Despite its moderate surface area (∼7 %), the continental shelf accounts for 14 %–30 % of net ecosystem production (Gattuso et al., 1998), 80 % of organic matter burial (Gattuso et al., 1998), and 15 %–21 % of the CO2 uptake of the global ocean (Cai, 2011; Cai et al., 2006; Chen and Borges, 2009; Laruelle et al., 2010). Moreover, anthropogenic impacts have substantially changed the nutrient and carbon loads delivered to the coastal oceans (Bauer et al., 2013; Regnier et al., 2013; Yang et al., 2018), which have in turn resulted in a series of environmental problems (e.g., coastal eutrophication, hypoxia, and acidification) in some coastal regions (Cai et al., 2011; Diaz and Rosenberg, 2008; Rabalais et al., 2014; Wallace et al., 2014). Understanding and quantifying how these impacts affect the metabolic balance and CO2 fluxes of coastal systems is of critical interest to scientists and policy-makers. However, the substantial heterogeneity resulting from physical and biogeochemical interactions makes assessing metabolic state and carbon flux a challenging task in dynamic coastal environments.
Net community production (NCP) is defined as the difference between gross primary production and community respiration and indicates whether the ecosystem is a net source or sink of organic matter (Eppley and Peterson, 1979; Sarmiento and Gruber, 2006). NCP in the mixed layer plays an important role in regulating the surface CO2 and O2 dynamics. It also represents the amount of organic carbon available for export to the subsurface, which is closely related to bottom-water biogeochemical processes, e.g., the development and maintenance of hypoxia.
The northern Gulf of Mexico (nGOM) is a river-dominated continental shelf (Mckee et al., 2004) with NCP and CO2 dynamics significantly affected by the terrestrial inputs of carbon and nutrients from the Mississippi–Atchafalaya River system (Lohrenz et al., 2014). CO2 variability in the nGOM was extensively investigated by high-resolution underway measurement of the partial pressure of CO2 (pCO2) (Huang et al., 2015). High terrestrial inorganic and organic carbon loading results in CO2 oversaturation and net CO2 efflux to the atmosphere in the river channel and estuary of the Mississippi River (Cai, 2003; Guo et al., 2012; Huang et al., 2015; Lohrenz et al., 2010). On the continental shelf, reduced pCO2 observed in the Mississippi plume (sink for atmospheric CO2) was attributed to strong primary production supported by the excessive riverine nutrient loads (Guo et al., 2012; Huang et al., 2015; Lohrenz et al., 1990, 1999, 2014). Enhanced surface production and subsequent subsurface respiration of the sinking organic matter has led to recurring bottom-water hypoxia covering large portions of the Louisiana–Texas shelf in summer when stratification limits O2 replenishment (Bianchi et al., 2010; Obenour et al., 2013; Rabalais et al., 2002). Springtime riverine nutrient flux and subsequent biological production in surface water play a critical role in determining the size of the summertime bottom-water hypoxia area in the nGOM (Justić et al., 1993; Turner et al., 2012). Rapid subsurface respiration also leads to a significant decrease in pH and a weakening of acid–base buffer capacity, which further results in enhancement of the coastal ocean acidification problem (Cai et al., 2011).
Previous NCP studies in the nGOM have been mainly based on dissolved oxygen changes during light/dark bottle oxygen incubations and non-conservative removal of dissolved inorganic carbon or nutrients (Cai, 2003; Huang et al., 2012; Guo et al., 2012; Murrell et al., 2009, 2013). However, the detailed relationship between NCP and CO2 dynamics remains unclear because of the low spatial resolution of the conventional NCP measurements based on discrete samples. In this study, we present the first attempt to obtain high-resolution NCP estimates from continuous underway measurement of the oxygen-to-argon ratio (O2∕Ar) in the nGOM in spring. The NCP result was compared to those derived from traditional approaches to evaluate the consistency of NCP estimates from various methods. Meanwhile, these NCP methods are associated with different temporal and spatial scales and are differently affected by biological and physical processes. By comparing NCP estimates from multiple methods we can get a more robust understanding of the overall metabolism of the system. The simultaneous underway determination of NCP and pCO2, together with measurements of dissolved oxygen (DO), dissolved inorganic carbon (DIC), total alkalinity (TA), nutrients, and other environmental parameters, allow us to better constrain the variability and controls on the metabolic balance and CO2 flux in the nGOM. We also use a box model to investigate the relationship between NCP and air–sea fluxes of O2 and CO2.
2.1 Sample collection and measurements
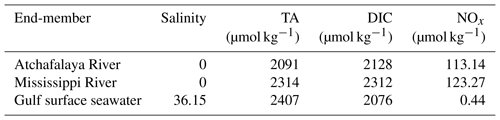
The cruise was conducted onboard RV Pelican during 6–16 April 2017. The study region covered the northern Gulf of Mexico including the Mississippi and Atchafalaya estuaries and the adjacent Louisiana continental shelf where summer hypoxia repeatedly occurs (Fig. 1). Vertical water column profiles of temperature, salinity, DO, chlorophyll fluorescence (Chl a), and photosynthetically active radiation (PAR) were measured by a Sea-Bird conductivity–temperature–depth (CTD) system (SBE 911plus) at 83 sampling stations (Fig. 1). Discrete water samples for DIC, TA, DO, and nutrients (n=382) were collected from 3 to 12 depths depending on the bottom depth and vertical profiles of temperature, salinity, and DO. River water samples of the Mississippi (89.98∘ W, 29.85∘ N) and Atchafalaya (91.21∘ W, 29.70∘ N, Fig. 1) were taken on 5 April, 1 day prior to the cruise, to identify the DIC and TA concentrations of the river end-members. Samples for DIC and TA were collected in 250 mL borosilicate glass bottles and preserved with 50 µL of saturated HgCl2 solution (Dickson et al., 2007). DIC was measured by non-dispersive infrared measurement on the CO2 stripped from the acidified sample (AS-C3, Apollo SciTech). TA titrations were conducted with a ROSS™ combination electrode 8102 (Thermo Fisher Scientific) on a semi-automated titrator (AS-ALK2, Apollo SciTech). The precisions of DIC and TA measurements were both 2 µmol kg−1. DIC and TA measurements were calibrated, both with accuracy better than 0.1 %, with certified reference materials provided by Andrew G. Dickson, Scripps Institution of Oceanography. DO in discrete samples was measured by a Shimadzu UV-1700 at 25 ∘C using the spectrophotometric method following Pai et al. (1993) with an accuracy of 0.2 %. For nutrient analysis, water from each Niskin bottle was immediately filtered through 0.22 µm, sterile, polyethersulfone syringe filters and stored frozen for subsequent nutrient characterization. Samples were analyzed in duplicate for dissolved NOx () by Cu–Cd reduction followed by azo dye colorimetry using a Lachat Instruments QuikChem® FIA+8000 Series Automated Ion Analyzer at the Louisiana Universities Marine Consortium as described previously (Roberts and Doty, 2015). Standard curves were prepared using standard NO3−N and NO2−N stock solutions (Hach, Loveland CO) and yielded r2 values of ≥0.999.
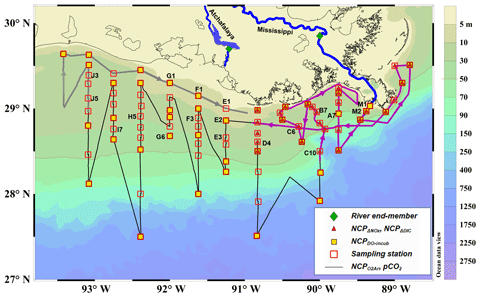
Figure 1Map and sampling sites in the northern Gulf of Mexico during the April 2017 cruise. The black dotted line is the cruise track along which the high-resolution underway measurements were made. The tracks in the Mississippi plume (purple line, 8–11 April) and in the Atchafalaya coastal regions (grey line, 15–17 April) are highlighted. Also shown are the 83 CTD sampling stations (hollow red squares), the 43 stations where light/dark bottle DO incubations were conducted (solid yellow squares), the 30 stations where non-conservative changes in DIC and NOx were used to estimate NCP rates (solid red triangles), and the 2 stations where the properties of river end-members were measured (solid green diamonds). The vertical CTD profiles of the labeled stations are shown in the Supplement. Figure generated by Ocean Data View (Schlitzer, 2018).
2.2 Underway measurements
The underway system was fed by the ship's seawater supply from an inlet located at an approximate depth of 2.5 m. The flow-through system and the Multiple Instrument Data Acquisition System (MIDAS) provided measurements on sea surface temperature, conductivity (Sea-Bird SBE 21 Thermosalinograph), Chl a (Turner Model 10 Series Fluorometers), and light transmittance (WETLabs 25 cm path length transmissometer). MIDAS also integrated data from the ship's meteorological suite: wind, barometric pressure, temperature, and relative humidity (TS05327 R. M. Young) and PAR (LI-COR LI-190SZ).
Underway seawater pCO2 was measured with a precision of 0.1 µatm by an automated flow-through pCO2 measuring system (AS-P2, Apollo SciTech) with a shower head equilibrator and a non-dispersive infrared gas detector (LI-7000, LI-COR) (Huang et al., 2015). The pCO2 measurement was calibrated twice daily against three certified gas standards (150.62, 404.72, and 992.54 ppm), and the accuracy was better than ±2 µatm. The underway pCO2 system alternated measurements on a stream of seawater split from the same inlet for the MIDAS and a stream of outside air from the bow of the vessel away from chimney contamination. The atmospheric pCO2 was measured every 3 h automatically. The underway DO was measured by an Aanderaa 4835 optode which was calibrated against discrete surface water values by spectrophotometric measurements.
Underway high-resolution measurements of O2∕Ar were made by equilibrator inlet mass spectrometry as described by Cassar et al. (2009). Briefly, a fraction of underway seawater (the same supplied to the pCO2 measuring system) was pumped through a gas-permeable membrane contactor cartridge at a flow rate of 100 mL min−1. The cartridge was connected to a quadrupole mass spectrometer (Pfeiffer Prisma) through a fused-silica capillary which continuously sampled headspace gases for O2∕Ar measurement. As atmospheric O2∕Ar is essentially constant relative to that in the surface water, calibrations of the O2∕Ar ion current ratio were conducted by sampling the ambient air every 3 h through a second capillary (Cassar et al., 2009). The instrument precision estimated from the repeated measurements of atmospheric O2∕Ar was 0.3 %.
2.3 Calculations
The mixed layer depth (MLD) was defined as the depth at which the density changed by 0.03 kg m−3 relative to the surface value and was calculated according to the density profiles at sampling stations. Air–sea CO2 flux () was calculated as
where is the gas transfer velocity of CO2 calculated using the daily mean wind speed from the three-dimensional Coupled Ocean/Atmosphere Mesoscale Prediction System (COAMPS) (Hodur, 1997) and the coefficients of Sweeney et al. (2007). The COAMPS daily wind speed agreed well (mean difference = 0.4 m s−1, figure not shown) with buoy measurements in our study region (s42047, s8768094, FRWL1, MRSL1, LOPL1, GISL1, PSTL1, and PILL1, data from the National Data Buoy Center, http://www.ndbc.noaa.gov/maps/WestGulf.shtml, last access: 25 August 2018). K0 is the CO2 solubility coefficient calculated from the measured sea surface temperature and salinity (Weiss, 1974). ΔpCO2(sea–air) is the difference between the measured pCO2 in the surface water (pCO2meas) and in the atmosphere (pCO2air). pCO2air variability was negligible (405±4 µatm) compared to the large variations in pCO2meas (110–1800 µatm), so pCO2air was set at the cruise average value of 405 µatm for all flux calculations. Negative values correspond to net CO2 uptake by the ocean (ocean as a CO2 sink for the atmosphere). Air–sea O2 flux () was calculated as
where is the gas exchange velocity of O2 which was calculated in a similar way to that of and ΔO2(sea–air) is the difference between the seawater DO concentration from the calibrated underway optode measurement ([O2]meas) and the saturated DO concentration ([O2]sat) calculated from the measured sea surface temperature and salinity (Garcia and Gordon, 1992). The oxygen saturation percentage (DO %) is calculated as DO % = [O2]meas ∕ [O2]sat.
2.4 NCP estimates
In this study, NCP rates were estimated by three different approaches: underway O2∕Ar measurements (NCP), light/dark bottle dissolved oxygen (DO) incubations (NCPDO-incub), and non-conservative changes in DIC (NCPΔDIC) or NOx (NCP).
NCP from the O2∕ Ar method. DO concentration in the surface water is affected by physical (e.g., changes in temperature, salinity, atmospheric pressure, and bubble dissolution and injection) and biological processes (e.g., photosynthesis and respiration). Ar and O2 have similar responses to physical processes as they have similar solubility and temperature dependency (Garcia and Gordon, 1992; Hamme and Emerson, 2004). However, Ar is biologically inert and can therefore be used to infer abiotic influences on oxygen. Contemporaneous measurements of O2 and Ar thus allow the biologically induced O2 changes to be isolated (Craig and Hayward, 1987). By measuring the biologically mediated oxygen supersaturation Δ(O2∕Ar) (Cassar et al., 2011; Craig and Hayward, 1987; Jonsson et al., 2013; Kaiser et al., 2005),
the surface NCP can be approximated by the net air–sea biological oxygen flux (bioflux, mmol O2 m−2 d−1) under a physically isolated mixed layer assumption (Jonsson et al., 2013):
The modeling study by Teeter et al. (2018) suggested that the bioflux accurately represents the exponentially weighted NCP over the past several residence times of O2. The residence times of O2 (MLD∕gas transfer velocity of O2, ∼2.3 d during our cruise) refers to the length of time required to exchange O2 between the mixed layer and the atmosphere (Kaiser et al., 2005; Teeter et al., 2018). To account for the wind speed history prior to the arrival of the ship at each station, the weighting technique of Reuer et al. (2007) modified by Teeter et al. (2018) was applied to calculate the gas exchange velocity of O2 in this study.
NCP from the DO incubation. NCP was estimated by the light/dark bottle incubation method at 43 CTD stations (Fig. 1). Surface water samples (∼1.5 m) were collected from Niskin bottles into triplicate clear and black 300 mL Wheaton BOD bottles. The initial oxygen saturation percentage and temperature in each bottle were measured by inserting a luminescent/optical dissolved oxygen probe (Hach LDO101, Hach Hq40d meter) into the bottle. Care was taken to avoid introducing air bubbles during this step. After recording the initial oxygen saturation percentage value, the probe was removed and the small volume displaced by the probe (∼3 mL) was replaced with filtered seawater from an offshore, low-nutrient site. The addition of DO to the bottle from the replacement water was considered small, on the order of the method detection limit of approximately 2 mmol m−3 d−1 (Murrell et al., 2009, 2013). Clear and dark bottles were placed into a deck incubator screened at 50 % of ambient sunlight for 24 h. The deck incubator was plumbed with flowing seawater from the MIDAS in order to maintain surface water temperatures. After 24 h, the oxygen saturation percentage and temperature were measured again with the oxygen probe. DO concentrations obtained from the LDO probe were verified by a comparison with DO concentrations measured by the spectrophotometric method of Pai et al. (1993) in a subset of samples (n=14). The mean difference between the two methods of ±5 % was consistent with previous comparisons of probe-measured versus Winkler-measured DO based on several hundred comparisons (Murrell et al., 2013).
The respiration rate was calculated from the DO changes in the dark bottles (Rdark, mmol O2 m−3 d−1). The respiration rate was assumed to be uniform in the mixed layer; thus, the integrated respiration over the MLD (RespInt, mmol O2 m−2 d−1) was calculated as Resp. The gross primary production (GPP) varied with depth due to the reduction in light availability with increasing depth. The mean percentage of PAR (% PAR) in the water column in relation to surface PAR (E0) was calculated at each station as
where E0 is 100 % and light attenuation (Kd, m−1) is the rate of exponential decline in PAR as a function of depth as measured by the CTD. In our study, we assumed that GPP linearly dependent on light up to a maximum GPPmax occurred when % PAR = 50 %. This assumption is based on previous measurements from this shelf that indicate photosynthesis begins to saturate at a light level of ∼200 µmol quanta m−2 s−1 (Lohrenz et al., 1994), which is roughly 50 % of light in the surface mixed layer (Lohrenz et al., 1999). GPPmax was thus estimated as GPP, where Rlight is the DO change rate in the light bottles. To calculate the integrated GPP in the mixed layer (GPPInt, mmol O2 m−2 d−1), the GPP was scaled by the light environment in the MLD:
The coefficient 2 in Eq. (7) was used so that the product of 2×% PAR would scale from 0 to 1; i.e., GPP approaches GPPmax at % PAR = 50 %. Finally, the NCP integrated over the MLD (NCPDO-incub, mmol O2 m−2 d−1) was estimated as
The mean standard errors of NCPDO-incub estimates from triplicate bottle incubations across all sites were approximately 16 % of the mean rates.
NCP from the non-conservative changes in DIC or nutrients. NCP can also be estimated from the biologically induced deviations of DIC or nutrients from conservative mixing. We applied a three-end-member mixing model (Huang et al., 2012) to distinguish the contribution from conservative mixing (Xmix) and the biologically induced change (ΔXbiol). The Xmix was calculated from the fractions of Gulf of Mexico surface seawater (fsw), Mississippi River water (fMR), and Atchafalaya River water (fAR) together with the corresponding end-member concentrations shown in Table 1:
We used salinity and potential alkalinity (PTA = TA + NOx) (Brewer and Goldman, 1976) as the two conservative tracers to constrain fsw, fMR, and fAR using a non-negative least square method (Lawson and Hanson, 1974). The concentrations of DICmix and NOxmix from conservative mixing can then be calculated from Eq. (10), and the biologically induced changes in DIC (ΔDICNCP) and NOx (ΔNOxNCP) were estimated as
where DICmeas and NOxmeas are the observed concentrations of DIC and NOx, and ΔDICgas is the DIC changes induced by air–sea CO2 exchange. Note that ΔDICNCP (mmol C m−3) and ΔNOxNCP (mmol N m−3) represent the cumulative NCP-induced changes in the concentrations of DIC and NOx since the mixing of river water with oceanic water. In order to calculate the NCP rates derived from DIC (NCPΔDIC, mmol C m−2 d−1) or NOx (NCP, mmol N m−2 d−1), the MLD and plume residence time (τ) need to be considered (Cai, 2003):
To facilitate comparison with previous studies (Guo et al., 2012; Huang et al., 2012; Cai, 2003), τ values for the Mississippi plume were taken from Green et al. (2006) as 1, 1.5, and 6 d for salinity ranges of 0–18, 18–27, and 27–34.5, respectively. In our study, we only calculated NCPΔDIC and NCP for stations in the Mississippi plume because τ for the Atchafalaya plume is not available.
NCP unit conversion. To facilitate the comparison of NCP estimates from the different approaches, NCP rates were converted to the same carbon units (mmol C m−2 d−1) using the Redfield ratio of . The photosynthetic molar ratio of C∕O2 for new and recycled production may vary between 1.1 ( as nitrogen source) and 1.4 ( as nitrogen source) (Laws, 1991). In our study region, the riverine input of was the main nitrogen source for biological uptake (Table 1), and we considered the average Redfield ratio of to be appropriate. Although biological C∕N uptake may differ from the Redfield stoichiometry (Geider and La Roche, 2002; Sambrotto et al., 1993), the applicability of the Redfield C∕N ratio has been previously demonstrated in our study region (Huang et al., 2012; Xue et al., 2015) and confirmed in this study.
2.5 Box model for NCP and gas exchange
A simple box model was used to examine the relationship between NCP and air–sea fluxes of O2 and CO2. The environmental settings of the box model were taken from the averaged condition during our study period: temperature = 22 ∘C, salinity = 35, TA = 2400 µmol L−1, pCO2air=405 µatm, MLD = 6 m, and wind speed = 6 m s−1. The initial state of the seawater was set to be in equilibrium with the atmosphere, and the concentrations of DO and pCO2 in the seawater were modulated by time-dependent NCP functions and air–sea gas exchange at hourly time steps. At each time step, the relative changes in concentrations of DIC, TA, and DO resulting from NCP were assumed to follow the ratio of (Zeebe and Wolf-Gladrow, 2001). The pCO2 was calculated from DIC and TA using the CO2SYS program (Pierrot and Wallace, 2006). The air–sea fluxes of O2 and CO2 were calculated following Eqs. (1) and (2).
3.1 General hydrological and biogeochemical characteristics
The Mississippi and Atchafalaya rivers typically experience peak discharge and NOx loading in spring (Fig. S1 in the Supplement). These peaks in spring 2017 occurred later than the average condition during 1997–2017 and the monthly mean values of discharge and NOx loading in April 2017 were slightly lower than the long-term mean values (Fig. S1). Surface water parameters (temperature, salinity, light transmittance, Chl a, DO %, pCO2, and ΔO2∕Ar) showed high spatial variability on the inner and middle shelves (bottom depth < 50 m), with much lower variability observed on the outer shelf (bottom depth > 50 m) (Fig. 2). The highest physical and biogeochemical variations were observed in the Mississippi plume during 8–11 April and in the Atchafalaya coastal region during 15–17 April (Fig. 3). In spring when river discharge is high and the wind is typically downwelling-favorable, the Mississippi River freshwater generally flows westward in a contained nearshore current (Zhang et al., 2012; Lehrter et al., 2013). Our three-end-member mixing model accurately reproduced the westward extension of the Mississippi freshwater on the Louisiana shelf from the Mississippi bird's foot delta (Figs. 2b and 4a). The mixing model also suggested a westward Atchafalaya plume trajectory in a narrow band along the coast, with little Atchafalaya freshwater transported upcoast toward the Mississippi Delta (Fig. 4b). The pattern of the Mississippi and Atchafalaya freshwater transport agreed well with the multiple-year average condition (2005–2010) in April by hydrodynamic numerical simulation (Zhang et al., 2012). To better investigate the variability of surface water parameters, we divided the coastal region into four sub-regions: (1) the lower Mississippi River channel (Fig. S2, salinity < 2); (2) the Mississippi plume (Fig. 4a, east of 90.75∘ W, north of 28.30∘ N); (3) the high-turbidity Atchafalaya coastal water (Figs. 4a and 2d, 90.75–92.35∘ W, light transmittance < 20 %, named HTACW hereafter); and (4) the Atchafalaya plume (Fig. 4b, 92.35–93.50∘ W, north of 29.00∘ N). Typical vertical CTD profiles are shown in the Supplement (Figs. S2–S4) to demonstrate the different mixing conditions observed in the four sub-regions as well as other regions in the nGOM.
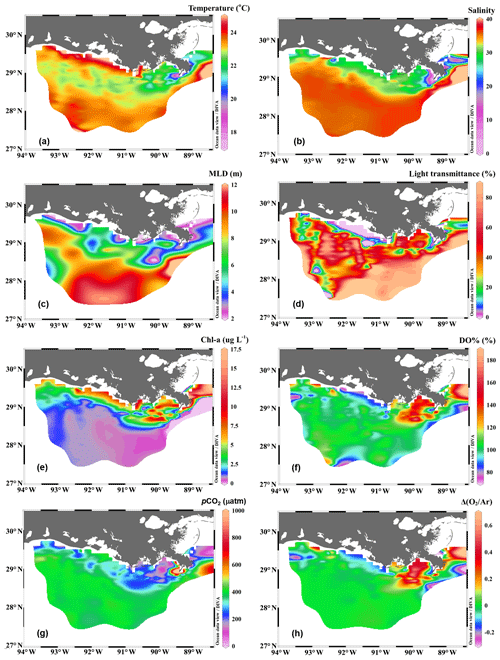
Figure 2The distribution of (a) temperature, (b) salinity, (c) mixed layer depth (MLD), (d) light transmittance, (e) chlorophyll a concentration (Chl a), (f) oxygen saturation percentage (DO %), (g) partial pressure of CO2 (pCO2), and (h) biologically induced oxygen supersaturation (ΔO2∕Ar) in the surface water of the nGOM. Figure generated by Ocean Data View (Schlitzer, 2018).
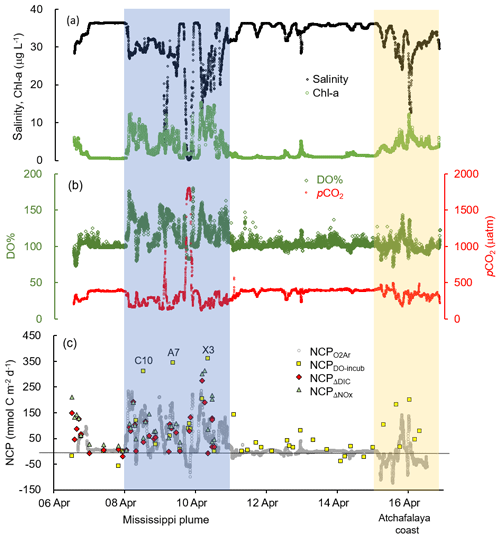
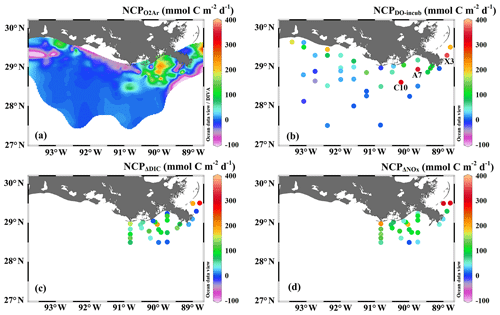
Figure 3The underway measurements of (a) salinity and Chl a, (b) DO % and pCO2, and (c) NCP rates estimated from the O2∕Ar measurement (NCP, grey circles). Also shown in (c) are the NCP rates estimated from the light/dark DO incubation (NCPDO-incub, yellow squares), non-conservative changes in DIC (NCPΔDIC, red diamonds), or NOx (NCPΔNOx, green triangles). See Fig. 1 for the cruise track in the Mississippi plume (8–11 April) and Atchafalaya coast (15–17 April). See Fig. 5 for the positions of stations C10, A7, and X3 in the Mississippi plume.
3.2 Estimates of NCP
In comparison to the discrete measurements of NCPDO-incub, NCPΔDIC, and NCP, the underway O2∕Ar measurements provided NCP estimates with the highest resolution and most complete spatial coverage (Fig. 5). The NCPDO-incub, NCPΔDIC, and NCP were mostly obtained at salinities higher than 20, while the NCP covered the whole salinity range (0 to 36.4), providing more information on the NCP variability in the dynamic estuary environments. All methods suggested high variability of NCP in the surface water of the nGOM (Figs. 3c, 5), and these methods yielded similar spatial patterns with high production rates in the plume region around the Mississippi bird's foot delta (Fig. 5). The results of NCPΔDIC (−19.0 to 274.9 mmol C m−2 d−1) and NCP (1.6 to 314.0 mmol C m−2 d−1) were close to each other (Fig. 5c, d), and their ranges were similar to that of NCP in the Mississippi plume (−99.6 to 235.4 mmol C m−2 d−1) (Fig. 3c). NCPDO-incub (−56.0 to 360.7 mmol C m−2 d−1) gave the highest NCP estimates in the Mississippi plume (stations C10, A7, and X3 in Figs. 5b and 3c). As NCP is a backward exponentially weighted average rate (Teeter et al., 2018), it is less able to capture high NCP values due to the inherent averaging of the O2∕Ar approach. Moreover, NCP could be a poor estimate of daily production rate (e.g., NCPDO-incub in our study) when the mixed layer is not at steady state (Teeter et al., 2018). These could partly explain the observed difference between NCP and NCPDO-incub in the dynamic Mississippi plume. In the high-salinity offshore waters, NCP and NCPDO-incub both suggest low NCP rates close to zero (Fig. 5a, b). One major difference between NCP and NCPDO-incub is that the O2∕Ar method generated negative NCP estimates in the lower Mississippi River channel and in the HTACW, while NCPDO-incub suggested positive NCP rates in these regions (Fig. 5a, b).
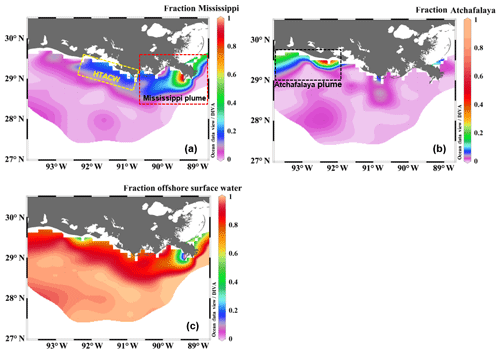
Figure 4The fractional contribution of (a) the Mississippi River, (b) the Atchafalaya River, and (c) offshore surface water to the surface water of the nGOM estimated from the three-end-member mixing model. The sub-regions shown in (a) and (b) are the Mississippi plume, the high-turbidity Atchafalaya coastal water (HTACW), and the Atchafalaya plume. Figure generated by Ocean Data View (Schlitzer, 2018).
3.3 Mississippi River channel and plume
Vertical CTD profiles showed strong surface stratification in the lower Mississippi River channel (Fig. S2). The light transmittance in the surface water of the river channel was close to zero (Fig. 6a) and the Chl a concentrations were low (Fig. 6b) despite ample nutrient availability (NOx up to 123.3 µmol kg−1, Table 1). Similar to most inner estuaries (Borges and Abril, 2011; Chen et al., 2012; Chen and Swaney, 2012), high pCO2 (up to 1803.0 µatm, Fig. 6c), undersaturated DO (83.7±0.8 %, Fig. 6d) and net CO2 efflux (55.5±7.6 mmol C m−2 d−1, Fig. 6e) was observed in the lower Mississippi River channel. The negative NCP ( mmol C m−2 d−1, Fig. 6f) suggested net heterotrophic condition in the Mississippi River channel, which contrasts with the positive NCPDO-incub (94.5±11.6 mmol C m−2 d−1 Fig. 7c) measured by the DO incubation method.
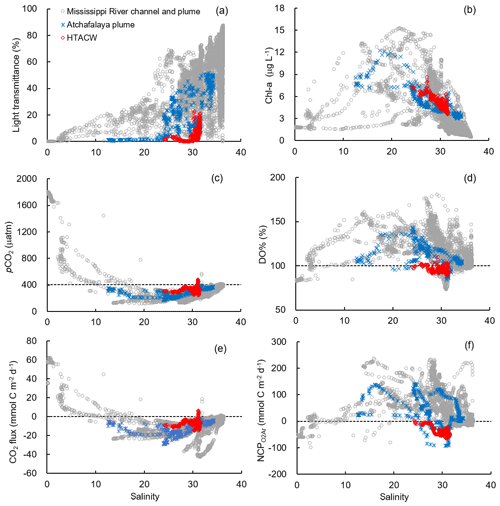
Figure 6The distribution of (a) light transmittance, (b) Chl a, (c) pCO2, (d) DO%, (e) CO2 flux, and (f) NCP along the salinity gradient in different sub-regions. The dash lines in (c) to (f) are the atmospheric pCO2 (405 µatm), DO % of 100 %, zero CO2 flux, and zero NCP, respectively.
The Mississippi plume and most offshore regions were characterized by surface stratification, which was mainly caused by the buoyancy of fresher surface water in the plume and vertical temperature gradient in the offshore region (Fig. S3). With increasing light transmittance (Fig. 6a) in conjunction with persistence of riverine-derived nutrient concentrations (Fig. 7a) along the Mississippi plume flow path, phytoplankton biomass reached high levels at intermediate salinities of 15–30 (Fig. 6b). High Chl a concentrations in the plume region corresponded to large decreases in pCO2 (down to 113.9 µatm, Fig. 6c) and strong oceanic CO2 uptake (up to −42.7 mmol m−2 d−1, Fig. 6e), as well as elevated DO % (up to 180.1 %, Fig. 6d) and NCP rates (Fig. 6f). The observed high NCP rates (e.g., up to 235.4 mmol C m−2 d−1 in NCP, up to 360.7 mmol C m−2 d−1 in NCPDO-incub, Fig. 7c) are within the range of prior estimates for this region during the spring season (−238 to 624 mmol C m−2 d−1, Cai, 2003; Guo et al., 2012; Huang et al., 2012; Lohrenz et al., 1990, 1997, 1999) and are among the highest in large river estuarine and shelf waters (Cooley and Yager, 2006; Dagg et al., 2004; Ning et al., 1988; Ternon et al., 2000).
3.4 Atchafalaya plume and HTACW
The Atchafalaya River discharges in a shallow broad, low-gradient shelf (10 m isobath does not occur until more than 40 km offshore of the delta, Fig. 1) which frequently experiences cross-shelf currents (Roberts and Doty, 2015). The Atchafalaya plume water extended westward in a narrow band along the coast (Fig. 4b) and generally showed similar biogeochemical variability to that observed in the Mississippi plume (Fig. 6). Elevated Chl a, DO %, and NCP were also observed at intermediate salinities (15–30) in the Atchafalaya plume, which also exhibited decreases in pCO2 and oceanic CO2 uptake (Fig. 6). For both the Mississippi and Atchafalaya plume regions, the three-end-member mixing model suggests that the enhanced biological production resulted in significant deviations of DIC and NOx from the conservative mixing lines (Fig. 8). The amplitudes of the non-conservative biological removal of nutrients (up to 35 µmol kg−1 in ΔNOxNCP, Fig. 8a) and DIC (up to 250 µmol kg−1 in ΔDICNCP, Fig. 8b) are similar to the findings of previous studies in the nGOM (Cai, 2003; Guo et al., 2012; Huang et al., 2012). The biological uptake ratio of ΔNOxNCP and ΔDICNCP (0.14 in Fig. 8c) was close to the Redfield N∕C ratio (16∕106 = 0.15). However, NCP suggested that the southwestern part of the Atchafalaya plume (around 29.30∘ N, 93.50∘ W) was heterotrophic (Fig. 5a). A detailed examination of the CTD profiles revealed that the water column in this area was vertically well-mixed (Fig. S4), which was different than the stratification observed in other plume regions.
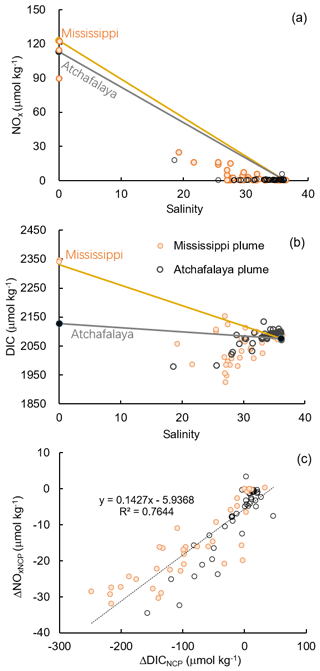
Figure 8Scatter plots of (a) DIC and salinity, (b) NOx and salinity, and (c) the non-conservative changes in DIC (ΔDICNCP) and NOx (ΔNOxNCP) in the Mississippi and Atchafalaya plumes. The end-member concentrations of the Mississippi River, the Atchafalaya River, and offshore gulf surface water are shown in (a) and (b) together with the conservative mixing lines.
The HTACW was characterized by a well-mixed water column and low light transmittance (Fig. S4). Although the Chl a concentrations in the HTACW were similar to those in the Atchafalaya plume in the salinity range of 24 to 32 (Fig. 6b), the DO % was much lower in the HTACW (94.7±12.1 %, Fig. 6d). The pCO2 in the HTACW (327.8±34.6 µatm) was higher than that in the Atchafalaya plume (288.7±43.7 µatm) at the same salinities (Fig. 6c), but the HTACW still acted as a weak sink for atmospheric CO2 ( mmol C m−2 d−1, Fig. 6e). Similar to that in the Mississippi River channel, the two approaches for NCP estimation presented contrasting results in the HTACW: negative NCP ( mmol C m−2 d−1, Fig. 5a) suggest net heterotrophic conditions, while positive NCPDO-incub rates (62.6±23.3 mmol C m−2 d−1, Fig. 5b) suggest net autotrophic conditions.
4.1 Comparison of NCP estimations
A comparison of NCP estimated from various methods should be interpreted with caution as each approach has its independent assumptions and limitations and refers to different temporal and spatial scales (Ulfsbo et al., 2014). However, applying multiple methods provides complementary information to better understand the processes affecting estimations of and controls on ecosystem metabolism.
NCP from the DO incubation method. The NCPDO-incub was estimated from 24 h DO changes in incubation bottles, which gives a daily NCP estimate for the plankton community at the sampling location. The DO incubation method is a direct measurement of NCP and is free from the influences of lateral advection and sediment metabolism. NCPDO-incub thus equals the MLD-integrated NCP in the stratified regions (NCPMLD in Fig. 9a, c) or the water column-integrated NCP in the well-mixed regions (NCPwater in Fig. 9b). However, there are uncertainties related to scaling from samples collected at discrete depths to integrated mixed layer NCP values. First, the scaling method used here assumes a homogenous distribution of respiration rate over the MLD. Second, we only measured GPP at one light level (50 %) and we assumed that the GPP below 50 % surface PAR was linearly scaled to % PAR (Eqs. 6 and 7). Similar assumptions for the Louisiana shelf were tested previously by Murrell and Lehrter (2011), who found that single-point measurements (vs. multi-point measurements in a layer) provided robust estimates of integrated rates. However, in the current study, the assumption has been further applied to shallow nearshore sites (< 10 m depth), which may exhibit greater heterogeneity in vertical PAR distributions due to the high algal biomass and suspended sediment particle concentrations. More importantly, for high-turbidity water samples (e.g., samples collected in the Mississippi River channel and in the HTACW), the incubated samples were not mixed in the same way as that in the natural environment, and the sedimentation of particles in incubation bottles could alleviate the light limitation for phytoplankton. As a result, the gross primary production (GPPInt in Eq. 8) could be overestimated and NCPDO-incub would not represent the true in situ NCP in high-turbidity waters.
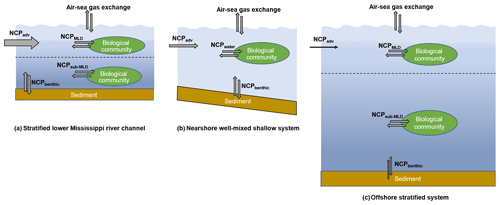
Figure 9The differences in water column mixing conditions in the nGOM and their influences on NCP estimation. The dotted lines in (a) and (c) indicate the mixed layer depth. In the stratified lower Mississippi River channel (a) and the offshore stratified system (c), NCPDO-incub equals the in situ community production in the mixed layer (NCPMLD), while NCP reflects the combined result of the NCPMLD and the influence of lateral advection of the river water (NCPadv). In the nearshore well-mixed shallow system (b), NCPDO-incub equals the water column community production (NCPwater), while NCP reflects the combined result of NCPwater, NCPbenthic, and NCPadv. Note that the influence of NCPadv decreases offshore with the increasing water residence time.
NCP from the O2 ∕ Ar method. NCP is derived from the air–sea biological oxygen flux (Eq. 4), which represents the exponentially weighted NCP over the past several residence times of O2 (Kaiser et al., 2005; Teeter et al., 2018). When using the O2∕Ar method to estimate NCPMLD, a key assumption is that physical inputs to the mixed layer are negligible. However, this assumption can be invalid in the dynamic coastal environments. Recent studies have shown that entrainment and upwelling processes (mixing with O2-depleted subsurface water) can lead to significant underestimation in NCPMLD using the O2∕Ar method, especially in coastal upwelling zones (Castro-Morales et al., 2013; Nicholson et al., 2012; Shadwick et al., 2015; Teeter et al., 2018). As most regions in our study were characterized by the persistent surface stratification (Figs. S2 and S3), the influences of sub-pycnocline (NCPsub-MLD in Fig. 9a, c) and benthic metabolisms (NCPbenthic in Fig. 9a, c) on the surface O2∕Ar ratio were expected to be minor. However, the surface O2∕Ar ratio in the well-mixed nearshore regions (e.g., the HTACW, Fig. S4) was affected by both water column (NCPwater) and benthic metabolisms (NCPbenthic) (Fig. 9b). Moreover, both Mississippi and Atchafalaya River end-members were highly heterotrophic, and lateral transportation of this heterotrophic signal carried by river water (NCPadv in Fig. 9) should be considered. As it generally takes a few days for O2 to become in equilibrium with the atmosphere (see the discussion below), NCPadv could play an important role in affecting the O2∕Ar ratio in the river channel and estuary where water transport speed was rapid (Fig. 9a, b). The influence of NCPadv decreased offshore and the impact of remote source water heterotrophy was negligible in most offshore regions where water residence time was sufficiently long (Fig. 9c). Therefore, NCP represented the metabolic state of the water which was affected not only by the local aquatic ecosystem (NCPMLD or NCPwater in Fig. 9), but also by additional factors including NCPbenthic and NCPadv (Fig. 9). Depending on the different mixing conditions in the nGOM, NCP reflected either (1) the combined result of NCPMLD and NCPadv in the stratified river channel and plume region; (2) the combined result of NCPwater, NCPbenthic, and NCPadv in the well-mixed nearshore waters (e.g., HTACW); or (3) NCPMLD in the offshore stratified regions where riverine influence was minor. As NCPbenthic only affected a small portion of the nearshore water in the Atchafalaya coastal region (Fig. S4), the NCP measured in this study was mainly modulated by NCPMLD and NCPadv. Considering the nGOM as a whole, lateral advection of NCPadv can be considered to be internal transport within the system given that the NCP was measured with adequate spatial coverage. As a result, the NCP measured in this study well represented the overall metabolic state of the surface water of the nGOM.
NCP from the non-conservative changes in DIC and nutrients. The NCPΔDIC and NCP in the Mississippi plume reflected the average community production rate along the flow path during the river–ocean mixing process. There are several sources of uncertainty associated with the NCP estimated from the non-conservative mixing change in DIC and nutrients. First, errors in estimating water residence time and the changes in MLD over the transit time of the plume water lead to proportional errors in the calculation of NCPΔDIC and NCP (Eqs. 13 and 14). The plume water residence time is a function of river discharge and other physical conditions; it is therefore expected that using a set of past model-assessed τ values probably would introduce the largest uncertainty into the estimation of NCPΔDIC and NCP. Second, uncertainty may be caused by the changes in the concentrations of DIC and nutrients of the river end-members. However, this uncertainty decreases with salinity (Huang et al., 2012) and was generally low in our study.
To better investigate the NCP rates estimated from different methods, we focused on the regions where NCP and NCPDO-incub provided contrasting results: NCP suggested heterotrophy in the Mississippi River channel and in the HTACW where positive NCPDO-incub rates were presented. The contrasting results of NCP and NCPDO-incub can be mainly explained by the different spatial and temporal scales associated with the two methods responding to the mixing conditions. In the high-turbidity Mississippi River channel (light transmittance close to zero) and HTACW (light transmittance < 20 %), the GPP was strongly limited by light availability and the DO incubation method could significantly overestimate the in situ NCP due to the improved light environment in the incubation bottles. However, the measured community respiration rates (RespInt in Eq. 8) in the lower Mississippi River channel (14.0±0.8 mmol C m−2 d−1) and in the HTACW (30.5±10.7 mmol C m−2 d−1) were not able to fully account for the heterotrophy suggested by NCP ( and mmol C m−2 d−1 in the lower Mississippi River channel and HTACW, respectively), even when the GPP was not taken into account. This indicates sources of heterotrophic signals other than the local community respiration in these two regions. In the stratified lower Mississippi River channel (Fig. 9a), the influence of lateral transportation of the heterotrophic river water from the upper river channel was significant because of the short water residence time (∼1 d, Green et al., 2006). The heterotrophic condition in the lower Mississippi River channel could be attributed to the dominant influence of the heterotrophic NCPadv over the local biological production. In the vertically well-mixed HTACW (Fig. 9b), NCP reflected the combined result of the water column community production, the lateral advection of CO2-rich Atchafalaya River water (NCPadv), and sediment metabolism (NCPbenthic). High sediment oxygen consumption and bottom water community respiration rates were observed in the Atchafalaya River delta estuary (Roberts and Doty, 2015) and on the Louisiana continental shelf (Murrell and Lehrter, 2011; Murrell et al., 2013). These studies suggested that the total below-pycnocline respiration rates show low variability over a large geographic and temporal range in the nGOM (46.4 to 104.5 mmol O2 m−2 d−1). The negative NCP observed in the HTACW by our study ( mmol C m−2 d−1) agreed with the finding of Murrell et al. (2013) which showed shelf-scale net water column heterotrophy on the Louisiana shelf. This water column heterotrophy can be well explained by the combined results of NCPwater, NCPbenthic, and NCPadv. The same logic can be applied to explain the net heterotrophy observed in the southwestern part of the Atchafalaya plume with a well-mixed water column (negative NCP around 29.30∘ N, 93.50∘ W, Fig. 5a).
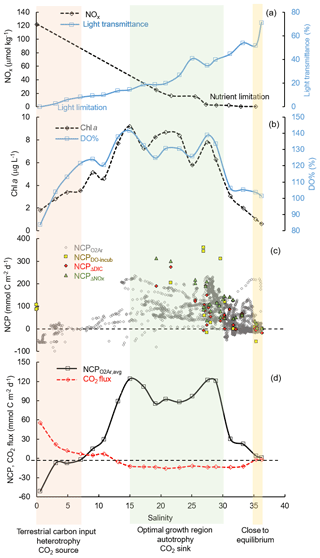
4.2 Controls on the surface NCP and CO2 flux
As the underway O2∕Ar method provided the highest-resolution NCP estimation coupled with pCO2 measurement, NCP was presented together with the CO2 variables in the following sections to investigate the variability and controls on the metabolic balance of the system. Nutrients, irradiance, and mixing were considered to be the major controlling factors of biological production in coastal waters of the nGOM (Lehrter et al., 2009; Lohrenz et al., 1999; Murrell et al., 2013; Turner and Rabalais, 2013). Here we use the results in the Mississippi plume (data averaged over increments of 2 salinity units, Fig. 7) to demonstrate the controlling mechanisms of the changes in surface NCP and CO2 flux with the increasing salinity. There is an ecological gradient along the river–ocean mixing continuum: from turbid, eutrophic freshwater to clear, oligotrophic offshore oceanic waters (Fig. 7a). The freshwater input from the Mississippi River was characterized by strong heterotrophy with high DIC and pCO2 supported by the decomposition of terrestrial organic carbon (Bianchi et al., 2010). Meanwhile, phytoplankton growth and production were limited by light availability in the high-turbidity Mississippi River channel despite the high nutrient concentration (Fig. 7a–c). The net heterotrophy of the water at the low-salinity end and the corresponding CO2 outgassing (Fig. 7d) were attributed to the terrestrial carbon input, light limitation on primary production, and short water residence time (Lehrter et al., 2009; Lohrenz et al., 1990, 1999; Roberts and Doty, 2015). While high CO2 efflux was observed at low salinities, its contribution to the overall regional CO2 flux was relatively small due to the limited spatial coverage of low-salinity regions (Huang et al., 2015).
Due to the alleviation of light limitation in conjunction with persistence of riverine nutrient concentrations, Chl a, DO % and NCP all showed an increasing trend with salinity along the flow path of the Mississippi plume (Fig. 8). A positive correlation between the mean NCP rates and Chl a concentrations (Fig. 7b, d) was observed in the Mississippi plume (r2 = 0.75, figure not shown) where light availability generally determined the onset of the biological growth and the river-borne nutrient loading set the magnitude of biological production (Figs. 7, 8). At intermediate salinities (15 to 30) in the Mississippi plume, there existed an “optimal growth region” where light and nutrient availability were both favorable for phytoplankton growth (Fig. 7) (Cloern et al., 2013; DeMaster et al., 1996; Seguro et al., 2015). High NCP (114.8±54.6 mmol C m−2 d−1) was observed in this optimal growth region corresponding to an oceanic CO2 uptake of mmol C m−2 d−1 (Fig. 7d). In high-salinity offshore water, phytoplankton growth and production were primarily limited by depleted nutrient concentration (Lehrter et al., 2009; Lohrenz et al., 1990, 1999). Because of the minor terrestrial influence and low biological production, DO and pCO2 in the offshore gulf water were close to equilibrium with the atmosphere and NCP and CO2 flux were close to zero (Fig. 7).
The spatial variability of NCP and CO2 flux in the nGOM are associated with the trajectory of the Mississippi and Atchafalaya plume as the surface biogeochemical variations are strongly affected by riverine influences. For instance, an unusually broad plume extension in the nGOM in March 2010, driven by upwelling-favorable wind and high freshwater discharge, was associated with elevated chlorophyll concentrations and stronger biological CO2 uptake (Huang et al., 2013). Modeling studies also suggest that NCP and CO2 fluxes in the nGOM are susceptible to changes in river and wind forcing (Fennel et al., 2011; Xue et al., 2016). To better study the variability of surface NCP and CO2 flux, further studies are needed to investigate how the seasonal and inter-annual variations in environmental conditions (freshwater discharge, riverine inputs of carbon and nutrients, wind forcing, coastal circulation, etc.) affect the trajectory of the river plume and the biological processes therein.
4.3 Coupling between NCP and CO2 flux
Overall, the surface water of the nGOM (93.00–89.25∘ W, 28.50–29.50∘ N) was estimated to be net autotrophic during our study period with an area-weighted mean NCP rate of 21.2 mmol C m−2 d−1 and as a CO2 sink of −6.7 mmol C m−2 d−1. When plotting the paired CO2 flux and NCP data (Fig. 10), most data collected in the lower Mississippi River channel fall into quadrant 2, suggesting net heterotrophy coupled with CO2 outgassing to the atmosphere. The Mississippi plume and Atchafalaya plume exhibited opposite patterns, with most data in these regions being in quadrant 4 (net autotrophy coupled with CO2 uptake from the atmosphere). However, the data in quadrant 1 (autotrophic water as a CO2 source observed near the Mississippi River mouth) and quadrant 3 (heterotopic water as a CO2 sink in the HTACW) suggest decoupling between NCP and CO2 flux.
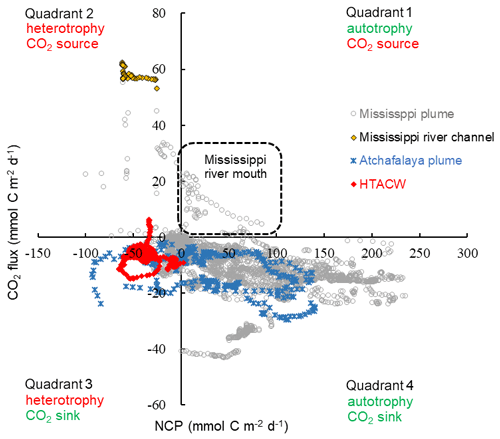
Figure 10Scatter plot of NCP and CO2 flux observed in the surface water of the nGOM. Positive NCP implies net autotrophy and negative CO2 flux implies net oceanic CO2 uptake from the atmosphere.
Here we use the box model (Sect. 2.5) to investigate the relationship between NCP and air–sea gas fluxes of O2 and CO2. We calculated the re-equilibrium time for O2 and CO2 following the occurrence of 10 d biological modification: NCP was set to 50 (net autotrophy) or −50 (net heterotrophy) mmol C m−2 d−1 from days 0 to 10, and to zero after day 11 (Fig. S5). The air–sea O2 flux rapidly reached a balance with the NCP-induced O2 changes for both the autotrophy and heterotrophy simulations with the re-equilibrium time for O2 for each estimation to be a few days (Fig. S5). Given the same environmental settings, the re-equilibrium time for CO2 was much longer (more than 1 month, Fig. S5). This is related to the relatively slow air–sea CO2 exchange rate, and, more importantly the carbonate buffering system; i.e., the gas exchange-induced changes in aquatic CO2 are buffered by a much larger carbon pool of (Zeebe and Wolf-Gladrow, 2001).
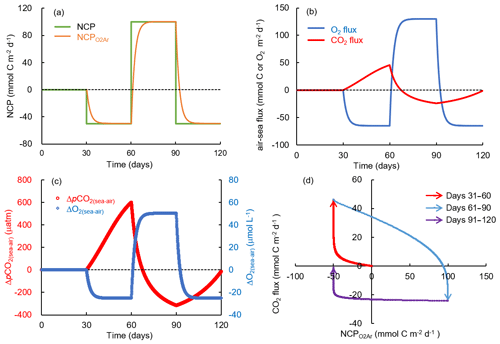
Figure 11Simulation of carbon and oxygen dynamics responding to time-dependent varying NCP rates and gas exchange using a box model. The variations of (a) NCP and exponentially weighted NCP (NCP), (b) air–sea CO2 flux and O2 flux, and (c) air–sea pCO2 difference (ΔpCO2(sea–air)) and O2 difference (ΔO2(sea–air)). (d) Scatter plot of CO2 flux and NCP. Positive NCP implies net autotrophy and negative O2 and CO2 fluxes imply gas influxes into the water. See the text for details.
NCP affects air–sea gas exchange of CO2 through its influence on pCO2 in the surface water. Net autotrophy results in a net biological uptake of CO2 from the seawater (decrease in ΔpCO2(sea–air) in Eq. 1), while net heterotrophy has the opposite effect. However, ΔpCO2(sea–air) is not only affected by in situ NCP (ΔpCO2NCP), but also by the background level of ΔpCO2, which is related to the preceding mixing and biological processes (ΔpCO2background): . Therefore, local ecosystem net autotrophy (negative ΔpCO2NCP) does not necessarily result in CO2 uptake from the atmosphere (negative ΔpCO2(sea–air)) if the NCP-induced pCO2 decrease occurs in a water with a high heterotrophic background (highly positive ΔpCO2background). Similarly, net heterotrophy does not necessarily result in a CO2 outgassing if the source water is highly autotrophic.
In the simulation with time-dependent varying NCP rates (Fig. 11), we demonstrated how the preceding biological processes and the lingering background pCO2 affect the relationship between NCP and CO2 flux. The NCP rate in this simulation was set to 0 during days 0 to 30, changed to −50 mmol C m−2 d−1 (net heterotrophy) during days 31 to 60, then to 100 mmol C m−2 d−1 (net autotrophy) during days 61 to 90, and to −50 mmol C m−2 d−1 again during days 91 to 120 (Fig. 11a). Although NCP changed instantly, the backward exponentially weighted NCP derived from the bioflux of O2 (NCP in Fig. 11a) lagged a few days behind NCP. After each change in NCP, the memory effect of the preceding NCP on DO was small as the air–sea O2 exchange quickly balanced the NCP-induced O2 production or consumption within several days (Fig. 11b, c). In contrast, the slow CO2 gas exchange and long re-equilibrium time of CO2 generated a significant memory effect of the preceding NCP on ΔpCO2(sea–air) (Fig. 11b, c). The combined result of in situ production and the lingering effect of background pCO2 thus resulted in the decoupling between NCP and CO2 flux (data in quadrant 1 and quadrant 3 in Fig. 11d). One typical example is the results during days 91 to 120 (data in quadrant 3 in Fig. 11d): the strong preceding autotrophic production during days 61 to 90 led to highly negative ΔpCO2background (−315.5 µatm on day 90, Fig. 11c), which resulted in the water acting as a CO2 sink during days 91 to 120 (Fig. 11b), although the in situ heterotrophic NCP increased pCO2 during this time period (Fig. 11c).
In summary, the decoupling between NCP and CO2 flux can be the result of competing effects of ΔpCO2background and ΔpCO2NEP. In our observations, surface waters with oversaturated pCO2 and positive NCP (data in quadrant 1 in Fig. 10) were observed directly outside of the Mississippi River mouth. This is the region where in situ autotrophic biological productivity began to increase due to alleviated light limitation, but the highly heterotrophic ΔpCO2background from the river channel resulted in the water in this region still acting as a CO2 source. Decoupling was also observed in the HTACW, where CO2 uptake occurred under heterotrophic conditions (data in quadrant 3 in Fig. 10). As discussed above, this phenomenon can be explained by in situ heterotrophy superimposed on surface water with low background pCO2 resulting from the preceding autotrophic biological production.
During a spring cruise in the northern Gulf of Mexico in April 2017, we found encouraging agreement among NCP estimates from multiple approaches despite the different temporal and spatial resolutions and uncertainties associated with each approach. Our study showed that the DO incubation approach represents the daily NCP by the local plankton community, while the O2∕Ar method reflects the metabolic state of the water relating to both biological and physical processes over longer timescales. The DO incubation method may significantly overestimate NCP rates for high-turbidity water samples due to the improved light environment in the incubation bottles. The O2∕Ar method has the advantage of being able to provide high-resolution NCP estimates matching the underway pCO2 measurement, which provides more accurate estimation of the overall metabolic condition of the surface water of the nGOM and also allows a better examination of the NCP and CO2 dynamics. The NCP and CO2 flux showed higher spatial variability on the inner and middle shelves, which was strongly influenced by the Mississippi–Atchafalaya River system. Along the river–ocean mixing gradient, NCP and CO2 flux were characterized by (1) heterotrophy and CO2 release at low salinities resulting from the decomposition of terrestrial carbon and light limitation on photosynthesis, (2) strong autotrophy and CO2 uptake at intermediate salinities of 15–30 where light and nutrient are both favorable for phytoplankton growth, and (3) close-to-zero NCP rate and CO2 flux in the offshore seawater resulting from nutrient limitation. This study also demonstrated that, due to the slow air–sea CO2 exchange and the buffering effect of the carbonate system, decoupling between NCP and CO2 flux could be observed as the competing result of in situ biological production and the lingering effect of background pCO2 of the source water.
Data of this study are available from the Biological and Chemical Oceanography Data Management Office: https://www.bco-dmo.org/project/751332 (Cai et al., 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-16-3507-2019-supplement.
ZPJ, JL, BC, ZO, NH, MKS, and JZ attended the nGOM cruise and all the authors contributed to the data collection: O2∕Ar (ZPJ, ZO), incubation experiments (JL), pCO2 (BC), DO (NH), DIC and TA (MKS, JZ, YX), nutrient (BJR), and model and remote sensing (CL). WJC designed and led the whole project. WJC is the PI who supervised the sample analysis, data analysis, and writing. ZPJ is the primary author, while all the co-authors were involved in discussion and writing by providing comments.
The authors declare that they have no conflict of interest.
We thank the captain and crew of RV Pelican for their excellent work. We are grateful for the comments and suggestions from Isabel Seguro, an anonymous reviewer, and editor Jack Middelburg, which significantly improved the quality of this paper. We thank Ariella Chelsky and Ekaterina Bulygina for collection and laboratory analyses of nutrient samples, respectively.
This research has been supported by the National Key Research and Development Program of China (grant no. 2016YFA0601404), the National Science Foundation, US (grant no. NSF-OCE 1559279 and NSF-OCE 1760660), and the National Natural Science Foundation of China (grant no. 41506090). Zong-Pei Jiang and Junxiao Zhang recognize the support by the China Scholarship Council for supporting their 1-year visit of the Cai laboratory during which the fieldwork was accomplished.
This paper was edited by Jack Middelburg and reviewed by Isabel Seguro and one anonymous referee.
Bauer, J. E., Cai, W. J., Raymond, P. A., Bianchi, T. S., Hopkinson, C. S., and Regnier, P. A. G.: The changing carbon cycle of the coastal ocean, Nature, 504, 61–70, https://doi.org/10.1038/nature12857, 2013.
Bianchi, T. S., DiMarco, S. F., Cowan, J. H., Hetland, R. D., Chapman, P., Day, J. W., and Allison, M. A.: The science of hypoxia in the Northern Gulf of Mexico: A review, Sci. Total Environ., 408, 1471–1484, https://doi.org/10.1016/j.scitotenv.2009.11.047, 2010.
Borges, A. V. and Abril, G.: Carbon dioxide and methane dynamics in estuaries, in: Treatise on Estuarine and Coastal Science, edited by: Wolanski, E. and McLusky, D., Academic Press, Waltham, 119–161, 2011.
Brewer, P. G. and Goldman, J. C.: Alkalinity changes generated by phytoplankton growth, Limnol. Oceanogr., 21, 108–117, 1976.
Cai, W. J.: Riverine inorganic carbon flux and rate of biological uptake in the Mississippi River plume, Geophys. Res. Lett., 30, 1032, https://doi.org/10.1029/2002gl016312, 2003.
Cai, W. J.: Estuarine and coastal ocean carbon paradox: CO2 sinks or sites of terrestrial carbon incineration?, Annu. Rev. Mar. Sci., 3, 123–145, https://doi.org/10.1146/annurev-marine-120709-142723, 2011.
Cai, W. J., Dai, M. H., and Wang, Y. C.: Air-sea exchange of carbon dioxide in ocean margins: A province-based synthesis, Geophys. Res. Lett., 33, L12603, https://doi.org/10.1029/2006GL026219, 2006.
Cai, W. J., Hu, X. P., Huang, W. J., Murrell, M. C., Lehrter, J. C., Lohrenz, S. E., Chou, W. C., Zhai, W. D., Hollibaugh, J. T., Wang, Y. C., Zhao, P. S., Guo, X. H., Gundersen, K., Dai, M. H., and Gong, G. C.: Acidification of subsurface coastal waters enhanced by eutrophication, Nat. Geosci., 4, 766–770, https://doi.org/10.1038/NGEO1297, 2011.
Cai, W., Rabalais, N., and Fennel, K.: Underway pCO2 from the R∕V Pelican cruise GOM_UW_1704 conducted in the Northern Gulf of Mexico in April 2017. Biological and Chemical Oceanography Data Management Office (BCO-DMO), Dataset version 2019-07-01, https://doi.org/10.1575/1912/bco-dmo.770864.1, 2019.
Cassar, N., Barnett, B. A., Bender, M. L., Kaiser, J., Hamme, R. C., and Tilbrook, B.: Continuous high-frequency dissolved O2∕Ar measurements by equilibrator inlet mass spectrometry, Anal. Chem., 81, 1855–1864, https://doi.org/10.1021/ac802300u, 2009.
Cassar, N., DiFiore, P. J., Barnett, B. A., Bender, M. L., Bowie, A. R., Tilbrook, B., Petrou, K., Westwood, K. J., Wright, S. W., and Lefevre, D.: The influence of iron and light on net community production in the Subantarctic and Polar Frontal Zones, Biogeosciences, 8, 227–237, https://doi.org/10.5194/bg-8-227-2011, 2011.
Cloern, J. E. and Jassby, A. D.: Patterns and scales of phytoplankton variability in estuarine-coastal ecosystems, Estuar. Coast., 33, 230–241, https://doi.org/10.1007/s12237-009-9195-3, 2010.
Castro-Morales, K., Cassar, N., Shoosmith, D. R., and Kaiser, J.: Biological production in the Bellingshausen Sea from oxygen-to-argon ratios and oxygen triple isotopes, Biogeosciences, 10, 2273–2291, https://doi.org/10.5194/bg-10-2273-2013, 2013.
Chen, C.-T. A. and Borges, A. V.: Reconciling opposing views on carbon cycling in the coastal ocean: Continental shelves as sinks and near-shore ecosystems as sources of atmospheric CO2, Deep-Sea Res. Pt. II, 56, 578–590, 2009.
Chen, C.-T. A. and Swaney, D. P.: Terrestrial-ocean transfers of carbon and nutrient across the coastal boundary: Editorial overview, Curr. Opin. Env. Sust., 4, 159–161, 2012.
Chen, C.-T. A., Huang, T.-H., Fu, Y.-H., Bai, Y., and He, X.: Strong sources of CO2 in upper estuaries become sinks of CO2 in large river plumes, Curr. Opin. Env. Sust., 4, 179–185, https://doi.org/10.1016/j.cosust.2012.02.003, 2012.
Cooley, S. R. and Yager, P. L.: Physical and biological contributions to the western tropical North Atlantic Ocean carbon sink formed by the Amazon River plume, J. Geophys. Res., 111, C08018, https://doi.org/10.1029/2005JC002954, 2006.
Craig, H. and Hayward, T.: Oxygen supersaturation in the ocean: Biological versus physical contributions, Science, 235, 199–202, https://doi.org/10.1126/science.235.4785.199, 1987.
Dagg, M., Benner, R., Lohrenz, S., and Lawrence, D.: Transformation of dissolved and particulate materials on continental shelves influenced by large rivers: plume processes, Cont. Shelf Res., 24, 833–858, https://doi.org/10.1016/j.csr.2004.02.003, 2004.
DeMaster, D. J., Smith, W. O., Nelson, D. M., and Aller, J. Y.: Biogeochemical processes in Amazon shelf waters: Chemical distributions and uptake rates of silicon, carbon and nitrogen, Cont. Shelf Res., 16, 617–643, https://doi.org/10.1016/0278-4343(95)00048-8, 1996.
Diaz, R. J. and Rosenberg, R.: Spreading dead zones and consequences for marine ecosystems, Science, 321, 926–929, https://doi.org/10.1126/science.1156401, 2008.
Dickson, A. G., Sabine, C. L., and Christian, J. R. (Eds.): Guide to best practices for ocean CO2 measurements, North Pacific Marine Science Organization (PICES), Sidney, British Columbia, 2007.
Eppley, R. W. and Peterson, B. J.: Particulate organic matter flux and planktonic new production in the deep ocean, Nature, 282, 677–680, https://doi.org/10.1038/282677a0, 1979.
Fennel, K., Hetland, R., Feng, Y., and DiMarco, S.: A coupled physical-biological model of the Northern Gulf of Mexico shelf: model description, validation and analysis of phytoplankton variability, Biogeosciences, 8, 1881–1899, https://doi.org/10.5194/bg-8-1881-2011, 2011.
Garcia, H. E. and Gordon, L. I.: Oxygen solubility in seawater: Better fitting equations, Limnol. Oceanogr., 37, 1307–1312, 1992.
Gattuso, J.-P., Frankignoulle, M., and Wollast, R.: Carbon and carbonate metabolism in coastal aquatic ecosystems, Annu. Rev. Ecol. Evol. S., 29, 405–434, 1998.
Geider, R. J. and La Roche, J.: Redfield revisited: variability of C∕N:P in marine microalgae and its biochemical basis, Eur. J. Phycol., 37, 1–17, https://doi.org/10.1017/S0967026201003456, 2002.
Green, R. E., Bianchi, T. S., Dagg, M. J., Walker, N. D., and Breed, G. A.: An organic carbon budget for the Mississippi River turbidity plume and plume contributions to air-sea CO2 fluxes and bottom water hypoxia, Estuar. Coast., 29, 579–597, 2006.
Guo, X., Cai, W.-J., Huang, W.-J., Wang, Y., Chen, F., Murrell, M. C., Lohrenz, S. E., Jiang, L.-Q., Dai, M., Hartmann, J., Lin, Q., and Culp, R.: Carbon dynamics and community production in the Mississippi River plume, Limnol. Oceanogr., 57, 1–17, https://doi.org/10.4319/lo.2012.57.1.0001, 2012.
Hamme, R. C. and Emerson, S. R.: The solubility of neon, nitrogen and argon in distilled water and seawater, Deep-Sea Res. Pt. I, 51, 1517–1528, https://doi.org/10.1016/j.dsr.2004.06.009, 2004.
Hodur, R. M.: The Naval Research Laboratory's coupled ocean/Atmosphere Mesoscale Prediction System (COAMPS), Mon. Weather Rev., 125, 1414–1430, 1997.
Huang, W. J., Cai, W. J., Powell, R. T., Lohrenz, S. E., Wang, Y., Jiang, L. Q., and Hopkinson, C. S.: The stoichiometry of inorganic carbon and nutrient removal in the Mississippi River plume and adjacent continental shelf, Biogeosciences, 9, 2781–2792, https://doi.org/10.5194/bg-9-2781-2012, 2012.
Huang, W. J., Cai, W. J., Castelao, R. M., Wang, Y. C., and Lohrenz, S. E.: Effects of a wind-driven cross-shelf large river plume on biological production and CO2 uptake on the Gulf of Mexico during spring, Limnol. Oceanogr., 58, 1727–1735, https://doi.org/10.4319/lo.2013.58.5.1727, 2013.
Huang, W. J., Cai, W. J., Wang, Y. C., Lohrenz, S. E., and Murrell, M. C.: The carbon dioxide system on the Mississippi River-dominated continental shelf in the northern Gulf of Mexico: 1. Distribution and air-sea CO2 flux, J. Geophys. Res., 120, 1429–1445, https://doi.org/10.1002/2014JC010498, 2015.
Jonsson, B. F., Doney, S. C., Dunne, J., and Bender, M.: Evaluation of the Southern Ocean O2∕Ar-based NCP estimates in a model framework, J. Geophys. Res., 118, 385–399, https://doi.org/10.1002/jgrg.20032, 2013.
Justić, D., Rabalais, N. N., Eugene Turner, R., and Wiseman, W. J.: Seasonal coupling between riverborne nutrients, net productivity and hypoxia, Mar. Pollut. Bull., 26, 184–189, https://doi.org/10.1016/0025-326X(93)90620-Y, 1993.
Kaiser, J., Reuer, M. K., Barnett, B., and Bender, M. L.: Marine productivity estimates from continuous O2∕Ar ratio measurements by membrane inlet mass spectrometry, Geophys. Res. Lett., 32, https://doi.org/10.1029/2005gl023459, 2005.
Laruelle, G. G., Durr, H. H., Slomp, C. P., and Borges, A. V.: Evaluation of sinks and sources of CO2 in the global coastal ocean using a spatially-explicit typology of estuaries and continental shelves, Geophys. Res. Lett., 37, L15607, https://doi.org/10.1029/2010gl043691, 2010.
Laws, E. A.: Photosynthetic quotients, new production and net community production in the open ocean, Deep-Sea Res. Pt. A, 38, 143–167, https://doi.org/10.1016/0198-0149(91)90059-O, 1991.
Lawson, C. L. and Hanson, R. J.: Solving Least Squares Problems, Prentice-Hall, chap. 23, 161 pp., 1974.
Lehrter, J. C., Ko, D. S., Murrell, M. C., Hagy, J. D., Schaeffer, B. A., Greene, R. M., Gould, R. W., and Penta, B.: Nutrient distributions, transports, and budgets on the inner margin of a river-dominated continental shelf, J. Geophys. Res., 118, 4822–4838, 2013.
Lehrter, J. C., Murrell, M. C., and Kurtz, J. C.: Interactions between freshwater input, light, and phytoplankton dynamics on the Louisiana continental shelf, Cont. Shelf Res., 29, 1861–1872, https://doi.org/10.1016/j.csr.2009.07.001, 2009.
Lohrenz, S. E., Dagg, M. J., and Whitledge, T. E.: Enhanced primary production at the plume pceanic interface of the Mississippi River, Cont. Shelf Res., 10, 639–664, https://doi.org/10.1016/0278-4343(90)90043-L, 1990.
Lohrenz, S. E., Fahnenstiel, G. L., and Redalje, D. G.: Spatial and temporal variations of photosynthetic parameters in relation to environmental-conditions in coastal waters of the northern Gulf of Mexico, Estuaries, 17, 779–795, https://doi.org/10.2307/1352747, 1994.
Lohrenz, S. E., Fahnenstiel, G. L., Redalje, D. G., Lang, G. A., Chen, X. G., and Dagg, M. J.: Variations in primary production of northern Gulf of Mexico continental shelf waters linked to nutrient inputs from the Mississippi River, Mar. Ecol. Prog. Ser., 155, 45–54, https://doi.org/10.3354/meps155045, 1997.
Lohrenz, S. E., Fahnenstiel, G. L., Redalje, D. G., Lang, G. A., Dagg, M. J., Whitledge, T. E., and Dortch, Q.: Nutrients, irradiance, and mixing as factors regulating primary production in coastal waters impacted by the Mississippi River plume, Cont. Shelf Res., 19, 1113–1141, https://doi.org/10.1016/S0278-4343(99)00012-6, 1999.
Lohrenz, S. E., Cai, W.-J., Chen, F., Chen, X., and Tuel, M.: Seasonal variability in air-sea fluxes of CO2 in a river-influenced coastal margin, J. Geophys. Res.-Ocean., 115, C10034, https://doi.org/10.1029/2009JC005608, 2010.
Lohrenz, S. E., Cai, W. J., Chakraborty, S., Gundersen, K., and Murrell, M. C.: Nutrient and carbon dynamics in a large river-dominated coastal ecosystem: the Mississippi-Atchafalaya River system, in: Biogeochemical Dynamics at Major River-Coastal Interfaces: Linkages with Global Change, edited by: Allison, M. A., Bianchi, T. S., and Cai, W.-J., Cambridge University Press, Cambridge, 448–472, 2014.
McKee, B. A., Aller, R. C., Allison, M. A., Bianchi, T. S., and Kineke, G. C.: Transport and transformation of dissolved and particulate materials on continental margins influenced by major rivers: benthic boundary layer and seabed processes, Cont. Shelf Res., 24, 899–926, https://doi.org/10.1016/j.csr.2004.02.009, 2004.
Muller-Karger, F. E., Varela, R., Thunell, R., Luerssen, R., Hu, C. M., and Walsh, J. J.: The importance of continental margins in the global carbon cycle, Geophys. Res. Lett., 32, L01602, https://doi.org/10.1029/2004gl021346, 2005.
Murrell, M. C. and Lehrter, J. C.: Sediment and Lower Water Column Oxygen Consumption in the Seasonally Hypoxic Region of the Louisiana Continental Shelf, Estuar. Coast., 34, 912–924, https://doi.org/10.1007/s12237-010-9351-9, 2011.
Murrell, M. C., Campbell, J. G., Hagy, J. D., and Caffrey, J. M.: Effects of irradiance on benthic and water column processes in a Gulf of Mexico estuary: Pensacola Bay, Florida, USA, Estuar. Coast. Shelf Sci., 81, 501–512, https://doi.org/10.1016/j.ecss.2008.12.002, 2009.
Murrell, M. C., Stanley, R. S., Lehrter, J. C., and Hagy, J. D.: Plankton community respiration, net ecosystem metabolism, and oxygen dynamics on the Louisiana continental shelf: Implications for hypoxia, Cont. Shelf Res., 52, 27–38, https://doi.org/10.1016/j.csr.2012.10.010, 2013.
Nicholson, D. P., Stanley, R. H. R., Barkan, E., Karl, D. M., Luz, B., Quay, P. D., and Doney, S. C.: Evaluating triple oxygen isotope estimates of gross primary production at the Hawaii Ocean Time-series and Bermuda Atlantic Time-series Study sites, J. Geophys. Res., 117, C05012, https://doi.org/10.1029/2010jc006856, 2012.
Ning, X. R., Vaulot, D., Liu, Z. S., and Liu, Z. L.: Standing stock and production of phytoplankton in the estuary of the Changjiang (Yangtse River) and the adjacent East China Sea, Mar. Ecol. Prog. Ser., 49, 141–150, 1988.
Obenour, D. R., Scavia, D., Rabalais, N. N., Turner, R. E., and Michalak, A. M.: Retrospective analysis of midsummer hypoxic area and volume in the Northern Gulf of Mexico, 1985–2011, Environ. Sci. Technol., 47, 9808–9815, https://doi.org/10.1021/es400983g, 2013.
Pai, S.-C., Gong, G.-C., and Liu, K.-K.: Determination of dissolved oxygen in seawater by direct spectrophotometry of total iodine, Mar. Chem., 41, 343–351, https://doi.org/10.1016/0304-4203(93)90266-Q, 1993.
Pierrot, D., Lewis, E. and Wallace, D. W. R.: MS Excel program developed for CO2 system Calculations, ORNL/CDIAC-105a, Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, US Department of Energy, Oak Ridge, TN, https://doi.org/10.3334/CDIAC/otg.CO2SYS_XLS_CDIAC105a, 2006.
Rabalais, N. N., Turner, R. E., and Wiseman, W. J.: Gulf of Mexico hypoxia, aka “The dead zone”, Annu. Rev. Ecol. S., 33, 235–263, https://doi.org/10.1146/annurev.ecolsys.33.010802.150513, 2002.
Rabalais, N. N., Cai, W. J., Carstensen, J., Conley, D. J., Fry, B., Hu, X. P., Quinones-Rivera, Z., Rosenberg, R., Slomp, C. P., Turner, R. E., Voss, M., Wissel, B., and Zhang, J.: Eutrophication-driven deoxygenation in the coastal ocean, Oceanography, 27, 172–183, 2014.
Regnier, P., Friedlingstein, P., Ciais, P., Mackenzie, F. T., Gruber, N., Janssens, I. A., Laruelle, G. G., Lauerwald, R., Luyssaert, S., Andersson, A. J., Arndt, S., Arnosti, C., Borges, A. V., Dale, A. W., Gallego-Sala, A., Godderis, Y., Goossens, N., Hartmann, J., Heinze, C., Ilyina, T., Joos, F., LaRowe, D. E., Leifeld, J., Meysman, F. J. R., Munhoven, G., Raymond, P. A., Spahni, R., Suntharalingam, P., and Thullner, M.: Anthropogenic perturbation of the carbon fluxes from land to ocean, Nat. Geosci., 6, 597–607, 2013.
Reuer, M. K., Barnett, B. A., Bender, M. L., Falkowski, P. G., and Hendricks, M. B.: New estimates of Southern Ocean biological production rates from O2∕Ar ratios and the triple isotope composition of O2, Deep-Sea Res. Pt. I, 54, 951–974, https://doi.org/10.1016/j.dsr.2007.02.007, 2007.
Roberts, B. J. and Doty, S. M.: Spatial and temporal patterns of benthic respiration and net nutrient fluxes in the Atchafalaya River Delta Estuary, Estuar. Coast., 38, 1918–1936, 2015.
Sambrotto, R. N., Savidge, G., Robinson, C., Boyd, P., Takahashi, T., Karl, D. M., Langdon, C., Chipman, D., Marra, J., and Codispoti, L.: Elevated consumption of carbon relative to nitrogen in the surface ocean, Nature, 363, 248–250, https://doi.org/10.1038/363248a0, 1993.
Sarmiento, J. L. and Gruber, N.: Ocean Biogeochemical Dynamics, Princeton University Press, Princeton, NJ, 528 pp., 2006.
Schlitzer, R.: Ocean Data View, available at: https://odv.awi.de/ (last access: 9 September 2019), 2018.
Seguro, I., García, C. M., Papaspyrou, S., Gálvez, J. A., García-Robledo, E., Navarro, G., Soria-Píriz, S., Aguilar, V., Lizano, O. G., Morales-Ramírez, A., and Corzo, A.: Seasonal changes of the microplankton community along a tropical estuary, Regional Studies in Marine Science, 2, 189–202, https://doi.org/10.1016/j.rsma.2015.10.006, 2015.
Shadwick, E. H., Tilbrook, B., Cassar, N., Trull, T. W., and Rintoul, S. R.: Summertime physical and biological controls on O2 and CO2 in the Australian Sector of the Southern Ocean, J. Mar. Syst., 147, 21–28, https://doi.org/10.1016/j.jmarsys.2013.12.008, 2015.
Sweeney, C., Gloor, E., Jacobson, A. R., Key, R. M., McKinley, G., Sarmiento, J. L., and Wanninkhof, R.: Constraining global air-sea gas exchange for CO2 with recent bomb 14C measurements, Global Biogeochem. Cy., 21, GB2015, https://doi.org/10.1029/2006gb002784, 2007.
Teeter, L., Hamme, R. C., Ianson, D., and Bianucci, L.: Accurate estimation of net community production grom O2∕Ar measurements, Global Biogeochem. Cy., 32, 1163–1181, https://doi.org/10.1029/2017GB005874, 2018.
Ternon, J. F., Oudot, C., Dessier, A., and Diverres, D.: A seasonal tropical sink for atmospheric CO2 in the Atlantic ocean: the role of the Amazon River discharge, Mar. Chem., 68, 183–201, 2000.
Turner, R. E., Rabalais, N. N., and Justic, D.: Predicting summer hypoxia in the northern Gulf of Mexico: Redux, Mar. Pollut. Bull., 64, 319–324, 2012.
Turner, R. E. and Rabalais, N. N.: Nitrogen and phosphorus phytoplankton growth limitation in the northern Gulf of Mexico, Aquat. Microb. Ecol., 68, 159–169, https://doi.org/10.3354/ame01607, 2013.
Ulfsbo, A., Cassar, N., Korhonen, M., van Heuven, S., Hoppema, M., Kattner, G., and Anderson, L. G.: Late summer net community production in the central Arctic Ocean using multiple approaches, Global Biogeochem. Cy., 28, 1129–1148, https://doi.org/10.1002/2014GB004833, 2014.
Wallace, R. B., Baumann, H., Grear, J. S., Aller, R. C., and Gobler, C. J.: Coastal ocean acidification: The other eutrophication problem, Estuar. Coast. Shelf Sci., 148, 1–13, https://doi.org/10.1016/j.ecss.2014.05.027, 2014.
Weiss, R. F.: Carbon dioxide in water and seawater: the solubility of a non-ideal gas, Mar. Chem., 2, 203–215, https://doi.org/10.1016/0304-4203(74)90015-2, 1974.
Wolf-Gladrow, D. A., Zeebe, R. E., Klaas, C., Kortzinger, A., and Dickson, A. G.: Total alkalinity: The explicit conservative expression and its application to biogeochemical processes, Mar. Chem., 106, 287–300, https://doi.org/10.1016/j.marchem.2007.01.006, 2007.
Xue, J. H., Cai, W. J., Hu, X. P., Huang, W. J., Lohrenz, S. E., and Gundersen, K.: Temporal variation and stoichiometric ratios of organic matter remineralization in bottom waters of the northern Gulf of Mexico during late spring and summer, J. Geophys. Res., 120, 8304–8326, https://doi.org/10.1002/2015JC011453, 2015.
Xue, Z., He, R. Y., Fennel, K., Cai, W. J., Lohrenz, S., Huang, W. J., Tian, H. Q., Ren, W., and Zang, Z. C.: Modeling pCO2 variability in the Gulf of Mexico, Biogeosciences, 13, 4359–4377, https://doi.org/10.5194/bg-13-4359-2016, 2016.
Yang, X. F., Xue, L., Li, Y. X., Han, P., Liu, X. Y., Zhang, L. J., and Cai, W. J.: Treated wastewater changes the export of dissolved inorganic carbon and its isotopic composition and leads to acidification in coastal oceans, Environ. Sci. Technol., 52, 5590–5599, 2018.
Zeebe, R. E. and Wolf-Gladrow, D. (Eds.): CO2 in seawater: Equilibrium, kinetics, isotopes, Elsevier, Amsterdam, 2001.
Zhang, X. Q., Hetland, R. D., Marta-Almeida, M., and DiMarco, S. F.: A numerical investigation of the Mississippi and Atchafalaya freshwater transport, filling and flushing times on the Texas-Louisiana Shelf, J. Geophys. Res., 117, C11009, https://doi.org/10.1029/2012jc008108, 2012.