the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Modeling oceanic nitrate and nitrite concentrations and isotopes using a 3-D inverse N cycle model
Taylor S. Martin
François Primeau
Karen L. Casciotti
Nitrite () is a key intermediate in the marine nitrogen (N) cycle and a substrate in nitrification, which produces nitrate (), as well as water column N loss processes denitrification and anammox. In models of the marine N cycle, is often not considered as a separate state variable, since occurs in much higher concentrations in the ocean. In oxygen deficient zones (ODZs), however, represents a substantial fraction of the bioavailable N, and modeling its production and consumption is important to understand the N cycle processes occurring there, especially those where bioavailable N is lost from or retained within the water column. Improving N cycle models by including is important in order to better quantify N cycling rates in ODZs, particularly N loss rates. Here we present the expansion of a global 3-D inverse N cycle model to include as a reactive intermediate as well as the processes that produce and consume in marine ODZs. accumulation in ODZs is accurately represented by the model involving reduction, reduction, oxidation, and anammox. We model both 14N and 15N and use a compilation of oceanographic measurements of and concentrations and isotopes to place a better constraint on the N cycle processes occurring. The model is optimized using a range of isotope effects for denitrification and oxidation, and we find that the larger (more negative) inverse isotope effects for oxidation, along with relatively high rates of , oxidation give a better simulation of and concentrations and isotopes in marine ODZs.
- Article
(3456 KB) -
Supplement
(2287 KB) - BibTeX
- EndNote
Nitrogen (N) is an important nutrient to consider when assessing biogeochemical cycling in the ocean. The N cycle is intrinsically tied to the carbon (C) cycle, whereby N can be the limiting nutrient for primary production and carbon dioxide uptake (Moore et al., 2004; Codispoti, 1989). Understanding the distribution and speciation of bioavailable N in the ocean allows us to make inferences about the effects on other nutrient cycles and potential roles that N may play in a regime of climate change (Gruber, 2008).
There are several chemical species in which N can be found in the ocean. The largest pool of bioavailable N is nitrate (), a dissolved inorganic species, which can be taken up by microbes for use in assimilatory or dissimilatory processes. Another dissolved inorganic species, nitrite (), accumulates in much lower concentrations but is a key intermediate in many N cycling processes. Models of the marine N cycle often include and together as a single dissolved inorganic N (DIN) pool, or exclude entirely (DeVries et al., 2013; Deutsch et al., 2007; Brandes and Devol, 2002). However, does accumulate significantly in oxygen deficient zones (ODZs) in features known as secondary maxima, and it is an intermediate or substrate in many important N cycle processes occurring there.
ODZs are hotspots for marine N loss (Codispoti et al., 2001; Deutsch et al., 2007), which is driven by processes that result in conversion of bioavailable DIN to dinitrogen gas (N2). The two main water column N loss processes, denitrification and anammox, use as a substrate. Denitrification involves the stepwise reduction of to and then to gaseous nitric oxide (NO), nitrous oxide (N2O), and N2. Anammox consists of the anaerobic oxidation of ammonium () to N2 using as the electron acceptor. is also oxidized to during anammox, representing an alternative fate for in ODZs. Indeed, oxidation appears to be prevalent in ODZs, with more oxidation occurring than can be explained by anammox alone (Gaye et al., 2013; Peters et al., 2016, 2018b; Babbin et al., 2017; Buchwald et al., 2015; Casciotti et al., 2013; Martin and Casciotti, 2017). oxidation results in the regeneration of that would otherwise be converted to N2 and lost from the system. The close coupling between reduction to and oxidation back to , represents a control valve on the marine N budget (Penn et al., 2016; Bristow et al., 2016). Where oxidation can outcompete reduction via denitrification and anammox, bioavailable N is retained. Water column N losses may occur primarily where oxidation rates are limited by oxygen availability. Thus, understanding the dynamics in ODZ waters is critical to assess the N loss occurring there.
The observed and concentrations alone do not allow us to fully characterize the N cycling processes occurring in a given region. Stable isotope measurements of and provide additional insight and constraints on marine N cycle processes. There are two stable isotopes of N: 14N and 15N. The isotopic ratios for a given N species, usually expressed in delta notation as δ15N (‰) = , are an integrated measure of the processes that have produced and consumed that N species. Each process imparts a unique isotope effect (ε (‰) = , where 14k and 15k are the first-order rate constants for the 14N and 15N containing molecules, respectively) that impacts the isotopic composition of the substrate and the product (Mariotti et al., 1981). In particular, cycling processes have distinct isotope effects, where reduction occurs with normal isotopic fractionation (Bryan et al., 1983; Martin and Casciotti, 2016; Brunner et al., 2013) and oxidation occurs with an unusual inverse kinetic isotope effect (Casciotti, 2009; Buchwald and Casciotti, 2010; Brunner et al., 2013). Thus, the isotopes of are sensitive to the relative importance of oxidation and reduction in consumption (Casciotti, 2009; Casciotti et al., 2013).
Models of the marine N cycle have employed isotopes and isotope effects in conjunction with N concentrations to elucidate N cycle processes (Brandes and Devol, 2002; Sigman et al., 2009; Somes et al., 2010; DeVries et al., 2013; Casciotti et al., 2013; Buchwald et al., 2015; Peters et al., 2016). A model can either assume a set of processes and infer the underlying isotope effects, or assume isotope effects and infer a set of processes. The latter isotope models are highly dependent on the chosen isotope effects used for given processes. Although there are estimates of isotope effects for processes based on both environmental measurements and laboratory studies, there is not always agreement between them. For example, laboratory cultures of oxidizers indicate an N isotope effect of to −20 ‰ (Casciotti, 2009; Buchwald and Casciotti, 2010), while measured concentrations and isotopes of and in ODZs indicate that isotope effects closer to −30 ‰ are needed to explain the observations (Buchwald et al., 2015; Casciotti et al., 2013; Peters et al., 2016).
Here we present an expansion of an existing global ocean 3-D inverse isotope-resolving N cycling model (DeVries et al., 2013) to investigate the isotopic constraints on N cycling in ODZs and the impact of these regions on global ocean N isotope patterns. An important step was to include and its isotopes as tracers. The addition of allows us to include additional internal N cycling processes, as well as a more nuanced and realistic version of the processes occurring in ODZs. We used a database of and observations in order to assess the performance of the model as well as optimize the model N cycle parameters for which we do not have good prior estimates. In the model we employ a variety of isotope effect estimates for three important ODZ processes – reduction, reduction, and oxidation – to discern what isotope effects result in the best fit to the observations.
2.1 Inverse N cycle model overview
The model used here is a steady-state inverse model that solves for the concentration and δ15N of , , particulate organic N (PON), and dissolved organic N (DON) using a set of linear equations. Because the model assumes that the system is in steady state, it is not able to capture time-dependent properties of the system such as seasonality and anthropogenic change. However, on interannual timescales the N cycle is thought to be approximately in balance (Gruber, 2004; Bianchi et al., 2012). The residence time of N in the ocean, which is thought to be on the order of 2000–3000 years (Gruber, 2008), is sufficiently long to preclude any detectable changes in the global N inventory to date on timescales commensurate with the global overturning circulation. An important advantage of the steady-state assumption for our linear model is that it is possible to find solutions by direct matrix inversion without the need for a spin-up period as required by forward models. The solution to the system provides 14N and 15N concentrations of the N species of interest at every grid point in the model system. Working with a linear system imposes some restrictions on how complicated the rate equations can be, but there are improvements in model performance and ease of use, allowing us to test hypotheses about the processes that govern the marine N cycle and budget, particularly those occurring in and around oceanic ODZs. We aimed to produce a realistic N cycle model that represented ODZ processes accurately while limiting the number of free parameters. The description below outlines the dependencies and simplifications employed in this version of the model.
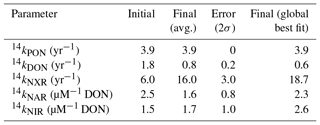
The model's uncertain biological parameters were determined through an optimization process that minimizes the difference between the modeled and observed and concentration and isotope data. Computational time limits the number of parameters that we were able to optimize. We therefore focused our investigation on parameters that are poorly constrained by literature values and to which the model solution is most sensitive. In order to determine the parameters for optimization, a sensitivity analysis was performed on each parameter, varying them individually by ±10 % and computing the change in the modeled 14N and 15N. Those parameters that resulted in modeled 14N and 15N variability of >5 % were chosen for optimization in the model. The sensitivity analysis and the optimal values of the parameters contribute to an improved understanding of the cycling of N in the ocean in general and in the ODZs in particular. The optimization process is discussed in further detail in Sect. 2.6.
The sensitivity analysis revealed that the modeled distribution of 15N was very sensitive to chosen isotope effects, those parameters that control the relative rates of 15N and 14N in chemical and biological processes. There are literature estimates for each of the isotope effects of interest in this work, although there is often a discrepancy between isotope effects estimated in laboratory studies and those expressed in oceanographic measurements (Kritee et al., 2012; Casciotti et al., 2013; Bourbonnais et al., 2015; Martin and Casciotti, 2017; Fuchsman et al., 2017; Marconi et al., 2017; Peters et al., 2018b). Rather than optimizing the isotope effect values, we have chosen to use multiple cases with different combinations of previously estimated isotope effects in order to assess which values best fit the observations.
In addition to the optimized parameters and isotope effects, there were some nonsensitive parameters that were fixed prior to the optimization and whose values were chosen using literature estimates (Table 1). Some N cycle processes are also dependent on prescribed input fields that are not explicitly modeled, such as temperature, phosphate, oxygen, and net primary production. These external input fields will be discussed in detail in the relevant sections for each N cycle process.
2.2 Model grid and transport
The model uses a uniform 2∘ × 2∘ grid with 24 depth levels. The thickness of each model layer increases with depth, from 36 m at the top of the water column to 633 m near the bottom. Bottom topography was determined using 2 min gridded bathymetry (ETOPO2v2) that was then interpolated to the model grid. Our linear N cycle model relies on the transport of dissolved N species (, , and DON) in the ocean. For this we use the annual averaged circulation as captured by a tracer transport operator that governs the rate of transport of dissolved species (, , and DON) between boxes. The original version of the tracer data-assimilation procedure used to generate the transport operator for dissolved species (Tf) is described by DeVries and Primeau (2011), and the higher resolution version used here is described by DeVries et al. (2013).
2.3 N cycle
In the N cycling portion of the model, we track four different N species (Fig. 1). There are two organic N (ON) pools: dissolved (DON) and particulate (PON). There are also two dissolved inorganic N (DIN) pools: and . We did not explicitly model ammonium () because it typically occurs in low concentrations throughout the ocean, and scarcity of data (especially δ15N data) would make model validation difficult. Although has been observed to accumulate to micromolar concentrations in some ODZs (Bristow et al., 2016; Hu et al., 2016), this occurs largely in shallow, coastal shelf regions that are not resolved by the model.
Because we used the concentrations of both 14N and 15N of each N species to constrain the rate parameters, two sets of governing equations were employed: one that depends on 14N and another that depends on 15N. Generally, the rate for 15N processes was dependent on the rate of 14N processes and an isotopic fractionation factor () that is specific to each process and substrate. By solving for steady-state solutions to both 14N and 15N concentrations, we were able to model global distributions of [], [], and their corresponding δ15N values.
2.3.1 N cycle parameterization
We first describe the 14N equations and the general format of the N cycle in the model. Each equation is then broken down into its component parts for further explanation of the biological processes and their parameterization. The 15N equations and isotope implementation will be discussed in a later section.
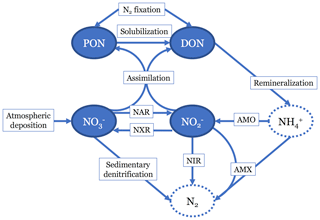
Figure 1Diagram showing the nitrogen (N) cycle processes represented in the model. Two organic N pools are modeled: particulate organic N (PON) and dissolved organic N (DON). Two inorganic N pools are modeled: nitrate () and nitrite (). N source processes are nitrogen (N2) fixation and atmospheric deposition. N sink processes are sedimentary denitrification, reduction (NIR), and anammox (AMX). Internal cycling processes that transform N from one species to another are solubilization, remineralization, assimilation, reduction (NAR), ammonia oxidation (AMO), and oxidation (NXR). Neither ammonia (NH3) nor ammonium () are tracked in this model, since they are assumed to not accumulate. N2 is also not explicitly accounted for in the model.
The governing equations for the 14N-containing DIN ( and ) and organic N (DON and PON) state variables can be written as follows:
The model is designed to represent a steady state, thus the term is 0. The J terms represent the source and sink processes for each state variable, expressed in units of mmol m−3 yr−1 and will be described in more detail below. Briefly, is the spatially variable deposition of from the atmosphere to the sea surface. In the DIN model equations, and represent the assimilation of and , respectively, by phytoplankton in the upper two box levels. This assimilated produces DON and PON, with proportions set by a spatially variable term, σ. Assimilation in the DON and PON equations is represented by and is dependent on 2013 World Ocean Atlas (WOA) [] interpolated to the model grid. N2 fixation () is split between DON and PON with the same σ term. reduction (), reduction (), oxidation (), and anammox () act on the and pools. represents the removal of via benthic denitrification. represents the dissolution of PON into DON. represents the degradation of DON, which feeds into ammonia oxidation () and as described below.
Through the use of these J terms, the governing equations are all linear with respect to the state variables. However, in order to introduce dependence of rates on the concentrations of multiple state variables, for example allowing heterotrophic reduction to be dependent on organic N as well as , we run the organic N equations and the DIN equations seperately. When [DON] is found in the [DIN] governing equations, that [DON] value has already been determined for each grid box from the organic N model. When [] is found in the DON governing equations, it is drawn from 2013 World Ocean Atlas annual data interpolated to the model grid.
2.3.2 N source processes
Atmospheric deposition and N2 fixation are the two largest sources of N to the ocean (Gruber and Galloway, 2008) and the only sources of new bioavailable N in the model. We do not consider the third largest source of N, riverine fluxes, in the model due to a lack of coastal resolution and the expectation that much of the river-derived N is denitrified in the shelf sediments (Nixon et al., 1996; Seitzinger and Giblin, 1996). Representing these processes may be possible in a future version of the model, but is beyond the scope of the current model, given its coarse resolution near the coasts.
Atmospheric deposition
N deposition is assumed to only occur in the top box of the model. We assume that most of the N deposited is as , and that the other species would be rapidly oxidized to in the oxic surface waters.
To calculate , the atmospheric deposition rate of 14N, we use modeled total inorganic N deposition for 1993, Sdep (Galloway et al., 2004; Dentener et al., 2006; data available online at https://daac.ornl.gov/CLIMATE/guides/global_N_deposition_maps.html, last access: November 2017), which was interpolated to our model grid. This term, Sdep, is then multiplied by a prescribed fractional abundance of 14N in the deposited N (), which is calculated from the isotopic composition of deposited N (δ15Ndep, −4 ‰; Eq. 6), to yield the deposition of 14N to the sea surface in each box (). To calculate from δ15Ndep, we first calculate using , a standard with a value of 0.003676 (Eq. 6; Mariotti, 1983).
Then, using the approximation that 15N∕14N = , we calculate as (). The units of Sdep are given in mg N m−2 yr−1, which we convert to mmol m−3 yr−1 by dividing by the depth of the surface box. This source term of N to the model is spatially variable but independent of the modeled N terms.
N2 fixation
N2 fixation is the other source of new N to the model, and is assumed to only occur in the top box of the model. It is parameterized similarly to N2 fixation in the model of DeVries et al. (2013), with partial inhibition by (Holl and Montoya, 2005) and dependence on iron (Fe) and phosphate () availability (Monteiro et al., 2011).
F0 is the maximum rate of N2 fixation (1.5 mmol m−3 yr−1; Table 1) and is calculated from the estimated areal rate of N2 fixation in the western tropical Atlantic (Capone et al., 2005) divided by the depth of the top model box. NO3,obs is the 2013 World Ocean Atlas annually averaged surface interpolated to the model grid (Garcia et al., 2013b). The parameter λ is an inhibition constant for N2 fixation in the presence of (Table 1).
The temperature (T) terms scale the rate of N2 fixation based on the observed temperature (Tobs), maximum observed sea surface temperature (Tmax), and the minimum preferred growth temperature for Trichodesmium (T0; Capone et al., 2005). The temperature data were taken from 2013 World Ocean Atlas annually averaged temperature interpolated to the model grid (Locarnini et al., 2013). We recognize that this will likely provide a conservative estimate of N2 fixation, given the growing recognition of N2 fixation outside of the tropical and subtropical ocean by organisms other than Trichodesmium (Shiozaki et al., 2017; Harding et al., 2018; Landolfi et al., 2018).
Fe is the modeled deposition of soluble Fe interpolated to the model grid (mmol Fe m−2 yr−1; Chien et al., 2016) divided by the depth of the top model grid box to give units of mmol Fe m−3 yr−1. Fe and are assumed to limit N2 fixation at low concentrations via Michaelis–Menten kinetics. KFe and KP are their respective half-saturation constants. Additionally, there is a term that allows us to set the isotopic ratio of newly fixed N, , which is the fractional abundance of 14N in newly fixed N and is calculated as in Eq. (6) from δ15Nfix (−1 ‰; Table 1). All of the N2 fixation parameters are fixed rather than optimized (Table 1). Due to the use of non-optimized parameters and an input field rather than modeled , N2 fixation serves as an independent check that our modeled N cycle produces reasonable N concentrations and overall N loss rates. However, N2 fixation is not explicitly modeled here and is instead taken as a fixed, though spatially variable, input field (Fig. S1 in the Supplement). The global rate of N2 fixation produced by this parameterization is 131 Tg N yr−1, which is in line with several current estimates (Table S1 in the Supplement).
In the model, N2 fixation and assimilation (Sect. 2.3.3) are assumed to be the two processes that create exportable organic N. A fraction, σ, of this organic N is partitioned into DON rather than PON (Eqs. 3–4). In order to create spatial variability in this constant, we assumed that 1−σ, the fraction of assimilated N partitioned to PON, is equal to the particle export (Pe) ratio. This Pe ratio is the ratio of particle export to primary production, and is equivalent to the fraction of organic N that is exported from the euphotic zone as particulate matter rather than recycled or solubilized into DON. The Pe ratio is calculated for each model grid square from the mixed layer temperature (Tml) and net primary production (NPP) as described by Dunne et al. (2005):
The constant Φ has a value of −0.0101 ∘C−1 as determined by Dunne et al. (2005). Net primary production estimates (in units of mmol carbon m−2 yr−1) were taken from a satellite-derived productivity model (Westberry et al., 2008), annually averaged, and interpolated onto the model grid. Tml is calculated from the 2013 World Ocean Atlas annual average (Locarnini et al., 2013), which has been interpolated to the model grid. The temperature of the top two model boxes were averaged to give Tml. As temperature increases, the Pe ratio decreases and less PON is exported, resulting in more DON recycling in the surface with several possible explanatory mechanisms discussed in greater detail by Dunne et al. (2005). As net primary production increases, the Pe ratio increases and relatively more PON is exported; net primary production explains 74 % of the observed variance in particle export (Dunne et al., 2005).
2.3.3 Internal N cycling processes
Assimilation of nitrate and nitrite
Assimilation accounts for the uptake of DIN and its incorporation into organic matter in the shallowest two layers of the global model. Since assimilation affects both the organic and inorganic N pools, we must account for it in both sets of model runs. We will first address assimilation in the organic N model (Eqs. 9 and 10).
Since the organic N model is run first and the assimilation rates are dependent on DIN concentrations, assumptions must be made about the DIN field in order to account for assimilation prior to the DIN model runs. Here we used observed [] from the 2013 World Ocean Atlas annual product interpolated to the model grid []obs (Garcia et al., 2013b) to calculate the assimilation rates for DON and PON production (). For this assumption to be valid, our modeled surface [] must be close to the observed values, which we will test in Sect. 3.1. The rate constant for assimilation, 14kassim, varies spatially and is determined using observations of surface [] and satellite-derived net primary production (NPP; Westberry et al., 2008). The rate constant is converted to N units using the ratio of carbon (C) to N in organic matter (rC:N), which we assume to be 106:16 (Redfield et al., 1963). The value of the rate constant is only nonzero in the top two boxes of the model, where we assume primary production to be occurring. The same rate constant is used in both the organic N and DIN assimilation equations. We also assume from the perspective of organic N that only is being assimilated, since is present at relatively low concentrations in the surface ocean, and it may be characterized as recycled production. Assimilated N is partitioned between PON and DON using the Pe ratio as previously described and shown in Eqs. (3) and (4).
The setup for assimilation in the DIN model (Eqs. 11 and 12) is similar, but can use modeled [] and [] rather than the World Ocean Atlas values. In order to appropriately reflect surface and concentrations, both and are assimilated. 14kassim is calculated as described above and is assumed to be the same for both and . We justify using only [] to parameterize 14kassim because generally makes up the bulk of DIN available for assimilation at the surface, but this assumption will be discussed in more detail below.
Solubilization
Solubilization is the transformation of PON to DON, and is dependent only on [PON] and a solubilization rate constant (14ksol), which is optimized (Table 2).
The solubilization of PON, together with the particle transport operator (Tp), produces a particle flux attenuation curve similar to a Martin curve with exponent (Table 1; Martin et al., 1987). While in the real world, the length scale for particle flux attenuation is somewhat longer in ODZs compared to oxygenated portions of the water column, and also varies regionally (Berelson, 2002; Buesseler et al., 2008; Buesseler and Boyd, 2009), our model uses a spatially invariant 14ksol. A spatially variable 14ksol that accounts for lower apparent values in ODZs is a refinement that could be introduced in future model versions.
Remineralization
Remineralization, or ammonification, is the release of DON into the DIN pool. This is parameterized using the concentration of DON and a remineralization rate constant (14kremin), which is optimized (Table 2).
The removal of this remineralized DON, since it does not accumulate as , is either through ammonia oxidation (AMO) or anammox (AMX), depending on [O2] as described below and in Sect. 2.3.4. We use the same remineralization rate constant regardless of the utilized electron acceptor (e.g., O2, ). Since particle flux attenuation is observed to be somewhat weaker in ODZs compared with oxygenated water (Van Mooy et al., 2002), this may slightly overestimate the rates of heterotrophic remineralization occurring in ODZs.
Ammonia oxidation (AMO)
AMO uses ammonia (NH3) as a substrate. Since we do not include NH3 or in the model system, we treat remineralized DON as the substrate for AMO. In order to maintain consistency between the organic N and DIN model runs, remineralized DON is routed either to AMO or AMX (lost from the system) based on the O2 dependencies of AMO and AMX. Rather than using a strict O2 cutoff for AMO, it is limited by O2 using Michaelis–Menten kinetics. The half-saturation constant for O2, (Table 1), sets the O2 concentration at which AMO reaches half of its maximal value.
Recent studies have shown that AMO and oxidation (NXR), both O2-requiring processes, have very low O2 half saturation constants and can occur down to nanomolar levels of [O2] (Peng et al., 2016; Bristow et al., 2016). In contrast, O2-inhibited processes such as AMX are only allowed to occur at O2 concentrations below a given threshold. The handling of O2 thresholds for anaerobic processes is discussed in more detail below (Sect. 2.3.4), though we describe it briefly here due to the interplay between AMO and AMX in the model. Briefly, the O2 dependence of AMX is represented by the parameter ηAMX, which has a value between 0 and 1 for a given grid box depending on the average number of months in a year its 2013 World Ocean Atlas [O2] falls below the [O2] threshold for anammox (, Table 1). If, for example, the [O2] in a given grid box is always above the threshold for AMX, ηAMX=0 and all of the remineralized DON (represented by ) will be oxidized via AMO. If [O2] is less than , ηAMX will be nonzero and a smaller fraction of the remineralized DON will be oxidized via AMO. The fraction ultimately oxidized by AMO is thus determined by the Michaelis–Menten parameterization of AMO, as well as the O2 threshold for anammox.
Nitrite oxidation
The rates of oxidation (NXR) are dependent on the availability of as well as O2. Similar to AMO, we parameterize O2 dependence using Michaelis–Menten kinetics and a fixed half-saturation constant for O2 (, Table 1). was taken to be 0.8 µM O2, based on kinetics experiments performed with natural populations of oxidizing bacteria (Bristow et al., 2016). Finally, we employ an optimized rate constant (14kNXR, Table 2) to fit the available data.
2.3.4 N sink processes
Nitrate and nitrite reduction
reduction (NAR) and reduction (NIR) are two processes within the stepwise reductive pathway of canonical denitrification. The end result of denitrification is the conversion of DIN to N2 gas, rendering it bioavailable to only a restricted set of marine organisms. Although there are intermediate gaseous products between and N2, we treat NIR as the rate-limiting step in the denitrification pathway, where DIN is removed from the system.
For both NAR and NIR, we introduce a dependency on two state variables, their respective N substrates, and organic matter availability. Where NAR and NIR occur heterotrophically, they consume organic matter in addition to their main N substrates or electron receptors. When NAR occurs chemoautotrophically, it would be dependent primarily on the presence of and an electron donor, such as hydrogen sulfide (Lavik et al., 2009). Since we do not model the production of reduced sulfur species in our model, our estimates of denitrification would not explicitly include the effects of this process. However, chemolithotrophic denitrification could be tacitly accounted for in the optimization process, since the rate constants that control the rates of NAR and NIR are optimized in order to best fit the observations, and the isotope effect for chemolithotrophic denitrification is thought to be similar to that of heterotrophic denitrification (Frey et al., 2014).
In order to maintain levels of heterotrophic NAR and NIR that are dependent on both the available or and the available organic matter in a linear model, it was necessary to run organic N and DIN equations separately, since it is not possible to include dependencies on two state variables (e.g., DON and ) in the linear system. Both NAR and NIR are dependent on the remineralization rate () that is calculated in the organic N model run. In model boxes where NAR and NIR are occurring, some of the remineralization is carried out with electron acceptors other than O2. As mentioned above, we assume that does not depend on the choice of electron acceptor.
The rate coefficients for NAR (14kNAR) and NIR (14kNIR) are optimized rather than fixed (Table 2). Further, the dependence of and on means that kNAR and kNIR are not first-order rate constants and have different units than kPON, kDON, and kNXR (Table 2).
The inhibition of NAR and NIR by O2, like AMX, is parameterized by a parameter η, which inhibits these processes when [O2] is above their maximum threshold. Originally, we treated this term as a binary operator that would be set to 0 if the empirically corrected 2013 World Ocean Atlas annually averaged [O2] was above the threshold for the process and 1 if [O2] was below the threshold. On further refinement, we wanted to account for the possibility of seasonal shifts in [O2] in ODZs. Thus, for each month, we assigned a value of 0 or 1 to each model grid box. These values were then averaged over the 12 months of the year to give a sliding value of η between 0 and 1 for each grid box. The O2 thresholds used to calculate ηNAR and ηNIR were fixed (7 and 5 µM, respectively; Table 1). Since we do not explicitly model O2, [O2] was predetermined using the 2013 World Ocean Atlas monthly O2 climatology (Garcia et al., 2013a) interpolated to the model grid. We also applied an empirical correction that improves the fit of World Ocean Atlas [O2] data to observed suboxic measurements (Bianchi et al., 2012).
Anammox
Anammox (AMX) catalyzes the production of N2 from and . Since we do not use as a variable in our N cycling equations, we substituted remineralized DON () as a proxy for availability. As described above in Sect. 2.3.3, remineralized DON is routed through either AMO or AMX depending on [O2] and the O2 dependencies of AMO and AMX.
The O2 threshold used to calculate ηAMX from monthly O2 climatology is fixed (10 µM; Table 1). In order to maintain mass balance on remineralized DON, we do not include dependence on [] in Eq. (19), although removes (Eq. 2). This parameterization inherently assumes that AMX is limited primarily by [] supply and not [NO2], which may not always be correct (Bristow et al., 2016). Anammox also produces 0.3 moles of via associated NXR for every 1 mole of N2 gas produced (Strous et al., 1999). For this reason, anammox appears in the state equation for (Eq. 1).
Sedimentary denitrification
Sedimentary (or benthic) denitrification () is an important loss term for N in the marine environment, and in order to encapsulate it within the model grid we assume that it is occurring within the bottom depth box for any particular model water column. The parameterization for sedimentary denitrification is based on a transfer function described by Bohlen et al. (2012). The original transfer function was dependent on bottom water [O2], bottom water [], and the rain rate of particulate organic carbon (RRPOC). Here, RRPOC was calculated via a Martin curve (Martin et al., 1987) using the Pe ratio, net primary production (NPP), depth (z), euphotic zone depth (zeu), and a Martin curve exponent (b):
Net primary production is derived from the productivity modeling of Westberry et al. (2008) as described in Sect. 2.3.2. The Pe ratio is calculated as previously described in Sect. 2.3.2. The depth for any given model box is assumed to be the depth at the bottom of the box. The euphotic zone depth is the bottom depth of the second box (73 m), since all production is assumed to be occurring in the top two boxes. As described above, the Martin curve exponent, b, is a fixed value in our model (; Table 1), though this may result in underestimation of the particulate matter reaching the seafloor below ODZs (Van Mooy et al., 2002).
The transfer function for sedimentary denitrification was originally described using a nonlinear dependence of the rate on . In order for sedimentary denitrification to be properly implemented in our linear model, we broke the original nonlinear relationship into three roughly linear segments to create a piecewise relationship between and sedimentary denitrification rate (Fig. S2). We obtained three linear relationships between and sedimentary denitrification rate, each applicable across a given range of values. Due to the nature of our linear model, we needed to express the interval cutoff points that define the transition between the piecewise relationship segments in terms of O2 rather than . Therefore, a linear relationship between O2 and was determined using the 2013 World Ocean Atlas annually averaged data (Garcia et al., 2013a, b; Fig. S3). The cutoff points were determined to be 75 and 175 µM O2. The linear relationships were then rearranged in order to estimate sedimentary denitrification rate as a function of RRPOC, [O2], and []. These equations were then further broken down into a component that is dependent on [] and a component that is dependent on [O2] (see Supplement).
An additional term is introduced that reduces the sedimentary denitrification rate by 27 % if the depth of the bottom model box is less than 1000 m. This term represents the potential for efflux of into the water column from shallow, organic rich shelf sediments (Bohlen et al., 2012). This decreases overall sedimentary denitrification by approximately 6 Tg N yr−1. This transfer function also assumes that all of the efflux is immediately oxidized to and does not alter its isotopic composition in bottom water. This is a conservative estimate of the effects of benthic N loss on water column isotopes, as several studies suggest that benthic N processes may contribute to water column nitrate 15N-enrichment (Lehmann et al., 2007; Granger et al., 2011; Somes and Oschlies, 2015; Brown et al., 2015). However, our current model parameterization does not require enhanced fractionation during benthic N loss to fit deep ocean . Additionally, our spatial resolution does not well represent regions where this effect might be significant on bottom water , such as the shallow shelves.
2.4 N isotope implementation
In our model, we are interested in using the isotopic composition of and to constrain the rates of N cycling and loss from the global ocean. As DON and PON are ultimate substrates for and production, it is essential to track the 15N in the organic N pools as well. The matrix setup for 15N is similar to that for the 14N species, but the rates were changed as follows:
is the rate of each relevant 14N process as described above, and is the rate of each 15N process. The αprocess is the fractionation factor for a given process, which is given by the ratio between the rate constants for 14N and 15N (). A fractionation factor greater than 1 indicates a normal isotope effect and a fractionation factor less than 1 indicates an inverse isotope effect. Several of these fractionation factors are well known, but others are more poorly constrained, especially when values are calculated from in situ concentration and isotope ratio measurements (Hu et al., 2016; Casciotti et al., 2013; Ryabenko et al., 2012). For this reason, we ran several model cases with different fractionation factors for NAR, NIR, and NXR during the optimization process (Sect. 2.6, Table 3). The other fractionation factors were fixed (Table 1). In order to produce the 15N concentrations of N species from our observations to constrain the model, we calculated 15N∕14N from measured δ15N and multiplied by the measured concentration of each modeled N species, assuming that .
This simple 15N implementation was used with fixed fractionation factors for remineralization (αremin=1), solubilization (αsol=1), assimilation (αassim=1.004), sedimentary denitrification (αsed=1), and AMO (αAMO=1) (Table 1). Isotope effects for NAR (εNAR), NIR (εNIR), and NXR (εNXR) were varied in different combinations during model optimization (Table 3). Distinct isotopic parameterizations were also required for atmospheric deposition, N2 fixation, and anammox, as described below.
Atmospheric deposition
For atmospheric deposition of N, we prescribe fixed δ15N value of −4 ‰ (Table 1), which can be related to the fractional abundance of 14N (), previously described in Sect. 2.3.2, as well as the fractional abundance of 15N () in deposited N. We multiply by Sdep, the estimated rate of total N deposition to obtain .
Nitrogen fixation
Similar to atmospheric deposition, newly fixed N has a δ15N value (−1 ‰; Table 1). In Sect. 2.3.2 we described , the fractional abundance of 14N in newly fixed N. Here we multiply the fractional abundance of 15N, , by the other terms in the N2 fixation equation (Eq. 6) to obtain the rate of 15N fixation.
Anammox
Anammox is the most complicated process to parameterize isotopically because it has three different N isotope effects associated with it. There is an isotope effect on both substrates that are converted to N2 ( and ), as well as for the associated oxidation to . We assume that the fractionation factor for ammonium oxidation via AMX () is 1, setting it to match the fractionation factor for AMO (αAMO; Table 1), both with no expressed fractionation since does not accumulate in the model. Since all remineralized DON must be routed either through AMO or AMX, this simplifies the mass balance and ensures that all remineralized 14N and 15N is accounted for. is removed with the isotope effects of reduction (αAMX,NIR) and oxidation (αAMX,NXR) in the expected 1:0.3 proportion (Brunner et al., 2013).
2.5 Model inversion
Once our N cycle equations were set up as described above, we input them into MATLAB in block matrix form. The equations were of the general form Ax=b. All model ocean boxes (200 160 in total) are accounted for in the matrices. Matrix A (400 320 × 400 320) contained the rate constants and other parameters that are multiplied by the vector of state variables, x (400 320 × 1). Vector x contained the state variables (i.e., [] and [] or [DON] and [PON]) to be solved for by the linear solver. Vector b (400 320 × 1) contained the rates that were independent of the state variables, such as N2 fixation and N deposition. Let us consider, as an example, the DIN model setup. The top left corner of matrix A would contain rate constants for processes that produce and consume that are also dependent on []. The top right corner of matrix A would contain rate constants for processes that produce and consume but are dependent on []. The bottom left corner of matrix A would contain rate constants for processes that produce and consume but are dependent on []. The bottom right corner of matrix A would contain rate constants that produce and consume and are also dependent on []. The top half of vector x would be [] for each model box, and the bottom half of vector x would be [] for each model box. The top half of vector b would be independent processes that produce or consume [], and the bottom half of vector b would be independent processes that produce or consume [].
In MATLAB, we used METIS ordering, which is part of the SuiteSparse (http://faculty.cse.tamu.edu/davis/suitesparse.html, last access: December 2017) to order our large, sparse matrix A. We then used the built-in function “umfpack” with METIS to factorize matrix A. The built-in matrix solver “mldivide” was then used with the factorized components of matrix A and matrix b to solve for x.
2.6 Parameter optimization
There are many parameters in the model that control the rates of the different N cycle processes (Tables 1–3). Some of these parameters are well constrained by literature values (Table 1). Others, such as the rate constants, were objects of our investigation and were optimized against available observations (Table 2). For our optimization, we compared model output using different parameter values to a database of and concentrations and isotopes. The database was originally compiled by Rafter et al. (2019) and has been expanded to include some additional unpublished data (Table S2). All of the database observations were binned and interpolated to the model grid. If multiple observations occurred within the same model grid box, the values were averaged and a standard deviation was calculated. The database was divided randomly into a training set, used for optimization, and a test set, used to assess model performance. The same number of grid points with observations was used in the training and test sets.
The optimization procedure used the MATLAB function “fminunc” to obtain values for the nonfixed parameters that minimized a cost function (Eq. 22). In each iteration of the optimization, the model system was solved by running the 14N-organic N model, 15N-organic N model, 14N-DIN model, and 15N-DIN model. The modeled output [], [], , and were compared to values from the database training set. Though DON and PON observations were not used to optimize the model, the open ocean and deep water values were useful in constraining the parameters that control PON solubilization and DON remineralization. The entire model was run using a set of initial parameter values (Table 2) and the optimization scheme continued to alter those starting parameters until a minimum in the cost function was attained. We optimized the logarithm of the parameter values rather than the original parameters themselves so the unconstrained optimization returned positive values. The transformed starting parameters and subsequent modified parameter sets were then fed back into the model equations as ex, where x denotes the log-transformed parameter. The cost function in the optimization procedure is as follows:
The w terms are weighting terms introduced to scale the contributions of the four observed parameters to equalize their contributions to the cost function. The n terms and standard deviation (sd) terms were used to normalize the contributions of each measurement type to the cost function. Each n term is equal to the number of each type of measurement in the training dataset (e.g., the number of [] data points ). The sd term is equal to the standard deviation of all the measurements of a given type (e.g., the standard deviation of all the [] data points within the training set).
In order to account for error in our model parameter estimates, we also iterated over several possible values for three of the most important isotope effects for processes in ODZs: εNAR, εNIR, and εNXR (Table 3). We chose to iterate over these parameters rather than optimize them since there is a large range of estimates for each of these parameters. We assigned different possible values for each of these parameters (Table 3), resulting in 12 possible combinations. The optimization protocol was performed for each of those combinations and unique optimized parameter sets were obtained. The parameter results were then averaged (final values, Table 2) and their spread is categorized as the error (error, Table 2).
3.1 Global model–data comparison
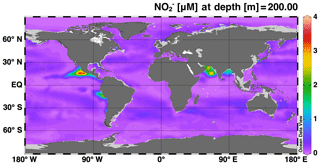
The simulations of concentration and isotopic composition are the most unique features of this model in comparison to existing global models of the marine N cycle. As such, accumulation in ODZs is a feature that should be well represented by the model in order to use it to test hypotheses about processes that control N cycling and loss in ODZs. Overall, we see accumulating at 200 m in the major ODZs of the Eastern Tropical North Pacific (ETNP), Eastern Tropical South Pacific (ETSP), and the Arabian Sea (AS) (Fig. 2), which is consistent with observations and expected based on the low O2 conditions found there. However, accumulation of in the model ETSP was lower than expected. The model also accumulated in the Bay of Bengal, which is a low-O2 region off the east coast of India that does not generally accumulate or support water column denitrification, but is thought to be near the “tipping point” for allowing N loss to occur (Bristow et al., 2017). Possible reasons for the underestimation of in the ETSP and overestimation in the Bay of Bengal will be discussed further in Sect. 4.2.
The model optimization described above yielded a set of isotope effects that best fit the global dataset of [], [], and . The best fit was achieved for isotope effects of 13 ‰ for reduction (εNAR), 0 ‰ for reduction (εNIR), and −13 ‰ for oxidation (εNXR). Figure 3 shows the test set comparison for the global best-fit set of isotope effects overlaid with a 1:1 line, which the data would follow if there was perfect agreement between model results and observations. There is general agreement between model and observations, with most of the data clustering near the 1:1 lines. Agreement between the observations and the training data are similar (Fig. S4), indicating that we did not overfit the training data.
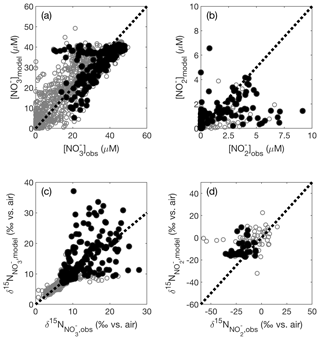
Figure 3Modeled (a) [], (b) [], (c) , and (d) are compared against the corresponding values from the database test set. Shown on each panel is a 1:1 line starting at the origin. Data in black have corresponding [O2]<10 µM, and data in gray have [O2]≥10 µM.
In the test set, there were some low [O2] points where our model [] exceeded observations (Fig. 3a, filled black circles); these are largely within the ETSP. In contrast, the AS tended to show slightly lower modeled [] than expected. The [] accumulation (Fig. 3b) and signals (Fig. 3c) in the ETSP were also generally too low compared with observations. These signals are likely tied to insufficient reduction occurring in the model ETSP. Another consideration is that there may be a mismatch in resolution between the model and the time and space scales needed to resolve the high accumulations observed sporadically (Anderson et al., 1982; Codispoti et al., 1985, 1986).
Overall, the representation of was fairly good (RMSE = 2.4 ‰), though there were a subset of points above ‰ where the modeled exceeded the observed , and others where modeled was lower than observations (Fig. 3c). Many of the points with overestimated were located within the AS ODZ, where there may be too much reduction occurring, leading to artificially elevated values. As indicated above, the underestimated points largely fell within the ETSP where we believe the model is underestimating reduction. The representation of was also fairly good (RMSE = 8.6 ‰), though the modeled was generally not low enough (Fig. 3d), indicating an underestimated sink of “heavy” .
3.2 ODZ model–data comparison using station profiles
To further investigate the distribution of model N species within the three main ODZs, we selected representative offshore grid boxes within each ODZ that contained observations to directly compare with model results in station profiles. Overall, the modeled and concentration and isotope profiles in the AS and ETNP were consistent with the observations, with [] slightly underestimated in the AS ODZ and overestimated in the ETSP (Fig. 4). As [O2] goes to zero, the O2-intolerant processes NAR, NIR, and AMX are released from inhibition. These processes result in a decrease in [] (via NAR) which corresponds to an increase in , since NAR has a normal isotope effect. also starts to accumulate in the secondary maximum as a result of NAR. The is lower than since light is preferentially created via NAR, and this fractionation is further reinforced by the inverse isotope effect of NXR (Casciotti, 2009). These patterns are readily observed in the AS and ETNP, but were less apparent in the ETSP, where [] depletion and [] accumulation in the model were lower than observed. This could be due in part to the time-independent nature of this steady-state inverse model, which does not capture the effects of upwelling events in the ETSP on N supply and cycling (Canfield, 2006; Chavez and Messié, 2009).
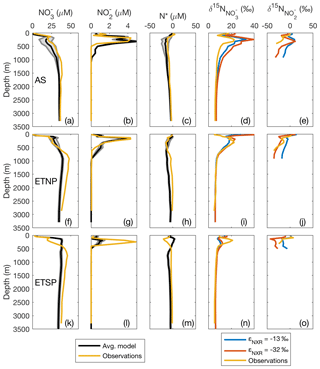
Figure 4Depth profiles comparing model results with binned and averaged database observations from a model water column. Results are shown for offshore regions of the three main oxygen deficient zones (ODZs): the Arabian Sea (AS; a–e), the Eastern Tropical North Pacific (ETNP; f–j), and the Eastern Tropical South Pacific (ETSP; k–o). Average modeled nitrate concentration ([]), nitrite concentration ([]), and N* are shown in black. Gray error lines around the black line show the 2σ spread from the average from the 12 different optimized model results using the different combinations of isotope effects for nitrate reduction (εNAR), nitrite reduction (εNIR), and nitrite oxidation (εNXR). Observed data are shown in yellow in all panels. Modeled and are shown for three different combinations of isotope effect. The blue lines represent εNAR=13, , and εNIR=0, which are the best fit isotope effects globally and in the ETSP. The red lines represent εNAR=13, , and εNIR=0, which are the best fit isotope effects in the AS.
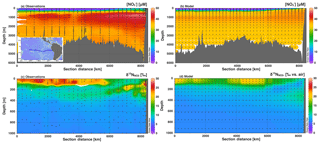
Figure 5Section profiles of concentrations and isotopes over the GEOTRACES GP16 cruise track (panel a inset) in the South Pacific. Section distance runs from west to east in each panel. Comparison of (a) observed [] to (b) modeled [] is presented over the full depth range (0–6000 m). Comparison of (c) observed to (d) modeled is presented over a shortened depth range (0–1000 m) to better assess surface and ODZ values. GEOTRACES data are from Peters et al. (2018a) and available from Biological and Chemical Oceanography Data Management Office (BCO-DMO).
In order to gauge the model results for N loss, we also calculated N*, a measure of the availability of DIN relative to compared to Redfield ratio stoichiometry (; Deutsch et al., 2001). Negative N* values are associated with N loss due to AMX or NIR or release of from anoxic sediments (Noffke et al., 2012), while positive N* values are associated with input of new N through N2 fixation (Gruber and Sarmiento, 1997). Although we did not model , we used the modeled [] and [] together with World Ocean Atlas data interpolated to the model grid to calculate N* resulting from the model. Both the AS and ETNP showed a decrease in model N* in the ODZ, as expected for water column N loss. Below the ODZ, N* increased again and returned to expected deep water values. Modeled N* in the ETSP, however, did not follow the observed trend, consistent with an underestimate of N loss in the model ETSP.
Though the global best fit isotope effects for NAR, NIR, and NXR produced good agreement to the data in general, the isotope effects that best fit individual ODZ regions differed when the cost function was restricted to observations from a given ODZ. For the ETSP, the best fit isotope effects were the same as the previously stated global best fit. For the AS, the best fit isotope effects were εNAR=13 ‰, εNIR=0 ‰, and ‰. For the ETNP, the best fit isotope effects were εNAR=13 ‰, εNIR=15 ‰, and ‰, though the performance is only marginally better than with εNIR=0 ‰. The lower (more inverse) value for εNXR resulted in higher and lower , which better fit the ODZ data compared to the global best fit ‰. These results are consistent with earlier isotope modeling studies in the ETSP (Casciotti et al., 2013; Peters et al., 2016, 2018b) and in the AS (Martin and Casciotti, 2017). Although, in the AS, modeled values were too high, likely in part due to overpredicted rates of NAR, which also resulted in lower modeled [] (Fig. 4).
3.3 Model–data comparison in GEOTRACES sections
We also investigated the agreement between global best fit model concentration and isotope distributions with data from two GEOTRACES cruise sections: GP16 in the South Pacific, and GA03 in the North Atlantic. For GP16, we see that [] is low in surface waters and increases to a mid-depth maximum between 1000 and 2000 m. The highest [] are found at mid-depth in the eastern boundary of the section. The model reproduces the general patterns, matching observations fairly well in the surface waters, but diverges below 500 m (Fig. 5). Although the patterns are generally correct, insufficient is accumulated in the deep waters of the model Pacific. This could be due to an underestimate of preformed (over estimate of assimilation in the Southern Ocean), or inadequate supply of organic matter to be remineralized at depth. In the Southern Ocean, model surface [] are 5–10 µM lower than observations (Fig. S5), which could be enough to explain the lower-than-expected [] in the deep Pacific, which is largely sourced from the Southern Ocean (Rafter et al., 2013; Sigman et al., 2009; Peters et al., 2018a, b).
In the GP16 section, we also see that there are elevated values in the model surface waters and in the ETSP ODZ (Fig. 5d), as expected from observations (Fig. 5c). However, we can also see that the insufficient depletion of and increase in in the ETSP ODZ (Fig. 5b and d) extends beyond the single grid box highlighted earlier (Fig. 4). The less-than-expected increase of in the ETSP ODZ and the upper thermocline in the eastern part of the section is consistent with an underestimate of reduction. In GP16 we were also able to compare modeled and observed [] and (Fig. S6). Patterns of modeled [] and showed accumulation of in the ODZ, with an appropriate value (Fig. S6). Although, generally lower modeled concentrations of in the ODZ also support an underestimate of NAR (Fig. S6).
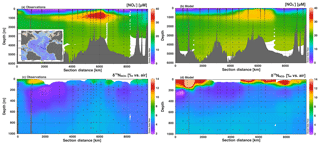
Figure 6Section profiles of concentrations and isotopes over the GA03 cruise track (panel a inset) in the North Atlantic. In each panel, section distance runs from west to east for the first 6000 km, and then runs from south to north. Comparison of (a) observed [] to (b) modeled [] is presented over the full depth range (0–6000 m). Comparison of (c) observed to (d) modeled is presented over a shortened depth range (0–1000 m) to better assess surface and the low contribution from N2 fixation. GEOTRACES data are from Marconi et al. (2015) and available from BCO-DMO.
Surface values were also not as high in the model as in the observations (Fig. 5), which could result from insufficient assimilation or too low supplied (Peters et al., 2018a). However, we do see a similar depth range for high surface and a local minimum between the surface and ODZ propagating westward in both the model and observations, indicating that the physical and biogeochemical processes affecting are represented by the model. Additionally, the model shows slightly elevated in the thermocline depths (200–500 m) west of the ODZ, which is consistent with the observations (Fig. 5c), though not of the correct magnitude. This is partly related to the muted ODZ signal as mentioned above and its lessened impact on thermocline across the basin. Peters et al. (2018a) and Rafter et al. (2013) also postulated that these elevated values were in part driven by remineralization of organic matter with high δ15N. The δ15N of sinking PON in the model (6 ‰–10 ‰) was similar to those observed in the South Pacific (Raimbault et al., 2008), as well as those predicted from aforementioned N isotope studies (Rafter et al., 2013; Peters et al., 2018a). The model also shows slightly elevated in the intermediate depths (500–1500 m), which is consistent with observations, again reflecting remineralization of PON with δ15N greater than mean ocean . Overall, the patterns of for the model GP16 are correct but the magnitudes of isotopic variation are muted, largely due to the lack of N loss in the ODZ and modeled surface values that are lower than observations. The simplification of dynamics in the model could also contribute to underestimation of values if there was a large flux of 15N-enriched from sediments (Granger et al., 2011), or if 15N-depleted was preferentially transferred to the N2 pool via anammox. While the isotope effect on during anammox (Brunner et al., 2013) is indeed higher than that applied here, we chose to balance this with a low isotope effect during aerobic oxidation (Table 1).
In the North Atlantic along GEOTRACES section GA03, we see good agreement between the observed and modeled [] (Fig. 6). There is generally low surface [] with a distinct area of high [] propagating from near the African coast. Deep water (>2000 m) [] is lower than we see in the Pacific section, and the model matches well with the Atlantic observations. Again, there is not quite enough present in Southern Ocean-sourced intermediate waters (500–1500 m; Marconi et al., 2015). Modeled values at first glance appear higher than observed values at the surface (Fig. 6). However, many of the surface [] were below the operating limit for analysis and were not determined. Focusing on areas where both measurements and model results are present yields excellent agreement. For example, we do see low values in upper thermocline waters in both the model and observations, likely corresponding to low δ15N contributions from N2 fixation that is remineralized at depth and accumulated in North Atlantic Central Water (Marconi et al., 2015; Knapp et al., 2008). The model input includes significant rates of N2 fixation in the North Atlantic that are consistent with this observation (Fig. S1). However, rates of N deposition in the North Atlantic are also fairly high and can contribute to the low δ15N signal (Knapp et al., 2008). In our model, atmospheric N deposition contributed between 0 % and 50 % of N input along the cruise track.
4.1 Assumption checks
As previously mentioned (Sect. 2.3), organic N and DIN were modeled separately in order to introduce dependence on both organic N and substrate availability for the heterotrophic processes NAR and NIR. These separate model runs required several assumptions to be made regarding the processes that impact both organic N and DIN, namely assimilation and remineralization.
The first assumption was that the rates of N assimilation are equal between the organic N and DIN model runs. The organic N model run uses World Ocean Atlas surface [] to estimate the contribution of DIN assimilation to the production of organic N, whereas the DIN model uses modeled [] and [] to estimate DIN removal via assimilation. Though these two methods used the same rate constants for assimilation, differences in DIN concentrations could cause some discrepancies between the overall rates. Analysis of the results revealed that slightly more overall DIN assimilation occurred in the DIN model run than organic N produced in the organic N model (Fig. S7). This could be due in part to assimilation of in the top two boxes of the DIN model, since assimilation is unaccounted for in the organic N model. This is largely an issue in the oligotrophic gyres, where surface [] is very low and accumulates to low but nonzero concentrations (Fig. 2). Assimilation of accounts for a significant fraction of DIN assimilation in these regions, but the overall assimilation rates there are low and the resulting influence on the whole system is also low. Another source of discrepancy would be where modeled surface [] is higher than the World Ocean Atlas surface [] that is supplied to the organic N model, which would result in higher assimilation rates in the DIN model run. Indeed, points at which the DIN assimilation rates are higher than the organic N production rates do tend to have modeled [] that was higher than observed [] (Fig. S7). Likewise, points with relatively lower DIN assimilation had modeled [] less than observed []. However, the majority of DIN assimilation estimates were within 10 µM yr−1 of the organic N production estimates, with an average offset of approximately 3.5 % compared to DIN assimilation. The total global assimilation rates were within 0.4 %, with some spatially variable differences due to offset between surface [] and modeled []. However, we find that the World Ocean Atlas surface values are fairly well represented by our modeled surface (Fig. S5). We conclude that though the assimilation rates are not identical in the organic N and DIN model runs, the discrepancy in modeled DIN assimilation is less than 0.1 %, and there is unlikely to be significant creation or loss of N as a result of the split model.
4.2 Model dependency on input O2
The modeled concentration and isotope profiles for the ETSP, unlike in the AS and ETNP, reflected an underestimation of water column denitrification in the best-fit model. In ETSP measurements, there is a clear deficit in [], coincident with the secondary maximum and N* minimum (Fig. 4). In our modeled profiles, this deficit is missing, and although a secondary maximum is present, its magnitude is lower than observed (Fig. 4). The model also does not capture the negative N* excursion (Fig. 4), which we think reflects a model underestimation of NAR and NIR in the ETSP. The cause of this missing denitrification is likely to be poor representation of the ETSP O2 conditions in the model grid space. Since our model grid is fairly coarse (), only a few boxes within the ETSP had averaged [O2] below the thresholds that would allow processes such as NAR and NIR to occur. The anoxic region of the ETSP is adjacent to the coast and not as spatially extensive as in the AS and ETNP (Fig. S8); therefore, this region in particular was less compatible with the model grid. In order to test whether the parameterization of O2 dependence was the cause of the low N loss, we ran the model using the globally optimized parameters (Table 3) but with higher O2 thresholds (15 µM) for NAR, NIR, and AMX (Table 1). This extended the region over which ODZ processes could occur and resulted in an increase in water column N loss from 6 to 32 Tg N yr−1 in the ETSP, which is more consistent with previous estimates (DeVries et al., 2012; Deutsch et al., 2001). This change also stimulated the development of a deficit, larger secondary maximum, and N* minimum within the ODZ (Fig. 7).
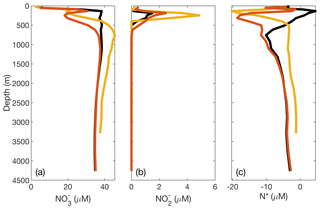
Figure 7Plots of DIN concentrations and N* from the ETSP ODZ comparing modified O2 thresholds for N loss. In the original optimized version of the model, there is insufficient N loss and accumulation in the ETSP. To demonstrate that this issue may be caused by the parameterization of O2 and dependence and/or model grid size in the ETSP, we raised the O2 thresholds for N loss-related processes (NAR, NIR, and AMX) to 15 µM. This effectively lowers the observed [O2] in order to stimulate N loss. The resulting (a) [], (b) [], and (c) N* are shown with the observed values from the database (yellow), original optimized model values (black), and lowered O2 threshold model values (red).
As previously mentioned (Sect. 3.1), modeled [] in the Bay of Bengal is higher than observations. The accumulation of here in the model is likely due to O2 concentrations falling below the set threshold for NAR but above the threshold for NIR, so can accumulate via NAR but cannot be consumed via NIR. Although AMX and NXR occur there, the modeled rates of their consumption are rather low, which supports a higher accumulation of in the steady-state model. This is in contrast to observations that production is tightly matched with oxidation in the Bay of Bengal, which limits accumulation and N loss there (Bristow et al., 2017). The fact that the model over predicts NAR in the AS may also be connected with overprediction of NAR in the Bay of Bengal. It is possible that the oxygen thresholds for ODZ processes are not the same in all ODZs, and further work on oxygen sensitivities of N cycle processes will be addressed in a companion study (Martin et al., 2019).
A global inverse ocean model was modified to include 14N and 15N in both and as state variables. Adding the processes required to describe the cycling of in the global ocean, including oxic and anoxic processes, resulted in a globally representative distribution of [], [], , and . In particular, the patterns of variation in both oxic and anoxic waters are generally consistent with observations, though some magnitudes of variation were somewhat muted by the model. This could be due to an underestimation of a process rate, due to parameterization or model resolution, or an underestimation of the isotope effect involved.
Importantly, we were able to generate a roughly balanced steady-state ocean N budget without the need for an artificial restoring force. The [] and [] distributions that were required to achieve this roughly balanced budget are well within the range of observed values. Some interesting take-home messages from this work are the following: (1) a relatively low isotope effect for reduction (εNAR=13 ‰) gives a good fit to data, similar to that concluded in some recent studies (Marconi et al., 2017; Bourbonnais et al., 2015; Casciotti et al., 2013); (2) low O2 half-saturation constants for oxidation allowing oxidation to occur in parallel with reduction, reduction, and anammox were needed to achieve reasonable distributions of , , and their isotopes in the ocean water column ODZs.
Though we have been able to adequately represent and assess N cycling in ODZs, there are many areas in which this model could be improved in order to expand its usefulness. Improving resolution of the model, particularly in coastal regions where there are steep gradients in nutrient and O2 concentrations, would improve the accuracy of the model in regions such as the ETSP. Further, in regions that have high seasonal or interannual variability, an annually averaged steady-state model may not represent some important temporal dynamics. While we attempted to account for seasonal variation in the strength of the ODZs through use of monthly O2 climatologies, we did not simulate seasonal variations in net primary production and the strength of the biological pump. Variations in these parameters are likely to drive variations in N loss (Kalvelage et al., 2013; Ward, 2013; Babbin et al., 2014).
In addition to the dependency on external static nutrient and parameter fields, this N cycle model is highly dependent on isotope effects for N cycle processes. Previous work has shown that the laboratory-derived isotope effects for some N cycle processes are not the same as their expressed isotope effects in environmental samples or under conditions relevant to environmental samples (Casciotti et al., 2013; Bourbonnais et al., 2015; Buchwald et al., 2015; Kritee et al., 2012; Marconi et al., 2017). Further probing the isotope effects using an inverse model such as this could provide insight into the expressed isotope effects that should be used in other modeling efforts involving field data. As presented in Sect. 3.1, the larger magnitude isotope effect for oxidation best fit the ETNP and AS ODZs, where most of the ODZ volume resides. However, most model values still do not reach the lowest values observed on the edges of marine ODZs, indicating that further work is needed to understand the expression of these isotope effects.
The larger isotope effects resulted in better fits to observations of δ15N and DIN concentrations with lower rates of N cycling. This reinforces the importance of obtaining realistic isotope effect estimates for each process that are relevant on an environmental scale. Additionally, this highlights the need for critical consideration of isotope effects used in N cycle models that use isotope balance to predict N cycling rates. Though isotopes provide us with a useful tool to assess the relative contributions of different processes, these estimates are highly subject to the isotope effects employed. Also, as illustrated by the regional optimizations, the isotope effect for a given process may vary, or be expressed differently, in different regions.
This model provides an excellent framework for further testing hypotheses about controls on the marine N inventory and cycling of N on a global scale. The distribution and sensitivities of N cycle rates resulting from this model will be explored in a companion manuscript (Martin et al., 2019). Incorporation of variable environmental input data, such as temperature, productivity, and [O2], could also help us predict how the N cycle might be affected by past and future environmental changes.
Model code and model output from the three optimal ODZ isotope effect combinations, including the global best fit, are available in the Stanford Digital Repository (https://doi.org/10.25740/VA90-CT15; Martin et al., 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-16-347-2019-supplement.
KLC, FP, and TSM designed the study. TSM and FP constructed the model. TSM and KLC analyzed and interpreted the results. TSM, KLC, and FP wrote the manuscript.
The authors declare that they have no conflict of interest.
Thanks to Patrick Rafter for sharing a pre-publication version of his
isotope database. Thanks to Tim Davis for guidance on sparse matrix solvers. Thanks to
Tim DeVries for helpful discussions about earlier versions of the inverse model. Thanks
to Kevin Arrigo and Leif Thomas for comments on an earlier draft of this manuscript. This
work was partly supported by National Science Foundation (NSF) Chemical
Oceanography grant 1657868 to KLC.
Edited by: Jack
Middelburg
Reviewed by: Annie Bourbonnais and Itzel Ruvalcaba Baroni
Anderson, J. J., Okubo, A., Robbins, A. S., and Richards, F. A.: A model for nitrate distributions in oceanic oxygen minimum zones, Deep-Sea Res., 29, 1113–1140, https://doi.org/10.1016/0198-0149(82)90031-0, 1982.
Babbin, A. R., Keil, R. G., Devol, A. H., and Ward, B. B.: Organic Matter Stoichiometry, Flux, and Oxygen Control Nitrogen Loss in the Ocean, Science, 344, 406–408, https://doi.org/10.1126/science.1248364, 2014.
Babbin, A. R., Peters, B. D., Mordy, C. W., Widner, B., Casciotti, K. L., and Ward, B. B.: Multiple metabolisms constrain the anaerobic nitrite budget in the Eastern Tropical South Pacific, Global Biogeochem. Cy., 31, 258–271, https://doi.org/10.1002/2016GB005407, 2017.
Berelson, W. M.: Particle settling rates increase with depth in the ocean, Deep-Sea Res. Pt. II, 49, 237–251, https://doi.org/10.1016/S0967-0645(01)00102-3, 2002.
Bianchi, D., Dunne, J. P., Sarmiento, J. L., and Galbraith, E. D.: Data-based estimates of suboxia, denitrification, and N2O production in the ocean and their sensitivities to dissolved O2, Global Biogeochem. Cy., 26, 1–13, https://doi.org/10.1029/2011GB004209, 2012.
Bohlen, L., Dale, A. W., and Wallmann, K.: Simple transfer functions for calculating benthic fixed nitrogen losses and regeneration ratios in global biogeochemical models, Global Biogeochem. Cy., 26, GB3029, https://doi.org/10.1029/2011GB004198, 2012.
Bonin, P., Gilewicz, M., and Bertrand, J. C.: Effects of oxygen on each step of denitrification on Pseudomonas nautica, Can. J. Microbiol., 35, 1061–1064, https://doi.org/10.1139/m89-177, 1989.
Bourbonnais, A., Altabet, M. A., Charoenpong, C. N., Larkum, J., Hu, H., Bange, H. W., and Stramma, L.: N-loss isotope effects in the Peru oxygen minimum zone studied using a mesoscale eddy as a natural tracer experiment, Global Biogeochem. Cy., 29, 793–811, https://doi.org/10.1002/2013GB004679, 2015.
Brandes, J. A. and Devol, A. H.: Isotopic fractionation of oxygen and nitrogen in coastal marine sediments, Geochim. Cosmochim. Ac., 61, 1793–1801, https://doi.org/10.1016/S0016-7037(97)00041-0, 1997.
Brandes, J. A. and Devol, A. H.: A global marine-fixed nitrogen isotopic budget: Implications for Holocene nitrogen cycling, Global Biogeochem. Cy., 16, 67-1–67-14, https://doi.org/10.1029/2001GB001856, 2002.
Bristow, L. A., Dalsgaard, T., Tiano, L., Mills, D. B., Bertagnolli, A. D., Wright, J. J., Hallam, S. J., Ulloa, O., Canfield, D. E., Revsbech, N. P., and Thamdrup, B.: Ammonium and nitrite oxidation at nanomolar oxygen concentrations in oxygen minimum zone waters, P. Natl. Acad. Sci. USA, 113, 10601–10606, https://doi.org/10.1073/pnas.1600359113, 2016.
Bristow, L. A., Callbeck, C. M., Larsen, M., Altabet, M. A., Dekaezemacker, J., Forth, M., Gauns, M., Glud, R. N., Kuypers, M. M. M., Lavik, G., Milucka, J., Naqvi, S. W. A., Pratihary, A., Revsbech, N. P., Thamdrup, B., Treusch, A. H., and Canfield, D. E.: N2 production rates limited by nitrite availability in the Bay of Bengal oxygen minimum zone, Nat. Geosci., 10, 24–29, https://doi.org/10.1038/ngeo2847, 2017.
Brown, Z. W., Casciotti, K. L., Pickart, R. S., Swift, J. H., and Arrigo, K. R.: Aspects of the marine nitrogen cycle of the Chukchi Sea shelf and Canada Basin, Deep-Sea Res. Pt. II, 118, 73–87, https://doi.org/10.1016/j.dsr2.2015.02.009, 2015.
Brunner, B., Contreras, S., Lehmann, M. F., Matantseva, O., Rollog, M., Kalvelage, T., Klockgether, G., Lavik, G., Jetten, M. S. M., Kartal, B., and Kuypers, M. M. M.: Nitrogen isotope effects induced by anammox bacteria, P. Natl. Acad. Sci. USA, 110, 18994–18999, https://doi.org/10.1073/pnas.1310488110, 2013.
Bryan, B. A., Shearer, G., Skeeters, J. L., and Kohl, D. H.: Variable expression of the nitrogen isotope effect associated with denitrification of nitrite, J. Biol. Chem., 258, 8613–8617, 1983.
Buchwald, C. and Casciotti, K. L.: Oxygen isotopic fractionation and exchange during bacterial nitrite oxidation, Limnol. Oceanogr., 55, 1064–1074, https://doi.org/10.4319/lo.2010.55.3.1064, 2010.
Buchwald, C., Santoro, A. E., Stanley, R. H. R., and Casciotti, K. L.: Nitrogen cycling in the secondary nitrite maximum of the eastern tropical North Pacific off Costa Rica, Global Biogeochem. Cy., 29, 2061–2081, https://doi.org/10.1002/2015GB005187, 2015.
Buesseler, K. O. and Boyd, P. W.: Shedding light on processes that control particle export and flux attenuation in the twilight zone of the open ocean, Limnol. Oceanogr., 54, 1210–1232, https://doi.org/10.4319/lo.2009.54.4.1210, 2009.
Buesseler, K. O., Trull, T. W., Steinberg, D. K., Silver, M. W., Siegel, D. A., Saitoh, S.-I., Lamborg, C. H., Lam, P. J., Karl, D. M., Jiao, N. Z., Honda, M. C., Elskens, M., Dehairs, F., Brown, S. L., Boyd, P. W., Bishop, J. K. B., and Bidigare, R. R.: VERTIGO (VERtical Transport In the Global Ocean): A study of particle sources and flux attenuation in the North Pacific, Deep-Sea Res. Pt. II, 55, 1522–1539, https://doi.org/10.1016/j.dsr2.2008.04.024, 2008.
Canfield, D. E.: Models of oxic respiration, denitrification and sulfate reduction in zones of coastal upwelling, Geochim. Cosmochim. Ac., 70, 5753–5765, https://doi.org/10.1016/j.gca.2006.07.023, 2006.
Capone, D. G., Burns, J. A., Montoya, J. P., Subramaniam, A., Mahaffey, C., Gunderson, T., Michaels, A. F., and Carpenter, E. J.: Nitrogen fixation by Trichodesmium spp.: An important source of new nitrogen to the tropical and subtropical North Atlantic Ocean, Global Biogeochem. Cy., 19, GB2024, https://doi.org/10.1029/2004GB002331, 2005.
Carpenter, E. J., Harvey, H. R., Brian, F., and Capone, D. G.: Biogeochemical tracers of the marine cyanobacterium Trichodesmium, Deep-Sea Res. Pt. I, 44, 27–38, https://doi.org/10.1016/S0967-0637(96)00091-X, 1997.
Casciotti, K. L.: Inverse kinetic isotope fractionation during bacterial nitrite oxidation, Geochim. Cosmochim. Ac., 73, 2061–2076, https://doi.org/10.1016/j.gca.2008.12.022, 2009.
Casciotti, K. L., Trull, T. W., Glover, D. M., and Davies, D.: Constraints on nitrogen cycling at the subtropical North Pacific Station ALOHA from isotopic measurements of nitrate and particulate nitrogen, Deep-Sea Res. Pt. II, 55, 1661–1672, https://doi.org/10.1016/j.dsr2.2008.04.017, 2008.
Casciotti, K. L., Buchwald, C., and McIlvin, M.: Implications of nitrate and nitrite isotopic measurements for the mechanisms of nitrogen cycling in the Peru oxygen deficient zone, Deep-Sea Res. Pt. I, 80, 78–93, https://doi.org/10.1016/j.dsr.2013.05.017, 2013.
Chavez, F. P. and Messié, M.: A comparison of Eastern Boundary Upwelling Ecosystems, Prog. Oceanogr., 83, 80–96, https://doi.org/10.1016/j.pocean.2009.07.032, 2009.
Chien, C.-T., Mackey, K. R. M., Dutkiewicz, S., Mahowald, N. M., Prospero, J. M., and Paytan, A.: Effects of African dust deposition on phytoplankton in the western tropical Atlantic Ocean off Barbados, Global Biogeochem. Cy., 30, 716–734, https://doi.org/10.1002/2015GB005334, 2016.
Codispoti, L. A.: Phosphorus vs. Nitrogen limitation of new and export production, in: Productivity of the Oceans: Present and Past, Vol. 44, John Wiley & Sons Ltd., New York City, NY, USA, 377–394, 1989.
Codispoti, L. A. and Christensen, J. P.: Nitrification, denitrification and nitrous oxide cycling in the eastern tropical South Pacific ocean, Mar. Chem., 16, 277–300, https://doi.org/10.1016/0304-4203(85)90051-9, 1985.
Codispoti, L. A., Friederich, G. E., Packard T. T., Glover, H. E., Kelly, P. J., Spinrad, R. W., Barber, R. T., Elkins, J. W., Ward, B. B., Lipschultz, F., and Lostaunau, N.: High Nitrite Levels off Northern Peru: A Signal of Instability in the Marine Denitrification Rate, Science, 233, 1200–1202, https://doi.org/10.1126/science.233.4769.1200, 1986.
Codispoti, L. A., Brandes, J. A., Christensen, J. P., Devol, A. H., Naqvi, S. W. A., Paerl, H. W., and Yoshinari, T.: The oceanic fixed nitrogen and nitrous oxide budgets: Moving targets as we enter the anthropocene?, Sci. Mar., 65, 80–105, https://doi.org/10.3989/scimar.2001.65s285, 2001.
Dalsgaard, T., Stewart, F. J., Thamdrup, B., De Brabandere, L., Revsbech, N. P., Ulloa, O., Canfield, D. E., and DeLong, E. F.: Oxygen at nanomolar levels reversibly suppresses process rates and gene expression in anammox and denitrification in the oxygen minimum zone off Northern Chile, MBio, 5, e01966-14, https://doi.org/10.1128/mBio.01966-14, 2014.
Dentener, F., Drevet, J., Lamarque, J. F., Bey, I., Eickhout, B., Fiore, A. M., Hauglustaine, D., Horowitz, L. W., Krol, M., Kulshrestha, U. C., Lawrence, M., Galy-Lacaux, C., Rast, S., Shindell, D., Stevenson, D., Van Noije, T., Atherton, C., Bell, N., Bergman, D., Butler, T., Cofala, J., Collins, B., Doherty, R., Ellingsen, K., Galloway, J., Gauss, M., Montanaro, V., Müller, J. F., Pitari, G., Rodriguez, J., Sanderson, M., Solmon, F., Strahan, S., Schultz, M., Sudo, K., Szopa, S., and Wild, O.: Nitrogen and sulfur deposition on regional and global scales: A multimodel evaluation, Global Biogeochem. Cy., 20, GB4003, https://doi.org/10.1029/2005GB002672, 2006.
Deutsch, C., Gruber, N., Key, R. M., Sarmiento, J. L., and Ganachaud, A.: Denitrification and N2 fixation in the Pacific Ocean, Global Biogeochem. Cy., 15, 483–506, https://doi.org/10.1029/2000GB001291, 2001.
Deutsch, C., Sarmiento, J. L., Sigman, D. M., Gruber, N., and Dunne, J. P.: Spatial coupling of nitrogen inputs and losses in the ocean, Nature, 445, 163–167, https://doi.org/10.1038/nature05392, 2007.
DeVries, T. and Primeau, F.: Dynamically and Observationally Constrained Estimates of Water-Mass Distributions and Ages in the Global Ocean, J. Phys. Oceanogr., 41, 2381–2401, https://doi.org/10.1175/JPO-D-10-05011.1, 2011.
DeVries, T., Deutsch, C., Primeau, F., Chang, B., and Devol, A.: Global rates of water-column denitrification derived from nitrogen gas measurements, Nat. Geosci., 5, 547–550, https://doi.org/10.1038/ngeo1515, 2012.
DeVries, T., Deutsch, C., Rafter, P. A., and Primeau, F.: Marine denitrification rates determined from a global 3-D inverse model, Biogeosciences, 10, 2481–2496, https://doi.org/10.5194/bg-10-2481-2013, 2013.
Dunne, J. P., Armstrong, R. A., Gnanadesikan, A., and Sarmiento, J. L.: Empirical and mechanistic models for the particle export ratio, Global Biogeochem. Cy., 19, GB4026, https://doi.org/10.1029/2004GB002390, 2005.
Follows, M. J., Dutkiewicz, S., Grant, S., and Chisholm, S. W.: Emergent Biogeography of Microbial Communities in a Model Ocean, Science, 315, 1843–1846, https://doi.org/10.1126/science.1138544, 2007.
Frey, C., Hietanen, S., Jürgens, K., Labrenz, M., and Voss, M.: N and O isotope fractionation in nitrate during chemolithoautotrophic denitrification by Sulfurimonas gotlandica, Environ. Sci. Technol., 48, 13229–13237, https://doi.org/10.1021/es503456g, 2014.
Fuchsman, C. A., Devol, A. H., Casciotti, K. L., Buchwald, C., Chang, B. X., and Horak, R. E. A.: An N isotopic mass balance of the Eastern Tropical North Pacific Oxygen Deficient Zone, Deep-Sea Res. Pt. II, 156, 137–147, https://doi.org/10.1016/j.dsr2.2017.12.013, 2017.
Galloway, J. N., Dentener, F. J., Capone, D. G., Boyer, E. W., Howarth, R. W., Seitzinger, S. P., Asner, G. P., Cleveland, C. C., Green, P. A., Holland, E. A., Karl, D. M., Michaels, A. F., Porter, J. H., Townsend, A. R., and Vörösmarty, C. J.: Nitrogen cycles: past, present, and future, Biogeochemistry, 70, 153–226, https://doi.org/10.1007/s10533-004-0370-0, 2004.
Garcia, H. E., Boyer, T. P., Locarnini, R. A., Boyer, T. P., Antonov, J. I., Mishonov, A. V., Baranova, O. K., Zweng, M. M., Reagan, J. R., and Johnson, D. R.: World Ocean Atlas 2013, Volume 3: dissolved oxygen, apparent oxygen utilization, and oxygen saturation, NOAA Atlas NESDIS 75, Silver Spring, MD, USA, 27 pp., 2013a.
Garcia, H. E., Locarnini, R. A., Boyer, T. P., Antonov, J. I., Baranova, O. K., Zweng, M. M., Reagan, J. R., and Johnson, D. R.: World Ocean Atlas 2013, Volume 4: Dissolved inorganic nutrients (phosphate, nitrate, silicate), NOAA Atlas NESDIS 76, Silver Spring, MD, USA, 25 pp., 2013b.
Gaye, B., Nagel, B., Dähnke, K., Rixen, T., and Emeis, K-C.: Evidence of parallel denitrification and nitrite oxidation in the ODZ of the Arabian Sea from paired stable isotopes of nitrate and nitrite. Global Biogeochem. Cy., 27, 1059–1071, https://doi.org/10.1002/2011GB004115, 2013.
Granger, J., Sigman, D. M., Lehmann, M. F., and Tortell, P. D.: Nitrogen and oxygen isotope fractionation during dissimilatory nitrate reduction by denitrifying bacteria, Limnol. Oceanogr., 53, 2533–2545, https://doi.org/10.4319/lo.2008.53.6.2533, 2008.
Granger, J., Sigman, D. M., Rohde, M. M., Maldonado, M. T., and Tortell, P. D.: N and O isotope effects during nitrate assimilation by unicellular prokaryotic and eukaryotic plankton cultures, Geochim. Cosmochim. Ac., 74, 1030–1040, https://doi.org/10.1016/j.gca.2009.10.044, 2010.
Granger, J., Prokopenko, M. G., Sigman, D. M., Mordy, C. W., Morse, Z. M., Morales, L. V., Sambrotto, R. N., and Plessen, B.: Coupled nitrification-denitrification in sediment of the eastern Bering Sea shelf leads to 15N enrichment of fixed N in shelf waters, J. Geophys. Res.-Oceans, 116, 1–18, https://doi.org/10.1029/2010JC006751, 2011.
Gruber, N.: The Dynamics of the Marine Nitrogen Cycle and its Influence on Atmospheric CO2 Variations, in: The Ocean Carbon Cycle and Climate, Springer, the Netherlands, 2004.
Gruber, N.: The Marine Nitrogen Cycle: Overview and Challenges, in: Nitrogen in the Marine Environment, edited by: Capone, D. G., Bronk, D. A., Mulholland, M. R., and Carpenter, E. J., Elsevier, Amsterdam, the Netherlands, 2008.
Gruber, N. and Galloway, J. N.: An Earth-system perspective of the global nitrogen cycle, Nature, 451, 293–296, https://doi.org/10.1038/nature06592, 2008.
Gruber, N. and Sarmiento, J. L.: Global patterns of marine nitrogen fixation and denitrification, Global Biogeochem. Cy., 11, 235–266, https://doi.org/10.1029/97GB00077, 1997.
Harding, K., Turk-Kubo, K. A., Sipler, R. E., Mills, M. M., Bronk, D. A., and Zehr, J. P.: Symbiotic unicellular cyanobacteria fix nitrogen in the Arctic Ocean, P. Natl. Acad. Sci. USA, 115, 13371–13375, https://doi.org/10.1073/pnas.1813658115, 2018.
Hastings, M. G., Jarvis, J. C., and Steig, E. J.: Anthropogenic Impacts on Nitrogen Isotopes of Ice-Core Nitrate, Science, 324, 1288, https://doi.org/10.1126/science.1170510, 2009.
Hoering, T. C. and Ford, H. T.: The Isotope Effect in the Fixation of Nitrogen by Azotobacter, J. Am. Chem. Soc., 82, 376–378, https://doi.org/10.1021/ja01487a031, 1960.
Holl, C. M. and Montoya, J. P.: Interactions between nitrate uptake and nitrogen fixation in continuous cultures of the marine diazotroph Trichodesmium (Cyanobacteria), J. Phycol., 41, 1178–1183, https://doi.org/10.1111/j.1529-8817.2005.00146.x, 2005.
Hu, H., Bourbonnais, A., Larkum, J., Bange, H. W., and Altabet, M. A.: Nitrogen cycling in shallow low-oxygen coastal waters off Peru from nitrite and nitrate nitrogen and oxygen isotopes, Biogeosciences, 13, 1453–1468, https://doi.org/10.5194/bg-13-1453-2016, 2016.
Jensen, M. M., Kuypers, M. M. M., Lavik, G., and Thamdrup, B.: Rates and regulation of anaerobic ammonium oxidation and denitrification in the Black Sea, Limnol. Oceanogr., 53, 23–36, https://doi.org/10.4319/lo.2008.53.1.0023, 2008.
Kalvelage, T., Jensen, M. M., Contreras, S., Revsbech, N. P., Lam, P., Günter, M., LaRoche, J., Lavik, G., and Kuypers, M. M. M.: Oxygen Sensitivity of Anammox and Coupled N-Cycle Processes in Oxygen Minimum Zones, PLoS One, 6, e29299, https://doi.org/10.1371/journal.pone.0029299, 2011.
Kalvelage, T., Lavik, G., Lam, P., Contreras, S., Arteaga, L., Loscher, C. R., Oschlies, A., Paulmier, A., Stramma, L., and Kuypers, M. M. M.: Nitrogen cycling driven by organic matter export in the South Pacific oxygen minimum zone, Nat. Geosci., 6, 228–234, https://doi.org/10.1038/ngeo1739, 2013.
Knapp, A. N., DiFiore, P. J., Deutsch, C., Sigman, D. M., and Lipschultz, F.: Nitrate isotopic composition between Bermuda and Puerto Rico: Implications for N2 fixation in the Atlantic Ocean, Global Biogeochem. Cy., 22, GB3014, https://doi.org/10.1029/2007GB003107, 2008.
Knapp, A. N., Sigman, D. M., Lipschultz, F., Kustka, A. B., and Capone, D. G.: Interbasin isotopic correspondence between upper-ocean bulk DON and subsurface nitrate and its implications for marine nitrogen cycling, Global Biogeochem. Cy., 25, GB4004, https://doi.org/10.1029/2010GB003878, 2011.
Kritee, K., Sigman, D. M., Granger, J., Ward, B. B., Jayakumar, A., and Deutsch, C.: Reduced isotope fractionation by denitrification under conditions relevant to the ocean, Geochim. Cosmochim. Ac., 92, 243–259, https://doi.org/10.1016/j.gca.2012.05.020, 2012.
Kuypers, M. M. M., Lavik, G., Woebken, D., Schmid, M., Fuchs, B. M., Amann, R., Jorgensen, B. B., and Jetten, M. S. M.: Massive nitrogen loss from the Benguela upwelling system through anaerobic ammonium oxidation, P. Natl. Acad. Sci. USA, 102, 6478–6483, https://doi.org/10.1073/pnas.0502088102, 2005.
Landolfi, A., Kähler, P., Koeve, W., and Oschlies, A.: Global marine N2 fixation estimates: From observations to models, Front. Microbiol., 9, 1–8, https://doi.org/10.3389/fmicb.2018.02112, 2018.
Lavik, G., Stührmann, T., Brüchert, V., Van Der Plas, A., Mohrholz, V., Lam, P., Mußmann, M., Fuchs, B. M., Amann, R., Lass, U., and Kuypers, M. M. M.: Detoxification of sulphidic African shelf waters by blooming chemolithotrophs, Nature, 457, 581–584, https://doi.org/10.1038/nature07588, 2009.
Lehmann, M. F., Bernasconi, S. M., Barbieri, A., Simona, M., and McKenzie, J. A.: Interannual variation of the isotopic composition of sedimenting organic carbon and nitrogen in Lake Lugano: A long-term sediment trap study, Limnol. Oceanogr., 49, 839–849, https://doi.org/10.4319/lo.2004.49.3.0839, 2004.
Lehmann, M. F., Sigman, D. M., McCorkle, D. C., Granger, J., Hoffmann, S., Cane, G., and Brunelle, B. G.: The distribution of nitrate 15N∕14N in marine sediments and the impact of benthic nitrogen loss on the isotopic composition of oceanic nitrate, Geochim. Cosmochim. Ac., 71, 5384–5404, https://doi.org/10.1016/j.gca.2007.07.025, 2007.
Locarnini, R. A., Mishonov, A. V., Antonov, J. I., Boyer, T. P., Garcia, H. E., Baranova, O. K., Zweng, M. M., Paver, C. R., Reagan, J. R., Johnson, D. R., Hamilton, M., and Seidov, D.: World Ocean Atlas 2013, Vol. 1: Temperature, NOAA Atlas NESDIS 73, Silver Spring, MD, USA, 40 pp., 2013.
Marconi, D., Weigand, M. A., Rafter, P. A., McIlvin, M. R., Forbes, M., Casciotti, K. L., and Sigman, D. M.: Nitrate isotope distributions on the US GEOTRACES North Atlantic cross-basin section: Signals of polar nitrate sources and low latitude nitrogen cycling, Mar. Chem., 177, 143–156, https://doi.org/10.1016/j.marchem.2015.06.007, 2015.
Marconi, D., Kopf, S., Rafter, P. A., and Sigman, D. M.: Aerobic respiration along isopycnals leads to overestimation of the isotope effect of denitrification in the ocean water column, Geochim. Cosmochim. Ac., 197, 417–432, https://doi.org/10.1016/j.gca.2016.10.012, 2017.
Mariotti, A.: Atmospheric nitrogen is a reliable standard for natural 15N abundance measurements, Nature, 303, 685–687, https://doi.org/10.1038/303685a0, 1983.
Mariotti, A., Germon, J. C., Hubert, P., Kaiser, P., Letolle, R., Tardieux, A., and Tardieux, P.: Experimental determination of nitrogen kinetic isotope fractionation: Some principles; illustration for the denitrification and nitrification processes, Plant Soil, 62, 413–430, https://doi.org/10.1007/BF02374138, 1981.
Martin, J. H., Knauer, G. A., Karl, D. M., and Broenkow, W. W.: VERTEX: carbon cycling in the northeast Pacific, Deep-Sea Res., 34, 267–285, https://doi.org/10.1016/0198-0149(87)90086-0, 1987.
Martin, T. S. and Casciotti, K. L.: Nitrogen and oxygen isotopic fractionation during microbial nitrite reduction, Limnol. Oceanogr., 61, 1134–1143, https://doi.org/10.1002/lno.10278, 2016.
Martin, T. S. and Casciotti, K. L.: Paired N and O isotopic analysis of nitrate and nitrite in the Arabian Sea oxygen deficient zone, Deep-Sea Res. Pt. I, 121, 121–131, https://doi.org/10.1016/j.dsr.2017.01.002, 2017.
Martin, T. S., Primeau, F., and Casciotti, K. L.: Model output from N isotope global inverse model, Stanford Digital Repository, https://doi.org/10.25740/VA90-CT15, 2018.
Martin, T. S., Primeau, F., and Casciotti, K. L.: Assessing marine nitrogen cycle rates and process sensitivities with a global 3D inverse model, Global Biogeochem. Cy., in review, 2019.
Möbius, J.: Isotope fractionation during nitrogen remineralization (ammonification): Implications for nitrogen isotope biogeochemistry, Geochim. Cosmochim. Ac., 105, 422–432, https://doi.org/10.1016/j.gca.2012.11.048, 2013.
Monteiro, F. M., Dutkiewicz, S., and Follows, M. J.: Biogeographical controls on the marine nitrogen fixers, Global Biogeochem. Cy., 25, GB2003, https://doi.org/10.1029/2010GB003902, 2011.
Moore, J. K. and Doney, S. C.: Iron availability limits the ocean nitrogen inventory stabilizing feedbacks between marine denitrification and nitrogen fixation, Global Biogeochem. Cy., 21, GB2001, https://doi.org/10.1029/2006GB002762, 2007.
Moore, J. K., Doney, S. C., and Lindsay, K.: Upper ocean ecosystem dynamics and iron cycling in a global three-dimensional model, Global Biogeochem. Cy., 18, GB4028, https://doi.org/10.1029/2004GB002220, 2004.
Nixon, S. W., Ammerman, J. W., Atkinson, L. P., Berousky, V. M., Billen, G., Boicourt, W. C., Boynton, W. R., Church, T. M., Ditoro, D. M., Elmgren, R., Garber, J. H., Giblin, A. E., Jahnke, R. A., Owens, N. J. P., Pilson, M. E. Q., and Seitzinger, S. P.: The fate of nitrogen and phosphorus at the land-sea margin of the North Atlantic Ocean Five major rivers with an average water flow exceeding 3000 m3 s−1 discharge, Biogeochemistry, 35, 141–180, 1996.
Noffke, A., Hensen, C., Sommer, S., Scholz, F., Bohlen, L., Mosch, T., Graco, M., and Wallmann, K.: Benthic iron and phosphorus fluxes across the Peruvian oxygen minimum zone, Limnol. Oceanogr., 57, 851–867, https://doi.org/10.4319/lo.2012.57.3.0851, 2012.
Peng, X., Fuchsman, C. A., Jayakumar, A., Warner, M. J., Devol, A. H., and Ward, B. B.: Revisiting nitrification in the Eastern Tropical South Pacific: A focus on controls, J. Geophys. Res.-Oceans, 121, 1667–1684, https://doi.org/10.1002/2015JC011455, 2016.
Penn, J., Weber, T., and Deutsch, C.: Microbial functional diversity alters the structure and sensitivity of oxygen deficient zones, Geophys. Res. Lett., 43, 9773–9780, https://doi.org/10.1002/2016GL070438, 2016.
Peters, B. D., Babbin, A. R., Lettmann, K. A., Mordy, C. W., Ulloa, O., Ward, B. B., and Casciotti, K. L.: Vertical modeling of the nitrogen cycle in the eastern tropical South Pacific oxygen deficient zone using high-resolution concentration and isotope measurements, Global Biogeochem. Cy., 30, 1661–1681, https://doi.org/10.1002/2016GB005415, 2016.
Peters, B. D., Lam, P. J., and Casciotti, K. L.: Nitrogen and oxygen isotope measurements of nitrate along the US GEOTRACES Eastern Pacific Zonal Transect (GP16) yield insights into nitrate supply, remineralization, and water mass transport, Mar. Chem., 201, 137–150, https://doi.org/10.1016/j.marchem.2017.09.009, 2018a.
Peters, B. D., Horak, R., Devol, A., Fuchsman, C., Forbes, M., Mordy, C. W., and Casciotti, K. L.: Estimating fixed nitrogen loss and associated isotope effects using concentration and isotope measurements of , , and N2 from the Eastern Tropical South Pacific oxygen deficient zone, Deep-Sea Res. Pt. II, https://doi.org/10.1016/j.dsr2.2018.02.011, 2018b.
Rafter, P. A., DiFiore, P. J., and Sigman, D. M.: Coupled nitrate nitrogen and oxygen isotopes and organic matter remineralization in the Southern and Pacific Oceans, J. Geophys. Res.-Oceans, 118, 4781–4794, https://doi.org/10.1002/jgrc.20316, 2013.
Rafter, P. A., Bagnell, A., Marconi, D., and DeVries, T.: Global trends in marine nitrate N isotopes from observations and a neural network-based climatology, Biogeosciences Discuss., https://doi.org/10.5194/bg-2018-525, in review, 2019.
Raimbault, P., Garcia, N., and Cerutti, F.: Distribution of inorganic and organic nutrients in the South Pacific Ocean – evidence for long-term accumulation of organic matter in nitrogen-depleted waters, Biogeosciences, 5, 281–298, https://doi.org/10.5194/bg-5-281-2008, 2008.
Redfield, A. C., Ketchum, B. H., and Richards, F. A.: The Influence of Organisms on the Composition of Sea Water, Sea, 2, 26–77, 1963.
Ryabenko, E., Kock, A., Bange, H. W., Altabet, M. A., and Wallace, D. W. R.: Contrasting biogeochemistry of nitrogen in the Atlantic and Pacific Oxygen Minimum Zones, Biogeosciences, 9, 203–215, https://doi.org/10.5194/bg-9-203-2012, 2012.
Seitzinger, S. P. and Giblin, A. E.: Estimating denitrification in North Atlantic continental shelf sediments, Biogeochemistry, 35, 235–260, https://doi.org/10.1007/BF02179829, 1996.
Shiozaki, T., Bombar, D., Riemann, L., Hashihama, F., Takeda, S., Yamaguchi, T., Ehama, M., Hamasaki, K., and Furuya, K.: Basin scale variability of active diazotrophs and nitrogen fixation in the North Pacific, from the tropics to the subarctic Bering Sea, Global Biogeochem. Cy., 31, 996–1009, https://doi.org/10.1002/2017GB005681, 2017.
Sigman, D. M., DiFiore, P. J., Hain, M. P., Deutsch, C., Wang, Y., Karl, D. M., Knapp, A. N., Lehmann, M. F., and Pantoja, S.: The dual isotopes of deep nitrate as a constraint on the cycle and budget of oceanic fixed nitrogen, Deep-Sea Res. Pt. I, 56, 1419–1439, https://doi.org/10.1016/j.dsr.2009.04.007, 2009.
Somes, C. J. and Oschlies, A.: On the influence of “non-Redfield” dissolved organic nutrient dynamics on the spatial distribution of N2 fixation and the size of the marine fixed nitrogen inventory, Global Biogeochem. Cy., 29, 973–993, https://doi.org/10.1002/2014GB005050, 2015.
Somes, C. J., Schmittner, A., Galbraith, E. D., Lehmann, M. F., Altabet, M. A., Montoya, J. P., Letelier, R. M., Mix, A. C., Bourbonnais, A., and Eby, M.: Simulating the global distribution of nitrogen isotopes in the ocean, Global Biogeochem. Cy., 24, GB4019, https://doi.org/10.1029/2009GB003767, 2010.
Strous, M., Fuerst, J. A., Kramer, E. H. M., Logemann, S., Muyzer, G., van de Pas-Schoonen, K. T., Webb, R., Kuenen, J. G., and Jetten, M. S. M.: Missing lithotroph identified as new planctomycete, Nature, 400, 446–449, https://doi.org/10.1038/22749, 1999.
Van Mooy, B. A. S., Keil, R. G., and Devol, A. H.: Impact of suboxia on sinking particulate organic carbon: Enhanced carbon flux and preferential degradation of amino acids via denitrification, Geochim. Cosmochim. Ac., 66, 457–465, https://doi.org/10.1016/S0016-7037(01)00787-6, 2002.
Ward, B. B.: How Nitrogen Is Lost, Science, 341, 352–353, https://doi.org/10.1126/science.1240314, 2013.
Westberry, T., Behrenfeld, M. J., Siegel, D. A., and Boss, E.: Carbon-based primary productivity modeling with vertically resolved photoacclimation, Global Biogeochem. Cy., 22, GB2024, https://doi.org/10.1029/2007GB003078, 2008.