the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Technical Note: Isotopic corrections for the radiocarbon composition of CO2 in the soil gas environment must account for diffusion and diffusive mixing
Jocelyn E. Egan
David R. Bowling
David A. Risk
Earth system scientists working with radiocarbon in organic samples use a stable carbon isotope (δ13C) correction to account for mass-dependent fractionation, but it has not been evaluated for the soil gas environment, wherein both diffusive gas transport and diffusive mixing are important. Using theory and an analytical soil gas transport model, we demonstrate that the conventional correction is inappropriate for interpreting the radioisotopic composition of CO2 from biological production because it does not account for important gas transport mechanisms. Based on theory used to interpret δ13C of soil production from soil CO2, we propose a new solution for radiocarbon applications in the soil gas environment that fully accounts for both mass-dependent diffusion and mass-independent diffusive mixing.
Radiocarbon allows us to measure the age of soil-respired CO2 (CO2 diffusing from the soil surface to the atmosphere, also called soil flux as in Cerling et al., 1991), but the traditional reporting convention for radiocarbon was not established for soil gas-phase sampling; rather, it was established for solid (organic matter) sample analysis. The validity of this convention has never been explicitly tested for soil-respired CO2.
The traditional radiocarbon reporting convention, Δ14C (Stuiver and Polach, 1977), uses a mass-dependent correction based on the isotopic composition of wood. Its purpose is to correct for biochemical fractionation against the radiocarbon isotopologue (14CO2) abundance during photosynthesis, which is assumed to be twice as strong as for 13CO2 based on their respective departures in molecular mass from 12CO2. The classical reference describing these conventional calculations is Stuiver and Polach (1977).
In the soil gas environment, researchers have different implicit expectations for fractionation processes. They generally assume that 14C of CO2 is not biochemically fractionated in the gas phase between the points of CO2 production (biological production of CO2 by soil organisms and roots) and measurement (subsurface or flux chamber samples). This assumption is reasonable based on the short residence time of CO2 (minutes to days) in the soil profile before emission to the atmosphere. However, soil gas isotopic signatures depart in predictable ways from the signature of production because of physical fractionation. It has been recognized for decades that δ13C of CO2 at any point in the soil profile will never equal the isotopic signature of production because of transport fractionations that alter produced CO2 before it is measured (Cerling et al., 1991). This theory readily extends to 14C.
We argue here that in the case of soil pore space 14C in which mixing of air masses occurs, the assumption that mass-dependent fractionation is twice as large for 14C as δ13C by biochemical and physical processes no longer holds. Using theory and the physical modeling of soil gas transport to illustrate the issue with the current reporting convention correction, we propose an alternative approach for specific use cases.
To understand why the mass-dependent correction used in the Stuiver and Polach (1977) radiocarbon reporting convention may be a poor fit for soil gas studies, we can look at our current understanding of the stable isotopic composition, δ13C, of soil CO2 (pore space CO2, mole fraction with respect to dry air). We use delta notation to present the stable isotopic composition of CO2:
where δ13C is the isotopic composition in per mill (see Table 1 for a full list of abbreviations), Rs is the 13C∕12C ratio of the sample, and RVPDB is the 13C∕12C ratio of the international standard, Vienna Pee Dee Belemnite.
Table 1List of symbols used. Note that the isotope composition ratios are also unitless but traditionally expressed using per mill (‰) notation.
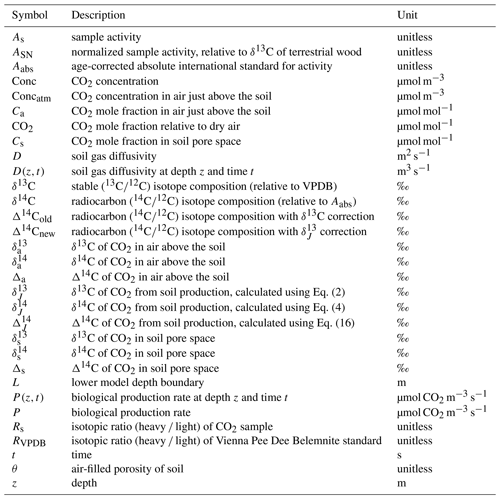
From foundational work done by Cerling et al. (1991) we know that the isotopic composition of soil CO2 is different from that of soil-respired CO2. Any change in δ13C of soil CO2 with depth is influenced by (1) mixing of atmospheric and biological (or biogeochemical) sources of isotopically distinct CO2, which may occur via diffusion (no bulk gas flow; referred to as diffusive mixing for the remainder of the paper) or advection (bulk gas flow), and (2) kinetic fractionation by diffusion. The effect of these is illustrated in Fig. 1 using a simulated soil gas profile. In panel (a) two depth profiles of δ13C of CO2 that were modeled in a steady-state environment are shown (the model will be described in Sect. 3). The profiles differ only in soil diffusivity; all other characteristics were held constant, including rates of production, δ13C of CO2 in the atmosphere (−8 ‰; circle), and biological production (−25 ‰; square with dashed line). In the resultant depth profile with higher soil diffusivity in panel (a), the δ13C of soil CO2 ranges from −8 ‰ to −15.1 ‰. In the depth profile representing a soil with lower diffusivity, the δ13C of soil CO2 ranges from −8 ‰ to −20.6 ‰. We stress again that these two isotopic depth profiles differ only due to differences in transport as a result of their varying soil diffusivities. In the depth profile with lower soil diffusivity, atmospheric CO2 does not penetrate downwards as readily, so the profile shape is much steeper near the soil–atmosphere boundary and is more reflective of the production source composition, −25 ‰, at depth. In the depth profile with higher soil diffusivity, atmospheric air of −8 ‰ more readily mixes from the surface downward by diffusion, so the near-surface isotopic composition will be more reflective of the atmosphere due to diffusive mixing of these end-members near the soil surface.
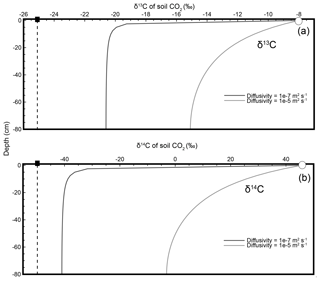
Figure 1Modeled steady-state diffusive vertical depth profiles for δ13C and δ14C of soil CO2. In panel (a) the δ13C of atmospheric CO2 (circle) is −8 ‰ and CO2 from biological production (square with dashed line; δJ) is −25 ‰. In panel (b) the δ14C of atmospheric CO2 (circle) is 45.5 ‰ and CO2 from biological production (square with dashed line) is −50 ‰. Both profiles have the same biological production rates and isotopic composition of biological production, but each profile has a different soil diffusivity as indicated.
Importantly, the soil CO2 never equals the δ13C of production (−25 ‰) at any depth in either profile in Fig. 1a. It is not possible to directly measure δ13C of production in situ because diffusion and diffusive mixing alter the character of CO2 immediately after its production. From the site of production in the soil, 12CO2 diffuses somewhat faster through the soil than 13CO2 because the former has a lower mass. This diffusive difference leads to isotopic fractionation and results in depth profiles of δ13C of soil CO2 that are isotopically enriched (less negative) compared to the source of production. Work by Cerling (1984) and later by Cerling et al. (1991) demonstrated that the mass differences between the two isotopologues led to a difference in the diffusion rate of each in air, amounting to a fractionation of 4.4 ‰ (note that this applies only to binary diffusion of CO2 in air and will differ if CO2 diffuses in other gases). As a result, the δ13C of soil CO2 measured at any depth will be enriched by a minimum of 4.4 ‰ relative to the biological production CO2 source. However, the δ13C of soil-respired CO2 can be considerably more enriched than 4.4 ‰ relative to production due to diffusive mixing with the atmosphere as shown in Fig. 1a.
A convenient theoretical formulation for correcting δ13C for both diffusion fractionation and diffusive mixing was introduced by Davidson (1995), following on the work of Cerling (1984) and Cerling et al. (1991). This approach allows one to combine measurements of CO2 and its isotopic composition within the soil and the air above it to infer the isotopic composition of CO2 produced in the soil. This only applies when transport within the soil is purely by diffusion (no bulk air movement). The Davidson (Davidson, 1995) solution uses the difference between the diffusion coefficients for 12C and 13C as follows:
where is the δ13C composition of CO2 from soil production (biological respiration within the soil), Cs and are the mole fraction and isotopic composition of soil CO2, and Ca and are the mole fraction and isotopic composition of CO2 in the air just above the soil. In Fig. 2a the mole fraction and isotopic composition of soil CO2 at a 40 cm depth and of the air just above the soil were “sampled” from model-generated soil depth profiles and the (unrounded) values were used to calculate the isotopic composition of production using Davidson's equation (Cs= 14 780 ppm, ‰, Ca=380 ppm, and ‰). The resulting (e.g., Eq. 2) at this depth equals the true isotopic composition of production (see inset box, Fig. 2a). However, because the Davidson approach accounts for diffusion and diffusive mixing, at any given soil depth, not just 40 cm, the modeled values of Cs and in Figs. 1a and 2a will always yield (via Eq. 2) the true isotopic composition of production, ‰ (dashed line). If δ13C of soil CO2 were (erroneously) interpreted to represent the δ13C of soil-respired CO2, the error could be as large as the absolute value of ( ‰. This Davidson (1995) approach has been shown to be robust when applied to field data from natural soils (Breecker et al., 2012; Bowling et al., 2015; Liang et al., 2016).
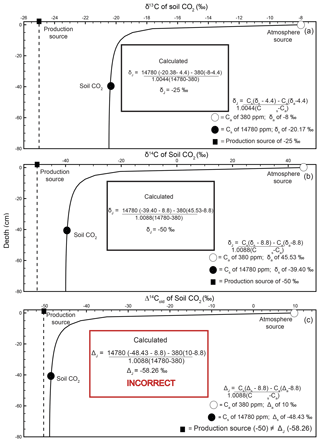
Figure 2Modeled steady-state diffusive vertical depth profiles for δ13C (a), δ14C (b), and Δ14Cold (c) of soil CO2. The three soil profiles were generated using the same soil production and diffusivity rates (2 µmol m−3 s−1 and m2 s−1, respectively). Panels (a) and (b) were prepared using δ13C and δ14C as noted. Panel (c) shows an approach consistent with present day, whereby the Δ14C profile generated by the model incorporates the traditional Stuiver and Polach (1974) correction for biochemical fractionation. Inset “Calculated” panels show how, using input data read directly from each depth profile, a user would arrive at either the correct or incorrect isotopic value of production using a Davidson approach to adjust for in-soil gas transport. The atmospheric source (Ca) composition is presented as a white circle, the soil CO2 composition (Cs) is a black circle, and the isotopic composition of production is a black square. Note that values for the isotopic composition of soil in the three panels are rounded for ease of reading but are actually −20.3832 ‰, −39.3989 ‰, and −48.4319 ‰, respectively, for panels (a–c). These values are drawn from the curve at a depth of 40 cm.
While 14C is a radioactive isotope and thus decays with time, the half-life is sufficiently long so that 14CO2 behaves similarly to stable isotopes on the timescales at which diffusion occurs in a soil gas system. In this way, δ13C diffusive fractionation theory can be applied to the radiocarbon isotopic composition, δ14C, so long as we account for the mass difference. The larger mass of 14C means that the diffusion fractionation factor is calculated to be 8.8 ‰ based on the atomic masses of 14CO2, 12CO2, and bulk air (Southon, 2011).
We can show that the 14CO2 distribution in soils will be like that of 13CO2 if we model its distribution through depth in the same synthetic soil gas environment. In Fig. 1b we present a modeled soil environment with defined atmospheric and production source CO2 isotopic composition boundary conditions for δ14C, the 14C equivalent to δ13C (Stuiver and Polach, 1977):
where δ14C is the isotopic composition in per mill, As is the measured activity of the sample, and Aabs is the activity of the oxalic acid standard (both unitless). As in Fig. 1a, in panel (b), the profile with lower soil diffusivity, the downward penetration of atmospheric CO2 into the soil profile is reduced, and as a consequence the isotopic depth profile more closely reflects (but does not equal) the composition of production (−50 ‰; dashed line). When the diffusion rate is high and transport is rapid, the atmospheric source is more readily able to penetrate the profile and mix with the production source. In both profiles, the measured value of soil CO2 at a given depth will not equal the isotopic production value of −50 ‰ because of diffusion and diffusive mixing. Similar profiles of δ14C of soil CO2 with depth, highlighting the diffusive effects, have been presented by Wang et al. (1994).
Since δ14C transport of soil CO2 is like that of δ13C, it follows that we should apply corrections for δ14C like those in Eq. (2) in order to calculate the isotopic composition of production. The δ14C reformulation of Davidson's equation is as follows:
where is the δ14C composition of soil production, Cs and are the mole fraction and δ14C composition of the soil CO2, and Ca and are the mole fraction and δ14C composition of CO2 in the air just above the soil. This Davidson reformulation for δ14C, , was applied to a model-generated profile of soil δ14C at a 40 cm depth in Fig. 2b, like in panel (a) for δ13C (Cs= 14 780 ppm, ‰, Ca=380 ppm, and ‰; see inset box, Fig. 2b). As was the case for δ13C in Fig. 2a, the modeled values of Cs and at any depth will yield the true isotopic composition of production, −50 ‰ (dashed line), because this approach accounts for diffusion and diffusive mixing.
The typical approach that has been used for interpreting the 14C composition of soil CO2 and soil-respired CO2 (e.g., Trumbore, 2000) differs from the δ14C example above because a δ13C correction is applied to account for the mass-dependent isotopic fractionation of biochemical origin, ultimately converting δ14C to a variant called Δ14C (Stuiver and Polach, 1977). The derivation of the mass-dependent correction is provided in Stuiver and Robinson (1974), wherein observations are normalized to an arbitrary baseline value of −25 ‰ for δ13C (a value for terrestrial wood), and the 13C fractionation factors are squared to account for the 14C∕12C fractionation factor as follows:
where ASN is the normalized sample activity, As is the sample activity, and δ13C is the isotopic composition of the sample (soil CO2 in our case). As explained in Stuiver and Robinson (1974), the 0.975 term sometimes used in forms of ASN is equivalent to , which we will retain for clarity. The equation for Δ14C, the δ13C-corrected variant of δ14C, can then be created from Eq. (5) by substituting in delta notation for Δ14C of Δ14C = (ASN∕Aabs -1) × 1000 following Stuiver and Robinson (1974):
Combining Eqs. (3) and (6) leads to
For more information on the derivation of Eqs. (6) and (7) see Stuiver and Robinson (1974), page 88. In Eq. (7) we have added the subscript “old” to highlight that this is the common approach used to date for soil gas applications – we will introduce a “new” method with Eq. (15). The terms on the left-hand side of Eqs. (6) and (7) are identical. Note that Aabs in our notation is equivalent to AO in Stuiver and Robinson (1974).
Equation (7) uses δ13C as an input parameter to make a mass-dependent correction to obtain Δ14C, but the profiles of δ13C and δ14C of soil CO2 (Fig. 1) highlight the fact that both vary within the soil because of diffusion and diffusive mixing. This makes it unclear what form of δ13C should actually be used in the place of the mass-dependent correction in the soil gas environment (δ13C of the soil CO2 is measured but δ13C of biological production is not) as diffusive mixing is not a mass-dependent process. When Δ14Cold is modeled through depth like δ13C and δ14C in Figs. 1 and 2 it also varies with depth as shown in Fig. 2c. However, using a Δ14C variant of Davidson's δJ (as for δ14C in Fig. 2b) at the same 40 cm depth does not correctly reproduce the specified model value for the Δ14C of production of −50 ‰ like it did for δ13C and δ14C (Cs= 14 780 ppm, ‰, Ca=380 ppm, and Δa=10 ‰; see inset box, 2c). We therefore adapted the mass-dependent correction in Δ14Cold using Davidson's (1995) theory to demonstrate how and why it should be used for Δ14C soil gas applications.
We used an analytical gas transport model to simulate a range of natural soil profiles of 12CO2, 13CO2, and 14CO2 in order to present soil gas transport theory. The model is based on Fick's second law of diffusion:
where θ is the soil air-filled pore space, Conc is the concentration, t is time, D(z,t) is the soil gas diffusion function, and P(z,t) is the biological production function, with the latter two dependent on both depth z and time t.
The model was run in steady state,
and both diffusion and production rates were constant with depth:
The following boundary conditions were used:
where Concatm is the concentration of CO2 in air just above the soil and L is the model lower spatial boundary, the point below which no production or diffusion occurs. Equation (8) is solved analytically to yield the following equation:
In the model, isotopologues of CO2 are treated as independent gases, with their own specific concentration gradients and diffusion rates (Cerling et al., 1991; Risk and Kellman, 2008; Nickerson and Risk, 2009). We assume total CO2 to be 12CO2 because of its high abundance. The error associated with this assumption is less than 0.01 % (Amundson et al., 1998). Equation (14) is thus applied for 13CO2 and 14CO2. For the full derivation see Nickerson et al. (2014) Sect. 2.3.
The analytical gas transport model was applied across a range of soil diffusivity (, , and m2 s−1) and soil production rates (0.5, 1, 2, and 4 µmol CO2 m−3 s−1). The specific soil diffusivity and production rates used to generate each profile are stated in the figure caption of that profile. We used a δ13C of biological production (−25 ‰) and atmospheric CO2 (δa; −8‰) and Δ14C of biological production (−50 ‰) and atmospheric CO2 (Δa; 10 ‰) to represent realistic conditions found in nature. The other model boundary conditions were as follows: L=0.8 m, z=0.025 m, and Concatm= 15 833 µmol m−3 (∼380 ppm). The output of the model under these applied conditions were profiles of 12CO2, 13CO2, and 14CO2 for each depth (z) down to the bottom boundary (L).
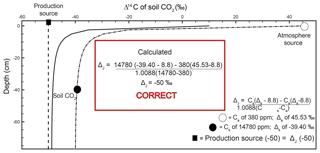
Figure 3Modeled steady-state diffusive vertical depth profiles for Δ14Cold (solid line; same profile as in Fig. 2c) and Δ14Cnew (dashed line) of soil CO2. The Δ14Cnew soil profile was calculated from the profiles in Fig. 2 (soil production and diffusivity rates of 2 µmol m−3 s−1 and m2 s−1, respectively). The inset “Calculated” panels show how, using input data read directly from the depth profile of Δ14Cnew, a user would arrive at the correct value of production using a Davidson approach to adjust for in-soil gas transport. The atmospheric source (Ca) composition is presented as a white circle, the soil CO2 composition (Cs) is a black circle, and the isotopic composition of production is a black square. Note that values for the isotopic composition of soil and atmosphere are rounded for ease of reading but are actually −39.3989 ‰ and 45.5276 ‰, respectively. These values are drawn from the curve at a depth of 40 cm.
4.1 Adapted correction for interpreting radiocarbon values of soil and soil-respired CO2
Based on Davidson's (1995) theory and what we demonstrated with Fig. 2c, rather than using the δ13C soil pore space as a mass-dependent correction, we suggest instead using the value (Eq. 2), the biological production of δ13C, in its place in the denominator of Eq. (7) as follows:
Values of Δ14Cnew through depth represent transport-fractionation-corrected soil CO2 values of radiocarbon, and in comparison to Δ14Cold, they are corrected for mass-independent diffusive mixing.
A depth profile of Δ14Cnew is presented in Fig. 3 (dashed line). To generate this soil depth profile we used the numbers from the simulated profiles in Fig. 2 and inserted them into Eq. (2) to determine at each depth. These values were then used in Eq. (15) to obtain Δ14Cnew of soil CO2 through depth. The Δ14Cnew profile (dashed line) is more isotopically enriched compared to the Δ14Cold profile (solid line) in Fig. 3. Values sampled from the Δ14Cold profile (the same as the one presented in Fig. 2c) were not able to reproduce the specified model value for the Δ14C of production of −50 ‰ using a Δ14C variant of Davidson's δJ. To demonstrate that Δ14Cnew does correct for gas transport fractionations, it can be placed into , a Δ14C adaption of Davidson (1995) for 14C (Eq. 4), as follows:
where is the Δ14C composition of soil production, Cs and Δ14Cnew are the mole fraction and Δ14C composition of the soil CO2, and Ca and are the mole fraction and Δ14C composition of CO2 in the air just above the soil.
Unlike in the case of Δ14Cold demonstrated in the inset box in Fig. 2c, using the same 40 cm depth from the Δ14Cnew profile, we were able to reproduce the specified model value for the Δ14C of production of −50 ‰ (Cs= 1 780 ppm, ‰, Ca=380 ppm, and Δa=45.5276 ‰; see inset box, Fig. 3).
4.2 Work-arounds and establishing new best practice
In the soil gas environment, Δ14Cnew convention should be used to properly interpret soil-respired CO2 from soil CO2, as it corrects for all related transport fractionations. For researchers who have soil CO2 data previously interpreted using Δ14Cold, the following steps will help correct for transport fractionations: (1) use and Δ14Cold to back out the activity of the sample (As); (2) calculate the isotopic composition of production for δ13C using Eq. (2), ; (3) use and As in Eq. (7) to calculate Δ14Cnew; and finally (4) determine the radiocarbon isotopic composition of production using Eq. (16), .
Going forward, several changes to best practice are recommended. On a lab level, for new soil CO2 data, we propose that laboratories report radiocarbon using Eq. (3) for δ14C, the uncorrected radiocarbon variant, so that the first step above (use and Δ14Cold to back out the activity of the sample; As) can be avoided, and researchers can proceed with steps 2–4. We also suggest that researchers measure δ13 alongside Δ14C so that they are not dependent on the AMS-measured δ13 for potential back corrections.
The Davidson (1995) δJ method was the gradient approach we used in our study, but alternative gradient approaches, such as those presented for δ13C by Goffin et al. (2014) and Nickerson et al. (2014) and for Δ14C by Phillips et al. (2013), would likely be similarly successful in producing depth-dependent compositions of production. They are, however, not quite as straightforward as the δJ method.
This traditional Δ14C solution, which uses δ13C of soil CO2 as a mass-dependent correction, is not appropriate for the soil gas environment, as it does not account for mass-independent mixing processes. We propose a new best practice for Δ14C work in the soil gas environment that accounts for gas transport fractionations and produces true estimates of Δ14C of production.
No data sets were used in this article.
JEE, DRB, and DAR conceptualized the theory and method for proving the new solution for radiocarbon applications in the soil gas environment. JEE carried out the modeling, validation, visualization, and writing of the original draft. DRB, DAR, and JEE reviewed and edited the draft.
The authors declare that they have no conflict of interest.
Thanks to Thure Cerling for helpful discussions on the paper and to anonymous reviewers whose input was important in shaping the final presentation of this material.
Jocelyn E. Egan is grateful for support from a Research-in-Residence Award from the Inter-University Training in Continental-scale Ecology Project, National Science Foundation, Directorate for Biological Sciences (grant no. EF-1137336). Jocelyn E. Egan was also funded by the Natural Sciences and Engineering Research Council of Canada (NSERC). This research was also supported by the US Department of Energy, Office of Science (grant no. DE-SC0010625).
This paper was edited by Dan Yakir and reviewed by three anonymous referees.
Bowling, D. R., Egan, J. E., Hall, S. J., and Risk, D. A.: Environmental forcing does not induce diel or synoptic variation in the carbon isotope content of forest soil respiration, Biogeosciences, 12, 5143–5160, https://doi.org/10.5194/bg-12-5143-2015, 2015.
Breecker, D. O., Payne, A. E., Quade, J., Banner, J. L., Ball, C. E., Meyer, K. W. and Cowan, B. D.: The sources and sinks of CO2 in caves under mixed woodland and grassland vegetation, Geochim. Cosmochim. Ac., 96, 230–246, https://doi.org/10.1016/j.gca.2012.08.023, 2012.
Cerling, T. E.: The stable isotopic composition of modern soil carbonate and its relationship to climate, Earth Planet. Sc. Lett., 71, 229–240, 1984.
Cerling, T. E., Solomon, K. D., Quade, J., and Bowman, J. R.: On the isotopic composition of carbon in soil carbon dioxide, Geochim. Cosmochim. Ac., 55, 3403–3405, 1991.
Davidson, G. R.: The stable isotopic composition and measurement of carbon in soil CO2, Geochim. Cosmochim. Ac., 59, 2485–2489, 1995.
Goffin, S., Aubinet, M., Maier, M., Plain, C., Schack-Kirchner, H., and Longdoz, B.: Characterization of the soil CO2 production and its carbon isotope composition in forest soil layers using the flux-gradient approach, Agric. Forest Meteorol., 188, 45–57, https://doi.org/10.1016/j.agrformet.2013.11.005, 2014.
Liang, L. L., Riveros-Iregui, D. A., and Risk, D. A.: Spatial and seasonal variabilities of the stable carbon isotope composition of soil CO2 concentration and flux in complex terrain, J. Geophys. Res.-Biogeo., 121, 2015JG003193, https://doi.org/10.1002/2015JG003193, 2016.
Nickerson, N. and Risk, D.: Physical controls on the isotopic composition of soil-respired CO2, J. Geophys. Res., 114,https://doi.org/10.1029/2008JG000766, 2009.
Nickerson, N., Egan, J., and Risk, D.: Subsurface approaches for measuring soil CO2 isotopologue flux: Theory and application, J. Geophys. Res.-Biogeo., 119, 2013JG002508, https://doi.org/10.1002/2013JG002508, 2014.
Phillips, C. L., McFarlane, K. J., Risk, D., and Desai, A. R.: Biological and physical influences on soil 14CO2 seasonal dynamics in a temperate hardwood forest, Biogeosciences, 10, 7999–8012, https://doi.org/10.5194/bg-10-7999-2013, 2013.
Risk, D. and Kellman, L.: Isotopic fractionation in non-equilibrium diffusive environments, Geophys. Res. Lett., 35, https://doi.org/10.1029/2007GL032374, 2008.
Southon, J. R.: Are the fractionation corrections correct: Are the isotopic shifts for 14C∕12C ratios in physical processes and chemical reactions really twice those for 13C∕12C?, Radiocarbon, 53, 691–704, 2011.
Stuiver, M. and Polach, H. A.: Discussion: Reporting of 14C Data, Radiocarbon, 19, 355–363, 1977.
Stuiver, M. and Robinson, S. W.: University of Washington Geosecs North Atlantic carbon-14 results, Earth Planet. Sc. Lett., 23, 87–90, 1974.
Trumbore, S.: Age of soil organic matter and soil respiration: radiocarbon constraints on belowground C dynamics, Ecol. Appl., 10, 399–411, 2000.
Wang, Y., Amundson, R., and Trumbore, S.: A model for soil 14CO2 and its implications for using 14C to date pedogenic carbonate, Geochim. Cosmochim. Ac., 58, 393–399, 1994.





