the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Theoretical uncertainties for global satellite-derived burned area estimates
Jose L. Gómez-Dans
Mathias Disney
Philip Lewis
Quantitative information on the error properties of global satellite-derived burned area (BA) products is essential for evaluating the quality of these products, e.g. against modelled BA estimates. We estimate theoretical uncertainties for three widely used global satellite-derived BA products using a multiplicative triple collocation error model. The approach provides spatially unique uncertainties at 1∘ for the Moderate Resolution Imaging Spectroradiometer (MODIS) Collection 6 burned area product (MCD64), the MODIS Collection 5.1 (MCD45) product, and the European Space Agency (ESA) Climate Change Initiative Fire product version 5.0 (FireCCI50) for 2001–2013. The uncertainties on mean global burned area for three products are km2 for MCD64, km2 for FireCCI50, and km2 for MCD45. These correspond to relative uncertainties of 4 %–5.5 % and also indicate previous uncertainty estimates to be underestimated. Relative uncertainties are 8 %–10 % in Africa and Australia, for example, and larger in regions with less annual burned area. The method provides uncertainties that are likely to be more consistent with modelling and data analysis studies due to their spatially explicit properties. These properties are also intended to allow spatially explicit validation of current burned area products.
Several global satellite-derived burned area (BA) products have been generated for the past two decades. These products, generated from coarse spatial resolution (250–1000 m) satellite imagery, have provided vital information to fire-related disciplines (Mouillot et al., 2014). They have provided new information on global pyrogeography and changes in fire occurrence (Archibald et al., 2013; Andela et al., 2017), been used to calibrate and validate fire models within dynamic global vegetation models (DGVMs) (Thonicke et al., 2001; Hantson et al., 2016), as well as to drive “bottom-up” estimates of fire emissions (Seiler and Crutzen, 2008; van der Werf et al., 2017). Despite such value, the true information content of such datasets is still to be fully quantified. The trust that users can place into these products can be improved by providing estimates of product uncertainty. This entails providing a quantitative statement about the lack of knowledge of the true burned area – described by a probability density function (PDF) characterising the range and likelihood of possible values (IPCC, 2008; ISO/BPIM, 2008). Burned area products display large intra- and interannual differences in the magnitude and timing of fire activity (Giglio et al., 2010; Padilla et al., 2015). Humber et al. (2018) indicated that the range of total recorded burned area for 2005–2011 varied by 90 % between four global satellite-derived burned area products. These ranges imply considerable uncertainty in the global burned area satellite record. Previous burned area product intercomparison initiatives have attempted to explore and explain the spatial and temporal differences observed between different products. Large differences between product estimates have been highlighted in tropical regions, boreal Eurasia, and sub-Saharan Africa (Giglio et al., 2010; Humber et al., 2018). These divergences have been interpreted to be driven by differences in the observing properties of the satellites used to create products, as well as the mapping algorithms used within each product. A key determinant on the accuracy of burned area detection originates from the spatial mapping scale of products, with evidence that products produced from higher-resolution observations have reduced omission errors (Roy and Boschetti, 2009). Others have highlighted the importance of the temporal revisit time of the utilised satellite instrument (Boschetti et al., 2004). Similarly, the role of persistent cloud cover in some regions has been highlighted, with large divergences between burned area estimates in southeastern Asia ascribed to differences in algorithm observational requirements (Humber et al., 2018). Differences in algorithm decisions and assumptions have also been emphasised, with evidence that even non-vegetated areas (i.e. deserts) display burning for some products (Giglio et al., 2010).
While these intercomparison and validation exercises have provided insight into product performance, the global estimation of product uncertainties from such exercises is difficult. Even the largest and most sophisticated validation datasets correspond to only a small sampling of global fire activity, and it is not clear whether this is sufficient information to build an understanding of uncertainties at global and decadal scales. Uncertainty quantification (UQ) has been requested by users of burned area products for several years (Mouillot et al., 2014; Rabin et al., 2017). Fire modellers have indicated that the discrepancies between products and lack of systematic uncertainty information have restricted efforts for improving models. Poulter et al. (2015) considered the sensitivity of a dynamic global vegetation model to the driving satellite burned area product used. They indicated that the model displayed large sensitivities to deviations between the satellite products, and greater UQ would help to drive improvements in model development and benchmarking. Concerns have also been expressed about the calibration of fire models against burned area products which lack the necessary uncertainty information to evaluate model performance in a systematic manner against the observations (Knorr et al., 2014; Yue et al., 2014).
This paper addresses the requirement for uncertainties on global satellite-derived burned area by estimating the uncertainties of three widely used burned area products. Section 2 outlines the sources of uncertainties in burned area products and previous estimates of uncertainties. Section 3 then describes the uncertainty estimation procedure used here. Section 4 presents the results of the uncertainty model and compares the uncertainty estimates against two other available estimates of burned area uncertainties. Section 5 considers the assumptions of the error model used, and Sect. 6 discusses potential mechanisms for the reported uncertainties. Section 7 concludes the paper.
2.1 Sources of uncertainty
The production of global records of burned area involves the processing of considerable volumes of coarse-resolution satellite observations. Burned area products lie at the top of a measurement process involving the transformation of the initial satellite measurements to higher-level burned area inferences (Merchant et al., 2017). Uncertainties enter this measurement process at all levels. The initial satellite measurements are not error-free and these uncertainties are thus propagated through the burned area retrieval algorithm. In addition, the detection of changes and the attribution to burning naturally involve an uncertain inference on the state of the land surface.
The optical surface reflectance and thermal measurements used to map burned area have inherent uncertainties due to the measurement process. The optical surface reflectance products, for example, are themselves derived geophysical variables which involve the application of retrieval algorithms (e.g. atmospheric correction), introducing additional uncertainties into the measurement (Vermote et al., 2002).
The sampling provided by Earth-orbiting sensors contributes additional uncertainties. Satellite instruments collect measurements of an area of the land surface infrequently in time and from different acquisition geometries of the Sun and sensor. Variations in sampling geometry alter both the ground area sampled by the sensor and the apparent reflectance signal. The wide-swath instruments typically used to produce burned area products provide the temporal sampling necessary to detect the ephemeral signal of fire on the land surface. However, large variations in the sampling geometries from these sensors complicate the detection of changes in the land surface related to fire (Roy et al., 2005). Zhang et al. (2003) found that changes in the viewing geometries between pre- and post-fire reflectance resulted in enhanced difficulty of identifying burned areas in boreal forests. Similarly, variations in the area sampled led to a significant proportion of the recorded signal originating from outside of the pixel. Huang et al. (2002) indicated that the blurring due to the sensor point spread function (PSF) reduced the accuracy of land cover classifications by around 5 %.
The temporal sampling of the land surface is a key feature in the ability to resolve burned areas. Most significant for burned area mapping is the relationship between observation opportunity and the persistence of the burn signal on the land surface. This persistence is determined by the characteristics of the post-fire recovery of vegetation, as well as the dissipation of ash and char from the burn site. In boreal forests, an observable signal may last many years, savannas typically register a persistent signal for only a few weeks, and the subsequent ploughing of croplands may remove evidence for burning within a week (Trigg and Flasse, 2000; Sukhinin et al., 2004; Hall et al., 2016). The timely observation of the land surface pre- and post-fire then serves as a key determinant on the successful detection of burned areas. Melchiorre and Boschetti (2018) indicated that the median global persistence of an observable burn signal is 29 d, and that within 48 d 87 % of global burned area is undetectable.
The procedures and assumptions built into detection algorithms also determine the error properties of individual products. Burned area products display regional disparities in performance that are in line with differences in fire characteristics (Padilla et al., 2015). Developers of burned area products have previously highlighted limitations within their algorithms. Simon et al. (2004) indicated that parameters within their algorithm may lead to commission/omission errors in different regions. Roy et al. (2005) suggested that their algorithm may miss fires which display a rise in post-fire reflectance. And Giglio et al. (2009) suggested that the assumption of a decline in a post-fire vegetation index within their algorithm is not met in around 20 % of fires over validation data from northwestern Australia.
2.2 Present uncertainty estimates
Previous estimates of product uncertainties have been largely driven by validation initiatives. In these analyses, product commission and omission errors have been computed in comparison to reference datasets, which are typically generated by the manual or semi-automated mapping of area burned from higher-resolution images. The extents of these validation exercises range from regional comparisons against a few selected sites to larger global validation designs (Roy and Boschetti, 2009; Padilla et al., 2015, 2017; Boschetti et al., 2016). The derived validation statistics are then interpreted as providing estimates of the uncertainties of the product in light of these commission/omission statistics. The clearest example of this is the estimate of burned area standard error σA provided in the Global Fire Emissions Database (GFED) 4 product (Giglio et al., 2010):
where A is the aggregated burned area in the grid cell. cB serves as an uncertainty coefficient which scales the standard error based on an analysis of residuals against Landsat-validated burned area.
A natural concern that arises from these approaches is the quality of the sampling provided by such validation datasets. Even larger and more systematic validation efforts may still provide only a limited sampling of the true uncertainties. For example, the validation of products against 103 validation sites by Padilla et al. (2015) is derived from active fire observations, which display their own issues and uncertainties (Giglio et al., 2006a). Similarly, the challenge of generating sufficient validation data to enumerate global uncertainties in burned area is considerable. The estimated uncertainties provided by GFED4 are derived from three unique values for cB (covering Siberia, southern Africa, and the western United States), and regions not sharing sufficient similarities with these are given a median value of cB (Giglio et al., 2010). An additional limitation of the regional enumeration of cB is that it must replicate contributions from additional uncertainty sources. These will be features such as variations in cloud cover obscuring burned area detection and uncertainties arising from variations in the distribution and local mixture of vegetation type. This variability will alter the value of cB within each region.
An exception to this approach is provided by the European Space Agency (ESA) Climate Change Initiative Fire product version 5.0 (FireCCI50) which provides per-pixel estimates of uncertainty in the detection of burned areas (Chuvieco et al., 2018). These uncertainties are computed by considering a number of features of the detection problem such as the number of observations available and the magnitude of the reflectance change signal. These pixel-level uncertainties are then aggregated into the lower-resolution FireCCI50 product to provide per 0.25∘ grid cell standard errors. The validity of these standard errors will be dependent upon the quality of the per-pixel uncertainty estimates (in terms of modelling the true uncertainty) and the aggregation process from pixel to coarser grid cell scales (Bellprat et al., 2017).
In the absence of product-provided uncertainty estimates, others have also derived estimates of uncertainties. Le Page et al. (2015) proposed uncertainties of 25 %–50 % in burned area as provided by GFED4 based on an inspection of the GFED data. Most frequently, the range in burned area reported by different products has been used to provide upper and lower bounds on global burned area (Knorr et al., 2012; Poulter et al., 2015; Rabin et al., 2017; Forkel et al., 2019). The large uncertainty in global burned area implied by this figure contributes considerably to emission uncertainties (Knorr et al., 2012). It also introduces additional problems into the evaluation of the performance of fire models against satellite-derived observations (Rabin et al., 2017).
3.1 Burned area datasets
The present study estimates theoretical uncertainties for three global burned area products. The Moderate Resolution Imaging Spectroradiometer (MODIS) Collection 6 burned area product (MCD64C6) provides a global record of burned area for the MODIS period (i.e. 2000–present). The algorithm uses active fire observations to refine a classifier based on the application of a temporal change spectral index derived from MODIS short-wave infrared channels 5 (1230–1250 nm) and 7 (2105–2155 nm) (Giglio et al., 2018).
The MODIS Collection 5.1 burned area product (MCD45C5.1) was produced with a different algorithm and provides a global record of burned area for a reduced period covering 2000–2016. The product uses a multi-temporal modelling algorithm which flags for changes in the land surface based on differences between predicted and observed reflectance. The algorithm then filters changes to those that match the expected reflectance characteristics of burned surfaces in the near-infrared (841–876 nm) and short-wave infrared (1230–1250 nm) reflectance. The algorithm does not utilise active fire observations (Roy et al., 2005).
The ESA FireCCI50 product provides global burned area for 2001–2016. The algorithm uses changes in MODIS near-infrared (841–876 nm) surface reflectance inside a classifier that, like MCD64C6, is locally trained with active fire observations from the MODIS sensors (Chuvieco et al., 2018). The product is novel in that it provides burned area at a spatial resolution of 250 m compared to the 500 m spatial resolution of the other two products. This limits the algorithm to use only the red and near-infrared spectral bands.
The MCD45C5.1 product has now been deprecated by the Collection 6 MCD64 algorithm. The operational 1 km Copernicus burned area product was also considered; however, issues have been found in the product which has resulted in the product being withdrawn for reprocessing (Copernicus Global Land Service, 2019). The newer 300 m Copernicus burned area product covers a more limited temporal span from 2014 to the present. In terms of dataset selection, the three chosen products represent the longest available combined satellite record.
3.2 Computation of uncertainties
Stoffelen (1998) first proposed triple collocation (TC) as a method to estimate uncertainties in three collocated data products. The method has now been used across a considerable range of remote-sensing-derived geophysical variables including soil moisture, precipitation, leaf area index, and fraction of photosynthetically absorbed radiation (Fang et al., 2012; Roebeling et al., 2012; D'Odorico et al., 2014; Gruber et al., 2016). Consider three observational records of a variable with an unknown but true value T. The TC error model specifies that each observational record may be related to the truth via a linear measurement equation:
where α and β represent additive and multiplicative biases, respectively. ϵ denotes the residual (random) errors of the relation and is considered here to be normally distributed.
As posited, the three measurement equations indicate a system that is underdetermined. However, by making three assumptions, the system can be solved to provided estimates of the random errors of each product. First, each product is assumed to have zero mean residual errors (E[ϵ]=0). Second, the errors of each product are assumed to be uncorrelated (but not necessarily independent) with each other. Finally, the random error distribution is assumed to be uncorrelated with the true value T, as systematic errors are incorporated into β. The last assumption is not met for geophysical variables which show random errors that are functionally related to the magnitude of the signal (Tian et al., 2013).
Figure 1 shows mean annual burned area of the three products against individual product estimates. The shaded area represents the standard deviation between the products binned by the mean of the three products. It can be observed that the deviations between the products grow with the magnitude of burned area reported. This indicates that the constraint imposed on the burned area becomes more uncertain with the magnitude of burned area detected. This occurs because the random errors in burned area are heteroscedastic (Giglio et al., 2006b). The TC model in Eqs. (2–4) assumes, however, that the random errors ϵ are homoscedastic – in that the error variance model is not a function of the true (unobserved) burned area. This feature of the errors is common to several other geophysical variables (e.g. precipitation, aboveground biomass) (Tian et al., 2013; Alemohammad et al., 2015; Gonzalez de Tanago et al., 2018).
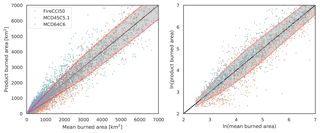
Figure 1Differences between the burned area reported by the three products and the mean of the three products. Also shown is the standard deviation of the products (grey) binned by the mean burned area of the three products. Increasing standard deviation with the magnitude of burned area implies heteroscedastic errors, while log-transformed burned areas have errors which are more homoscedastic.
In log space, however, the differences between products do not increase with the logarithmic burned area and are closer to being homoscedastic. Alemohammad et al. (2015) proposed that for heteroscedastic datasets, an alternative TC error model is suitable in which the random error is a multiplicative signal on the truth T. Instead, the error model for X can be related as
where α is a multiplicative error, β is the deformation error, and eϵ is the residual (random error). Taking the natural logarithm of Eq. (5) leads to an additive measurement model:
with the assumption that, in the log space, the random errors are normally distributed: . Representing x=ln(X) and t=ln(T), Eq. (6) is equivalent to
which provides a linear system equivalent to Eq. (2). Given the same assumptions of the classical TC method, the residual error estimates of each product (in log space) can be derived from the following manipulations of the sample covariance matrix C of the three log-transformed products (McColl et al., 2014):
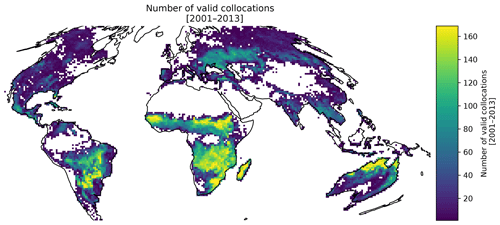
A requirement of the TC method is that the three datasets explicitly cover the same temporal and spatial domain and are of the same variable (Yilmaz and Crow, 2014). To achieve this, the three burned area datasets were aggregated to a shared temporal and spatial grid. The three products were aggregated from the original pixel resolution products to a common sinusoidal grid g with a resolution of 1∘ at the Equator. For each 16 d period between January 2001 and December 2013, the burned area reported by each product within the cell was aggregated to form a full temporal record for each cell through time of length Nt. The temporal span of the datasets provided potentially Nt=286 observations. A feature of solving the multiplicative error model in log space is that any product that reports no burned area will prevent the estimation of the covariance matrix C. As a result, any 16 d period where at least one product reported no reported burned area was excluded. This meant that approximately 40 % of cells globally had no agreed burned area between the products and therefore do not have error estimates. Nevertheless, the major fire regions are well sampled across the record (see Fig. 2). The TC method is able to sample the majority of the reported fire activity by the products. Total burned area over the study period for cells which do not have associated uncertainties is less than 0.5 % of the total burned area of each product.
3.2.1 Annualised uncertainties
Beyond product standard errors, annualised uncertainties on the total burned area are also of particular interest to the users of burned area products. To produce 16 d uncertainties in the burned area for each product, reconsider the error model specified in Eq. (5). The random errors back-transformed into burned area are defined by a log-normal distribution specified as log normal . Therefore, the distribution of 16 d burned area, P(X), can be defined in reference to Eq. (5) as
where Xo is the observed burned area for the product and Z the standard normal distribution. To produce an annual uncertainty estimate, each 16 d burned area distribution P(X) was sampled from and integrated over the year to provide a distribution of annual burned area for each grid cell. The independence assumption of individual observation errors in this scheme is also a requirement of the TC method (Gruber et al., 2016). To summarise the annual distribution, it was then approximated as a normal distribution based on matching the moments of the samples. Figure 3 shows an example of the procedure for producing 16 d and annualised uncertainties for an area covering northern Australia. Large absolute uncertainties are associated with the peak in the burning season here.
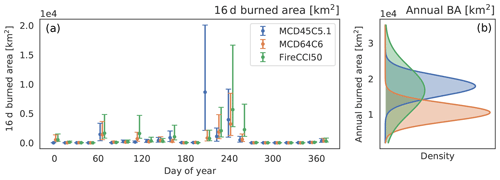
Figure 3The 16 d and annual uncertainties for a grid cell covering northern Australia. (a) The multiplicative error model provides unique uncertainties on each 16 d observation for each product (95 % confidence intervals shown). (b) To produce an annual uncertainty on the reported burned area, these are aggregated to produce an annual distribution which is then approximated as a normal distribution.
Given the regional variability in absolute burned area, the relative magnitude of the annual uncertainties to the reported burned area of each product was also considered. The relative uncertainty in mean annual burned area is defined by
where BAyear is the total burned area reported by the product for the grid cell for each individual year.
3.2.2 Regional and global uncertainties
Given that we may expect the performance of each product to vary with the local fire behaviour, we considered the uncertainty estimates with regard to the International Geosphere-Biosphere Programme (IGBP) land cover type classification provided in the MODIS Collection 6 land cover product (MCD12Q1.006) (Friedl et al., 2010). We simplified the University of Maryland (UMD) land cover classification into five more primary categories of (1) forest including all forest types, (2) croplands, (3) shrublands including both open and closed shrublands, (4) savannas, and (5) grasslands. The simplified land cover product was then aggregated to the sinusoidal 1∘ resolution grid by considering the dominant land cover type in each cell. We also considered product errors within the 14 fire regions specified by GFED which have been previously used for regional comparisons of burned area products (Giglio et al., 2013)
A complicating feature of the aggregation to the regional scales is that the spatial correlation of the uncertainties at the grid cell level is unknown. It would generally be expected that the uncertainties in adjacent grid cells may be similar due to correlations in the driving features of the uncertainties, e.g. land cover, cloud statistics and algorithmic limitations. The integration of grid-cell-level uncertainties via an independent quadrature summation would imply a strong constraint on there being no spatial correlation in the uncertainties (Bellprat et al., 2017). Instead, to produce the regional estimates, 16 d burned area for each product was aggregated for the whole region or land cover stratification and the TC error model then applied. This allows for the effective spatial error correlation in the products to be present in the regional uncertainties while requiring no additional assumptions about the error structure.
Figure 4 displays global maps of the residual errors (in log space) for each product. Spatial patterns in uncertainties show general similarities at broad scales. The patterns are also different from the spatial distribution of burning, indicating that systematic errors are not leaking into the random errors. The largest random errors for each product are located in eastern China, corresponding to regions of agricultural fires. Here, errors are greater than 1 for all products, which indicates a random error of greater than 100 % in the detected burned area. This would indicate that the level of agreement between the products is lower than the precision of the products.
Local patterns of the errors then diverge for each product. MCD45 has larger random errors in central and eastern Europe, in regions with predominantly agricultural fires. The lowest uncertainties are found in savanna ecosystems of Southern Hemisphere Africa and northern Australia. MCD64 shows the largest uncertainties in agricultural and tundra regions of eastern Eurasia. It also has the largest uncertainties in western Africa, in areas where deforestation fires are common. MCD64 has larger uncertainties in savannas relative to MCD45 and lower random errors in areas with agricultural burning. FireCCI has smaller errors in agricultural regions of eastern Eurasia compared to the other two products. FireCCI also has smaller random errors in regions of agricultural burning and deforestation areas around the Amazon compared to MCD45 and MCD64.
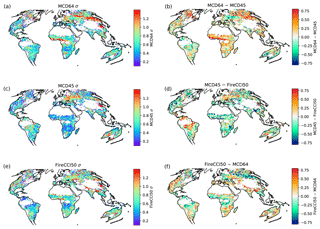
Figure 4(a, c, e) TC random errors for the three products and (b, d, f) differences between product random errors.
Figure 5 displays global maps of mean annual burned area and associated uncertainties for the three products. Between the products, similar spatial distributions in burned area and TC-estimated uncertainties can be observed. The heteroscedastic nature of burned area uncertainties is apparent with standard uncertainties scaling with the magnitude of burned area. Absolute uncertainties for each product are largest in sub-Saharan Africa and northern Australia which corresponds to regions with the greatest burned area. Greater disagreement in the magnitude of burning occurs in regions with less frequent burning or typically compounding factors on detection. In equatorial Asia, MCD64 and FireCCI50 detect, respectively, 1310 % and 940 % more burned area than MCD45. Greater detection by MCD64 here has been associated with the use of active fires (Humber et al., 2018). These higher estimates are also better constrained with relative uncertainties of 35 % and 36 %, respectively, for FireCCI50 and MCD64, compared to a higher relative uncertainty of 70 % on the MCD45 burned area. FireCCI50 detects 66 % more burned area in the agricultural burning regions of central and eastern Europe than MCD64 and 48 % more than MCD45. However, the large uncertainties on these estimates indicate them to be consistent within the uncertainties: with relative uncertainties of 141 % on FireCCI50, 168 % on MCD45, and 95 % on MCD64. Regions where MCD45 reports no burning prevents the estimation of TC uncertainties due to the requirement of the multiplicative error model used here. This is most noticeable in equatorial Asia and South America.
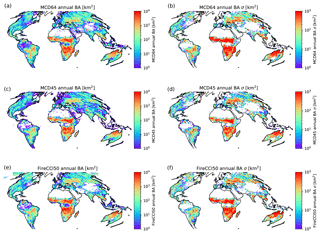
Figure 5(a, c, e) Mean annual burned area (km2) and (b, d, f) associated standard errors of mean annual burned area (km2).
Globally, MCD64 reports the greatest mean annual burned area ( km2). This is followed by FireCCI50 which reports km2 and MCD45 km2. In terms of relative uncertainties, MCD64 has the smallest relative uncertainty of 3.9 %, FireCCI50 has 4.5 %, and MCD45 has the largest uncertainty (5.5 %). MCD64 and MCD45 provide consistent estimates of mean annual burned area for 76 % of grid cells with TC-estimated uncertainties. In these locations, estimates from both products are within the range of standard uncertainties provided from the TC method. MCD64 and FireCCI50 agree across a slightly broader spatial extent, with 80 % of available cells agreeing within the uncertainties of each product. MCD45 and FireCCI50 have the lowest agreement of the three products, with consistent estimates across 72 % of TC cells. Figure 6 shows locations where all three products agree within their standard uncertainties for mean annual burned area. Overall, all three products agree within their uncertainties for 60 % of available TC cells. Within a broader distribution of two standard errors, the three products agree across 85 % of the valid cells. Regions where the products do not agree within 2 standard deviations are concentrated in equatorial Asia, the northern Amazon region, the southwestern United States, and parts of the Indian subcontinent.
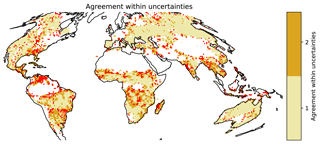
Figure 6Consistency of mean annual burned area for the three products. Light brown regions correspond to regions where all three products agree within 1 standard error. Brown regions correspond to agreement within 2 standard errors. Red regions indicate areas which do not agree within 2 standard errors.
Figure 7 shows a regional breakdown of mean annual burned area and uncertainties stratified by land cover. Globally, burned area estimates are most uncertain for cropland and shrublands for all products. All three products perform comparatively better in savannas and grasslands and less well in forested biomes. For nearly all land covers, MCD45 has the largest relative uncertainties of the three products. It has the largest uncertainties in shrublands, with a relative uncertainty of 25 %, followed by FireCCI50 (13 %) and then MCD64 (8 %). The uncertainty for the MCD45 product in shrublands is contributed to in large part by a poor constraint on burning in Australian (AUST) shrublands where the relative uncertainty exceeds 40 % ( km2), compared to 15 % and 8 % for the FireCCI50 and MCD64 products, respectively. FireCCI50 uncertainties in shrublands are driven by large uncertainties on comparatively small reported shrubland burned area in Central America (CEAM) of 765±1846 km2 and temperate North America (TENA) of 1175±2115 km2. This contrasts with much smaller uncertainties on a similar reported burned area from MCD64 in TENA 1172±449 km2.
All products have a poor constraint on global cropland burning with relative uncertainties of 8 %–10 %. MCD45 generally has the largest relative uncertainties on cropland burning across all fire regions, with confidence intervals larger than the magnitude of reported burned area for Europe (EURO), boreal Eurasia (BOAS), and equatorial Asia (EQAS). Exceptions are found in TENA and southeast Asia (SEAS), where MCD45 reports the most cropland burning and also has the lowest relative uncertainties.
An interesting feature occurs in boreal forest ecosystems, where MCD45 and FireCCI have smaller uncertainties in boreal Eurasian (BOAS) forests compared to boreal North American (BONA) forests. Uncertainties for MCD45 are around 2 times larger in BONA forests and 40 % larger for FireCCI50 in BOAS as compared to BONA forests. Alternatively, MCD64 has lower relative uncertainties in BONA compared to BOAS, with uncertainties 70 % larger in boreal Eurasia.
In the key burning regions of Northern Hemisphere (NHAF) and Southern Hemisphere Africa (SHAF), MCD45 typically has the most constrained estimate of burned area. The three products provide consistent estimates in grasslands and savannas in both regions, with reported burned area for each product agreeing within the uncertainties estimated for all products. The uncertainties are still considerable, however, with relative uncertainties for all three products largest in savannas and grasslands. In these land covers, relative uncertainties exceed 13 % in NHAF and 8 % in SHAF. This leads to broad standard errors on each product in NHAF, with reported mean annual burned area of km2 for MCD64, km2 for MCD45, and km2 for FireCCI50. Table 1 summarises the mean annual burned area and uncertainties by fire region.
Table 1Mean annual burned area (×103 km2), standard uncertainty (×103 km2), and relative uncertainty (%) for the products by fire region.
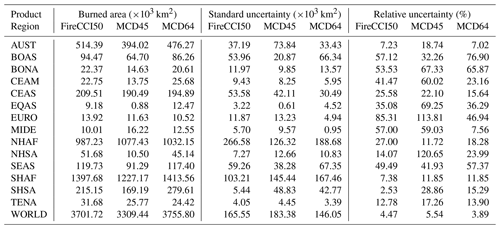
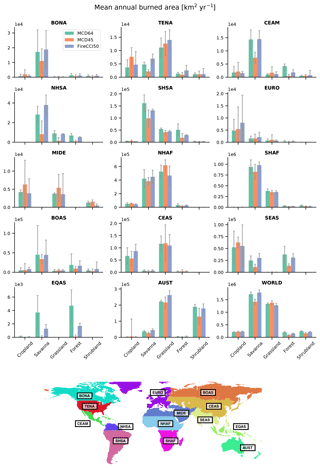
Figure 7Mean annual burned area and uncertainties (km2 yr−1) for the fire regions stratified by land cover: (BONA) boreal North America, (TENA) temperate North America, (CEAM) Central America, (NHSA) Northern Hemisphere South America, (SHSA) Southern Hemisphere South America, (EURO) Europe, (MIDE) Middle East, (NHAF) Northern Hemisphere Africa, (SHAF) Southern Hemisphere Africa, (BOAS) boreal Asia, (CEAS) central Asia, (SEAS) southeast Asia, (EQAS) equatorial Asia, (AUST) Australia and New Zealand.
4.1 Comparison against other uncertainty estimates
4.1.1 GFED4 uncertainties
We contrast the uncertainties from the TC method with two other available uncertainty estimates. First, in relation to the MCD64 product, we consider the uncertainties provided with the GFED4 burned area product. The GFED4 burned area and uncertainty are derived exclusively from the MCD64 product for the period considered here. GFED4, however, utilised the older MCD64 Collection 5.1 product, which detects significantly less global burned area than the present Collection 6 product (Giglio et al., 2018). Nevertheless, in the absence of other uncertainty estimates, it is sensible to consider the relative uncertainties for the GFED4 product against the TC estimates. To align the uncertainties with those provided by the TC method, the total annual burned area uncertainties were considered. To produce annual uncertainties for GFED4, the monthly variances provided by the GFED4 product were added in quadrature.
Figure 8 shows global differences between mean annual relative uncertainties in GFED4 vs. TC-derived uncertainties. TC uncertainties generally exceed GFED uncertainties in most regions. The global median for TC uncertainties is 38 % and GFED 34 %; however, mean global GFED uncertainties exceed those provided by the TC method. Mean global GFED uncertainties are 65 % compared to 45 % provided by the TC method, though this figure is skewed by a greater range in the GFED uncertainties (GFED interquartile range (IQR): 15 %–80 % vs. TC IQR: 26 %–57 %). Areas of higher TC uncertainties are found in the agricultural burning regions of northern China and eastern Russia, where TC uncertainties exceed GFED by 70 %–100 %. TC uncertainties also exceed GFED uncertainties in western Africa (90 %) and areas of North America, especially in boreal forest regions of eastern Canada. GFED uncertainties also exceed TC uncertainties in several regions. For example, GFED uncertainties are larger in boreal Eurasia (40 %–60 %), eastern India (30 %–70 %), and parts of South America (35 %–65 %).
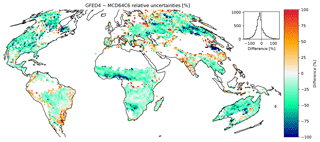
Figure 8Differences in relative uncertainties between GFED4- and TC-estimated relative uncertainties.
We conceive two probable causes for differences between the two uncertainty estimates. Primarily, GFED4 is based on an older collection of the MCD64 product which detected globally around 26 % less burned area than the present Collection 6 product (Giglio et al., 2018). An equally important consideration is that the uncertainty assumptions of the two methods are different. For the GFED uncertainties, Giglio et al. (2010) indicated that these are likely to be conservative due to the potential cancelling of omission and commission errors in the total reported burned area, with the effect being that GFED uncertainties are also likely overestimated for the MCD64 Collection 5.1 product. The TC method accounts for any potential cancelling of errors by focusing on the observed burned area irrespective of the error source.
4.1.2 FireCCI50 product uncertainties
The FireCCI50 climate model grid (CMG) product also provides standard errors per grid cell at the coarse spatial resolutions considered here. These are produced from an aggregation of individual uncertainties in the 250 m pixel product to produce fortnightly standard errors in burned area. In the same manner as with the GFED4 uncertainties, we produce annual uncertainties from the FireCCI50 product by adding the uncertainties in quadrature for each fortnightly product.
The uncertainties provided with the FireCCI50 product represent the first attempt to provide a full uncertainty traceability chain for burned area datasets. We find that the reported uncertainties are considerably smaller than those provided by the TC error model as well as the uncertainty estimates provided by GFED4. Figure 9 shows a comparison of relative uncertainties for TC-derived uncertainties and the uncertainties provided with the FireCCI50 product. TC uncertainties exceed product uncertainties in 98 % of the valid grid cells. Globally, the median relative uncertainty implied by the product is 2 % compared to 41 % from the TC uncertainties. The product uncertainties have a much smaller global range (IQR: 1 %–5 %) compared to the TC estimate (IQR: 27 %–58 %). The differences between TC uncertainties and product uncertainties are largest in cropland areas of northern China (150 %–200 %), eastern Russia (50 %–100 %), and eastern India (60 %–120 %). TC uncertainties are also around (70 %–100 %) larger in regions of the western United States.
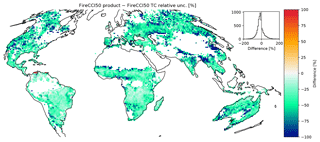
Figure 9Differences in relative uncertainties between product uncertainties for FireCCI50- and TC-estimated relative uncertainties.
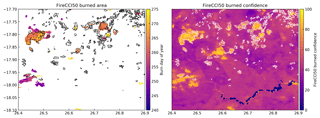
Figure 10 shows an example of the pixel-level uncertainties provided with the FireCCI50 product. Reference burned area is overlaid from the analysis of two Landsat acquisitions. We see that the product correctly detects the larger burn scars in the image extent. For these larger burn scars, the provided confidence is 70 %–100 %. However, smaller burn scars which are not classified as burned by the algorithm show burn probabilities which are similar to the unburned background (20 %–40 %). These values do not correspond well with the likely fire signal at these locations, with the apparent pattern in unburned confidence values arising from the interpretation of the composited observations used within the algorithm.
As previously indicated in Sect. 3.2, the TC error model has several key assumptions which must be considered. An initial requirement of the TC method is that the three products correspond to three temporally and spatially collocated data products. Here, this was achieved by considering the products at coarse spatial and temporal scales. The aggregation of daily pixel products to 16 d windows should help to reduce the influence of differences in reporting dates of fires between products. Similarly, the aggregation to a 1∘ spatial resolution grid reduces the chance of highly local differences in reported burned area and therefore should provide more robust estimates for each product. Nevertheless, due to the requirements of the TC method, around 40 % of global land cells do not have uncertainties – although this figure includes desert regions. Zwieback et al. (2012) indicated that the relative error in uncertainty estimates from the TC method can be approximated by , where n is the valid number of collocated observations used to compute the product covariance matrix. Users should be aware that the accuracy of uncertainties in regions with less frequent burning will therefore be lower than those regions with longer fire seasons. Given the available temporal span of the products, the mean global relative uncertainty in TC error estimates is expected to be around 33 %.
The most significant assumption of the TC method for the presented analysis is that the products do not have error cross-correlations (ECCs) (Zwieback et al., 2012; Gruber et al., 2016). ECC structures between burned area products may occur due to (1) the use of the same satellite instruments, (2) shared observation opportunity at the 1∘ spatial scale, and (3) similarities in the retrieval algorithms. We now consider each. A key concern is that the three products all utilise observations from the MODIS instruments. All three products utilise MODIS surface reflectance measurements, with FireCCI50 and MCD64 additionally using MODIS active fire detections. In terms of the second ECC source, grid cell uncertainty estimates may also be affected by the general observational opportunity available within the TC cell. Active fire products have a better sampling at higher latitudes relative to the Equator (Giglio et al., 2006b), and persistent cloudiness may introduce additional error correlations between the products. Finally, similarities within the mapping algorithms may introduce additional ECC sources. For example, similar thresholds on fire-related changes in reflectance may cause error correlations between the products. In regard to each source of potential ECCs, we judge that product uncertainties are most significantly determined by algorithmic decisions. This is because the three algorithms use considerably different decision structures for mapping the pixel-level burned areas. For example, while MCD64 and FireCCI41 both use active fire observations, the two algorithms utilise distinct expectations of fire properties in different spectral regions. Similarly, several intercomparison activities of these three products have indicated considerable differences between estimates at both the pixel-level product and regional burned area estimates (Padilla et al., 2015; Humber et al., 2018).
We also stress that the uncertainties estimated with the TC method likely represent a lower bound on the true uncertainties of these products. The TC measurement model can only explicitly estimate random errors but not systematic errors (i.e. bias) present in the data products from fires which are undetectable. The underestimation bias observed for these coarse-resolution products in validation studies indicates that the products likely have considerable systematic errors. Chuvieco et al. (2018) have estimated that the FireCCI50 product has global omission errors of 70 % and MCD64C6 of 62 %, which are partially balanced by commission errors of 50 % and 35 %, respectively. Roteta et al. (2019) also indicated that a higher-spatial-resolution 20 m burned area product provided 80 % more burned area than the MCD64C6 product for sub-Saharan Africa, which while not providing a true validation indicates considerable biases in coarse-resolution products. Users should therefore be aware that the likely systematic biases in coarse-resolution products mean that the TC uncertainties provide a lower bound on the true uncertainty.
This study has estimated theoretical uncertainties for three global satellite-derived burned area datasets. This study provides an update on ongoing efforts to provide quantitative uncertainties for remotely sensed global burned area estimates initiated with GFED4 (Giglio et al., 2006b) and continued within the FireCCI products (Chuvieco et al., 2018). Within the four-stage validation scheme developed for land remote sensing products developed by the Committee on Earth Observation Satellites (CEOS) Land Product Validation (LPV) group, the majority of current burned area products have only achieved stage-3 validation (Morisette et al., 2006; Boschetti et al., 2009, 2016; Padilla et al., 2017; Chuvieco et al., 2018). Meeting the stage-4 requirement for statistically robust and validated uncertainties remains an open challenge for the burned area community. While new large-scale validation datasets of burned area have been recently developed (Padilla et al., 2017; Chuvieco et al., 2018), these provide regional-to-global commission/omission error statistics which need to be interpolated with a statistical model of the measurement process to provide explicit spatiotemporally dense uncertainties (such as is done in GFED4). Specifying and then parameterising such models spatially and temporally is a considerable challenge. Instead, the presented TC error model provides a data-driven method to independently and automatically estimate uncertainties in three global burned area products post hoc, and in a manner suitable for inclusion as part of stage-4 validation campaigns.
A feature of the TC analysis shown here is the large relative uncertainties across croplands and shrublands globally. The large relative uncertainties in shrubland burning have not been previously highlighted for global satellite burned area products. A potential mechanism for this is a detection threshold associated with the limited and discontinuous fuel bed in shrublands. The limited vegetation density in shrublands will limit the magnitude of the radiometric burn signal pre-to-post fire – limiting the change signal the algorithms use to classify burning. Combing the limited vegetation signal with the general sparseness of vegetation ground cover in shrublands will lead to this “patchiness” of the burn signal which when observed at 500 m will fall around the detection thresholds of the mapping algorithms considered here (Roy and Landmann, 2005). The large relative uncertainty for MCD45 recorded in Australian (primarily xeric) shrublands is potentially a feature of the limited performance of the algorithm over surfaces with bright soils (Roy et al., 2005; de Klerk et al., 2012). This is an interesting feature that represents a promising area for future research. Cropland burning has been a persistent problem for coarse-resolution burned area products. Particular features which obscure detection in croplands are the transient nature of the burn signal before ploughing, and the highly fragmented nature of burning on the land surface. Given these circumstances, the ability to detect cropland burn scars from MODIS resolution data has been previously questioned (Hall et al., 2016). Zhu et al. (2017) indicated omission errors for the MCD64 product greater than 60 % for small cropland fires. Similarly, MCD45 has been reported to considerably underreport cropland burning globally (Roy et al., 2008). However, discrepancies between the products are likely to still be driving the TC uncertainties, for example, observed commission errors by MCD64 for harvesting in Eurasia and MCD45 in Australia (Giglio et al., 2009; Humber et al., 2018). It remains an open question whether the higher spatial resolution available in the FireCCI50 products improves performance over croplands, with some evidence that it might (Chuvieco et al., 2016). The FireCCI50 product detects the greatest magnitude of cropland burning globally and has the smallest relative uncertainties of the three products. Future studies may be better able to indicate whether the increase in spatial resolution has produced this.
Previous validation activities have indicated that satellite-derived burned area products typically perform best in regions where fire activity is more prevalent (Padilla et al., 2015). We also find that the smallest relative uncertainties are typically found in the frequently burning savannas and grasslands of Africa, Australia, and South America. Nevertheless, relative uncertainties in burned area estimates for these regions were found to be in excess of 8 %–10 %. Given the predominance of fire activity in these areas, they contribute considerably to the uncertainty on reported global burned area. In areas with more infrequent burning or more barriers to detection, relative uncertainties were found to be higher. In such circumstances, the particular limitations of each detection algorithm are most likely to drive the differences observed. For example, differing observational requirements of the products drive large uncertainties in equatorial Asia (EQAS) where persistent clouds reduce the mapped area of all algorithms. The MCD45 algorithm has been found to suffer uniquely in cloudier regions due to the greater sampling requirement of the algorithm as well as over-restrictive cloud masking conditions (Roy et al., 2002; Giglio et al., 2010; Humber et al., 2018). Changes made to the MCD64 Collection 6 product, including relaxations on cloud masking, have increased the mapped area in these cloudier regions (Giglio et al., 2018).
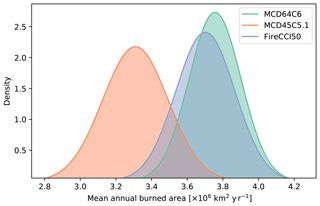
Globally, MCD64 reports the greatest burned area ( km2), followed by FireCCI50 ( km2), and then MCD45 ( km2). In terms of the global agreement between products, Fig. 11 shows the distribution of mean annual burned area for the three products. A higher level of agreement between the FireCCI50 and MCD64 products can be observed with the two products, agreeing well within 1 standard deviation. The MCD45 product disagrees most with the MCD64 product and slightly less with the FireCCI50 product. The three products overlap within 2 standard deviations. Even so, the degree of discrepancy on global burned area estimates would indicate that the previously used confidence bounds (i.e. from the range of products; Rabin et al., 2017) provide an underestimate in the global burned area uncertainty.
Estimates of the mean annual burned area from the three products agree within their respective uncertainties in around 60 % of valid TC estimates. Nevertheless, while estimates are consistent, regional estimates remain poorly constrained by the products considered. Uncertainties in excess of 10 % are found for all products in at least one land cover, including uncertainties > 24 % for MCD45 in shrublands, 11 % for MCD64 in croplands, and 13 % in shrublands for FireCCI50. Regional uncertainties are often larger than these figures, with relative uncertainties in excess of 100 % for MCD45 in croplands and grasslands in central America and boreal Asia, and for forests in Europe and boreal North America. Uncertainties larger than 100 % for MCD64 are also found in forests and croplands in boreal and central Asia. FireCCI50 also has relative uncertainties > 100 % for croplands and forests in Australia, boreal North America, and Europe. As these products are often also used at national to regional scales, it is important to consider the reliability of the current products at these scales (Roy and Boschetti, 2009; Zhu et al., 2017; Liu et al., 2019). The uncertainty estimates here are therefore useful for these users to discern any limitations of products at the appropriate scale. While the TC-estimated uncertainties cannot directly provide information on uncertainties at the pixel level, we would also encourage users to consider the quality assurance (QA) information provided in these products.
The presented TC uncertainties have many uses. The uncertainties could, for example, be used to drive development and refinement of parameters in DGVMs related to fire processes or improve optimisation routines for parameter selection (Poulter et al., 2015; Forkel et al., 2019). They could also be used to better constrain uncertainties on emission estimates derived from “bottom-up” inventory approaches (French et al., 2004; Knorr et al., 2012; Randerson et al., 2012; Van Der Werf et al., 2017). Explicit uncertainties per observation additionally allow for the development of more advanced assimilation of the satellite observations into models through mathematical frameworks in data assimilation. Similarly, they open up the ability to calibrate model parameters x against observations of burned area. For example, assume a DGVM has a fire model that predicts burned area at a time t (BAmodel(t)) as a function of, e.g. meteorological drivers, vegetation parameters, and some fire-related parameters I (e.g. Thonicke et al., 2010; Mangeon et al., 2016):
Under the assumption that the burned area estimates are normal, one could derive the (log) likelihood function L(BAobs∣x), which can be written as
Minimisation of this function would result in the parameters that provide a closer fit to the observations, weighted by how much one could trust these observations.
The wide application and interpretation of remote sensing products of burned area require explicit estimates of the uncertainties of these products. This paper has presented theoretical uncertainties for three global satellite-derived burned area products. A TC error model was applied to produce unique, near-global uncertainties for the MCD64 Collection 6, MCD45 Collection 5.1, and FireCCI50 burned area products. While products were found to provide consistent estimates in a majority of the sampled global fire extent, the constraint on burned area in many regions was found to be poor, with uncertainties in each product exceeding 8 %–10 % in the most burned regions. Uncertainties on burned area in regions with less burned area were also found to be considerable. Individual products were shown to have uncertainties exceeding 100 % in specific regions and land covers. The present study would suggest that previous estimates of uncertainty in global burned area from satellite products appear to be underestimates. Users of these products should therefore be aware of the uncertainties both in the limited constraint on burned area even from multiple products, and the regional and land-cover-specific differences in product confidence as provided by these uncertainties.
The TC-estimated uncertainties are available at https://catalogue.ceda.ac.uk/uuid/2d9162f949e042adbdd6ec82c910ee5b (last access: 2 August 2019) (Brennan et al., 2019).
JB designed the study and performed the analysis with input from MD, JLGD, and PL. JB wrote the manuscript with contributions from all authors.
The authors declare that they have no conflict of interest.
The authors were supported by the Natural Environment Research Council’s (NERC) (agreement PR140015 between NERC and the National Centre for Earth Observation; NCEO). JGD and PL would like to acknowledge financial support from the European Union Horizon 2020 research and innovation programme under grant agreement no. 687320 MULTIPLY (MULTIscale SENTINEL land surface information retrieval platform). We thank colleagues involved in ESA FireCCI phase 2 for helpful discussions.
This research has been supported by the NERC NCEO (grant no. PR140015) and the H2020 (grant no. 687320).
This paper was edited by Alexey V. Eliseev and reviewed by two anonymous referees.
Alemohammad, S. H., McColl, K. A., Konings, A. G., Entekhabi, D., and Stoffelen, A.: Characterization of precipitation product errors across the United States using multiplicative triple collocation, Hydrol. Earth Syst. Sci., 19, 3489–3503, https://doi.org/10.5194/hess-19-3489-2015, 2015. a, b
Andela, N., Morton, D., Giglio, L., Chen, Y., van der Werf, G., Kasibhatla, P., DeFries, R., Collatz, G., Hantson, S., Kloster, S., Bachelet, D., Forrest, M., Lasslop, G., Li, F., Man- geon, S., Melton, J. R., Yue, C., and Randerson, J. T.: A human-driven decline in global burned area, Science, 356, 1356–1362, 2017. a
Archibald, S., Lehmann, C. E., Gómez-Dans, J. L., and Bradstock, R. A.: Defining pyromes and global syndromes of fire regimes, P. Natl. Acad. Sci. USA, 110, 6442–6447, 2013. a
Bellprat, O., Massonnet, F., Siegert, S., Prodhomme, C., Macias-Gómez, D., Guemas, V., and Doblas-Reyes, F.: Uncertainty propagation in observational references to climate model scales, Remote Sens. Environ., 203, 101–108, 2017. a, b
Boschetti, L., Eva, H., Brivio, P. A., and Grégoire, J.-M.: Lessons to be learned from the comparison of three satellite-derived biomass burning products, Geophys. Res. Lett., 31, L21501, https://doi.org/10.1029/2004GL021229, 2004. a
Boschetti, L., Roy, D., and Justice, C.: International Global Burned Area Satellite Product Validation Protocol Part I – production and standardization of validation reference data (to be followed by part II – accuracy reporting), Committee on Earth Observation Satellites: Maryland, MD, USA, 2009. a
Boschetti, L., Stehman, S. V., and Roy, D. P.: A stratified random sampling design in space and time for regional to global scale burned area product validation, Remote Sens. Environ., 186, 465–478, 2016. a, b
Brennan, J., Gomez-Dans, J., Disney, M., and Lewis, P.: Theoretical uncertainties for three global satellite-derived burned area estimates, Centre for Environmental Data Analysis, 26 July 2019, https://catalogue.ceda.ac.uk/uuid/2d9162f949e042adbdd6ec82c910ee5b, 2019 a
Chuvieco, E., Yue, C., Heil, A., Mouillot, F., Alonso-Canas, I., Padilla, M., Pereira, J. M., Oom, D., and Tansey, K.: A new global burned area product for climate assessment of fire impacts, Global Ecol. Biogeogr., 25, 619–629, 2016. a
Chuvieco, E., Lizundia-Loiola, J., Pettinari, M. L., Ramo, R., Padilla, M., Tansey, K., Mouillot, F., Laurent, P., Storm, T., Heil, A., and Plummer, S.: Chuvieco, E., Lizundia-Loiola, J., Pettinari, M. L., Ramo, R., Padilla, M., Tansey, K., Mouillot, F., Laurent, P., Storm, T., Heil, A., and Plummer, S.: Generation and analysis of a new global burned area product based on MODIS 250 m reflectance bands and thermal anomalies, Earth Syst. Sci. Data, 10, 2015–2031, https://doi.org/10.5194/essd-10-2015-2018, 2018. a, b, c, d, e, f
Copernicus Global Land Service: Burnt Area 1 km from SPOT/VGT unavailable, available at: https://land.copernicus.eu/global/content/burnt-area-1km-spotvgt-unavailable, last access: 5 July 2019. a
de Klerk, H. M., Wilson, A. M., and Steenkamp, K.: Evaluation of satellite-derived burned area products for the fynbos, a Mediterranean shrubland, Int. J. Wildland Fire, 21, 36–47, 2012. a
D'Odorico, P., Gonsamo, A., Pinty, B., Gobron, N., Coops, N., Mendez, E., and Schaepman, M. E.: Intercomparison of fraction of absorbed photosynthetically active radiation products derived from satellite data over Europe, Remote Sens. Environ., 142, 141–154, 2014. a
Fang, H., Wei, S., Jiang, C., and Scipal, K.: Theoretical uncertainty analysis of global MODIS, CYCLOPES, and GLOBCARBON LAI products using a triple collocation method, Remote Sens. Environ., 124, 610–621, 2012. a
Forkel, M., Andela, N., P Harrison, S., Lasslop, G., Van Marle, M., Chuvieco, E., Dorigo, W., Forrest, M., Hantson, S., Heil, A., Li, F., Melton, J., Sitch, S., Yue, C., and Arneth, A.: Emergent relationships with respect to burned area in global satellite observations and fire-enabled vegetation models, Biogeosciences, 16, 57–76, https://doi.org/10.5194/bg-16-57-2019, 2019. a, b
French, N. H., Goovaerts, P., and Kasischke, E. S.: Uncertainty in estimating carbon emissions from boreal forest fires, J. Geophys. Res.-Atmos., 109, D14S08, https://doi.org/10.1029/2003JD003635, 2004. a
Friedl, M. A., Sulla-Menashe, D., Tan, B., Schneider, A., Ramankutty, N., Sibley, A., and Huang, X.: MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets, Remote Sens. Environ., 114, 168–182, 2010. a
Giglio, L., Csiszar, I., and Justice, C. O.: Global distribution and seasonality of active fires as observed with the Terra and Aqua Moderate Resolution Imaging Spectroradiometer (MODIS) sensors, J. Geophysical Res.-Biogeo., 111, G02016, https://doi.org/10.1029/2005JG000142, 2006a. a
Giglio, L., van der Werf, G. R., Randerson, J. T., Collatz, G. J., and Kasibhatla, P.: Global estimation of burned area using MODIS active fire observations, Atmos. Chem. Phys., 6, 957–974, https://doi.org/10.5194/acp-6-957-2006, 2006b. a, b, c
Giglio, L., Loboda, T., Roy, D. P., Quayle, B., and Justice, C. O.: An active-fire based burned area mapping algorithm for the MODIS sensor, Remote Sens. Environ., 113, 408–420, 2009. a, b
Giglio, L., Randerson, J. T., van der Werf, G. R., Kasibhatla, P. S., Collatz, G. J., Morton, D. C., and DeFries, R. S.: Assessing variability and long-term trends in burned area by merging multiple satellite fire products, Biogeosciences, 7, 1171–1186, https://doi.org/10.5194/bg-7-1171-2010, 2010. a, b, c, d, e, f, g
Giglio, L., Randerson, J. T., and van der Werf, G. R.: Analysis of daily, monthly, and annual burned area using the fourth-generation global fire emissions database (GFED4), J. Geophys. Res.-Biogeo., 118, 317–328, 2013. a
Giglio, L., Boschetti, L., Roy, D. P., Humber, M. L., and Justice, C. O.: The Collection 6 MODIS burned area mapping algorithm and product, Remote Sens. Environ., 217, 72–85, 2018. a, b, c, d
Gonzalez de Tanago, J., Lau, A., Bartholomeus, H., Herold, M., Avitabile, V., Raumonen, P., Martius, C., Goodman, R. C., Disney, M., Manuri, S., et al.: Estimation of above-ground biomass of large tropical trees with terrestrial LiDAR, Methods Ecol. Evol., 9, 223–234, 2018. a
Gruber, A., Su, C.-H., Zwieback, S., Crow, W., Dorigo, W., and Wagner, W.: Recent advances in (soil moisture) triple collocation analysis, Int. J. Appl. Earth Obs., 45, 200–211, 2016. a, b, c
Hall, J. V., Loboda, T. V., Giglio, L., and McCarty, G. W.: A MODIS-based burned area assessment for Russian croplands: Mapping requirements and challenges, Remote Sens. Environ., 184, 506–521, 2016. a, b
Hantson, S., Arneth, A., Harrison, S. P., Kelley, D. I., Prentice, I. C., Rabin, S. S., Archibald, S., Mouillot, F., Arnold, S. R., Artaxo, P., Bachelet, D., Ciais, P., Forrest, M., Friedlingstein, P., Hickler, T., Kaplan, J. O., Kloster, S., Knorr, W., Lasslop, G., Li, F., Mangeon, S., Melton, J. R., Meyn, A., Sitch, S., Spessa, A., van der Werf, G. R., Voulgarakis, A., and Yue, C.: The status and challenge of global fire modelling, Biogeosciences, 13, 3359–3375, https://doi.org/10.5194/bg-13-3359-2016, 2016. a
Huang, C., Townshend, J. R., Liang, S., Kalluri, S. N., and DeFries, R. S.: Impact of sensor's point spread function on land cover characterization: assessment and deconvolution, Remote Sens. Environ., 80, 203–212, 2002. a
Humber, M. L., Boschetti, L., Giglio, L., and Justice, C. O.: Spatial and temporal intercomparison of four global burned area products, Int. J. Digit. Earth, 12, 460–484, https://doi.org/10.1080/17538947.2018.1433727, 2018. a, b, c, d, e, f, g
IPCC: IPCC Guidelines for National Greenhouse Gas Inventories, Tech. Rep., National Greenhouse Gas Inventories Programme, https://www.ipcc-nggip.iges.or.jp/public/2006gl (last accessed: 15 August 2019), 2008. a
ISO/BPIM: Evaluation of measurement data – Guide to the expression of uncertainty in measurement, Tech. Rep. JCGM 100:2008, Joint Committee for Guides in Metrology, 134 pp., http://www.iso.org/sites/JCGM/GUM-introduction.htm (last accessed: 15 August 2019), 2008. a
Knorr, W., Lehsten, V., and Arneth, A.: Determinants and predictability of global wildfire emissions, Atmos. Chem. Phys., 12, 6845–6861, https://doi.org/10.5194/acp-12-6845-2012, 2012. a, b, c
Knorr, W., Kaminski, T., Arneth, A., and Weber, U.: Impact of human population density on fire frequency at the global scale, Biogeosciences, 11, 1085–1102, https://doi.org/10.5194/bg-11-1085-2014, 2014. a
Le Page, Y., Morton, D., Bond-Lamberty, B., Pereira, J. M. C., and Hurtt, G.: HESFIRE: a global fire model to explore the role of anthropogenic and weather drivers, Biogeosciences, 12, 887–903, https://doi.org/10.5194/bg-12-887-2015, 2015. a
Liu, T., Marlier, M., Karambelas, A., Jain, M., Singh, S., Singh, M., Gautam, R., and DeFries, R. S.: Missing emissions from post-monsoon agricultural fires in northwestern India: regional limitations of MODIS burned area and active fire products, Environ. Res. Commun., 1, 011007, https://doi.org/10.1088/2515-7620/ab056c, 2019. a
Mangeon, S., Voulgarakis, A., Gilham, R., Harper, A., Sitch, S., and Folberth, G.: INFERNO: a fire and emissions scheme for the UK Met Office's Unified Model, Geosci. Model Dev., 9, 2685–2700, https://doi.org/10.5194/gmd-9-2685-2016, 2016. a
McColl, K. A., Vogelzang, J., Konings, A. G., Entekhabi, D., Piles, M., and Stoffelen, A.: Extended triple collocation: Estimating errors and correlation coefficients with respect to an unknown target, Geophys. Res. Lett., 41, 6229–6236, 2014. a
Melchiorre, A. and Boschetti, L.: Global Analysis of Burned Area Persistence Time with MODIS Data, Remote Sensing, 10, 750, https://doi.org/10.3390/rs10050750, 2018. a
Merchant, C. J., Paul, F., Popp, T., Ablain, M., Bontemps, S., Defourny, P., Hollmann, R., Lavergne, T., Laeng, A., de Leeuw, G., Mittaz, J., Poulsen, C., Povey, A. C., Reuter, M., Sathyendranath, S., Sandven, S., Sofieva, V. F., and Wagner, W.: Uncertainty information in climate data records from Earth observation, Earth Syst. Sci. Data, 9, 511–527, https://doi.org/10.5194/essd-9-511-2017, 2017. a
Morisette, J., Heinsch, F. A., and Running, S. W.: Monitoring global vegetation using moderate-resolution satellites, Eos, Transactions American Geophysical Union, 87, 568–568, 2006. a
Mouillot, F., Schultz, M. G., Yue, C., Cadule, P., Tansey, K., Ciais, P., and Chuvieco, E.: Ten years of global burned area products from spaceborne remote sensing – A review: Analysis of user needs and recommendations for future developments, Int. J. Appl. Earth Obs., 26, 64–79, https://doi.org/10.1016/j.jag.2013.05.014, 2014. a, b
Padilla, M., Stehman, S. V., Ramo, R., Corti, D., Hantson, S., Oliva, P., Alonso-Canas, I., Bradley, A. V., Tansey, K., Mota, B., Pereira, J., and Chuvieco, E.: Comparing the accuracies of remote sensing global burned area products using stratified random sampling and estimation, Remote Sens. Environ., 160, 114–121, 2015. a, b, c, d, e, f
Padilla, M., Olofsson, P., Stehman, S. V., Tansey, K., and Chuvieco, E.: Stratification and sample allocation for reference burned area data, Remote Sens. Environ., 203, 240–255, 2017. a, b, c
Poulter, B., Cadule, P., Cheiney, A., Ciais, P., Hodson, E., Peylin, P., Plummer, S., Spessa, A., Saatchi, S., Yue, C., and Zimmermann, E.: Sensitivity of global terrestrial carbon cycle dynamics to variability in satellite-observed burned area, Global Biogeochem. Cy., 29, 207–222, 2015. a, b, c
Rabin, S. S., Melton, J. R., Lasslop, G., Bachelet, D., Forrest, M., Hantson, S., Kaplan, J. O., Li, F., Mangeon, S., Ward, D. S., Yue, C., Arora, V. K., Hickler, T., Kloster, S., Knorr, W., Nieradzik, L., Spessa, A., Folberth, G. A., Sheehan, T., Voulgarakis, A., Kelley, D. I., Prentice, I. C., Sitch, S., Harrison, S., and Arneth, A.: The Fire Modeling Intercomparison Project (FireMIP), phase 1: experimental and analytical protocols with detailed model descriptions, Geosci. Model Dev., 10, 1175–1197, https://doi.org/10.5194/gmd-10-1175-2017, 2017. a, b, c, d
Randerson, J., Chen, Y., Van Der Werf, G., Rogers, B., and Morton, D.: Global burned area and biomass burning emissions from small fires, J. Geophys. Res.-Biogeo., 117, G04012, https://doi.org/10.1029/2012JG002128, 2012. a
Roebeling, R., Wolters, E., Meirink, J., and Leijnse, H.: Triple collocation of summer precipitation retrievals from SEVIRI over Europe with gridded rain gauge and weather radar data, J. Hydrometeorol., 13, 1552–1566, 2012. a
Roteta, E., Bastarrika, A., Padilla, M., Storm, T., and Chuvieco, E.: Development of a Sentinel-2 burned area algorithm: Generation of a small fire database for sub-Saharan Africa, Remote Sens. Environ., 222, 1–17, 2019. a
Roy, D., Lewis, P., and Justice, C.: Burned area mapping using multi-temporal moderate spatial resolution data – A bi-directional reflectance model-based expectation approach, Remote Sens. Environ., 83, 263–286, 2002. a
Roy, D., Jin, Y., Lewis, P., and Justice, C.: Prototyping a global algorithm for systematic fire-affected area mapping using MODIS time series data, Remote Sens. Environ,, 97, 137–162, 2005. a, b, c, d
Roy, D. P. and Boschetti, L.: Southern Africa validation of the MODIS, L3JRC, and GlobCarbon burned-area products, IEEE T. Geosci Remote, 47, 1032–1044, 2009. a, b, c
Roy, D. P. and Landmann, T.: Characterizing the surface heterogeneity of fire effects using multi-temporal reflective wavelength data, Int. J. Remote Sens., 26, 4197–4218, 2005. a
Roy, D. P., Boschetti, L., Justice, C. O., and Ju, J.: The collection 5 MODIS burned area product – Global evaluation by comparison with the MODIS active fire product, Remote Sens. Environ., 112, 3690–3707, 2008. a
Seiler, W. and Crutzen, P. J.: Estimates of gross and net fluxes of carbon between the biosphere and the atmosphere from biomass burning, Clim. Change, 2, 207–247, 1980. a
Simon, M., Plummer, S., Fierens, F., Hoelzemann, J. J., and Arino, O.: Burnt area detection at global scale using ATSR-2: The GLOBSCAR products and their qualification, J. Geophys. Res.-Atmos., 109, D14S02, https://doi.org/10.1029/2003JD003622, 2004. a
Stoffelen, A.: Toward the true near-surface wind speed: Error modeling and calibration using triple collocation, J. Geophys. Res.-Oceans, 103, 7755–7766, 1998. a
Sukhinin, A. I., French, N. H., Kasischke, E. S., Hewson, J. H., Soja, A. J., Csiszar, I. A., Hyer, E. J., Loboda, T., Conrad, S. G., Romasko, V. I., et al.: AVHRR-based mapping of fires in Russia: New products for fire management and carbon cycle studies, Remote Sens. Environ., 93, 546–564, 2004. a
Thonicke, K., Venevsky, S., Sitch, S., and Cramer, W.: The role of fire disturbance for global vegetation dynamics: coupling fire into a Dynamic Global Vegetation Model, Global Ecol. Biogeogr., 10, 661–677, 2001. a
Thonicke, K., Spessa, A., Prentice, I. C., Harrison, S. P., Dong, L., and Carmona-Moreno, C.: The influence of vegetation, fire spread and fire behaviour on biomass burning and trace gas emissions: results from a process-based model, Biogeosciences, 7, 1991–2011, https://doi.org/10.5194/bg-7-1991-2010, 2010. a
Tian, Y., Huffman, G. J., Adler, R. F., Tang, L., Sapiano, M., Maggioni, V., and Wu, H.: Modeling errors in daily precipitation measurements: Additive or multiplicative?, Geophys. Res. Lett., 40, 2060–2065, 2013. a, b
Trigg, S. and Flasse, S.: Characterizing the spectral-temporal response of burned savannah using in situ spectroradiometry and infrared thermometry, Int. J. Remote Sens., 21, 3161–3168, 2000. a
Van Der Werf, G. R., Randerson, J. T., Giglio, L., Van Leeuwen, T. T., Chen, Y., Rogers, B. M., Mu, M., Van Marle, M. J., Morton, D. C., Collatz, G. J., Yokelson, R. J., and Kasibhatla, P. S.: Global fire emissions estimates during 1997–2016, Earth Syst. Sci. Data, 9, 697–720, https://doi.org/10.5194/essd-9-697-2, 2017. a
van der Werf, G. R., Randerson, J. T., Giglio, L., van Leeuwen, T. T., Chen, Y., Rogers, B. M., Mu, M., van Marle, M. J. E., Morton, D. C., Collatz, G. J., Yokelson, R. J., and Kasibhatla, P. S.: Global fire emissions estimates during 1997–2016, Earth Syst. Sci. Data, 9, 697–720, https://doi.org/10.5194/essd-9-697-2017, 2017. a
Vermote, E. F., El Saleous, N. Z., and Justice, C. O.: Atmospheric correction of MODIS data in the visible to middle infrared: first results, Remote Sens. Environ., 83, 97–111, 2002. a
Yilmaz, M. T. and Crow, W. T.: Evaluation of assumptions in soil moisture triple collocation analysis, J. Hydrometeorol., 15, 1293–1302, 2014. a
Yue, C., Ciais, P., Cadule, P., Thonicke, K., Archibald, S., Poulter, B., Hao, W. M., Hantson, S., Mouillot, F., Friedlingstein, P., Maignan, F., and Viovy, N.: Modelling the role of fires in the terrestrial carbon balance by incorporating SPITFIRE into the global vegetation model ORCHIDEE – Part 1: simulating historical global burned area and fire regimes, Geosci. Model Dev., 7, 2747–2767, https://doi.org/10.5194/gmd-7-2747-2014, 2014. a
Zhang, Y.-H., Wooster, M., Tutubalina, O., and Perry, G.: Monthly burned area and forest fire carbon emission estimates for the Russian Federation from SPOT VGT, Remote Sens. Environ., 87, 1–15, 2003. a
Zhu, C., Kobayashi, H., Kanaya, Y., and Saito, M.: Size-dependent validation of MODIS MCD64A1 burned area over six vegetation types in boreal Eurasia: Large underestimation in croplands, Sci. Rep.-UK, 7, 4181, https://doi.org/10.1038/s41598-017-03739-0, 2017. a, b
Zwieback, S., Scipal, K., Dorigo, W., and Wagner, W.: Structural and statistical properties of the collocation technique for error characterization, Nonlin. Processes Geophys., 19, 69–80, https://doi.org/10.5194/npg-19-69-2012, 2012. a, b