the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Interpreting eddy covariance data from heterogeneous Siberian tundra: land-cover-specific methane fluxes and spatial representativeness
Juha-Pekka Tuovinen
Mika Aurela
Juha Hatakka
Aleksi Räsänen
Tarmo Virtanen
Juha Mikola
Viktor Ivakhov
Vladimir Kondratyev
Tuomas Laurila
The non-uniform spatial integration, an inherent feature of the eddy covariance (EC) method, creates a challenge for flux data interpretation in a heterogeneous environment, where the contribution of different land cover types varies with flow conditions, potentially resulting in biased estimates in comparison to the areally averaged fluxes and land cover attributes. We modelled flux footprints and characterized the spatial scale of our EC measurements in Tiksi, a tundra site in northern Siberia. We used leaf area index (LAI) and land cover class (LCC) data, derived from very-high-spatial-resolution satellite imagery and field surveys, and quantified the sensor location bias. We found that methane (CH4) fluxes varied strongly with wind direction (−0.09 to 0.59 on average) during summer 2014, reflecting the distribution of different LCCs. Other environmental factors had only a minor effect on short-term flux variations but influenced the seasonal trend. Using footprint weights of grouped LCCs as explanatory variables for the measured CH4 flux, we developed a multiple regression model to estimate LCC group-specific fluxes. This model showed that wet fen and graminoid tundra patches in locations with topography-enhanced wetness acted as strong sources (1.0 during the peak emission period), while mineral soils were significant sinks (−0.13 ). To assess the representativeness of measurements, we upscaled the LCC group-specific fluxes to different spatial scales. Despite the landscape heterogeneity and rather poor representativeness of EC data with respect to the areally averaged LAI and coverage of some LCCs, the mean flux was close to the CH4 balance upscaled to an area of 6.3 km2, with a location bias of 14 %. We recommend that EC site descriptions in a heterogeneous environment should be complemented with footprint-weighted high-resolution data on vegetation and other site characteristics.
- Article
(3323 KB) -
Supplement
(1199 KB) - BibTeX
- EndNote
Biosphere–atmosphere exchange of greenhouse gases (GHGs) is commonly measured using the micrometeorological eddy covariance (EC) method (Aubinet et al., 2012). This tower-based, non-intrusive technique provides spatially integrated flux data at the ecosystem scale with a typical integration domain of a few hectares. This is in stark contrast to flux chamber measurements that can be focused on homogeneous small-scale (<1 m2) patches of an ecosystem or on individual plant communities (Livingston and Hutchinson, 1995; Virkkala et al., 2017). The spatial aggregation inherent in the EC data is a strong asset if one's objective is to study functioning or GHG exchange of an extensive, relatively homogeneous ecosystem. Heterogeneous landscapes consisting of a mosaic of differing vegetation and land cover patches, however, may entail issues on the interpretation of the spatial representativeness of measurements. This stems from the fact that the EC integration process is equivalent to non-uniform weighting of the upwind surface elements that influence the measured flux, thus potentially resulting in an unequal and temporally varying contribution from different land cover types (Schmid, 2002). Especially isolated zones of high source–sink density may bias the estimated average flux of the area surrounding the EC tower. The spatial distribution of relative weights, a function that Leclerc and Thurtell (1990) coined “footprint”, depends on the measurement height and strongly on wind direction. As the flux footprint is also affected by other properties of the atmospheric flow, e.g. hydrostatic stability, directional averaging does not guarantee an unbiased flux estimate either.
Arctic tundra serves as a prime example of a surface that is heterogeneous with respect to biogeochemical processes. The vegetation, soil and land cover structure of tundra areas are fragmented, the landscape typically comprising patches of different plant communities, water bodies and other land cover types (Stow et al., 2004; Virtanen and Ek, 2014; Mikola et al., 2018). Such heterogeneity concerns both the composition and configuration of land cover properties. This is clearly manifested by the leaf area index (LAI), which shows a higher relative variation among sites in tundra than in any other biome (Asner et al., 2003), and there are pronounced spatial and temporal LAI patterns at the landscape scale (Marushchak et al., 2013; Juutinen et al., 2017). Surface heterogeneity also generates high variability in the ecosystem–atmosphere fluxes of GHGs, including methane (CH4) (Olefeldt et al., 2013). Tundra biomes are responsible for approximately 3 % of the total CH4 emissions estimated at 560 Tg yr−1, 40 % of which is biogenic (McGuire et al., 2012; Saunois et al., 2016). The emissions from tundra are predicted to increase substantially, as a fraction of the vast reservoir of organic carbon in permafrost soils may be released into the atmosphere as a result of warming-induced thawing, creating a positive feedback to climate change (Schuur et al., 2015).
The heterogeneity in the ecosystem–atmosphere CH4 flux originates from the multitude of biochemical and physical controls of the anaerobic production, bacterial oxidation and transport of CH4 (Whalen and Reeburgh, 1990; Lai, 2009; Bridgham et al., 2013). Methane can be released into the atmosphere through gradual diffusion in soil and water, in ebullition (bubbling) events and via plant-mediated advective transport. These processes involve different residence times and thus expose the produced CH4 to different degree of oxidation. As a result of this complexity, field studies have identified a wide range of factors that are associated with the level and variation of observed fluxes. Of these, soil temperature and moisture (or water table level) typically constitute the key environmental controls (Olefeldt et al., 2013). As a general rule, wet carbon-rich soils emit substantial amounts of CH4, while dry tundra soils act as small net sinks (Lau et al., 2015). Even if lesser in magnitude, the uptake flux in dry areas may dominate the regional CH4 balance (Jørgensen et al., 2015; D'Imperio et al., 2017). Methane flux strongly depends on vegetation and soil characteristics, such as the abundance of vascular plants with aerenchyma tissue facilitating gas transport; other important variables include substrate availability, and soil acidity and redox potential (Lai, 2009; Bridgham et al., 2013; Olefeldt et al., 2013).
Landscape heterogeneity not only calls for further measurements of fluxes and their controls on multiple spatial scales, preferably including multiple EC towers for spatial replication (Hill et al., 2017), but also necessitates development of techniques for data interpretation, including down- and upscaling methods for generalization of observations. Micrometeorological models are available for estimating the flux footprint (Leclerc and Foken, 2014) and have been utilized in various ways when dealing with the representativeness of flux measurements. In its simplest form, such an analysis involves determination of footprint dimensions for typical flow conditions, to ensure that the expected “field of view” of EC measurements is sufficiently confined to the area of interest (e.g. Aurela et al., 2009). Averaged footprints, or footprint “climatologies”, can be calculated from time series of actual short-term (typically 30 min) meteorological data, thus providing a fuller view of the spatial extent of EC aggregation (e.g. Amiro, 1998). When combined with a land cover map, footprint time series can be used for data quality control by quantifying the contribution of different land cover types or, specifically, that of a certain ecosystem intended to be observed (Tuovinen et al., 1998; Rebmann et al., 2005; Göckede et al., 2008). The footprint function can also be used for a formal expression of the spatial, or more precisely the point-to-area (Nappo et al., 1982), representativeness of the EC measurements performed at a certain location. A suitable metric for this, termed the “sensor location bias” by Schmid and Lloyd (1999), can be defined by comparing the footprint-weighted average of a surface-related quantity, mapped across the study area, to the corresponding arithmetic average.
While EC data from a heterogeneous environment are still commonly compared with plot-scale data without considering the differential weighting of the plots in the EC signal (e.g. Heikkinen et al., 2002; Sachs et al., 2010; Yu et al., 2013), footprint modelling has been successfully combined with land cover information in various studies for a representative upscaling of chamber-based fluxes (e.g. Marushchak et al., 2016), plot-scale model results (e.g. Budishchev et al., 2014), remotely sensed fluxes (e.g. Chen et al., 2009) and vegetation data for model input (e.g. Stoy et al., 2013). The temporally varying footprint weights of different land cover types can also be taken as a basis for constructing statistical models that unravel land-cover-specific fluxes from the spatially aggregated EC data, but this depends on the quality of land cover data (Fan et al., 1992; Forbrich et al., 2011). The very-high-spatial-resolution (VHSR) satellite imagery makes it possible to derive reliable land cover maps with as high as a ∼1 m resolution. By utilizing such a detailed vegetation map, Budishchev et al. (2014) showed that footprint-weighting of modelled plot-scale CH4 emissions from permafrost tundra resulted in a good agreement with EC measurements, while areally averaged fluxes failed to reproduce the heterogeneity-induced temporal variability. A similar conclusion was reached by Davidson et al. (2017), who upscaled chamber-based CH4 fluxes for four sites in Alaska by means of VHSR vegetation maps.
The aims of the present study are threefold. First, we characterize the dimensions of the field of view and the point-to-area representativeness of the EC measurements carried out at a micrometeorological measurement station, located on permafrost tundra in Tiksi in northern Siberia, during summer 2014. We demonstrate and quantify the heterogeneity of this site, producing information that is essential for any further study exploiting these flux data. For this, we combine a micrometeorological footprint model and detailed maps of ecosystem characteristics, including land cover classes (LCCs), LAI and topographic wetness index (TWI). These are based on VHSR satellite imagery and extensive field surveys, which still are scant for Siberian tundra. Second, we hypothesize that distinguishable mean fluxes can be determined for LCC groups that represent different CH4 source–sink capacities; this can be accomplished by developing a multiple regression model that links these fluxes to the EC measurements via footprint weighting. This approach was motivated by the findings of Davidson et al. (2016), who demonstrated that a simple vegetation classification could explain the variation in CH4 emissions from Arctic tundra as accurately as a set of key environmental drivers. Furthermore, the flux chamber measurements made in Tiksi showed that the effect of LCC was much larger than that of environmental controls (Vähä, 2016). Because of this objective, we limit our data to the growing season. Finally, the LCC group-specific fluxes obtained in this way offer us an opportunity to upscale the CH4 balance to the landscape scale and thus to evaluate the representativeness of EC measurements also with respect to CH4 exchange. We emphasize that the scope of this study is focused on the ramifications of the unavoidable non-uniform spatial sampling involved in EC measurements rather than on ecosystem processes.
2.1 Site and data
2.1.1 Site description and meteorological conditions
The study area covers the surroundings of the micrometeorological GHG flux measurement station in Tiksi in north-eastern Russia, near the Tiksi Observatory operated by Yakutian Service for Hydrometeorology and Environmental Monitoring. The EC tower of the station is located at 71.5943∘ N, 128.8878∘ E, 7 m above sea level, approximately 500 m from the shoreline of the Laptev Sea and 50 km from the Lena River delta. The flux measurements are run by the Finnish Meteorological Institute and constitute part of the International Arctic Systems for Observing the Atmosphere (IASOA) activities (Uttal et al., 2016).
Tiksi is located within the continuous permafrost zone, and the climate is arctic: the winters are long and cold, while the summers are cool. The mean annual temperature and precipitation in Tiksi in 1981–2010 were −12.7 ∘C and 323 mm, respectively; the year 2014 was somewhat warmer (−10.9 ∘C) and drier (249 mm) (AARI, 2018). Air temperature typically falls below 0 ∘C in the end of September, and the soil temperatures reach the freezing point at approximately the same time. During the winter, air temperatures are typically below −20 ∘C, and the soil temperatures are reduced to levels below −10 ∘C. Snow appears typically in October and melts in early June. After the snowmelt, the top (a few centimetres) layer of soil warms quickly, but the thawing rate of deeper layers varies depending on the soil type and vegetation (Mikola et al., 2018).
The soil type ranges from mineral soil to peatlands with a high organic content (>60 % of dry soil mass) (Mikola et al., 2018). The landscape around the EC tower represents the coastal tundra zone of eastern Siberia with a high diversity of plant species and community types, including fens, bogs, tundra heaths and meadows, but there are also areas of bare ground (Juutinen et al., 2017; Mikola et al., 2018). The terrain is relatively flat, sloping gently (2–3∘) towards the south. This generates a hydrological gradient, and a small brook runs through the site; there are also ponds and small lakes within the study area. Further details of vegetation and soil characteristics are presented in Sect. 2.1.3 and 2.1.4.
The data analysed in this study cover the period of 5 July to 29 August 2014, which represents the thermal growing season of that year, using the daily mean air temperature of 5 ∘C as the threshold (Fig. S1 in the Supplement). During this period, the mean air temperature was higher (10.2 ∘C) than the corresponding 1981–2010 mean (7.8 ∘C), which was also the case for the precipitation sum (116 mm vs. the long-term mean 86 mm). In 2014, the soil temperature at 10 cm depth, measured with a Pt100 sensor in dry fen soil, varied within the typical summertime range of 5±2 ∘ C from early July to the end of August (Fig. S1). The depth of the active soil layer mostly varied within 0.2–0.4 m in early July–mid-August 2014 (Mikola et al., 2018).
2.1.2 Flux measurements
The CH4 and energy fluxes used in the present study were measured continuously with the micrometeorological eddy covariance method (Aubinet et al., 2012). The EC instrumentation consisted of a USA-1 (METEK GmbH, Elmshorn, Germany) sonic anemometer/thermometer, an LI-7000 (LI-COR, Inc., Lincoln, NE, USA) CO2 ∕ H2O analyser and an RMT-200 (Los Gatos Research, Inc., San Jose, CA, USA) CH4 analyser. The measurement height was 3 m. The sampling frequency was 10 Hz, and the turbulent fluxes were calculated with the in-house PyBARFluxCalc programme with 30 min block averaging according to standard procedures, including double coordinate rotation, lag determination and wet-to-dry mole fraction conversion where necessary (Aubinet et al., 2012). The high-frequency CH4 flux loss was corrected for using an empirical approach described by Laurila et al. (2005); for this, a half-power frequency of 1.1 Hz was estimated from the data. The CH4 flux data were screened for instationarity by removing cases in which the relative non-stationarity of either momentum or CH4 flux exceeded 30 % (Foken and Wichura, 1996). In addition, periods of weak turbulence (friction velocity <0.12 m s−1) were discarded. In total, 911 half-hourly observations were included in the analysis. No gap-filling of the time series was necessary for the purposes of the present study.
In addition to the EC technique, CH4 exchange was measured with a static flux chamber (Vähä, 2016). The surface area of this chamber was 0.25 m2 and its height 0.3 m. The sample air from the chamber was directed to a DLT-100 (Los Gatos Research, Inc., San Jose, CA, USA) CH4 analyser. The chamber closure time was either 4 or 10 min, depending on the LCC and the expected magnitude of CH4 flux. The measurements were carried out between 15 July and 16 August 2014. However, the number of chamber plots was modest and the reach of these measurements from the EC mast was limited due to the use of an online gas analyser; moreover, the measurement plots do not fully correspond to the land cover classification that was developed subsequently (Mikola et al., 2018) and used in the present study. Therefore, instead of aiming at a full analysis of the chamber data, we utilized them for a partial validation of the estimated LCC-specific fluxes, using four plots on dry fen, two plots on wet fen and one plot on bare soil, with 31 or 32 measurements taken on each plot.
2.1.3 Mapping of landscape characteristics
The land cover classification consists of nine classes visually distinguished according to their key characteristics (Table 1). The LCCs were identified within an area of 1 km2 around the EC tower on the basis of a vegetation and soil survey and verified using statistical ordination of the 92 established study plots according to plant species composition and functional plant and soil attributes (Mikola et al., 2018). To extrapolate the LCCs to the landscape scale (Figs. 1a and S2), a supervised object-based classification with the random forest method was carried out using two VHSR multispectral satellite images (12 August 2012 and 11 July 2015; WorldView-2, DigitalGlobe, Inc., Westminster, CO, USA) and a digital elevation model (DEM) constructed from the 2015 WorldView-2 stereo pair (Fig. 1b). The internal (cross-validation of training data) and external (validation data) classification accuracies of the land cover classification were 80 % and 49 %, respectively. For details, see Mikola et al. (2018).
Table 1Land cover classes and their dominating vegetation and other characteristics, derived from Juutinen et al. (2017) and Mikola et al. (2018).
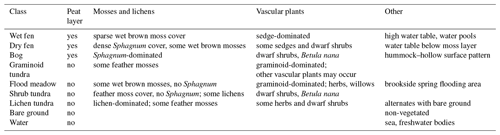
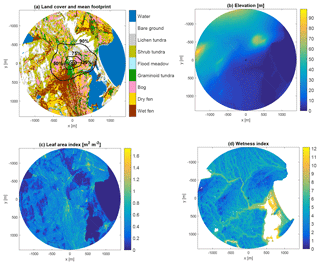
Figure 1Land cover classes and the mean cumulative footprint during the growing season of 2014 (a), terrain elevation (b), maximum leaf area index (on 12 August 2012) (c) and topographic wetness index for terrestrial surfaces (d). The isopleths in panel (a) indicate the areas with a 25 %, 50 %, 75 % and 90 % contribution to the measured flux (only the further distance visible). The plus sign indicates the location of the EC tower.
Using non-linear regression, the LAI of vascular plants was estimated from the normalized difference vegetation index (NDVI) calculated from the reflectance data of the 2012 WorldView-2 image (Fig. 1c). This map represents the period of maximum LAI in 2012; for the estimated development of the LAI of different LCCs in 2014, see Juutinen et al. (2017) and Fig. S1. The topographic wetness index (TWI) was calculated from the DEM using the method of Böhner and Selige (2006) (Fig. 1d). TWI is defined as a function of the upslope contributing area and the local terrain slope and thus serves as a proxy for potential soil moisture. For details of the DEM and TWI data, see Mikola et al. (2018). All maps have a 2 m pixel size, and in this study they were limited to a circle with a radius of 1.4 km from the EC tower, which defines the domain of the present study. For upscaling to a regional scale, we also considered the LCCs determined within a larger area of 35.8 km2 (Fig. S2).
2.1.4 Main features of the land cover classes
The LCCs employed in the present study are described by Juutinen et al. (2017) and in greater detail by Mikola et al. (2018); a summary of observed vegetation characteristics is provided in Table 1. Briefly, the dry fen, wet fen and bog classes represent peat-forming environments, while the other LCCs refer to environments with no discernible peat layer. The vascular plant vegetation of fens, i.e. the wetter peatlands, is characterized by sedges (Carex spp.). In 2014, the LAI of this vegetation reached its maximum in early August, estimated at 1.1 and 0.5 for wet and dry fens, respectively (Fig. S1; Juutinen et al., 2017). Sphagnum mosses are abundant in the dry fens, while in the wet fens the moss cover is sparse and water pools are common. The bogs are drier and show microtopographic variation; their vegetation consists mainly of dwarf shrubs, dwarf birch (Betula nana) and Sphagnum and other mosses. The vegetation of flood meadows and graminoid tundra is dominated by graminoids (sedges and grasses), which yield a relatively high maximum vascular-plant LAI of 0.9 and 0.7, respectively, for these LCCs during the study period (Juutinen et al., 2017). The areas defined as shrub tundra have an abundant coverage of feather mosses and dwarf shrubs. In addition, lichen tundra patches with lesser biomass alternate with stony bare-ground areas.
In terms of soil properties of the vegetated areas, the dry fen, wet fen, bog and graminoid tundra LCCs stand out with their high organic matter (on average 38 % of soil dry mass) and water concentration (on average 73 % of fresh mass) in the top 10 cm soil layer, while the lowest concentrations (4 % and 22 %, respectively) were found in the soils of the lichen tundra LCC, as measured on 9–14 August 2014 (Mikola et al., 2018). The soil temperature at a depth of 15 cm was clearly highest in the lichen tundra sampling plots, and flood meadow and wet fen soils mostly had a higher temperature than those of the other remaining LCCs. The depth of the biologically active soil layer approximately doubled from early July to mid-August 2014 (the period when weekly measurements were taken). In mid-August, the active layer depth was highest, approximately 40 cm, at the wet fen and flood meadow plots and lowest, 25 cm, at the shrub tundra and lichen tundra plots (Mikola et al., 2018).
2.2 Application of footprints
2.2.1 Footprint-weighted averaging and sensor location bias
In this section, we first present an exposition of the footprint-weighting of continuous variables and LCC maps and then define the sensor location bias, which are needed for the heterogeneity assessment and regression modelling. The footprint function (Horst and Weil, 1992) specific to a certain measurement configuration (f) is expressed here in polar coordinates as
where F is the surface flux density distribution, 〈F〉 is the vertical flux density at the measurement point above the surface, and θ and r are the horizontal direction and distance with respect to this location. Equation (1) postulates that the flux at a certain location above the ground represents a spatial weighting of the surface flux distribution, where the weighting is defined by the footprint function f, , ∀θ, r and , which describes the turbulent transport between each surface element and the reference point. In the context of EC measurements, f can be estimated by micrometeorological modelling, and 〈F〉 denotes the measured flux, while F(θ, r) is unknown.
Based on f(θ, r), we define, analogously to Eq. (1), footprint-weighted averages of other quantities. For a continuous variable X, such as LAI and terrain elevation, we write this average, or the “effective” value of X related to a certain footprint f, as
We apply a similar averaging operation to an LCC map, in which each location (in practice, a pixel) is allocated to a single LCC. We denote the LCC map by , where the integer j=1 … N specifies the LCC at (θ, r), and define the weighted LCC corresponding to f as
where
This provides the proportion of each LCC within the footprint, which can be calculated for a footprint climatology as well as a single footprint distribution. If the variable X in Eq. (2) is LCC-specific but otherwise does not depend on location, i.e. we can specify constants Xj, j=1…N, then we combine Eqs. (2) and (3) to obtain the footprint-weighted X as
To describe the point-to-area representativeness of the flux measurements with respect to a variable related to a surface property or exchange, we follow Schmid and Lloyd (1999) and define a metric that quantifies how well the measurement at a certain location reflects the actual conditions averaged over the area of interest. The sensor location bias for X is calculated here as
where denotes the mean X within the study area. This definition differs from the one introduced by Schmid and Lloyd (1999), who expressed the sensor location bias as . As 〈X〉 depends on the footprint and thus varies with time, ΔX is not temporally invariant either.
We calculated the sensor location bias with Eqs. (2) and (6) for terrain elevation, the maximum LAI and TWI that were mapped across the study area (Fig. 1). In addition, to investigate the effect of landscape heterogeneity, this bias was calculated for the mean CH4 flux, for which the areal reference was obtained from LCC group-specific fluxes. These fluxes were estimated with a multiple regression model derived from Eq. (5) (to be described in Sect. 2.3), in which the LCC group proportions calculated with Eq. (3) were used as explanatory variables.
2.2.2 Footprint modelling
We calculated the flux footprints f for each 30 min flux averaging period in a horizontal 2 m × 2 m grid by using the analytical footprint model developed by Kormann and Meixner (2001) (here “KM model”). The KM model is based on a stationary gradient diffusion formulation, building on the classical solution of the two-dimensional advection–diffusion equation with vertical power law profiles assumed for the mean wind speed and eddy diffusivity (Pasquill and Smith, 1983). As a novel feature, these profiles are related to the corresponding Monin–Obukhov similarity (MOS) profiles. The crosswind diffusion is assumed to be Gaussian and height-independent.
Our EC measurements provide the necessary input data for the KM model, including mean wind direction (θ), mean horizontal wind speed at anemometer height (U), friction velocity (u*), hydrostatic stability (L−1) and the standard deviation of lateral wind velocity (σv). When matching the wind and diffusivity power laws to the MOS profiles at the measurement height, the KM model does not require an explicit definition of roughness length (z0), since the input data (i.e. U, u*, L−1) implicitly specify z0 according to the MOS profile of the horizontal wind speed. In the case of a heterogeneous surface, this simplifies the computations significantly as compared to models that require additional flux aggregation procedures for estimating the effective z0 (Göckede et al., 2006).
Independent of the flow conditions, a part of each footprint distribution formally extends beyond any finite target area. Therefore, in those footprint calculations that involve a surface property distribution such as the LCC map, we normalize the footprint integrated over the map area to 1, unless indicated otherwise. This means that the upper distance of radial integration in Eqs. (2), (3) and (5) is set to a finite limit of rm and the footprint-weighted averages are scaled by dividing by , where rm (≈1.4 km) is the radius of the present land cover maps.
2.2.3 Examples of flow conditions
To demonstrate how the EC flux measurement in Tiksi is affected by surface heterogeneity, we calculated the footprint-weighted averages of the surface attributes LAI, terrain elevation and TWI using Eq. (2) and the data illustrated in Fig. 1b–d as the continuous variable X, while Eq. (5) was used for the footprint-weighted LCC areas of the nine classes shown in Fig. 1a. For this demonstration, we defined three flow situations in terms of the variables that affect the footprint in a given θ, i.e. U, u*, L−1 and σv (Table 2). These cases represent differing stability conditions, for which typical parameter combinations were derived from the measurement data employed in this study. The U–u*–L−1 combination was constrained by z0=0.01 m as calculated from the MOS profile of the horizontal wind speed (Pasquill and Smith, 1983). For lateral wind velocity fluctuations, which only affect turbulent diffusion in the crosswind direction, we used the scaling . This corresponds to the median of our data and, for simplicity, was adopted here for all stabilities.
2.3 Statistical model
2.3.1 Land cover class aggregation and upscaling of CH4 fluxes
We hypothesize that mean CH4 fluxes can be determined for LCC groups, each composed of LCCs of similar expected source–sink capacity. This grouping was based on the documented vegetation and soil characteristics, reported in detail by Mikola et al. (2018) and Nyman (2015), and summarized here in Sect. 2.1.4. In addition, we utilized the TWI map and defined areas of potentially wet soils as those with TWI >4 (Fig. 1d). Using these data and syntheses of CH4 production and fluxes in similar ecosystems (Olefeldt et al., 2013; Nicolini et al., 2013; Turetsky et al., 2014; Lau et al., 2015; Petrescu et al., 2015; Treat et al., 2015) as background information, we defined four aggregated classes (Table 3, Fig. 2), for which the LCC group-specific fluxes were determined with the statistical model described below (Sect. 2.3.2).
The data sources listed above suggest that wet fens typically are strong CH4 emitters, and thus the pixels of the wet fen LCC with TWI > 4 were selected for the first LCC group (“strong source”; Table 3). We also assumed that the pixels of the graminoid tundra LCC in the potentially wet locations should be included in this category as the graminoids at the site are dominated by aerenchymatous Carex spp. and Eriophorum spp. (e.g. E. vaginatum), i.e. plants known to be associated with substantial CH4 emissions. The drier fens within the study area likely act as weaker emitters, so these were combined into another LCC group (“moderate source”), together with the bodies of freshwater (water LCC above the sea level). The syntheses cited above also justify an assumption that mineral soils, i.e. here the bare ground and lichen tundra LCCs, act as weak CH4 sinks (“sink”). The proportional areas of these three LCC groups were used as the explanatory variables in the regression model. The remaining pixels were allocated to the fourth group consisting of the LCCs that either are expected to have a very small CH4 flux on average or cover only a limited area in flux footprints (“neutral”). This group is included as an intercept in the regression model, and we hypothesize that its estimated value is not statistically different from zero.
The CH4 fluxes determined for the aggregated LCCs defined above were upscaled by a simple mosaic approach, i.e. by areal weighting of the group-specific fluxes. To illustrate how the upscaled flux depends on land cover heterogeneity at different spatial scales, the upscaling was performed for different subdomains as a function of the distance from the EC tower, and also for a larger area of 35.8 km2 (Fig. S2).
2.3.2 Model formulation and validation
Assuming that the CH4 flux does not vary among the LCC-map pixels attributed to a certain LCC, we applied Eq. (5) and expressed each flux measurement as a weighted arithmetic mean of the LCC-specific fluxes Fj, j=1 … N (number of LCCs),
where these fluxes are unknown, and the weights 〈Λ〉j (Eq. 3) are the fractional areas of the corresponding LCCs. Assuming further that the LCC-specific fluxes remain constant within a data set of M observations but the proportional LCC areas vary with the temporally changing footprint, we obtained a set of linear algebraic equations, from which a solution could be sought for Fj. We applied this idea by first defining aggregated LCC groups according to the expected CH4 source–sink capacity of each LCC (Sect. 2.3.1) and formulated a linear regression problem as
where the matrix contains the proportional LCC areas of the aggregated LCCs for each observation, is a vector of the unknown parameters, m[M×1] denotes the measurement vector, and e[M×1] is the error term. NA (equal to 3 here) denotes the number of those aggregated LCCs whose proportional area was included as an explanatory variable. This does not cover all the LCCs, and we included an intercept term in this regression equation so as to represent the remaining LCCs and the proportion of footprint extending beyond the study area; i.e. we did not scale the sum of 〈Λ〉j to 100 %.
We estimated q with the ordinary least square (OLS) estimator. Before calculating the standard errors of these estimates, we tested the model residuals for heteroskedasticity and serial correlation. Heteroskedasticity was tested with the White test that is based on an auxiliary regression, where squared residuals are regressed on original explanatory variables and their squares and cross products, and the inference is based on a Lagrange multiplier (LM) test statistic (Greene, 2012). Serial correlation was tested with the Breusch–Godfrey test, which is based on a similar LM principle where the OLS residuals are regressed on the original explanatory variables augmented by lagged residuals. If heteroskedasticity and serial correlation could not be ruled out, the standard errors for the model parameters were calculated with the Newey–West estimator, which is a robust estimator for the asymptotic covariance matrix of the OLS estimator (Greene, 2012). This would result in wider confidence intervals than the traditional OLS-based standard errors. We assume that these confidence intervals reflect the overall uncertainty emerging from measurement data, LCC classification and footprint modelling; therefore, no “bottom-up” error analysis addressing individual error sources was attempted.
The agreement between the model and the observations was evaluated on the basis of the coefficient of determination (R2), root mean squared error (RMSE) and mean absolute error (MAE). The agreement was also examined as a function of wind direction, to verify that we can replicate the pronounced directional dependency of the observed CH4 fluxes (Aurela et al., 2015). The performance of the statistical model against independent data was assessed with 10-fold cross-validation (James et al., 2013).
The random error of the measured mean CH4 flux was estimated as , where σ is the standard deviation of flux and M=911. To minimize the wind direction dependency of fluxes, σ was calculated relative to a varying mean obtained from the data binned as a function of wind direction into 50 groups of similar size.
To investigate the temporal trend of the fluxes, we performed the statistical modelling and upscaling separately for weekly periods in addition to the full 8-week data set. These results also shed light on the performance of the statistical method when the number of input data is limited and the coverage of different wind directions may be incomplete.
3.1 Demonstrating surface heterogeneity
Our footprint analysis shows that those surface elements that had the greatest influence on the EC measurements in Tiksi were typically located within a distance of 10–200 m (Table S1 in the Supplement). However, the actual range depended strongly on atmospheric stability, as expected (Horst and Weil, 1992). The distance of maximal influence in a single footprint varied from 18 to 35 m depending on stability, and the estimated far end of the source area ranged from 200 to 3500 m for the 90 % flux contribution, for instance. The 1.4 km radius of the circle centred at the EC tower, which defines our primary study area, was selected to result in a 95 % footprint coverage within this area in the neutral case. About 15 % of the footprint calculated for the stable flow example extended beyond the limits of this area, while in the unstable case 99.7 % of the footprint was confined to the target circle (Fig. 3).
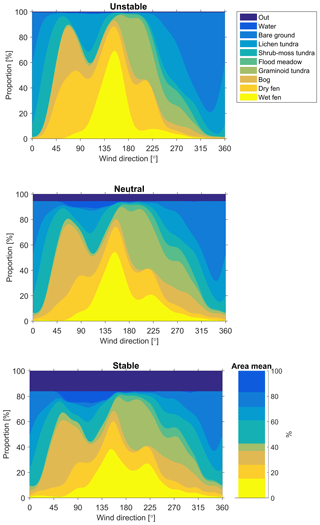
Figure 3Proportion of different land cover classes in the flux footprint as a function of wind direction for the three flow condition cases specified in Table 2. The rightmost panel shows the relative coverage of these classes within the study area.
The variation of the footprint-weighted LCC contributions, calculated with Eq. (5), as a function of wind direction demonstrates how the heterogeneity inherent in tundra landscape manifests itself in the EC measurement data (Fig. 3; see also Fig. S3). As is obvious from the LCC map (Fig. 1a), the distribution of contributing LCCs varied a lot among different wind directions (Fig. 3). In the neutral case, for example, there were seven different LCCs dominating at least in one sector. Turbulent mixing also played a substantial role in the magnitude of relative LCC contributions, as the weighting of longer distances increased with increasing stability. In some directions, the contribution of the most common LCCs was highly sensitive to atmospheric stability. In the north-east-to-east sector, for example, the relatively small dry fen patch located within a few tens of metres from the EC tower (Fig. 1a) contributed 45 % in the unstable case but only 13 % in the stable case (Fig. 3). Similarly, the relative importance of the extensive bare-ground area between the west and the north-east strongly depended on atmospheric stability.
The footprint-weighted surface characteristics, calculated with Eq. (2) for the cases detailed in Table 2, further demonstrate the landscape heterogeneity-induced variations. The effective LAI originating from the footprint-weighting of the LAI map showed a strong dependency on wind direction: in the neutral case, for example, 〈LAI〉 ranged from 0.19 to 0.64 m2 m−2 (Fig. 4a). In the unstable case, the direction dependency was similar; however, 〈LAI〉 was up to 0.12 m2 m−2 lower than in neutral conditions due to the dominance of bare ground in the vicinity of the EC tower in the north-western sector (Fig. 1a). As averaged over all directions, here assumed equally frequent, 〈LAI〉 was in all stability cases somewhat higher than the arithmetic areal average (Fig. 4a). Due to the directional variations in 〈LAI〉, the maximum sensor location bias (ΔLAI, Eq. 6) may exceed 90 % in the direction of the maximum 〈LAI〉.
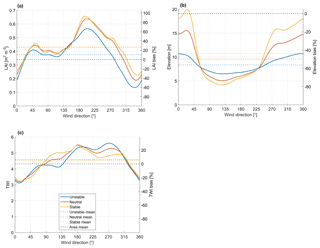
Figure 4The footprint-weighted and areally averaged leaf area index (a), terrain elevation (b) and topographic wetness index (c) as a function of wind direction for the three flow condition cases specified in Table 2. The right-hand ordinate indicates the corresponding sensor location bias.
Based on a corresponding footprint-weighting, an effective mean value could also be determined for terrain elevation (Fig. 4b). This shows that, even though the topographic variability within the flux footprint was small, slightly different terrain elevation patterns are associated with each flux measurement depending on both wind direction and stability. The sensor location bias for elevation was negative in almost all flow conditions, as the elevation is on average lower within the area that typically dominates the flux footprint (Figs. 1b and 4b). The area of predominantly bare ground was also apparent in the effective TWI (Fig. 4c). In the east-to-south sector, the differences between the stability classes are due to the higher TWI values determined along the coast (Fig. 1d) that gain in importance in stable conditions. Between the south-west and the north-west, in contrast, 〈TWI〉 was higher in unstable conditions, which results from the more pronounced influence of the brook running near the EC tower. The footprint-weighted TWI averaged over all directions was, in all cases, close to the arithmetic area average, with the magnitude of the corresponding ΔTWI being lower than 30 % (Fig. 4c).
In addition to the examples presented above, we demonstrated the heterogeneity of the Tiksi landscape by calculating the mean LAI and LCC contributions from the time series of EC measurements adopted for the present analysis. Figure 1a shows the footprint climatology for the growing season of 2014, depicted as the smallest bounded region containing the surface elements that contribute to EC measurements by a certain fraction (Eq. S1 in the Supplement). This source area is clearly asymmetric, and comparison with the data in Table S1 indicates that the source area is more limited than the corresponding area in typical neutral conditions; i.e. it effectively reflects slightly unstable conditions. Weighting the LAI distribution by the mean footprint resulted in a bias of ΔLAI=20.2 %. For comparison, this is much larger than the bias in the NDVI estimated for EC sites in northern China: at the 1 km2 scale, ΔNDVI ranged from −6.9 % to 4.2 % at eight sites with low vegetation, and even at a land model scale of ∼300 km2 the mean absolute ΔNDVI was not more than 6.5 % (Wang et al., 2016). Notwithstanding such a high degree of agreement, one of the sites was considered “disturbed”. In another study, the EC measurements at two sites with a ΔNDVI of less than 4 % reported for the 1 km2 scale were considered unbiased, while a ΔNDVI of 28 % determined for a grassland site was judged as problematic; the mean NDVI, and hence ΔNDVI, was very similar up to the maximum scale of 4 km2 investigated (Kim et al., 2006).
For most of the LCCs in Tiksi, the field of view of the EC sensors averaged over the growing season clearly differed from the areal coverage of the LCCs within the study area (Table 4; see also Fig. S4 for the effect of wind direction and stability). Here, we have excluded the large marine areas, which have a minor weight in the EC data. The difference is still largest for the water LCC, as the freshwater bodies are concentrated on the fringes of the study area, and for the flood meadow category with a limited coverage. However, there were also major differences among the dominating terrestrial classes, such as shrub tundra and wet fen: the surface elements attributed to these LCCs contributed to the EC observations less (by 40 %) than their total areal coverage would suggest.
Table 4Proportions (%) of different land cover classes as weighted by the mean footprint function during the growing season (“weighted”) and their areal coverages within the study area (“area”), within the source area defined by the 90 % cumulative footprint (“area, 90 %”, Fig. 1a) and within a 35.8 km2 region (“region”, Fig. S2). The marine areas are excluded, and the integrated footprint within the study area is scaled to 100 %.
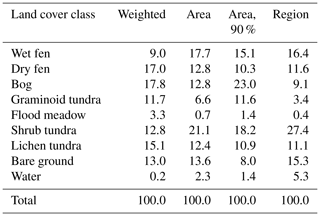
If the areal LCC proportions were calculated within the non-circular area defined by the 90 % cumulative footprint (Fig. 1a), some of these proportions changed dramatically (Table 4). We also included in the comparison the LCC distributions for a 35.8 km2 area (Fig. S2). Compared to this, the study area has a similar coverage of fens, bare ground and lichen tundra, whereas the water and shrub tundra LCCs are under-represented and bogs and graminoid tundra over-represented. Overall, these results demonstrate the multiscale heterogeneity of the site and indicate that here the representativeness cannot be described as a proportional coverage of a single target LCC in the footprint climatology, as is the case for most EC sites (Göckede et al., 2008).
3.2 Land cover group-specific CH4 fluxes
The parameters of the regression model introduced in Sect. 2.3.2 were estimated with OLS for the LCC aggregation presented in Sect. 2.3.1. As this produced model residuals that exhibited both heteroscedasticity and autocorrelation (White LM test statistic , Breusch–Godfrey LM test statistic ), the confidence intervals were based on the Newey–West estimator. Even when these (larger) confidence intervals were introduced, all the estimated parameters except for the constant, i.e. those representing aggregated LCCs with expected CH4 exchange, proved to be statistically different from zero (p<0.05; Table 5). The results were also in perfect accord with our qualitative hypothesis on CH4 flux variability among the LCCs: the model could differentiate between the high emitters, moderate emitters and sinks without any explicit prior information on this pattern. Concerning the quantitative differences, Treat et al. (2018) reported the same degree of spatial variation (standard deviation/mean of 155 %) in the modelled annual CH4 fluxes on low Arctic tundra, highly heterogeneous similarly to Tiksi, and showed that the differences among LCCs clearly dominate over the interannual variation in the regional CH4 fluxes.
The temporal variation of the estimated 30 min ecosystem-scale CH4 fluxes was consistent with observations, even though it is obvious that the full range of variability, most notably the peak values, could not be reproduced (R2=0.797, RMSE of 0.0994 , MAE of 0.0686 ; Fig. S5). However, part of this variation arose from measurement noise, and in this context it is crucial that the mean fluxes were modelled accurately also when considering the strong wind direction dependence of observations (Fig. 5). Estimated from the mean fluxes of binned data shown in Fig. 5, the variance related to wind direction accounted for up to 80 % of the total variance of measured fluxes. This dependence, obviously generated by the systematic LCC variations within the flux footprint (Fig. 3), is a key pattern in this data set and must be taken into consideration when calculating representative CH4 balances (Aurela et al., 2015). The model residuals differed significantly (p<0.05) from zero only in a narrow south-eastern wind sector, where the model slightly overestimated the fluxes. The 10-fold cross-validation statistics show that the model performed against independent data only marginally worse than the fit to the full data set (R2=0.794, RMSE of 0.1000 , MAE of 0.0691 ).
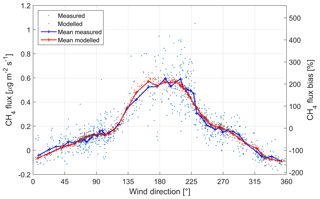
Figure 5Measured and modelled CH4 fluxes as a function of wind direction (left axis). The averaged data were calculated in 50 direction classes. The right axis indicates the sensor location bias of the measured data shown (both individual points and the mean) with respect to the mean upscaled flux within the study area (0.183 ).
Forbrich et al. (2011) have shown that the footprint variations dominate the short-term (hourly to daily) variations in the CH4 flux on a boreal fen with a pronounced flark–lawn–hummock structure, while soil temperature only explains the seasonal trend. As 80 % of the CH4 flux variance in Tiksi was explained by the variation in the proportions of the LCCs contributing to the measurement, we can expect a similar pattern, i.e. a limited role of other environmental controls in the short-term variability (30 min data). The linear correlation between CH4 flux and soil temperature (at 10 cm depth) was indeed weak (R2=0.101) and did not get any stronger for an exponential fit or if one considered the model residual, i.e. the unexplained part of observation. For u*, this correlation was even weaker (R2=0.053); u* acts as a measure of turbulence that affects surface diffusion and ebullition and has been found to explain a major part of the CH4 flux variance observed on polygonal tundra (Sachs et al., 2008). Our results also contrasted with the findings of Parmentier et al. (2011), who, similarly to our study, observed a major effect of wind direction on the CH4 flux measured on Siberian tundra but were also able to relate the short-term flux variation to environmental variables, including atmospheric stability. In that study, however, the LCC proportions were not used as an explanatory factor, but the data were grouped according to the wind sector characterized by qualitative soil wetness (“wet”, “dry” and “mixed”), and environmental responses were determined separately for these groups. On the other hand, Tagesson et al. (2012) found that the only significant factor controlling the CH4 flux on a wet tundra ecosystem in north-east Greenland was the relative contribution of fen areas, indicating that the controls are site-specific and that any turbulence-related dependency may partly reflect footprint variations, in addition to the actual control of surface exchange processes.
Chamber-based CH4 flux measurements would constitute the most logical means for validating the estimated LCC-specific fluxes. As explained in Sect. 2.1.2, some chamber data were available for the period of the EC data but their temporal and spatial coverage was limited. Despite the limitations, these measurements lend support to our EC-based results shown in Table 5: the two wet fen plots were strong CH4 emitters with observed fluxes of 0.56 and 3.8 , while the mean CH4 emission from dry fen plots ranged from 0.06 to 0.67 (mean 0.25 ) (Vähä, 2016). The LCC group-specific fluxes (Table 5) were also in accordance with the extensive synthesis of chamber-based CH4 flux measurements across permafrost zones conducted by Olefeldt et al. (2013). Their database indicates that the mean flux at peatland sites during the growing season ranges from 0.03 on dry tundra to 0.75 on wet tundra (medians of site-specific fluxes), while the mean flux at the sites classified as permafrost fen is within 0.48–1.70 at 50 % of the sites. The micrometeorological measurements that integrate over the heterogeneity of tundra landscape typically show lower CH4 fluxes. For example, Sachs et al. (2008) and Wille et al. (2008) measured a mean emission of 0.22 from polygonal tundra in the Lena River delta in July–August (in 2004 and 2006), which is close to our mean flux (0.21 in July–August 2014). Seven other comparable Arctic tundra sites in Siberia, Alaska and Greenland had a mean summer flux within the range of 0.13–1.05 (Fan et al., 1992; Friborg et al., 2000; Zona et al., 2009; Parmentier et al., 2011; Tagesson et al., 2012; Castro-Morales et al., 2018). These data also show that variation among sites can be much larger than the interannual variation at a site.
The sink efficiency estimated for the mineral soil LCCs in Tiksi ( , 95 % confidence interval) seems high in comparison to previous data (Turetsky et al., 2014; Lau et al., 2015; Jørgensen et al., 2015; D'Imperio et al., 2017). However, this estimate is consistent with the measured EC fluxes and thus not an artefact of the modelling procedure. This can be observed by inspecting the cases in which the proportion of the assumed sink LCCs in the flux footprint exceeds 80 % (within the wind direction sector of 330–360∘). By ignoring the other LCCs, we obtained an apparent mean CH4 flux of −0.109 for these cases, while the corresponding modelled (for all LCCs) and measured fluxes were −0.093 and −0.094 , respectively. Furthermore, the chamber measurements conducted on bare ground at the site in summer 2014 yielded a consistent mean of −0.12 (Vähä, 2016).
So far, our discussion has been based on fluxes averaged over the whole study period of 8 weeks. The weekly resolved LCC group-specific fluxes, however, indicate that there was temporal variation in CH4 emissions that was not generated by footprint dynamics (Fig. 6). Most notably, the drier fens (dry fen LCC, and wet fen LCC with a low TWI) showed only weak emissions in the beginning of the period. The maximum emissions occurred during the 2-week period around mid-August (9–22 August); these emissions were on average 0.44±0.14 for the “moderate source” LCC group and 1.00±0.10 for the “strong source” LCC group. The weekly averages of model residuals during the whole study period were positively correlated with the corresponding soil temperatures, but the correlation was not statistically significant (R2=0.444, p=0.102). However, the maximum emissions occurred when soil temperatures were highest, approximately 5 ∘C (at 10 cm depth), on 9–22 August. During this period, the LAI of vascular plants on the fens and graminoid tundra was still high, even though it was already declining on the fens (Juutinen et al., 2017). The positive correlation between the vascular LAI of graminoid tundra and the weekly model residuals (R2=0.556, p=0.054) points to the role of both primary production and plant-mediated CH4 transport, associated with the close relationship between LAI and the maximum photosynthesis rate (Laurila et al., 2001; Street et al., 2007) and the dominance of aerenchymatous plants (Bridgham et al., 2013). However, the depth of the active layer also increased during the study period in some soils, especially in dry fens, but the data are too limited for statistical analysis of this effect (Mikola et al., 2018).
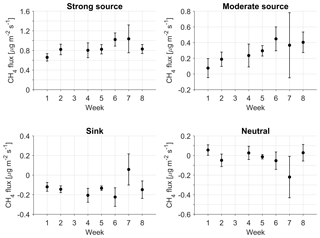
Figure 6Estimates of the LCC group-specific fluxes calculated from weekly data (1 indicates 5–11 July; 2 indicates 12–18 July; 3 indicates 19–25 July, data missing; 4 indicates 26 July–1 August; 5 indicates 2–8 August; 6 indicates 9–15 August; 7 indicates 16–22 August; 8 indicates 23–29 August). The vertical bars indicate the 95 % confidence intervals.
3.3 Upscaled CH4 fluxes
By upscaling the mean CH4 fluxes estimated for the LCC groups, we estimated the effect of the EC tower location on the spatial representativeness of the mean CH4 flux observed during the growing season of 2014 (0.208 ). In other words, adopting the data shown in Table 5 as a reference for the CH4 flux averaged over the study area, we could calculate the sensor location bias for CH4 flux (Fig. 5) similarly to the results shown in Sect. 3.1 for LAI, terrain elevation, TWI and LCC proportions. As the relative area of the coastal waters is significant within the study area but minor in the average flux footprint (Fig. 1, Table 4), these areas were excluded from the upscaling domain.
Calculating the sensor location bias for CH4 flux is equivalent to a linear transformation of the observed fluxes. Thus, the pronounced directional dependence of CH4 fluxes translates into an equally pronounced variation in this bias estimate, which ranged approximately from −200 % to 400 % for individual data points and from −170 % to 230 % on average (Fig. 5). The bias was smallest in eastern and western wind directions. However, the effective LCC composition is very different in these directions, with a much smaller coverage of fens in the west (Fig. 3).
The areally averaged CH4 flux depended on the upscaling domain in a non-monotonous manner (Fig. 7). The uncertainty of the mean measured CH4 flux (Sect. 2.3.2) was small (0.007 ) due to a large number of observations and was ignored in Fig. 7b. Defining the reference area as a function of the radius of a circular area centred at the EC tower, the magnitude of sensor location bias was less than 10 % for the distances of 640–1350 m. Acknowledging the statistical uncertainty in the upscaled fluxes, determined from the LCC group-specific uncertainty estimates (Table 5), the measured mean flux was within the 95 % confidence interval for distances larger than approximately 600 m. For the primary study area, the mean bias during the growing season was 13.9 % and the corresponding 95 % confidence interval was [−0.3 %, 32.9 %] (Table 6). While formally the overestimation of EC measurements of the CH4 flux averaged over the study area was not statistically significant (p>0.05), the estimated sensor location bias would be lower if the study area were originally defined by a radius of 800–1000 m (Fig. 7). Here, we do not suggest that the study area should be defined post hoc but advocate a footprint-based analysis to assess the representativeness of measurements at different spatial scales. Adopting the regional upscaling area of 35.8 km2 as the reference results in a sensor bias of 30 % [12 %, 55 %] for the CH4 flux (Table 6).
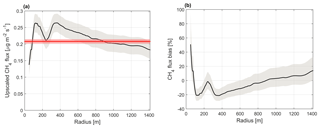
Figure 7Upscaled CH4 flux within a circular area as a function of the distance from the EC tower (a) and the corresponding sensor location bias according to Eq. (6) (b). The red line indicates the mean measured flux. The shaded areas represent the 95 % confidence intervals.
Table 6Upscaling of CH4 fluxes () based on the LCC group-specific flux data shown in Table 5.
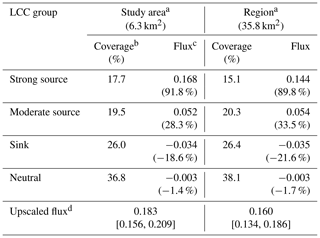
a “Study area” refers to the circle with a radius of 1.4 km centred at the EC mast. “Region” is shown in Fig. S2. b Marine areas are excluded from upscaling. c Calculated as LCC group-specific flux multiplied by the relative coverage. The value in parentheses is equivalent to this flux divided by the upscaled flux. d The values in square brackets indicate the 95 % confidence interval.
Even though the coverage of our nine basic LCCs clearly differed from their footprint-weighted contributions (Table 4), the four LCC groups, aggregated according to the assumed CH4 emission potential of LCCs, covered areas rather similar to those within the original study domain (Table 6). Within the regional upscaling area of 35.8 km2, the strong emitters were less common, but the total flux was only 13 % lower than within the original study area. On the other hand, freshwater bodies occupy a larger relative area (Table 4). These were included here in the “moderate source” LCC group, but the actual emissions from these ecosystems could not be estimated as their total area within the flux footprint is minute. Nevertheless, there is increasing evidence that Arctic lakes and ponds emit significant amounts of CH4 (Wik et al., 2016). At all scales, it was necessary to allow for the sink areas that play a significant role in the upscaled balance. However, the agreement of CH4 fluxes between different scales may be considered somewhat fortuitous and implies little about carbon dioxide and other scalar fluxes that have different spatial patterns.
3.4 Methodological issues
Our results obviously depend on the quality of the land cover classification. The LCC accuracy assessment indicates that especially the flood meadow LCC is poorly classified (Mikola et al., 2018); however, this LCC only appears along the brook and has a very limited coverage. More importantly, the dry fen, wet fen and graminoid tundra pixels may be partly mixed up. The field data and multivariate data analysis of Mikola et al. (2018) indicate that the variations in plant functional type composition within these LCCs indeed overlap, which impairs the classification of the “strong source” and “moderate source” LCC groups and effectively precludes modelling that resolves individual LCCs. On the other hand, the large areas of bare ground and lichen tundra with low organic soil content, i.e. the assumed CH4 sink areas, can be identified reliably (Mikola et al., 2018).
Despite the uncertainties, the land cover classification allowed us to meaningfully group the surface elements according to their CH4 exchange potential. This relationship shows that the LCC reflects the integrated effect of a range of processes that control net production and efflux of CH4, such as the availability of substrates and gas transport routes (Davidson et al., 2016, 2017). Thus, a vegetation classification based on VHSR satellite imagery provided us with a straightforward means of upscaling the average LCC group-specific fluxes. As the predominant part of CH4 flux variance resulted from the varying contributions of different LCCs, we did not consider additional environmental controls. Such simplicity is welcome since statistically robust EC-based flux estimates for scales exceeding the flux footprint would require spatial replication with multiple EC towers (Hill et al., 2017). Our approach serves as an alternative to a common method of deriving LCC-specific data from (a typically more limited set of) flux chamber measurements and upscaling these either directly (e.g. Schneider et al., 2009; Davidson et al., 2017) or by first modelling their temporal variation (e.g. Marushchak et al., 2016). Matthes et al. (2014) showed that more nuanced insights into the spatial drivers can be achieved by the use of multiple EC towers and periodic remote sensing images and by examination of both the abundance and spatial fractal structure of vegetation.
Even though the KM model constitutes an appropriate tool for describing turbulent transport over an aerodynamically smooth surface such as tundra, any footprint estimate involves both structural and input-related modelling uncertainties. The KM model has been tested by Kljun et al. (2003), Marcolla and Cescatti (2005), Neftel et al. (2008) and Arriga et al. (2017) against experimental data and more complex footprint models. All these studies conclude that the KM model performs well, but we note here that there may be a tendency for too-smooth footprint distributions in the along-wind direction. As pointed out in Sect. 2.3.2, we did not try to explicitly estimate the errors related to the flux footprints but assumed that the confidence intervals determined for the LCC group-specific fluxes reflect the overall uncertainty contained in any data employed in the statistical model. Because of this approach, the uncertainty of the results shown in Figs. 3 and 4 could not be quantified. Overestimation of footprint distribution in larger distances would mean that the contribution of graminoid tundra might be slightly underestimated and that of shrub tundra overestimated as the proportions of these LCCs have a rather systematic dependency on the distance from the EC mast. If the overall LCC heterogeneity of a site became more apparent when viewing it as a function of distance rather than direction, our statistical method would be more dependent on the footprint model and the results would probably be more uncertain.
We obtained statistically significant estimates for the LCC group-specific fluxes when employing the whole data set of 8 weeks, but the performance of the model was observed to deteriorate as the number of data was reduced. This can be observed from the weekly results (Fig. 6), in which the confidence intervals are temporally varying and larger than those for the whole data set; in some cases, the results were not consistent with the original flux hypotheses (at the chosen significance level). As wind direction is the primary control of the flux footprint, and consequently the LCC proportions associated with EC measurements (Fig. 3), it is necessary that the variation in wind directions during each period sufficiently covers all the relevant LCCs. This obviously depends on the degree and nature of LCC heterogeneity at the site in question. In our weekly results for Tiksi, the directional coverage was clearly incomplete during 16–22 August 2014, when there were few observations for the sector extending from the north-west to the south-east, leading to uncertain flux estimates for that particular period (Fig. 6). Nevertheless, the LCC group-specific fluxes estimated on a weekly basis improved the overall model performance during the whole study period (R2=0.836, RMSE of 0.0894 , MAE of 0.0619 ).
While the weekly results indicated that there is temporal variation in the LCC group-specific fluxes, the longer-term upscaling was rather insensitive to temporal resolution of these data. The weekly values produced an upscaled flux of 0.162±0.063 for the original study area, i.e. only slightly lower (by 11 %) but a much more uncertain estimate than the one obtained for the whole data set (Table 6).
We suggest that estimation of LCC-specific fluxes, accomplished here with a regression model, provides a new avenue to filling the inevitable gaps in the measurement data time series. This proposition is supported by the good out-of-sample validation statistics obtained (Sect. 3.2), as holding the validation data out during parameter estimation is equivalent to generating missing data that need to be gap-filled. This kind of an approach is potentially applicable to those data gaps that are related to the gas concentration measurement, for example due to malfunctioning of the gas analyser, i.e. gaps that appear in the CH4 flux data but not in the momentum and sensible heat fluxes.
Another methodological implication of our results concerns the definition of a study area. It is customary to report a “site description” that documents the key ecological characteristics of the area of interest. Within a homogeneous environment, collating the necessary site data is straightforward in terms of statistical representativeness because the outcome is insensitive to the spatial sampling design. Furthermore, the representativeness of EC measurements can be simply assessed by considering the coverage of a single target LCC within the flux footprints. In heterogeneous environments, however, there is a risk for a serious mismatch between the EC flux measurements and the site data, even in cases of an unbiased description of the study area. Our results show that the land cover type composition sampled by the EC measurement was significantly different from the actual LCC coverage within our study area, which as such was originally chosen to be consistent with the dimensions of a typical flux footprint and considered characteristic of the landscape.
The eddy covariance flux measurement technique is commonly considered to have an advantageous spatial averaging property, sometimes to the extent that it is assumed to “provide an accurate integration of the overall flux from the [heterogeneous] ecosystem” (Turner and Chapin III, 2006). However, this notion is limited and potentially misleading as a universal premise, since this integration process involves differential weighting within a temporally varying flux footprint, a well-known but frequently overlooked feature of EC measurements, which we in the present study demonstrated and quantified for a heterogeneous tundra site in north-eastern Russia. The CH4 fluxes measured in Tiksi were highly variable due to the variation in vegetation composition and soil wetness within the landscape around the EC tower. During summer 2014, the bias of observations with respect to the upscaled flux varied strongly with wind direction, ranging from −170 % to 230 % on average.
By combining VHSR satellite imagery and footprint modelling, we could statistically estimate the contribution of the main land cover types to EC measurements. Methane emissions mainly originated from wet fen and graminoid tundra patches in locations with topography-enhanced soil wetness, where conditions are favourable for CH4 production and efflux (mean flux 1.0 during the 2-week peak period). Another noteworthy feature is that the areas of bare soil and lichen tundra acted as strong CH4 sinks (−0.13 during the summer). Despite the ecosystem heterogeneity and directional variations in the point-to-area representativeness of EC measurements, the mean CH4 flux measured during this season can be considered unbiased, and even more so if the present area of interest were halved, i.e. considered to extend up to 1 km from the EC tower. On the other hand, the measured fluxes overestimate the regional (35.8 km2) balance by 30 %.
Even though the EC-sampled LCC distribution proved to be representative in terms of the mean CH4 flux during a growing season, the small-scale heterogeneity at the site was so high as to result in rather unfavourable representativeness metrics for key land cover features such as LAI and LCC fractions. This suggests that it would generally be beneficial to present a more integrated site and flux data description than what has been considered standard, i.e. to also include data on footprint-weighted surface attributes and point-to-area representativeness.
In a follow-up study, we will investigate longer-term CH4 flux data from Tiksi to better understand the seasonal and interannual variations and their environmental controls. These data will also make it possible to further assess the statistical method suggested here, including its use as a gap-filling tool. Furthermore, we anticipate that flux sites with more than one EC tower provide new opportunities for the estimation of LCC-specific fluxes (e.g. Matthes et al., 2014; Hill et al., 2017); more advanced inverse modelling techniques should be explored for this.
The micrometeorological data used in this study can be accessed via the Zenodo data repository (Tuovinen et al., 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-16-255-2019-supplement.
JPT designed the study, performed the computations, interpreted the results and wrote the paper, with contributions from MA, AR, TV, JM and TL. MA, JH, VI, VK and TL carried out the flux measurements. AR and TV provided the remote sensing and vegetation data, and JM provided the soil data. All authors reviewed the paper.
The authors declare that they have no conflict of interest.
This study was financially supported by the Academy of Finland, projects
“Greenhouse gas, aerosol and albedo variations in the changing Arctic”
(project no. 269095), “Carbon balance under changing processes of Arctic and
subarctic cryosphere” (project no. 285630), “Constraining uncertainties in
the permafrost-climate feedback” (project no. 291736) and “Carbon dynamics
across Arctic landscape gradients: past, present and future” (project no.
296888); the European Commission, FP7 project “Changing permafrost in the
Arctic and its global effects in the 21st century (PAGE21, project no.
282700)”; and the Nordic Council of Ministers, DEFROST Nordic Centre of
Excellence within NordForsk.
Edited by: Lutz Merbold
Reviewed by: two anonymous referees
AARI: Archive of Tiksi standard meteorological observations (1932–2016), Russian Federal Service for Hydrometeorology and Environmental Monitoring, St Petersburg, Russia, available at: http://www.aari.ru/resources/d0024/archive/description_e.html, last access: 13 September 2018.
Amiro, B. D.: Footprint climatologies for evapotranspiration in a boreal catchment, Agr. Forest Meteorol., 90, 195–201, 1998.
Arriga, N., Rannik, Ü, Aubinet, M., Carrara, A., Vesala, T., and Papale, D.: Experimental validation of footprint models for eddy covariance CO2 flux measurements above grassland by means of natural and artificial tracers, Agr. Forest Meteorol., 242, 75–84, 2017.
Asner, G. P., Scurlock, J. M. O., and Hicke, J. A.: Global synthesis of leaf area observations: implications for ecological and remote sensing studies, Global Ecol. Biogeogr., 12, 191–205, 2003.
Aubinet, M., Vesala, T., and Papale, D. (Eds.): Eddy Covariance: A Practical Guide to Measurement and Data, Springer Science+Business Media B.V., Dordrecht, 2012.
Aurela, M., Lohila, A., Tuovinen, J.-P., Hatakka, J., Riutta, T., and Laurila, T.: Carbon dioxide exchange on a northern boreal fen, Boreal Environ. Res., 14, 699–710, 2009.
Aurela, M., Laurila, T., Tuovinen, J.-P., Hatakka, J., Linkosalmi, M., Virtanen, T., Mikola, J., Asmi, E., Ivakhov, V., Kondratyev, V., Uttal, T., and Makshtas, A.: CH4 and CO2 exchange on permafrost tundra in Tiksi, Siberia, in: Proceedings of the 1st Pan-Eurasian Experiment (PEEX) Conference and the 5th PEEX Meeting, edited by: Kulmala, M., Zilitinkevich, S., Lappalainen, H. K., Kyrö, E.-M., and Kontkanen, J., Report Series in Aerosol Science, 163, 60–62, 2015.
Böhner, J. and Selige, T.: Spatial prediction of soil attributes using terrain analysis and climate regionalisation, in: SAGA – Analysis and Modelling Applications, edited by: Böhner, J., McCloy, K. R., and Strobl, J., Göttinger Geographische Abhandlungen, 115, University of Göttingen, Germany, 13–28, 2006.
Bridgham, S. D., Cadillo-Quiroz, H., Keller, J. K., and Zhuang, Q.: Methane emissions from wetlands: biogeochemical, microbial, and modeling perspectives from local to global scales, Glob. Change Biol., 19, 1325–1346, 2013.
Budishchev, A., Mi, Y., van Huissteden, J., Belelli-Marchesini, L., Schaepman-Strub, G., Parmentier, F. J. W., Fratini, G., Gallagher, A., Maximov, T. C., and Dolman, A. J.: Evaluation of a plot-scale methane emission model using eddy covariance observations and footprint modelling, Biogeosciences, 11, 4651–4664, https://doi.org/10.5194/bg-11-4651-2014, 2014.
Castro-Morales, K., Kleinen, T., Kaiser, S., Zaehle, S., Kittler, F., Kwon, M. J., Beer, C., and Göckede, M.: Year-round simulated methane emissions from a permafrost ecosystem in Northeast Siberia, Biogeosciences, 15, 2691–2722, https://doi.org/10.5194/bg-15-2691-2018, 2018.
Chen, B., Black, T. A., Coops, N. C., Hilker, T., Trofymow, J. A., and Morgenstern, K.: Assessing tower flux footprint climatology and scaling between remotely sensed and eddy covariance measurements, Bound.-Lay. Meteorol., 130, 137–167, 2009.
Davidson, S. J., Sloan, V. L., Phoenix, G. K., Wagner, R., Fisher, J. P., Oechel, W. C., and Zona, D.: Vegetation type dominates the spatial variability in CH4 emissions across multiple arctic tundra landscapes, Ecosystems, 19, 1116–1132, 2016.
Davidson, S. J., Santos, M. J., Sloan, V. L., Reuss-Schmidt, K., Phoenix, G. K., Oechel, W. C., and Zona, D.: Upscaling CH4 fluxes using high-resolution imagery in Arctic tundra ecosystems, Remote Sens., 9, 1227, 2017.
D'Imperio, L., Nielsen, C. S., Westergaard-Nielsen, A., Michelsen, A., and Elberling, B.: Methane oxidation in contrasting soil types: responses to experimental warming with implication for landscape-integrated CH4 budget, Glob. Change Biol., 23, 966–976, 2017.
Fan, S. M., Wofsy, S. C., Bakwin, P. S., Jacob, D. J., Anderson, S. M., Kebabian, P. L., McManus, J. B., Kolb, C. E., and Fitzjarrald, D. R.: Micrometeorological measurements of CH4 and CO2 exchange between the atmosphere and subarctic tundra, J. Geophys. Res., 97, 16627–16643, 1992.
Foken, T. and Wichura, B.: Tools for quality assessment of surface-based flux measurements, Agr. Forest Meteorol., 78, 83–105, 1996.
Forbrich, I., Kutzbach, L., Wille, C., Becker, T., Wu, J., and Wilmking, M.: Cross-evaluation of measurements of peatland methane emissions on microform and ecosystem scales using high-resolution landcover classification and source weight modelling, Agr. Forest Meteorol., 151, 864–874, 2011.
Friborg, T., Christensen, T. R., Hansen, B. U., Nordstroem, C., and Soegaard, H.: Trace gas exchange in a high-arctic valley 2. Landscape CH4 fluxes measured and model using eddy correlation data, Global Biogeochem. Cy., 14, 715–723, 2000.
Göckede, M., Markkanen, T., Hasager, C. B., and Foken, T.: Update of a footprint-based approach for the characterisation of complex measurement sites, Bound.-Lay. Meteorol., 118, 635–655, 2006.
Göckede, M., Foken, T., Aubinet, M., Aurela, M., Banza, J., Bernhofer, C., Bonnefond, J. M., Brunet, Y., Carrara, A., Clement, R., Dellwik, E., Elbers, J., Eugster, W., Fuhrer, J., Granier, A., Grünwald, T., Heinesch, B., Janssens, I. A., Knohl, A., Koeble, R., Laurila, T., Longdoz, B., Manca, G., Marek, M., Markkanen, T., Mateus, J., Matteucci, G., Mauder, M., Migliavacca, M., Minerbi, S., Moncrieff, J., Montagnani, L., Moors, E., Ourcival, J.-M., Papale, D., Pereira, J., Pilegaard, K., Pita, G., Rambal, S., Rebmann, C., Rodrigues, A., Rotenberg, E., Sanz, M. J., Sedlak, P., Seufert, G., Siebicke, L., Soussana, J. F., Valentini, R., Vesala, T., Verbeeck, H., and Yakir, D.: Quality control of CarboEurope flux data – Part 1: Coupling footprint analyses with flux data quality assessment to evaluate sites in forest ecosystems, Biogeosciences, 5, 433–450, https://doi.org/10.5194/bg-5-433-2008, 2008.
Greene, W. H.: Econometric Analysis, 7th edn., Pearson Education Ltd., Harlow, UK, 2012.
Heikkinen, J. E. P., Maljanen, M., Aurela, M., Hargreaves, K. J., and Martikainen, P. J.: Carbon dioxide and methane dynamics in a sub-Arctic peatland in northern Finland, Polar Res., 21, 49–62, 2002.
Hill, T., Chocholet, M., and Clement, R.: The case for increasing the statistical power of eddy covariance ecosystem studies: why, where and how?, Glob. Change Biol., 23, 2154–2165, 2017.
Horst, T. W. and Weil, J. C.: Footprint estimation for scalar flux measurements in the atmospheric surface layer, Bound.-Lay. Meteorol., 59, 279–296, 1992.
James, G., Witten, D., Hastie, T., and Tibshirani, R.: An Introduction to Statistical Learning with Applications in R, Springer Science+Business Media, Inc., New York, 2013.
Jørgensen, C. J., Lund Johansen, K. M., Westergaard-Nielsen, A., and Elberling, B.: Net regional methane sink in High Arctic soils of northeast Greenland, Nat. Geosci., 8, 20–23, 2015.
Juutinen, S., Virtanen, T., Kondratyev, V., Laurila, T., Linkosalmi, M., Mikola, J., Nyman, J., Räsänen, A., Tuovinen, J.-P., and Aurela, M.: Spatial variation and seasonal dynamics of leaf-area index in the arctic tundra – implications for linking ground observations and satellite images, Environ. Res. Lett., 12, 095002, https://doi.org/10.1088/1748-9326/aa7f85, 2017.
Kim, J., Guo, Q., Baldocchi, D. D., Leclerc, M. Y., Xu, L., and Schmid, H. P.: Upscaling fluxes from tower to landscape: Overlaying flux footprints on high-resolution (IKONOS) images of vegetation cover, Agr. Forest Meteorol., 136, 132–146, 2006.
Kljun, N., Kormann, R., Rotach, M. W., and Meixner, F. X.: Comparison of the Lagrangian footprint model LPDM-B with an analytical footprint model, Bound.-Lay. Meteorol., 106, 349–355, 2003.
Kormann, R. and Meixner, F. X.: An analytical footprint model for non-neutral stratification, Bound.-Lay. Meteorol., 99, 207–224, 2001.
Lai, D. Y. F.: Methane dynamics in northern peatlands: A review, Pedosphere, 19, 409–421, 2009.
Lau, M. C. Y., Stackhouse, B. T., Layton, A. C., Chauhan, A., Vishnivetskaya, T. A., Chourey, K., Ronholm, J., Mykytczuk, N. C. S., Bennett, P. C., Lamarche-Gagnon, G., Burton, N., Pollard, W. H., Omelon, C. R., Medvigy, D. M., Hettich, R. L., Pfiffner, S. M., Whyte, L. G., and Onstott, T. C.: An active atmospheric methane sink in high Arctic mineral cryosols, ISME J., 9, 1880–1891, 2015.
Laurila, T., Soegaard, H., Lloyd, C. R., Aurela, M., Tuovinen, J.-P., and Nordstroem, C.: Seasonal variations of net CO2 exchange in European Arctic ecosystems, Theor. Appl. Climatol., 70, 183–201, 2001.
Laurila, T., Tuovinen, J.-P., Lohila, A., Hatakka, J., Aurela, M., Thum, T., Pihlatie, M., Rinne, J., and Vesala, T.: Measuring methane emissions from a landfill using a cost-effective micrometeorological method, Geophys. Res. Lett., 32, L19808, https://doi.org/10.1029/2005GL023462, 2005.
Leclerc, M. Y. and Foken, T.: Footprints in Micrometeorology and Ecology, Springer-Verlag, Berlin, 2014.
Leclerc, M. Y. and Thurtell, G. W.: Footprint prediction of scalar fluxes using a Markovian analysis, Bound.-Lay. Meteorol., 52, 247–258, 1990.
Livingston, G. P. and Hutchinson, G. L.: Enclosure-based measurement of trace gas exchange: applications and sources of error, in: Biogenic Trace Gases: Measuring Emissions from Soil and Water, edited by: Matson, P. A. and Harriss, R. C., Blackwell Science Ltd., Oxford, UK, 14–51, 1995.
Marcolla, B. and Cescatti, A.: Experimental analysis of flux footprint in varying conditions in an alpine meadow, Agr. Forest Meteorol., 135, 291–301, 2005.
Marushchak, M. E., Kiepe, I., Biasi, C., Elsakov, V., Friborg, T., Johansson, T., Soegaard, H., Virtanen, T., and Martikainen, P. J.: Carbon dioxide balance of subarctic tundra from plot to regional scales, Biogeosciences, 10, 437–452, https://doi.org/10.5194/bg-10-437-2013, 2013.
Marushchak, M. E., Friborg, T., Biasi, C., Herbst, M., Johansson, T., Kiepe, I., Liimatainen, M., Lind, S. E., Martikainen, P. J., Virtanen, T., Soegaard, H., and Shurpali, N. J.: Methane dynamics in the subarctic tundra: combining stable isotope analyses, plot- and ecosystem-scale flux measurements, Biogeosciences, 13, 597–608, https://doi.org/10.5194/bg-13-597-2016, 2016.
Matthes, J. H., Sturtevant, C., Verfaillie, J., Knox, S., and Baldocchi, D.: Parsing the variability in CH4 flux at spatially heterogeneous wetland: Integrating multiple eddy covariance towers with high-resolution flux footprint analysis, J. Geophys. Res.-Biogeo., 119, 1322–1339, 2014.
McGuire, A. D., Christensen, T. R., Hayes, D., Heroult, A., Euskirchen, E., Kimball, J. S., Koven, C., Lafleur, P., Miller, P. A., Oechel, W., Peylin, P., Williams, M., and Yi, Y.: An assessment of the carbon balance of Arctic tundra: comparisons among observations, process models, and atmospheric inversions, Biogeosciences, 9, 3185–3204, https://doi.org/10.5194/bg-9-3185-2012, 2012.
Mikola, J., Virtanen, T., Linkosalmi, M., Vähä, E., Nyman, J., Postanogova, O., Räsänen, A., Kotze, D. J., Laurila, T., Juutinen, S., Kondratyev, V., and Aurela, M.: Spatial variation and linkages of soil and vegetation in the Siberian Arctic tundra – coupling field observations with remote sensing data, Biogeosciences, 15, 2781–2801, https://doi.org/10.5194/bg-15-2781-2018, 2018.
Nappo, C. J., Caneill, J. Y., Furman, R. W., Gifford, F. A., Kaimal, J. C., Kramer, M. L., Lockhart, T. J., Pendergast, M. M., Pielke, R. A., Randerson, D., Shreffler, J. H., and Wyngaard, J. C.: The workshop on the representativeness of meteorological observations, June 1981, Boulder, Colo., B. Am. Meteorol. Soc., 63, 761–764, 1982.
Neftel, A., Spirig, C., and Ammann, C.: Application and test of a simple tool for operational footprint evaluations, Environ. Pollut., 152, 644–652, 2008.
Nicolini, G., Castaldi, S., Fratini, G., and Valentini, R.: A literature overview of micrometeorological CH4 and N2O flux measurements in terrestrial ecosystems, Atmos. Environ., 81, 311–319, 2013.
Nyman, J.: The composition and phenological development of the vegetation and its impact on carbon fluxes in the Siberian tundra, MSc thesis, Department of Environmental Sciences, University of Helsinki, Finland, 2015.
Olefeldt, D., Turetsky, M. R., Crill, P. M., and McGuire, A. D.: Environmental and physical controls on northern terrestrial methane emissions across permafrost zones, Glob. Change Biol., 19, 589–603, 2013.
Parmentier, F. J. W., van Huissteden, J., van der Molen, M. K., Schaepman-Strup, G., Karsanaev, S. A., Maximov, T. C., and Dolman, A. J.: Spatial and temporal dynamics in eddy covariance observations of methane fluxes at a tundra site in northeastern Siberia, J. Geophys. Res., 116, G03016, https://doi.org/10.1029/2010JG001637, 2011.
Pasquill, F. and Smith, F. B.: Atmospheric Diffusion, 3rd edn., Ellis Horwood Ltd., Chichester, UK, 1983.
Petrescu, A. M. R., Lohila, A., Tuovinen, J.-P., Baldocchi, D. D., Desai, A. R., Roulet, N. T., Vesala, T., Dolman, A. J., Oechel, W. C., Marcolla, B., Friborg, T., Rinne, J., Matthes, J. H., Merbold, L., Meijide, A., Kiely, G., Sottocornola, M., Sachs, T., Zona, D., Varlagin, A., Lai, D. Y. F., Veenendaal, E., Parmentier, F.-J. W., Skiba, U., Lund, M., Hensen, A., van Huissteden, J., Flanagan, L. B., Shurpali, N. J., Grünwald, T., Humphreys, E. R., Jackowicz-Korczyński, M., Aurela, M. A., Laurila, T., Grüning, C., Corradi, C. A. R., Schrier-Uijl, A. P., Christensen, T. R., Tamstorf, M. P., Mastepanov, M., Martikainen, P. J., Verma, S. B., Bernhofer, C., and Cescatti, A.: The uncertain climate footprint of wetlands under human pressure, P. Natl. Acad. Sci. USA, 112, 4594–4599, 2015.
Rebmann, C., Göckede, M., Foken, T., Aubinet, M., Aurela, M., Berbigier, P., Bernhofer, C., Buchmann, N., Carrara, A., Cescatti, A., Ceulemans, R., Clement, R., Elbers, J. A., Granier, A., Grünwald, T., Guyon, D., Havránková, K., Heinesch, B., Knohl, A., Laurila, T., Longdoz, B., Marcolla, B., Markkanen, T., Miglietta, F., Moncrieff, J., Montagnani, L., Moors, E., Nardino, M., Ourcival, J.-M., Rambal, S., Rannik, Ü, Rotenberg, E., Sedlak, P., Unterhuber, G., Vesala, T., and Yakir, D.: Quality analysis applied on eddy covariance measurements at complex sites using footprint modelling, Theor. Appl. Climatol., 80, 121–141, 2005.
Sachs, T., Wille, C., Boike, J., and Kutzbach, L.: Environmental controls on ecosystem-scale CH4 emission from polygonal tundra in the Lena River Delta, Siberia, J. Geophys. Res., 113, G00A03, https://doi.org/10.1029/2007JG000505, 2008.
Sachs, T., Giebels, M., Boike, J., and Kutzbach, L.: Environmental controls on CH4 emission from polygonal tundra on the microsite scale in the Lena river delta, Siberia, Glob. Change Biol., 16, 3096–3110, 2010.
Saunois, M., Jackson, R. B., Bousquet, P., Poulter, B., and Canadell, J. G.: The growing role of methane in anthropogenic climate change, Environ. Res. Lett., 11, 120207, https://doi.org/10.1088/1748-9326/11/12/120207, 2016.
Schmid, H. P.: Footprint modeling for vegetation atmosphere exchange studies: a review and perspective, Agr. Forest Meteorol., 113, 159–183, 2002.
Schmid, H. P. and Lloyd, C. R.: Spatial representativeness and the location bias of flux footprints over inhomogeneous areas, Agr. Forest Meteorol., 93, 195–209, 1999.
Schuur, E. A. G., McGuire, A. D., Schädel, C., Grosse, G., Harden, J. W., Hayes, D. J., Hugelius, G., Koven, C. D., Kuhry, P., Lawrence, D. M., Natali, S. M., Olefeldt, D., Romanovsky, V. E., Schaefer, K., Turetsky, M. R., Treat, C. C., and Vonk, J. E.: Climate change and the permafrost carbon feedback, Nature, 520, 171–179, 2015.
Schneider, J., Grosse, G., and Wagner, D.: Land cover classification of tundra environments in the Arctic Lena Delta based on Landsat 7 ETM+ data and its application for upscaling of methane emissions, Remote Sens. Environ., 113, 380–391, 2009.
Stow, D. A., Hope, A., McGuire, D., Verbyla, D., Gamon, J., Huemmrich, F., Houston, S., Racine, C., Sturm, M., Tape, K., Hinzman, L., Yoshikawa, K., Tweedie, C., Noyle, B., Silapaswan, C., Douglas, D., Griffith, B., Jia, G., Epstein, H., Walker, D., Daeschner, S., Petersen, A., Zhou, L., and Myneni, R.: Remote sensing of vegetation and land-cover change in Arctic Tundra Ecosystems, Remote Sens. Environ., 89, 281–308, 2004.
Stoy, P. C., Williams, M., Evans, J. G., Prieto-Blanco, A., Disney, M., Hill, T. C., Ward, H. C., Wade, T. J., and Street, L. E.: Upscaling tundra CO2 exchange from chamber to eddy covariance tower, Arct. Antarct. Alp. Res., 45, 275–284, 2013.
Street. L. E., Shaver, G. R., Williams, M., and Van Wijk, M. T.: What is relationship between changes in canopy leaf area and changes in photosynthetic CO2 flux in arctic ecosystems?, J. Ecol., 95, 139–150, 2007.
Tagesson, T., Mölder, M., Mastepanov, M., Sigsgaard, C., Tamstorf, M. P., Lund, M., Falk, J. M., Lindroth, A., Christensen, T. R., and Ström, L.: Land-atmosphere exchange of methane from soil thawing to soil freezing in a high-Arctic wet tundra ecosystem, Glob. Change Biol., 18, 1928–1940, 2012.
Treat, C. C., Natali, S. M., Ernakovich, J., Iversen, C. M., Lupascu, M., McGuire, A. D., Norby, R. J., Chowdhury, T. R., Richter, A., Šantrůčková, H., Schädel, C., Schuur, E. A. G., Sloan, V. L., Turetsky, M. R., and Waldrop, M. P.: A pan-Arctic synthesis of CH4 and CO2 production from anoxic soil incubations, Glob. Change Biol., 21, 2787–2803, 2015.
Treat, C. C., Marushchak, M. E., Voigt, C., Zhang, Y., Tan, Z., Zhuang, Q., Virtanen, T. A., Räsänen, A., Biasi, C., Hugelius, G., Kaverin, D., Miller, P. A., Stendel, M., Romanovsky, V., Rivkin, F., Martikainen, P. J., and Shurpali, N. J.: Tundra landscape heterogeneity, not inter-annual variability, controls the decadal regional carbon balance in the Western Russian Arctic, Glob. Change Biol., 24, 5188–5204, 2018.
Tuovinen, J.-P., Aurela, M., and Laurila, T.: Resistances to ozone deposition to a flark fen in the northern aapa mire zone, J. Geophys. Res., 103, 16953–16966, 1998.
Tuovinen, J.-P., Aurela, M., Hatakka, J., Räsänen, A., Virtanen, T., Mikola, J., Ivakhov, V., Kondratyev, V., and Laurila, T.: Dataset for “Interpreting eddy covariance data from heterogeneous Siberian tundra: land cover-specific methane fluxes and spatial representativeness” [Data set], Zenodo, https://doi.org/10.5281/zenodo.2348842, 2018.
Turetsky, M. R., Kotowska, A., Bubier, J., Dise, N. B., Crill, P., Hornibrook, E. R. C., Minkkinen, K., Moore, T. R., Myers-Smith, I. H., Nykänen, H., Olefeldt, D., Rinne, J., Saarnio, S., Shurpali, N., Tuittila, E.-S., Waddington, J. M., White, J. R., Wickland, K. P., and Wilmking, M.: A synthesis of methane emissions from 71 northern, temperate, and subtropical wetlands, Glob. Change Biol., 20, 2183–2197, 2014.
Turner, M. G. and Chapin III, F. S.: Causes and consequences of spatial heterogeneity in ecosystem function, in: Ecosystem Function in Heterogeneous Landscapes, edited by: Lovett, G. M., Jones, C. G., Turner, M. G., and Weathers, K. C., Springer Science+Business Media, Inc., New York, 9–30, 2006.
Uttal, T., Starkweather, S., Drummond, J. R., Vihma, T., Makshtas, A. P., Darby, L. S., Burkhart, J. F., Cox, C. J., Schmeisser, L. N., Haiden, T., Maturilli, M., Shupe, M. D., de Boer, G., Saha, A., Grachev, A. A., Crepinsek, S. M., Bruhwiler, L., Goodison, B., McArthur, B., Walden, V. P., Dlugokencky, E. J., Persson, P. O. G., Lesins, G., Laurila, T., Ogren, J. A., Stone, R., Long, C. N., Sharma, S., Massling, A., Turner, D. D., Stanitski, D. M., Asmi, E., Aurela, M., Skov, H., Eleftheriadis, K., Virkkula, A., Platt, A., Førland, E. J., Iijima, Y., Nielsen, I. E., Bergin, M. H., Candlish, L., Zimov, N. S., Zimov, S. A., O'Neill, N. T., Fogal, P. F., Kivi, R., Konopleva-Akish, E. A., Verlinde, J., Kustov, V. Y., Vasel, B., Ivakhov, V. M., Viisanen, Y., and Intrieri, J. M.: International Arctic Systems for Observing the Atmosphere (IASOA): An International Polar Year Legacy Consortium, B. Am. Meteorol. Soc., 97, 1034–1056, 2016.
Vähä, E.: Kasvillisuus- ja maaperämuuttujien välinen yhteys ja niiden merkitys hiilidioksidin ja metaanin vaihdossa arktisen tundraekosysteemin ja ilmakehän välillä [The relationship between vegetation and soil variables and their importance in the carbon dioxide and methane exchange between an Arctic tundra ecosystem and the atmosphere], MSc thesis, Department of Environmental Sciences, University of Helsinki, Finland, 2016.
Virkkala, A.-M., Virtanen, T., Lehtonen, A., Rinne, J., and Luoto, M.: The current state of CO2 flux chamber studies in the Arctic tundra: a review, Prog. Phys. Geog., 42, 162–184, 2017.
Virtanen, T. and Ek, M.: The fragmented nature of tundra landscape, Int. J. Appl. Earth Obs., 27, 4–12, 2014.
Wang, H., Jia, G., Zhang, A., and Miao, C.: Assessment of spatial representativeness of eddy covariance flux data from flux tower to regional grid, Remote Sens., 8, 742, https://doi.org/10.3390/rs8090742, 2016.
Whalen, S. C. and Reeburgh, W. S.: Consumption of atmospheric methane by tundra soils, Nature, 346, 160–162, 1990.
Wik, M., Varner, R. K., Walter Anthony, K., MacIntyre, S., and Bastviken, D.: Climate-sensitive northern lakes and ponds are critical components of methane release, Nat. Geosci., 9, 99–106, 2016.
Wille, C., Kutzbach, L., Sachs, T., Wagner, D., and Pfeiffer, E-M.: Methane emission from Siperian arctic polygonal tundra: eddy covariance measurements and modeling, Glob. Change Biol., 14, 1395–1408, 2008.
Yu, L., Wang, H., Wang, G., Song, W., Huang, Y., Li, S.-G., Liang, Y., Tang, Y., and He, J.-S.: A comparison of methane emission measurements using eddy covariance and manual and automated chamber-based techniques in Tibetan Plateau alpine wetland, Environ. Pollut., 181, 81–90, 2013.
Zona, D., Oechel, W. C., Kochendorfer, J., Paw U, K. T., Salyuk, A. N., Olivas, P. C., Oberbauer, S. F., and Lipson, D. A.: Methane fluxes during the initiation of a large-scale water table manipulation experiment in the Alaskan Arctic tundra, Global Biogeochem. Cy., 23, GB2013, https://doi.org/10.1029/2009GB003487, 2009.