the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
The role of soil pH on soil carbonic anhydrase activity
Sam P. Jones
Lisa Wingate
Steven Wohl
Carbonic anhydrases (CAs) are metalloenzymes present in plants and microorganisms that catalyse the interconversion of CO2 and water to bicarbonate and protons. Because oxygen isotopes are also exchanged during this reaction, the presence of CA also modifies the contribution of soil and plant CO18O fluxes to the global budget of atmospheric CO18O. The oxygen isotope signatures (δ18O) of these fluxes differ as leaf water pools are usually more enriched than soil water pools, and this difference is used to partition the net CO2 flux over land into soil respiration and plant photosynthesis. Nonetheless, the use of atmospheric CO18O as a tracer of land surface CO2 fluxes requires a good knowledge of soil CA activity. Previous studies have shown that significant differences in soil CA activity are found in different biomes and seasons, but our understanding of the environmental and ecological drivers responsible for the spatial and temporal patterns observed in soil CA activity is still limited. One factor that has been overlooked so far is pH. Soil pH is known to strongly influence microbial community composition, richness and diversity in addition to governing the speciation of CO2 between the different carbonate forms. In this study we investigated the CO2–H2O isotopic exchange rate (kiso) in six soils with pH varying from 4.5 to 8.5. We also artificially increased the soil CA concentration to test how pH and other soil properties (texture and phosphate content) affected the relationship between kiso and CA concentration. We found that soil pH was the primary driver of kiso after CA addition and that the chemical composition (i.e. phosphate content) played only a secondary role. We also found an offset between the δ18O of the water pool with which CO2 equilibrates and total soil water (i.e. water extracted by vacuum distillation) that varied with soil texture. The reasons for this offset are still unknown.
Please read the corrigendum first before continuing.
-
Notice on corrigendum
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
-
Article
(1663 KB)
- Corrigendum
-
Supplement
(132 KB)
-
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(1663 KB) - Corrigendum
-
Supplement
(132 KB) - BibTeX
- EndNote
The build-up of carbon dioxide (CO2) in the atmosphere is increasing rapidly because of anthropogenic activities (IPCC, 2013). The terrestrial biosphere currently mitigates about 25 % of anthropogenic CO2 emissions as a result of a small disequilibrium between two large gross CO2 fluxes, photosynthetic CO2 uptake and respiratory CO2 release (Le Quéré et al., 2015). It is clear from recent studies that this disequilibrium is highly variable from year to year with climate and is difficult to measure directly (Ballantyne et al., 2012; Gurney and Eckels, 2011; Poulter et al., 2014; Le Quéré et al., 2015). Currently this disequilibrium is estimated as a residual term in atmospheric budgets of CO2 after reconciling the various fluxes between the oceans, the atmosphere and anthropogenic emissions (including land use change). These mass budgets rely heavily on coupled climate–carbon models that require accurate representations of how key ecosystem processes such as respiration and stomatal conductance respond to changes in climate and other environmental factors (Friedlingstein et al., 2006). However, it is difficult to evaluate the performance of these models at large scales, as it is difficult to estimate gross CO2 fluxes directly (Beer et al., 2010; Wingate et al., 2009, 2010). Therefore, additional datasets and tools that can track the behaviour of these processes and bring independent information on how to constrain their representation in models are now urgently required.
One potential approach takes advantage of the observed variability in the oxygen isotope composition of CO2 molecules in the atmosphere (δ18Oa) (Ciais et al., 1997; Cuntz, 2003; Farquhar et al., 1993; Francey and Tans, 1987; Welp et al., 2011; Wingate et al., 2009). This variability in δ18Oa is driven principally by the seasonal and inter-annual variability in the oxygen isotope composition of leaf and soil water pools that are strongly regulated by climate (Welp et al., 2011). Furthermore, large differences between the oxygen isotope composition of soil and leaf water pools exist and can be used to track rapidly the relative contributions of soil and leaf CO2 exchange (Ciais et al., 1997; Farquhar et al., 1993; Francey and Tans, 1987; Welp et al., 2011; Wingate et al., 2010). This large-scale and rapid hydration of CO2 by the biosphere is accelerated by the family of carbonic anhydrase enzymes (CAs), which are ubiquitous in bacteria, algae, fungi and plants (Badger, 2003; Elleuche and Poggeler, 2010; Moroney et al., 2001; Smith and Ferry, 2000). In leaves the activity and concentration of CAs are high enough to expect that CO2 diffusing out of the leaf is in nearly full isotopic equilibrium with leaf water (Farquhar and Cernusak, 2012; Gillon and Yakir, 2001). In soils full isotopic equilibration between CO2 and water can also occur below a certain depth (Miller et al., 1999; Tans, 1998) but will depend strongly on the distribution and activity of CA in the soil profile (Gangi et al., 2015; Wingate et al., 2009). This is because when the rate of CO2 diffusion through a soil layer exceeds the CA-catalysed CO2 hydration rate in that layer, full isotopic equilibration cannot occur (Tans, 1998; Wingate et al., 2008, 2009, 2010). Thus variations in soil CA activity and CO2 diffusion rates dictate the shallowest depth where full isotopic equilibration between CO2 and water can occur.
By compiling datasets of depth-resolved soil water δ18O composition and soil–air CO18O exchange rates for a range of biomes, Wingate et al. (2009) found a tendency for larger soil CA activities in warmer and drier regions, and proposed three relatively simple but spatially explicit scenarios of soil CA activity at the global scale (Wingate et al., 2009). Subsequently, using the lower range of soil CA activity estimates made by Wingate et al. (2009), an atmospheric CO18O inversion was performed and led to a surprisingly high rate of global photosynthesis, of ca. 175 GtC yr−1 over the period 1980–2010 (Welp et al., 2011), a surprisingly high value compared to the accepted global estimate of 115–130 GtC yr−1 (Beer et al., 2010; IPCC, 2013). This global-scale estimate of photosynthesis over land was also highly sensitive to the range of soil CA activities used, demonstrating that a better understanding of the environmental and ecological drivers of soil CA activity was key to reduce the uncertainty in large-scale gross CO2 fluxes using atmospheric CO18O budgets.
Changes in the abundance and diversity of soil microbial communities were proposed as possible drivers of the observed spatial and temporal changes in soil CA activity (Seibt et al., 2006; Wingate et al., 2008, 2009, 2010). In particular, soil pH is known to strongly influence microbial community composition, richness and diversity (Fierer and Jackson, 2006; Griffiths et al., 2011; Hartman et al., 2008; Lauber et al., 2009) and could thus influence soil CA activity indirectly via changes in the microbial populations that would translate into difference in CA requirements and in the expression of classes of CA with different enzymatic efficiencies. Indeed, α- and β-CA classes are not represented equally in all kingdoms. Very schematically, α-CAs tend to be more abundant in algae and micro-algae while β-CAs are more commonly found in fungi (Elleuche and Poggeler, 2010; Moroney et al., 2001). In addition, α-CAs can be extracellular enzymes unlike β-CAs that are, to our knowledge, only intracellular enzymes. Soil pH should also influence CA-driven CO2 hydration kinetics directly as CA reactivation is known to be limited by its de-protonation with a pKa around 7.2 (Rowlett et al., 2002). This may not be true for intracellular CA activity, as it has been shown that soil micro-organisms have the ability to regulate and maintain their intracellular pH within one pH unit near neutral (Krulwich et al., 2011). However, in certain micro-organisms, extracellular CAs have also been found (e.g. Hopkinson et al., 2013) whose activity should be directly affected by external (soil) pH. Thus a direct link between (at least a fraction of) soil CA activity and soil pH should exist.
Actually, part of the reported variations in soil CA activity derived from the isotopic exchange rates between soil water and CO2 can be explained by differences in soil pH. This is because soil CA activities are often reported as an enhancement factor relative to an un-catalysed CO2–H2O isotopic exchange rate, assumed equal to ca. 0.012 s−1 at 25 ∘C (Miller et al., 1999). However, because soil pH governs the speciation of CO2 between the different carbonate forms, with dissolved CO2 being predominant only in acidic environments (pH < 6), the true un-catalysed rate (kiso,uncat) is not the same for all soils and is strongly reduced in alkaline conditions (Mills and Urey, 1940; Uchikawa and Zeebe, 2012). Thus for the same soil CA activity – or more precisely for the same soil CO2–water isotopic exchange rate (kiso) – the enhancement factor should rather be defined relative to the true un-catalysed rate (kiso ∕ kiso,uncat) and would then be much greater in alkaline soils than in acidic ones.
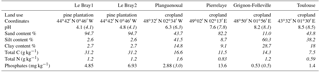
Table 1Main characteristics of the soils investigated in this study. Numbers in italics indicate literature data (Achat et al., 2014).
The chemical composition of the soil solution is another potentially important factor that should be considered when reporting soil CA activity. Several studies have shown that some anions commonly found in soils could act as CA inhibitors or activators, depending on their ability to exchange protons. For example, at neutral pH, phosphate ions were reported to be activators of bovine α-CA as CO2 hydration rates increased up to 6.5-fold relative to a solution without phosphates, whilst sulfate ions on the other hand were shown to act as a weak inhibitor on the same α-CA (Rowlett et al., 1991). The presence of these ions also modifies, sometimes dramatically, the pH response of CA activity in vitro (Rowlett et al., 1991), questioning our previous idea that pH might be the only chemical factor controlling soil CA activity.
The aim of this study was to investigate the relationship between soil CA activity and soil pH. For this we used a setup that allowed us to retrieve simultaneously the soil CA activity and the δ18O of the soil water pool with which CO2 equilibrates, without destructive sampling. Using six different soils differing in pH by almost 4 pH units, we investigated the influence of soil pH on the CO2 hydration rate (kh) and CO2–H2O equilibration (kiso). We also artificially increased the CA concentration in each soil by adding solutions of bovine CA. This CA isoform was chosen because it is well characterised in terms of enzymatic activity (Uchikawa and Zeebe, 2012) and pH response (Rowlett et al., 1991) and it has been demonstrated that its activity was very stable in time even after several hours in solution (Uchikawa and Zeebe, 2012). Thus it was possible to investigate whether CA concentrations and soil pH were the only factors affecting the activity of this exogenous CA. Because of the direct role of pH on CO2 speciation and CO2 hydration rate, we hypothesised that exogenous CA activity should be inhibited in acidic soils, but that the native soil phosphate concentration might also influence the activity of CA for soils differing in pH.
2.1 Soil sampling
A range of soils that differed naturally in terms of pH, texture, land use and chemical composition were investigated (Table 1). Soil samples from Le Bray, a maritime pine forest located at about 20 km southwest of Bordeaux (France), were collected in November 2014 (LeBray1) and April 2016 (LeBray2). The four other soils were sampled from croplands. The soils from Planguenoual (France, 95 km northwest of Rennes) and Grignon-Folleville (France, 20 km southwest of Paris) were collected in May 2013. More details about these soils can be found in Achat et al. (2014). The soil from Pierrelaye (France, 30 km northwest of Paris) was sampled in October 2014 and May 2016 but mixed in one batch and the soil from Toulouse was sampled once in May 2016.
All soil samples were taken from the soil surface (0–15 cm) after removal of the coarse litter elements. They were sieved with a 4 mm mesh, homogenised and air-dried for several weeks in the laboratory. A first set of experiments was conducted in March 2015 with the soils from LeBray1, Planguenoual and Grignon-Folleville. Prior to gas exchange measurements, 330 to 440 g of soil was repacked in a 500 mL Teflon pot to obtain a common soil depth (ca. 7 cm). For each soil type, we prepared three repacked Teflon pots. Each soil pot was then irrigated with 125 mL of water and allowed to drain for 12 to 24 h at room temperature and light conditions. Drainage was facilitated by a small hole (3 mm inner diameter) drilled at the bottom of the pot to avoid the accumulation of water and anoxic conditions in deeper soil layers. During gas exchange measurements this hole was closed with a Teflon screw. Preliminary results from this first set of experiments indicated substantial evaporation-induced isotopic enrichment of soil water in the top layer, as well as soil-to-soil variations in water-filled pore space (WFPS), which could complicate the interpretation of the results. Thus a second set of experiments was conducted in June 2016 where the WFPS was better controlled and soil evaporation was minimised by allowing the soils to drain prior to measurement inside a dark chamber controlled at 21 ∘C and with a saturating water vapour generated from an evaporating reservoir filled with the same water that was used for irrigation. The soils from LeBray2, Pierrelaye and Toulouse were chosen for this second set of experiments, to minimise differences between soil texture, whilst keeping a large range of pH (Table 1). Prior to gas exchange measurements, 280 to 300 g of soil was repacked in a 500 mL Teflon pot to a common soil depth of ca. 5–6 cm. Each soil pot was then irrigated in order to reach a WFPS of 25 % and left in the dark chamber for 24 h. All Teflon pots used in the experiment had a constant surface area of 41.85 cm2.
2.2 Carbonic anhydrase addition
For a set of gas exchange measurements, lyophilised α-CA powder from bovine erythrocytes (C3934-100MG, Sigma-Aldrich, France) was diluted into the irrigation water. For each set of experiments, CA concentrations of ca. 24 and 80 mg L−1 were used. We chose these concentration because they would correspond to the upper range of CA concentrations expected in natural soils, assuming a cytoplasmic CA concentration of 0.1 mM (Ogée et al., 2016). Apart from this addition of CA into the irrigation water, all other preparation steps of the soil microcosms were kept identical to the ones described above for the microcosms without CA addition.
CA activities from soil microcosms without CA powder addition are qualified hereafter as “native” and CA activities related to the CA addition are called “non-native” and estimated, for a given soil, as the difference between the activities on the CA-added microcosms and their native rates.
2.3 Experimental setup and working sequence
Prior to gas exchange measurements, each soil pot was closed using a screw-tight lid connected to inlet and outlet tubes (Fig. 1) and immersed into a 6.5 L water bath, thermally regulated at 20 ∘C. An acclimation time of at least 20 min was used to allow the soil column to re-equilibrate to the new air supply CO2 composition and the new temperature. The soil CO2 efflux and its oxygen isotopic composition were then measured using the experimental setup illustrated in Fig. 1. To simultaneously retrieve soil CA activity, reported here as the CO2–H2O isotopic exchange rate kiso, and the δ18O of the soil water pools with which CO2 equilibrates (δsw-eq), we designed a system that allowed us to measure CO2 isotope fluxes under two, quasi-simultaneous isotopic steady states that only differ in the isotopic composition of the CO2 entering the soil chamber (Fig. 1). The air supplied to the chamber came directly from a tank containing dry air during the first steady state (SS1) and from a mix of dry, CO2-free air and a tank of pure CO2 during the second steady state (SS2). In practice, the air was supplied to the microcosms during SS2 using a compressor (FM2 Atlas Copto, Nacka, Sweden), coupled to a chemical scrub column (Ecodry K-MT6, Parker Hannifin, Cleveland, OH, US) that removed water vapour and CO2 from the air before being mixed with pure CO2, with a δ18O isotopic composition significantly different from the CO2-in-air mixture used in SS1. During SS2 mixing valves adjusted the CO2 concentration of the inlet air to maintain it close to the value of the inlet air used in SS1 within acceptable error (423 ± 5 ppm), whilst their oxygen isotope compositions differed markedly (Fig. 2). The transition between SS1 and SS2 was operated by means of a three-way valve (Fig. 1) and a transition period of 20 min was necessary to attain the new steady state (Fig. 2). A full sequence of measurements lasted about 1h (Fig. 2) and consisted of two steady states. During each steady state, the by-pass (i.e. the air entering the soil chamber) and the outlet of the chamber were alternately selected via a manifold connected to a stable isotope CO2 analyser (Fig. 2). During the first set of experiments each working sequence was repeated three times on each soil and CA treatment (pseudo-replication) at a temperature of 25 ∘C. During the second set of experiments each soil and CA treatment were made in triplicates but measured only once over a single working sequence (true replication) at a temperature of 21 ∘C.
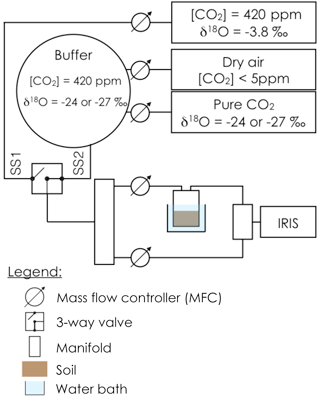
Figure 1Schematic of the experimental setup used to estimate simultaneously the CO2–H2O isotope exchange rate (kiso) in a soil microcosm and the oxygen isotopic composition of the soil water pool with which the CO2 equilibrates (δsw-eq). The soil microcosm consists of 280–300 g of dry soil previously re-humidified to 25 % of the water holding capacity using mineral water containing different amounts of exogenous CA powder. The soil column is thermally regulated using a 6.5 L water bath and the air entering the chamber is a mixture of CO2 in dry air whose oxygen isotopic composition is alternatively enriched (steady state 1, −3.8 ‰ VPDBg) and depleted (steady state 2, between −24 and −27 ‰ VPDBg, depending on the experiment).
To account for possible non-linearity and drift of the stable isotope analyser during the experiments, gas from two calibration tanks of known CO2 concentration and isotopic composition was regularly recorded in-between sample measurements (Fig. 2). For both sets of experiments the calibration tanks, whose 12C16O2 and 12C16O18O mixing ratios bracketed our measurements, were measured at approximately 16 min intervals, consistent with the expected stability of the analyser (see below).
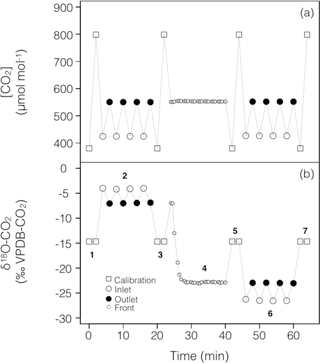
Figure 2Typical time series of the measured CO2 mixing ratio and isotope composition (δ18O) over the course of a working sequence. The sequence is composed of seven steps (indicated in b) to successively measure: (1) two calibration bottles spanning the expected range of CO2 mixing ratios, (2) inlet and outlet lines of the soil microcosm, measured 4 times consecutively, using a CO2 with an enriched δ18O (steady state 1), (3) calibration bottles, (4) the outlet of the chamber during the switch of the air supplying the soil chamber (front), (5) calibration bottles, (6) inlet and outlet lines of the soil chamber, measured 4 times consecutively, using a CO2 with a depleted δ18O (steady state 2) and (7) calibration bottles.
2.4 CO2 mixing ratio and stable isotope measurements
Mixing ratios of 12C16O2, 13C16O2 and 12C16O18O were measured using an Isotope Ratio Infrared Spectrometer (IRIS, Delta Ray, Thermo Fisher Scientific, USA). The cell pressure was controlled and maintained at 100 mbar throughout the experiment. The air sample passed through a multi-pass Herriot cell at a flow of 85 mL min−1 with a total path length of 5 m, leading to a theoretical residence time in the analyser of ca. 35 s. To minimise carry-over effects caused by this residence time, each line (inlet or chamber air or calibration tanks) was measured for 2 min and only the last 40 s of measurements were averaged to provide a single mean and standard deviation.
Calibration tank mixing ratios for the different isotopologues (12CO2, 13CO2 and CO18O) were averaged as described above (2 min of measurement and only the last 40 s were averaged) and interpolated in time using a spline function. These interpolated time series were then used to perform a two-point calibration regression on the mixing ratios for each sample measurement. Total CO2 mixing ratio was computed following Wingate et al. (2010):
where the factor 0.999179 accounts for the presence of 12C16O17O in the gas mixture. The δ18O of CO2 was expressed on the VPDB-CO2 scale using the formula
where 0.00208835 is the 18O ∕ 16O isotope ratio of the VPDB-CO2 reference standard (Allison et al., 1995) and the factor 0.5 accounts for the fact that there are two oxygen atoms per molecule of CO2 but only one 18O atom in 12C16O18O.
Standard deviations on CO2 mixing ratios of the different isotopologues were used to compute measurement error on total CO2 concentration. In contrast, measurement error on the isotope ratios was not calculated using Eq. (2) but computed from the standard deviation over the last 20 s of measurements of the instantaneous ratio [12C16O18O] ∕ [12C16O2]. This is because fluctuations in one CO2 isotopologue was always highly correlated with fluctuations in the other CO2 isotopologue leading to much smaller fluctuations in their ratios than the one calculated from simple error propagation using Eq. (2). Using this approach, typical errors on [CO2] and δ18O-CO2 values were around 0.1 ppm and 0.3 ‰, respectively.
Under steady-state conditions (i.e. during SS1 or SS2 in Fig. 2), and according to the mass balance of total CO2 in the chamber headspace, the soil CO2 efflux is proportional to the total CO2 concentration difference between the inlet and outlet airstreams:
where uin (mol s−1) is the flow rate of dry air on the inlet of the chamber, S is the soil surface (m2) and cin and cout are the mixing ratios of total CO2 (mol mol−1) in the air entering and leaving the chamber respectively. Because these mixing ratios were determined on a dry air basis (because of the Nafion dryer upstream before the CO2 isotope analyser) only the flow of dry air on the inlet of the chamber was required to perform the mass balance.
The fluxes of 12C16O2 (16F) and 12CO18O (18F) can be computed using Eq. (3), and the oxygen isotopic signature of the soil CO2 flux (δF = 0.5 − 1, also expressed on the VPDB-CO2 scale) can thus be calculated from the 12C16O2 concentrations and δ18O of the inlet (16Cin, 18δin) and outlet (16Cout, 18δout) air:
For each steady state, three or four inlet/outlet measurements were performed leading to three or four individual values of δF from which a mean and standard deviation could be computed.
2.5 Theoretical retrieval of soil CA activity and δeq
Assuming uniform soil properties (i.e. uniform soil porosity, moisture and temperature), δF can be computed as (Tans, 1998; Wingate et al., 2010)
where δeq (‰ VPDB-CO2) is the CO2 oxygen isotopic composition in equilibrium with soil water, εD (−8.7 ‰) is the oxygen isotope fractionation factor during diffusion of CO2 in air, Ca (mol m−3) and δa (‰ VPDB-CO2) are the concentration and δ18O of CO2 in the air at the soil–air interface, respectively, F is the soil CO2 efflux (µmol m−2 s−1) and Vinv (m s−1) is the piston velocity (i.e. the rate at which a column of air gets pushed into the soil; Tans, 1998). In the following we will assume full mixing inside the chamber so that δa = 18δout and Ca = , where p (Pa) and T (K) are air pressure and temperature inside the chamber headspace. The piston velocity is a function of soil moisture and temperature and soil CA activity only (Tans, 1998; Wingate et al., 2010) so that it should be the same between the two steady states. Because cout and F were also maintained constant between the two steady states it was possible to retrieve δeq and Vinv from the two steady-state measurements:
where δa,1 and δa,2 are δa during steady states 1 and 2 and δF,1 and δF,2 are the corresponding δF, computed from Eq. (4).
Strictly speaking, Eq. (5) is valid only for a semi-infinite soil column. In our experiments the soil depths were of a few centimetres only and mass transport was not possible at the bottom of the soil column (i.e. zero CO2 flux), because the microcosms were closed at the bottom. With this new boundary condition, Eq. (5) should be slightly modified (see Appendix A for a full derivation):
with and , where zmax is soil depth and with and Deff (m2 s−1) the effective diffusivity of gaseous CO2 through the soil matrix (Tans, 1998; Wingate et al., 2010). The latter was computed using the formulation of Moldrup et al. (2003) for repacked soils: , where φ (m3 m−3) is total soil porosity and D0 (m2 s−1) is the molecular diffusivity of CO2 in soil air at temperature Ts (K): (Ts∕273.15)1.81 (Massman, 1998). The right-hand side of Eq. (6b) was then used to estimate and Vinv was solved iteratively to satisfy the equation , from which z1 and then and δeq could be deduced (using Eq. 6b replacing εD by .
The soil CO2–H2O isotopic exchange rate (kiso, in s−1) was then derived from the piston velocity according to
where B (m3 m−3) is the solubility coefficient for CO2 in water (Weiss, 1974) and θ (m3 m−3) is the volumetric soil water content.
The soil CO2–H2O isotopic exchange rate kiso was further converted into a CO2 hydration rate (kh). Following Uchikawa and Zeebe (2012) we have
where C (mol m−3) is the CO2 concentration in soil water and S = [H2CO3] + [HCO] + [CO]. Assuming that the ratio C ∕ S is close to its equilibrium value (this assumption is actually required to derive Eq. 10), the ratio kh ∕ kiso is only a function of temperature and pH (Uchikawa and Zeebe, 2012). In acidic soils, this ratio approaches 3 at any temperature, because there are three oxygen atoms in the CO2–H2O system and in this pH range, CO2 is the dominant dissolved inorganic carbon species.
Following the same reasoning as in Ogée et al. (2016) for carbonyl sulfide (OCS) hydrolysis, the soil CO2 hydration rate can also be expressed as a function of bulk CA concentration [CA] (mol m−3):
where kh,uncat (s−1) is the un-catalysed CO2 hydration rate at a given temperature T (K) and pH and kcat and KM are the (community-averaged) CA-catalysed maximum hydration rate and Michaelis–Menten constant at the same temperature and pH. The expected pH dependency of kh and kiso for different levels of CA concentrations are shown in Fig. 3.
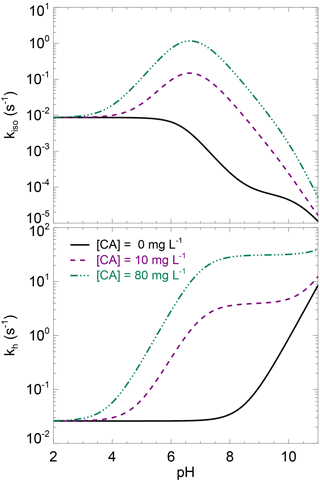
Figure 3Theoretical rates of CO2 hydration (kh) and CO2–H2O oxygen isotope exchange (kiso) as a function of pH, for three levels of carbonic anhydrase concentration. These theoretical curves have been obtained using the un-catalysed rate formula compiled in Uchikawa and Zeebe (2012) and enzymatic parameters of s−1 µM−1 and pKa=7, which are typical values for CA-catalysed CO2 hydration (Rowlett et al., 2002; Smith and Ferry, 2000). Using enzymatic parameter values more specific to the α-CA powder used here for the CA treatment (i.e. s−1 µM−1 and ) would not change qualitatively this figure.
Values of δeq were converted into a soil water isotope composition equivalent (δsw-eq, in ‰ VSMOW) according to Brenninkmeijer et al. (1983): δsw-eq = δeq + 0.20 (Ts − 297.15). According to Wingate et al. (2009) this δsw-eq should correspond to the soil water δ18O at a depth zeq (m) given by
2.6 Water extraction and isotopic measurements
These estimated profiles of soil water δ18O were further compared to δ18O measurements of soil water extracts (δsw). For this, after completion of the full gas exchange sequence shown in Fig. 2, soil samples were collected at 1, 2 and 4 cm below the soil surface and stored in Weaton glass jars with Parafilm in a refrigerator. Water from these soil samples was then extracted by vacuum distillation and the extracted water analysed for stable isotope composition using a Triple Isotope Water Analyser (TIWA 45EP; Los Gatos Research Inc., CA, USA) coupled to a liquid auto sampler (PAL System, Switzerland). The δ18O values of soil water samples were calibrated on the VSMOW-SLAP scale using three internal laboratory water standards that covered the expected range of δ18O in soil water (−10.16 ± 0.06, −5.59 ± 0.14 and +5.21 ± 0.13 ‰ in 2015 and −10.31 ± 0.06, −4.84 ± 0.06 and +0.62 ± 0.06 ‰ in 2016, on the VSMOW-SLAP scale). Two internal standards (the most depleted and more enriched ones) were used for calibration whilst the third internal standard was used for quality check. These in-house standards were kept in 25 L kegs that were over-pressured with dry air and measured against IAEA standards before and after the experiments, with no drift observed.
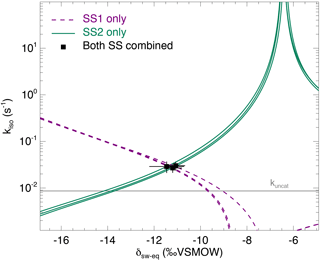
Figure 4The CO2–H2O isotopic exchange rate (kiso) and isotopic composition of soil water equilibrated with CO2 (δsw) retrieved using the two-steady-state approach described in the main text (Eqs. 6a and 6b), for one single microcosm (LeBray1 with an α-CA addition of 24 mg L−1). Relationships between kiso and δsw for steady state 1 (dotted lines) and steady state 2 (solid lines) are also shown. In this example the microcosm was measured over three consecutive sequences, resulting in three curves for each steady state and three intersection points that coincide well with the two-steady-state solution for each sequence (black squares). The pH-dependent, un-catalysed CO2–H2O isotopic exchange rate (Uchikawa and Zeebe, 2012) is indicated by the grey horizontal line.
Both soil water samples and internal working standards were transferred into 2 mL glass vials and the vials were then closed with pre-pierced PTFE caps and silicone septa. Vials with internal standard waters were interspaced every five sample vials following the International Atomic Energy Agency (IAEA) recommendations. A small water volume (0.2–1.0 µL) from each vial was sampled using a 5 µL syringe (SGE Analytical Science, Ringwood, Australia) and injected through a septum in a vaporiser unit maintained at 80 ∘C to ensure complete vaporisation of the liquid water straight after injection. The vapour was then transferred through a Teflon tube to the pre-evacuated optical cavity of the water isotope analyser. Before each measurement the syringe was rinsed three times in deionised water. Each vial was then measured eight times in total and only the last five measurements, subject to data filtering, were retained and averaged. Based on measurements on the internal standard used for quality check, the accuracy (i.e. the mean absolute difference between calibrated and true δ18O values) and reproducibility (i.e. the standard deviation of these means) of our δ18O measurements were always below 0.15 and 0.1 ‰ respectively.
2.7 Phosphate concentration measurements
Because phosphate ions can act as either strong CA activators (Rowlett et al., 1991) or CA inhibitors (Rusconi et al., 2004), total phosphate concentration in the different soils was measured using the water extraction and colorimetric method (Van Veldhoven and Mannaerts, 1987). On 10 g of dry soil we added 99 mL of deionised water and 1 mL of a biocide (Toluene) to stop any microbial activity. Soil suspensions were incubated at 20 ∘C for 16 h on an agitating roller, then sampled with plastic syringes and filtered through 0.2 mm membrane filters. The filtered solutions were then analysed for phosphate concentrations (mg(P) L−1) using a malachite green colorimetric method (Van Veldhoven and Mannaerts, 1987). Results were then expressed on a dry soil mass basis (mg(P) kg(soil)−1).
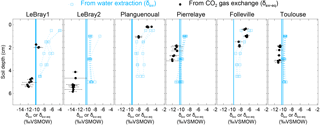
Figure 5The isotopic composition of soil water at different depths in the replicated soil microcosms from each site, estimated either by vacuum distillation and water isotope analysis (δsw, blue squares) or online CO2–H2O isotopic exchange using the two-steady-state approach (δsw-eq, at depth zeq, black circles; see text). Profiles for the different CA treatments are plotted together without distinction (because exogenous CA addition should not affect the isotopic composition of soil water). The blue vertical line also indicates the isotopic composition of the irrigation water used for the re-wetting of the air-dried soils. According to Eq. (11), the addition of exogenous CA shifts the gas exchange results (δsw-eq) to shallower depths (zeq).
3.1 Illustration of the non-destructive soil CA activity measurement method
From each sequence and steady state, it was possible to compute a relationship between the soil CO2–H2O isotopic exchange rate, kiso and the isotope composition of soil water in equilibration with soil CO2, δsw-eq by combining Eqs. (7) and (8). This approach, when presented graphically, leads to a plot with up to six curves (two curves per sequence; see Fig. 4 in the case of LeBray1 with 24 mg L−1 of exogenous CA addition) that intersect at very similar locations within the kiso–δsw-eq space. Combining the two steady states from the same sequence of measurement (Fig. 2) and using the iterative procedure described above, it is also possible to estimate kiso and δsw-eq numerically, as indicated by the symbols in Fig. 4. These values corresponded closely to the intersection points of the two curves for each steady state in the kiso–δsw-eq space (Fig. 4). Errors on the CO2 isotope measurements were also algebraically propagated into the equations in order to estimate uncertainties on kiso and δsw-eq. The repeatability of the measurements between the three sequences was very good with a standard deviation equal to or lower than the propagated error on individual estimates (i.e. the spread of the squares in Fig. 4 was always smaller than the error bars on each individual square). Sometimes the intersection between the two lines was not as clearly defined as the one shown in Fig. 4 but the combination of the two steady states always provided very consistent and repeatable estimates of both kiso and δsw-eq between the different sequences. For example, in the experiment shown in Fig. 4, we obtained kiso values of 0.022 ± 0.005, 0.025 ± 0.006 and 0.025 ± 0.005 s−1 and δsw-eq values of −11.3 ± 0.6, −11.5 ± 0.7 and −11.2 ± 0.3 ‰ VSMOW for the three sequences. These estimated values of δsw-eq were significantly different (P < 0.05) from the δ18O of irrigation water (−10.1 ‰ VSMOW) and from the mean cryogenically extracted soil water averaged over the entire soil column and weighted by volumetric soil water content (Fig. 5). Similar results were also observed on LeBray2 where the water pool “seen” by CO2 had an isotopic composition (δsw-eq, black circles in Fig. 5) that was strongly depleted (by about 5 ‰) compared to the cryogenically extracted soil water pool (blue squares in Fig. 5). In contrast, more enriched CO2-derived δsw-eq values and shallower zeq were found in soils containing a larger clay fraction (i.e. Planguenoual and Folleville; see Table 1), also in much better agreement with the δ18O profile of cryogenically extracted soil water (Fig. 5).
3.2 Effect of soil pH on soil CA activity
The native (i.e. without any addition of exogenous α-CA during irrigation) isotopic exchange rates (kiso,native) of the six soils were always higher than the un-catalysed rate (kiso,uncat) and tended to increase slightly with more alkaline conditions (Fig. 6). These values of native isotopic exchange rates are consistent with what we would theoretically predict using β-CA concentrations between 10 and 80 mg L−1 (Fig. 3).
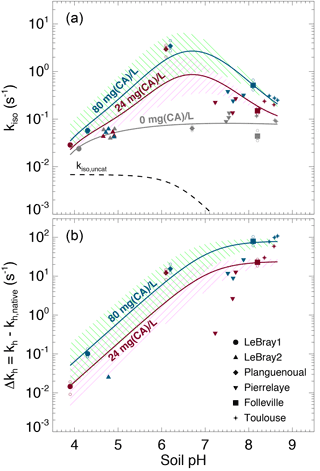
Figure 6(a) Measured CO2–H2O isotopic exchange rates (kiso) in the different soils for different levels of α-CA addition and (b) associated enhancement hydration rates ( caused by the α-CA addition. In (a), the un-catalysed isotope exchange rate (kiso,uncat; see Uchikawa and Zeebe, 2012) is shown for reference (black dotted curve). The pH dependence of the native isotope exchange rates (grey points in a) is interpolated over the entire pH range explored here using a third-order polynomial fit (grey curve in a). The range of the theoretical rates above this native rate curve that we would expect from α-CA addition of 24 mg L−1 (purple curve and hatched area) and 80 mg L−1 (green curve and hatched area) are also shown and have been obtained using s−1 µM−1 and . For those microcosms that were measured multiple times (several sequences), smaller open symbols are displayed to indicate the results from each individual sequence. In some cases (e.g. LeBray 2), some points could not be displayed in (b) because the kiso measured after CA addition was smaller than the mean native kiso, resulting in negative Δkh values (within the measurement uncertainty).
The addition of exogenous CA generally led to higher kiso values compared to the native rates, and also enhanced CO2 hydration rates kh, with marked differences depending on the pH range (Fig. 6a). On the most acidic soils, the addition of exogenous α-CA barely increased kh above its native rate (kh,native), by 0.1 s−1 or less (the native rate was around 0.06 s−1), but within the uncertainties on the measurements. On the other hand for the most alkaline soils (Toulouse, Folleville) kh increased to about 20 s−1 with 24 mg L−1 of CA added to the irrigation water and up to 65–100 s−1 at 80 mg L−1. Results from the soils with more neutral pH (Planguenoual, Pierrelaye) were intermediate between these two cases with enhanced hydration rates of the order of 10 s−1 or less.
This influence of soil pH on the enhancement of kh by exogenous CA was anticipated as the kcat∕KM (appearing in Eq. 10) is known to be strongly reduced in acidic pH with a pH response of the form (Rowlett et al., 1991)
To test whether our results only reflected the pH response of the exogenous α-CA, we rewrote Eq. (10) as follows:
where kh,native (s−1) represents the native value of kh and [CA]exogenous (mol m−3) is the concentration of exogenous CA in soil water. For a given pH (and temperature) the difference should then be proportional to [CA]exogenous and the slope of the relationship should be given by kcat∕KM and thus be influenced by soil pH. The theoretical pH response of Δkh at the two CA concentration values used in this study (24 and 80 mg L−1) is shown in Fig. 6b, using Eq. (12) with and ( s−1 µM−1 and a molar mass of 30 kg mol−1, typical values for bovine α-CA (Lindskog and Coleman, 1973; Rowlett et al., 1991; Uchikawa and Zeebe, 2012). For LeBray1, Folleville and Toulouse, our results were in very close agreement with Eq. (12) for the two different CA concentrations we tested, but this was not the case for the other soils. For LeBray2 and Pierrelaye, the observed enhanced hydration rates were smaller than the ones predicted by Eq. (12) while for Planguenoual, they were higher.
4.1 Can we predict the enhancement in soil CA activity associated with exogenous CA addition?
Results presented in Fig. 6b demonstrate that a low (acidic) soil pH clearly inhibits the non-native, additional hydration rate of CO2 induced by a supply of exogenous CA to the soil water. Our data from three of the soils (LeBray1, Folleville and Toulouse) agreed remarkably well with the pH response described by Eq. (12) and parameterised with kcat ∕ KM and pKa values previously estimated from independent studies on the same α-CA than the one used here (Uchikawa and Zeebe, 2012) or other bovine CA (Rowlett et al., 1991). This indicates that our gas exchange method to estimate CO2 hydration rates in soil water is robust, despite possible complications caused by CO2 diffusion through the soil matrix and the potential for heterogeneity in soil water content and pore space in our microcosms. A further possible complication could have arisen because of the necessity to subtract the native hydration rate from our Δkh calculations. This approach could have introduced a possible bias in our calculations of Δkh if the native hydration rates were markedly different between soils with and without CA addition – i.e. if the addition of water with exogenous CA over the 12–24 h prior to our gas exchange measurements was enough to induce changes in microbial growth and diversity and/or their CA gene expression compared to soils where only water was added. We estimated the bacterial and fungal abundance using qPCR for some of our microcosms and could not find any clear trend in the number of 16S and 18S DNA gene copies with the amount of exogenous CA added to the soil (not shown). These results suggest that within the timeframe of our experiment, exogenous CA addition did not affect the community structure. However, conservation of the community structure does not necessarily translate into conservation of the native CO2 hydration rate as microbial communities may have modulated their CA gene expression in response to the availability and activity of exogenous CA. Actually, the observed values of Δkh were not always consistent with those predicted for three of the soils (LeBray2, Pierrelaye and Planguenoual), which may indicate changes in native CO2 hydration rates with exogenous CA addition that would have biased our Δkh estimations.
Another possible reason for these discrepancies between observed and predicted Δkh could be that the model we are using to derive kiso and thus kh from our gas exchange data (Eq. 8) assumes that the soil column is homogeneous in terms of soil water content, temperature, porosity, CA concentration and respiration rate (Tans, 1998; see also Appendix A). Care was taken to remain as close as possible to these conditions: the soils had been sieved and homogenised before being placed into the soil chambers, the irrigation of the soil was performed at least 12 h prior to the gas exchange measurements and the soil microcosms were immersed in a water bath to minimise temperature gradients during the gas exchange measurements. Furthermore, in 2016 we also increased the preparation time to 24 h and minimised soil water evaporation and isotopic enrichment (see Sect. 2). However, despite these precautions, soil water content and its oxygen isotope composition was not always homogeneous throughout the soil column (Fig. 5).
Also, on the most alkaline soils, we noticed that the CO2 mixing ratio on the outlet of the soil microcosm was not always constant but decreased slightly, indicating that steady state was not reached. This could be explained by the fact that these alkaline soils contain a large pool of total dissolved inorganic carbon that takes much longer to re-equilibrate after a change in the CO2 concentration in the microcosm headspace, especially if this concentration differed markedly from the CO2 concentration seen by the soil prior to measurement. On these soils, the acclimation time of 20 min was certainly too short, but was chosen as a compromise in order to minimise other possible artefacts caused by soil evaporation whilst the microcosm was flushed with dry air during the measurements.
In order to explore the possible consequences of the deviations from non-steady state and soil water inhomogeneity on our kiso estimates, we also used a numerical model that simulates explicitly the transport and rate of change of the different CO2 isotopologues throughout the soil column and inside the chamber headspace. The model was similar to the one used in Gangi et al. (2015) but with prescribed vertical profiles of soil water content (θ) and isotopic composition (δsw). The model was run over the entire sequence shown in Fig. 2 and three model parameters were optimised in order to find the best match between the modelled and observed time series of CO2 mixing ratio and its carbon and oxygen isotopic composition in the chamber headspace. These model parameters were the ratio kiso ∕ kiso,uncat (assumed constant through the soil column), the CO2 mixing ratio of the air prior to connecting the microcosm to the air supply and a possible offset between δsw and δsw,eq (also assumed constant throughout the soil column). The latter parameter seemed necessary given the results shown in Fig. 5. Soil CO2 production rate was assumed to be uniform throughout the soil column and computed iteratively to match the observed CO2 efflux. Soil temperature was set to the constant value of the water bath and vertical profiles of soil water content and isotopic composition (δsw) were prescribed from depth-resolved measurements (Fig. 5). Surprisingly, the results from this numerical model differed only marginally from those shown in Figs. 5 and 6 (see Supplement Fig. S1). Values of Δkh were slightly affected by non-steady-state effects, either positively (Pierrelaye) or negatively (Planguenoual). Soil water inhomogeneity could also affect Δkh values slightly both positively (Folleville) or negatively (LeBray1). Overall, the discrepancies between Δkh estimates and the theoretical predictions (Eq. 12) were only marginally reduced, even after non-steadiness and soil water inhomogeneity had been accounted for.
Another factor that could explain the deviation of Δkh from theory is the presence of phosphate ions in the soil solution (Table 1) that could either activate or inhibit CA compared to its activity in the absence of such anions (Rowlett et al., 1991; Rusconi et al., 2004). We tested this hypothesis by exploring how the ratio between Δkh predicted by Eq. (12) (Δkh,theory) and the observed Δkh varied with total phosphate concentration (Pi), as well as with the concentrations in mono- and di-hydrogen phosphate ions (HPO and H2PO respectively). Although the relationships between Δkh,theory ∕ Δkh and the different phosphate ion concentrations were quite dispersed, we could observe a positive trend (not shown). Also, two of the soils with the highest total Pi and H2PO molar concentrations (LeBray2 and Pierrelaye) had the largest Δkh,theory ∕ Δkh ratio, corresponding to an inhibitory factor of about 10 in Pierrelaye and even higher in LeBray2. This could indicate that phosphate ions act as an inhibitor of the exogenous CA used in our experiments, explaining the reduced response to CA addition in these two soils (Fig. 6).
4.2 With which soil water pool does the CO2 equilibrate?
Our results also revealed large differences between the isotopic composition of the water pool “seen” by the CO2 (δsw-eq) and that of cryogenically extracted soil water (δsw), with significantly (P < 0.05) more depleted δsw-eq values compared to δsw (Fig. 5 and Table S2 in the Supplement). Interestingly, very similar “offsets” between δsw and δsw,eq were also predicted by the numerical model (not shown), except for LeBray1 where even larger offsets were found. For a given soil the offset did not seem to vary with soil CA activity (i.e. the difference between δsw and δsw,eq was the same for soils with and without CA addition; see Table S2) and, at least for the only soil tested, did not seem to be affected by small change in soil water content (similar offsets were observed between LeBray1 and LeBray2). However, in-between the different soils, it seemed that those with the highest CA activity (Planguenoual, Folleville) also had the smallest offset (Table S2). Also for LeBray soil, Jones et al. (2017) showed that the offset between δsw and δsw-eq decreased when the soil was approaching saturation.
The exact reason for this offset between δsw and δsw,eq is still unknown. Noting that δsw and δsw,eq are estimated from measurements coming from different analysers, we verified that the calibrations of the two analysers were consistent with one another. We thus pressurised pure CO2 into a keg partially full of water of known isotopic composition and let the water–CO2 mixture equilibrate for several weeks. The pure CO2 was then diluted into CO2-free air to reach ambient CO2 concentrations and the air mixture was analysed with our CO2 isotope analyser. We found a small difference of about −0.31 ‰ between the δ18O of the equilibrated CO2 and the δ18O of the water in the keg. Clearly, such a bias would only explain a small fraction of the measured offset between δsw and δsw,eq, down to −6 ‰ on some soils. Also the fact that this offset cancels in soils with high CA activity indicates that our calibration scheme is clearly not the only cause of the existence of such an offset.
A possible explanation for the observed difference between δsw and δsw,eq could be that, at any given depth, soil water is not isotopically homogeneous and that CO2 “sees” a different water pool to that extracted during cryogenic distillation, with different thermodynamic and chemical properties between the different soil water pools. This idea has been proposed by several studies already. For example Hsieh et al. (1998) allowed pure CO2 to equilibrate for several weeks with different soils at different water contents and found that the isotopic composition of equilibrated CO2 could differ by several ‰ compared to the δ18O of the soil water extracted by vacuum distillation, even at relatively high (i.e. 32 %) gravimetric water contents. They explained this difference by recognising that soil surfaces contain a lot of ions that could modify the isotopic composition of the “bound” water pool and also the CO2–H2O isotopic fractionation factor.
More recently, Chen et al. (2016) performed laboratory experiments that suggest the existence of two isotopically distinct pools of water around hydrophilic materials such as silage, litter or soil organic matter. They found a negative apparent isotopic fractionation between total water (extracted by cryogenic distillation) and unconfined water (estimated by water liquid–vapour equilibration), suggesting a depletion of the water bound to the hydrophilic material. They also found that the magnitude of this apparent fractionation increased with the solid to water ratio. To reconcile these results with ours, we would need to assume that CO2 equilibrates with bound water, even when exogenous CA is added to the soil. This is somewhat surprising, because once in solution we would expect the exogenous CA to be equally spread between bound and unbound water. Another explanation could be that water around the CA reaction sites is depleted. Chen et al. (2016) found large apparent fractionation factors with water adsorbed onto casein, another protein found in milk. However, according to their theory, at high water contents (or low solid-to-water ratios), the fractionation factor should vanish. In addition, Uchikawa and Zeebe (2012) found that the isotopic equilibration between BaCO3 and water was not affected by the presence of CA in the solution, thus rejecting the hypothesis of different water composition around the CA reaction sites. Clearly, more experiments on CO2–H2O equilibration in soils such as those performed by Hsieh et al. (1998) are needed to better understand the underlying mechanisms leading to this apparent oxygen isotope disequilibrium between soil CO2 and soil water, even below the equilibrium depth.
Our experimental results demonstrate that our two-steady-state approach is robust and sensitive enough to detect changes in the CO2–H2O isotope exchange rate when the concentration of CA enzyme in the soil matrix is augmented artificially. We also found that natural variations in soil pH had a strong control over the variability of soil CA activity, with a smaller influence of the phosphate ion concentration, and these variations reassuringly followed similar patterns to those observed in other studies on α-CA activity in buffered solutions. This is a real advancement in our understanding of the spatial variations of soil CA activity across biomes reported by Wingate et al. (2009) and the associated impact on the atmospheric budget of CO18O. However, our results should still be taken with caution. Although α-CAs may be present in certain soil microbial communities with a high abundance of phototrophs such as cyanobacteria and micro-algae, the majority of microbial CAs in soils are more likely represented by the β-CA class (Smith and Ferry, 2000). In addition, β-CAs are seldom active externally like α-CAs and are rather found in the internal cell components of the microbe, in particular the cytoplasm (e.g. Merlin et al., 2003). Thus, although β-CAs also exhibit a strong dependence of CA activity with pH (Rowlett et al., 2002), it remains to be investigated whether the location and relative abundance of different CAs in soil communities modifies the expected relationship with pH. In addition, it is not clear whether the impact of anions such as phosphate ions will remain important when the CA is active internally. This was beyond the scope of the present study but is an obvious next step to be addressed in future experiments to help understand and model better the spatio-temporal variations in atmospheric CO18O at large scales.
The raw data, the meta-data and data processing codes are stored on data servers and repositories and available upon request to the corresponding authors.
Following Tans (1998) we will assume that the CO2 concentration profile within the soil column is driven by two processes: respiration, characterised by a production density S (mol m−3 s−1) and diffusion, characterised by an effective diffusivity Deff (m2 s−1). At steady state, the mass balance equation (see also Eq. 3 in Tans, 1998) is
where C (mol m−3) is the CO2 concentration at depth z (m) within the soil column. Assuming S constant throughout the soil column (a fair assumption when working on repacked, temperature-controlled soil columns), and with the boundary conditions C=Ca at z=0 and at , the solution of Eq. (A1) is (see for example Eq. 23a in Tans, 1998)
Denoting by R, RS and Req the 18O ∕ 16O ratio of soil air CO2, soil respired CO2 and CO2 in equilibrium with soil water, respectively, the steady-state CO18O mass balance equation is (see also Eq. 9 in Tans, 1998)
Defining y=RC, Eq. (A3) becomes
The general solution of this differential equation is of the form , where A and B are constants to be defined and Y is a particular solution of Eq. (A4). Choosing Y of the form , the coefficients a, b and c must satisfy Eq. (A4) for any depth z. Using the expression of C(z) from Eq. (A2), this gives
With the boundary conditions y=CaRa at z=0 and at , the solution of Eq. (A4) can be found (i.e. constants A and B can be identified) and this gives
The CO2 and CO18O fluxes at the soil surface are given by
From Eq. (A2) we get and from Eq. (A6) we obtain
where . Defining and using the delta notation (i.e. – 1 where Rstd is the 18O ∕ 16O ratio of the international standard VPDBg), Eq. (A8) becomes
where and noting that the second-order term εDδeq has been discarded. Now, assuming RS=Req (or equivalently δS=δeq), Eq. (A9) simplifies to Eq. (8) in the main text.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-15-597-2018-supplement.
JS, SPJ, LW, SW and JO conceived and designed the experiment. JS, SPJ and SW conducted the gas-exchange and water isotope measurements. JS, SPJ and JO analysed the data. JS, JO and LW wrote the paper. All authors commented and contributed to the final version.
The authors declare that they have no conflict of interest.
Pierre-Alain Maron and Virginie Nowak are gratefully acknowledged for
quantitative PCR analysis performed on some of our soil samples. We also
thank Alain Mollier for helping us with the phosphate concentration
measurements. This project received funding from the European Research
Council (ERC) starting grant SOLCA under the European Union's Seventh
Framework Programme (FP7/2007-2013) (grant agreement no. 338264), the French
Agence Nationale de la Recherche (ANR) (grant agreement
no. ANR-13-BS06-0005-01) and the Institut National de la Recherche
Agronomique (INRA) departments EFPA and EA (PhD studentship of
Joana Sauze).
Edited by: Elise
Pendall
Reviewed by: three anonymous referees
Achat, D. L., Daumer, M. L., Sperandio, M., Santellani, A. C., and Morel, C.: Solubility and mobility of phosphorus recycled from dairy effluents and pig manures in incubated soils with different characteristics, Nutr. Cycl. Agroecosys., 99, 1–15, https://doi.org/10.1007/s10705-014-9614-0, 2014.
Allison, C. E., Francey, R. J., and Meijer, H. A. J.: Recommendations for the reporting of stable isotope measurements of carbon and oxygen in CO gas, Ref. Intercomp. Mater. Stable Isot., 24, 155–162, https://doi.org/10.1016/0020-708X(73)90108-7, 1995.
Badger, M.: The roles of carbonic anhydrases in photosynthetic CO2 concentrating mechanisms, Photosynth. Res., 77, 83–94, https://doi.org/10.1023/A:1025821717773, 2003.
Ballantyne, A. P., Alden, C. B., Miller, J. B., Tans, P. P., and White, J. W. C.: Increase in observed net carbon dioxide uptake by land and oceans during the past 50 years, Nature, 488, 70–72, https://doi.org/10.1038/nature11299, 2012.
Beer, C., Reichstein, M., Tomelleri, E., Ciais, P., Jung, M., Carvalhais, N., Rodenbeck, C., Arain, M. A., Baldocchi, D., Bonan, G. B., Bondeau, A., Cescatti, A., Lasslop, G., Lindroth, A., Lomas, M., Luyssaert, S., Margolis, H., Oleson, K. W., Roupsard, O., Veenendaal, E., Viovy, N., Williams, C., Woodward, F. I., and Papale, D.: Terrestrial Gross Carbon Dioxide Uptake: Global Distribution and Covariation with Climate, Science, 329, 834–838, https://doi.org/10.1126/science.1184984, 2010.
Brenninkmeijer, C. A. M., Kraft, P., and Mook, W. G.: Oxygen isotope fractionation between CO2 and H2O, Chem. Geol., 41, 181–190, https://doi.org/10.1016/S0009-2541(83)80015-1, 1983.
Chen, G., Auerswald, K., and Schnyder, H.: 2H and 18O depletion of water close to organic surfaces, Biogeosciences, 13, 3175–3186, https://doi.org/10.5194/bg-13-3175-2016, 2016.
Ciais, P., Denning, A. S., Tans, P. P., Berry, J. A., Randall, D. A., Collatz, G. J., Sellers, P. J., White, J. W. C., Trolier, M., Meijer, H. A. J., Francey, R. J., Monfray, P., and Heimann, M.: A three-dimensional synthesis study of δ18O in atmospheric CO2?: 1. Surface fluxes, J. Geophys. Res.-Atmos., 102, 5857–5872, https://doi.org/10.1029/96JD02360, 1997.
Cuntz, M.: A comprehensive global three-dimensional model of δ18O in atmospheric CO2?: 1. Validation of surface processes, J. Geophys. Res., 108, 1–24, https://doi.org/10.1029/2002JD003153, 2003.
Elleuche, S. and Poggeler, S.: Carbonic anhydrases in fungi, Microbiology, 156, 23–29, https://doi.org/10.1099/mic.0.032581-0, 2010.
Farquhar, G. D. and Cernusak, L. A.: Ternary effects on the gas exchange of isotopologues of carbon dioxide, Plant. Cell Environ., 35, 1221–1231, https://doi.org/10.1111/j.1365-3040.2012.02484.x, 2012.
Farquhar, G. D., Lloyd, J., Taylor, J. A., Flanagan, L. B., Syvertsen, J. P., Hubick, K. T., Wong, S. C., and Ehleringer, J. R.: Vegetation effects on the isotope composition of oxygen in atmospheric CO2, Nature, 363, 439–443, https://doi.org/10.1038/363439a0, 1993.
Fierer, N. and Jackson, R. B.: The diversity and biogeography of soil bacterial communities, P. Natl. Acad. Sci. USA, 103, 626–631, https://doi.org/10.1073/pnas.0507535103, 2006.
Francey, R. J. and Tans, P. P.: Latitudinal variation in oxygen-18 of atmospheric CO2, Nature, 327, 495–497, https://doi.org/10.1038/327495a0, 1987.
Friedlingstein, P., Cox, P., Betts, R., Bopp, L., von Bloh, W., Brovkin, V., Cadule, P., Doney, S., Eby, M., Fung, I., Bala, G., John, J., Jones, C., Joos, F., Kato, T., Kawamiya, M., Knorr, W., Lindsay, K., Matthews, H. D., Raddatz, T., Rayner, P., Reick, C., Roeckner, E., Schnitzler, K.-G., Schnur, R., Strassmann, K., Weaver, A. J., Yoshikawa, C., and Zeng, N.: Climate–Carbon Cycle Feedback Analysis: Results from the C4 MIP Model Intercomparison, J. Climate, 19, 3337–3353, https://doi.org/10.1175/JCLI3800.1, 2006.
Gangi, L., Rothfuss, Y., Ogée, J., Wingate, L., Vereecken, H., and Brüggemann, N.: A New Method for In Situ Measurements of Oxygen Isotopologues of Soil Water and Carbon Dioxide with High Time Resolution, Vadose Zone J., 14, https://doi.org/10.2136/vzj2014.11.0169, 2015.
Gillon, J. and Yakir, D.: Influence of Carbonic Anhydrase Activity in Terrestrial Vegetation on the 18O Content of Atmospheric CO2, Science, 291, 2584–2587, https://doi.org/10.1126/science.1056374, 2001.
Griffiths, R. I., Thomson, B. C., James, P., Bell, T., Bailey, M., and Whiteley, A. S.: The bacterial biogeography of British soils, Environ. Microbiol., 13, 1642–1654, https://doi.org/10.1111/j.1462-2920.2011.02480.x, 2011.
Gurney, K. R. and Eckels, W. J.: Regional trends in terrestrial carbon exchange and their seasonal signatures, Tellus B, 63, 328–339, https://doi.org/10.1111/j.1600-0889.2011.00534.x, 2011.
Hartman, W. H., Richardson, C. J., Vilgalys, R., and Bruland, G. L.: Environmental and anthropogenic controls over bacterial communities in wetland soils, P. Natl. Acad. Sci. USA, 105, 17842–17847, https://doi.org/10.1073/pnas.0808254105, 2008.
Hopkinson, B. M., Meile, C., and Shen, C.: Quantification of Extracellular Carbonic Anhydrase Activity in Two Marine Diatoms and Investigation of Its Role, Plant Physiol., 162, 1142–1152, https://doi.org/10.1104/pp.113.217737, 2013.
Hsieh, J. C. C., Savin, S. M., Kelly, E. F., and Chadwick, O. A.: Measurement of soil-water δ18O values by direct equilibration with CO2, Geoderma, 82, 255–268, https://doi.org/10.1016/S0016-7061(97)00104-3, 1998.
IPCC: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK and New York, NY, USA, 1535 pp., https://doi.org/10.1017/CBO9781107415324, 2013.
Jones, S. P., Ogée, J., Sauze, J., Wohl, S., Saavedra, N., Fernández-Prado, N., Maire, J., Launois, T., Bosc, A., and Wingate, L.: Non-destructive estimates of soil carbonic anhydrase activity and associated soil water oxygen isotope composition, Hydrol. Earth Syst. Sci., 21, 6363–6377, https://doi.org/10.5194/hess-21-6363-2017, 2017.
Krulwich, T. A., Sachs, G., and Padan, E.: Molecular aspects of bacterial pH sensing and homeostasis, Nat. Rev. Microbiol., 9, 330–343, https://doi.org/10.1038/nrmicro2549, 2011.
Lauber, C. L., Hamady, M., Knight, R., and Fierer, N.: Pyrosequencing-Based Assessment of Soil pH as a Predictor of Soil Bacterial Community Structure at the Continental Scale, Appl. Environ. Microb., 75, 5111–5120, https://doi.org/10.1128/AEM.00335-09, 2009.
Le Quéré, C., Moriarty, R., Andrew, R. M., Canadell, J. G., Sitch, S., Korsbakken, J. I., Friedlingstein, P., Peters, G. P., Andres, R. J., Boden, T. A., Houghton, R. A., House, J. I., Keeling, R. F., Tans, P., Arneth, A., Bakker, D. C. E., Barbero, L., Bopp, L., Chang, J., Chevallier, F., Chini, L. P., Ciais, P., Fader, M., Feely, R. A., Gkritzalis, T., Harris, I., Hauck, J., Ilyina, T., Jain, A. K., Kato, E., Kitidis, V., Klein Goldewijk, K., Koven, C., Landschützer, P., Lauvset, S. K., Lefèvre, N., Lenton, A., Lima, I. D., Metzl, N., Millero, F., Munro, D. R., Murata, A., Nabel, J. E. M. S., Nakaoka, S., Nojiri, Y., O'Brien, K., Olsen, A., Ono, T., Pérez, F. F., Pfeil, B., Pierrot, D., Poulter, B., Rehder, G., Rödenbeck, C., Saito, S., Schuster, U., Schwinger, J., Séférian, R., Steinhoff, T., Stocker, B. D., Sutton, A. J., Takahashi, T., Tilbrook, B., van der Laan-Luijkx, I. T., van der Werf, G. R., van Heuven, S., Vandemark, D., Viovy, N., Wiltshire, A., Zaehle, S., and Zeng, N.: Global Carbon Budget 2015, Earth Syst. Sci. Data, 7, 349–396, https://doi.org/10.5194/essd-7-349-2015, 2015.
Lindskog, S. and Coleman, J. E.: The Catalytic Mechanism of Carbonic Anhydrase, P. Natl. Acad. Sci. USA, 70, 2505–2508, https://doi.org/10.1073/pnas.70.9.2505, 1973.
Massman, W. J.: A review of the molecular diffusivities of H2O, CO2, CH4, CO, O3, SO2, NH3, N2O, NO, and NO2 in air, O2 and N2 near STP, Atmos. Environ., 32, 1111–1127, https://doi.org/10.1016/S1352-2310(97)00391-9, 1998.
Merlin, C., Masters, M., Mcateer, S., and Coulson, A.: Why Is Carbonic Anhydrase Essential to Escherichia coli?, J. Bacteriol., 185, 6415–6424, https://doi.org/10.1128/JB.185.21.6415-6424.2003, 2003.
Miller, J. B., Yakir, D., White, J. W. C., and Tans, P. P.: Measurement of 18O ∕ 16O in the soil-atmosphere CO2 flux, Global Biogeochem. Cy., 13, 761–774, https://doi.org/10.1029/1999GB900028, 1999.
Mills, G. A. and Urey, H. C.: The Kinetics of Isotopic Exchange between Carbon Dioxide, Bicarbonate Ion, Carbonate Ion and Water 1, J. Am. Chem. Soc., 62, 1019–1026, https://doi.org/10.1021/ja01862a010, 1940.
Moldrup, P., Olesen, T., Komatsu, T., Yoshikawa, S., Schjønning, P., and Rolston, D. E.: Modeling Diffusion and reaction in soils: X. A unifying model for solute and gas diffusivity in unsaturated soil, Soil Sci., 168, 321–337, https://doi.org/10.1097/01.ss.0000070907.55992.3c, 2003.
Moroney, J. V., Bartlett, S. G., and Samuelsson, G.: Carbonic anhydrases in plants and algae, Plant Cell Environ., 24, 141–153, https://doi.org/10.1046/j.1365-3040.2001.00669.x, 2001.
Ogée, J., Sauze, J., Kesselmeier, J., Genty, B., Van Diest, H., Launois, T., and Wingate, L.: A new mechanistic framework to predict OCS fluxes from soils, Biogeosciences, 13, 2221–2240, https://doi.org/10.5194/bg-13-2221-2016, 2016.
Poulter, B., Franck, D., Ciais, P., Myneni, R. B., Andela, N., Bi, J., Broquet, G., Canadell, J. G., Chevallier, F., Liu, Y. Y., Running, S. W., Sitch, S., and van der Werf, G. R.: Contribution of sem-arid ecosystems to interannual variability of the global carbon cycle, Nature, 509, 600–603, https://doi.org/10.1038/nature13376, 2014.
Rowlett, R. S., Gargiulo, N. J., Santoli, F. A., Jackson, J. M., and Corbett, A. H.: Activation and Inhibition of Bovine Carbonic Anhydrase III by Dianions, J. Biol. Chem., 266, 933–941, 1991.
Rowlett, R. S., Tu, C., McKay, M. M., Preiss, J. R., Loomis, R. J., Hicks, K. A., Marchione, R. J., Strong, J. A., Donovan, G. S., and Chamberlin, J. E.: Kinetic characterization of wild-type and proton transfer-impaired variants of β-carbonic anhydrase from Arabidopsis thaliana, Arch. Biochem. Biophys., 404, 197–209, https://doi.org/10.1016/S0003-9861(02)00243-6, 2002.
Rusconi, S., Innocenti, A., Vullo, D., Mastrolorenzo, A., Scozzafava, A. and Supuran, C. T.: Carbonic anhydrase inhibitors. Interaction of isozymes I, II, IV, V, and IX with phosphates, carbamoyl phosphate, and the phosphonate antiviral drug foscarnet, Bioorg. Med. Chem. Lett., 14, 5763–5767, https://doi.org/10.1016/j.bmcl.2004.09.064, 2004.
Seibt, U., Wingate, L., Lloyd, J., and Berry, J. A.: Diurnally variable δ18O signatures of soil CO2 fluxes indicate carbonic anhydrase activity in a forest soil, J. Geophys. Res., 111, G04005, https://doi.org/10.1029/2006JG000177, 2006.
Smith, K. and Ferry, J. G.: Prokaryotic carbonic anhydrases, FEMS Microbiol. Rev., 24, 335–366, https://doi.org/10.1016/S0168-6445(00)00030-9, 2000.
Tans, P.: Oxygen isotopic equilibrium between carbon dioxide and water in soils, Tellus B, 50, 163–178, https://doi.org/10.1034/j.1600-0889.1998.t01-1-00004.x, 1998.
Uchikawa, J. and Zeebe, R. E.: The effect of carbonic anhydrase on the kinetics and equilibrium of the oxygen isotope exchange in the CO2–H2O system: Implications for δ18O vital effects in biogenic carbonates, Geochim. Cosmochim. Ac., 95, 15–34, https://doi.org/10.1016/j.gca.2012.07.022, 2012.
Van Veldhoven, P. P. and Mannaerts, G. P.: Inorganic and organic phosphate measurements in the nanomolar range, Anal. Biochem., 161, 45–48, https://doi.org/10.1016/0003-2697(87)90649-X, 1987.
Weiss, R. F.: Carbon dioxide in water and seawater: the solubility of a non-ideal gas, Mar. Chem., 2, 203–215, https://doi.org/10.1016/0304-4203(74)90015-2, 1974.
Welp, L. R., Keeling, R. F., Meijer, H. A. J., Bollenbacher, A. F., Piper, S. C., Yoshimura, K., Francey, R. J., Allison, C. E., and Wahlen, M.: Interannual variability in the oxygen isotopes of atmospheric CO2 driven by El Niño, Nature, 477, 579–582, https://doi.org/10.1038/nature10421, 2011.
Wingate, L., Seibt, U., Maseyk, K., Ogée, J., Almeida, P., Yakir, D., Pereira, J. S., and Mencuccini, M.: Evaporation and carbonic anhydrase activity recorded in oxygen isotope signatures of net CO2 fluxes from a Mediterranean soil, Glob. Change Biol., 14, 2178–2193, https://doi.org/10.1111/j.1365-2486.2008.01635.x, 2008.
Wingate, L., Ogee, J., Cuntz, M., Genty, B., Reiter, I., Seibt, U., Yakir, D., Maseyk, K., Pendall, E. G., Barbour, M. M., Mortazavi, B., Burlett, R., Peylin, P., Miller, J., Mencuccini, M., Shim, J. H., Hunt, J., and Grace, J.: The impact of soil microorganisms on the global budget of 18O in atmospheric CO2, P. Natl. Acad. Sci. USA, 106, 22411–22415, https://doi.org/10.1073/pnas.0905210106, 2009.
Wingate, L., Ogée, J., Burlett, R., and Bosc, A.: Strong seasonal disequilibrium measured between the oxygen isotope signals of leaf and soil CO2 exchange, Glob. Change Biol., 16, 3048–3064, https://doi.org/10.1111/j.1365-2486.2010.02186.x, 2010.
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(1663 KB) - Full-text XML
- Corrigendum
-
Supplement
(132 KB) - BibTeX
- EndNote





