the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Field-warmed soil carbon changes imply high 21st-century modeling uncertainty
Katherine Todd-Brown
Bin Zheng
Thomas W. Crowther
The feedback between planetary warming and soil carbon loss has been the focus of considerable scientific attention in recent decades, due to its potential to accelerate anthropogenic climate change. The soil carbon temperature sensitivity is traditionally estimated from short-term respiration measurements – either from laboratory incubations that are artificially manipulated or from field measurements that cannot distinguish between plant and microbial respiration. To address these limitations of previous approaches, we developed a new method to estimate soil temperature sensitivity (Q10) of soil carbon directly from warming-induced changes in soil carbon stocks measured in 36 field experiments across the world. Variations in warming magnitude and control organic carbon percentage explained much of field-warmed organic carbon percentage (R2 = 0.96), revealing Q10 across sites of 2.2 [1.6, 2.7] 95 % confidence interval (CI). When these field-derived Q10 values were extrapolated over the 21st century using a post hoc correction of 20 Coupled Model Intercomparison Project Phase 5 (CMIP5) Earth system model outputs, the multi-model mean soil carbon stock changes shifted from the previous value of 88 ± 153 Pg carbon (weighted mean ± 1 SD) to 19 ± 155 Pg carbon with a Q10-driven 95 % CI of 248 ± 191 to −95 ± 209 Pg carbon. On average, incorporating the field-derived Q10 values into Earth system model simulations led to reductions in the projected amount of carbon sequestered in the soil over the 21st century. However, the considerable parameter uncertainty led to extremely high variability in soil carbon stock projections within each model; intra-model uncertainty driven by the field-derived Q10 was as great as that between model variation. This study demonstrates that data integration should capture the variation of the system, as well as mean trends.
- Article
(672 KB) - Companion paper 1
- Companion paper 2
-
Supplement
(5982 KB) - BibTeX
- EndNote
The flux of carbon dioxide between the soil and atmosphere is a major control on atmospheric carbon dioxide concentrations. Warming temperatures, driven by increases in atmospheric carbon dioxide, have the potential to stimulate carbon decomposition, accelerating its release into the atmosphere (Davidson and Janssens, 2006). If this is not counterbalanced by an equivalent increase in primary productivity (the opposing carbon flux), then it has the potential to drive a land carbon–climate feedback that will accelerate anthropogenic climate change. Recent global compilations of data from ecosystem warming experiments lend support to this idea (Carey et al., 2016), suggesting that warming alone could drive a loss of carbon from the upper soil horizons (Crowther et al., 2016). However, these studies addressed the impact of warming in isolation, and it remains unclear how this process will interact with the variety of other global change drivers to affect the global soil carbon stock over the rest of this century. Reflective of such uncertainty, soil carbon changes projected for 2100 under the Representative Concentration Pathway (RCP) 8.5, business-as-usual, scenario for the Coupled Model Intercomparison Project Phase 5 (CMIP5) range from −70 to 250 Pg carbon across different Earth system models (ESMs; Todd-Brown et al., 2014), making the land–carbon feedback one of the largest sources of uncertainty in future climate projections (Friedlingstein et al., 2014). Improving the soil carbon component of the Earth system models is essential to predicting the future evolution of the Earth system and thus establishing meaningful greenhouse gas emissions targets.
A fundamental parameter describing soil temperature sensitivity in soil carbon models is the Q10 – the factor of the change in decomposition rate associated with 10 ∘C of warming from a reference temperature (Davidson and Janssens, 2006; Lloyd and Taylor, 1994). Traditional laboratory incubations have found a wide range of Q10 values, varying from 1.4 (Townsend et al., 1997) to > 3 (Davidson et al., 1998, 2006), with 2 being the most commonly accepted value. Complicating this, theoretical analyses based on chemical kinetics suggest Q10 is itself dependent on temperature (Davidson and Janssens, 2006; Lloyd and Taylor, 1994), though these values are typically very close to 2 in most environmental temperature ranges (Lloyd and Taylor, 1994). More recently, large-scale analyses of field respiration have converged on Q10 estimates of 1.4 to 1.5 (Bond-Lamberty and Thomson, 2010; Hashimoto et al., 2015; Mahecha et al., 2010). Unsurprisingly, this temperature response is also critical in Earth system models, where the temperature sensitivity parameter is known to be a major driver of variation (Booth et al., 2012; Jones and Cox, 2001; Jones et al., 2006). However, it is unclear what is driving the lower Q10 estimates in these field-based syntheses compared to the average lab-based estimates from single-site studies, and there appears to be a relatively wide range of “typical” Q10 values in the literature. Nevertheless, most Earth system models use values that range from 1.5 (Oleson et al., 2013; Raddatz et al., 2007) to 2 (Bonan, 1996; Cox, 2001).
Traditionally, these Q10 values have been calculated from warming-induced changes in soil respiration rates. However, this approach has two main limitations: (1) respiration rates measured under idealized laboratory conditions fail to reflect the structure, heterogeneity, and variability of natural systems, and (2) field measurements cannot directly isolate heterotrophic soil respiration from autotrophic root respiration without substantially altering the system. Estimating Q10 directly from warming-induced changes in soil carbon stocks could be a valuable approach to addressing these limitations, but the variability and relative imprecision of soil carbon stock data necessitate a large sample size to adequately describe variation at the global scale (Bradford et al., 2016). Yet results from a recent Earth system model meta-analysis indirectly suggest that, with enough sample coverage, it may be possible to infer Q10 directly from changes in soil carbon stocks (Todd-Brown et al., 2014).
Here we present a new approach to estimating the global Q10 value from net changes in soil carbon stocks under warming, rather than soil respiration measurements, and examine the consequences of these estimates – with associated uncertainty – on CMIP5 Earth system model projections of global carbon storage over the rest of the 21st century. To do this, we use a global database of soil carbon stock data from 36 field-warming experiments around the world, each of which includes control (ambient) plots, and those which have been warmed for extended (years to decades) periods of time (Crowther et al., 2016) (Table S1 in the Supplement), and outputs from 20 Earth system models in the CMIP5 RCP 8.5, business-as-usual, scenario (Taylor et al., 2011; see Table 1 and S3 for model and output details). These field data were used previously to derive Earth system model independent estimates of global soil carbon temperature sensitivity where the effect of warming was isolated from other global change drivers or the interacting climate system (Crowther et al., 2016). In this study we develop a novel approach that enables us to explore these field results in the context of the temperature sensitivity function (Q10) used in an integrated Earth system model. We then examine the consequences of the data-driven Q10 estimates, and the associated uncertainty, for CMIP5 Earth system model projections of global carbon storage over the rest of the 21st century using a novel post hoc modification of the CMIP5 simulation outputs.
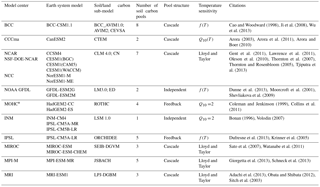
Table 1This is a summary of the soil decomposition sub-models for the ESMs used in this study and includes the number of pools, structure of the carbon exchange between those pools, temperature sensitivity function, and citations. Temperature sensitivity function is denoted as f(T), borrowed from the Century model (Parton et al., 1987, 1988); Lloyd and Taylor, taken from the recommended form from Lloyd and Taylor (1994); Q10(T), a temperature-dependent Q10 as defined by Arora (2003); or a Q10 parameter for the Q10 function as defined in this paper.
2.1 Field sites
The field sites were drawn from a previous analysis (Crowther et al., 2016). From this initial database of 48 paired case–control studies, we selected 36 studies that were run longer than 2 years to match the metastable state assumption articulated below. Eighteen of these sites were temperate grasslands, savannas, and shrublands; 10 were temperate broadleaf and mixed forests; six were tundra; one boreal forests or taiga; and one site was in a Mediterranean forest, woodland, and scrub. A traditional statistical analysis of the sites is provided by Crowther et al. (2016). For this study, we used the increase in soil temperature due to warming, length of the study, and the percent of soil organic carbon in paired warmed and control plots (Table S1).
2.2 Q10 calculations
We calculated traditional Q10 estimates based on these warming-induced soil carbon losses, enabling us to embed this temperature sensitivity information into a soil decomposition model framework. Traditional soil decomposition models follow a first-order linear decay framework:
where C is a vector of soil carbon pools with unique turnover times, t is time, uin is a scaler of soil carbon inputs, b is an allocation vector describing how the inputs are divided between the soil carbon pools, K is a diagonal matrix representing the decomposition rates of the pools, Q10 is a diagonal matrix with entries of the form representing the temperature sensitivity factor, T is a scalar describing the soil temperature and T0 an arbitrary reference temperature, and A is the transfer matrix representing movement of carbon between soil carbon pools.
The temperature sensitivity was assumed to be constant across pools. This allows the diagonal Q10 matrix to be collapsed into a single scalar value of the form . This constant temperature sensitivity assumption is discussed below and follows the structure of the CMIP5 Earth system models.
In general, there are three classes of pool structure for traditional models: independent, where there was no exchange between soil carbon pools, making A the identity matrix; cascade, where pools with faster turnover times passed carbon to pools with slower turnover times, making A a lower triangular matrix; and full-feedback models, where carbon was exchanged between faster and slower pools and vice versa, making A a fully dense matrix. In all cases KA is an M matrix, implying there exists an inverse with all positive entries. For the independent and cascade pools KA is diagonalizable, implying it can be broken down into a diagonal matrix D and an invertible matrix P such that KA = P−1DP.
For most well-developed soils, soil carbon stocks are at a metastable state where soil inputs approximately equal outputs (see Results for discussion of Earth system model outputs). Given that KA is an M matrix and this metastable state approximation, we can describe the total soil organic carbon as follows:
where C is the total organic carbon stock, u the sum of the soil inputs, and k a bulk decomposition rate that can be constructed from the decay matrix KA and allocation vector of the soil inputs b. For details of this derivation see the Supplement, Sect. “Mathematical Analysis”.
We can now describe the soil carbon stock difference between two soils with the same decay rate but different temperatures and inputs. This could either be two time points from a simulation where the soil output is close (within 10 %) of the soil inputs or a warmed treatment and a control:
For the field sites, we assume that the relative change in inputs due to warming is negligible compared to the effect on the decomposition rate across sites and that the main driver of differences in decomposition rates between control and treatment is the warming treatment, leading us to
Finally, we assume that the bulk density of the soil at a given site was unaffected by the warming treatment. This allows us to use the mass percent soil organic carbon instead of the soil organic carbon density for Eq. (4).
2.3 Model–data integration: parameter fitting
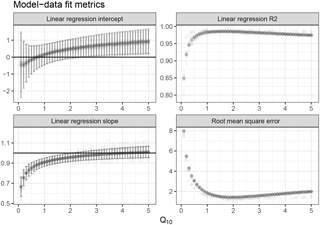
Given the relatively small parameter space, we chose a brute-force model–data integration approach where we iteratively calculated the predicted change in soil carbon stock given the control soil carbon (Eq. 4) across a range of Q10 values from 0.1 to 5 in 0.1 increments. We set the lower bound of the Q10 range to 0.1 instead of 1 for two reasons. First, while it is generally accepted that warmer soil temperatures will increase soil respiration (constraining Q10 > 1), it is possible that a warmer soil would result in drier soils and suppress soil respiration. In addition, numerically we wanted to bracket the expected parameter range with our prior. Data–model fits were scored using root mean squared error (RMSE) and linear regression (R2, slope and intercept).
A Q10 value was considered a good fit if the resulting model–data linear regression showed a low bias (slopes and intercepts within 2 standard deviations of 1 and 0, respectively); standard fit metrics like the R2 and RMSE were relatively insensitive to the Q10 parameter (see Fig. 1). By selecting the parameter based on model–data fit instead of deriving a direct Q10 value for each site and using the distribution, we demonstrate the robustness of the model and have a clear metric to select the parameter range. To test for statistical power, we randomly sampled the data 1000 times with sample sizes from 5 to 34 sites and compared this to samples with randomly assigned control vs. warming (for each study the percent carbon of control and treatment has a 50 % chance of being switched). These random and sample-generated Q10 distributions were compared using a two-sample Kolmogorov–Smirnov test to test that the distributions were statistical distinct.
2.4 Earth system model analysis
Earth system model simulations were drawn from CMIP5, the Coupled Model Intercomparison Project to support the IPCC Fifth Assessment Report (Taylor et al., 2011). We downloaded simulation outputs from the RCP 8.5 scenario, representing the “business-as-usual” scenario, including heterotrophic respiration (rh), soil temperature (tsl), and heterotrophic carbon stock (cSoil and cLitter) from the CMIP5 repository on the Earth System Federation Grid. Ten-year means were taken at the beginning and end of the 21st century for each variable (corresponding to 2006–2015 and 2090–2099). Soil temperature was averaged for the first 10 cm to correspond with experimental soil temperature readings. Soil carbon stock was calculated by adding all heterotrophic-respiration pools (including soil cSoil and litter cLitter) where multiple pools were reported. Soil carbon inputs were calculated from the monthly change in soil carbon stock plus the reported heterotrophic respiration. Model variable summaries can be found in Table S3, and processing code is documented in the Supplement.
These 20 Earth system models are built from previous models which contain 10 distinct soil sub-models (Table 1). The number of soil carbon pools in these ESMs varied from one (INM-CM4) to eight (BCC-CSM1.1), with most models having two to five pools. None of the models reported soil carbon with depth, although GFDL-ESM2G and GFDL-ESM2M document a depth-dependent model. There were three classes of pool structure for these models: independent, where there was no exchange between soil carbon pools; cascade, where pools with faster turnover times passed carbon to pools with slower turnover times; and full-feedback models, where carbon was exchanged between faster and slower pools and vis-versa. In this set of models, two of these soil models were full-feedback models (HadGEM, ISPL-CM), six were cascade pool structure (MRI-ESM1, MIROC-ESM, MPI-ESM, CLM4.0 (CESM1, CCSM4, NorESM1), CanESM2, BCC-CSM1.1), and two were independent pools (GFDL-ESM2, INM-CM4). Only two models documented an explicitly constant Q10 (INM-CM2 and HadGEM2, Q10 = 2), one model documented a soil-temperature-dependent Q10 (CanESM2), four models documented a soil temperature sensitivity from Lloyd and Taylor which behaves very similarly to Q10 = 2 at moderate temperatures (Lloyd and Taylor, 1994), and the remaining three (ISPL-CM5, GFDL-ESM2, BCC-CM1.1) all used a variation of the soil temperature sensitivity proposed in CENTURY (Parton et al., 1987, 1988) which also behaves very similarly to Q10 = 2 at moderate temperatures but declines at high temperatures (Lloyd and Taylor, 1994). The ESMs considered had a single global Q10, or Q10 formula, dependent on soil temperature, uniformly applied to the decay pools. This documented structure should be approached with caution due to frequent lags between model development and documentation; actual values and functions may differ. For details with citations see Table 1.
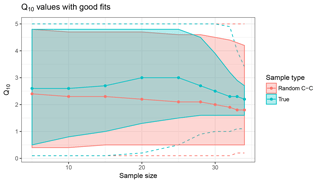
Figure 2The Q10 with good one-to-one model–data fits defined in Fig. 1, at 90 % confidence interval (band) with minimum and maximum values (dotted line) and median value (solid line), across 10 different sample sizes ranging from 5 to 34, for the original data set (true: blue) and randomized case–control (random C-C: red).
Soil carbon stocks at the beginning of Earth system model simulations are typically documented to be spun up to close to steady state, and there is numerical support that this holds throughout the simulation (see Results and Fig. S3 in the Supplement). Thus Eq. (3) can be extended to the change in soil carbon stock over the 21st century. This leads to the following explicit calculation for a Q10 value at each grid cell:
where the Q10 value is related to the modern soil temperature Tm, future soil temperature at the end of the 21st century Tf, modern soil inputs um, future soil inputs uf, modern soil carbon stock Cm, and future soil carbon stock Cf.
For soils that are very close to zero soil carbon stocks, have minimal shifts in soil temperature, or have very low soil inputs, the estimated Q10 is not finite. Similarly soils which are not well described by their shift in soil temperature (for example, if there is a significant shift in the moisture regime) may have non-typical Q10 values that are either less than 0.5 or greater than 5. We examined the amount of shift in soil carbon stocks associated with the four categories of Q10 values (nonfinite, less than 0.5, greater than 5, or typical), as well as the spatial patterns associated with these categories.
To support the assertion that the Q10 value can be calculated from relatively short timescales found in the field experiments, we examined the distribution-typical Q10 values associated with similar soil temperature steps experienced by the field experiments on 1-, 5-, 10-, 15-, 20-, 50-, 75-, and 84-year timescales using 10-year mean gridded values of soil carbon stocks, soil inputs, and soil temperature. It should be noted, however, that changes in the moisture conditions over the 21st century may complicate this analysis of the Earth system model simulations; thus it is not an exact proxy for the field experiments where the control and treatment plots experienced similar baseline climate conditions and a more or less constant offset throughout the experiment.
Finally, the Q10 distribution was scaled to reflect the best estimate and uncertainty from the field data. This distribution shift was done by normalizing the Q10 map to the mean of the distribution and multiplying it by the experimentally derived values. The Q10 correction was only applied to grids with typical Q10's (non-typical Q10's were considered to have predominately non-temperature driving variables, and their soil carbon stocks were not altered). This normalization shifted the global Q10 distribution within the models to match the most common (geographically likely) Q10 with the data-driven Q10 value, yet by preserving the distribution we preserved other factors affecting changes in decomposition rate (i.e., moisture shifts) in the model. We then recalculated the change in soil carbon for each grid cell with this modified Q10 according to Eq. (3) and calculated the global area-weighted totals.
The full analysis script and those used to generate the figures are available in the Supplement.
From the changes in soil carbon stocks across field studies, we find a global Q10 of 2.2 (90 % CI: 1.6, 2.7; R2 > 0.95; root mean squared error < 2; Figs. 1, S2). The model–data fit was evaluated using a linear regression and root mean squared error (Fig. 1). While the R2 of the model–data comparison was relatively insensitive to the Q10 value, there was a notable improvement in the bias with Q10 (as defined as the slope within 2 standard deviations of 1 and intercept within 2 standard deviations of 0). These bias-driven selection criteria were used to select Q10 values from a prior range of (0.1, 5); see Methods for details.
The Q10 distribution was compared with a random null distribution and was significantly distinct (Kolmogorov-Smirnov D = 0.441, p < 2 × 10−16; see Table S2, Figs. 2 and S1). Five to 34 randomly selected sites from the full data set were compared to a null distribution where control vs. warmed labels were randomized. The quartiles of the data subsets notably converged at a sample size of 25, where the null distribution was relatively invariant across sample size (Fig. 2). The distribution of the Q10 values under null appeared lognormal, centered around 1, demonstrating no temperature effect (Fig. S1). The distribution of the Q10 range for the data subsets converged to around 2.2 (Fig. S1).
The balance between gridded soil inputs and heterotrophic respiration at both the initial and final 10-year mean for the 21st century was within 10 % for over 93 % of the grid cells across all models with half of the grid cells within 0.1 %. Most models had 95 % and two models consistently had 100 % of their grid cells within 10 % – the absolute value of the net flux was within 10 % of the highest primary flux (Fig. S3). Thus, the soil inputs are on the same order of magnitude as the soil outputs. This was reflected in very similar Q10 distributions regardless of whether soil inputs or heterotrophic respiration was used to derive the Q10 value (Fig. S4). A notable exception to this was the MIROC-ESM model, which did see differences in inputs and heterotrophic respiration drive different Q10 distributions (Fig. S4).
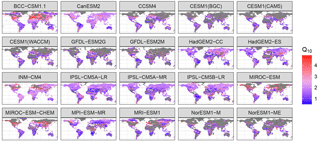
Figure 3Inferred Q10 values from the Earth system models (CMIP5, RCP 8.5). The color scheme is centered around the field-driven Q10 median value of 2.2. Grey indicates non-typical Q10 values that were nonfinite, less than 0.5, or greater then 5.
The inferred Q10 values in the Earth system models derived from 10-year mean changes across different time steps (1, 5, 10, 15, 20, 50, 75, and 84 years) had similar distributions in most of the models (Fig. S4). There were minor shifts in the mode of most models, which could be attributable to changes in the moisture conditions or other (non-temperature or input) environmental variables in the simulation. Models aggregated across common land models showed marked similarity in their Q10 distributions (Fig. S5). There was also an extremely high correlation between Q10 values derived from soil inputs compared to those derived for heterotrophic respiration across all models (Fig. S6).
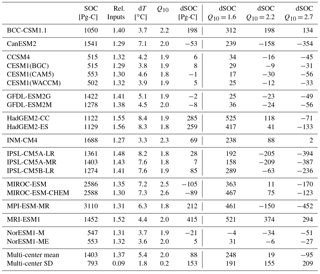
Table 2Global model summary with multi-center mean and standard deviation for modern soil organic carbon (SOC) stocks (Pg-C), relative shift in soil inputs (uf∕um), absolute change in soil temperature (dT) (∘C), inferred mean of Q10 as calculated by grid cell (see Eq. 5), change in soil organic carbon (dSOC) over the 21st century (Pg-C), and change in soil organic carbon with rescaled Q10 values (1.6, 2.2, and 2.7).
The inferred Q10 values in the Earth system models from the decadal average across the 21st century fell into four categories (nonfinite, less than 0.5, greater than 5, or typical; Fig. S7); however most of the change in soil carbon stocks over the 21st century occurred in grid cells with typical Q10 values between 0.5 and 5 (Fig. S6). A notable exception to this trend was the MRI-ESM1 model, where roughly half of the change in carbon stocks occurred in grid cells with Q10 values greater than 5 (Fig. S6). Spatially the Q10 categories showed strong geographical patterns (Fig. S7). The GFDL-ESM2 models were dominated by nonfinite values at high northern latitudes (Fig. S7). MIROC-ESM, CCSM4, CESM1, and NorESM1 models were dominated by Q10 values above 5 at the high northern latitudes (Fig. S7). Unless otherwise noted, only typical Q10 values are addressed for the remainder of this study.
The inferred Q10 values for the decadal average across the 21st century also showed strong geographic patterns (Fig. 3) and were typically unimodal (Fig. S6). MIROC-ESM and MIROC-ESM-CHEM showed the weakest spatial patterns with high grid-to-grid variation (Fig. 3). Mean Q10 values fell within the 90 % CI of the field data Q10, ranging between 1.8 (CESM1(CAM5), HadGEM2-ES, ISPL-CM5A, and MPI-ESM-MR) and 2.6 (MIROC-ESM-CHEM), with the multi-center Q10 values at 2.0 ± 0.2 (Table 2).
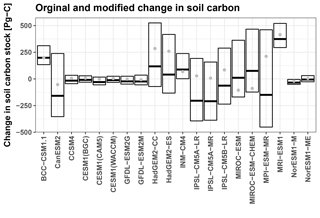
When the inferred Q10 values were modified to reflect the data-driven Q10 range, resulting variation in the multi-center mean was almost as large as the variation across model projections (Fig. 4, Table 2). Re-centering the global Q10 distribution to reflect the range of field-driven Q10 values (Fig. S8) resulted in changes in soil carbon stocks over the 21st century of between −452 Pg carbon (MPI-ESM-MR) and 525 Pg carbon (HadGEM2-CC), with a best-estimate Q10 (Q10 = 2.2) resulting in 19 ± 155 Pg carbon (multi-center mean ± 1 SD) and a field-drive bound (Q10 = 1.6, 2.7) of [248 ± 191, −95 ± 209] Pg carbon (Fig. 4, Table 2).
By capturing information about warming-induced changes to relatively undisturbed field soil carbon stocks directly rather than inferring this from soil respiration rates, this is the first study to generate field Q10 estimates of soil carbon losses without needing to correct for belowground autotrophic respiration. Using a simplified version of a traditional decomposition model with a soil temperature sensitivity function, we estimate that the global Q10 value is 2.2 ([1.6, 2.7] 95 % CI, Figs. 1, S2). This Q10 is notably higher than previous global estimates based on field soil respiration data (Q10 = 1.4 to 1.5; Bond-Lamberty and Thomson, 2010; Mahecha et al., 2010) yet well within the range of estimates from laboratory-based studies (Davidson and Janssens, 2006) as well as close to documented soil temperature sensitivity parameters (∼ 2) of Earth system models (Table 1).
This Q10 range is statistically significant. Resampling the 36-study data set demonstrates the need for over 25 sites to distinguish the Q10 range from random (Figs. 2 and S1). While the Q10 distribution for the 34-study subset is distinct from the null distribution (Kolmogorov-Smirnov D = 0.441; p < 2 × 10−16), there appears to be some minor drift in the range, suggesting that more study sites could be informative, and we hope future studies will include data recently identified (van Gestel et al., 2018).
Inferring decadal-scale environmental sensitivity from an annual-scale experiment is generally controversial. However, in this case, traditional model structures assume a temperature sensitivity function that is invariant across space and time, and numerical trends in the Earth system model reflect this. In the traditional model structure the soil temperature sensitivity function is applied as a single scaler to multi-pool models, causing the relative decomposition response in both fast and slow pools to be the same (for example, Parton et al., 1987). Examining the inferred gridded Q10 values from annual means across timescales from 1 to 84 years in Earth system models shows a strong similarity in the distribution of most models (Fig. S4). Similarly using soil inputs as opposed to heterotrophic respiration did not affect the distribution of the gridded Q10 values, with the notable exception of MIROC-ESM, which is explained by unusual differences in soil inputs and outputs (Figs. S3, S4). Differences in the Q10 distribution across timescales are likely driven then by interaction with other sensitivity functions like moisture or in shifts in the allocation of dead vegetation to different pools as the plant type distribution changes over time.
If soils are more sensitive to warming than previously expected, then how would this affect future soil carbon stocks over the 21st century? To address this question, we turned to the CMIP5 Earth system models run under RCP 8.5 (Taylor et al., 2011). In order to modify the Earth system model output to reflect the data-driven Q10, we applied similar assumptions used in the field data analysis. We first examine the soil temperature sensitivity of soil carbon stocks simulated by CMIP5 Earth system models. In contrast to the field data, we take into account the effect of the change in soil inputs on soil carbon stocks in the Earth system models because these coupled simulations include CO2 fertilization and other climate effects known to influence primary production (see Methods, Eq. 5). Though these inferred Q10 values (Q10 = 1.8, 2.6) fall within the uncertainty of the field-derived Q10 values (Q10 = 1.6, 2.7), most ESM Q10 means fell under the median data Q10 value of 2.2 (Table 2), implying ESMs were, on average, less sensitive to soil temperature shifts than the field-warmed data would imply. It should be noted that this inferred Q10 value is not exactly the parameterized Q10 value but instead a combination of the soil temperature sensitivity and other environmental sensitivities. If there were, on average, an additional constraint on respiration (such as moisture), we might expect the inferred Q10 parameter to be lower than the model-parameterized Q10.
There were notable regional patterns across all but two of the Earth-system-model-inferred Q10's (Figs. 3, S7). High northern latitudes tended to have either large or nonfinite Q10 values, suggesting that something other than soil temperature and input shifts were driving changes in soil carbon stock. This alternative driver could be a shift in moisture regimes or dynamics driven by thaw thresholds, which could similarly affect the analysis of the field data. Additional drivers of soil decomposition dynamics, beyond temperature and inputs considered here, have the potential to explain some of the variation in the Q10 range, and new model structures are being explored to take some of these mechanisms into account (Luo et al., 2015; Wieder et al., 2015a). This remains an active area of research.
Propagating this field Q10 range into the ESM projections resulted in greater carbon losses from the soil by the end of the 21st century (multi-center means of the soil carbon change shifted from 88 to 19 Pg carbon) with large uncertainties; ESM multi-center standard deviation was initially 152 Pg carbon, which is half of the range of the multi-model mean attributed to Q10 95 % CI [248, −95] Pg carbon (Fig. 4, Table 2). To calculate these modified projections, means of the model-specific Q10 distributions were re-centered to reflect the best-estimate Q10 and associated 95 % CI from the field data analysis. By preserving the distribution within the model, we attempted to propagate soil moisture sensitivities and other model-specific effects into the modified projections. We also did not modify grid cells with non-typical Q10 values (nonfinite, below 0.5, or above 5) since those grids likely governed other non-temperature drivers. The large range of carbon shifts in each ESM driven by this Q10 CI confirms the importance of considering parameter uncertainty in the land carbon component of Earth system model projections. The post hoc correction that we present provides an innovative way to account for this parameter variation without the computational burden of additional ensemble runs.
This analysis includes several basic assumptions and caveats. Specifically, we assume that the difference between treatment and control is driven entirely by the soil warming effect, and those warming effects are uniform across soil carbon quality. Though warming-induced changes in soil inputs are, on average, relatively small, they are have been shown to be highly variable at similar sites (Lu et al., 2013). The analysis of field data could be extended to account for these changes in inputs in follow-up studies (Eq. 3). A large increase in soil inputs would cause an underestimation of the Q10 value, while a decrease in soil inputs would cause an overestimation of the Q10 value (see Eq. 3). While there is some evidence to support soil temperature sensitivity dependency on soil carbon quality (Knorr et al., 2005), there is also evidence for a uniform soil temperature sensitivity (Hicks Pries et al., 2017), as is represented in the Earth system models considered in this study (Table 1). A quality-dependent Q10 would not be separable from the bulk decay term, and thus a one-pool model would be inappropriate in this case (see Supplement). In addition, the data set has acknowledged biases (see Crowther et al., 2016), which are typical of field studies.
One-pool simplification
We find that multi-year soil carbon dynamics can be well described by a one-pool model at a specific timescale in both the Earth system models and field experiment. If we restrict the decomposition models to those with either independent or cascade pool structures (that is, no carbon passed from the slow to the fast pools), then the temporal dynamics of the total soil carbon of the system at a specific timescale can be approximated by a single pool due to the fact that the lower triangular decomposition–transfer matrix is diagonalizable (see Supplement for details). While this diagonalizable property does not hold for full-feedback models where carbon is transferred from the slower to faster carbon pools, all decomposition–transfer matrices are M matrices. If we combine the positive-inverse properties resulting from this M matrix structure and assume that the soils are close to metastable state (that is, soil inputs are roughly equal to the heterotrophic respiration outputs, as we show in Fig. S3 for the Earth system models considered and would expect for soils from intact systems), then the total soil carbon can be described by a bulk decay rate that is a linear combination of the transfer coefficients, decay rates, and input allocations of the component pools (see Supplement for analytical details). This provides analytical support for the one-pool simplification seen numerically in the Earth system models in the CMIP5 project (Todd-Brown et al., 2013, 2014).
The one-pool simplifications described above are controversial assertions. The one-pool model has proven inadequate to describe laboratory incubations where heterotrophic respiration over time is compared to the soil carbon stock (Thornton, 1998; Weng and Luo, 2011). This is due to the multiple timescales considered (daily, monthly, and annual) and, more importantly, the fact that these laboratory incubations are by their nature not at steady state since any inputs to the system are generally removed. Thus this analysis would not be expected to hold for laboratory incubation, and we would further expect the bulk decay rate to change with timescales for sites undergoing rapid changes in inputs (in other words, the bulk decay rate inferred at a 1-year time step would not match the 100-year time step at a site undergoing transition from grassland to forest). Another key assumption is that soil organic carbon of different quality responds the same to warming. However, the scalar multiplier representing environmental sensitivities is independent of pools in most models (e.g., Parton et al., 1988). These scalar multiplies (like the Q10 temperature sensitivity examined in this study) would be invariant to the timescale if this modeling assumption were applied to the field analysis. Finally shifts in the allocation of dead vegetation to the different soil pools would shift the bulk decay rate of the one-pool approximation (see Supplement: Analytical proofs). With these caveats in mind, we feel that the one-pool approximation is extremely valuable in analyzing soil carbon models and data.
It is still unclear how the terrestrial carbon cycle in general, and soils in particular, will respond to climate change over the 21st century. The CMIP5 models, representing our best coupled climate models to date, have a wide range of soil carbon responses over the 21st century (Todd-Brown et al., 2014). While it would be nice to have all the models agree on a tightly bound answer, the question we should be asking scientifically is, does the variation in the models reflect our best scientific understanding? Models must capture not only mean trends but also system variance and must accurately represent scientific uncertainty.
Post hoc correction of simulation results can provide some insight into known gaps in Earth system models without the computational hurdle of re-running simulation results. Previous studies have applied post hoc corrections to address nutrient limitations on net primary production (Wieder et al., 2015b), and this study demonstrates the high level of uncertainty that can be driven by the soil temperature response parameter. This study suggests that soil carbon response to warming is highly variable in the field and ESMs should increase their variability to reflect this field variation. Future studies increasing the number of field-warmed studies (van Gestel et al., 2018), as well as extending the field data to include changes in plant productivity in response to warming, would inform the field-derived Q10 analysis explored here. In addition, explaining field moisture and applying that understanding to a post hoc Earth system model analysis is a logical next step.
The code for this study is included in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-15-3659-2018-supplement.
KTB and TWC both contributed to the writing of the manuscript. KTB was responsible for the analysis. TWC coordinated the field data set. BZ was responsible for the mathematical analysis and made contributions to the revisions of the manuscript.
The authors declare that they have no conflict of interest.
We thank Ben Bond-Lamberty and Vanessa Bailey for their reviews of the manuscript before submission, Will Wieder and Mark Bradford for discussions in formulating this analysis, and Donald Jorgensen for his work on the graphical abstract. We would also like to thank the reviewers for their feedback.
Part of the research described in this paper was conducted under the Laboratory Directed Research and Development Program at the Pacific Northwest National Laboratory, a multiprogram national laboratory operated by Battelle for the U.S. Department of Energy; Katherine Todd-Brown is grateful for the support of the Linus Pauling Distinguished Postdoctoral Fellowship program. TWC was supported by a Marie Skłodowska-Curie Action fellowship. Bin Zheng was supported in part by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, as part of the Uncertainty Quantification for Complex Systems project.
We thank the experimentalists who generously made their data available for this analysis.
We acknowledge the World Climate Research Programme's Working Group on
Coupled Modelling, which is responsible for CMIP, and we thank the climate
modeling groups (listed in Table S3) for producing and making available their
model output. For CMIP the U.S. Department of Energy's Program for Climate
Model Diagnosis and Intercomparison provides coordinating support and led
development of software infrastructure in partnership with the Global
Organization for Earth System Science Portals.
Edited by: Michael Weintraub
Reviewed by: Chris Jones, Melanie
Mayes, and three anonymous referees
Adachi, Y., Yukimoto, S., Deushi, M., Obata, A., Nakano, H., Tanaka, T. Y., Hosaka, M., Sakami, T., Yoshimura, H., Hirabara, M., Shindo, E., Tsujino, H., Mizuta, R., Yabu, S., Koshiro, T., Ose, T., and Kitoh, A.: Basic performance of a new earth system model of the Meteorological Research Institute (MRI-ESM1), Pap. Meteorol. Geophys., 64, 1–19, https://doi.org/10.2467/mripapers.64.1, 2013.
Arora, V. K.: Simulating energy and carbon fluxes over winter wheat using coupled land surface and terrestrial ecosystem models, Agr. Forest Meteorol., 118, 21–47, https://doi.org/10.1016/S0168-1923(03)00073-X, 2003.
Arora, V. K. and Boer, G. J.: Uncertainties in the 20th century carbon budget associated with land use change, Glob. Change Biol., 16, 3327–3348, https://doi.org/10.1111/j.1365-2486.2010.02202.x, 2010.
Arora, V. K., Scinocca, J. F., Boer, G. J., Christian, J. R., Denman, K. L., Flato, G. M., Kharin, V. V, Lee, W. G., and Merryfield, W. J.: Carbon emission limits required to satisfy future representative concentration pathways of greenhouse gases, Geophys. Res. Lett., 38, L05805, https://doi.org/10.1029/2010GL046270, 2011.
Bonan, G. B.: A land surface model (LSM version 1.0) for ecological, hydrological and atmospheric studies: technical discription and user's guide, NCAR Tech. note NCAR/TN-417+STR, https://doi.org/10.5065/D6DF6P5X, 1996.
Bond-Lamberty, B. and Thomson, A.: Temperature-associated increases in the global soil respiration record, Nature, 464, 579–582, https://doi.org/10.1038/nature08930, 2010.
Booth, B. B. B., Jones, C. D., Collins, M., Totterdell, I. J., Cox, P. M., Sitch, S., Huntingford, C., Betts, R. A., Harris, G. R., and Lloyd, J.: High sensitivity of future global warming to land carbon cycle processes, Environ. Res. Lett., 7, 24002, https://doi.org/10.1088/1748-9326/7/2/024002, 2012.
Bradford, M. A., Wieder, W. R., Bonan, G. B., Fierer, N., Raymond, P. A., and Crowther, T. W.: Managing uncertainty in soil carbon feedbacks to climate change, Nat. Clim. Chang., 6, 751–758, https://doi.org/10.1038/nclimate3071, 2016.
Cao, M. and Woodward, F. I.: Net primary and ecosystem production and carbon stocks of terrestrial ecosystems and their responses to climate change, Glob. Change Biol., 4, 185–198, https://doi.org/10.1046/j.1365-2486.1998.00125.x, 1998.
Carey, J. C., Tang, J., Templer, P. H., Kroeger, K. D., Crowther, T. W., Burton, A. J., Dukes, J. S., Emmett, B., Frey, S. D., Heskel, M. A., Jiang, L., Machmuller, M. B., Mohan, J., Panetta, A. M., Reich, P. B., Reinsch, S., Wang, X., Allison, S. D., Bamminger, C., Bridgham, S., Collins, S. L., de Dato, G., Eddy, W. C., Enquist, B. J., Estiarte, M., Harte, J., Henderson, A., Johnson, B. R., Larsen, K. S., Luo, Y., Marhan, S., Melillo, J. M., Peñuelas, J., Pfeifer-Meister, L., Poll, C., Rastetter, E., Reinmann, A. B., Reynolds, L. L., Schmidt, I. K., Shaver, G. R., Strong, A. L., Suseela, V., and Tietema, A.: Temperature response of soil respiration largely unaltered with experimental warming, P. Natl. Acad. Sci. USA, 113, 13797–13802, https://doi.org/10.1073/pnas.1605365113, 2016.
Coleman, K. and Jenkinson, D. S.: ROTHC-26.3, A model for the turnover of carbon in soils, Model Descr. Wind. user Guid., available at: http://www.rothamsted.ac.uk/ssgs/RothC/mod26_3_win.pdf, 1999.
Collins, W. J., Bellouin, N., Doutriaux-Boucher, M., Gedney, N., Halloran, P., Hinton, T., Hughes, J., Jones, C. D., Joshi, M., Liddicoat, S., Martin, G., O'Connor, F., Rae, J., Senior, C., Sitch, S., Totterdell, I., Wiltshire, A., and Woodward, S.: Development and evaluation of an Earth-System model – HadGEM2, Geosci. Model Dev., 4, 1051–1075, https://doi.org/10.5194/gmd-4-1051-2011, 2011.
Cox, P.: Discription of “TRIFFID” Dynamic Global Vegetation Model, Hadley Centre technical note 24, London Road, Bracknell, Berks R12 2SY, UK, available at: http://climate.uvic.ca/model/common/HCTN_24.pdf (last access: 8 June 2018), 2001.
Crowther, T. W., Todd-Brown, K. E. O., Rowe, C. W., Wieder, W. R., Carey, J. C., Machmuller, M. B., Snoek, B. L., Fang, S., Zhou, G., Allison, S. D., Blair, J. M., Bridgham, S. D., Burton, A. J., Carrillo, Y., Reich, P. B., Clark, J. S., Classen, A. T., Dijkstra, F. A., Elberling, B., Emmett, B. A., Estiarte, M., Frey, S. D., Guo, J., Harte, J., Jiang, L., Johnson, B. R., Kröel-Dulay, G., Larsen, K. S., Laudon, H., Lavallee, J. M., Luo, Y., Lupascu, M., Ma, L. N., Marhan, S., Michelsen, A., Mohan, J., Niu, S., Pendall, E., Peñuelas, J., Pfeifer-Meister, L., Poll, C., Reinsch, S., Reynolds, L. L., Schmidt, I. K., Sistla, S., Sokol, N. W., Templer, P. H., Treseder, K. K., Welker, J. M., and Bradford, M. A.: Quantifying global soil carbon losses in response to warming, Nature, 540, 104–108, https://doi.org/10.1038/nature20150, 2016.
Davidson, E. A. and Janssens, I. A.: Temperature sensitivity of soil carbon decomposition and feedbacks to climate change, Nature, 440, 165–173, https://doi.org/10.1038/nature04514, 2006.
Davidson, E. A., Belk, E., and Boone, R. D.: Soil water content and temperature as independent or confounded factors controlling soil respiration in a temperate mixed hardwood forest, Glob. Change Biol., 4, 217–227, https://doi.org/10.1046/j.1365-2486.1998.00128.x, 1998.
Davidson, E. A., Janssens, I. A., and Luo, Y.: On the variability of respiration in terrestrial ecosystems: moving beyond Q10, Glob. Change Biol., 12, 154–164, https://doi.org/10.1111/j.1365-2486.2005.01065.x, 2006.
Dufresne, J. L., Foujols, M. A., Denvil, S., Caubel, A., Marti, O., Aumont, O., Balkanski, Y., Bekki, S., Bellenger, H., Benshila, R., Bony, S., Bopp, L., Braconnot, P., Brockmann, P., Cadule, P., Cheruy, F., Codron, F., Cozic, A., Cugnet, D., de Noblet, N., Duvel, J. P., Ethé, C., Fairhead, L., Fichefet, T., Flavoni, S., Friedlingstein, P., Grandpeix, J. Y., Guez, L., Guilyardi, E., Hauglustaine, D., Hourdin, F., Idelkadi, A., Ghattas, J., Joussaume, S., Kageyama, M., Krinner, G., Labetoulle, S., Lahellec, A., Lefebvre, M. P., Lefevre, F., Levy, C., Li, Z. X., Lloyd, J., Lott, F., Madec, G., Mancip, M., Marchand, M., Masson, S., Meurdesoif, Y., Mignot, J., Musat, I., Parouty, S., Polcher, J., Rio, C., Schulz, M., Swingedouw, D., Szopa, S., Talandier, C., Terray, P., Viovy, N., and Vuichard, N.: Climate change projections using the IPSL-CM5 Earth System Model: From CMIP3 to CMIP5, Clim. Dynam., 40, 2123–2165, https://doi.org/10.1007/s00382-012-1636-1, 2013.
Dunne, J. P., John, J. G., Shevliakova, E., Stouffer, R. J., Krasting, J. P., Malyshev, S. L., Milly, P. C. D., Sentman, L. T., Adcroft, A. J., Cooke, W., Dunne, K. A., Griffies, S. M., Hallberg, R. W., Harrison, M. J., Levy, H., Wittenberg, A. T., Phillips, P. J., and Zadeh, N.: GFDL's ESM2 Global Coupled Climate–Carbon Earth System Models. Part II: Carbon System Formulation and Baseline Simulation Characteristics*, J. Climate, 26, 2247–2267, https://doi.org/10.1175/JCLI-D-12-00150.1, 2013.
Friedlingstein, P., Meinshausen, M., Arora, V. K., Jones, C. D., Anav, A., Liddicoat, S. K., and Knutti, R.: Uncertainties in CMIP5 climate projections due to carbon cycle feedbacks, J. Climate, 27, 511–526, https://doi.org/10.1175/JCLI-D-12-00579.1, 2014.
Gent, P. R., Danabasoglu, G., Donner, L. J., Holland, M. M., Hunke, E. C., Jayne, S. R., Lawrence, D. M., Neale, R. B., Rasch, P. J., Vertenstein, M., Worley, P. H., Yang, Z.-L., and Zhang, M.: The Community Climate System Model version 4, J. Climate, 24, 4973–4991, https://doi.org/10.1175/2011JCLI4083.1, 2011.
Giorgetta, M. A., Jungclaus, J., Reick, C. H., Legutke, S., Bader, J., Böttinger, M., Brovkin, V., Crueger, T., Esch, M., Fieg, K., Glushak, K., Gayler, V., Haak, H., Hollweg, H.-D., Ilyina, T., Kinne, S., Kornblueh, L., Matei, D., Mauritsen, T., Mikolajewicz, U., Mueller, W., Notz, D., Pithan, F., Raddatz, T., Rast, S., Redler, R., Roeckner, E., Schmidt, H., Schnur, R., Segschneider, J., Six, K. D., Stockhause, M., Timmreck, C., Wegner, J., Widmann, H., Wieners, K.-H., Claussen, M., Marotzke, J., and Stevens, B.: Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the Coupled Model Intercomparison Project phase 5, J. Adv. Model. Earth Sy., 5, 572–597, https://doi.org/10.1002/jame.20038, 2013.
Hashimoto, S., Carvalhais, N., Ito, A., Migliavacca, M., Nishina, K., and Reichstein, M.: Global spatiotemporal distribution of soil respiration modeled using a global database, Biogeosciences, 12, 4121–4132, https://doi.org/10.5194/bg-12-4121-2015, 2015.
Hicks Pries, C. E., Castanha, C., Porras, R. C., and Torn, M. S.: The whole-soil carbon flux in response to warming, Science, 355, 1420–1423, https://doi.org/10.1126/science.aal1319, 2017.
Ji, J., Huang, M., and Li, K.: Prediction of carbon exchanges between China terrestrial ecosystem and atmosphere in 21st century, Sci. China Ser. D, 51, 885–898, https://doi.org/10.1007/s11430-008-0039-y, 2008.
Jones, C. and Cox, P. M.: Constraints on the temperature sensitivity of global soil respiration from the observed interannual variability in atmospheric CO2, Atmos. Sci. Lett., 2, 166–172, https://doi.org/10.1006/asle.2001.0041, 2001.
Jones, C. D., Cox, P. M., and Huntingford, C.: Climate-carbon cycle feedbacks under stabilization: uncertainty and observational constraints, Tellus B, 58, 603–613, https://doi.org/10.1111/j.1600-0889.2006.00215.x, 2006.
Knorr, W., Prentice, I. C., House, J. I., and Holland, E. A.: Long-term sensitivity of soil carbon turnover to warming, Nature, 433, 298–301, https://doi.org/10.1038/nature03226, 2005.
Krinner, G., Viovy, N., de Noblet-Ducoudré, N., Ogée, J., Polcher, J., Friedlingstein, P., Ciais, P., Sitch, S., and Prentice, I. C.: A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system, Global Biogeochem. Cy., 19, GB1015, https://doi.org/10.1029/2003GB002199, 2005.
Lawrence, D. M., Oleson, K. W., Flanner, M. G., Thornton, P. E., Swenson, S. C., Lawrence, P. J., Zeng, X., Yang, Z.-L., Levis, S., Sakaguchi, K., Bonan, G. B., and Slater, A. G.: Parameterization improvements and functional and structural advances in Version 4 of the Community Land Model, J. Adv. Model. Earth Sy., 3, M03001, https://doi.org/10.1029/2011MS000045, 2011.
Lloyd, J. and Taylor, J. A.: On the temperature dependence of soil respiration, Funct. Ecol., 8, 315–323, 1994.
Lu, M., Zhou, X., Yang, Q., Li, H., Luo, Y., Fang, C., Chen, J., Yang, X., and Li, B.: Responses of ecosystem carbon cycle to experimental warming: a meta-analysis, Ecology, 94, 726–738, https://doi.org/10.1890/12-0279.1, 2013.
Luo, Y., Ahlström, A., Allison, S. D., Batjes, N. H., Brovkin, V., Carvalhais, N., Chappell, A., Ciais, P., Davidson, E. A., Finzi, A., Georgiou, K., Guenet, B., Hararuk, O., Harden, J. W., He, Y., Hopkins, F., Jiang, L., Koven, C., Jackson, R. B., Jones, C. D., Lara, M. J., Liang, J., McGuire, A. D., Parton, W., Peng, C., Randerson, J. T., Salazar, A., Sierra, C. A., Smith, M. J., Tian, H., Todd-Brown, K. E. O., Torn, M., van Groenigen, K. J., Wang, Y. P., West, T. O., Wei, Y., Wieder, W. R., Xia, J., Xu, X., Xu, X., and Zhou, T.: Towards More Realistic Projections of Soil Carbon Dynamics by Earth System Models, Global Biogeochem. Cy., 30, 40–56, https://doi.org/10.1002/2015GB005239, 2015.
Mahecha, M. D., Reichstein, M., Carvalhais, N., Lasslop, G., Lange, H., Seneviratne, S. I., Vargas, R., Ammann, C., Arain, M. A., Cescatti, A., Janssens, I. A., Migliavacca, M., Montagnani, L., and Richardson, A. D.: Global convergence in the temperature sensitivity of respiration at ecosystem level, Science, 329, 838–840, https://doi.org/10.1126/science.1189587, 2010.
Moorcroft, P. R., Hurtt, G. C., and Pacala, S. W.: A method for scaling vegetation dynamics: The ecosystem demography model (ED), Ecol. Monogr., 71, 557–586, https://doi.org/10.2307/3100036, 2001.
Obata, A. and Shibata, K.: Damage of Land Biosphere due to Intense Warming by 1000-Fold Rapid Increase in Atmospheric Methane: Estimation with a Climate–Carbon Cycle Model, J. Climate, 25, 8524–8541, https://doi.org/10.1175/JCLI-D-11-00533.1, 2012.
Oleson, K. W., Lawrence, D. M., Bonan, G. B., Flanner, M. G., Kluzek, E., Lawrence, P. J., Levis, S., Swenson, S. C., and Thornton, P. E.: Technical Description of version 4.0 of the Community Land Model (CLM), NCAR Technical Note NCAR/TN-478+STR, https://doi.org/10.5065/D6FB50WZ, 2010.
Oleson, K. W., Lawrence, D. M., Bonan, G. B., Drewniak, B., Huang, M., Koven, C. D., Levis, S., Li, F., Riley, W. J., Subin, Z. M., Swenson, S. C., Thornton, P. E., Bozbiyik, A., Fisher, R., Heald, C. L., Kluzek, E., Lamarque, J.-F., Lawrence, P. J., Leung, L. R., Lipscomb, W., Muszala, S., Ricciuto, D. M., Sacks, W., Sun, Y., Tang, J., and Yang, Z.-L.: Technical Description of version 4.5 of the Community Land Model (CLM), 2013.
Parton, W. J., Schimel, D. S., Cole, C. V., and Ojima, D. S.: Analysis of factors controlling soil organic matter levels in great plains grasslands, Soil Sci. Soc. Am. J., 51, 1173–1179, https://doi.org/10.2136/sssaj1987.03615995005100050015x, 1987.
Parton, W. J., Stewart, J. W. B., and Cole, C. V.: Dynamics of C, N, P and S in grassland soils: a model, Biogeochemistry, 5, 109–131, https://doi.org/10.1007/BF02180320, 1988.
Raddatz, T. J., Reick, C. H., Knorr, W., Kattge, J., Roeckner, E., Schnur, R., Schnitzler, K.-G. G., Wetzel, P., and Jungclaus, J.: Will the tropical land biosphere dominate the climate-carbon cycle feedback during the twenty-first century?, Clim. Dynam., 29, 565–574, https://doi.org/10.1007/s00382-007-0247-8, 2007.
Sato, H., Itoh, A., and Kohyama, T.: SEIB–DGVM: A new dynamic global vegetation model using a spatially explicit individual-based approach, Ecol. Model., 200, 279–307, https://doi.org/10.1016/j.ecolmodel.2006.09.006, 2007.
Schneck, R., Reick, C. H., and Raddatz, T.: Land contribution to natural CO2 variability on time scales of centuries, J. Adv. Model. Earth Sy., 5, 354–365, https://doi.org/10.1002/jame.20029, 2013.
Shevliakova, E., Pacala, S. W., Malyshev, S., Hurtt, G. C., Milly, P. C. D., Caspersen, J. P., Sentman, L. T., Fisk, J. P., Wirth, C., and Crevoisier, C.: Carbon cycling under 300 years of land use change: Importance of the secondary vegetation sink, Global Biogeochem. Cy., 23, GB2022, https://doi.org/10.1029/2007GB003176, 2009.
Sitch, S., Smith, B., Prentice, I. C., Arneth, A., Bondeau, A., Cramer, W., Kaplan, J. O., Levis, S., Lucht, W., Sykes, M. T., Thonicke, K., and Venevsky, S.: Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model, Glob. Change Biol., 9, 161–185, https://doi.org/10.1046/j.1365-2486.2003.00569.x, 2003.
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An overview of CMIP5 and the experiment design, B. Am. Meteorol. Soc., 93, 485–498, https://doi.org/10.1175/BAMS-D-11-00094.1, 2011.
Thornton, P. E.: Regional ecosystem simulation: combining surface- and satellite-based observations to study linkages between terrestrial energy and mass budgets, Univ. of Montana, Missoula., 1998.
Thornton, P. E. and Rosenbloom, N. A.: Ecosystem model spin-up: Estimating steady state conditions in a coupled terrestrial carbon and nitrogen cycle model, Ecol. Model., 189, 25–48, https://doi.org/10.1016/j.ecolmodel.2005.04.008, 2005.
Thornton, P. E., Lamarque, J.-F., Rosenbloom, N. A., and Mahowald, N. M.: Influence of carbon-nitrogen cycle coupling on land model response to CO2 fertilization and climate variablity, Global Biogeochem. Cy., 21, GB4018, https://doi.org/10.1029/2006GB002868, 2007.
Tjiputra, J. F., Roelandt, C., Bentsen, M., Lawrence, D. M., Lorentzen, T., Schwinger, J., Seland, Ø., and Heinze, C.: Evaluation of the carbon cycle components in the Norwegian Earth System Model (NorESM), Geosci. Model Dev., 6, 301–325, https://doi.org/10.5194/gmd-6-301-2013, 2013.
Todd-Brown, K. E. O., Randerson, J. T., Post, W. M., Hoffman, F. M., Tarnocai, C., Schuur, E. A. G., and Allison, S. D.: Causes of variation in soil carbon simulations from CMIP5 Earth system models and comparison with observations, Biogeosciences, 10, 1717–1736, https://doi.org/10.5194/bg-10-1717-2013, 2013.
Todd-Brown, K. E. O., Randerson, J. T., Hopkins, F., Arora, V., Hajima, T., Jones, C., Shevliakova, E., Tjiputra, J., Volodin, E., Wu, T., Zhang, Q., and Allison, S. D.: Changes in soil organic carbon storage predicted by Earth system models during the 21st century, Biogeosciences, 11, 2341–2356, https://doi.org/10.5194/bg-11-2341-2014, 2014.
Townsend, A. R., Vitousek, P. M., Desmarais, D. J., and Tharpe, A.: Soil carbon pool structure and temperature sensitivity inferred using CO2 and 13CO2 incubation fluxes from five Hawaiian soils, Biogeochemistry, 38, 1–17, https://doi.org/10.1023/A:1017942918708, 1997.
van Gestel, N., Shi, Z., van Groenigen, K. J., Osenberg, C. W., Andresen, L. C., Dukes, J. S., Hovenden, M. J., Luo, Y., Michelsen, A., Pendall, E., Reich, P. B., Schuur, E. A. G., and Hungate, B. A.: Predicting soil carbon loss with warming, Nature, 554, E4–E5, https://doi.org/10.1038/nature25745, 2018.
Volodin, E. M.: Atmosphere-ocean general circulation model with the carbon cycle, Izv. Atmos. Ocean. Phys., 43, 266–280, https://doi.org/10.1134/S0001433807030024, 2007.
Watanabe, S., Hajima, T., Sudo, K., Nagashima, T., Takemura, T., Okajima, H., Nozawa, T., Kawase, H., Abe, M., Yokohata, T., Ise, T., Sato, H., Kato, E., Takata, K., Emori, S., and Kawamiya, M.: MIROC-ESM 2010: model description and basic results of CMIP5-20c3m experiments, Geosci. Model Dev., 4, 845–872, https://doi.org/10.5194/gmd-4-845-2011, 2011.
Weng, E. and Luo, Y.: Relative information contributions of model vs. data to short- and long-term forecasts of forest carbon dynamics, Ecol. Appl., 21, 1490–1505, https://doi.org/10.1890/09-1394.1, 2011.
Wieder, W. R., Allison, S. D., Davidson, E. A., Georgiou, K., Hararuk, O., He, Y., Hopkins, F., Luo, Y., Smith, M. J., Sulman, B., Todd-Brown, K., Wang, Y.-P., Xia, J., and Xu, X.: Explicitly representing soil microbial processes in Earth system models, Global Biogeochem. Cy., 29, 1782–1800, https://doi.org/10.1002/2015GB005188, 2015a.
Wieder, W. R., Cleveland, C. C., Smith, W. K., and Todd-Brown, K.: Future productivity and carbon storage limited by terrestrial nutrient availability, Nat. Geosci., 8, 441–444, https://doi.org/10.1038/ngeo2413, 2015b.
Wu, T., Li, W., Ji, J., Xin, X., Li, L., Wang, Z., Zhang, Y., Li, J., Zhang, F., Wei, M., Shi, X., Wu, F., Zhang, L., Chu, M., Jie, W., Liu, Y., Wang, F., Liu, X., Li, Q., Dong, M., Liang, X., Gao, Y., and Zhang, J.: Global carbon budgets simulated by the Beijing Climate Center Climate System Model for the last century, J. Geophys. Res.-Atmos., 118, 1–22, https://doi.org/10.1002/jgrd.50320, 2013.
- Article
(672 KB) - Full-text XML