the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
Evaluating the effect of nutrient redistribution by animals on the phosphorus cycle of lowland Amazonia
Corina Buendía
Axel Kleidon
Stefano Manzoni
Björn Reu
Amilcare Porporato
Phosphorus (P) availability decreases with soil age and potentially limits the productivity of ecosystems growing on old and weathered soils. Despite growing on ancient soils, ecosystems of lowland Amazonia are highly productive and are among the most biodiverse on Earth. P eroded and weathered in the Andes is transported by the rivers and deposited in floodplains of the lowland Amazon basin creating hotspots of P fertility. We hypothesize that animals feeding on vegetation and detritus in these hotspots may redistribute P to P-depleted areas, thus contributing to dissipate the P gradient across the landscape. Using a mathematical model, we show that animal-driven spatial redistribution of P from rivers to land and from seasonally flooded to terra firme (upland) ecosystems may sustain the P cycle of Amazonian lowlands. Our results show how P imported to land by terrestrial piscivores in combination with spatial redistribution of herbivores and detritivores can significantly enhance the P content in terra firme ecosystems, thereby highlighting the importance of food webs for the biogeochemical cycling of Amazonia.
- Article
(3199 KB) -
Supplement
(49 KB) - BibTeX
- EndNote
1.1 The phosphorus biogeochemical cycle
Phosphorus (P) is a crucial element for life, providing structure to RNA and DNA and with a key function in energy transfer and storage (ATP and ADP). In general, weathering is the main source of P to terrestrial ecosystems. Theories on pedogenesis suggest that under humid climates and slow tectonic uplift, rock weathering becomes negligible, preventing input of “fresh” phosphorous to the biosphere (Chadwick et al., 1999; Crews et al., 1995; Walker and Syers, 1976; Wardle, 2004; Wardle et al., 2009). Under such conditions, without major disturbances (e.g., glaciation resetting soil development), P availability and with it net primary productivity decrease, leading to a so-called retrogressive phase (Wardle, 2004; Wardle et al., 2009) or terminal steady-state (Walker and Syers, 1976). However, despite their ∼ 100-million-year-old soils (Hoorn et al., 2010), some ecosystems in the lower Amazonian basin are among the most diverse and productive on Earth (Gentry, 1992). This raises the question as to what prevents Amazon ecosystems from falling into a retrogressive phase or terminal steady-state?
1.2 Amazon basin
The Amazon basin is one of the most biodiverse regions on Earth, including highly productive ecosystems, essential to the regulation of the global climate system. It extends over about 7 million km2, 13 % of which is covered by the Andes, while the rest is characterized by relatively flat topography. Over millions of years, the topographical gradient has resulted in a gradient of soil fertility from young and nutrient-rich Andean soils to ancient and highly weathered soils in the central and lower Amazon basin (Hoorn et al., 2010). Consequently, rivers originating in the Andes (called “white water rivers”) transport nutrient-rich sediments, whereas rivers originating in the lowlands tend to be nutrient poor (“black water rivers” if they carry organic acids and “clear water rivers” if they do not). River floodplains cover about 30 % of the basin (Junk et al., 2011b); ecosystems that are seasonally flooded by white waters are traditionally called várzea and are characterized by a high primary productivity and tree diversity (Wittmann et al., 2006), as compared to the ecosystems seasonally flooded by clear or black waters, which are called igapó. Because of nutrient transport by the white water rivers, an even steeper nutrient availability gradient exists between várzea and the terra firme ecosystems, which do not receive nutrients from seasonal floods. As the Amazon River is on the Equator, its sub-basins exhibit different seasonality, with rainy season and high waters occurring during each hemispheric summer, that is May–August north of the Equator and November–February south of Equator. Not only differences in nutrients but also differences in precipitation result in diversity among Amazon ecosystems, such as seasonally flooded rainforests, terra firme rainforests, dry forests, wetlands, and tropical savannas (Cerrado). In the lower part of the Amazon where water is less limiting, these ecosystems sustain a particularly high productivity and diversity of life forms (Antonelli and Sanmartín, 2011; Gentry, 1992).
1.3 P dynamics in the lowland Amazon basin
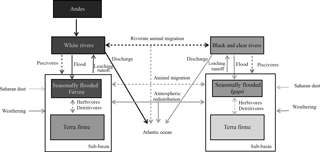
Figure 1Conceptual diagram of processes transferring P within the Amazon basin's ecosystems. Conceptual diagram of processes transferring P across ecosystems in the Amazon basin. The boxes represent the major ecoregions of Amazonia and dashed arrows represent animal-driven fluxes and solid arrows represent abiotic-driven fluxes. The grey tone represents the P content of these ecoregions from dark (high P content) to light tones (lower P content).
Here we shortly review the main processes contributing to the P budget of lowland Amazonian ecosystems as illustrated in Fig. 1. We start by discussing the inputs from the bedrock by weathering and then the likelihood that deocclusion of P in clays could serve as a long-term P source. Later, we discuss exogenous P input fluxes – first those mediated by the atmosphere and then those mediated by rivers – and finally how these inputs could reach seasonally flooded and terra firme ecosystems.
1.3.1 Weathering
Weathering in the central Amazon basin was estimated to be about 75 based on data taken at the mouth of Rio Negro river, which is an important tributary of the Amazon River draining only the lowlands (Gardner, 1990). This measurement contrast to trends observed in soil chronosequences like the Hawaiin Islands and Franz Joseph Glacier retrogression (Walker and Syers, 1976; Wardle, 2004; Wardle et al., 2009), where at terminal steady state no weathering is detectable. The Amazon basin experiences continental isostatic rebound, where the slow erosion rates are compensated by slow uplift and weathering of new material (Buendía et al., 2010; Porder et al., 2007). However, because bedrock can be as deep as 100 m, it is not clear whether or not P released by weathering can reach the terrestrial biotic cycle (Gardner, 1990). Nevertheless, as dissolved P reaches the rivers by groundwater flow, it can be used by freshwater ecosystems and redistributed across sub-basins with floods.
1.3.2 P deocclusion
High amounts of P are found in occluded forms in the old soils of central Amazon. Life has evolved energetically costly mechanisms, like cluster roots and mycorrhizal associations to make some of this P available to vegetation (Lambers et al., 2008). In a previous paper (Buendía et al., 2014) this possibility was explored by formulating a model that in a simple but explicit way, accounts for physical and chemical weathering, secondary mineral formation, P occlusion, and P deocclusion at a carbon cost. Our modeling study suggests that because Amazonian soils are very old and the pool of occluded P is finite, it cannot support the ecosystems in the long run. Nevertheless, it can act as a reserve of P for the ecosystems.
1.3.3 Atmospheric inputs
Dust originating from African deserts carry P to the Amazon basin, but this contribution is highly uncertain, spanning 2 orders of magnitude, from 4.8 (Mahowald et al., 2005) to 11–47 (Swap et al., 1992) and 125–426.47 (Bristow et al., 2010). Dust comprises only about 7 to 17 % of atmospheric deposition, while a much larger fraction is composed of biogenic particles (83–90 %) originating from the Amazon basin itself.
1.4 Redistribution of P within the Amazon basin
1.4.1 P redistribution between and within sub-basins
Biogenic particles, such as pollen, spores, bacteria, algae, protozoa, fungi, and leaf fragments, are generated by the forest and although to a great extent most of them are deposited in the forest again, some (about 19 ) fall into the Atlantic Ocean (Mahowald et al., 2005), where they become an important nutrient source to Atlantic marine ecosystems near the continent. Fires caused by the amplification of the agricultural frontier also contribute to the internal P redistribution and export (Artaxo and Hansson, 1994; Mahowald et al., 2005; Pauliquevis et al., 2012). Therefore, according to some of these estimates, the atmosphere could even drive more P losses than inputs to whole Amazon basin.
In addition to abiotic-driven P fluxes, migratory animals, like fish, caimans, turtles, and birds, migrate on a seasonal basis between the Andean-influenced white waters to P-deficient lowland black and clear waters. Animal migration thus results in a redistribution of nutrients within and across different sub-basins. This connection between sub-basins is well studied for some catfish species and has been shown to be significant but difficult to quantify for the clear and black water sub-basins (McClain and Naiman, 2008; Barthem and Goulding, 1997).
1.4.2 P redistribution between riverine and terrestrial ecosystems
Junk et al. (2011a) estimated that 30 % of the Amazon basin complies with international criteria for wetland definition. Rivers seasonally flood wide lowland areas, providing sediments and P inputs – a concept referred to as “flood pulse” (Junk, 1997; Junk et al., 1989). Despite flood pulses being well documented (Junk, 1997; Junk et al., 1989, 2011a), it is difficult to quantify the magnitude of this P flux as it varies depending on the flooding intensity, type of sediments and suspended matter transported, soil type, and the functional composition of the várzea and igapó ecosystems.

Figure 2Painting illustrating the fauna that can be observed near the Miritî, a black water tributary of the Caquetá river. The upper half-sphere represents the dry season, when most of the terrestrial animals are present in this area. The lower half-sphere represents rainy season, when animals move deep into the terra firme forest or to the head waters. With the beginning of the dry season animals feed on what remained from the flood and some species (turtles and caimans) lay their eggs, which are often consumed by terrestrial animals. This original water painting was illustrated by Marcela and Johana Yucuna, indigenous of the Yucuna ethnic group from the Mirití region (Caquetá, Colombia). The painting is reproduced with the permission of the artist.
Within the sub-basins, P may be transported from aquatic to terrestrial ecosystems by animals feeding on riverine food sources, terrestrial piscivores like the jaguar, the giant otter, and fishing birds. Figure 2 presents an illustration of the different animals that can be seen during the dry (lower half) and wet (upper half) seasons in a black water rivers, as perceived by indigenous people of the Rio Negro sub-basin. For example, an adult giant otter (Pteronura brasiliensis) consumes about 3 kg of fish per day (Carter and Rosas, 1997). Assuming fish dry weight is 20 % and P content of fish at about 1.1–4.5 % (Sterner and Elser, 2002), an adult otter could transfer about 6.6–27 g P per day to terrestrial ecosystems (2409–9855 g P a−1). Using the population density reported for Suriname, of 1.2 individuals per km−2 (Duplaix et al., 2008), giant otters could contribute about 28–118 . Although this species is listed as endangered, currently there are no population density estimates available and it is likely that population sizes have been larger than those observed today.
1.4.3 P redistribution between and within seasonally flooded and terra firme ecosystems
P transport by and around rivers can be complemented by terrestrial animals including soil fauna, insects, and mammals that frequently utilize both seasonally flooded and terra firme habitats (see Fig. 2). The movement between habitats further enhances the P redistribution potential on finer spatial scales. In other words, animal movement generates a net transport of P from relatively nutrient-rich to relatively nutrient-poor areas, analogous to a diffusion process, but acting against the gradients of physical flow processes driven by topographic relief. For example, in a study of a woolly monkey (Lagothrix lagotricha lugens) population in northwestern Amazon, Stevenson and Guzmán-Caro (2010) showed that this population could import about 1–4 from lowland to uplands through seed dispersal. A model based on animal movement as an agent of P redistribution illustrated how megafauna before the Pleistocene extinction could have sustained P cycling in this basin (Doughty et al., 2013).
However, it has not been demonstrated that entire ecosystems involving different trophic levels can achieve a net P redistribution effect in a similar manner as large herbivores. Here we show, using a simple mathematical framework, that P from seasonally flooded ecosystems can be redistributed from the floodplains, enriching P-poor terra firme ecosystems. Because the model accounts for different transport pathways, including contrasting animal foraging strategies (piscivory, herbivory, and detritivory) in a minimal parameterization, it allows us to evaluate the relative importance of different redistribution mechanisms.
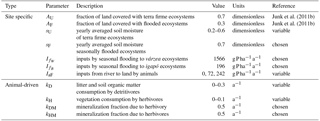
Due to the high complexity of food webs and biotic interactions, it is impossible to consider all P fluxes driven by animal migration and movement and the differences across ecosystems. Therefore, it is our objective to quantitatively evaluate the importance of the different redistribution mechanisms using a spatially lumped model synthesizing the major processes of P cycling, including P redistribution by animals (Fig. 1). As a first approximation, rather than focusing on a single mode of transport (as in Doughty et al., 2013), we consider two foraging strategies of consumer animals – herbivory and detritivory. Both strategies allow the spatial redistribution of P. To assess the importance of biomass consumption by animals on P redistribution under different environmental settings, we parameterized our model for three contrasting Amazonian lowland sub-basins, each subdivided into seasonally flooded (P-richer várzea or P-poorer igapó) and terra firme areas: (1) the Caquetá-Japurá sub-basin, a white water river rich in Andean sediments and hence relatively rich in P; (2) the Rio Negro sub-basin, a lowland black water tributary of the Amazon River which is regarded as P-poor; and (3) the Xingu sub-basin, a lowland clear water tributary draining Cerrados, a dry tropical savanna ecosystem seasonally flooded by P-poor clear waters. By doing so, we account for the main environmental variability affecting our model results, such as differences in P load of the flooding river (white waters vs. black and clear waters) and differences in soil moisture regime affecting the P losses from the ecosystem (dry vs. humid).
The model includes a “local” P cycling module (based on Buendía et al., 2010), a description of plant–animal and detritus–animal interactions, and an animal-driven P redistribution mechanism between seasonally flooded and terra firme ecosystems. The local module, indicated by an E subscript to identify a specific ecosystem type, consists of six ordinary differential equations representing the dynamics of weatherable material, secondary minerals, occluded P, P in available forms (PdE), P in vegetation biomass (PvE), and P in soil and litter biomass (PoE). All P stocks and fluxes are normalized by the area of the corresponding ecosystem (here we use the fractional areas AF and AU for flooded and terra firme ecosystems, respectively). The model uses annually averaged soil moisture content to characterize water availability, and the processes are interpreted on the annual timescale. Since animal dynamics are much faster than weathering and occlusion, it is safe to assume that animal pools are in quasi-equilibrium, whereas weathered P, occluded P, and P in secondary minerals are at steady state, thereby reducing the number of equations in the local module from six to three. We parameterized the system for seasonally flooded (F) and terra firme (or upland, U) ecosystems, coupling these two ecosystems through two biotic P fluxes representing the effect of herbivores (H) and detritivores (D; refer to Fig. 3). This distinction determines from which biomass pool animals feed (i.e., from live or dead biomass, respectively). A summary and description of symbols and parameters is given in Tables 1 and 2. Our model assumes that herbivory and detritivory redistribute P within a sub-basin and between both types of ecosystems (flooded and terra firme) in proportion to the ecosystem area. As a result of this assumption, a net P transfer occurs between the ecosystem with higher P in the vegetation or organic matter compartment to the ecosystem with lower P. This approximation could be relaxed in the future to account for the fact that animals may preferably consume nutrient-rich foliage and detritus, which is more abundantly available in the seasonally flooded forest (Andersen et al., 2004) and hence a greater proportion of it may be transferred to terra firme ecosystems (i.e., directional P redistribution). Therefore, the proposed model provides a conservative estimate of the net P transfer rate.
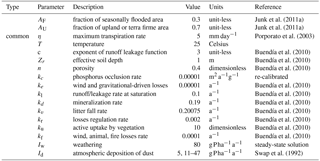
Table 1Description of symbols. Subscript E may stand for either terra firme (replaced by U) or seasonally flooded ecosystem (replaced by F).
2.1 Herbivory and detritivory
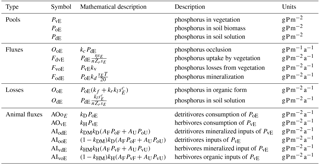
Two P consumption pathways control P redistribution by terrestrial animals – one that is supported by live vegetation biomass (herbivory) and one that is supported by litter and soil organic matter (detritivory). The rate of vegetation P (PvE) consumption by herbivores is described by a first-order process with a rate constant kH. This foraging strategy is characteristic of, e.g., monkeys, birds, and leaf cutter ants together with their supported food webs (see Fig. 3). The rate of organic matter P (PoE) consumption by detritivores is also modeled as a first-order process with rate constant kD. This foraging strategy is adopted by species such as termites, soil fauna, and their food webs. These P consumption and redistribution fluxes are defined mathematically in the following.
With reference to Fig. 3, we can define the rate of herbivory per unit area in a generic E ecosystem as AOvE=kHPvE (where AO stands for animal-driven output). When accounting for the areal extent of each ecosystem, herbivores consume kH(AUPvU+AFPvF). Phosphorus is then released by animals in proportion to the area of the receiving ecosystem. The flux of P returned to a generic ecosystem is then calculated as the rate of consumption over the whole basin weighed by the area receiving P (i.e., kHAE(AUPvU+AFPvF)). Therefore, the area-normalized input P fluxes to each ecosystem are obtained as AI (where AI stands for animal-driven input).
Of this P input to an ecosystem, animals mineralize a fraction kHM (transferred to the dissolved pool PdE), whereas the remaining fraction (1−kHM) is transferred to the soil organic matter pool PoE. This choice is motivated by the fact that animals have limited assimilation efficiency, resulting in excretion of P in easily available forms (i.e., reaching the dissolved pool Pd; Sterner and Elser, 2002). Based on these assumptions, the non-mineralized organic inputs to both ecosystems from herbivores (first subscript v) and detritivores (first subscript o) are, respectively, expressed as
The inputs in mineralized forms to the PdE compartments are similarly described as
The net P flux from flooded to upland ecosystems mediated by herbivores can be also calculated on a whole-basin area basis as
Using the definitions of P fluxes, HF→U is thus found as
This equation demonstrates that herbivores mediate a net P transport from ecosystems with more vegetation P to ecosystems with less vegetation, thus dissipating P gradients across the landscape. Interestingly, the more uniform the partition between flooded and upland ecosystems, the larger the flux is, because AU(1−AU) is maximized at AU=0.5. The same reasoning can be applied to detritivory, and the corresponding equations are obtained by substituting the subscript H by D.
Junk et al. (2011a)Junk et al. (2011a)Porporato et al. (2003)Buendía et al. (2010)Buendía et al. (2010)Buendía et al. (2010)Buendía et al. (2010)Buendía et al. (2010)Buendía et al. (2010)Buendía et al. (2010)Buendía et al. (2010)Buendía et al. (2010)Buendía et al. (2010)Swap et al. (1992)Note that, if herbivore consumption is set to 10 % per year, the model assumes that the same amount of biomass of both seasonally flooded (F) and terra firme ecosystems (U) is consumed. Therefore, the magnitude of the redistribution linearly depends on the P stocks in each ecosystem. Animal population dynamics are effectively neglected here (e.g., the model would not properly describe herbivore outbreaks that defoliate large areas), although other approaches to modeling herbivory include an animal pool and employ nonlinear consumption kinetics (e.g., Doughty et al., 2013; de Mazancourt and Schwartz, 2010). The advantage of our minimal approach is that it does not require any parameter except the consumption rate of vegetation and detritus, for which we show sensitivity analyses, and the partitioning of animal P to organic and available pools, which does not play a major role at steady state.
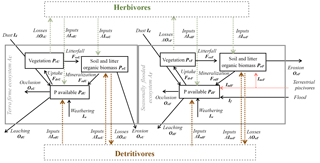
Figure 3Model structure diagram representing the redistribution of P due to herbivory and detritivory. Diagram of model structure representing P fluxes and pools. Black arrows represent the P fluxes among pools representing the basin dynamics of the P cycle and color arrows represent the P fluxes due to animal consumption and dual habitat use: green arrows for herbivory fluxes and brown arrows for detritivory fluxes; red arrow for terrestrial piscivores.
2.2 Model parameterization and inputs
2.2.1 Weathering inputs
For the weathering input Iw, we assumed an average molar P concentration in the bedrock of 75 mol P m−3 (Porder et al., 2007) and a tectonic uplift rate for the lowland basin of 0.0057 mm a−1 (Kronberg et al., 1979). We assumed that uplift rates are the same for the lowland basin and that only 60 % of the material in the rock is weatherable. The steady-state solution corresponds to a weathering flux of about 80 . Furthermore, we assume that the P from weathering is available for plants.
2.2.2 Atmospheric input Id
While P in gaseous phase forms is not common, the atmosphere can transport P-carrying particles. As it has already been discussed in the Introduction, deposition of Saharan dust has been found to contribute to the P budget of the Amazon basin and we chose to work with 5 . The atmospheric deposition of biogenic particles, which accounts for the highest percentage of atmospheric deposition (about 80 % in the Amazon), should not be considered as a system input but rather as a sub-basin recycling process (Mahowald et al., 2005). It should be noted that the term identified in our model as detritivory could also be considered as a sub-basin recycling process. Hence, the production of biogenic particles by forests has a similar effect as detritivore redistribution within the basin.
2.2.3 Flooding inputs
To constrain the range of parameter values in the sensitivity analyses, we estimate the maximum possible P input based on weathering estimates of a lowland sub-basin compared to the Amazon basin. The calculation is based on the assumption that the P cycle is at steady state, i.e., P transport by rivers out of the basin equals the weathering rate as it was explained in the introduction.
Gardner (1990) estimated the P weathering rate for the Amazon and Rio Negro basins to be 457 and 242 , respectively. Assuming that the lowlands of the Amazon have a similar weathering rates as the Rio Negro sub-basin, which is a black water tributary draining only the lowland, and taking into account that lowlands occupy about 87 % of the whole basin, their contribution to the total is about . Hence, the Andes contribute with the remaining .
Since the Andes cover 13 % of the total basin, the in situ weathering must be around 1895.84 . Because our goal here is to define an upper limit for the sensitivity analysis, we assume that all the P from Andean weathering is deposited through flooding to the seasonally flooded areas. These areas occupy 30 % of the drained area, so that the total amount of P that is deposited amounts to mol P (i.e., 1957 ). Following similar calculations, for igapó ecosystems the deposition rate is estimated as 700 mol P (i.e., 217 ). Considering that most of the material is transported during the raining season, flood plains are inundated during some months the year, and P can recycle within the basin more times before it is discharged into the ocean, we let the flooding input for the várzea Ifw be 80 % of the estimated 1566 and the flooding input to the igapó ffB 90 % of estimated 196 .
2.2.4 Terrestrial piscivores
In addition to flooding, terrestrial animals that transport P from river to flooded ecosystems, for example giant otters, fishing birds, and humans, are represented here as annual fluxes of P to flooded areas as the animals will probably use terra firme areas close to the rivers.
For the animal P flux from rivers to the flooded areas, simulations with three different P inputs were run, with values of 0, 72, and 242 . The first value simulates a scenario with no animals, the second simulates a scenario in which P transfer is like the one estimated for giant otter (Pteronura brasiliensis; see calculation in the introduction), and the last one simulates a scenario in which otters and other animals contribute; since this contribution is unknown, the limit for the sensitivity analysis was set to a value between 3 to 4 times the second estimate, 242 .
2.2.5 Balance equations
The following equations represent the P balances of a generic ecosystem (subscript E). The specific equations for terra firme and seasonally flooded ecosystems are obtained by replacing subscript E with U for upland and F for flooded. The parameters used for seasonally flooded and terra firme ecosystems are the same, with the exception of yearly averaged soil moisture sE and the ecosystem spatial extent (AU and AF). Vegetation obtains P from available forms in the soil (PdE) through water uptake (passive mechanism) and symbiotic organisms (FdvE); losses are due to herbivory (AOvE) and litterfall (FvoE; see Fig. 3):
Soil and litter organic biomass (PoE) increase due to litterfall (FvoE) from the same ecosystem as well as from the connected ecosystem due to the contribution of herbivores (AIvoE), detritivores (AIooE), and terrestrial animals feeding on riverine food sources (piscivores) that transport P to flooded ecosystems (IaoF). P release due to mineralization of soil organic matter is a function of soil moisture and temperature. Detritivores also induce mineralization and redistribution of PoE through the flux AOoE. Accordingly, the mass balance equation for organic matter P reads
P in available forms (Pd) receives inputs from atmospheric dust deposition (Id), weathering (Iw), flooding in seasonally flooded ecosystems (IfF), terrestrial piscivore imports to flooded ecosystems (IadF), mineralization of PoE (FodE), and mineralization and redistribution through animals (AIodE+AIvdE). Losses are driven mainly by runoff and leaching OdE, vegetation uptake FdvE, and occlusion OdcE, so that the mass balance equation for available P can be written as
Sensitivities to parameters like soil moisture, vegetation active uptake, and runoff are presented in Buendía et al. (2010), and the values chosen for simulations are listed in Table 1.
Junk et al. (2011b)Junk et al. (2011b)2.3 Parameterization of animal dynamics
The parameterization of animal dynamics requires only a few parameters. P from animal turnover and excreta is assumed to be transferred equally to either available P and soil organic matter P (i.e., ). Altering this assumption did not significantly affect the results. Herbivore and detritivore consumption rate constants (kH and kD) are varied in a sensitivity analysis over a range consistent with observations (Cebrian and Lartigue, 2004)
2.4 Scenarios for Amazonian sub-basins
To assess the importance of biomass consumption by animals on P redistribution under different environmental settings, we parameterized our model for three contrasting Amazonian lowland sub-basins: (1) the Caquetá-Japurá sub-basin, a white water river rich in Andean sediments and hence relatively richer in P; (2) the Rio Negro sub-basin, a lowland black water tributary of the Amazon River which is generally poor in P; and (3) the Xingu sub-basin, clear water tributary of the Amazon, draining mainly Cerrados, dry tropical savanna ecosystem.
On the regional scale, the average fluxes are calculated with the assumption that 30 % of the terrestrial area is seasonally flooded and the 70 % is terra firme (non-flooded; Junk et al., 2011). We run the model for terra firme ecosystems (U) using yearly averaged relative soil water content (sU) of 0.35 for the Cerrado (Runyan and D'Odorico, 2012), and 0.6 for the Caquetá-Japurá and Rio Negro sub-basins. Furthermore, for all seasonally flooded areas in the three sub-basins (F), we assumed yearly averaged soil water content (sF) of 0.7.
2.5 Simulation setup
The solution of the system of six ordinary differential equations was obtained using the deSolve package in R (Soetaert et al., 2010). The model approaches steady state at around 7000 simulation years. Since the initial state of the system is not known, we use here only the steady-state solutions for our results.
Herbivores and detritivores affect the P cycle in the simulated sub-basins in multiple ways, as illustrated in Figs. 4 and 5. These figures show contour plots of the parameter of interest (P fluxes in Fig. 4 and P stocks in Fig. 5), as a function of herbivore and detritivore consumption rates. These patterns are described first regarding the more humid sub-basins (Caquetá/Japurá, Rio Negro) and then to explore different climatic conditions using the Xingu sub-basin as a case study. The two subsequent Figs. (4) and (5) show the effect of either herbivory or detritivory (respectively), while also considering piscivore-mediated P redistribution.
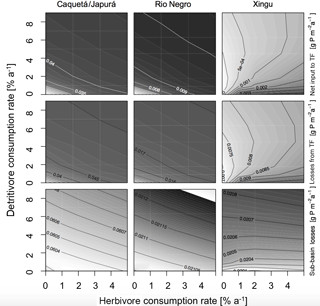
Figure 4Sensitivity of P fluxes of the model at steady state to herbivore and detritivore consumption rates. The first row of panels show the net P input to terra firme due to herbivory and detritivory (total animal input to TF – animal output of TF). The second row shows the P dissolved losses to the terra firme and the last row the sub-basin total losses. This simulation assumes a terrestrial piscivore input to the seasonally flooded ecosystem of 72 .
Our model results show that at steady state, in general, terra firme ecosystems have less P in biomass than their associated seasonally flooded ecosystem (Fig. 5, middle row), this is expected due to the P inputs with seasonal flooding. The gradient between the coupled ecosystems is steeper when P inputs are higher, and therefore Caquetá/Japurá receiving Andean sediments flooding inputs has the steepest gradient. The redistribution of P due to animals (herbivores and detritivores) helps to dissipate the P gradient between the coupled ecosystems, resulting in a net P transfer from seasonally flooded to terra firme ecosystems (Fig. 4, top row). Animals mediate this P transfer, but the feedbacks of animal consumption on the various P pools in the model make the role of animals non-trivial – involving both positive and negative effects on vegetation P depending on the intensity of herbivory and detritivory.
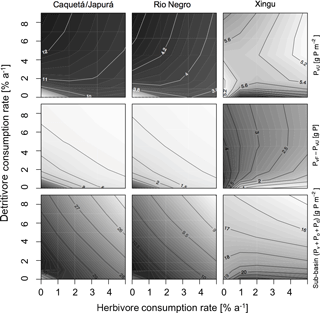
Figure 5Sensitivity of P states of the model at steady state to herbivore and detritivore consumption rates. The first row of panels show the status of P in terra firme due to herbivory and detritivory. The second row shows the difference between P in vegetation in terra firme ecosystem and in seasonally flooded ecosystem to represent the P gradient and how this differentially gets dissipated with herbivory and detritivory (AFPvF−AUPvU). The last row shows total P at the sub-basin (). This simulation assumes a terrestrial piscivore input to the seasonally flooded ecosystem of 72 .
In humid sub-basins, increasing consumption rates by either herbivores or detritivores speeds up the P cycle by increasing cycling and mineralization of organic P. The effect is similar for P-rich (left columns in Figs. 4–5) and P-poor sub-basins (middle columns), despite the latter showing smaller P stocks and fluxes than the P-rich systems. On one hand, this enhanced P cycling increases P transfer from the flooded to the terra firme ecosystem (Fig. 4, top row); on the other hand, due to the larger available P pool, P losses from the terra firme ecosystem and overall on the sub-basin scale also increase (Fig. 4, middle row). Despite the enhanced P losses, the net transfer of P from flooded to terra firme ecosystems sustains a larger terra firme vegetation than in absence of herbivores and detritivores (Fig. 5, top row). The two consumption pathways appear largely complementary, as indicated by approximately hyperbolic contour curves for these fluxes (left two columns in Fig. 4). Under the humid conditions of the Caquetá/Japurá and Rio Negro sub-basins, both strategies acting simultaneously enhance P in vegetation at low herbivory and detritivory rates (< 1.5 % per year), whereas intensifying herbivore consumption eventually decreases the vegetation P stocks, especially at high detritivore consumption rates (Fig. 5, top row). Therefore, animal contribution to P redistribution is optimal for vegetation P in the terra firme at intermediate values of herbivore consumption (1–2 % per year) and only under low to moderate detritivore consumption rates (< 3 % per year).
While a rate of herbivore consumption of 1–2 % maximizes P in living biomass of the terra firme ecosystem, a rate of only 1 % or less maximizes the P status of the whole sub-basin (Fig. 5, bottom row), and this maximum only occurs at low detritivore consumption rates. This difference originates from the P gains of the terra firme ecosystem but also takes into account the losses of the seasonally flooded ecosystem that occupies 30 % of the sub-basins area. Therefore, despite larger vegetation P under certain combinations of consumption rates, the steady-state total P stocks on the sub-basin scale tend to decrease with increasing consumption rates, except at very low consumptions rates (Fig. 5, bottom row) due to the corresponding increasing P losses.
Herbivory and detritivory affect the P status of vegetation in the terra firme ecosystems in a different way under more arid conditions, suggesting a potentially important role of climate in mediating P redistribution, as illustrated in Figs. 4 and 5 (right columns). In the dry Xingu sub-basin, patterns are more complex than in the moister sub-basins. There, the effect of the two consumption pathways on the net P transfer between flooded and terra firme ecosystems is mainly additive (rather than complementary as in the humid sub-basins), as shown by the monotonically increasing contour curves in Fig. 4 (top-right panel). Despite the positive effect of both consumption pathways on P transfer, the steady-state vegetation P in the terra firme ecosystem does not increase monotonically with increasing consumption rates (Fig. 5, top right). Intermediate values of herbivory (1–2 % per year) maximize vegetation P for detritivory rates below 6 % per year, while no maximum occurs under very intense detritivore consumption. For a given herbivory rate, increasing detritivore consumption increases vegetation P, at low kD, but has a negative at high kD values (top right panel in Fig. 5).
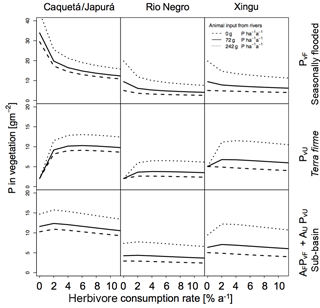
Figure 6Sensitivities of herbivory on P in vegetation for the three sub-basins with different terrestrial piscivores P inputs. Effect of herbivory rates on P in vegetation (g P m−2) for the three sub-basins (columns) at seasonally flooded and terra firme ecosystems and on the sub-basin scale (rows). The different line types refer to different input estimates to the flooded ecosystem by terrestrial piscivores (none, otters only, otters and other species). Simulations were run without detritivory.
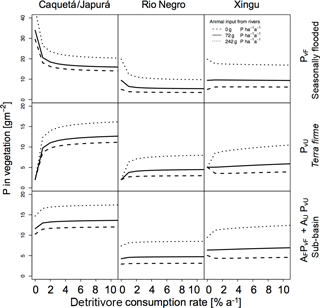
Figure 7Sensitivities of detritivory on P in vegetation for the three sub-basins with different terrestrial piscivores P inputs. Effect of detritivory on P in vegetation (g P m−2) for the three sub-basins (columns) with different terrestrial piscivores P inputs. P in vegetation is shown for seasonally flooded and terra firme ecosystems and on the sub-basin scale (rows). The different line types refer to different mechanisms of P input to the flooded ecosystem by terrestrial piscivores (none, otters only, otters and other species). Simulations were run without herbivory.
In Figs. 6 and 7 we also tested the role of P transport by piscivores from the rivers to the flooded areas, from which it may be transported further inland by detritivores and herbivores as described above. In all sub-basins, piscivore activity (solid and dotted lines compared to the dashed line) significantly improves the P status of both flooded and terra firme ecosystems. In particular, higher piscivore activity emphasizes the maximum in vegetation P in terra firme ecosystems at intermediate levels of herbivore grazing pressure.
We explored the effect of P redistribution through herbivory and detritivory on P availability in three different sub-basins within the Amazon basin. We also considered different P inputs originating from terrestrial piscivores and we investigated the interactions between herbivory and detritivory, flooding regime, and the role of soil moisture. Our results highlight four important points: first, plants growing in terra firme ecosystems can gain P from redistribution induced by both herbivory and detritivory. Second, animal-driven redistribution leads to contrasting P in vegetation depending on herbivore grazing pressure. While small herbivory rates significantly enhance the P in vegetation in terra firme ecosystems with a maximum around 1–2 %, detritivory monotonically increases the P availability in these ecosystems, resulting in a saturation at high consumption rates. Third, differences in soil moisture conditions as well as in P input through flooding across the three sub-basins lead to differences in the absolute amount of P in vegetation and to different responses to herbivory and detritivory. Fourth, terrestrial piscivores importing P to flooded ecosystems in combination with the redistribution by detritivores and herbivores can fertilize terra firme ecosystems. For terra firme at the dry Xingu, the extra P input by piscivores switches the redistribution effect of herbivory and detritivory from decreasing to increasing vegetation P (Figs. 6 and 7).
Our results show that herbivory annual consumption rates of 1–2 % led to a maximum in P availability in the terra firme ecosystem. In a terra firme forest in the Rio Negro basin, leaves account for about 0.51 g P m−2, stems 2.60 g P m−2, and roots 1.71 g P m−2 (Uhl and Jordan, 1984), adding up to about 5 g P m−2(a value consistent with those obtained in our simulations; Fig. 5). Leaf cutter ants in the tropical forest of Barro Colorado Island (Panama) consume about 10 % of foliar biomass per year (Hudson et al., 2009; Metcalfe et al., 2014). Assuming that ant consumption rates are similar across tropical terra firme forests, 10 % of the foliage consumed in the Rio Negro basin leads to an overall P annual consumption rate of 1 % of vegetation biomass. Considering the presence of other herbivores, the overall consumption rate probably ranges between 1 and 3 % per year, which is also in agreement with the predicted range that maximizes vegetation P in the terra firme ecosystem, and in the upper range of our estimate of 1 % herbivory, maximizing the P status on the sub-basin scale (Fig. 6). Moreover, our model suggests that herbivory rates greater than 2.5 % exert a negative effect on P availability in ecosystems that lack substantial sources of P (like the Rio Negro basin).
It would be interesting to assess whether other models of nutrient redistribution exhibit a similar transition from positive to negative effects (for example, in the case of megaherbivores before the megafauna extinction; see Doughty et al., 2013). It is worth noting in this context that in about 50 % of the world ecosystems, the fraction of biomass consumed by herbivores is indeed lower than 5 % (Cebrian and Lartigue, 2004).
Furthermore, our model simulations suggest that P redistribution through detritivores is in general of similar importance than that of herbivores. Observations from central Amazonian forests showing that the proportion of animals feeding on living plant material is rather small (about 7 %) while the proportion of animals feeding on detritus is about half of the total (Fittkau and Klinge, 1973) are in agreement with our finding that higher detritivory than herbivory is necessary to maximize P in vegetation. For example, termites are present in most Amazonian ecosystems (Rückamp et al., 2010), where they abandon nests at a rate of approximately 165 nests . In terms of P, this rate translates to a turnover rate of about 600 , comprising 95 % woody turnover and 8.5 % total litter turnover (Salick et al., 1983).
These dynamics create micro-sites of fertility, but over larger scales and in the long-term they offer a mechanism for P transfer from flooded to terra firme ecosystems. The study of McKey et al. (2010) on abandoned raised agricultural fields in a seasonal flooded ecosystem found a positive correlation between P content of the fields and the number of termites, ants, and worms. This is consistent with our model finding that redistribution is key to the P budget of the terra firme ecosystems and that detritivores are particularly important in this process (Figs. 4 and 5).
4.1 P dynamics of the Amazon basin and its implications
Our results follow from the assumption that herbivores and detritivores can effectively transport P deep into the terra firme ecosystems. Is this assumption reasonable, considering current Amazonian fauna? Amazonian food webs are poorly understood from the perspective of modern science, but communities inhabiting the Amazon have a deep understanding of how they function. As an example Fig. 2 illustrates some of the animals (birds, insects, snakes, and big cats) that are driving the P transfer associated with the Mirití, a black water tributary to the Caquetá, based on the personal experiences of the native people.
Leaf cutting ants, although not herbivores in the strict sense, take amounts of leaves much greater than one would assume based on their body size. This is because ants do not directly feed on leaves but on the fungi they grow with them. Other animals in turn feed on ants, like birds, anteaters, and monkeys, which in turn are eaten by large predators like the jaguar (Fig. 2). Thus leaf P can be later excreted by a jaguar in the deepest part of the terra firme ecosystems due to the activity of the whole food web. This means that a complex food web may allow P transport to areas far away from seasonally flooded ecosystems and rivers. To illustrate this process, one may consider it in analogy to a wave: a wave moves over long distances, but the particles (animals in our context) transfer the energy (P) from particle to particle. It is not necessary that a single animal moves far, but it is the total action of the movement that could result in a net input of P to the P depleted regions. We can imagine how a P atom may travel in complex ways across the Amazon, but a deterministic model of such movement is unfeasible. Animal movement due to dual habitat use is not restricted to invertebrates as in the example above, but it is also documented for fructivorous vertebrates, which use both seasonally flooded and terra firme habitats. Some animals move on a daily basis, while others move on a seasonal basis. Haugaasen and Peres (2007, 2008, 2009) showed that this movement is related to spatial variations in fruit availability. The arboreal species take advantage of the newly available immature and mature fruits, while terrestrial vertebrates mainly profit from fruits remaining after the flood. As we already mention in the introduction, a study on a population of woolly monkeys (Lagothrix lagotricha lugens) shows that their dual habitat use results in a net P flux of 1–4 from seasonally flooded forest to terra firme forest (Stevenson and Guzmán-Caro, 2010). The magnitude of P imported by this single monkey population is of the same order of magnitude of the P inputs through the atmosphere originating from the Saharan desert. Hence, the finding of our model that animals contribute substantially to P redistribution in the Amazon basin appears reasonable.
Our results also illustrate how terrestrial animals and the associated food webs that feed on riverine sources of food together with herbivores and/or detritivores can fertilize terra firme ecosystems (Figs. 4 and 5). Those P imports are particularly important in sub-basins drained by clear and black water rivers, which do not receive large amounts of P because the waters that flood those sub-basins are very poor in P (as illustrated in Fig. 2). This flow of P associated with the Amazonian food webs has implications for human effects on the Amazon basin. Humans have inhabited the Amazon basin for at least 19 000 years and also rely in riverine sources of food. They have created a soil of high fertility, the terra preta, which has been shown to be widespread in the western part of the Amazon and it is associated with clear and black water rivers (McMichael et al., 2014). The population density of pre-Colombian societies in the Amazon before European arrival is still highly uncertain. However, one could imagine that humans were and to some degree are still are as important as other predators for the transfer of P from rivers to land.
So far, we solely considered the transfer of P from rivers to land, but not the P transfer between sub-basins. Although this is not included in our model, fish migration in the Amazon River network constitutes an important mechanism transferring P from the nutrient-rich white waters to the nutrient-poor black and clear water rivers (McClain and Naiman, 2008). Large predator species such as the catfish and detrital-feeding fish species migrate from rivers relying on the Andean nutrient supply to rivers that drain nutrient-poor lowlands (McClain and Naiman, 2008; Barthem and Goulding, 1997). Although fish migrations are well studied, the reasons why they occur remain unclear. One reason might be stoichiometric constraints during ontogenesis (Sterner and Elser, 2002). Juveniles migrate to the estuaries (Barthem and Goulding, 1997), where P is abundantly available due to the mixture of sediments with saltwater. There, they can feed on nutrient-rich resources for growth. Adults mainly require energy and locations for reproduction, which are mainly found upstream in small rivers in the forests (Sterner and Elser, 2002). This migration potentially results in a depletion of the P gradient between rivers originating in the Andes, the mouth of the Amazon River, and the black water lowland rivers (McClain and Naiman, 2008). Using information on the productivity of the forest and how fish change their nutritional needs through the life cycle could help to better understand this remarkable animal-driven P redistribution mechanism.
4.1.1 Comparison with other modeling approaches
A publication presenting a model of P redistribution due to herbivory in the Amazon basin by Doughty et al. (2013) argued that the last extinction of megaherbivores, about 13 000 years ago, decreased significantly P redistribution within the Amazon basin. They suggest “major human impacts on global biogeochemical cycles stretch back to well before the dawn of agriculture. Aspects of the Anthropocene may have begun with the Pleistocene megafaunal extinctions”. Our results agree with those of Doughty et al. (2013) in identifying animals as important drivers of the P cycle and therefore essential to Amazon productivity. However, we obtain different insights about P dynamics in the Amazon and how important herbivory and detritivory might be. We find that excessive herbivory can have negative effects of the P budget. Thus the expansion of cattle farming in the Amazon (i.e., human associated megafauna) is not only a driver of deforestation but may also have long-term effects on biogeochemical cycling of the Amazon. If cattle feeds on vegetation in the basin, but is transported elsewhere for consumption, it represents a net P loss from the system. Locally, cattle movement can concentrate P around drinking or resting areas, thus substituting the natural redistribution processes with a P concentration mechanism. P would then be easily lost via leaching from these biogeochemical hot spots, which would also represent a net loss, but via a different route. In contrast to our approach, Doughty et al. (2013) only consider herbivores feeding in the seasonally flooded ecosystems, and base their model on the behavior of current large herbivores living in African savannas. Herbivore movement is approximated by a Brownian motion and the redistribution of P is assumed to be proportional to the size of the herbivore (Doughty et al., 2013; Wolf et al., 2013). Therefore, the effects of detritivores and small organisms, such as leaf cutter ants that harvest a disproportionately large amount of biomass compared to their size, are neglected, and the role of complex food webs that may allow long-distance transport may be underestimated. This model also does not consider terrestrial animals feeding on riverine food sources, like birds, humans, and otters, which our model shows to be very important in terms of P redistribution.
At the same time most of the megaherbivores went extinct (as assumed by Doughty et al., 2013), pre-Columbian societies would have shifted their diet towards fish and thereby would have enhanced the flux of P from rivers to land. Terra preta soils widespread in many terra firme ecosystems in western Amazonia are evidence for this human action. Moreover, pre-Colombian societies may have increased the contact areas with rivers by creating ponds and channels (so-called earthworks, or geoplyphs), which may have increased nutrient input by flooding (Mann, 2008). Taking this one step further, one may speculate whether pre-Columbian cultures of the Amazon intentionally enhanced the nutrient flux from river to terrestrial ecosystems and whether they did this by creating channels, feeding primarily on riverine sources of food, and keeping their waste on land.
Following this reasoning, landscape changes that are currently occurring in the Amazon region, such as the construction of dams, canalization of the main channels, and land-use changes towards pastures and crops will likely have impacts on the intermediate and long-term P dynamics of Amazonia and, consequently, its productivity and ecosystems dynamics. For example, the canalization of rivers reduces the contact area between rivers and the terrestrial ecosystems, thereby reducing flood plains that constitute important fertility hotspots. Dams disrupt fish migrations, thus reducing the P flux from nutrient-rich freshwater ecosystems like the Caquetá-Japurá river to nutrient-poor rivers like the Xingu. Fish overexploitation, particularly for export, has a similar effect. Land-use changes are major drivers of biodiversity loss and may thus reduce the ways P is redistributed across the basin and thus terra firme ecosystem productivity. Therefore, a more holistic exploration of P fluxes associated with animals seems necessary for better understanding the mechanisms that prevent the Amazon region from reaching P depletion.
We used a simple model to illustrate and discuss our hypothesis that animals may significantly contribute to the internal redistribution of P within the Amazon basin by reducing P availability gradient across the landscape. While rivers tend to dissipate the large-scale P gradient between the Andes and the lowlands (McClain and Naiman, 2008), animals do the same across sub-basins and on the landscape scale between river, seasonally flooded, and terra firme ecosystems. Our model assumes that the P from the Andes that is redistributed by rivers and animals could prevent Amazon lowland forests from falling into a retrogressive phase despite deeply weathered and nutrient-poor soils. This is in contrast to previous studies that mainly attribute high Amazonian productivity to exogenous atmospheric P imports. We advocate the view that redistribution processes within the Amazon basin are at least as important as exogenous inputs, based on a synthesis of the available information and a modeling exercise for the three major ecosystem types within Amazonia. Keeping in mind future empirical tests and investigations, we summarize our results as follows.
Flooding not only provides P but also takes it away, especially through biomass removal. Therefore not only the strength of the P gradient between seasonally flooded and terra firme ecosystem is important but also the soil moisture regime and the duration of flooding when comparing different locations or sub-basins.
Herbivores dissipate the P gradient between seasonally flooded and terra firme ecosystems much more efficiently than detritivores, while consumption rates of detritivores can be an order of magnitude higher than consumption rates of herbivores. Herbivory annual consumption rates of 1–2 % led to a maximum in P availability in the terra firme ecosystem. Herbivory and detritivory are complementary pathways enriching the P content of terra firme ecosystems. To understand P Amazon dynamics it would be important to quantify those effects in the field, e.g., by measuring the consumption rates of herbivores and detritivores along a P availability gradient.
All information necessary to reproduce the results is included in the model description; additionally, the model R code is shared in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-15-279-2018-supplement.
Statement of authorship: CB, AK, and AP defined the research question; CB and SM designed the model; CB and BR performed model simulations and analyzed the results; CB wrote the first draft of the manuscript; and all authors contributed substantially to revisions.
The authors declare that they have no conflict of interest.
Corina Buendía would like to thank Alvaro Buendía, Carlos Rodriguez,
Johana Yucuna,
and Marcela Yucuna for pointing out ways animals transport P; Carlos Sierra
for comments on model structure; Lee Miller and Kerry Hinds for comments on
manuscript structure and language; Thomas Hickler for comments and
corrections of the manuscript; Natalie Mahowald and Carlos Jordan for
pointing out some important aspects of the Amazon P cycle; and the Max Planck
Society for supporting Corina Buendía with a doctoral scholarship and Amilcare Porporato by the
Agriculture and Food Research Initiative from the USDA National Institute of
Food and Agriculture (2011-67003-30222) and the National Science Foundation
(CBET-1033467, FESD 1338694, and EAR 1331846 for the Calhoun Critical Zone
Observatory). We also thank the two reviewers for constructive criticism.
The article processing charges for this open-access
publication were covered by the Max Planck Society.
Edited by: Akihiko Ito
Reviewed by: two anonymous referees
Andersen, T., Elser, J. J., and Hessen, D. O.: Stoichiometry and population dynamics, Ecol. Lett., 7, 884–900, 2004. a
Antonelli, A. and Sanmartín, I.: Why are there so many plant species in the Neotropics?, Taxon, 60, 403–414, 2011. a
Artaxo, P. and Hansson, H.: Size distribution of biogenic aerosol particles from the Amazon Basin, Atmos. Environ., 29, 393–402, 1994. a
Barthem, R. and Goulding, M.: The catfish connection: ecology, migration, and conservation of Amazon predators, Columbia University Press, 1997. a, b, c
Bristow, C. S., Hudson-Edwards, K. A., and Chappell, A.: Fertilizing the Amazon and equatorial Atlantic with West African dust, Geophys. Res. Lett., 37, L14807, https://doi.org/10.1029/2010GL043486, 2010. a
Buendía, C., Kleidon, A., and Porporato, A.: The role of tectonic uplift, climate and vegetation in the long-term terrestrial phosphorus cycle, Biogeosciences, 7, 2025–2038, https://doi.org/10.5194/bg-7-2025-2010, 2010. a, b, c, d, e, f, g, h, i, j, k, l, m
Buendía, C., Arens, S., Hickler, T., Higgins, S. I., Porada, P., and Kleidon, A.: On the potential vegetation feedbacks that enhance phosphorus availability – insights from a process-based model linking geological and ecological timescales, Biogeosciences, 11, 3661–3683, https://doi.org/10.5194/bg-11-3661-2014, 2014. a
Carter, S. and Rosas, F. C.: Biology and conservation of the giant otter Pteronura brasiliensis, Mammal Rev., 27, 1–26, 1997. a
Cebrian, J. and Lartigue, J.: Patterns of herbivory and decomposition in aquatic and terrestrial ecosystems, Ecol. Monogr., 74, 237–259, 2004. a, b
Chadwick, O. A., Derry, L. A., Vitousek, P. M., Huebert, B. J., and Hedin, L.: Changing sources of nutrients during four million years of ecosystem development, Nature, 397, 491–497, 1999. a
Crews, T., Kitayama, K., Fownes, J., and Riley, R.: Changes in soil phosphorus fractions and ecosystem dynamics across a long chronosequence in Hawaii, Ecology, 75, 1407–1424, 1995. a
de Mazancourt, C. and Schwartz, M. W.: A resource ratio theory of cooperation, Ecol. Lett., 13, 349–359, 2010. a
Doughty, C. E., Wolf, A., and Malhi, Y.: The legacy of the Pleistocene megafauna extinctions on nutrient availability in Amazonia, Nat. Geosci., https://doi.org/10.1038/NGEO1895, 2013. a, b, c, d, e, f, g, h
Duplaix, N., Waldemarin, H., Groenedijk, J., Munis, M., Valesco, M., and Botello, J.: Pteronura brasiliensis: In IUCN Red List of Threatened Species, 2008. a
Fittkau, E. J. and Klinge, H.: On biomass and trophic structure of the central Amazonian rain forest ecosystem, Biotropica, 2–14, 1973. a
Gardner, L.: The role of rock weathering in the phosphorus budget of terrestrial watersheds, Biogeochemistry, 11, 97–110, 1990. a, b, c
Gentry, A. H.: Tropical Forest Biodiversity: Distributional Patterns and Their Conservational Significance, Oikos, 63, 19–28, 1992. a, b
Haugaasen, T. and Peres, C. A.: Vertebrate responses to fruit production in Amazonian flooded and unflooded forests, Biodivers. Conserv., 16, 4165–4190, 2007. a
Haugaasen, T. and Peres, C. A.: Population abundance and biomass of large-bodied birds in Amazonian flooded and unflooded forests, Bird Conserv. Int., 18, 87–101 https://doi.org/10.1017/S0959270908000130, 2008. a
Haugaasen, T. and Peres, C. A.: Interspecific primate associations in Amazonian flooded and unflooded forests, Primates, 50, 239–251, 2009. a
Hoorn, C., Wesselingh, F. P., ter Steege, H., Bermudez, M. A., Mora, A., Sevink, J., Sanmartín, I., Sanchez-Meseguer, A., Anderson, C. L., Figueiredo, J. P., Jaramillo, C., Riff, D., Negri, F. R., Hooghiemstra, H., Lundberg, J., Stadler, T., Särkinen, T., and Antonelli, A.: Amazonia through time: Andean uplift, climate change, landscape evolution, and biodiversity, Science, 330, 927–931, 2010. a, b
Hudson, T. M., Turner, B. L., Herz, H., and Robinson, J. S.: Temporal patterns of nutrient availability around nests of leaf-cutting ants (Atta colombica) in secondary moist tropical forest, Soil Biol. Biochem., 41, 1088–1093, 2009. a
Junk, W. J. (Ed.): The central Amazon floodplain: ecology of a pulsing system, Vol. 126, Ecological Studies, 1997. a, b
Junk, W. J., Bayley, P. B., and Sparks, R. E.: The flood pulse concept in river-floodplain systems, Canadian special publication of fisheries and aquatic sciences, 106, 110–127, 1989. a, b
Junk, W. J., Piedade, M. T. F., Schöngart, J., Cohn-Haft, M., Adeney, J. M., and Wittmann, F.: A Classification of Major Naturally-Occurring Amazonian Lowland Wetlands, Wetlands, 31, 623–640, 2011a. a, b, c, d
Junk, W. J., Piedade, M. T. F., Schöngart, J., Cohn-Haft, M., Adeney, J. M., and Wittmann, F.: A Classification of Major Naturally-Occurring Amazonian Lowland Wetlands, Wetlands, 31, 623–640, 2011b. a, b, c
Kronberg, B., Fyfe, W., Leonardos, O., and Santos, A.: The chemistry of some Brazilian soils: Element mobility during intense weathering, Chem. Geol., 24, 211–229, 1979. a
Lambers, H., Raven, J. A., Shaver, G. R., and Smith, S. E.: Plant nutrient-acquisition strategies change with soil age, Trends Ecol. Evol., 23, 95–103, 2008. a
Mahowald, N. M., Artaxo, P., Baker, A. R., Jickells, T. D., Okin, G. S., Randerson, J. T., and Townsend, A. R.: Impacts of biomass burning emissions and land use change on Amazonian atmospheric phosphorus cycling and deposition, Global Biogeochem. Cy., 19, GB4030, https://doi.org/10.1029/2005GB002541, 2005. a, b, c, d
Mann, C. C.: Ancient Earthmovers Of the Amazon, Science, 321, 1148–1152, 2008. a
McClain, M. E. and Naiman, R. J.: Andean influences on the biogeochemistry and ecology of the Amazon River, BioScience, 58, 325–338, 2008. a, b, c, d, e
McKey, D., Rostain, S., Iriarte, J., Glaser, B., Birk, J. J., Holst, I., and Renard, D.: Pre-Columbian agricultural landscapes, ecosystem engineers, and self-organized patchiness in Amazonia, P. Natl. Acad. Sci. USA, 107, 7823–7828, 2010. a
McMichael, C. H., Palace, M. W., Bush, M. B.and Braswell, B., Hagen, S., Neves, E. G., Silman, M. R., Tamanaha, E. K., and C., C.: Predicting pre-Columbian anthropogenic soils in Amazonia, P. R. Soc. B, 22, 281, 1471–2954, https://doi.org/10.1098/rspb.2013.2475, 2014. a
Metcalfe, D. B., Asner, G. P., Martin, R. E., Silva Espejo, J. E., Huasco, W. H., Farfán Amázquita, F. F., Carranza-Jimenez, L., Galiano Cabrera, D. F., Baca, L. D., Sinca, F., Huaraca Quispe, L. P., Taype, I. A., Mora, L. E., Dávila, A. R., Solórzano, M. M., Puma Vilca, B. L., Laupa Román, J. M., Guerra Bustios, P. C., Revilla, N. S., Tupayachi, R., Girardin, C. A. J., Doughty, C. E., and Malhi, Y.: Herbivory makes major contributions to ecosystem carbon and nutrient cycling in tropical forests, Ecol. Lett., 17, 324–332, https://doi.org/10.1111/ele.12233, 2014. a
Pauliquevis, T., Lara, L. L., Antunes, M. L., and Artaxo, P.: Aerosol and precipitation chemistry measurements in a remote site in Central Amazonia: the role of biogenic contribution, Atmos. Chem. Phys., 12, 4987–5015, https://doi.org/10.5194/acp-12-4987-2012, 2012. a
Porder, S., Vitousek, P. M., Chadwick, O. A., Chamberlain, C. P., and Hilley, G. E.: Uplift, Erosion and Phosphorus limitation in Terrestrial Ecosystems, Ecosystems, 10, 158–170, 2007. a, b
Porporato, A., D'Odorico, P., Laio, F., and Rodriguez-Iturbe, I.: Hydrologic controls on soil carbon and nitrogen cycles. I. Modeling scheme, Adv. Water Resour., 26, 45–58, 2003. a
Rückamp, D., Amelung, W., Theisz, N., Bandeira, A. G., and Martius, C.: Phosphorus forms in Brazilian termite nests and soils: relevance of feeding guild and ecosystems, Geoderma, 155, 269–279, 2010. a
Runyan, C. W. and D'Odorico, P.: Hydrologic controls on phosphorus dynamics: A modeling framework, Adv. Water Resour., 35, 94–109, 2012. a
Salick, J., Herrera, R., and Jordan, C. F.: Termitaria: nutrient patchiness in nutrient-deficient rain forests, Biotropica, 15, 1–7, 1983. a
Soetaert, K., Petzoldt, T., and Setzer, R. W.: Solving Differential Equations in R: Package deSolve, J. Stat. Softw., 33, 1–25, 2010. a
Sterner, R. W. and Elser, J. J.: Ecological stoichiometry: the biology of elements from molecules to the biosphere, Princeton University Press, 2002. a, b, c, d
Stevenson, P. R. and Guzmán-Caro, D. C.: Nutrient transport within and between habitats through seed dispersal processes by woolly monkeys in north-western Amazonia, Am. J. Primatol., 72, 992–1003, 2010. a, b
Swap, R., Garstang, M., Greco, S., Talbot, R., and Kållberg, P.: Saharan dust in the Amazon Basin, Tellus B, 44, 133–149, 1992. a, b
Uhl, C. and Jordan, C. F.: Succession and Nutrient Dynamics Following Forest Cutting and Burning in Amazonia, Ecology, 65, 1476–1490, 1984. a
Walker, T. W. and Syers, J. K.: The fate of phosphorous during pedogenesis, Geoderma, 15, 1–19, 1976. a, b, c
Wardle, D. A.: Ecosystem Properties and Forest Decline in Contrasting Long-Term Chronosequences, Science, 305, 509–513, https://doi.org/10.1126/science.1098778, 2004. a, b, c
Wardle, D. A., Bellingham, P. J., Bonner, K. I., and Mulder, C. P. H.: Indirect effects of invasive predators on litter decomposition and nutrient resorption on seabird-dominated islands, Ecology, 90, 452–464, 2009. a, b, c
Wittmann, F., Schöngart, J., Montero, J. C., Motzer, T., Junk, W. J., Piedade, M. T. F., Queiroz, H. L., and Worbes, M.: Tree species composition and diversity gradients in white-water forests across the Amazon Basin, J. Biogeogr., 33, 1334–1347, 2006. a
Wolf, A., Doughty, C. E., and Malhi, Y.: Lateral Diffusion of Nutrients by Mammalian Herbivores in Terrestrial Ecosystems, PloS one, 8, e71352, https://doi.org/10.1371/journal.pone.0071352, 2013. a