the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Towards a global understanding of vegetation–climate dynamics at multiple timescales
Lina M. Estupinan-Suarez
Alexander Brenning
Nuno Carvalhais
Felix Cremer
Fabian Gans
Anja Rammig
Markus Reichstein
Carlos A. Sierra
Miguel D. Mahecha
Climate variables carry signatures of variability at multiple timescales. How these modes of variability are reflected in the state of the terrestrial biosphere is still not quantified or discussed at the global scale. Here, we set out to gain a global understanding of the relevance of different modes of variability in vegetation greenness and its covariability with climate. We used >30 years of remote sensing records of the normalized difference vegetation index (NDVI) to characterize biosphere variability across timescales from submonthly oscillations to decadal trends using discrete Fourier decomposition. Climate data of air temperature (Tair) and precipitation (Prec) were used to characterize atmosphere–biosphere covariability at each timescale.
Our results show that short-term (intra-annual) and longer-term (interannual and longer) modes of variability make regionally highly important contributions to NDVI variability: short-term oscillations focus in the tropics where they shape 27 % of NDVI variability. Longer-term oscillations shape 9 % of NDVI variability, dominantly in semiarid shrublands. Assessing dominant timescales of vegetation–climate covariation, a natural surface classification emerges which captures patterns not represented by conventional classifications, especially in the tropics. Finally, we find that correlations between variables can differ and even invert signs across timescales. For southern Africa for example, correlation between NDVI and Tair is positive for the seasonal signal but negative for short-term and longer-term oscillations, indicating that both short- and long-term temperature anomalies can induce stress on vegetation dynamics. Such contrasting correlations between timescales exist for 15 % of vegetated areas for NDVI with Tair and 27 % with Prec, indicating global relevance of scale-specific climate sensitivities.
Our analysis provides a detailed picture of vegetation–climate covariability globally, characterizing ecosystems by their intrinsic modes of temporal variability. We find that (i) correlations of NDVI with climate can differ between scales, (ii) nondominant subsignals in climate variables may dominate the biospheric response, and (iii) possible links may exist between short-term and longer-term scales. These heterogeneous ecosystem responses on different timescales may depend on climate zone and vegetation type, and they are to date not well understood and do not always correspond to transitions in dominant vegetation types. These scale dependencies can be a benchmark for vegetation model evaluation and for comparing remote sensing products.
- Article
(5834 KB) - Full-text XML
-
Supplement
(53408 KB) - BibTeX
- EndNote
Ecosystems and climate interact on multiple spatial and temporal scales. For example, the main driver of photosynthesis during the daily cycle typically is light availability, assuming no other resource limitation. At annual timescales, temperature can limit growth and development during certain phases of the year, particularly in the extratropics. While climate variability is traditionally very well characterized across timescales (e.g., Viles, 2003; Cao et al., 2012; Bala et al., 2010; Hannachi et al., 2017), it is less well known how the biosphere responds to variations in climate on different scales. Understanding the implications of such timescale dependencies of climate–vegetation interactions is challenging due to the variety of interwoven processes. These dependencies range from short-term climate extremes and biotic stress (e.g., insect outbreaks) to seasonal dynamics in climate-driven phenology and long-term dynamics that can again either reflect intrinsic ecosystem dynamics (e.g., vegetation successional dynamics) or climate-change- or land-use-induced process alterations. Investigating vegetation–climate dynamics globally across multiple timescales requires long-term observation on relevant vegetation dynamics and climate variables in combination with a method to separate ecosystem variability at different timescales.
The assessment of ecosystem variability, e.g., in responses to climate at the global scale, has only become feasible in the last decades. Long-term Earth observations (EOs) are now allowing us to assess ecosystem states consistently over more than 30 years. Vegetation indices such as the normalized difference vegetation index (NDVI) have often been interpreted as proxies for vegetation activity (Zeng et al., 2013; De Keersmaecker et al., 2015; Hawinkel et al., 2015; Kogan and Guo, 2017; Pan et al., 2018), despite well-known limitations of only reflecting vegetation greenness. While novel EOs may be more closely related to actual rates of photosynthesis (Sun-induced fluorescence, SIF; Guanter et al., 2007), NDVI from the Advanced Very High Resolution Radiometer (AVHRR) has the advantage of offering the longest updated records of vegetation remote sensing data every 15 d (d stands for day). In tandem with climate time series from the same period, this record provides a solid basis to globally assess biosphere–atmosphere interactions across timescales ranging from weeks to decades.
Temporal biosphere dynamics carry the imprint of different drivers across timescales, yet EOs can only record one integrated signal over time. This signal reflects a mixture of processes acting on different scales, which cannot be observed independently (Mahecha et al., 2007; Defriez and Reuman, 2017; Pan et al., 2018). Therefore, short-term and long-term processes can be obscured by the dominant influence of the annual cycle (Braswell et al., 2005; Mahecha et al., 2010c). In order to study relevant ecosystem–climate interactions across temporal scales, information contained for each timescale thus first needs to be extracted from this integrated signal. Time series decomposition allows us to extract different frequencies such as annual, intra-annual, and interannual oscillations from vegetation and climate time series. Such approaches have proven useful, e.g., to characterize at what scales vegetation responses are dampened or amplified in comparison with their climate forcing (Stoy et al., 2009), how ecosystem variability is confined by hydrometeorological variability (Pappas et al., 2017), what scales of variability need to be considered to relate forcing variables and vegetation state comprehensively (Katul et al., 2001; Braswell et al., 2005), or to remove confounding effects from processes acting on longer timescales than the process in question (Mahecha et al., 2010b). However, to date most studies employing time series decomposition to study vegetation dynamics have focused on disentangling timescales from minutes to a few years based on flux data (Stoy et al., 2009; Katul et al., 2001; Mahecha et al., 2007, 2010c). Studies investigating long-term vegetation records by time series decomposition do exist but focus only on a specific region (Martínez and Gilabert, 2009; Canisius et al., 2007; Hawinkel et al., 2015) or do not provide cointerpretation with climate signals (Pan et al., 2018). Earth observation time series of vegetation and climate covering more than 30 years now allow us to characterize the timescale-resolved variability in the biosphere and its relation to climate globally across several decades. Additionally, the global coverage of these records allows one to attain a broader understanding in climate space and across vegetation types, which to date is equally lacking.
In this study, we set out to gain a global understanding of the relevance of the different modes of variability in vegetation greenness and its covariability with climate at timescales from submonthly oscillations to long-term trends. These timescale-specific vegetation–climate co-oscillations are expected to serve as a reference benchmark for comparing remote sensing products and terrestrial biosphere models. Specifically, we aim to (i) characterize variability of biosphere and climate time series explicitly on multiple timescales; (ii) understand spatial patterns of this scale-resolved variability and covariability globally; (iii) assess whether characteristic timescale-specific dynamics in the biosphere and climate relate to established climate classifications or land cover; and (vi) assess differences in correlations of biosphere with climate on short-term, seasonal, and longer-term timescales.
The code to produce all primary figures is made available as supplementary notebook (https://doi.org/10.5281/zenodo.3611262, Linscheid et al., 2019).
2.1 Data
A global gridded dataset of AVHRR NDVI was retrieved from the Global Inventory Monitoring and Modeling System (GIMMS, Pinzon and Tucker, 2014) at 15 d temporal and 0.083∘ spatial resolutions (GIMMS NDVI v3.1). Original data were aggregated to 0.5∘ by taking the mean of the corresponding 0.083∘ pixels. Corresponding records of air temperature (Tair) from the European Centre for Medium-Range Weather Forecasts (ERA-Interim v4, Dee et al., 2011) and precipitation (Prec) from the Multi-Source Weighted-Ensemble Precipitation (MSWEP, Beck et al., 2019) were aggregated to match temporal resolution by summation (Prec) or averaging (Tair). Spatial resolution of Tair was preserved (0.5∘), while MSWEP values were averaged for spatial resampling (0.083 to 0.5∘). Spatial and temporal resolution were fixed based on the coarsest resolution among the input datasets to ensure conservative results. The time period considered was from 1 January 1982 to 31 December 2015.
2.2 Preprocessing
Gaps in NDVI time series were filled with values from the mean seasonal cycle computed separately for each grid cell. Missing values were mostly present at high northern latitudes (Fig. S1 in the Supplement). Each time series (for each pixel) was normalized to zero mean and unit variance prior to performing fast Fourier transformation (FFT). For further analysis, the gap-filled data were discarded. Normalization, gap-filling, and FFT were performed in the Earth System Data Lab (https://www.earthsystemdatalab.net/, last access: 1 August 2019, Mahecha et al., 2019), using the implementation based on the programming language Julia. Analyses were performed on a latitude–longitude grid due to software and data considerations. In all spatial analyses on the latitude–longitude grid, the difference in size of grid cells between high latitudes and the Equator was accounted for through weighting values by grid cell size. Similarly, in all analyses that involved sampling of data points, the sampling frequency was weighted by grid cell size.
2.3 Time series decomposition
All pixel time series were first detrended using a linear model. We then used discrete FFT to decompose the detrended time series into underlying harmonic functions at different frequencies (Brockwell and Davis, 2006). The resulting Fourier spectra (Fig. S2) were reconstructed by inverse FFT into binned scale-specific subsignals for short-term, seasonal, and longer-term oscillations: the seasonal signal was reconstructed from the Fourier spectrum at periods of 0.9–1.1 years, plus semiannual and 4-monthly harmonics (i.e., 0.5- and 0.33-year periods). The short-term signal was reconstructed from the Fourier spectrum of all periods <0.9 year, except the two seasonal harmonics, representing interannual oscillations that are not directly linked to periods of seasonality. The longer-term signal was reconstructed from all remaining periods >1.1 year, representing interannual and longer timescales. The subsignal binning was centered on the definition of the seasonal/annual bin similarly to Mahecha et al. (2010a) and Fürst (2009). The bin ranges were slightly adapted due to the FFT approach, which yields signals of different frequencies compared to the approach chosen by Mahecha et al. (2010a). To identify emerging features occurring at different latitudinal bands, mean values weighted by pixel area were calculated in the tropics (23.5∘ N to 23.5∘ S), extratropics (above 23.5∘ N and below 23.5∘ S), and globally.
2.4 Variance per timescale and co-oscillation regimes
For each timescale-specific signal, we calculated the proportion of variance of the original signal explained for each variable per grid cell. Each pixel of the global land surface was then classified into oscillation regimes depending on which scale explained the largest amount of variance in each variable (abbreviations: S – short term, A – seasonal, L – longer term, T – trend). For example, if the variance was dominated by the seasonal subsignal in NDVI and Tair, and by the short-term scale in Prec, this pixel would be classified as AAS (in the order of NDVI, Tair, and Prec). Theoretically, the superimposition yields 64 (43) possible combinations, of which only 26 occurred. For simplicity, our analysis was focused on the 11 most abundant oscillation regimes (99.7 % of pixels).
In order to complement static/traditional classifications, we compared our oscillation regimes with the Global Land Cover map project coordinated by the Joint Research Center (GLC2000, Bartholomé and Belward, 2005) and climate zones from the updated Köppen–Geiger global classification (Kottek et al., 2006, see Fig. S1). Only those pixels that contained data from all three data streams (Köppen–Geiger classes A–D, GLC2000, and our oscillation regimes) were considered in this analysis. Nonvegetated and nonnatural areas as defined by GLC2000 were disregarded for this analysis and onward (Table S1 in the Supplement). The final land surface assessed was 75 871 486 km2, corresponding to 70 % of the vegetated GLC2000 area (Fig. S1). For the same area, we calculated the V measure (V), a spatial association index based on homogeneity and complementarity criteria proposed specifically for thematic map comparison (Nowosad and Stepinski, 2018). The index ranges from 0 to 1, with 1 being a perfect association, and was used to provide an overall comparison between the co-oscillation regime map with Köppen–Geiger and GLC2000 maps.
To assess the influence of gap-filling performed in the original GIMMS NDVI data due to influence of cloud cover or snow, we excluded time points that were retrieved by splines or mean seasonal cycle due to the lack of direct observation in NDVI (Pinzon and Tucker, 2014) at five different quality flag thresholds in our classification of oscillation regimes. Quality flags were aggregated from 0.083 to 0.5∘ by calculating the fraction of direct observations per 0.5∘ pixel at each time step. Subsequently, the dominant classification was repeated, excluding time steps with less than 30 %, 50 %, 70 %, 90 %, and 95 % direct observations for each grid cell. Furthermore, we repeated the time series decomposition method for NDVI and the enhanced vegetation index (EVI) from the Moderate Resolution Imaging Spectroradiometer (MODIS). The vegetation indices product MOD13C1.006 is provided by NASA EOSDIS LP DAAC at 0.05∘. Data were aggregated spatially by averaging valid pixels to 0.5∘ for the overlapping period with GIMMS NDVI (2001–2015). A comparison of the dominant oscillation regimes between products was carried out at a pixel basis.
2.5 Correlations between variables at each timescale
We correlated timescale-specific subsignals of NDVI, Tair, and Prec using Pearson's correlation coefficient, Spearman correlation, and partial correlation. For this analysis, all time points with NDVI < 0.2 were masked in order to consider only data points corresponding to active vegetation (Fig. S1). NDVI was lagged one time step (15 d) behind Prec in order to allow for the response time of vegetation to changes in water availability. Due to the 15 d temporal resolution of the data, a response time of up to 15 d is intrinsically included in our analyses. Each time lag is therefore an additional 15 d, and shorter responses cannot be assessed. We compared six different lags (from 15 to 90 d, Fig. S3). When correlating NDVI and precipitation instantaneously, we found almost exclusively negative correlations for the short-term scale. A lag of one time step was sufficient to arrive at expected positive correlations between NDVI and precipitation, while increasing the lag time did not substantially improve or alter the results. We thus chose to globally use a lag of one time step (representing a 15–30 d response time) between precipitation and NDVI across all scales. Globally, temperature appeared to be most strongly correlated to NDVI instantaneously (not lagged); thus, no time lag was introduced between air temperature and NDVI. Recent studies assessing time lags and memory effects between vegetation and climate also indicate that time lags of around 1 month generally carry most of the explanatory power for predicting vegetation dynamics (Krich et al., 2019; Kraft et al., 2019; Papagiannopoulou et al., 2017). Correlations of NDVI–Tair and NDVI–Prec were binned into five quantiles and presented in a bivariate color map (Teuling et al., 2011). In addition, we compared differences in the sign of the correlation between seasonal and longer-term oscillations to detect areas where the correlation was inverted between scales.
2.6 Assessment of land cover change on time series decomposition
We assessed whether land cover change over the 30-year time period influenced our results by extracting pixels with substantial land cover change as determined by Song et al. (2018). While linear trends were removed from the time series before decomposition, changes in amplitude or piecewise linear and nonlinear trends may have an impact on our analyses. First, we aggregated original 0.05∘ data to match our 0.5∘ spatial resolution by averaging. We then determined 0.5∘ pixels with >25 % gain or loss of trees, short vegetation, or bare ground and assessed whether the observed changes in land cover (Song et al., 2018) were reflected in the NDVI time series to a degree that substantially affected the classification of dominant oscillation regimes.
2.7 Comparison of Fourier transform with empirical mode decomposition
While the FFT approach is the most classical time series decomposition technique, there are more data-adaptive alternatives available (Huang et al., 1998; Ghil, 2002; Paluš and Novotná, 2008). In order to understand whether different methods would lead to different insight, we compared the employed FFT approach with the more data-adaptive empirical mode decomposition (EMD). EMD repeatedly extracts subsignals (intrinsic mode functions, IMFs) from the time series by interpolating a spline between local minima and maxima until the residuals converge to approximately constant values (Huang et al., 1998). We used an ensemble-based modification of the EMD algorithm, the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN, Colominas et al., 2014; Torres et al., 2011), and a frequency-binning approach to obtain frequency bands comparable to the ones chosen for FFT. In contrast to the regular EMD, CEEMDAN employs an ensemble approach in which noise is added to the data before decomposition and ensemble averages for each IMF are returned, so that a more robust end result is obtained (Colominas et al., 2014; Torres et al., 2011). Briefly, in CEEMDAN each IMF is computed as the mean of an ensemble of IMFs retrieved from noisy data copies. This IMF is subtracted from the original signal, and the residual signal is used as input for retrieving the next IMF (Colominas et al., 2014; Torres et al., 2011). As such, CEEMDAN is less prone to mode mixing than EMD while still fulfilling the completeness property of EMD (i.e., the sum of all IMFs equals the original signal). As IMFs resulting from EMD do not have a fixed frequency assigned, we then associated each IMF with a timescale by measuring the distance between all local maxima and minima as a proxy for the dominating wavelength of the signal. Distances between each two maxima or minima were classified as short-term, seasonal, or longer-term depending on their length. The IMF was then categorized by the majority distance category and added into the respective timescale bin. For example, if an IMF contained 25 seasonal cycles and 5 short-term cycles, it was classified as seasonal and added to the seasonal signal bin. IMFs in each bin were combined by summation.
3.1 Time series variance across timescales
Assessing the contribution of each timescale subsignal to the signal variance at each grid cell, we find that for NDVI most of the temporal variability is expectedly captured by the seasonal cycle (71 % of the global variance), especially above the Tropic of Cancer (23.5∘ N) (Fig. 1, Table S2). Short-term oscillations contribute dominantly in parts of tropical America and Southeast Asia, while longer-term components are mainly observed in Australia, South Africa, parts of Argentina, and northern Mexico. Specifically, short-term and longer-term signals together contribute 27 % of the total NDVI variance globally and 38 % in the equatorial region (23.5∘N to 23.5∘S).
Similarly, Tair is strongly dominated by seasonal oscillations in the extratropics above/below 23.5∘ N/S (94 % and 90 %, respectively, Table S2) as would be expected. Even in the tropics, short-term and longer-term components contribute only 30 % of the variance (and 11 % and 4 % of global variance, respectively, Table S2). In contrast, short-term oscillations dominate global precipitation variance before the seasonal cycle (52 % and 41 % of global variance each, Table S2). An east–west gradient of precipitation over Eurasia stands out, changing from predominantly short-term to predominantly seasonal signal variance. In the tropics, a similar contribution from both oscillations is found (42 % and 41 %, respectively, Table S2). Linear trends removed before FFT decomposition had a minor influence on overall variance (Fig. 1). In summary, short-term and longer-term signals show substantial, regionally focused contributions to signal variance. These regions differ between variables, suggesting complex patterns of temporal interaction.
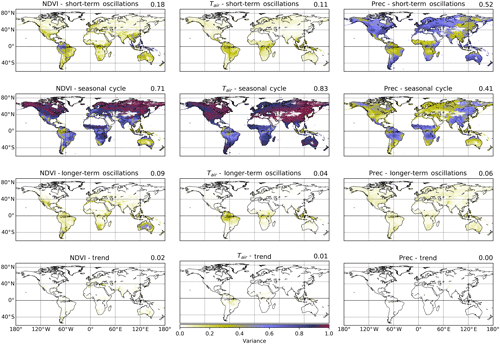
Figure 1Global distribution of timescale-specific variance (relative spectral powers) of the normalized difference vegetation index (NDVI), air temperature (Tair), and precipitation (Prec). Normalized time series of NDVI, Tair, and Prec (columns) were decomposed by fast Fourier transformation and reconstructed into short-term (intra-annual), seasonal (annual), and longer-term (interannual) components (rows). The relative contribution of each scale-specific signal to overall variance was determined at each grid cell. Globally, most of the variance of NDVI and Tair is contained in the seasonal component (red colors), while Prec shows a high contribution of variance from the short-term component. The semiannual cycle is included in the seasonal band. Upper-right-corner values show the percentage of overall variance explained by each timescale.
3.2 Classification of co-oscillations regimes
Given the contrasting, spatially heterogeneous patterns observed in different variables in Fig. 1, we investigated how scale-specific oscillations of biosphere and climate co-occur globally. We combined the dominant scale of variability for each variable in each grid cell (Fig. S4) and found that 84.5 % of the assessed area is dominated by seasonal oscillations of NDVI, 9 % by short-term oscillations in NDVI, and 6.5 % by longer-term oscillations in NDVI (0.03 % captured by the trend). Combining the maps for all three variables into a map of codominant oscillation regimes (Fig. 2, Table S3), we find that seasonal NDVI regimes co-occur predominantly with seasonal Tair, as well as seasonal or short-term Prec regimes (blue regions). Dominant seasonal cycles of NDVI and Tair, as well as fast oscillation regimes in Prec, are expected over large parts of the globe, which is reflected by the large extent of the AAS and AAA classes in this analysis. Beyond this expected solar-cycle-induced behavior, a number of differentiated oscillation classes stand out: short-term NDVI oscillations occur mainly in the South American and Asian tropics, in a multitude of combinations with predominantly seasonal or short-term Tair and Prec (light-green, red, and light-red regions). Longer-term oscillation regimes of NDVI co-occur with seasonal Tair and short-term Prec regimes (dark green regions) around southwestern Africa, southeastern South America, and Australia. Interestingly, the dominant scales in climatic variables are not always associated with similar dominant regimes in NDVI dynamics, suggesting complex or additional driving mechanisms in these heterogeneous regions. In fact, even in areas where temperature or precipitation has a seasonal cycle, NDVI can be dominated by short-term or longer-term oscillations: more than 90 % of the area with short-term NDVI regimes exhibits predominantly seasonal Tair, of which 36 % also shows predominantly seasonal Prec (SAA) and 55 % predominantly short-term Prec (SAS, Table S3). All areas where NDVI is predominantly longer term are classified as seasonal Tair and short-term Prec regimes (LAS, Table S3).
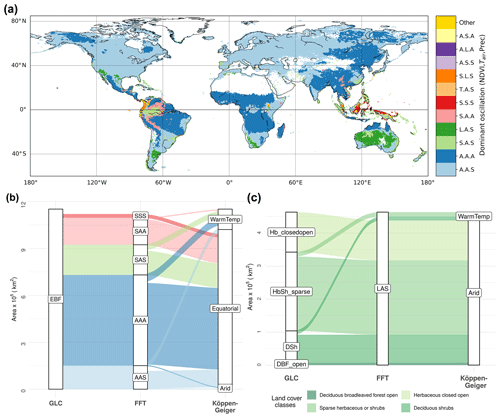
Figure 2Classification of land surface by dominant scale of variability in NDVI and climate, and its relation to land cover and mean climate. (a) Dominant scale of variability was determined for NDVI, Tair, and Prec separately for each grid cell and summarized as unique combinations between variables (S – short term, A – seasonal, L – longer term, T – trend, listed in the order of NDVI, Tair, and Prec). Only the 11 most common classes are shown. The semiannual cycle is included in the seasonal band. (b, c) Sankey diagrams (river plots) showing associations of pixels for (b) evergreen broadleaf forest (EBF) and (c) regions of dominant long-term oscillations in NDVI (LAS class) to oscillation regime (FFT), land cover class (GLC2000), and Köppen–Geiger (KG) climate class. The width of the ribbons is proportional to the area that is commonly classified into the corresponding GLC2000, KG, or oscillation classes. DBF: deciduous broadleaf forest; Hb_closedopen: herbaceous closed open land cover; DSh: deciduous shrublands; HbSh_sparse: sparse herbaceous and shrub vegetation; Equatorial: KG class A; Arid: KG class B; WarmTemp: KG class C; NDVI: normalized difference vegetation index; Tair: air temperature; Prec: precipitation.
To account for the influence of clouds and snow cover in the GIMMS NDVI record, especially in the tropics and northern regions, we excluded time points where pixels contained a high proportion of gap-filled values. We found that overall less than 1.5 % of pixels changed their dominant oscillation class when only pixels with more than 0.7 direct observation fraction were considered. Even when the highest-quality threshold was applied (0.95 direct observation fraction), only 2.6 % of pixels changed dominant oscillation class (Fig. S5). Short-term pixels were the most affected by changes in dominant oscillation (12.9 % and 20.8 % for 0.7 and 0.95 direct observation thresholds respectively), while seasonal pixels showed the highest fraction of gap-filling overall (Fig. S5). As a further validation, we found very similar results when repeating the time series decomposition and the dominant oscillation regime classification based on EVI and NDVI from MODIS (Didan et al., 2019; Huete, 1997; Huete et al., 2002) for the years 2001–2015 (Fig. S6).
We investigated to what extent our classification into oscillation regimes shows patterns of temporal vegetation–climate relations that are not represented by conventional static classifications of the land surface. To determine overlap and differences between the classification of temporal vegetation–climate co-oscillations with static classifications of land cover (GLC2000) and Köppen–Geiger climate classes, we assessed their spatial association by the V measure (Nowosad and Stepinski, 2018). The V measures of co-oscillation regimes with Köppen–Geiger and GLC2000 were V=0.17 and V=0.11, respectively, indicating weak association with both static classifications. Hence, our classification contains information largely complementary to the compared climate and land cover classifications. Yet we observed a slightly stronger association with Köppen–Geiger than with GLC2000, also when comparing homogeneity and complementarity (Table S4). Comparing the three classifications among each other, we find that dominant temporal patterns in NDVI can be linked to certain land cover types such as shrubs and broadleaf forest: Sankey diagrams (Fig. 2b and c) display which proportion of land surface is commonly classified across different class combinations in the three data layers of the co-oscillation regime, GLC2000, and Köppen–Geiger for evergreen broadleaf forest (EBF, Fig. 2b) and areas dominated by longer-term NDVI (Fig. 2c). We find that EBF is the most diverse among land cover classes in terms of our temporal classification, with 35 % dominated by short-term NDVI oscillation (Fig. 2b). In contrast, more than 95 % of deciduous and evergreen needleleaf forests (DNF and ENF) and deciduous broadleaf forests (DBF) are dominated by seasonal NDVI regimes (Table S3). We further find a strong association of longer-term NDVI regimes with shrubs (21 % of the area dominated by longer-term NDVI), herbaceous (26 %), and sparse shrubs/herbaceous (49 %) land cover types in arid regions (Fig. 2c, overall 93 % of the LAS area coincides with Köppen–Geiger class B). Thus, differences within and among land cover and climate types exist when assessing temporal co-oscillations of vegetation and climate.
3.3 Assessment of land cover change on time series decomposition
In the above analyses we did not aim to explicitly detect the effect of land cover or land use change (LCLUC), but nevertheless LCLUC could have an influence on our NDVI classification (Fig. 2). We assessed whether changes in vegetation cover over the 30-year period severely affected our classification by inspecting pixels with >25 % change in the fraction of trees, short vegetation, or bare ground according to Song et al. (2018). Notably, very few of such pixels showed marked signs of land cover change reflected in NDVI time series at all, which is likely due to the coarse spatial resolution of the data used in this study as compared to previous studies focused on detecting LCLUC (Song et al., 2018; Fensholt et al., 2015): at 0.5∘ resolution, most pixels represent mixed signals which obscure most of the details that would allow for detecting land cover changes. In those pixels where we did see a clear progression in NDVI over time, the method did adequately capture this progression, e.g., by correctly reflecting an increasing amplitude of the seasonal cycle and/or shifting baseline (Fig. S7). However, the majority of such pixels with pronounced positive or negative NDVI progression were located in agricultural areas or areas of urbanization, which had a priori been excluded from downstream analyses. Overall, the change in vegetation over time did not have a widespread influence on the classification of dominant scale and oscillation regimes at the given spatial resolution.
3.4 Correlations of NDVI with climate on multiple scales
To inspect relationships of vegetation with climate at multiple timescales, we correlated NDVI with Tair and Prec at each pixel for each timescale (Fig. 3). We found different correlation patterns depending on the timescale: while all possible combinations of correlation between NDVI and Tair or Prec exist at the seasonal scale, short-term and longer-term scales show predominantly or relationships. On the seasonal scale, NDVI correlates positively with Tair and Prec above 40∘ N, whereas in the other latitudes all possible relations are observed. In particular, South America shows a highly diverse pattern of correlations. Differences exists across the tropics, where South America and Southeast Asia display mainly negative correlation with Prec, whereas African tropics display positive correlation with Prec. Semiarid regions show negative correlations with Tair as would be expected. While some of the patters are known, this correlation of decomposed oscillations reveals a more differentiated picture of ecosystem variability in comparison with the undecomposed data (Fig. S8). Notably, correlations on short- and longer-term scales partially show opposite signs compared to the seasonal scale, e.g., in South America, southern Africa, and Central America. Repeating the analysis with Spearman correlation and partial correlation returned similar results (Figs. S9 and S10). Due to the known saturation effects of NDVI against plant productivity over areas of dense biomass, we repeated the analysis with MODIS EVI. We found overall similar results across timescales, but correlations with Tair turned from negative to positive in parts of Central and South America, as well as India (Fig. S11), indicating that NDVI saturation may affect the results obtained from GIMMS long-term records in some areas.
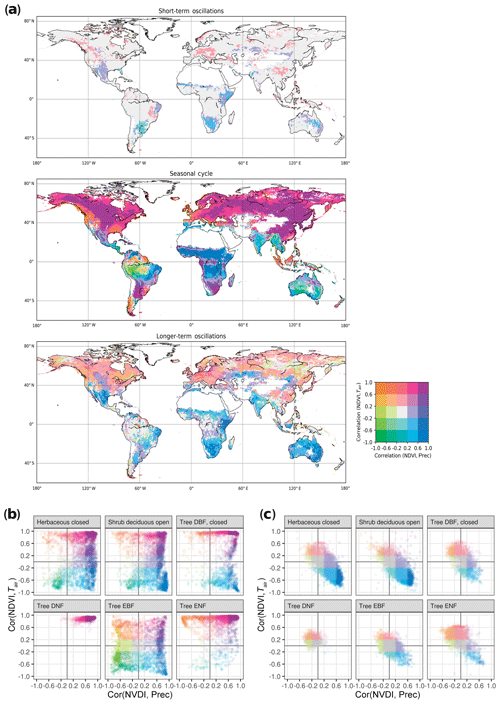
Figure 3Global distribution of timescale-specific correlation of NDVI with air temperature (Tair) and precipitation (Prec). (a) Correlations of NDVI with Tair and NDVI with Prec were calculated between decomposed signals at each grid cell. NDVI was lagged one time step (15 d) behind precipitation to allow for the response time; Tair was correlated instantaneously. Color scale represents both correlations, binned into quantiles (e.g., purple – high positive correlation of NDVI with both Tair and Prec, green – high negative correlation of NDVI with both Tair and Prec). Data points with NDVI<0.2 were excluded to avoid influence of inactive vegetation or nonvegetated time points. (b, c) Correlations for different land cover classes (GLC2000) in the seasonal (b) and longer-term (c) scale.
We again compared the observed patterns with vegetation types, to understand how different ecosystems react at different timescales, and found that different land cover classes showed distinct correlation patterns (Fig. 3b and c). Broadleaf evergreen forest shows the most diverse correlations on a seasonal scale (Fig. 3b). For short-term oscillations, the strongest correlations were found in semiarid shrublands and savannas, which spatially coincide with patterns observed in the longer term: for longer-term oscillations, the strong correlation Prec+ and Tair− was again related primarily to shrublands and savannas (Fig. 3a blue areas, Fig. 3c). We also observed a widespread positive longer-term correlation of NDVI with Tair in the northern latitudes.
Comparing with static classifications, we found that Köppen–Geiger climate classes had the most prominent differentiating effect for correlation patterns, and different climate classes occupy distinct patterns in this correlation space across scales (Fig. S12). Different land cover types generally show similar correlations within one climate zone, but exceptions exist (Fig. S13). Most prominently, EBF shows the most heterogeneous, spatially varying correlations on a seasonal scale. All land cover types show a confined correlation pattern of mainly or at the longer-term scale (Fig. 3c), which is further differentiated by climate zone (Fig. S14).
Assessing correlations across the different timescales, we find that the majority of northern temperate regions (Köppen class D) are positively correlated with Tair on all timescales, but correlation with Prec varies (zero for short-term and longer-term as well as seasonal scale: generally negative on the coast, positive in the interior continent). The equatorial region, South America, Africa, and Southeast Asia exhibit different correlation patterns with climate despite similar land cover types (tropical forest). In some regions, opposing correlations can be observed across timescales (Fig. 4a). For example, correlation of NDVI with Tair in southern Africa varies from negative on the short-term scale to positive on the seasonal scale and back to negative on the longer-term scale. As another example, on the east coast of Australia, NDVI has a low correlation with precipitation on the seasonal scale but high in the longer term. Assessing this globally, correlations between NDVI and Tair show inverted signs between seasonal and longer-term scales in 15.4 % of the vegetated land surface area (Fig. 4a and c). The same is true for NDVI and Prec in 27.3 % of the vegetated land surface area (Fig. 4b and c).
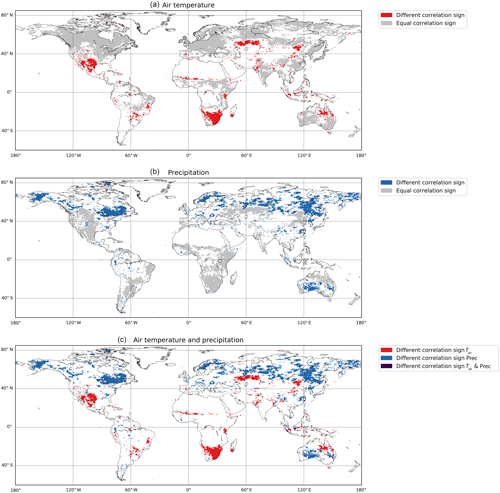
Figure 4Global comparison of differences in the sign of the correlation between the annual and long-term scale for NDVI and air temperature (a), NDVI and precipitation (b), and summary of both (c). Areas in which the sign of the correlation is inverted between seasonal and longer-term scales are highlighted in color, and areas where the sign of the correlation is identical between scales are highlighted in gray (a, b). Areas with correlations between −0.2 and 0.2 were not considered.
In summary, we find that correlations between NDVI and climate variables can change strongly between timescales. Semiarid ecosystems show most prominent short-term and longer-term signatures, while tropical rainforest show the most diverse relationships between variables. These patterns point to complex ecosystem responses to climate at different timescales, indicating that scale-specific ecosystem characterization is necessary to fully understand their temporal dynamics.
3.5 Comparison of fast Fourier transformation with empirical mode decomposition
FFT decomposes a signal in the frequency domain under the assumption that the underlying signals are sinusoidal, time-invariant, and additive (Brockwell and Davis, 2006). Although resulting power spectra and frequency-invariant modes of oscillation are conveniently interpretable, not all ecological processes can be expected to follow regular periodic and additive oscillatory patterns approximated by sine and cosine waves over time. We chose FFT decomposition due to its superior computational speed and stable global applicability, i.e., its ability to return homogeneous spatiotemporal patterns in our analysis. To ensure that the above limitations did not confound our results, we compared the FFT approach to the data-adaptive empirical mode decomposition, which could be expected to be better suited for exploring nonstationary ecological processes over time. In a test case over Europe, we found that our binning approach resulted in comparable results for the two methods, in terms of both spatial and temporal behavior of the signals (Figs. S15–S18). CEEMDAN generally attributed slightly less signal variance to the short-term and slightly more to the seasonal cycle for both Tair and NDVI and generally showed less modulation in the longer-term signals. Nevertheless, overall results were remarkably comparable. However, because CEEMDAN is a data-adaptive method a higher spatial heterogeneity and spatially varying sensitivity to the noise parameter were observed, which currently constrains a global implementation of the analysis.
In this study, we present a global characterization of biosphere variability at multiple timescales from weeks to decades where a natural surface classification emerges. We find that a substantial fraction of terrestrial ecosystems is characterized by either short- or longer-term NDVI oscillations (27 % of variance globally). The grid cells dominated by longer-term oscillations in NDVI concentrate mainly in semiarid shrublands, and the short-term-dominated grid cells concentrate mainly in equatorial latitude forests. Patterns in NDVI, air temperature, and precipitation variability are spatially heterogeneous: the classification of codominant oscillations is particularly homogeneous for temperate and boreal regions, while the tropics exhibit complex patterns of codominating timescales in vegetation and climate. This lack of correspondence in dominant temporal oscillations suggests that certain modes of variability in ecosystem–atmosphere interactions can be potentially induced by different exogenous, or even endogenous, dynamics. This picture is further differentiated by the finding that correlations between NDVI and climate variables differ between timescales. This highlights the need to assess vegetation sensitivity to climate specifically on different scales in order to understand complex patterns of atmosphere–biosphere interactions in time, where also confounding factors should be considered.
4.1 Comparison across timescales points to complex temporal signatures
The combination of timescale-specific classification (Fig. 2) and correlation (Fig. 3) allowed us to characterize the major scales of vegetation variability in relation to climate. The classification provides an additional layer of ecosystem characterization beyond common classifications such as land cover classes or the effective Köppen–Geiger climate classifications (Kottek et al., 2006; Koeppen, 1900; Geiger, 1954), which only consider seasonality besides mean climate states, increasing our understanding of dynamic vegetation properties across timescales. The complementarity of this data-driven classification of vegetation dynamics, extracted from the time series and summarized in the co-oscillation classification, is supported by the low spatial association calculated from the V measure. Our findings show that the dominant oscillation of NDVI is often, but not always, related to dominant oscillations of Tair and Prec (Fig. 2). For example, most of the land surface is dominated by annual oscillations in NDVI and Tair, combined with either seasonal or short-term dominance of Prec (AAA and AAS classes). In many of these regions, air temperature alone or both air temperature and precipitation are limiting factors for plant growth (Nemani, 2003; Seddon et al., 2016) and thus expected to drive vegetation dynamics. In contrast, heterogeneous spatial patterns are observed in equatorial and semiarid regions, where different dominant scales of oscillation are found for NDVI and climatic variables. Here, the relationship between variables may depend on additional factors, and/or scales may show interactive effects. In the tropics, radiation is proposed to be one of the main drivers of NDVI (Nemani, 2003; Seddon et al., 2016), which could partially explain the lack of temporal coherence between NDVI, Tair, and Prec. Dominant short-term oscillations of NDVI (SSS, SAS, SAA) might be explained by climate intraseasonality in the tropics due to the Madden–Julian Oscillation (MJO). The MJO is defined as anomalies in the atmospheric pressure between 10∘ N and 10∘ S in the Indian Ocean region that propagate eastward to the eastern Pacific (Madden and Julian, 1971). Depending on the region and phase, its oscillatory period ranges between 20 and 90 d. MJO is considered the dominant component of intraseasonal climate variability in the tropics (Zhang, 2013). We see MJO as one feasible driver of short-term NDVI oscillations through alterations of precipitation and temperature (Zhang, 2013; Hidayat, 2016; Mayta et al., 2019). However, MJO impacts, teleconnections, and predictability are still insufficiently understood (Zhang, 2013; Wang et al., 2019). Short-term oscillations of vegetation in those regions need to be further investigated, including other sources of intraseasonal variation, connections with climatic events, and data constraints. Additionally, regional analysis at higher spatial resolution might reveal details in local climatic variability, as well as other nonclimatic processes such as land use change or crop rotations, among others. Comparing variables across multiple timescales can point to areas with complex temporal signatures that require further attention.
4.2 Nondominant subsignals reveal short- and longer-term ecosystem dynamics
From assessing relationships among variables on multiple timescales, we conclude that (i) nondominant subsignals in climate variables may dominate the biospheric response, (ii) possible links may exist between short-term and longer-term scales, and (iii) correlations of NDVI with climate variables differ between scales.
The dominance of long-term NDVI in semiarid regions coincides with strong correlations of longer-term NDVI with Prec (positive) and Tair (negative). This indicates that longer-term variation in precipitation exerts a strong influence on NDVI variability in these regions despite contributing a minor portion of precipitation variation itself. Overall, longer-term correlation of precipitation with NDVI is higher than seasonal correlation (by at least 0.2) in 73 % of the area classified as LAS, where simultaneously longer-term variance of precipitation itself contributes <20 % of the variance (3 939 362 km2). Due to their highly plastic interannual vegetation dynamics, semiarid ecosystems exert a strong influence on interannual variability of the land CO2 sink (Ahlstrom et al., 2015; Poulter et al., 2014; Zhang et al., 2016). Longer-term correlations between variables also show broad patterns related to temperature-induced greening in the northern latitudes (Pan et al., 2018; Keenan and Riley, 2018; Zhu et al., 2016; Park et al., 2016). This is in agreement with previous findings using higher-resolution data (Clinton et al., 2014). Thus, nondominant subsignals in climate variables may dominate the biospheric response, stressing their possible long-term impact on vegetation dynamics.
Vegetation may respond to interannual climate variation on both intra- and interannual scales (Meir et al., 2018). Such interannual climate variation may occur, e.g., in the form of precipitation variation or periodic atmospheric fluctuations like the El Niño–Southern Oscillation (ENSO, Poveda and Salazar, 2004; Kogan and Guo, 2017; Liu et al., 2017), the Pacific Decadal Oscillation (Chen et al., 2017), or Indian Ocean dynamics (Hawinkel et al., 2015). As a prominent example in our study, for semiarid regions both short- and longer-term correlations indicate a strong coupling to variations in water availability for shrublands and herbaceous land cover. These results harmonize with the observed fast response of vegetation to water deficit in arid and semiarid regions (Vicente-Serrano et al., 2013; Wang et al., 2016), as well as the observation of strong water memory effects in these regions (Liu et al., 2018). Some of these patterns match regions where vegetation is stressed during ENSO events due to precipitation decrease (Ahlstrom et al., 2015; Kogan and Guo, 2017), generating a possible link between short-term and longer-term scales. Previous studies suggest that climate forcing on one timescale can be amplified or dampened in corresponding vegetation responses (Stoy et al., 2009), or transferred to another timescale (Katul et al., 2001), preserving the system's entropy but creating complex interactions across scales. This highlights the need to further investigate interactions between different timescales globally in long-term EO records.
Finally, for some regions the correlation of variables can differ between timescales. In southern Africa, for example, this may be due to a pronounced temperature-dependent annual cycle of vegetation but a longer-term negative effect of warming temperatures on vegetation productivity. Thus, time series decomposition offers important differentiation of atmosphere–biosphere covariation across scales. This may serve as a platform for generating hypotheses in areas where contrasting dominant oscillations and/or correlations across scales are observed.
4.3 Differences between land cover classes highlight the tropics
By characterizing the temporal behavior of NDVI and climate, we observed different vegetation dynamics between land cover types. Differences in power spectra between plant functional types have been shown before on shorter timescales with flux data (Stoy et al., 2009). Assessing this phenomenon globally, we find both homogeneous and heterogeneous behavior within land cover types, showing nontrivial global patterns of the influence of land cover and climate on vegetation variability across scales. For example, 36 % of evergreen broadleaf forests are dominated by short-term oscillations in NDVI, while other forest types are dominated almost exclusively by seasonal NDVI oscillations. Indeed, the most heterogeneous patterns of codominating oscillations and correlations were found for tropical regions, within and across continents. In African tropics, NDVI is predominantly seasonal and correlation of NDVI with precipitation is always positive, while in most of the remaining tropics, NDVI is dominated by short-term oscillations and shows a predominantly negative correlation with Prec on a seasonal scale in the central Amazon and Southeast Asian tropical forests. This could be explained by different amounts of mean annual precipitation (MAP) falling in these regions, which cause a pronounced wet–dry seasonality in Africa and the central Amazon but not in the northwest or outer regions of the Amazon and SE Asia where MAP is in excess of annual vegetation water demand (Guan et al., 2015). In such areas, correlation with Prec may, e.g., become negative when water is already in excess and clouded/rainy seasons cause limitation in radiation available for plant growth. Similarly, temperature is not usually limiting canopy development in the tropics (rather the contrary, Huang et al., 2019), which may explain negative correlations with Tair. As NDVI saturates over regions of dense vegetation, results in the tropics need to be interpreted with caution, and negative correlation with Tair could alternatively be explained by underestimation of the seasonal cycle over tropical EBF. In fact, negative correlations with Tair were observed less frequently when repeating the analysis with MODIS EVI (Fig. S11), indicating that saturation of NDVI against plant productivity might affect our results in densely vegetated areas such as the tropics. Overall, despite known drawbacks of NDVI as a proxy for plant productivity, the long-term NDVI record generally agrees well with results obtained from the considerably shorter EVI time series, suggesting that it is a good proxy for vegetation activity across timescales over large parts of the global land surface.
It is relevant to emphasize that our results might be affected by noise related to the continuous presence of clouds in the tropics and other atmospheric artifacts. To estimate this effect, we excluded pixels with a low number of direct observations and recalculated the dominant oscillation regime. Short-term oscillations were most affected in this analysis, but roughly 80 % were consistently dominated by short-term oscillation under the strictest scenario, providing higher confidence in our results for the tropics (Fig. S5).
The observed scale-specific patterns highlight the need to assess dynamic vegetation properties in time as differentiating factors beyond land cover type and mean climate.
4.4 Results prove robust against changes in data source and decomposition method
We used long-term GIMMS NDVI records in combination with Fourier transformation in this analysis, well aware of their potential limitations (van Leeuwen et al., 2006; Beck et al., 2011; Fensholt and Proud, 2012; Pinzon and Tucker, 2014). Further consolidating our results against methodological artifacts of the data source and decomposition method, we found that results were not broadly affected or conclusions changed when repeating analyses with MODIS NDVI and EVI or empirical mode decomposition, when excluding gap-filled values as discussed above, or when testing the effect of land use change on decomposed oscillations. Specifically, the analysis of MODIS NDVI and EVI returned a similar classification of dominant timescales in vegetation (Fig. S6). Although short-term oscillations in tropical NDVI may partly reflect noise introduced by cloud cover, heavy aerosol conditions, and biomass burning, our results based on EVI, which is less sensitive to aerosols and haze (Miura et al., 2012), resulted in even more, rather than less, pixels being classified into the short-term oscillation regime (Fig. S6). However, dense clouds are still a limitation when optical remote sensing data are used. EMD decomposition consistently reproduced results of FFT in space and time for all variables (Figs. S15–S18). Excluding gap-filled values originating from snow or cloud inference from the GIMMS NDVI dataset changed the dominant oscillation for only up to 2.3 % of pixels overall, and 20 % of short-term classified pixels, when the strictest threshold was applied (Fig. S5). Land cover and land use change were hardly detectable at the coarse spatial resolution of 0.5∘ employed and had a minor effect on the distribution of signal variance to the different timescale (Fig. S7). In summary, our results proved robust against data source and decomposition method.
4.5 Limitations and outlook
The current study presents a first global characterization of atmosphere–biosphere variability at multiple timescales from weeks to decades. We chose the longest available satellite-retrieved time series of vegetation, GIMMS NDVI, to be able to assess relations of atmosphere–biosphere covariability over more than three decades. We find heterogeneous temporal patterns of biosphere–climate responses across timescales. Known limitations of NDVI include saturation effect at high canopy cover, especially relevant in the tropics, as well as influence by soil reflectance in sparsely vegetated areas. These effects could thus influence our results and the emerging patterns should be compared with newer satellite products such as Sun-induced fluorescence (SIF), which are coupled more directly to plant physiology and photosynthesis (Badgley et al., 2017; Koren et al., 2018) but are only available for short time periods. Considering further variables influencing vegetation dynamics, such as radiation, cloud cover, soil moisture, fires, or storms could bring additional insight into the drivers of vegetation dynamics, especially for poorly explained regions in the current analysis, such as the tropics. In future studies, longer-term climate signals could be compared with climate oscillations such as ENSO to gain further understanding of their effect on long-term ecosystem variability.
Analysis of time lag effects between atmospheric forcing and vegetation response may bring additional valuable insight into ecosystem functioning, yet assessing meaningful time lags across timescales is challenging due to a variety processes involved. Plausible time lags from months to years have been suggested between climate forcing and vegetation response and/or ecosystem carbon exchange through direct and indirect effects (e.g., Braswell et al., 1997, 2005; Vukićević et al., 2001; Krich et al., 2019; Kraft et al., 2019; Papagiannopoulou et al., 2017). Assessing lagged vegetation responses across timescales may help to disentangle such coexisting time lags to form a global, timescale-resolved picture of vegetation responses to climate. To account for the confounding effect of autocorrelation and spurious links between variables, methods like causal inference (Runge et al., 2013, 2019; Krich et al., 2019) should be applied in order to retrieve causal time lags between variables.
Our analyses are conducted at 0.5∘ spatial and 15 d temporal resolution, which may obscure short-term and local vegetation–climate relations, and instead only provide average relationships of variables within each grid cell. Our analyses may thus not be representative in heterogeneous landscapes such as coastlines or mountains. Regions standing out through heterogeneous patterns, such as the Amazon, should be further investigated regionally at higher temporal and spatial resolution whenever consistent data streams permit this to better understand local influence of climate, vegetation and topography on atmosphere–biosphere covariation. Recently, studies in the Amazon based on products such as SIF have detected differences in vegetation anomalies within the basin during El Niño events (Koren et al., 2018). The identified asymmetry in the east–west gradient coincides with observed changes in temperature, soil moisture, and GRACE-derived water storage. Our results pave a way for better understanding the spatial heterogeneity of ecosystem responses to climate variability (van Schaik et al., 2018). Here, assessing temporal patterns beyond correlation (see Wu et al., 2015) will provide additional insight into the temporal evolution of vegetation dynamics and the carbon cycle variability.
In conclusion, decomposing vegetation and climate time series into discrete subsignals allows us to disentangle atmosphere–biosphere oscillations from short- to longer-term timescales. A key finding is that short-term and longer-term modes of variability can dominate regional patterns of ecosystem dynamics: 18 % of land area is effectively characterized by intra-annual variability and 9 % by longer-term modes of NDVI. We derived a global map of dominant patterns of vegetation–climate covariability on multiple timescales. The emerging classification of variability regimes allows us to generate new hypotheses on land–atmosphere interactions. In particular, we can now delineate areas with complex spatiotemporal vegetation signatures. For example, tropical evergreen forests are dominated by short-term oscillations (36 %), while shrublands and herbaceous land cover make up >90 % of the area dominated by longer-term NDVI, suggesting important roles in intra- and interannual biosphere dynamics of these land cover classes. Importantly, changing correlations of NDVI with climate across timescales suggest that climate sensitivities of vegetation can vary with timescale. Globally, 15.4 % of the land area shows opposing correlation of NDVI to Tair between annual and long-term modes of variability, while 27.3 % shows opposite correlations of NDVI and Prec. These findings underline the relevance of advancing our understanding of scale-specific climate sensitivities. In southern Africa, for instance, the relation of vegetation to temperature is inverted across scales, as well as in parts of Australia where the same is true for precipitation. Differentiating such responses is essential to fully comprehend long-term biosphere dynamics and project them into the future. Understanding the interaction of climate and vegetation on separate timescales, warranting that independent processes are not obscured by dominant ones, is essential in times where extreme climate conditions of increasing frequency exert a repeated perturbing influence on ecosystem dynamics (Defriez and Reuman, 2017). This needs to be considered for short- and long-term vegetation modeling under changing climate scenarios.
All remote sensing data are publicly available from the respective supplier. The co-oscillation classification (Fig. 2) is available as a NetCDF file from https://doi.org/10.5281/zenodo.3611262 (Linscheid et al., 2019). The code underlying all primary figures is made available as a supplementary notebook from https://doi.org/10.5281/zenodo.3611262 (Linscheid et al., 2019) and in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-17-945-2020-supplement.
LMES and NL have contributed equally to the paper and performed all analyses. The study was designed by NL, MDM, and LMES with input from all other authors. LMES and NL wrote the paper with substantial input from all other authors. FC and FG implemented the EmpiricalModeDecomposition.jl and libeemd.jl packages in Julia.
The authors declare that they have no conflict of interest.
This paper has been realized within the Earth System Data Lab project funded by the European Space Agency. The authors acknowledge Lina Fürst for initiation of the preliminary study laying the foundation for this project. The authors acknowledge support from Ulrich Weber for data management and preprocessing. Lina M. Estupinan-Suarez acknowledges the support of the DAAD and its Graduate School Scholarship Programme (57395813). Nora Linscheid acknowledges the support of the TUM Graduate School. Lina M. Estupinan-Suarez and Nora Linscheid acknowledge the continuous support of the International Max Planck Research School for Global Biogeochemical Cycles. Felix Cremer acknowledges the support of the German Research Foundation project HyperSense (grant no. TH 1435/4-1).
The article processing charges for this open-access publication were covered by the Max Planck Society.
This paper was edited by Akihiko Ito and reviewed by two anonymous referees.
Ahlstrom, A., Raupach, M. R., Schurgers, G., Smith, B., Arneth, A., Jung, M., Reichstein, M., Canadell, J. G., Friedlingstein, P., Jain, A. K., Kato, E., Poulter, B., Sitch, S., Stocker, B. D., Viovy, N., Wang, Y. P., Wiltshire, A., Zaehle, S., and Zeng, N.: The Dominant Role of Semi-Arid Ecosystems in the Trend and Variability of the Land CO2 Sink, Science, 348, 895–899, https://doi.org/10.1126/science.aaa1668, 2015. a, b
Badgley, G., Field, C. B., and Berry, J. A.: Canopy Near-Infrared Reflectance and Terrestrial Photosynthesis, Sci. Adv., 3, e1602244, https://doi.org/10.1126/sciadv.1602244, 2017. a
Bala, G., Caldeira, K., and Nemani, R.: Fast versus Slow Response in Climate Change: Implications for the Global Hydrological Cycle, Clim. Dynam., 35, 423–434, https://doi.org/10.1007/s00382-009-0583-y, 2010. a
Bartholomé, E. and Belward, A. S.: GLC2000: A New Approach to Global Land Cover Mapping from Earth Observation Data, Int. J. Remote Sens., 26, 1959–1977, https://doi.org/10.1080/01431160412331291297, 2005. a
Beck, H. E., McVicar, T. R., van Dijk, A. I. J. M., Schellekens, J., de Jeu, R. A. M., and Bruijnzeel, L. A.: Global Evaluation of Four AVHRR–NDVI Data Sets: Intercomparison and Assessment against Landsat Imagery, Remote Sens. Environ., 115, 2547–2563, https://doi.org/10.1016/j.rse.2011.05.012, 2011. a
Beck, H. E., Wood, E. F., Pan, M., Fisher, C. K., Miralles, D. G., van Dijk, A. I. J. M., McVicar, T. R., and Adler, R. F.: MSWEP V2 Global 3-Hourly 0.1∘ Precipitation: Methodology and Quantitative Assessment, B. Am. Meteorol. Soc., 100, 473–500, https://doi.org/10.1175/BAMS-D-17-0138.1, 2019. a
Braswell, B. H., Schimel, D. S., Linder, E., and Moore, B.: The Response of Global Terrestrial Ecosystems to Interannual Temperature Variability, Science, 278, 870–873, https://doi.org/10.1126/science.278.5339.870, 1997. a
Braswell, B. H., Sacks, W. J., Linder, E., and Schimel, D. S.: Estimating Diurnal to Annual Ecosystem Parameters by Synthesis of a Carbon Flux Model with Eddy Covariance Net Ecosystem Exchange Observations, Glob. Change Biol., 11, 335–355, https://doi.org/10.1111/j.1365-2486.2005.00897.x, 2005. a, b, c
Brockwell, P. J. and Davis, R. A.: Time Series: Theory and Methods, Springer Series in Statistics, Springer, New York, NY, 2nd Edn., reprint of the 1991 Edn., oCLC: 819807707, 2006. a, b
Canisius, F., Turral, H., and Molden, D.: Fourier Analysis of Historical NOAA Time Series Data to Estimate Bimodal Agriculture, Int. J. Remote Sens., 28, 5503–5522, https://doi.org/10.1080/01431160601086043, 2007. a
Cao, L., Bala, G., and Caldeira, K.: Climate Response to Changes in Atmospheric Carbon Dioxide and Solar Irradiance on the Time Scale of Days to Weeks, Environ. Res. Lett., 7, 034015, https://doi.org/10.1088/1748-9326/7/3/034015, 2012. a
Chen, M., Parton, W. J., Del Grosso, S. J., Hartman, M. D., Day, K. A., Tucker, C. J., Derner, J. D., Knapp, A. K., Smith, W. K., Ojima, D. S., and Gao, W.: The Signature of Sea Surface Temperature Anomalies on the Dynamics of Semiarid Grassland Productivity, Ecosphere, 8, e02069, https://doi.org/10.1002/ecs2.2069, 2017. a
Clinton, N., Yu, L., Fu, H., He, C., and Gong, P.: Global-Scale Associations of Vegetation Phenology with Rainfall and Temperature at a High Spatio-Temporal Resolution, Remote Sens., 6, 7320–7338, https://doi.org/10.3390/rs6087320, 2014. a
Colominas, M. A., Schlotthauer, G., and Torres, M. E.: Improved Complete Ensemble EMD: A Suitable Tool for Biomedical Signal Processing, Biomed. Signal Process. Control, 14, 19–29, https://doi.org/10.1016/j.bspc.2014.06.009, 2014. a, b, c
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
Defriez, E. J. and Reuman, D. C.: A Global Geography of Synchrony for Terrestrial Vegetation, Global Ecol. Biogeogr., 26, 878–888, https://doi.org/10.1111/geb.12595, 2017. a, b
De Keersmaecker, W., Lhermitte, S., Tits, L., Honnay, O., Somers, B., and Coppin, P.: A Model Quantifying Global Vegetation Resistance and Resilience to Short-Term Climate Anomalies and Their Relationship with Vegetation Cover: Global Vegetation Resistance and Resilience, Global Ecol. Biogeogr., 24, 539–548, https://doi.org/10.1111/geb.12279, 2015. a
Didan, K., Barreto-Munoz, A., Solano, R., and Huete, A.: MODIS Vegetation Index User's Guide (MOD13 Series). Version 3.00 (Collection 6), Vegetation Index and Phenology Lab The University of Arizona, available at: https://vip.arizona.edu/, last access: 1 August 2019. a
Fensholt, R. and Proud, S. R.: Evaluation of Earth Observation Based Global Long Term Vegetation Trends – Comparing GIMMS and MODIS Global NDVI Time Series, Remote Sens. Environ., 119, 131–147, https://doi.org/10.1016/j.rse.2011.12.015, 2012. a
Fensholt, R., Horion, S., Tagesson, T., Ehammer, A., Ivits, E., and Rasmussen, K.: Global-Scale Mapping of Changes in Ecosystem Functioning from Earth Observation-Based Trends in Total and Recurrent Vegetation: Mapping of Ecosystem Functioning Change from EO Data, Global Ecol. Biogeogr., 24, 1003–1017, https://doi.org/10.1111/geb.12338, 2015. a
Fürst, L. M. M.: Characterizing Global Spatiotemporal Patterns of the Fraction of Absorbed Photosynthetically Active Radiation, Diploma Thesis, University Bayreuth, Bayreuth, 2009. a
Geiger, R.: Ch. Klassifikation Der Klimate Nach W. Köppen, in: Landolt-Börnstein – Zahlenwerte Und Funktionen Aus Physik, Chemie, Astronomie, Geophysik Und Technik, Band III, alte Serie, 603–607, Springer, Berlin, 1954. a
Ghil, M.: Advanced Spectral Methods for Climatic Time Series, Rev. Geophys., 40, 3-1–3-41, https://doi.org/10.1029/2000RG000092, 2002. a
Guan, K., Pan, M., Li, H., Wolf, A., Wu, J., Medvigy, D., Caylor, K. K., Sheffield, J., Wood, E. F., Malhi, Y., Liang, M., Kimball, J. S., Saleska, S. R., Berry, J., Joiner, J., and Lyapustin, A. I.: Photosynthetic Seasonality of Global Tropical Forests Constrained by Hydroclimate, Nat. Geosci., 8, 284–289, https://doi.org/10.1038/ngeo2382, 2015. a
Guanter, L., Alonso, L., Gómez-Chova, L., Amorós-López, J., Vila, J., and Moreno, J.: Estimation of Solar-Induced Vegetation Fluorescence from Space Measurements, Geophys. Res. Lett., 34, L08401, https://doi.org/10.1029/2007GL029289, 2007. a
Hannachi, A., Straus, D. M., Franzke, C. L. E., Corti, S., and Woollings, T.: Low-Frequency Nonlinearity and Regime Behavior in the Northern Hemisphere Extratropical Atmosphere: Nonlinearity and Regime Behaviour, Rev. Geophys., 55, 199–234, https://doi.org/10.1002/2015RG000509, 2017. a
Hawinkel, P., Swinnen, E., Lhermitte, S., Verbist, B., Van Orshoven, J., and Muys, B.: A Time Series Processing Tool to Extract Climate-Driven Interannual Vegetation Dynamics Using Ensemble Empirical Mode Decomposition (EEMD), Remote Sens. Environ., 169, 375–389, https://doi.org/10.1016/j.rse.2015.08.024, 2015. a, b, c
Hidayat, R.: Modulation of Indonesian Rainfall Variability by the Madden–Julian Oscillation, Proc. Environ. Sci., 33, 167–177, https://doi.org/10.1016/j.proenv.2016.03.067, 2016. a
Huang, M., Piao, S., Ciais, P., Peñuelas, J., Wang, X., Keenan, T. F., Peng, S., Berry, J. A., Wang, K., Mao, J., Alkama, R., Cescatti, A., Cuntz, M., De Deurwaerder, H., Gao, M., He, Y., Liu, Y., Luo, Y., Myneni, R. B., Niu, S., Shi, X., Yuan, W., Verbeeck, H., Wang, T., Wu, J., and Janssens, I. A.: Air Temperature Optima of Vegetation Productivity across Global Biomes, Nature Ecol. Evol., 3, 772–779, https://doi.org/10.1038/s41559-019-0838-x, 2019. a
Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H., Zheng, Q., Yen, N.-C., Tung, C. C., and Liu, H. H.: The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis, P. Roy. Soc. A-Math. Phy., 454, 903–995, https://doi.org/10.1098/rspa.1998.0193, 1998. a, b
Huete, A.: A Comparison of Vegetation Indices over a Global Set of TM Images for EOS-MODIS, Remote Sens. Environ., 59, 440–451, https://doi.org/10.1016/S0034-4257(96)00112-5, 1997. a
Huete, A., Didan, K., Miura, T., Rodriguez, E., Gao, X., and Ferreira, L.: Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices, Remote Sens. Environ., 83, 195–213, https://doi.org/10.1016/S0034-4257(02)00096-2, 2002. a
Katul, G., Lai, C.-T., Schaefer, K., Ellsworth, D., and Oren, R.: Multiscale Analysis of Vegetation Surface Fluxes: From Seconds to Years, Adv. Water Resour., 24, 1119–1132, 2001. a, b, c
Keenan, T. F. and Riley, W. J.: Greening of the Land Surface in the World's Cold Regions Consistent with Recent Warming, Nature Clim. Change, 8, 825–828, https://doi.org/10.1038/s41558-018-0258-y, 2018. a
Koeppen, W.: Versuch einer Klassifikation der Klimate, vorzugsweise nach ihren Beziehungen zur Pflanzenwelt, Geogr. Z., 6, 657–679, 1900. a
Kogan, F. and Guo, W.: Strong 2015–2016 El Niño and Implication to Global Ecosystems from Space Data, Int. J. Remote Sens., 38, 161–178, https://doi.org/10.1080/01431161.2016.1259679, 2017. a, b, c
Koren, G., van Schaik, E., Araújo, A. C., Boersma, K. F., Gärtner, A., Killaars, L., Kooreman, M. L., Kruijt, B., van der Laan-Luijkx, I. T., von Randow, C., Smith, N. E., and Peters, W.: Widespread Reduction in Sun-Induced Fluorescence from the Amazon during the 2015/2016 El Niño, Philos. T. Roy. Soc. B, 373, 20170408, https://doi.org/10.1098/rstb.2017.0408, 2018. a, b
Kottek, M., Grieser, J., Beck, C., Rudolf, B., and Rubel, F.: World Map of the Köppen–Geiger Climate Classification Updated, Meteorol. Z., 15, 259–263, https://doi.org/10.1127/0941-2948/2006/0130, 2006. a, b
Kraft, B., Jung, M., Körner, M., Requena Mesa, C., Cortés, J., and Reichstein, M.: Identifying Dynamic Memory Effects on Vegetation State Using Recurrent Neural Networks, Front. Big Data, 2, 31, https://doi.org/10.3389/fdata.2019.00031, 2019. a, b
Krich, C., Runge, J., Miralles, D. G., Migliavacca, M., Perez-Priego, O., El-Madany, T., Carrara, A., and Mahecha, M. D.: Causal networks of biosphere–atmosphere interactions, Biogeosciences Discuss., https://doi.org/10.5194/bg-2019-297, in review, 2019. a, b, c
Linscheid, N., Estupinan-Suarez, L. M., Brenning, A., Carvalhais, N., Cremer, F., Gans, F., Rammig, A., Reichstein, M., Sierra, C. A., and Mahecha, M. D.: Supplementary Data and Notebook to “Towards a global understanding of vegetation-climate dynamics at multiple time scales”, Zenodo, https://doi.org/10.5281/zenodo.3611262, 2020. a, b, c
Liu, J., Bowman, K. W., Schimel, D. S., Parazoo, N. C., Jiang, Z., Lee, M., Bloom, A. A., Wunch, D., Frankenberg, C., Sun, Y., O'Dell, C. W., Gurney, K. R., Menemenlis, D., Gierach, M., Crisp, D., and Eldering, A.: Contrasting Carbon Cycle Responses of the Tropical Continents to the 2015–2016 El Niño, Science, 358, eaam5690, https://doi.org/10.1126/science.aam5690, 2017. a
Liu, L., Zhang, Y., Wu, S., Li, S., and Qin, D.: Water Memory Effects and Their Impacts on Global Vegetation Productivity and Resilience, Sci. Rep.-UK, 8, 2962, https://doi.org/10.1038/s41598-018-21339-4, 2018. a
Madden, R. A. and Julian, P. R.: Detection of a 40–50 Day Oscillation in the Zonal Wind in the Tropical Pacific, J. Atmos. Sci., 28, 702–708, https://doi.org/10.1175/1520-0469(1971)028<0702:DOADOI>2.0.CO;2, 1971. a
Mahecha, M. D., Reichstein, M., Lange, H., Carvalhais, N., Bernhofer, C., Grünwald, T., Papale, D., and Seufert, G.: Characterizing ecosystem-atmosphere interactions from short to interannual time scales, Biogeosciences, 4, 743–758, https://doi.org/10.5194/bg-4-743-2007, 2007. a, b
Mahecha, M. D., Fürst, L. M., Gobron, N., and Lange, H.: Identifying Multiple Spatiotemporal Patterns: A Refined View on Terrestrial Photosynthetic Activity, Pattern Recogn. Lett., 31, 2309–2317, https://doi.org/10.1016/j.patrec.2010.06.021, 2010a. a, b
Mahecha, M. D., Reichstein, M., Carvalhais, N., Lasslop, G., Lange, H., Seneviratne, S. I., Vargas, R., Ammann, C., Arain, M. A., Cescatti, A., Janssens, I. A., Migliavacca, M., Montagnani, L., and Richardson, A. D.: Global Convergence in the Temperature Sensitivity of Respiration at Ecosystem Level, Science, 329, 838–840, https://doi.org/10.1126/science.1189587, 2010b. a
Mahecha, M. D., Reichstein, M., Jung, M., Seneviratne, S. I., Zaehle, S., Beer, C., Braakhekke, M. C., Carvalhais, N., Lange, H., Le Maire, G., and Moors, E.: Comparing Observations and Process-Based Simulations of Biosphere-Atmosphere Exchanges on Multiple Timescales, J. Geophys. Res.-Biogeo., 115, G02003, https://doi.org/10.1029/2009JG001016, 2010c. a, b
Mahecha, M. D., Gans, F., Brandt, G., Christiansen, R., Cornell, S. E., Fomferra, N., Kraemer, G., Peters, J., Bodesheim, P., Camps-Valls, G., Donges, J. F., Dorigo, W., Estupiñan-Suarez, L., Gutierrez-Velez, V. H., Gutwin, M., Jung, M., Londoño, M. C., Miralles, D. G., Papastefanou, P., and Reichstein, M.: Earth system data cubes unravel global multivariate dynamics, Earth Syst. Dynam. Discuss., https://doi.org/10.5194/esd-2019-62, in review, 2019. a
Martínez, B. and Gilabert, M. A.: Vegetation Dynamics from NDVI Time Series Analysis Using the Wavelet Transform, Remote Sens. Environ., 113, 1823–1842, https://doi.org/10.1016/j.rse.2009.04.016, 2009. a
Mayta, V. C., Ambrizzi, T., Espinoza, J. C., and Dias, P. L. S.: The Role of the Madden–Julian Oscillation on the Amazon Basin Intraseasonal Rainfall Variability, Int. J. Climatol., 39, 343–360, https://doi.org/10.1002/joc.5810, 2019. a
Meir, P., Mencuccini, M., Binks, O., da Costa, A. L., Ferreira, L., and Rowland, L.: Short-Term Effects of Drought on Tropical Forest Do Not Fully Predict Impacts of Repeated or Long-Term Drought: Gas Exchange versus Growth, Philos. T. Roy. Soc. B, 373, 20170311, https://doi.org/10.1098/rstb.2017.0311, 2018. a
Miura, T., Huete, A. R., van Leeuwen, W. J. D., and Didan, K.: Vegetation Detection through Smoke-Filled AVIRIS Images: An Assessment Using MODIS Band Passes, J. Geophys. Res.-Atmos., 103, 32001–32011, https://doi.org/10.1029/98JD00051, 2012. a
Nemani, R. R.: Climate-Driven Increases in Global Terrestrial Net Primary Production from 1982 to 1999, Science, 300, 1560–1563, https://doi.org/10.1126/science.1082750, 2003. a, b
Nowosad, J. and Stepinski, T. F.: Spatial Association between Regionalizations Using the Information-Theoretical V-Measure, Int. J. Geogr. Inf. Sci., 32, 2386–2401, https://doi.org/10.1080/13658816.2018.1511794, 2018. a, b
Paluš, M. and Novotná, D.: Detecting Oscillations Hidden in Noise: Common Cycles in Atmospheric, Geomagnetic and Solar Data, in: Nonlinear Time Series Analysis in the Geosciences, edited by: Donner, R. V. and Barbosa, S. M., Vol. 112, 327–353, Springer Berlin Heidelberg, Berlin, Heidelberg, https://doi.org/10.1007/978-3-540-78938-3_15, 2008. a
Pan, N., Feng, X., Fu, B., Wang, S., Ji, F., and Pan, S.: Increasing Global Vegetation Browning Hidden in Overall Vegetation Greening: Insights from Time-Varying Trends, Remote Sens. Environ., 214, 59–72, https://doi.org/10.1016/j.rse.2018.05.018, 2018. a, b, c, d
Papagiannopoulou, C., Miralles, D. G., Dorigo, W. A., Verhoest, N. E. C., Depoorter, M., and Waegeman, W.: Vegetation Anomalies Caused by Antecedent Precipitation in Most of the World, Environ. Res. Lett., 12, 074016, https://doi.org/10.1088/1748-9326/aa7145, 2017. a, b
Pappas, C., Mahecha, M. D., Frank, D. C., Babst, F., and Koutsoyiannis, D.: Ecosystem Functioning Is Enveloped by Hydrometeorological Variability, Nature Ecol. Evol., 1, 1263–1270, https://doi.org/10.1038/s41559-017-0277-5, 2017. a
Park, T., Ganguly, S., Tømmervik, H., Euskirchen, E. S., Høgda, K.-A., Karlsen, S. R., Brovkin, V., Nemani, R. R., and Myneni, R. B.: Changes in Growing Season Duration and Productivity of Northern Vegetation Inferred from Long-Term Remote Sensing Data, Environ. Res. Lett., 11, 084001, https://doi.org/10.1088/1748-9326/11/8/084001, 2016. a
Pinzon, J. and Tucker, C.: A Non-Stationary 1981–2012 AVHRR NDVI3g Time Series, Remote Sens., 6, 6929–6960, https://doi.org/10.3390/rs6086929, 2014. a, b, c
Poulter, B., Frank, D., Ciais, P., Myneni, R. B., Andela, N., Bi, J., Broquet, G., Canadell, J. G., Chevallier, F., Liu, Y. Y., Running, S. W., Sitch, S., and van der Werf, G. R.: Contribution of Semi-Arid Ecosystems to Interannual Variability of the Global Carbon Cycle, Nature, 509, 600–603, https://doi.org/10.1038/nature13376, 2014. a
Poveda, G. and Salazar, L. F.: Annual and Interannual (ENSO) Variability of Spatial Scaling Properties of a Vegetation Index (NDVI) in Amazonia, Remote Sens. Environ., 93, 391–401, https://doi.org/10.1016/j.rse.2004.08.001, 2004. a
Runge, J., Petoukhov, V., and Kurths, J.: Quantifying the Strength and Delay of Climatic Interactions: The Ambiguities of Cross Correlation and a Novel Measure Based on Graphical Models, J. Climate, 27, 720–739, https://doi.org/10.1175/JCLI-D-13-00159.1, 2013. a
Runge, J., Bathiany, S., Bollt, E., Camps-Valls, G., Coumou, D., Deyle, E., Glymour, C., Kretschmer, M., Mahecha, M. D., Muñoz-Marí, J., van Nes, E. H., Peters, J., Quax, R., Reichstein, M., Scheffer, M., Schölkopf, B., Spirtes, P., Sugihara, G., Sun, J., Zhang, K., and Zscheischler, J.: Inferring Causation from Time Series in Earth System Sciences, Nat. Commun., 10, 2553, https://doi.org/10.1038/s41467-019-10105-3, 2019. a
Seddon, A. W. R., Macias-Fauria, M., Long, P. R., Benz, D., and Willis, K. J.: Sensitivity of Global Terrestrial Ecosystems to Climate Variability, Nature, 531, 229–232, https://doi.org/10.1038/nature16986, 2016. a, b
Song, X.-P., Hansen, M. C., Stehman, S. V., Potapov, P. V., Tyukavina, A., Vermote, E. F., and Townshend, J. R.: Global Land Change from 1982 to 2016, Nature, 560, 639–643, https://doi.org/10.1038/s41586-018-0411-9, 2018. a, b, c, d
Stoy, P. C., Richardson, A. D., Baldocchi, D. D., Katul, G. G., Stanovick, J., Mahecha, M. D., Reichstein, M., Detto, M., Law, B. E., Wohlfahrt, G., Arriga, N., Campos, J., McCaughey, J. H., Montagnani, L., Paw U, K. T., Sevanto, S., and Williams, M.: Biosphere-atmosphere exchange of CO2 in relation to climate: a cross-biome analysis across multiple time scales, Biogeosciences, 6, 2297–2312, https://doi.org/10.5194/bg-6-2297-2009, 2009. a, b, c, d
Teuling, A. J., Stöckli, R., and Seneviratne, S. I.: Bivariate Colour Maps for Visualizing Climate Data, Int. J. Climatol., 31, 1408–1412, https://doi.org/10.1002/joc.2153, 2011. a
Torres, M. E., Colominas, M. A., Schlotthauer, G., and Flandrin, P.: A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, in: 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 4144–4147, IEEE, Prague, Czech Republic, https://doi.org/10.1109/ICASSP.2011.5947265, 2011. a, b, c
van Leeuwen, W. J., Orr, B. J., Marsh, S. E., and Herrmann, S. M.: Multi-Sensor NDVI Data Continuity: Uncertainties and Implications for Vegetation Monitoring Applications, Remote Sens. Environ., 100, 67–81, https://doi.org/10.1016/j.rse.2005.10.002, 2006. a
van Schaik, E., Killaars, L., Smith, N. E., Koren, G., van Beek, L. P. H., Peters, W., and van der Laan-Luijkx, I. T.: Changes in Surface Hydrology, Soil Moisture and Gross Primary Production in the Amazon during the 2015/2016 El Niño, Philos. T. Roy. Soc. B, 373, 20180084, https://doi.org/10.1098/rstb.2018.0084, 2018. a
Vicente-Serrano, S. M., Gouveia, C., Camarero, J. J., Begueria, S., Trigo, R., Lopez-Moreno, J. I., Azorin-Molina, C., Pasho, E., Lorenzo-Lacruz, J., Revuelto, J., Moran-Tejeda, E., and Sanchez-Lorenzo, A.: Response of Vegetation to Drought Time-Scales across Global Land Biomes, P. Natl. Acad. Sci. USA, 110, 52–57, https://doi.org/10.1073/pnas.1207068110, 2013. a
Viles, H.: Interannual, Decadal and Multidecadal Scale Climatic Variability and Geomorphology, Earth-Sci. Rev., 61, 105–131, https://doi.org/10.1016/S0012-8252(02)00113-7, 2003. a
Vukićević, T., Braswell, B. H., and Schimel, D.: A Diagnostic Study of Temperature Controls on Global Terrestrial Carbon Exchange, Tellus B, 53, 150–170, https://doi.org/10.1034/j.1600-0889.2001.d01-13.x, 2001. a
Wang, B., Chen, G., and Liu, F.: Diversity of the Madden–Julian Oscillation, Sci. Adv., 5, eaax0220, https://doi.org/10.1126/sciadv.aax0220, 2019. a
Wang, J., Zeng, N., and Wang, M.: Interannual variability of the atmospheric CO2 growth rate: roles of precipitation and temperature, Biogeosciences, 13, 2339–2352, https://doi.org/10.5194/bg-13-2339-2016, 2016. a
Wu, D., Zhao, X., Liang, S., Zhou, T., Huang, K., Tang, B., and Zhao, W.: Time-Lag Effects of Global Vegetation Responses to Climate Change, Glob. Change Biol., 21, 3520–3531, https://doi.org/10.1111/gcb.12945, 2015. a
Zeng, F.-W., Collatz, G., Pinzon, J., and Ivanoff, A.: Evaluating and Quantifying the Climate-Driven Interannual Variability in Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) at Global Scales, Remote Sens., 5, 3918–3950, https://doi.org/10.3390/rs5083918, 2013. a
Zhang, C.: Madden–Julian Oscillation: Bridging Weather and Climate, B. Am. Meteorol. Soc., 94, 1849–1870, https://doi.org/10.1175/BAMS-D-12-00026.1, 2013. a, b, c
Zhang, Y., Xiao, X., Guanter, L., Zhou, S., Ciais, P., Joiner, J., Sitch, S., Wu, X., Nabel, J., Dong, J., Kato, E., Jain, A. K., Wiltshire, A., and Stocker, B. D.: Precipitation and Carbon-Water Coupling Jointly Control the Interannual Variability of Global Land Gross Primary Production, Sci. Rep.-UK, 6, 39748, https://doi.org/10.1038/srep39748, 2016. a
Zhu, Z., Piao, S., Myneni, R. B., Huang, M., Zeng, Z., Canadell, J. G., Ciais, P., Sitch, S., Friedlingstein, P., Arneth, A., Cao, C., Cheng, L., Kato, E., Koven, C., Li, Y., Lian, X., Liu, Y., Liu, R., Mao, J., Pan, Y., Peng, S., Peñuelas, J., Poulter, B., Pugh, T. A. M., Stocker, B. D., Viovy, N., Wang, X., Wang, Y., Xiao, Z., Yang, H., Zaehle, S., and Zeng, N.: Greening of the Earth and Its Drivers, Nature Climate Change, 6, 791–795, https://doi.org/10.1038/nclimate3004, 2016. a





