2.1 Study site and sampling campaigns

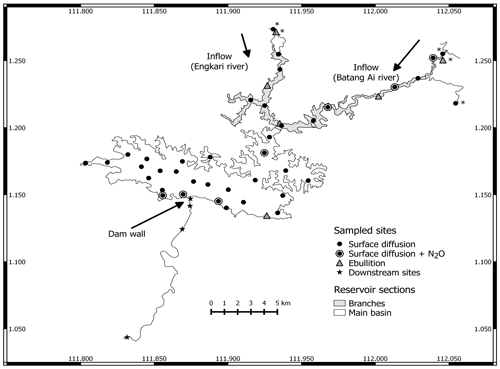
Batang Ai is a hydroelectric reservoir located on the island of Borneo in the Sarawak province of Malaysia (latitude 1.16^∘ and longitude 111.9^∘). The regional climate is tropical equatorial with a relatively constant temperature throughout the year, on average 23 ^∘C in the morning to 32 ^∘C during the day. Annual rainfall varies between 3300 and 4600 mm with two monsoon seasons: November to February (northeast monsoon) and June to October (southwest) (Sarawak Government, 2019). Batang Ai reservoir was impounded in 1985 with no prior clearing of the vegetation and has a dam wall of 85 m in height, a mean depth of 34 m, and a total area of 68.4 km². The reservoir catchment consists of 1149 km² of mostly forested land where human activities are limited to a few traditional habitations and associated croplands, as well as localized aquaculture sites within the reservoir main basin. The reservoir has two major inflows: the Batang Ai and Engkari rivers, which flow into two reservoir branches merging upstream of the main reservoir basin (Fig. 1). Four sampling campaigns were conducted: (1) 14 November to 5 December 2016 (November–December 2016), (2) 19 April to 3 May 2017 (April–May 2017), (3) 28 February to 13 March 2018 (February–March 2018), and (4) 12 to 29 August 2018 (August 2018).

Figure 1Map of Batang Ai showing the location of sampled sites and reservoir sections. * Represents the reservoir inflow sites.

2.2 Water chemistry

Samples for DOC, total phosphorus (TP), total nitrogen (TN), and chlorophyll a (Chl a) analyses were collected from the water surface (<0.5 m) at all surface diffusion sampling sites shown in Fig. 1 and during each campaign. For TP and TN, we collected non-filtered water in acid-washed glass vials stored at 4 ^∘C until analysis. TP was measured by spectrophotometry using the standard molybdenum blue method after persulfate digestion at 121 ^∘C for 20 min and a calibration with standard solutions from 10 to 100 µg L⁻¹ with a 5 % precision (Wetzel and Likens, 2000). TN analyses were performed by alkaline persulfate digestion to NO₃, subsequently measured on a flow Alpkem analyser (OI Analytical Flow Solution 3100) calibrated with standard solutions from 0.05 to 2 mg L⁻¹ with a 5 % precision (Patton and Kryskalla, 2003). Water filtered at 0.45 µm was used for DOC analysis with a total organic carbon analyser 1010-OI following sodium persulfate digestion and calibrated with standard solutions from 1 to 20 mg L⁻¹ with a 5 % precision (detection limit of 0.1 mg L⁻¹). Chl a was analysed through spectrophotometry following filtration on Whatman (GF/F) filters and extraction by hot 90 % ethanol solution (Sartory and Grobbelaar, 1984).

Figure 2Boxplots of measured CH₄ (on a log axis) and CO₂ fluxes grouped according to spatial position. Boxes are bounded by the 25th and 75th percentile and show medians (solid lines), and whiskers show 10th and 90th percentiles. Grey circles show single data points.

Download

2.3 Surface diffusion

Surface diffusion is the flux of gas between the water surface and the air driven by a gradient in gas partial pressure. Surface diffusion of CO₂ and CH₄ to the atmosphere was measured at 36 sites in the reservoir and 3 sites in the inflow rivers (Fig. 1), and sampling of the same sites was repeated in each campaign (with a few exceptions). Fluxes were measured using a static airtight floating chamber connected in a closed loop to an ultraportable gas analyser (UGGA from LGR). Surface diffusion rates (F_gas) were derived from the linear change in CO₂ and CH₄ partial pressures (continuously monitored at 1 Hz for a minimum of 5 min) through time inside the chamber using the following Eq. (1):

where s is the gas accumulation rate in the chamber, V=25 L the chamber volume, A=0.184 m² the chamber surface area, and m the gas molar volume at current atmospheric pressure.

N₂O surface diffusion was estimated at seven of the sampled sites (Fig. 1) using the following Eq. (2) (Lide, 2005):

where k_gas is the gas exchange coefficient, C_gas is the gas concentration in the water, and C_eq is the theoretical gas concentration at equilibrium given measured water temperature, atmospheric pressure, and ambient gas concentration. $C_{{\mathrm{N}}_{\mathrm{2}}\mathrm{O}}$ was measured using the headspace technique, with a 1.12 L sealed glass serum bottle containing surface water and a 0.12 L headspace of ambient air. After shaking the bottle for 2 min to achieve air–water equilibrium, the headspace gas was extracted from the bottle with an airtight syringe and injected in the previously evacuated 9 mL glass vial capped with an airtight butyl stopper and aluminium seal. Three analytical replicates and a local sample of ambient air were taken at each site and analysed by gas chromatography using a Shimadzu GC-2040, with a Poropaq Q column to separate gases and an electron capture detector (ECD) calibrated with 0.3, 1, and 3 ppm of N₂O certified standard gas. After analysis the original N₂O concentration of the water was back-calculated based on the water temperature before and after shaking (for gas solubility), the ambient atmospheric pressure, the ratio of water to air in the sampling bottle, and the headspace N₂O concentration before shaking. $k_{{\mathrm{N}}_{\mathrm{2}}\mathrm{O}}$ was derived from measured $k_{{\mathrm{CH}}_{\mathrm{4}}}$ values obtained by rearranging Eq. (2) for CH₄, with known values of F_gas, C_gas, and C_eq. The $k_{{\mathrm{CH}}_{\mathrm{4}}}$ to $k_{{\mathrm{N}}_{\mathrm{2}}\mathrm{O}}$ transformation was done using the following Eq. (3) (Cole and Caraco, 1998; Ledwell, 1984):

where Sc is the gas Schmidt number (Wanninkhof, 1992).

CH₄ and CO₂ concentrations in the water were measured using the headspace technique. Surface water was collected in a 60 mL gas-tight plastic syringe in which a 30 mL headspace was created (using either ambient air or carbon-free air). The syringe was shaken for 2 min to achieve gas equilibrium between air and water. The gas phase was then injected in a 12 mL airtight pre-evacuated vial and subsequently analysed through manual injection on a Shimadzu GC-8A gas chromatograph with a flame ionization detector following a calibration curve with certified gas standards (0–10 000 ppm for CO₂ and 0–50 000 ppm for CH₄). The samples were also analysed for isotopic δ¹³CO₂ and δ¹³CH₄ signatures by manually injecting 18 mL of gas in a cavity ring-down spectrometer (CRDS) equipped with a small sample isotopic module (SSIM A0314, Picarro G2201-i analyser) set in a non-continuous mode with a three-point calibration curve based on certified gas standards (−40 ‰, −3.9 ‰, and 25.3 ‰ for δ¹³CO₂, and −66.5 ‰, −38.3 ‰, and −23.9 ‰ for δ¹³CH₄).

2.4 Ebullition

Ebullition is the process through which gas bubbles formed in the sediments rise through the water column and are released to the atmosphere. Sediment gas ebullition was measured at four sites in the reservoir and two sites in the inflows (Fig. 1) by deploying 0.785 m² underwater inverted funnel traps at 2 to 3 m deep for approximately 20 d in the reservoir and 1 h in the inflows. The top part of a closed plastic syringe was fixed to the narrow end of the funnel trap where the emerging bubbles accumulated. Upon recovery, bubble gas volume was measured, collected from the syringe, and injected in 12 mL pre-evacuated airtight vials for CO₂ and CH₄ concentration analyses (using the aforementioned method). Ebullition rate was calculated assuming the original bubble composition was similar to bubbles collected almost right after ascent in the inflows sites, which was 100 % CH₄. Hence we considered CO₂ and N₂O ebullition to be null.

In order to estimate the potential for sediment accumulation fuelling ebullition in the littoral zone, we calculated the mud energy boundary depth (EBD in metres, below which fine-grained sediment accumulation occurs) using the reservoir surface area (E in km²) as the exposure parameter in the following Eq. (4) (Rowan et al., 1992):

Table 1CO₂ and CH₄ dynamics downstream of the dam: gas export rate from upstream to downstream of the dam, degassing, result of CH₄ oxidation (CO₂ production and CH₄ consumption), downstream emissions, and total emissions to the atmosphere below the dam. Uncertainties based on variation coefficients are reported in parentheses. Units are in $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ of reservoir surface area.

Download Print Version | Download XLSX

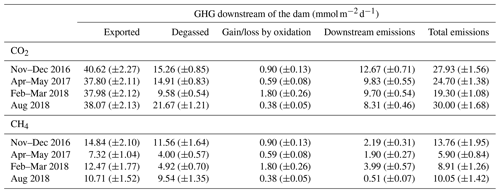
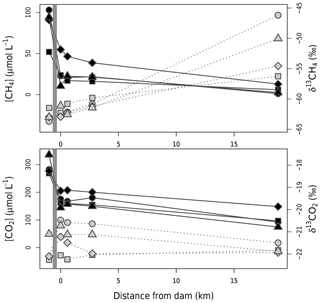
Figure 3Concentrations (black symbols and solid line) and δ¹³C (grey symbols and dotted lines) of CO₂ and CH₄ from right upstream of the dam (grey band) to 19 km downstream in the outflow river. Circles, squares, diamonds, and triangles represent values from November–December 2016, April–May 2017, February–Mar 2018, and August 2018 respectively.

Download

2.5 Degassing, downstream emissions, and CH₄ oxidation

Degassing of CO₂ and CH₄ right after water discharge (F_deg) and downstream emissions of the remaining reservoir-derived GHGs in the outflow river (F_dwn) were calculated using the following Eqs. (5) and (6):

where Q is the water discharge and C_up, C₀, and C₁₉ the measured gas concentrations upstream of the dam at the water withdrawal depth, at the powerhouse right after water discharge, and in the outflow 19 km downstream of the dam respectively. C_ox is the net change in gas concentration due to oxidation (loss for CH₄ and gain for CO₂). For downstream emissions, we considered that, after a river stretch of 19 km, all excess gas originating from the reservoir was evaded and gas concentration was representative of the outflow river baseline. This assumption potentially underestimates actual downstream emissions (in the case of remaining excess gas after 19 km). However, given the observed exponential decrease in gas concentration along the outflow (Fig. 3), emissions after 19 km are expected to be small compared to those in the 0 to 19 km river stretch, consistent with observations in other reservoirs (Guérin et al., 2006; Kemenes et al., 2007).

Gas concentrations upstream and downstream of the dam were obtained by measuring, in each campaign, CO₂ and CH₄ concentrations in a vertical profile right upstream of the dam at a 1 to 3 m interval from 0 to 32 m and at four locations in the outflow: at 0 (power house), 0.6, 2.7, and 19 km downstream of the dam (Fig. 1). Sampling was done using a multi-parameter probe equipped with depth, oxygen, and temperature sensors (Yellow Spring Instruments, YSI model 600XLM-M) attached to a 12 V submersible Tornado pump (Proactive Environmental Products) for water collection. Gas concentration and δ¹³C were measured as described in Sect. 2.3. Water withdrawal depth ranged from 20 to 23 m and was estimated based on known values of elevations of water intake and water level compared to sea level. Gas concentration in the water exiting the reservoir was defined as the average measured gas concentrations in the ±1 m range of the withdrawal depth.

Estimates of downstream CH₄ oxidation were obtained, for each sampling campaign, by calculating the fraction of CH₄ oxidized (F_ox) using the following Eq. (7):

Equation (7) is based on a non-steady-state isotopic model developed considering evasion (emission to the atmosphere) and oxidation as the two loss processes for CH₄ in the outflow river, assuming negligible isotopic fractionation for evasion (Knox et al., 1992) and a fractionation of α=1.02 for oxidation (Coleman et al., 1981) (see derivation in Supplement). [CH₄]_source, [CH₄]_resid, δ¹³CH_4source, and δ¹³CH_4resid are the concentrations of CH₄ and their corresponding isotopic signatures at the beginning of the outflow (km 0) and 19 km downstream, representing the source and residual pools of CH₄ respectively. The amount of CH₄ oxidized to CO₂ along the 19 km of river stretch for each sampling campaign was calculated as the product of F_ox and [CH₄]_source. The resulting loss of CH₄ and gain of CO₂ in the outflow were accounted for in downstream emissions (C_ox in Eq. 6). Note that downstream N₂O emissions were considered null since N₂O concentrations measured in the deep reservoir layer were lower than concentrations in the outflow.

2.6 Ecosystem-scale C footprint

Batang Ai annual C footprint was calculated as the sum of surface diffusion, ebullition, degassing, and downstream emissions of CO₂, CH₄, and N₂O considering a greenhouse warming potential of 1, 34, and 298 respectively over a 100-year lifetime period (Myhre et al., 2013). For each flux pathway, annual flux was estimated as the average of the sampling campaigns. Ecosystem-scale estimate of surface diffusion was calculated for each campaign as the average of measured flux rates applied to the reservoir area for N₂O, and for CO₂ and CH₄ it was obtained by spatial interpolation of measured fluxes over the reservoir area based on inverse distance weighting with a power of two (a power of one yields similar averages, CV <11 %) using package gstat version 1.1–6 in the R version 3.4.1 software (Pebesma, 2004; R Core Team, 2017). Ebullition at the reservoir scale was calculated as the average of measured reservoir ebullition rates applied to the littoral area (<3 m deep).

The estimated GHG emissions of Batang Ai based on measured data was compared to values derived from the G-res model (UNESCO/IHA, 2017) and the model presented in Barros et al. (2011). Both models predict surface CO₂ and CH₄ diffusion as a function of age and account for the effect of temperature using different proxies: the G-res uses effective temperature while the Barros et al. model uses latitude (an indirect proxy that integrates other spatial differences). In terms of CO₂ surface diffusion, the G-res uses reservoir area, soil C content, and TP to quantify the effect of C inputs fuelling CO₂ production, while the Barros et al. model uses DOC inputs directly (based on in situ DOC concentration). For CH₄ surface diffusion, both models account for morphometry using the fraction of littoral area (G-res) or the mean depth (Barros et al. model). Overall, both models predict surface diffusion based on the same conceptual framework but use different proxies. CH₄ ebullition and degassing are modelled only by the G-res, being the sole model available to this date. Details on model equations and input variables are presented in the Supplement (Tables S2 and S3).

3.1 Water chemistry

The reservoir is stratified throughout the year with a thermocline at a depth around 13 m and mostly anoxic conditions in the hypolimnion of the main basin (Fig. S1 in the Supplement). The system is oligotrophic, with very low concentrations of DOC, TP, TN, and Chl a averaging 0.9 (SD±0.2) mg L⁻¹, 5.9 (SD±2.4) µg L⁻¹, 0.11 (SD±0.04) mg L⁻¹, and 1.3 (SD±0.7) µg L⁻¹ respectively (Table S1) and high water transparency (Secchi depth >5 m). In the reservoir inflows, concentrations of measured chemical species are slightly higher but still in the oligotrophic range (Table S1); however, the transparency is much lower due to turbidity (Secchi <0.5 m). The oligotrophic status of the reservoir likely results from nutrient-poor soils (Wasli et al., 2011) and a largely undisturbed forested catchment in the protected Batang Ai National Park. The reservoir's low Chl a concentrations are comparable to the neighbouring Bakun reservoir (Ling et al., 2017), and its DOC concentrations are on the low end of the wide range of measured values in nearby rivers (Martin et al., 2018).

3.2 Surface diffusion

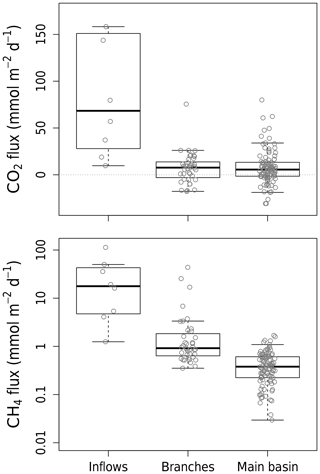
Measured CO₂ diffusion in the reservoir averaged 7.7 (SD±18.2) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ (Table S1), which is on the low end compared to other reservoirs (Deemer et al., 2016) and even to natural lakes (Sobek et al., 2005) but similar to CO₂ fluxes measured in two reservoirs in Laos (Chanudet et al., 2011). CO₂ diffusion across all sites ranged from substantial uptake to high emissions (from −30.8 to 593.9 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$, Table S1) reflecting a large spatial and temporal variability. Spatially, CO₂ fluxes measured in the main basin and branches had similar averages of 7.9 and 7.3 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ respectively (overall SD±18.2), contrasting with higher and more variable values in the inflows with a mean of 137.3 (SD±192.4) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ (Fig. 2). Within the reservoir, CO₂ fluxes varied (SD±18.2 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$) but did not follow a consistent pattern and might reflect pre-flooding landscape heterogeneity (Teodoru et al., 2011). Temporally, highest average reservoir CO₂ fluxes were measured in April–May 2017, when no CO₂ uptake was observed, contrary to other campaigns, especially February–March and August 2018, when CO₂ uptake was common (Fig. S2) and average Chl a concentrations were the highest. This reflects the important role of metabolism (namely CO₂ consumption by primary production) in modulating surface CO₂ fluxes in Batang Ai.

All CH₄ surface diffusion measurements were positive and ranged from 0.03 to 113.4 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ (Table S1). Spatially, CH₄ fluxes were progressively higher moving further upstream (Figs. 2 and S3), with decreasing water depth and increasing connection to the littoral. This gradient in morphometry induces an increasingly greater contact of the water with bottom and littoral sediments, where CH₄ is produced, explaining the spatial pattern of CH₄ fluxes. CH₄ surface diffusion also varied temporally but to a lesser extent than CO₂, being on average highest in August 2018 in the reservoir and in November–December 2016 in the inflows.

Reservoir N₂O surface diffusion (measured with a limited spatial resolution) averaged −0.2 (SD±2.1) $\mathrm{nmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ (Table S1). The negative value indicates that the system acts as a slight net sink of N₂O, absorbing an estimated 2.1 $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ (Table 2). Atmospheric N₂O uptake has previously been reported in aquatic systems and linked to low oxygen and nitrogen content conducive to complete denitrification, which consumes N₂O (Soued et al., 2016; Webb et al., 2019). These environmental conditions match observations in Batang Ai, with a low average TN concentration of 0.11 (0.04) mg L⁻¹ (Table S1) and anoxic deep waters (Fig. S1).

3.3 Ebullition

We calculated that CH₄ ebullition rates in Batang Ai's littoral area ranged from 0.02 to 0.84 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$, which contrasts with rates measured in its inflows, which are several orders of magnitude higher (52 to 103 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$). Similar patterns were observed in other reservoirs, where inflow arms where bubbling hot spots due to a higher organic C supply driven by terrestrial matter deposition (DelSontro et al., 2011; Grinham et al., 2018). Since ebullition rates are notoriously heterogeneous and were measured at only four sites in the reservoir, they may not reflect ecosystem-scale rates. However, our attempt to manually provoke ebullition at several other sites (by physically disturbing the sediments) did not result in any bubble release, confirming the low potential for ebullition in the reservoir littoral zone. Moreover, we calculated that fine-grained sediment accumulation is unlikely at depths shallower than 9.7 m (estimated EBD) in Batang Ai. This, combined with the reservoir steep slope, prevents the sustained accumulation of organic material in littoral zones (Blais and Kalff, 1995), hence decreasing the potential for CH₄ production and bubbling there. Also, apparent littoral sediment composition in the reservoir and dense clay with low porosity may further hinder bubble formation and emission (de Mello et al., 2018).

3.4 Degassing and downstream emissions

Emissions downstream of the dam, expressed on a reservoir-wide areal basis, ranged from 19.3 to 30.0 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ for CO₂ and from 5.9 to 13.8 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ for CH₄ (Table 1). The amount of CO₂ exiting the reservoir varied little between sampling campaigns (CV=3 %), contrary to CH₄ (CV=28 %, Table 1 and Fig. 3). Higher temporal variability of CH₄ concentration in discharged water is likely modulated by microbial CH₄ oxidation in the reservoir water column upstream of the dam. Evidence of high CH₄ oxidation is apparent in reservoir water column profiles, showing a sharp decline of CH₄ concentration and increase in δ¹³CH₄ right around the water withdrawal depth (Fig. S1). This vertical pattern results from higher oxygen availability when moving up in the hypolimnion (Fig. S1), promoting CH₄ oxidation at shallower depths.

Once GHGs have exited the reservoir, a large fraction (40 % and 65 % for CO₂ and CH₄ respectively) is immediately lost to the atmosphere as degassing emissions (Table 1), which is in line with previous literature reports (Kemenes et al., 2016). Along the outflow river, CO₂ and CH₄ concentrations gradually decreased, δ¹³CO₂ remained stable, and δ¹³CH₄ steadily increased (Fig. 3). Given the very small isotopic fractionation (0.9992) of CH₄ during gas evasion (Knox et al., 1992), the only process that can explain the observed δ¹³CH₄ increase is CH₄ oxidation (Bastviken et al., 2002; Thottathil et al., 2018). We estimated that riverine CH₄ oxidation ranged from 0.38 to 1.80 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ (expressed per squared metre of reservoir area for comparison), transforming 18 % to 32 % (depending on the sampling campaign) of the CH₄ to CO₂ within the first 19 km of the outflow. Riverine oxidation rates did not co-vary temporally with water temperature, oxygen availability, or CH₄ concentrations (known as typical drivers; Thottathil et al., 2019); hence, they might be regulated by other factors like light and microbial assemblages (Murase and Sugimoto, 2005; Oswald et al., 2015). Overall, riverine oxidation of CH₄ to CO₂ (which has a 34 times lower warming potential) reduced radiative forcing of downstream emissions (excluding degassing) by, on average, 21 %, and the total annual reservoir C footprint by 7 %. Despite having a measurable impact on reservoir GHG emissions, CH₄ oxidation downstream of dams was only considered in three other reservoirs to our knowledge (DelSontro et al., 2016; Guérin and Abril, 2007; Kemenes et al., 2007). Accounting for this process is particularly important in systems where downstream emissions are large, which is a common situation in tropical reservoirs (Demarty and Bastien, 2011). While additional data on the subject are needed, our results provide one of the first basis for understanding CH₄ oxidation downstream of dams and eventually integrating this component to global models (from which it is currently absent).

3.5 Importance of sampling resolution

High spatial and temporal sampling resolution have been recently highlighted as an important but often lacking aspect of reservoir C footprint assessments (Deemer et al., 2016; Paranaíba et al., 2018). Reservoir-scale fluxes are usually derived from applying an average of limited flux measurements to the entire reservoir area. For Batang Ai, this method overestimates CO₂ and CH₄ surface diffusion by 14 % (130 $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$) and 64 % (251 $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$) respectively compared to spatial interpolation. This is due to the effect of extreme values that are very constrained in space but have a disproportionate effect on the overall flux average. Also, reducing temporal sampling resolution to one campaign instead of four changes the reservoir C footprint estimate by up to 33 %. An additional source of uncertainty in reservoir flux estimates is the definition of a baseline value representing natural river emissions in order to calculate downstream emissions of excess gas in the outflow attributable to damming. In Batang Ai, downstream emission was estimated assuming the GHG concentration 19 km downstream of the dam is a representative baseline for the outflow; however, measured values in the pre-impounded river would have substantially reduced the estimate uncertainty. Results from Batang Ai reinforce the importance of pre- and post-impoundment sampling resolution and upscaling methods in annual reservoir-scale GHG flux estimates.

Table 2Estimated reservoir and inflow areal and total GHG fluxes to the atmosphere (±standard error for measured values, or 95 % confidence interval based on model standard error for G-res values) from different pathways based on measured and modelled approaches.

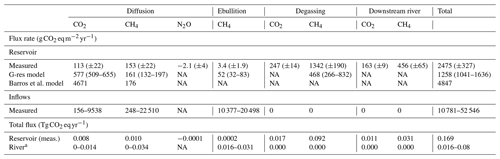
NA: not available. ^a Represents the estimated pre-impounded river fluxes assuming they were similar to current fluxes from the reservoir inflows.

Download Print Version | Download XLSX

3.6 Reservoir C footprint and potential mitigation

Most of the Batang Ai emissions occur downstream of the dam through degassing (64.2 %) and downstream emissions (25.0 %), while surface diffusion contributed only 10.6 % and ebullition 0.14 % (Table 2). In all pathways, radiative potential of CH₄ fluxes was higher than CO₂ and N₂O (especially for degassing), accounting for 79.0 % of Batang Ai CO₂ eq emissions. This distribution of the flux can be attributed mostly to the accumulation of large quantities of CH₄ in the hypolimnion, combined with the fact that the withdrawal depth is located within this layer, allowing the accumulated gas to escape to the atmosphere. Previous studies on reservoirs with similar characteristics to Batang Ai (tropical climate with a permanent thermal stratification and deep water withdrawal) have also found degassing and downstream emissions to be the major emission pathways, especially for CH₄ (Galy-Lacaux et al., 1997; Kemenes et al., 2007).

Overall, we estimated that the reservoir emits on average 2475 (±327) $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$, which corresponds to 0.169 Tg CO₂ eq yr⁻¹ over the whole system. In comparison, the annual areal emission rate (diffusion and ebullition) of the inflows, based on a more limited sampling resolution, is estimated to range from 10.8 to 52.5 $\mathrm{kg}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$, mainly due to extremely high ebullition. When applied to the approximated surface area of the river before impoundment (1.52 km²), this rate translates to 0.016–0.080 Tg CO₂ eq (Table 2), assuming similar flux rates in the current inflows and pre-impoundment river. While the emission rate of the river per unit of area is an order of magnitude higher than for the reservoir, its estimated total flux remains 2.1 to 10.6 times lower due to a much smaller surface. Higher riverine emissions rates are probably due to a shallower depth and higher inputs of terrestrial organic matter, both conducive to CO₂ and CH₄ production and ebullition. Changing the landscape hydrology to a reservoir drastically reduced areal flux rates, especially ebullition; however, it widely expanded the volume of anoxic environments (sediments and hypolimnion), creating a vast new space for CH₄ production. The new hydrological regime also created an opportunity for the large quantities of gas produced in deep layers to easily escape to the atmosphere through the outflow and downstream river.

One way to reduce reservoir GHG emissions is to ensure low CO₂ and CH₄ concentrations at the water withdrawal depth. In Batang Ai, maximum CO₂ and CH₄ concentrations are found in the reservoir deep layers and rapidly decrease from 20 to 10 m for CO₂ and from 25 to 15 m for CH₄ (Fig. S1). This pattern is commonly found in lakes and reservoirs and results from thermal stratification and biological processes (aerobic respiration and CH₄ oxidation). Knowing this concentration profile, degassing and downstream emissions could have been reduced in Batang Ai by elevating the water withdrawal depth to avoid hypolimnetic gas release. We calculated that elevating the water withdrawal depth by 1, 3, and 5 m would result in a reduction of degassing and downstream emissions by 1 %, 11 %, and 22 % for CO₂ and by 28 %, 92 %, and 100 % for CH₄, respectively (Fig. S4). Consequently, a minor change in the dam design could have drastically reduced Batang Ai's C footprint. This should be taken into consideration in future reservoir construction, especially in tropical regions.

3.7 Measured versus modelled fluxes

Based on measurements, Batang Ai emits on average 113 (±22) $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ via surface CO₂ diffusion. This value is 41 times lower than predicted by the Barros et al. model (4671 $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$, Table 2) based on reservoir age, DOC inputs (derived from DOC water concentration), and latitude (Barros et al., 2011). The high predicted value for Batang Ai, being a relatively old reservoir with very low DOC concentration, is mainly driven by its low latitude. While reservoirs in low latitudes globally have higher average CO₂ fluxes due to higher temperature and often dense flooded biomass (Barros et al., 2011; St. Louis et al., 2000), our results provide a clear example that not all tropical reservoirs have high CO₂ emissions by simple virtue of their geographical location. Despite high temperature, Batang Ai's very low water organic matter content (Table S1) offers little substrate for net heterotrophy, and its strong permanent stratification creates a physical barrier potentially retaining CO₂ derived from flooded biomass in the hypolimnion. The only three other sampled reservoirs in Southeast Asia (Nam Leuk and Nam Ngum in Laos, and Palasari in Indonesia) also exhibited low organic C concentration (for reservoirs in Laos) and low to negative average surface CO₂ diffusion despite their low latitude (Chanudet et al., 2011; Macklin et al., 2018). This suggests that, while additional data are needed, low CO₂ diffusion may be common in Southeast Asian reservoirs and is likely linked to the low organic C content.

In comparison, the G-res model predicts a CO₂ surface diffusion of 577 (509–655) $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$, which includes the flux naturally sustained by catchment C inputs (397 $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$, predicted flux 100 years after flooding) and the flux derived from organic matter flooding (180 $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$). While the predicted G-res value is much closer than that predicted from the Barros et al. model, it still overestimates measured flux, mostly the natural baseline (catchment derived) part of it. The G-res predicts baseline CO₂ effluxes as a function of soil C content, a proxy for C input to the reservoir. While Batang Ai soil is rich in organic C (∼50 g kg⁻¹), it also has a high clay content (>40 %) (ISRIC – World Soil Information, 2019; Wasli et al., 2011) which is known to bind with organic matter and reduce its leaching to the aquatic environment (Oades, 1988). This may explain the unusually low DOC concentration in the reservoir and its inflows (0.3 to 1.8 mg L⁻¹, Table S1) that are among the lowest reported in freshwaters globally (Sobek et al., 2007). Clay-rich soils are ubiquitous in tropical landscapes (especially in Southeast Asia, Central America, and central and eastern Africa) (ISRIC – World Soil Information, 2019); however, their impact on global-scale patterns of aquatic DOC remains unknown. This may be due to a lack of aquatic DOC data, with the most recently published global study on the subject featuring only one tropical system and a heavy bias towards North America and Europe (Sobek et al., 2007). Exploring the global-scale picture of aquatic DOC and its link to watershed soils characteristics would be a significant step forward in the modelling of reservoir CO₂ diffusion. Indeed, had the G-res model been able to capture the baseline emissions more correctly in Batang Ai (close to zero given the very low DOC inputs), predictions would have nearly matched observations. Finally, note that the G-res model is not suitable to predict CO₂ uptake, which was observed in 32 % of flux measurements in Batang Ai due to an occasionally net autotrophic surface metabolism favoured under low C inputs (Bogard and del Giorgio, 2016). Improving this aspect of the model depends on the capacity to predict internal metabolism of aquatic systems at a global scale, which is currently lacking. Overall, reservoir CO₂ diffusion models may be less performant in certain regions, like Southeast Asia, due to an uneven spatial sampling distribution and a general lack of knowledge and data on C cycling in some parts of the world.

Our field-based estimate of Batang Ai CH₄ surface diffusion is 153 (±22) $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$, which differs by only 5 % and 15 % from the G-res and Barros et al. modelled predictions of 161 (132–197) and 176 $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ respectively (Table 2). Both models use as predictors age, a proxy for water temperature (air temperature or latitude), and an indicator of reservoir morphometry (% littoral area or mean depth), and Barros et al. (2011) also uses DOC input (Table S3). Similar predictors were identified in a recent global literature analysis, which also pointed out the role of trophic state in CH₄ diffusion, with Batang Ai falling well in the range of flux reported in other oligotrophic reservoirs (Deemer et al., 2016). Overall, our results show that global modelling frameworks for CH₄ surface diffusion capture the reality of Batang Ai reasonably well.

Measured estimate of reservoir-scale CH₄ ebullition averaged 3.4 (±1.9) $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ (Table 2), which is one of the lowest reported globally in reservoirs (Deemer et al., 2016) and is an order of magnitude lower than the 52 (32–83) $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ predicted by the G-res model (the only available model for reservoir ebullition). This contrasts with the perception that tropical reservoirs consistently have high ebullitive emissions and supports the idea that the supply of sediment organic matter, rather than temperature, is the primary driver of ebullition (Grinham et al., 2018). Batang Ai sediment properties and focusing patterns mentioned earlier could explain the model overestimation of CH₄ ebullition. The G-res model considers the fraction of littoral area and horizontal radiance (a proxy for heat input) as predictors of ebullition rate but does not integrate other catchment properties. Building a stronger mechanistic understanding of the effect of sediment composition and accumulation patterns on CH₄ bubbling may improve our ability to more accurately predict reservoir ebullition flux.

Our empirical estimate shows that 409 (±23) and 1798 (±255) $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ are emitted as CO₂ and CH₄ respectively downstream of the dam (including degassing), accounting for 89 % of Batang Ai GHG emissions (Table 2). Currently there is no available model predicting downstream GHG emissions from reservoirs, except the G-res model which is able to predict only the CH₄ degassing part of this flux. Modelled CH₄ degassing in Batang Ai is 468 (266–832) $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ compared to an estimated 1342 (±190) $\mathrm{g}{\mathrm{CO}}_{\mathrm{2}}\mathrm{eq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ based on our measurements. Predictive variables used to model CH₄ degassing are modelled CH₄ surface diffusion (based on % littoral area and temperature) and water retention time (Table S3). In Batang Ai main basin, the strong and permanent stratification favours oxygen depletion in the hypolimnion, which promotes deep CH₄ accumulation combined with a decoupling between surface and deep water layers. The model relies strongly on surface CH₄ patterns to predict excess CH₄ in the deep layer, which could explain why it underestimates CH₄ degassing in Batang Ai. Similar strong stratification patterns are ubiquitous in the tropics, with a recent study suggesting a large majority of tropical reservoirs are monomictic or oligomictic (Lehmusluoto et al., 1997; Winton et al., 2019) and hence more often stratified than temperate and boreal ones. This suggests that CH₄ degassing is potentially more frequently underestimated in low-latitude reservoirs. The G-res effort to predict CH₄ degassing is much needed given the importance of this pathway, and the next step would be to refine this model and develop predictions for other currently missing fluxes like CO₂ degassing and downstream emissions in the outflow. Our results suggest that improving latter aspects requires a better capacity to predict GHG accumulation in deep reservoirs layers across a wide range of stratification regimes.