the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A meta-analysis on environmental drivers of marine phytoplankton C : N : P
Katsumi Matsumoto
The elemental stoichiometry of marine phytoplankton plays a critical role in global biogeochemical cycles through its impact on nutrient cycling, secondary production, and carbon export. Although extensive laboratory experiments have been carried out over the years to assess the influence of different environmental drivers on the elemental composition of phytoplankton, a comprehensive quantitative assessment of the processes is still lacking. Here, we synthesized the responses of P:C and N:C ratios of marine phytoplankton to five major drivers (inorganic phosphorus, inorganic nitrogen, inorganic iron, irradiance, and temperature) by a meta-analysis of experimental data across 366 experiments from 104 journal articles. Our results show that the response of these ratios to changes in macronutrients is consistent across all the studies, where the increase in nutrient availability is positively related to changes in P:C and N:C ratios. We found that eukaryotic phytoplankton are more sensitive to the changes in macronutrients compared to prokaryotes, possibly due to their larger cell size and their abilities to regulate their gene expression patterns quickly. The effect of irradiance was significant and constant across all studies, where an increase in irradiance decreased both P:C and N:C. The P:C ratio decreased significantly with warming, but the response to temperature changes was mixed depending on the culture growth mode and the growth phase at the time of harvest. Along with other oceanographic conditions of the subtropical gyres (e.g., low macronutrient availability), the elevated temperature may explain why P:C is consistently low in subtropical oceans. Iron addition did not systematically change either P:C or N:C. Overall, our findings highlight the high stoichiometric plasticity of eukaryotes and the importance of macronutrients in determining P:C and N:C ratios, which both provide us insights on how to understand and model plankton diversity and productivity.
- Article
(1504 KB) -
Supplement
(429 KB) - BibTeX
- EndNote
Elemental stoichiometry of biological production in the surface ocean plays a crucial role in the cycling of elements in the global ocean. The elemental ratio between carbon, nitrogen (N), and phosphorus (P) in exported organic matter expressed in terms of the ratio helps determine how much atmospheric carbon is sequestered in the deep ocean with respect to the availability of limiting nutrients. On geologic timescales, the N:P ratio reflects the relative availability of nitrate with respect to phosphate, both of which are externally supplied from the atmosphere via nitrogen fixation and/or continents via river supply and lost by denitrification and burial (Broecker, 1982; Lenton and Watson, 2000; Redfield, 1958; Tyrrell, 1999). On shorter timescales, the average stoichiometry of exported bulk particulate organic matter reflects the elemental stoichiometry of phytoplankton (Bonachela et al., 2016; Garcia et al., 2018; Martiny et al., 2013b), with additional influences from biological diversity and secondary processing of organic matter by zooplankton and heterotrophic bacteria. In the face of global change, understanding and quantifying the mechanisms that lead to variability in ratios are crucial in order to have an accurate projection of future climate change.
A key unresolved question is what determines of individual phytoplankton. Phytoplankton grows in the upper light-lit layer of the ocean, where the amount of inorganic nutrients, light, and temperature vary spatially and temporally. Laboratory studies show that these fluctuations trigger responses at the cellular level, whereby cells modify resource allocation in order to adapt optimally to their ambient environment (Geider and La Roche, 2002). For example, phytoplankton may alter resource allocation between the P-rich biosynthetic apparatus, N-rich light-harvesting apparatus, and C-rich energy storage reserves (Moreno and Martiny, 2018). Under a typical future warming scenario, the global ocean is expected to undergo changes in nutrient availability, temperature, and irradiance (Boyd et al., 2010). These changes are likely to have profound effects on the physiology of phytoplankton (Finkel et al., 2010; van de Waal et al., 2010), and observations show that competitive phytoplankton species can acclimate and adapt to changes in temperature, irradiance, and nutrients on decadal timescales (Irwin et al., 2015). Numerous laboratory and field experiments have been conducted thus far to study the relationship between the ratio of phytoplankton and environmental drivers. It is, however, challenging to synthesize those studies and generalize the response of phytoplankton to changes in environmental drivers. Individual studies employ different sets of statistical analyses to characterize the effects of the environmental driver(s) on elemental ratios, ranging from a simple t test to more complex mixed models, which makes interstudy comparisons challenging. In addition, since environmentally induced trait changes are driven by a combination of plasticity (acclimation), adaptation, and life history (Collins et al., 2020; Ward et al., 2019), stoichiometric responses of phytoplankton can be variable even amongst closely related species.
Meta-analysis/systematic review is a powerful statistical framework for synthesizing and integrating research results obtained from independent studies and for uncovering general trends (Gurevitch et al., 2018). The seminal synthesis by Geider and La Roche (2002), as well as the more recent work by Persson et al. (2010), has shown that C:P and N:P could vary by up to a factor of 20 between nutrient-replete and nutrient-limited cells. These studies have also shown that the C:N ratio can be modestly plastic due to nutrient limitation. A meta-analysis study by Hillebrand et al. (2013) highlighted the importance of growth rate in determining elemental stoichiometry and showed that both C:P and N:P ratios decrease with the increasing growth rate. Yvon-Durocher et al. (2015) investigated the role of temperature in modulating . Although their dataset was limited to studies conducted prior to 1996, they have shown a statistically significant relationship between C:P and temperature increase. MacIntyre et al. (2002) and Thrane et al. (2016) have shown that irradiance plays an important role in controlling optimal cellular C:N and N:P ratios. Most recently, Moreno and Martiny (2018) provided a comprehensive summary of how environmental conditions regulate cellular stoichiometry from a physiological perspective.
Here, we present results from a systematic literature review and subsequent meta-analysis to quantify how five key environmental drivers affect C:P and C:N ratios of marine phytoplankton. Unlike previous meta-analyses on the elemental stoichiometry of phytoplankton that strictly synthesized the effect of a single environmental driver, our study assessed the effects of five drivers, specifically for marine phytoplankton species. Importantly, we use a unique newly defined measure of effect size, a stoichiometry sensitivity factor (Tanioka and Matsumoto, 2017), which is a dimensionless parameter that relates a fractional change in P:C or N:C to a fractional change in a particular environmental driver. We compute the effect size for each driver–stoichiometry pair from independent studies and subsequently determine the weighted mean effect size for P:C and N:C ratios. Further, we compute the mean effect size within different subgroups of moderators such as plankton types and growth conditions to detect any systematic heterogeneity between those subgroups.
2.1 Bibliographic search and screening
We systematically screened peer-reviewed publications on monoculture laboratory experiment studies that assessed the effects of dissolved inorganic phosphorus, dissolved inorganic nitrogen, dissolved iron, irradiance, and temperature on P:C and N:C ratios of marine phytoplankton. These five environmental drivers are considered to be the top drivers of the open-ocean phytoplankton group in studies (Boyd et al., 2010, 2015). Although CO2 is another potentially important driver, we did not consider the effects of CO2 on elemental ratios. The previous meta-analysis studies showed that no generalization could be made concerning the direction of trends in P:C or N:C ratios as a function of CO2 concentration both in the laboratory-based experiments (Liu et al., 2010) and mesocosm/field-based experiments (Kim et al., 2018).
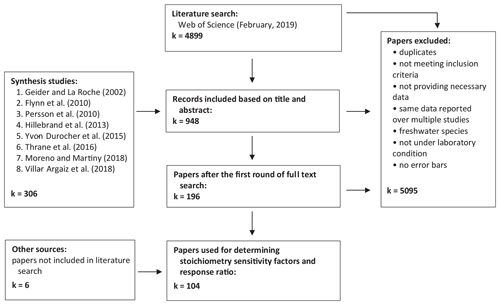
Firstly, we conducted a literature search using Web of Science (last accessed in February 2019) with the sequence of key terms (Table 1). This search yielded 4899 hits. We also closely inspected all the primary studies mentioned in the eight recent review papers on the elemental stoichiometry of phytoplankton in aquatic environments (Flynn et al., 2010; Geider and La Roche, 2002; Hillebrand et al., 2013; Moreno and Martiny, 2018; Persson et al., 2010; Thrane et al., 2016; Villar-Argaiz et al., 2018; Yvon-Durocher et al., 2015). The list is also augmented with six additional studies that did not appear in the literature search or the review papers but were cited elsewhere. Papers were further screened and selected to meet the following criteria. First, experiments must be carried out in controlled laboratory environments, where all the environmental factors, including temperature, photon flux density, salinity, and any other relevant conditions, are controlled. Second, all outdoor experiments, such as mesocosm or pond experiments, are excluded. Third, experiments must be conducted under unialgal/monoculture settings. However, we note that not all the experiments are carried out under strictly axenic conditions (i.e., not completely devoid of bacteria and viruses). Lastly, experiments must be conducted with replicates and must report either standard deviations or standard errors. Subsequent selection processes based on abstracts, graphs, tables, full text, and removal of duplicates led to a total of 104 journal articles (Fig. 1).
Table 1Keyword search terms used for literature search (Web of Science, February 2019). In the search field, “TS” refers to a field tag for “topic” and “*” is a wildcard search operator.

2.2 Data extraction
Data with means and standard deviations of P:C and N:C under varying environmental values provided by the original studies are used directly. GraphClick (Arizona Software Inc., 2010) was used to read off values from graphs when necessary. In cases where N:P and only one of either P:C or N:C is provided, the remaining ratio is determined by either multiplying or dividing by N:P. Similarly, elemental ratios are computed from the measurements of phytoplankton particulate organic carbon (POC), particulate organic nitrogen (PON), and particulate organic phosphorus (POP) when the ratios are not explicitly given in the original studies.
For nutrient (P, N, or Fe) manipulation studies, we selected two end-members (nutrient limited and nutrient replete) based on the definition given in the original studies. For batch and semicontinuous batch experiments, we compared the fractional change in initial concentrations between the nutrient-replete and nutrient-limited conditions when calculating the stoichiometry sensitivity factor (see Sect. 2.3.2). For continuous (chemostat or turbidostat) nutrient experiments, we used the difference in the inflow concentrations of the nutrient-replete and nutrient-limited cultures to determine the stoichiometry sensitivity factor. When multiple levels of concentrations are used, we selected two end-member points, one with the lowest growth rate and the other with the highest growth rate. When the growth rate was not provided in the original study, we selected two end-member values based on the highest and lowest nutrient uptake rate, chlorophyll concentration, or total concentration level with the underlying assumption that phytoplankton growth is nutrient limited within the range of nutrient levels considered.
For temperature and irradiance manipulations studies, we selected the lowest value and the optimal or saturating value that led to the maximum growth rate for phytoplankton. When the growth rate was not explicitly mentioned, we selected the lowest and the highest treatment values with the assumption that the phytoplankton is temperature or light limited within the range of values considered.
When more than two factors were manipulated in the same study, multiple experimental units are extracted if and only if each environmental driver was manipulated separately (i.e., conducted in a factorial manner). For example, we obtained a total of four experimental units from a two-by-two factorial study on temperature and nutrient: (1) comparing nutrient-limited vs. nutrient-replete treatment at low temperature; (2) same as in (1) at high temperature; (3) comparing low- vs. high-temperature response at nutrient-limited conditions; and (4) as in (3) at nutrient-replete conditions. An experimental unit refers to a controlled experiment of the same phytoplankton species between control and treatment groups, while all the other environmental factors are kept constant. If an experiment reported multiple measurements over time, only the final value was extracted.
We also extracted information on phytoplankton functional type (i.e., diatoms, coccolithophores, dinoflagellates, other eukaryotes, nondiazotrophic cyanobacteria, and diazotrophs; eukaryotes vs. prokaryotes; cold-water vs. temperate species), growth mode (i.e., batch vs. semicontinuous vs. continuous), growth phase at harvest (i.e., lag, exponential, stationary, decline), N form [, , , N2], and light regime (i.e., continuous vs. periodic light). Cold-water species is operationally defined if the control temperature (for P, N, Fe, or I manipulated experiments) or the maximum treatment temperature (for T manipulated experiments) was less than the threshold temperature of 10 ∘C. Attempted but ultimately discarded moderators for subsequent analysis mainly due to the lack of sample size include salinity, the axenic nature of the culture, and the number of generations required for acclimation before the start of the experiment.
Our final dataset consists of 241 experimental units of P:C and 366 experimental units of N:C from 104 journal articles encompassing seven taxonomic phyla (Bacillariophyta, Chlorophyta, Cryptophyta, Cyanobacteria, Haptophyta, Miozoa, and Ochrophyta) and six plankton functional types (diatoms, coccolithophores, dinoflagellates, other eukaryotes, nondiazotrophic cyanobacteria, and diazotrophs), and they are available in the Zenodo data repository (https://doi.org/10.5281/zenodo.3723121; Tanioka and Matsumoto, 2020).
2.3 Statistical analysis
We used two different measures of effect size for this study. One is a commonly used natural-logarithm-transformed response ratio, ln (RR) (Hedges et al., 1999), and the other is the stoichiometry sensitivity factor (Tanioka and Matsumoto, 2017). By using two separate measures, we can give a more robust prediction on how elemental stoichiometry varies with a change in a given environmental driver. All statistical analyses were performed with R v3.5.2 (R Core Team, 2018).
2.4 Response ratio
The natural-logarithm-transformed response ratio ln (RR) of the individual experimental unit and its variance (v) were calculated following Lajeunesse (2015):
Y denotes mean P:C or N:C, S is the standard deviation of that mean, and N is the sample size for the treatment (subscript t) and the control (subscript c) groups. We removed any experimental unit with a studentized residual value of ln (RR) exceeding the absolute value of 3 as an outlier (Viechtbauer and Cheung, 2010).
2.4.1 Stoichiometry sensitivity factor
The second effect size is the newly defined stoichiometry sensitivity factor (Tanioka and Matsumoto, 2017), which relates a fractional change in an elemental stoichiometry (response variable Y) to a fractional change in an environmental driver (variable X):
We estimated the variance of from the simple error propagation of Eq. (3) by assuming that the uncertainties associated with the environmental driver X are negligible compared to the errors associated with Y:
In essence, the magnitude of the s factor is a measure of how sensitive Y (P:C or N:C) is to a change in stressor level X, and the sign indicates whether Y changes in the same direction as X (positive sign) or in the opposite direction to X (negative sign). The s factor allows for different kinds of response: a linear response of Y with respect to X (), a near hyperbolic response that saturates at high X (), a logarithmic growth (), a decay (), and the null response (). This s-factor metric is conceptually similar to the homeostasis coefficient H (Persson et al., 2010), which relates the fractional change in resource nutrient stoichiometry to the fractional change in the organism's nutrient stoichiometry.
Importantly, the advantage of using as effect size is that its magnitude is a direct, quantitative measure of the strength of environmental drivers over the range of values examined. In contrast, ln (RR) only compares the effect of stressors without taking changes in the value of stressors into an account. Further, we can directly compare the strength of across different pairs of X and Y as it is nondimensional. For convenience, we use the term “s factor” in the rest of this paper when describing in a generic sense.
We used the same set of experimental units used in calculating ln (RR) to calculate s factors (i.e., any outliers are carried over). However, we did not calculate s factors for iron because the fractional change in dissolved iron concentration, often spanning multiple orders of magnitude, is substantially greater compared to the fractional change in P:C or N:C ratios, leading to an extremely low s factor. For temperature-manipulated experiments, we converted degrees Celsius into absolute temperature scale Kelvin. We used photon-flux density (PFD) measured in micromoles of photons per square meter per second (µmol photons m−2 s−1) for irradiance and micromolar (µM) for inorganic phosphorus and nitrogen experiments.
2.4.2 Meta-analysis and weighted mean responses
We calculated the weighted mean ln (RR) () and s factor () using the mixed-effects model with the R package metafor (Viechtbauer, 2010). The weighted mean (M) and its variance (V) were calculated as
where k is the total number of experimental units, Mj is effect size (ln (RR) or ) in experimental unit j, and Wj is the weighting factor, which is the inverse of the variance (Hedges et al., 1999). The 95 % confidence interval (CI) for the weighted mean was computed as
In the subsequent sections of this paper, the values of are back-transformed and represented as percent change:
and they are considered statistically significant if the 95 % CIs do not overlap with zero.
2.4.3 Testing the effect of moderators
We determined the effects of moderators by the rma function of the metafor package, which is an omnibus test of between-moderator heterogeneity based on χ2 distribution (Liang et al., 2020). The moderators we tested are plankton functional type (PFT), N form, growth mode, growth phase at extraction, and light regime (continuous vs. periodic). The effect of a moderator is considered significant when P value is less than 0.05. We use the weighted mean s factors in determining the effects of moderators except for iron experiments, where we used ln (RR) instead.
Phosphate addition increases both the mean P:C (235 % [95 % CI: 169 %, 322 %]) and N:C (23 % [13 %, 34 %]) significantly (Fig. 2b). The mean stoichiometric sensitivity factor of P:C () for change in phosphate is 0.21 [0.12, 0.29] (Table 2), which means that on average the P:C ratio of phytoplankton changes by 0.21 % for every 1 % increase in PO4 concentration. The effect of phosphate on N:C is an order of magnitude smaller but also statistically significant and positively correlated ( [0.004, 0.042]). Eukaryotic phytoplankton have significantly larger than prokaryotes (P<0.05, Fig. 3a), and the diatoms and coccolithophores especially have noticeably large (Fig. S1a, Table S1 in the Supplement). In addition, phytoplankton grown under chemostat experiments have significantly larger stoichiometric sensitivity compared to those grown under batch or chemostat conditions (Fig. 3b, P<0.001). There was no between-moderator heterogeneity in (Table S1).
Table 2Summary of the meta-analysis using the stoichiometry sensitivity factor and natural-logarithm-transformed response ratio. n, number of experimental units (numbers in bracket represent the number of outlier studies); , weighted mean stoichiometry sensitivity factor with environmental driver X and response variable Y; , weighted mean value of the natural-logarithm-transformed response ratio; ci.lb, lower boundary of 95 % CI; ci.ub, upper boundary of 95 % CI; sig., significance of the mean weighted effect size; ns, P>0.05; * P<0.05; P<0.01; P<0.001. Any experiment with a studentized residual value of ln (RR) exceeding 3 was removed as an outlier. Bold texts highlight statistically significant environmental drivers.
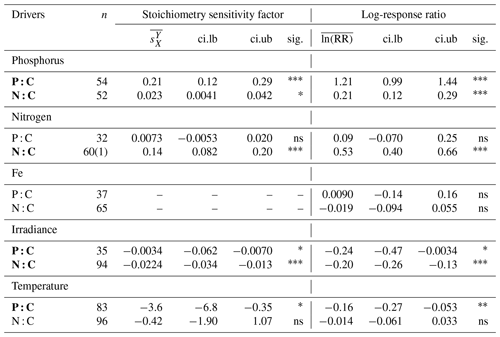
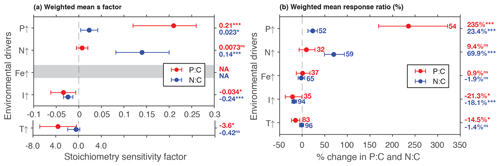
Figure 2Summary plot showing weighted mean responses of P:C and N:C using the (a) stoichiometry sensitivity factor and (b) % changes between control and treatment. Numbers next to the plots in (b) correspond to the number of experimental units, and the numbers are identical in (a). Numbers in the outside column are the weighted means. * P<0.05; P<0.01; P<0.001; ns, not significant. Note that the x axis is different for temperature experiments in (a).
The response of N:C to changes in inorganic nitrogen is similar to the response of P:C to PO4 changes where an increase in inorganic nitrogen raises N:C on average by 70 % [49 %, 93 %] (Fig. 2b), with the positive overall mean s factor of 0.14 [0.08, 0.20] (Table 2). Again, eukaryotic phytoplankton have higher stoichiometric sensitivity than prokaryotes (Fig. 3a, P<0.05). Nitrogen addition does not affect the weighted mean P:C (Fig. 2). Surprisingly, however, phytoplankton grown with the culture made up of nitrate and ammonia have significantly larger compared to those grown with nitrate only, with ammonia only, or under semidiazotrophic conditions (Fig. S2, Table S1). The small sample size, however, precludes us from making any firm conclusions.
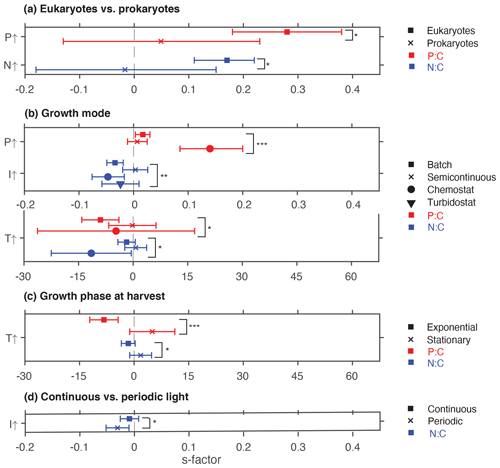
Figure 3Summary plot showing statistically significant effects of moderators. (a) Eukaryotes vs. prokaryotes, (b) growth mode, (c) growth phase at harvest, and (d) light regime. * P<0.05; P<0.01; P<0.001; ns, not significant.
An increase in iron availability does not lead to significant changes in both P:C and N:C (Fig. 2b). In addition, the effects of any moderators are not statistically significant (Table S1). Although diazotrophs that utilize N2 as their nitrogen source display a large response compared to other PFTs (−20 % [−36 %, 1 %]) (Table S1), their stoichiometric response is not quite statistically significant.
Increase in light availability significantly decreases both P:C (−21 % [−38 %, −0.4 %]) and N:C (−18 % [−23 %, −12 %]), with overall negative s factors ( [−0.062, −0.007], [−0.034, −0.013]). Although the magnitudes of both the response ratios and s factors are small compared to those of macronutrients, the responses across PFTs are consistent (Fig. S1c, f, Table S1). Phytoplankton grown under chemostat or batch conditions have significantly more negative compared to those grown under semicontinuous environments (Fig. 3b, P<0.01). Also, plankton grown under periodic light cycles have significantly lower compared to those grown under continuous light (Fig. 3d, P<0.05).
The response of P:C to warming is significant, where on average P:C decreases by 15 % [−24 %, −5 %] with negative mean s factor of [−6.8, −0.4] (Fig. 2a, b). The large magnitude of the s factor compared to that of other drivers reflects the fact that the fractional change in temperature (measured in kelvins) is considerably smaller than the fractional change in P:C. There is a significant variability due to growth mode where batch culture and chemostat culture experiments respectively have more negative s factors for P:C and N:C (Fig. 3b, P<0.05). Further, phytoplankton extracted during the exponential phase have noticeably more negative s factors than those extracted during the stationary growth phase (Fig. 3c) for both P:C (P<0.001) and N:C (P<0.05). The difference in mean response s-factor ratio amongst PFTs and between cold vs. temperate species is not statistically significant (Fig. S1e, Table S1). The responses of N:C are mixed, and the weighted mean effect sizes are therefore not statistically significant.
4.1 Basic framework
One of the fundamental tenets of chemical oceanography is the Redfield ratio, which implies that phytoplankton cells achieve a constant cellular ratio at the well-known molar ratio of 106 : 16 : 1 (Redfield et al., 1963). Constant is achieved for algal cells growing under steady-state conditions, where the balance is achieved between uptake of elements and assimilation into a cellular functional pool (Berman-Frank and Dubinsky, 1999; Klausmeier et al., 2004). Under such conditions, the growth rate of all cellular constituents averaged over one generation is the same, whether it is the carbon-specific, nitrogen-specific, or phosphorus-specific growth rates (Falkowski and Raven, 2007). In the real ocean, however, balanced growth is not always achieved due to short-term and long-term changes in the physical conditions of the ocean (Moore et al., 2013; Moore and Doney, 2007). For example, the deficiency of essential nutrients limits the formation of building blocks of new cells (e.g., N for proteins, P for nucleic acids and ATP), light limitation slows carbon assimilation (i.e., making of carbohydrates and reductants), and low temperature slows down the essential cellular transport and enzymatic reactions for growth (Madigan et al., 2006). A good example of unbalanced growth is phytoplankton blooms in the spring, where the transient changes in surface temperature, irradiance, and nutrient supply rate alter the growth rate and the elemental stoichiometry of phytoplankton (Polimene et al., 2015; Talarmin et al., 2016). In addition, future environmental variabilities caused by climate change are expected to cause temporal shifts in phytoplankton on longer timescales (Kwiatkowski et al., 2018, 2019; Tanioka and Matsumoto, 2017).
The degrees to which phytoplankton ratios are affected by environmental stresses depend both on the cellular stress response mechanisms and the magnitude of the environmental change as well as temporal variability of environmental drivers. Most types of stress responses can be divided into a stress-specific, primary response and a general secondary response (Brembu et al., 2017). The stress-specific responses are strong, robust, and consistently observed across photosynthetic organisms, while secondary responses are variable amongst different microorganisms. Primary and secondary responses are closely related to acclimation (plasticity response) and adaptation (evolutionary response), respectively. In essence, acclimation refers to the environmentally induced trait change of an organism in the absence of any genetic modification, while adaptation involves genetic changes driven by natural selection (Collins et al., 2020). Since primary responses do not involve genetic adjustment or natural selection, the responses are fast and often commonly shared amongst different marine phytoplankton. For example, changing the nutrient uptake affinity of a lineage within a generation in response to changing nutrient supply is a widely seen trait across all phytoplankton groups.
On the other hand, the secondary response depends both on the environmental condition and genotype (Brembu et al., 2017). The secondary responses take more time (usually up to a few hundred generations), and there is typically no single, unique response even when referring to a single species or functional group and a specific environmental driver (Collins et al., 2020). In the subsections below, we discuss any possible underlying cellular mechanisms responsible for producing changes in ratios (see Fig. 4 for schematic illustration).
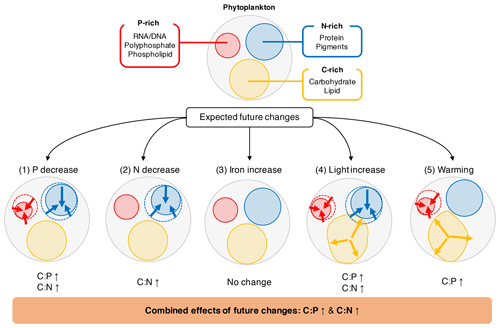
Figure 4Illustration of how the five environmental drivers under a typical future climate scenario affect the cellular allocation of volume between P-rich (red), N-rich (blue), and C-rich (orange) pools. The values for projected changes in C:P and C:N between 1981–2000 and 2081–2100 are given in Table 3.
4.2 Macronutrients (phosphate and nitrate)
Overall, we observe a consistent trend across all studies where P:C and N:C increases with an increase in the supply of dissolved inorganic phosphorus and nitrogen, respectively (Fig. 2). Since the changes in X:C and the supply of element X are positively related, and are both positive. Observations of phosphate (nitrate) against particulate organic matter P:C (N:C) across the global ocean indeed broadly follow this general trend (Galbraith and Martiny, 2015; Tanioka and Matsumoto, 2017).
Phytoplankton can temporally store excess nutrient intracellularly until the rate of carbon assimilation catches up to achieve steady-state balanced growth. Excess phosphorus, for example, can be stored mainly as polyphosphate (Dyhrman, 2016), and excess nitrate can be stored primarily as protein and free amino acids (Liefer et al., 2019; Sterner and Elser, 2002). Phytoplankton can consume these internal stores of nutrients (e.g., polyphosphates under P limitation) while maintaining the same level of carbon fixation, when the uptake of the nutrients does not meet their demand for growth (Cembella et al., 1984). Also, phytoplankton can reduce their number of ribosomes and RNA content under P limitation as RNA typically accounts for 50 % of nonstorage phosphorus (Hessen et al., 2017; Lin et al., 2016). Similarly, cells can reduce the synthesis of N-rich protein content under N limitation, resulting in a lower N:C ratio (Grosse et al., 2017; Liefer et al., 2019). These transient processes controlling the intracellular content of P or N (but not C content as much) likely result in a positive correlation between P:C and N:C with macronutrient concentrations.
Although and are consistently positive across all the studies, they are noticeably higher for eukaryotic phytoplankton than for prokaryotes (Fig. 3a). There are several hypotheses for explaining this trend. One of the most plausible explanations is related to the cell size and storage capacity difference amongst phytoplankton groups (Edwards et al., 2012; Lomas et al., 2014). Since eukaryotes are generally larger and possess more storage capacity, they are capable of greater luxury uptake and accumulation of internal P and N reserves when the nutrient is in excess (Talmy et al., 2014; Tozzi et al., 2004). When nutrients are scarce, the large cell size of eukaryotes allows them to increase their carbon content considerably by accumulating excess carbon as polysaccharides and lipids (Liefer et al., 2019; Lin et al., 2016). Another plausible hypothesis concerns variability in the acclimation/adaptation strategy at the genetic level (Dyhrman, 2016). Recent studies suggest that different phytoplankton groups exhibit different levels of transcriptional responsiveness and have different strategies for using nitrate (Lampe et al., 2019) and phosphate (Martiny et al., 2019). For example, diatoms have superior abilities to uptake and store nutrients by being able to quickly regulate their gene expression patterns required for nutrient uptake compared to other phytoplankton groups (Cáceres et al., 2019; Lampe et al., 2018, 2019). These hypotheses provide plausible explanations for why eukaryotes have elevated stoichiometry sensitivity to macronutrients compared to prokaryotes.
4.3 Iron
Iron is used in key biochemical processes such as electron transport, respiration, protein synthesis, and N fixation (Marchetti and Maldonado, 2016; Twining and Baines, 2013). Many of the iron-dependent processes are required for harvesting energy and for synthesizing biochemical intermediates (Price, 2005). As energy acquisition is equivalent to light acquisition in phototrophs, it makes sense that percent changes in stoichiometry for iron are similar in sign and magnitude to that of light (Fig. 2b). Although the effect of increasing iron on N:C is similar in sign and magnitude to that of light, increasing iron availability does not lead to a significant change in mean N:C (Fig. 2b). This suggests smaller-than-expected changes in the carbon or the nitrogen content (e.g., compounds such as porphyrin and phycobiliprotein that are essential for light harvesting) under Fe limitation (Falkowski and Raven, 2007; Twining and Baines, 2013). Alternatively, Fe availability may be affecting cellular C, N, and P more or less proportionally for all phytoplankton, leading to constant P:C and N:C (Greene et al., 1991; van Oijen et al., 2004; La Roche et al., 1993; Takeda, 1998). We also did not find noticeable heterogeneities in P:C and N:C amongst different moderators. Yet a number of laboratory studies, particularly those of picocyanobacteria (Prochlorococcus and Synechococcus), display significant effects of iron on (e.g., Cunningham and John, 2017). Despite their ecological importance (Biller et al., 2015; Flombaum et al., 2013), these taxa are understudied compared to diazotrophic cyanobacteria and diatoms. Future studies could focus on these picocyanobacteria and combine cellular information with other measures of phytoplankton physiology (e.g., chlorophyll fluorescence, Fv∕Fm ratio) to provide a more coherent, mechanistic picture of how changes in iron availability affect their physiology.
4.4 Irradiance
Light availability affects the photoacclimation strategy of phytoplankton and, subsequently, the cellular allocation of volume between the N-rich light-harvesting apparatus, P-rich biosynthetic apparatus, and C-rich energy storage reserves (Falkowski and LaRoche, 1991; Moreno and Martiny, 2018). At a fixed growth rate, high irradiance should downregulate the production of N-rich light-harvesting proteins and pigments to minimize the risk of photooxidative stress. Excess carbon fixed under high-irradiance conditions is stored as C-rich storage compounds such as lipids and polysaccharides (Berman-Frank and Dubinsky, 1999). As a result, N:C is expected to decrease under high light. In contrast, under low-light conditions, the macromolecular composition should favor the N-rich light-harvesting apparatus over C-rich storage reserves, thus elevating N:C. This line of reasoning would predict a negative relationship for the effect of irradiance increase on N:C, which is borne out in our meta-analysis (Fig. 2). Similarly, the P quota should be affected by a change in irradiance (Moreno and Martiny, 2018). P:C is expected to decrease at the increased light level because the total supply of inorganic phosphorus will not be able to keep up with the increase in photosynthetic carbon fixation, leading to a decoupled uptake of C and P (Hessen et al., 2002, 2008). Conversely, P:C is expected to increase at lower irradiance because carbon fixation decreases while phosphorus uptake remains constant (Urabe and Sterner, 1996).
The magnitudes of the weighted mean s factors for both P:C and N:C, however, are small, and the heterogeneity amongst PFTs is not discernible. This result agrees with a previous study that compiled experimental data prior to 1997 (MacIntyre et al., 2002). It is possible, however, that s factors obtained in our meta-analysis are underestimated as several factors may mute the effect of irradiance on the N:C ratio of phytoplankton. For example, an increase in nitrogen requirement for Rubisco (Li et al., 2015) and nutrient uptake machinery (Ågren, 2004) at high irradiance could partly offset the reduction in N content resulting from the downregulation of the light-harvesting apparatus. In addition, multiple studies have noted an increase in the protein demand (e.g., D1 protein) for repairing the damaged light-harvesting apparatus at high irradiance (Demmig-Adams and Adams, 1992; Li et al., 2015; Talmy et al., 2013), which also works in favor of stabilizing N content. Furthermore, we may have underestimated our s factor if the high end-member irradiance were above the optimal light level. This last reason is a fundamental limitation of s-factor determination as most studies we selected do not measure the actual optimal irradiance but simply report an arbitrary value that is either “high” or “light replete”.
Interestingly, we observed larger stoichiometric shifts in nutrient-replete batch and chemostat culture experiments compared to those conducted under semicontinuous settings (Fig. 3b). In addition, we found that experiments conducted under periodic daily light cycles have larger negative s factors compared to those experiments carried out under continuous light (Fig. 3d). These results are consistent with the global observation (Martiny et al., 2013a) and model studies (Arteaga et al., 2014; Talmy et al., 2014, 2016) which have shown that both the magnitude and temporal variability of N:C is higher in the nutrient-rich, light-limited polar regions than in the light-replete subtropics.
4.5 Temperature
We found that the P:C ratio decreases as temperature increases, while N:C remains relatively unchanged. Our result is consistent with a previous meta-analysis (Yvon-Durocher et al., 2015) that showed a decrease in phytoplankton P:C with temperature increase under laboratory and field settings. Moreover, our study and the study by Yvon-Durocher et al. (2015) support the idea that P:C is more flexible than N:C with respect to change in temperature, which suggests that intracellular P content is more sensitive to change in temperature than intracellular N content. Although the underlying mechanism for explaining lower P:C at higher temperature is not fully understood, there are currently three main hypotheses (Paul et al., 2015): (1) increase in metabolic stimulation of inorganic carbon uptake over phosphorus uptake; (2) increase in nutrient use efficiency which enables greater carbon fixation for given nutrient availability; and (3) translation compensation theory, which predicts that less P-rich ribosomes are required for protein synthesis and growth as the translation process becomes kinetically more efficient (McKew et al., 2015; Toseland et al., 2013; Woods et al., 2003; Xu et al., 2014; Zhu et al., 2017).
Differences in s factors amongst PFTs were not statistically significant, and none of the PFT displayed a statistically significant response in isolation. In other words, we did not see any PFT-specific adaptive/evolutionary response to warming (Schaum et al., 2018; Taucher et al., 2015). However, we observed noticeable variability due to the difference in culture growth mode (Fig. 3b) and the growth phase at extraction (Fig. 3c). The latter factor is particularly noticeable for P:C, where phytoplankton extracted during the nutrient-replete exponential growth phase have significantly more negative stoichiometric flexibility with a larger magnitude compared to those extracted during the nutrient-deplete stationary phase. This is consistent with multiple recent studies which suggest that the effect of temperature on growth and metabolic rates is greater when plankton are not nutrient or light limited (Aranguren-Gassis et al., 2019; Marañón et al., 2018; Roleda et al., 2013). This leads us to hypothesize that change in the P:C ratio due to ongoing warming will be more noticeable in the nutrient-rich polar regions, especially given the fact that temperature is already increasing at a startling rate due to polar amplification (Post et al., 2019).
4.6 Limitations and caveats
In the real ocean, none of the environmental changes discussed will likely occur in isolation because changes in irradiance, temperature, and nutrient availability are often linked. For example, an increase in sea surface temperature enhances the vertical stratification of the water column, which leads to greater levels of irradiance and nutrient limitation for phytoplankton trapped in a more shallow mixed layer (Boyd et al., 2015; Hutchins and Fu, 2017). Indeed, a meta-analysis on the pair-wise effects of environmental drivers on the elemental stoichiometry of phytoplankton has shown that the interactions of two environmental stressors can impose predominantly nonadditive effects to of phytoplankton so that the overall effect of multiple stressors is more than simply the sum of its parts (Villar-Argaiz et al., 2018). In addition to the individual phytoplankton stoichiometry, the bulk organic matter stoichiometry also reflects the phytoplankton community composition (Bonachela et al., 2016; Weber and Deutsch, 2010) as well as the stoichiometry of detrital material. Processes such as decomposition (Karl and Dobbs, 1998; Verity et al., 2000; Zakem and Levine, 2019), viral shunt (Jover et al., 2014), and preferential remineralization of phytoplankton macromolecules (Frigstad et al., 2011; Grabowski et al., 2019; Kreus et al., 2015) can also decouple phytoplankton from the bulk organic matter .
Table 3Projected changes in C:P (molar) and C:N (molar) between 1981–2000 and 2081–2100 given model-based projected changes in environmental drivers from Boyd et al. (2015). Changes in C:N and C:P are calculated separately for each driver, with s factors from Table 2 combined with reference of 146 : 20 : 1, a global biomass-weighted mean ratio of particulate organic matter (Martiny et al., 2013b). Ranges are derived from propagating uncertainties for the weighted mean s factors in Table 2. We used Eq. (9) in the main text for estimating the combined effect of multiple drivers.

4.7 Implications for global ocean biogeochemistry
Recent global biogeochemical models are starting to incorporate a more realistic representation of plankton physiology, which includes flexible phytoplankton (e.g., Buchanan et al., 2018). Modeling studies with flexible phytoplankton stoichiometry have demonstrated that proliferation of C-rich phytoplankton under future climate scenarios has the potential to buffer expected future decline in carbon export and net primary productivity caused by increased stratification (Kwiatkowski et al., 2018; Moreno et al., 2018; Tanioka and Matsumoto, 2017). This buffering effect cannot be simulated by biogeochemical models with fixed phytoplankton .
One way to model the dependencies of multiple environmental drivers (e.g., P, N, irradiance, and temperature) on of marine phytoplankton is the power-law formulation by Tanioka and Matsumoto (2017):
where subscript “0” indicates reference values. The s factors obtained from this meta-analysis are the exponents of Eq. (9) for different environmental drivers. Within the context of the power-law formulation, our results would indicate, for example, that eukaryotic phytoplankton would have the largest plasticity in P:C and N:C compared to prokaryotes with respect to the change in nutrient availability. Under future warming, high s factors of eukaryotes may thus play an important role in buffering the expected future decline in carbon export and net primary productivity (Kemp and Villareal, 2013).
We can give a first-order estimate of how much the elemental stoichiometry of marine phytoplankton may change in the future using Eq. (9) given a typical projection of the change in the key environmental drivers (Table 3; Fig. 4). Global climate models generally predict a decline in macronutrients and an increase in temperature and irradiance as a result of surface warming, increased vertical stratification, and reduced mixed layer depth (Bopp et al., 2013; Boyd et al., 2015). With large projected declines in macronutrients (−28.0 % for phosphate, −18.7 % for nitrate) we can predict an increase in C:P and C:N by ∼10 units (molar ratio) and ∼0.2 units, respectively, assuming the mean biomass-weighted particulate organic matter of as the present-day value (Martiny et al., 2013b). Further increase in C:P is expected due to the temperature increase of around 1 % (∼3 K). The total C:P change ranges from +6 to +25, considering all the uncertainties associated with the s factors. For C:N, we estimate an overall increase by 0.1–0.4 units largely driven by a decrease in nitrogen availability. The effect of change in irradiance is noticeably smaller (Table 3). In summary, this simple calculation highlights a potentially large shift for , whose change is predominantly driven by a reduction in macronutrients and temperature increase.
Our meta-analysis represents an important bottom-up approach in predicting how elemental stoichiometry of phytoplankton may evolve with climate change. We conclude that macronutrient availability is the most significant and shared environmental driver of . Changes in by macronutrients are driven by primary/plasticity responses commonly shared across phytoplankton. Our analysis shows that eukaryotic phytoplankton have higher stoichiometric plasticity compared to prokaryotes. Eukaryotes' large stoichiometric flexibility and high intrinsic growth rate can explain their unexpectedly high diversity (Malviya et al., 2016) and large contribution to carbon export globally, even in oligotrophic regions (Agusti et al., 2015; Nelson and Brzezinski, 1997). The effects of temperature on C:P are also significant, suggesting that a future ocean with elevated temperature and increased stratification will favor the production of carbon-rich organic matter. Future laboratory-based studies exploring how the multiple environmental drivers interactively alter the elemental composition of phytoplankton would be needed for a complete understanding. In addition, a further investigation on how a change in environmental drivers affects the stoichiometry of heterotrophs and zooplankton will be useful in filling the gaps to gain more mechanistic views on how these drivers affect the whole marine ecosystem.
All the data and codes used in the meta-analysis are available in the Zenodo data repository (https://doi.org/10.5281/zenodo.3723121, Tanioka and Matsumoto, 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-17-2939-2020-supplement.
TT and KM designed the study. TT carried out the literature review, data selection, and analysis and created the figures. Both TT and KM wrote the manuscript.
The authors declare that they have no conflict of interest.
Tatsuro Tanioka acknowledges support from the University of Minnesota Doctoral Dissertation Fellowship. Katsumi Matsumoto acknowledges sabbatical support by the Leverhulme Trust Visiting Professorship and the University of Oxford. We thank Carolyn Bishoff, Julia Kelly, and Amy Riegelman from the University of Minnesota Library for helping out the literature search and data selection. We also thank James Cotner for providing us feedback on the manuscript.
This research has been supported by the National Science Foundation, Division of Ocean Sciences (grant no. 1827948).
This paper was edited by Carol Robinson and reviewed by Alex Poulton and one anonymous referee.
Ågren, G. I.: The stoichiometry of autotrophs – Theory and observations, Ecol. Lett., 7, 185–191, https://doi.org/10.1111/j.1461-0248.2004.00567.x, 2004.
Agusti, S., González-Gordillo, J. I., Vaqué, D., Estrada, M., Cerezo, M. I., Salazar, G., Gasol, J. M., and Duarte, C. M.: Ubiquitous healthy diatoms in the deep sea confirm deep carbon injection by the biological pump, Nat. Commun., 6, 7608, https://doi.org/10.1038/ncomms8608, 2015.
Aranguren-Gassis, M., Kremer, C. T., Klausmeier, C. A., and Litchman, E.: Nitrogen limitation inhibits marine diatom adaptation to high temperatures, Ecol. Lett., 22, 1860–1869, https://doi.org/10.1111/ele.13378, 2019.
Arizona Software Inc.: GraphClick 3.0.2, available at: http://www.arizona-software.ch/graphclick/ (last access: 4 June 2020), 2010.
Arteaga, L., Pahlow, M., and Oschlies, A.: Global patterns of phytoplankton nutrient and light colimitation inferred from an optimality-based model, Global Biogeochem. Cy., 28, 648–661, https://doi.org/10.1002/2013GB004668, 2014.
Berman-Frank, I. and Dubinsky, Z.: Balanced Growth in Aquatic Plants: Myth or Reality?, Bioscience, 49, 29–37, https://doi.org/10.1525/bisi.1999.49.1.29, 1999.
Biller, S. J., Berube, P. M., Lindell, D., and Chisholm, S. W.: Prochlorococcus: The structure and function of collective diversity, Nat. Rev. Microbiol., 13, 13–27, https://doi.org/10.1038/nrmicro3378, 2015.
Bonachela, J. A., Klausmeier, C. A., Edwards, K. F., Litchman, E., and Levin, S. A.: The role of phytoplankton diversity in the emergent oceanic stoichiometry, J. Plankton Res., 38, 1021–1035, https://doi.org/10.1093/plankt/fbv087, 2016.
Bopp, L., Resplandy, L., Orr, J. C., Doney, S. C., Dunne, J. P., Gehlen, M., Halloran, P., Heinze, C., Ilyina, T., Séférian, R., Tjiputra, J., and Vichi, M.: Multiple stressors of ocean ecosystems in the 21st century: projections with CMIP5 models, Biogeosciences, 10, 6225–6245, https://doi.org/10.5194/bg-10-6225-2013, 2013.
Boyd, P. W., Strzepek, R., Fu, F., and Hutchins, D. A.: Environmental control of open-ocean phytoplankton groups: Now and in the future, Limnol. Oceanogr., 55, 1353–1376, https://doi.org/10.4319/lo.2010.55.3.1353, 2010.
Boyd, P. W., Lennartz, S. T., Glover, D. M., and Doney, S. C.: Biological ramifications of climate-change-mediated oceanic multi-stressors, Nat. Clim. Change, 5, 71–79, https://doi.org/10.1038/nclimate2441, 2015.
Brembu, T., Mühlroth, A., Alipanah, L., and Bones, A. M.: The effects of phosphorus limitation on carbon metabolism in diatoms, Philos. T. R. Soc. B, 372, 20160406, https://doi.org/10.1098/rstb.2016.0406, 2017.
Broecker, W. S.: Ocean chemistry during glacial time, Geochim. Cosmochim. Ac., 46, 1689–1705, https://doi.org/10.1016/0016-7037(82)90110-7, 1982.
Buchanan, P. J., Matear, R. J., Chase, Z., Phipps, S. J., and Bindoff, N. L.: Dynamic Biological Functioning Important for Simulating and Stabilizing Ocean Biogeochemistry, Global Biogeochem. Cy., 32, 565–593, https://doi.org/10.1002/2017GB005753, 2018.
Cáceres, C., Spatharis, S., Kaiserli, E., Smeti, E., Flowers, H., and Bonachela, J. A.: Temporal phosphate gradients reveal diverse acclimation responses in phytoplankton phosphate uptake, ISME J., 13, 2834–2845, https://doi.org/10.1038/s41396-019-0473-1, 2019.
Cembella, A. D., Antia, N. J., Harrison, P. J., and Rhee, G.-Y.: The Utilization of Inorganic and Organic Phosphorous Compounds as Nutrients by Eukaryotic Microalgae: A Multidisciplinary Perspective: Part 2, CRC Cr. Rev. Microbiol., 11, 13–81, https://doi.org/10.3109/10408418409105902, 1984.
Collins, S., Boyd, P. W., and Doblin, M. A.: Evolution, Microbes, and Changing Ocean Conditions, Annu. Rev. Mar. Sci., 12, 181–208, https://doi.org/10.1146/annurev-marine-010318-095311, 2020.
Cunningham, B. R. and John, S. G.: The effect of iron limitation on cyanobacteria major nutrient and trace element stoichiometry, Limnol. Oceanogr., 62, 846–858, https://doi.org/10.1002/lno.10484, 2017.
Demmig-Adams, B. and Adams, W. W.: Photoprotection and other responses of plants to high light stress, Annu. Rev. Plant Phys., 43, 599–626, https://doi.org/10.1146/annurev.pp.43.060192.003123, 1992.
Dyhrman, S. T.: Nutrients and Their Acquisition: Phosphorus Physiology in Microalgae, in: The Physiology of Microalgae, 155–183, Springer International Publishing, Cham., 2016.
Edwards, K. F., Thomas, M. K., Klausmeier, C. A., and Litchman, E.: Allometric scaling and taxonomic variation in nutrient utilization traits and maximum growth rate of phytoplankton, Limnol. Oceanogr., 57, 554–566, https://doi.org/10.4319/lo.2012.57.2.0554, 2012.
Falkowski, P. G. and LaRoche, J.: Acclimation to Spectral Irradiance in Algae, J. Phycol., 27, 8–14, https://doi.org/10.1111/j.0022-3646.1991.00008.x, 1991.
Falkowski, P. G. and Raven, J. A.: Aquatic Photosynthesis, Princeton University Press, Princeton, NJ, 2007.
Finkel, Z. V., Beardall, J., Flynn, K. J., Quigg, A., Rees, T. A. V., and Raven, J. A.: Phytoplankton in a changing world: cell size and elemental stoichiometry, J. Plankton Res., 32, 119–137, https://doi.org/10.1093/plankt/fbp098, 2010.
Flombaum, P., Gallegos, J. L., Gordillo, R. A., Rincón, J., Zabala, L. L., Jiao, N., Karl, D. M., Li, W. K. W., Lomas, M. W., Veneziano, D., Vera, C. S., Vrugt, J. A., and Martiny, A. C.: Present and future global distributions of the marine Cyanobacteria Prochlorococcus and Synechococcus, P. Natl. Acad. Sci. USA, 110, 9824–9829, https://doi.org/10.1073/pnas.1307701110, 2013.
Flynn, K. J., Raven, J. A., Rees, T. A. V., Finkel, Z., Quigg, A., and Beardall, J.: Is the growth rate hypothesis applicable to microalgae?, J. Phycol., 46, 1–12, https://doi.org/10.1111/j.1529-8817.2009.00756.x, 2010.
Frigstad, H., Andersen, T., Hessen, D. O., Naustvoll, L.-J., Johnsen, T. M., and Bellerby, R. G. J.: Seasonal variation in marine stoichiometry: can the composition of seston explain stable Redfield ratios?, Biogeosciences, 8, 2917–2933, https://doi.org/10.5194/bg-8-2917-2011, 2011.
Galbraith, E. D. and Martiny, A. C.: A simple nutrient-dependence mechanism for predicting the stoichiometry of marine ecosystems, P. Natl. Acad. Sci. USA, 112, 8199–8204, https://doi.org/10.1073/pnas.1423917112, 2015.
Garcia, C. A., Baer, S. E., Garcia, N. S., Rauschenberg, S., Twining, B. S., Lomas, M. W., and Martiny, A. C.: Nutrient supply controls particulate elemental concentrations and ratios in the low latitude eastern Indian Ocean, Nat. Commun., 9, 4868, https://doi.org/10.1038/s41467-018-06892-w, 2018.
Geider, R. and La Roche, J.: Redfield revisited: variability of in marine microalgae and its biochemical basis, Eur. J. Phycol., 37, 1–17, https://doi.org/10.1017/S0967026201003456, 2002.
Grabowski, E., Letelier, R. M., Laws, E. A., and Karl, D. M.: Coupling carbon and energy fluxes in the North Pacific Subtropical Gyre, Nat. Commun., 10, 1895, https://doi.org/10.1038/s41467-019-09772-z, 2019.
Greene, R. M., Geider, R. J., and Falkowski, P. G.: Effect of iron limitation on photosynthesis in a marine diatom, Limnol. Oceanogr., 36, 1772–1782, https://doi.org/10.4319/lo.1991.36.8.1772, 1991.
Grosse, J., van Breugel, P., Brussaard, C. P. D., and Boschker, H. T. S.: A biosynthesis view on nutrient stress in coastal phytoplankton, Limnol. Oceanogr., 62, 490–506, https://doi.org/10.1002/lno.10439, 2017.
Gurevitch, J., Koricheva, J., Nakagawa, S., and Stewart, G.: Meta-analysis and the science of research synthesis, Nature, 555, 175–182, https://doi.org/10.1038/nature25753, 2018.
Hedges, L. V., Gurevitch, J., and Curtis, P. S.: The Meta-Analysis of Response Ratios in Experimental Ecology, Ecology, 80, 1150, https://doi.org/10.2307/177062, 1999.
Hessen, D. O., Faerovig, P. J., and Andersen, T.: Light, Nutrients, and P:C Ratios in Algae: Grazer Performance Related to Food Quality and Quantity, Ecology, 83, 1886, https://doi.org/10.2307/3071772, 2002.
Hessen, D. O., Leu, E., Færøvig, P. J., and Falk Petersen, S.: Light and spectral properties as determinants of -ratios in phytoplankton, Deep-Sea Res. Pt. II, 55, 2169–2175, https://doi.org/10.1016/j.dsr2.2008.05.013, 2008.
Hessen, D. O., Hafslund, O. T., Andersen, T., Broch, C., Shala, N. K., and Wojewodzic, M. W.: Changes in Stoichiometry, Cellular RNA, and Alkaline Phosphatase Activity of Chlamydomonas in Response to Temperature and Nutrients, Front. Microbiol., 8, 18, https://doi.org/10.3389/fmicb.2017.00018, 2017.
Hillebrand, H., Steinert, G., Boersma, M., Malzahn, A., Léo Meunier, C., Plum, C., and Ptacnik, R.: Goldman revisited: Faster growing phytoplankton has lower N:P and lower stoichiometric flexibility, Limnol. Oceanogr., 58, 2076–2088, https://doi.org/10.4319/lo.2013.58.6.2076, 2013.
Hutchins, D. A. and Fu, F.-X.: Microorganisms and ocean global change, Nat. Microbiol., 2, 17058, https://doi.org/10.1038/nmicrobiol.2017.58, 2017.
Irwin, A. J., Finkel, Z. V., Müller-Karger, F. E., and Troccoli Ghinaglia, L.: Phytoplankton adapt to changing ocean environments, P. Natl. Acad. Sci. USA, 112, 5762–5766, https://doi.org/10.1073/pnas.1414752112, 2015.
Jover, L. F., Effler, T. C., Buchan, A., Wilhelm, S. W., and Weitz, J. S.: The elemental composition of virus particles: implications for marine biogeochemical cycles, Nat. Rev. Microbiol., 12, 519–528, https://doi.org/10.1038/nrmicro3289, 2014.
Karl, D. M. and Dobbs, F. C.: Molecular Approaches to Microbial Biomass Estimation in the Sea, in: Molecular Approaches to the Study of the Ocean, 29–89, Springer, the Netherlands, 1998.
Kemp, A. E. S. and Villareal, T. A.: High diatom production and export in stratified waters – A potential negative feedback to global warming, Prog. Oceanogr., 119, 4–23, https://doi.org/10.1016/j.pocean.2013.06.004, 2013.
Kim, J., Lee, K., Suh, Y., and Han, I.: Phytoplankton Do Not Produce Carbon-Rich Organic Matter in High CO2 Oceans, Geophys. Res. Lett., 45, 4189–4197, https://doi.org/10.1029/2017GL075865, 2018.
Klausmeier, C. A., Litchman, E., Daufresne, T., and Levin, S. A.: Optimal nitrogen-to-phosphorus stoichiometry of phytoplankton, Nature, 429, 171–174, https://doi.org/10.1038/nature02454, 2004.
Kreus, M., Schartau, M., Engel, A., Nausch, M., and Voss, M.: Variations in the elemental ratio of organic matter in the central Baltic Sea: Part I – Linking primary production to remineralization, Cont. Shelf Res., 100, 25–45, https://doi.org/10.1016/j.csr.2014.06.015, 2015.
Kwiatkowski, L., Aumont, O., Bopp, L., and Ciais, P.: The Impact of Variable Phytoplankton Stoichiometry on Projections of Primary Production, Food Quality, and Carbon Uptake in the Global Ocean, Global Biogeochem. Cy., 32, 516–528, https://doi.org/10.1002/2017GB005799, 2018.
Kwiatkowski, L., Aumont, O., and Bopp, L.: Consistent trophic amplification of marine biomass declines under climate change, Glob. Change Biol., 25, 218–229, https://doi.org/10.1111/gcb.14468, 2019.
Lajeunesse, M. J.: Bias and correction for the log response ratio in ecological meta-analysis, Ecology, 96, 2056–2063, https://doi.org/10.1890/14-2402.1, 2015.
Lampe, R. H., Cohen, N. R., Ellis, K. A., Bruland, K. W., Maldonado, M. T., Peterson, T. D., Till, C. P., Brzezinski, M. A., Bargu, S., Thamatrakoln, K., Kuzminov, F. I., Twining, B. S., and Marchetti, A.: Divergent gene expression among phytoplankton taxa in response to upwelling, Environ. Microbiol., 20, 3069–3082, https://doi.org/10.1111/1462-2920.14361, 2018.
Lampe, R. H., Wang, S., Cassar, N., and Marchetti, A.: Strategies among phytoplankton in response to alleviation of nutrient stress in a subtropical gyre, ISME J., 13, 2984–2997, https://doi.org/10.1038/s41396-019-0489-6, 2019.
La Roche, J., Geider, R. J., Graziano, L. M., Murray, H., and Lewis, K.: Induction of specific proteins in eukaryotic algae grown under iron-, phosphorus-, or nitrogen-deficient conditions, J. Phycol., 29, 767–777, https://doi.org/10.1111/j.0022-3646.1993.00767.x, 1993.
Lenton, T. M. and Watson, A. J.: Redfield revisited: 1. Regulation of nitrate, phosphate, and oxygen in the ocean, Global Biogeochem. Cy., 14, 225–248, https://doi.org/10.1029/1999GB900065, 2000.
Li, G., Brown, C. M., Jeans, J. A., Donaher, N. A., McCarthy, A., and Campbell, D. A.: The nitrogen costs of photosynthesis in a diatom under current and future pCO2, New Phytol., 205, 533–543, https://doi.org/10.1111/nph.13037, 2015.
Liang, X., Zhang, T., Lu, X., Ellsworth, D. S., BassiriRad, H., You, C., Wang, D., He, P., Deng, Q., Liu, H., Mo, J., and Ye, Q.: Global response patterns of plant photosynthesis to nitrogen addition: A meta-analysis, Glob. Change Biol., 26, 3585–3600, https://doi.org/10.1111/gcb.15071, 2020.
Liefer, J. D., Garg, A., Fyfe, M. H., Irwin, A. J., Benner, I., Brown, C. M., Follows, M. J., Omta, A. W., and Finkel, Z. V.: The Macromolecular Basis of Phytoplankton Under Nitrogen Starvation, Front. Microbiol., 10, 763, https://doi.org/10.3389/fmicb.2019.00763, 2019.
Lin, S., Litaker, R. W., and Sunda, W. G.: Phosphorus physiological ecology and molecular mechanisms in marine phytoplankton., J. Phycol., 52, 10–36, https://doi.org/10.1111/jpy.12365, 2016.
Liu, J., Weinbauer, M., Maier, C., Dai, M., and Gattuso, J.: Effect of ocean acidification on microbial diversity and on microbe-driven biogeochemistry and ecosystem functioning, Aquat. Microb. Ecol., 61, 291–305, https://doi.org/10.3354/ame01446, 2010.
Lomas, M. W., Bonachela, J. A., Levin, S. A., and Martiny, A. C.: Impact of ocean phytoplankton diversity on phosphate uptake, P. Natl. Acad. Sci., 111, 17540–17545, https://doi.org/10.1073/pnas.1420760111, 2014.
MacIntyre, H. L., Kana, T. M., Anning, T., and Geider, R. J.: Photoacclimation of photosynthesis irradiance response curves and photosynthetic pigments in microalgae and cyanobacteria, J. Phycol., 38, 17–38, https://doi.org/10.1046/j.1529-8817.2002.00094.x, 2002.
Madigan, M. T., Martinko, J. M., and Parker, J.: Brock biology of microorganisms, Pearson Prentice Hall, Upper Saddle River, 2006.
Malviya, S., Scalco, E., Audic, S., Vincent, F., Veluchamy, A., Poulain, J., Wincker, P., Iudicone, D., de Vargas, C., Bittner, L., Zingone, A., and Bowler, C.: Insights into global diatom distribution and diversity in the world's ocean, P. Natl. Acad. Sci., 113, E1516–E1525, https://doi.org/10.1073/pnas.1509523113, 2016.
Marañón, E., Lorenzo, M. P., Cermeño, P., and Mouriño-Carballido, B.: Nutrient limitation suppresses the temperature dependence of phytoplankton metabolic rates, ISME J., 12, 1836–1845, https://doi.org/10.1038/s41396-018-0105-1, 2018.
Marchetti, A. and Maldonado, M. T.: Iron, in: The Physiology of Microalgae, 233–279, Springer International Publishing, Cham., 2016.
Martiny, A. C., Vrugt, J. A., Primeau, F. W., and Lomas, M. W.: Regional variation in the particulate organic carbon to nitrogen ratio in the surface ocean, Global Biogeochem. Cy., 27, 723–731, https://doi.org/10.1002/gbc.20061, 2013a.
Martiny, A. C., Pham, C. T. A., Primeau, F. W., Vrugt, J. A., Moore, J. K., Levin, S. A., and Lomas, M. W.: Strong latitudinal patterns in the elemental ratios of marine plankton and organic matter, Nat. Geosci., 6, 279–283, https://doi.org/10.1038/ngeo1757, 2013b.
Martiny, A. C., Ustick, L., Garcia, A. C., and Lomas, M. W.: Genomic adaptation of marine phytoplankton populations regulates phosphate uptake, Limnol. Oceanogr., 65, S340–S350, https://doi.org/10.1002/lno.11252, 2019.
McKew, B. A., Metodieva, G., Raines, C. A., Metodiev, M. V., and Geider, R. J.: Acclimation of E miliania huxleyi (1516) to nutrient limitation involves precise modification of the proteome to scavenge alternative sources of N and P, Environ. Microbiol., 17, 4050–4062, https://doi.org/10.1111/1462-2920.12957, 2015.
Moore, C. M., Mills, M. M., Arrigo, K. R., Berman-Frank, I., Bopp, L., Boyd, P. W., Galbraith, E. D., Geider, R. J., Guieu, C., Jaccard, S. L., Jickells, T. D., La Roche, J., Lenton, T. M., Mahowald, N. M., Marañón, E., Marinov, I., Moore, J. K., Nakatsuka, T., Oschlies, A., Saito, M. A., Thingstad, T. F., Tsuda, A., and Ulloa, O.: Processes and patterns of oceanic nutrient limitation, Nat. Geosci., 6, 701–710, https://doi.org/10.1038/ngeo1765, 2013.
Moore, J. K. and Doney, S. C.: Iron availability limits the ocean nitrogen inventory stabilizing feedbacks between marine denitrification and nitrogen fixation, Global Biogeochem. Cy., 21, GB2001, https://doi.org/10.1029/2006GB002762, 2007.
Moreno, A. R. and Martiny, A. C.: Ecological Stoichiometry of Ocean Plankton, Annu. Rev. Mar. Sci., 10, 43–69, https://doi.org/10.1146/annurev-marine-121916-063126, 2018.
Moreno, A. R., Hagstrom, G. I., Primeau, F. W., Levin, S. A., and Martiny, A. C.: Marine phytoplankton stoichiometry mediates nonlinear interactions between nutrient supply, temperature, and atmospheric CO2, Biogeosciences, 15, 2761–2779, https://doi.org/10.5194/bg-15-2761-2018, 2018.
Nelson, D. M. and Brzezinski, M. A.: Diatom growth and productivity in an oligotropic midocean gyre: A 3-yr record from the Sargasso Sea near Bermuda, Limnol. Oceanogr., 42, 473–486, https://doi.org/10.4319/lo.1997.42.3.0473, 1997.
Paul, C., Matthiessen, B., and Sommer, U.: Warming, but not enhanced CO2 concentration, quantitatively and qualitatively affects phytoplankton biomass, Mar. Ecol.-Prog. Ser., 528, 39–51, https://doi.org/10.3354/meps11264, 2015.
Persson, J., Fink, P., Goto, A., Hood, J. M., Jonas, J., and Kato, S.: To be or not to be what you eat: regulation of stoichiometric homeostasis among autotrophs and heterotrophs, Oikos, 119, 741–751, https://doi.org/10.1111/j.1600-0706.2009.18545.x, 2010.
Polimene, L., Mitra, A., Sailley, S. F., Ciavatta, S., Widdicombe, C. E., Atkinson, A., and Allen, J. I.: Decrease in diatom palatability contributes to bloom formation in the Western English Channel, Prog. Oceanogr., 137, 484–497, https://doi.org/10.1016/j.pocean.2015.04.026, 2015.
Post, E., Alley, R. B., Christensen, T. R., Macias-Fauria, M., Forbes, B. C., Gooseff, M. N., Iler, A., Kerby, J. T., Laidre, K. L., Mann, M. E., Olofsson, J., Stroeve, J. C., Ulmer, F., Virginia, R. A., and Wang, M.: The polar regions in a 2 ∘C warmer world, Sci. Adv., 5, eaaw9883, https://doi.org/10.1126/sciadv.aaw9883, 2019.
Price, N. M.: The elemental stoichiometry and composition of an iron-limited diatom, Limnol. Oceanogr., 50, 1159–1171, https://doi.org/10.4319/lo.2005.50.4.1159, 2005.
R Core Team: R: A Language and Environment for Statistical Computing, available at: http://www.r-project.org/ (last access: 4 June 2020), 2018.
Redfield, A. C.: The biological control of chemical factors in the environment, Am. Sci., 46, 205–221, 1958.
Redfield, A. C., Ketchum, B. H., and Richards, F. A.: The influence of organisms on the composition of Seawater, in: The composition of seawater: Comparative and descriptive oceanography. The sea: ideas and observations on progress in the study of the seas, Vol. 2, edited by: Hill, M. N., 26–77, Interscience Publishers, New York, 1963.
Roleda, M. Y., Slocombe, S. P., Leakey, R. J. G., Day, J. G., Bell, E. M., and Stanley, M. S.: Effects of temperature and nutrient regimes on biomass and lipid production by six oleaginous microalgae in batch culture employing a two-phase cultivation strategy, Bioresource Technol., 129, 439–449, https://doi.org/10.1016/j.biortech.2012.11.043, 2013.
Schaum, C.-E., Buckling, A., Smirnoff, N., Studholme, D. J., and Yvon-Durocher, G.: Environmental fluctuations accelerate molecular evolution of thermal tolerance in a marine diatom, Nat. Commun., 9, 1719, https://doi.org/10.1038/s41467-018-03906-5, 2018.
Sterner, R. W. and Elser, J. J.: Ecological stoichiometry: the biology of elements from molecules to the biosphere, Princeton University Press, Princeton, NJ, 2002.
Takeda, S.: Influence of iron availability on nutrient consumption ratio of diatoms in oceanic waters, Nature, 393, 774–777, https://doi.org/10.1038/31674, 1998.
Talarmin, A., Lomas, M. W., Bozec, Y., Savoye, N., Frigstad, H., Karl, D. M., and Martiny, A. C.: Seasonal and long-term changes in elemental concentrations and ratios of marine particulate organic matter, Global Biogeochem. Cy., 30, 1699–1711, https://doi.org/10.1002/2016GB005409, 2016.
Talmy, D., Blackford, J., Hardman-Mountford, N. J., Dumbrell, A. J., and Geider, R. J.: An optimality model of photoadaptation in contrasting aquatic light regimes, Limnol. Oceanogr., 58, 1802–1818, https://doi.org/10.4319/lo.2013.58.5.1802, 2013.
Talmy, D., Blackford, J., Hardman-Mountford, N. J., Polimene, L., Follows, M. J., and Geider, R. J.: Flexible C : N ratio enhances metabolism of large phytoplankton when resource supply is intermittent, Biogeosciences, 11, 4881–4895, https://doi.org/10.5194/bg-11-4881-2014, 2014.
Talmy, D., Martiny, A. C., Hill, C., Hickman, A. E., and Follows, M. J.: Microzooplankton regulation of surface ocean POC : PON ratios, Global Biogeochem. Cy., 30, 311–332, https://doi.org/10.1002/2015GB005273, 2016.
Tanioka, T. and Matsumoto, K.: Buffering of Ocean Export Production by Flexible Elemental Stoichiometry of Particulate Organic Matter, Global Biogeochem. Cy., 31, 1528–1542, https://doi.org/10.1002/2017GB005670, 2017.
Tanioka, T. and Matsumoto, K.: Supporting Data for Tanioka and Matsumoto (2020), Zenodo, https://doi.org/10.5281/zenodo.3723121, 2020.
Taucher, J., Jones, J., James, A., Brzezinski, M. A., Carlson, C. A., Riebesell, U., and Passow, U.: Combined effects of CO2 and temperature on carbon uptake and partitioning by the marine diatoms Thalassiosira weissflogii and Dactyliosolen fragilissimus, Limnol. Oceanogr., 60, 901–919, https://doi.org/10.1002/lno.10063, 2015.
Thrane, J.-E., Hessen, D. O., and Andersen, T.: The impact of irradiance on optimal and cellular nitrogen to phosphorus ratios in phytoplankton, Ecol. Lett., 19, 880–888, https://doi.org/10.1111/ele.12623, 2016.
Toseland, A., Daines, S. J., Clark, J. R., Kirkham, A., Strauss, J., Uhlig, C., Lenton, T. M., Valentin, K., Pearson, G. A., Moulton, V., and Mock, T.: The impact of temperature on marine phytoplankton resource allocation and metabolism, Nat. Clim. Change, 3, 979–984, https://doi.org/10.1038/nclimate1989, 2013.
Tozzi, S., Schofield, O., and Falkowski, P.: Historical climate change and ocean turbulence as selective agents for two key phytoplankton functional groups, Mar. Ecol.-Prog. Ser., 274, 123–132, https://doi.org/10.3354/meps274123, 2004.
Twining, B. S. and Baines, S. B.: The Trace Metal Composition of Marine Phytoplankton, Annu. Rev. Mar. Sci., 5, 191–215, https://doi.org/10.1146/annurev-marine-121211-172322, 2013.
Tyrrell, T.: The relative influences of nitrogen and phosphorus on oceanic primary production, Nature, 400, 525–531, https://doi.org/10.1038/22941, 1999.
Urabe, J. and Sterner, R. W.: Regulation of herbivore growth by the balance of light and nutrients, P. Natl. Acad. Sci., 93, 8465–8469, https://doi.org/10.1073/pnas.93.16.8465, 1996.
van de Waal, D. B., Verschoor, A. M., Verspagen, J. M., van Donk, E., and Huisman, J.: Climate-driven changes in the ecological stoichiometry of aquatic ecosystems, Front. Ecol. Environ., 8, 145–152, https://doi.org/10.1890/080178, 2010.
van Oijen, T., van Leeuwe, M. A., Gieskes, W. W., and de Baar, H. J.: Effects of iron limitation on photosynthesis and carbohydrate metabolism in the Antarctic diatom Chaetoceros brevis (Bacillariophyceae), Eur. J. Phycol., 39, 161–171, https://doi.org/10.1080/0967026042000202127, 2004.
Verity, P. G., Williams, S. C., and Hong, Y.: Formation, degradation, and mass : volume ratios of detritus derived from decaying phytoplankton, Mar. Ecol.-Prog. Ser., 207, 53–68, https://doi.org/10.3354/meps207053, 2000.
Viechtbauer, W.: Conducting Meta-Analyses in R with the metafor Package, J. Stat. Softw., 36, 1–48, https://doi.org/10.18637/jss.v036.i03, 2010.
Viechtbauer, W. and Cheung, M. W.-L.: Outlier and influence diagnostics for meta-analysis, Res. Synth. Methods, 1, 112–125, https://doi.org/10.1002/jrsm.11, 2010.
Villar-Argaiz, M., Medina-Sánchez, J. M., Biddanda, B. A., and Carrillo, P.: Predominant Non-additive Effects of Multiple Stressors on Autotroph Ratios Propagate in Freshwater and Marine Food Webs, Front. Microbiol., 9, 69, https://doi.org/10.3389/fmicb.2018.00069, 2018.
Ward, B. A., Collins, S., Dutkiewicz, S., Gibbs, S., Bown, P., Ridgwell, A., Sauterey, B., Wilson, J. D., and Oschlies, A.: Considering the Role of Adaptive Evolution in Models of the Ocean and Climate System, J. Adv. Model. Earth Sy., 11, 1–19, https://doi.org/10.1029/2018MS001452, 2019.
Weber, T. S. and Deutsch, C. A.: Ocean nutrient ratios governed by plankton biogeography, Nature, 467, 550–554, https://doi.org/10.1038/nature09403, 2010.
Woods, H. A., Makino, W., Cotner, J. B., Hobbie, S. E., Harrison, J. F., Acharya, K., and Elser, J. J.: Temperature and the chemical composition of poikilothermic organisms, Funct. Ecol., 17, 237–245, https://doi.org/10.1046/j.1365-2435.2003.00724.x, 2003.
Xu, J., Gao, K., Li, Y., and Hutchins, D.: Physiological and biochemical responses of diatoms to projected ocean changes, Mar. Ecol.-Prog. Ser., 515, 73–81, https://doi.org/10.3354/meps11026, 2014.
Yvon-Durocher, G., Dossena, M., Trimmer, M., Woodward, G., and Allen, A. P.: Temperature and the biogeography of algal stoichiometry, Global Ecol. Biogeogr., 24, 562–570, https://doi.org/10.1111/geb.12280, 2015.
Zakem, E. J. and Levine, N. M.: Systematic variation in marine dissolved organic matter stoichiometry and remineralization ratios as a function of lability, Global Biogeochem. Cy., 33, 1389–1407, https://doi.org/10.1029/2019GB006375, 2019.
Zhu, Z., Qu, P., Gale, J., Fu, F., and Hutchins, D. A.: Individual and interactive effects of warming and CO2 on Pseudo-nitzschia subcurvata and Phaeocystis antarctica, two dominant phytoplankton from the Ross Sea, Antarctica, Biogeosciences, 14, 5281–5295, https://doi.org/10.5194/bg-14-5281-2017, 2017.