the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Current, steady-state and historical weathering rates of base cations at two forest sites in northern and southern Sweden: a comparison of three methods
Sophie Casetou-Gustafson
Harald Grip
Stephen Hillier
Sune Linder
Bengt A. Olsson
Magnus Simonsson
Johan Stendahl
Reliable and accurate methods for estimating soil mineral weathering rates are required tools in evaluating the sustainability of increased harvesting of forest biomass and assessments of critical loads of acidity. A variety of methods that differ in concept, temporal and spatial scale, and data requirements are available for measuring weathering rates. In this study, causes of discrepancies in weathering rates between methods were analysed and were classified as being either conceptual (inevitable) or random. The release rates of base cations (BCs; Ca, Mg, K, Na) by weathering were estimated in podzolised glacial tills at two experimental forest sites, Asa and Flakaliden, in southern and northern Sweden, respectively. Three different methods were used: (i) historical weathering since deglaciation estimated by the depletion method, using Zr as the assumed inert reference; (ii) steady-state weathering rate estimated with the PROFILE model, based on quantitative analysis of soil mineralogy; and (iii) BC budget at stand scale, using measured deposition, leaching and changes in base cation stocks in biomass and soil over a period of 12 years. In the 0–50 cm soil horizon historical weathering of BCs was 10.6 and 34.1 mmolc m−2 yr−1, at Asa and Flakaliden, respectively. Corresponding values of PROFILE weathering rates were 37.1 and 42.7 mmolc m−2 yr−1. The PROFILE results indicated that steady-state weathering rate increased with soil depth as a function of exposed mineral surface area, reaching a maximum rate at 80 cm (Asa) and 60 cm (Flakaliden). In contrast, the depletion method indicated that the largest postglacial losses were in upper soil horizons, particularly at Flakaliden.
With the exception of Mg and Ca in shallow soil horizons, PROFILE produced higher weathering rates than the depletion method, particularly of K and Na in deeper soil horizons. The lower weathering rates of the depletion method were partly explained by natural and anthropogenic variability in Zr gradients. The base cation budget approach produced significantly higher weathering rates of BCs, 134.6 mmolc m−2 yr−1 at Asa and 73.2 mmolc m−2 yr−1 at Flakaliden, due to high rates estimated for the nutrient elements Ca, Mg and K, whereas weathering rates were lower and similar to those for the depletion method (6.6 and 2.2 mmolc m−2 yr−1 at Asa and Flakaliden). The large discrepancy in weathering rates for Ca, Mg and K between the base cation budget approach and the other methods suggests additional sources for tree uptake in the soil not captured by measurements.
- Article
(2671 KB) -
Supplement
(1785 KB) - BibTeX
- EndNote
Silicate weathering is the major long-term source of base cations in forest ecosystems (Sverdrup and Warfvinge, 1988) and is therefore crucial for sustainable plant production and for proton consumption, counteracting soil and water acidification (Nilsson et al., 1982; Hedin et al., 1994; Likens et al., 1998; Bailey et al., 2003). These effects of weathering are important in areas where in the past high sulfur (S) deposition has caused severe acidification of forest soils and waters (Reuss and Johnson, 1986), for example in southern Scandinavia, the northeastern USA and southeastern Canada, regions where felsic igneous bedrock and less readily weatherable soils are abundant (Likens and Bormann, 1974; Nilsson and Tyler, 1995). To aid the multilateral negotiations on reducing emissions of acidifying air pollution, the effect-based concept of critical loads of acidity was developed in the late 1980s (Lidskog and Sundqvist, 2002). One advantage of the concept was that the critical loads could be calculated and mapped for different regions at various scales. Because weathering is a key component in estimates of critical loads, reliable applications of the critical load concept required that weathering rates could be estimated with sufficient accuracy at a regional scale (Sverdrup and de Vries, 1994).
By 1990 in most European countries, the trend of increasing S emissions since the 1950s started to abate (Grennfelt and Hov, 2005) with a simultaneous decrease in atmospheric deposition of base cations (Hedin et al., 1994). In Sweden, forest growth has at the same time gradually become a relatively more important source to soil acidity (Iwald et al., 2013). In addition to the reduction in S deposition, this change has partly been driven by increased use of logging residues for energy production (i.e. whole-tree harvesting), and probably also by a general higher forest production over recent decades in Sweden (Binkley and Högberg, 2016). Soil acidification by forest growth is principally caused by accumulation of base cations in tree biomass in excess of anion uptake (Nilsson et al., 1982). The return of base cations in remaining biomass and residues following harvesting determines to what extent the acid load can be neutralised. The soil acidification effect of whole-tree compared to stem-only harvesting has been demonstrated in long-term field experiments (Olsson et al., 1996; Zetterberg et al., 2013). The combined effects can therefore impede recovery from acidification and place increasing demands on nutrient supply.
The sustainability of increased harvest intensity of forest biomass has been questioned and analysed in many studies from various viewpoints and with various criteria with a focus on Europe and North America (e.g. Boyle et al., 1973; Paré et al., 2002; Thiffault et al., 2011; Achat et al., 2015; De Jong et al., 2017; Ranius et al., 2018), where the role of weathering in maintaining base cation balance is one criterion. The impact of increased use of logging residues on base cation balances in Swedish forest soils has been examined in several previous studies (Sverdrup and Rosén, 1998; Akselsson et al., 2007). A regional-scale study on Swedish forest soils found that, in parts of Sweden, base cation losses can occur at rates that lead to very low base saturation of the soils, possibly leading to negative effects on soil fertility and runoff water quality within just one forest rotation (Akselsson et al., 2007). In their study, base cation depletion in the soil was found to be more common after whole-tree harvesting than stem-only harvesting, especially for Norway spruce, with deficits being more common in southern than in northern (boreal) Sweden.
In regional assessments of the sustainability of different harvesting regimes, the estimated weathering rate has a strong influence on the base cation balance. Klaminder et al. (2011) found that different approaches to estimating weathering rates for a forested catchment in northern Sweden yielded results that differed substantially and that uncertainties in the methods had a great influence on the predicted sustainability of different harvesting practices. Futter et al. (2012) compiled weathering rates estimated at 82 sites on three continents, using different methods, and they found both large between-site and within-site differences in the values. Differences in input data can be attributed to different timescales used when acquiring different input data, challenges determining accurate mineralogical compositions and the use of field data compared with laboratory data (Van der Salm, 2001; Futter et al., 2012). Thus, they recommend that at least three different approaches be applied per study site to evaluate the precision in weathering estimates.
Different approaches to estimate weathering rates are likely to produce different estimates due to their conceptual differences, but additional sources to discrepancies of a more random nature will also appear. The latter may be due to misfits in spatial scales, measurement errors or uncertainties in model parameterisation. A number of studies comparing different approaches to estimating weathering rates have been published (e.g. Kolka et al., 1996; Sverdrup et al., 1998; Van der Salm et al., 2001; Ouimet and Dechesne, 2005; Whitfield et al., 2006, 2011; Koseva et al., 2010; Klaminder et al., 2011; Stendahl et al., 2013; Futter et al., 2012; Augustin et al., 2016) such that additional studies on this issue may seem redundant. However, several of these comparison studies can be criticised for poor harmonisation with respect to the spatial scale, or because nutrient uptake in biomass and soil change have been neglected or poorly quantified in approaches where these processes are relevant for the estimates. Poor harmonisation makes it difficult to separate conceptual from random sources of discrepancies. We therefore see a need for improved comparisons, performed with a spatially constrained and refined harmonisation in the sense of Futter et al. (2012) and combined with a focus on forest soils, tree nutrition and growth. Starting from the viewpoint that no method provides the “true” estimate of weathering, and acknowledging that different approaches are conceptually different and use different input data, in the present paper we examined three approaches: (1) “historical weathering” based on geochemical investigation of the soil profile, (2) modelled present weathering rate and (3) present weathering rate based on cation balances at the ecosystem level.
The choice of methods was primarily based on the fact that rates of weathering may (do) vary over time (Klaminder et al., 2011; Stendahl et al., 2013). The average weathering under long-term environmental change, i.e. historical weathering, is thus different from the weathering potential under present-day environmental conditions, i.e. “present-day weathering”, which is why we need to be able to consider historical weathering when assessing present-day weathering rates. Moreover, present-day weathering rates estimated by models based on the steady-state concept, which lacks the dimension of time, may differ from dynamic estimates of weathering rates derived from measured base cation budgets. These three different concepts of estimating weathering cannot be covered by a single method (Klaminder et al., 2011; Futter et al., 2012). Indeed, weathering estimates based on these concepts have often differed grossly from pedon to catchment scale, whereas truly harmonised comparisons of methods require that methods are tested uniformly at the same spatial scale. This spatial scale can be the pedon, which also contains the major part of the mineral nutrient sources in the soil available for forest growth. To our knowledge, Kolka et al. (1996) is the only study to have previously used this approach.
The first approach, the depletion method, makes use of soil-profile-based mass balances (Chadwick et al., 1990; Brimhall et al., 1991) to estimate total base cation losses in the soil above a reference soil depth. An element in a weathering-resistant mineral is used as a standard, most commonly zirconium (Zr, present in zircon) or titanium (Ti, present in rutile) (Sudom and St. Arnaud, 1971; Harden, 1987; Chadwick et al., 1990; Bain et al., 1994), due to their resistance to weathering at low temperatures (Schützel et al., 1963). To yield an annual average weathering rate (mmolc m−2), calculated element losses are commonly divided by an estimated soil age. In Nordic glacial tills situated above the marine limit, soil age is conventionally considered to be the number of years lapsed since the site of interest was finally deglaciated at the end of the Weichselian. Because the rate of weathering may vary over time (Klaminder et al., 2011; Stendahl et al., 2013), the average historical weathering rate may differ from the present-day weathering rate.
The second approach commonly involves the process-based PROFILE model, which has been used widely as a tool to estimate critical loads of acidity in the Nordic countries (e.g. Sverdrup et al., 1992) and North America (Whitfield and Watmough, 2012; Phelan et al., 2014). In PROFILE, release rates of base cations are estimated based on built-in assessments of the dissolution kinetics of a user-defined set of minerals present in the soil and the physical and chemical conditions that drive the dissolution of those minerals. Because it is a mechanistic model, its strength is its transparency, while its main weakness is the difficulty in setting values of model parameters and input variables to which it may have high sensitivity. Akselsson et al. (2019) concluded that the most important way to reduce uncertainties in modelled weathering rates is to reduce input data uncertainties, e.g. regarding soil texture, although there is still a need to improve process descriptions of biological weathering and weathering brakes (e.g. Erlandsson Lampa et al., 2019). The sensitivity of PROFILE to variations in soil physical parameters (e.g. soil texture, soil bulk density) and mineral composition was discussed by Jönsson et al. (1995) and Hodson et al. (1996). The importance of the ability to determine the precise identity and quantity of the minerals was analysed by Casetou-Gustafson et al. (2019a). They (Casetou-Gustafson et al., 2019a) also suggested that the dissolution kinetics of minerals used in the PROFILE model should be revised and the uncertainties assessed to improve the accuracy in model predictions.
The third approach to estimating weathering rate is the balanced base cation budget approach. This method has been applied to estimate current weathering rates at various temporal and spatial scales, mostly the catchment scale (Velbel, 1985; Likens et al., 1998). In one way of using the approach, mean weathering rates of individual minerals can be estimated at the catchment scale based on data for the mineralogical composition of soils along with element inputs in deposition and outputs in stream water and biomass uptake (e.g. Garrels and Mackenzie, 1967; Velbel, 1985; Velbel and Price, 2007). Others have estimated weathering as an unknown source from the missing balance between known sources (deposition, soil depletion) and known sinks (uptake, leaching, increase in soil BC stocks) (e.g. Sverdrup et al., 1998; Simonsson et al., 2015). The method requires measurements of known fluxes within a system with defined boundaries. The high data demand restricts the application of the base cation budget approach to a limited number of sites, essentially catchments with long-term monitoring of fluxes and well-defined boundaries. However, even then estimated weathering rates may suffer from large uncertainties, as errors in the sinks and sources accumulate in the mass balance equation (Simonsson et al., 2015). Furthermore, the base cation budget approach has mostly been applied under conditions where accumulation in biomass were not directly measured but estimated to be small, or base cation stocks in the soil were assumed to be at steady state (e.g. Kolka et al., 1996; Sverdrup et al., 1998; Whitfield et al., 2006). However, the nutrient demand is particularly large during the aggrading phase of a stand development where the foliage biomass is increasing rapidly. Hence, due to difficulties in application of the budget method to the regional scale, the PROFILE model and the depletion method are the most commonly used methods in Sweden to estimate weathering rates.
The principal aim of this study was to analyse the causes of discrepancies in estimations of weathering rates, with a focus on conceptual versus random sources of discrepancies between the depletion method, the PROFILE model and the balanced base cation budget approach. To accomplish this goal, the specific aims were to (1) perform a spatially harmonised comparison, sensu Futter et al. (2012) of the three approaches for a set of test criteria and (2) place weathering in the context of other base cation fluxes in aggrading Norway spruce forests, in particular the uptake in forest biomass. The base cation budgets were estimated at the period of stand development when nutrient demand was expected to peak. In combination with access to highly accurate data on biomass production, these conditions also provided opportunities to relate weathering to base cation accumulation in biomass at high nutrient uptake rates and possible simultaneous depletions of extractable base cation stocks in the soil. Furthermore, input data to PROFILE were characterised by high-quality quantitative mineralogical data, measured directly by quantitative X-ray powder diffraction (XRPD), as previously discussed by Casetou-Gustafson et al. (2018). Discrepancies between the PROFILE model and the depletion method were analysed by testing the sensitivity of PROFILE to changes in soil physical or mineralogical composition and by calculating the hypothetical time needed for PROFILE weathering rates to accomplish the element loss observed with the depletion method.
Three test criteria were used to examine the outputs of the depletion method and PROFILE model: (1) similarity in weathering estimates for the 0–50 cm soil profile, (2) similarity in depth gradients in weathering for the 0–100 cm soil profile and (3) similarity in ranking order of the base cations released.
2.1 Study sites
Two forest sites planted with Norway spruce (Picea abies (L.) Karst) were chosen for the study, Flakaliden in northern Sweden (64∘07′ N, 19∘27′ E) and Asa in southern Sweden (57∘08′ N, 14∘45′ E), because they have been used for long-term experimental studies on the effects of climate and nutrient and water supply on tree growth and element cycling (Linder, 1995; Bergh et al., 1999; Ryan, 2013) (Fig. 1).
The experiment at Flakaliden was established in 1986 in a 23-year-old Norway spruce stand, planted in 1963 with 4-year-old seedlings of local provenance after prescribed burning and soil scarification (Bergh et al., 1999). The experiment at Asa was established 1 year later (1987), in a 12-year-old Norway spruce stand planted in1975 with 2-year-old seedlings after clear-felling and soil scarification. The experimental design was similar at both sites and included control, irrigation and two nutrient optimisation treatments (Bergh et al., 1999). All treatments were replicated in 50 m × 50 m plots, arranged in a randomised block design. Only two of the four treatments were used in the present study: the control (C) and plots receiving an annual dose of an optimised mix of solid fertiliser (F), which among other elements per year contained about 10 kg ha−1 of Ca, 8 kg ha−1 of Mg and 45 kg ha−1 of K (Linder, 1995).
Flakaliden is located in the central boreal sub-zone with a harsh climate, with long cool days in summer and short cold days in winter. Mean annual temperature for the period 1990–2009 was 2.5 ∘C, and mean monthly temperature varied from −7.5 ∘C in February to 14.5 ∘C in July. Mean annual precipitation in the period was ∼650 mm, with approximately one-third falling as snow, which usually covers the frozen ground from mid-October to early May. Mean length of the growing season (daily mean temperature ≥5 ∘C) was 148 d, but with large between-year variations (see Table 1 in Sigurdsson et al., 2013).
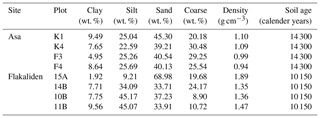
Table 1Soil profile characteristics at 50 cm depth in the mineral soil at the Asa and Flakaliden sites.
Asa is located in the hemi-boreal zone, where the climate is milder than at Flakaliden, which is reflected in a longer growing season (193 d). Mean annual temperature (1990–2009) was 6.3 ∘C, mean monthly temperature varied from −1.9 ∘C in February to 16.0 ∘C in July and mean annual precipitation was ∼750 mm. The soil is periodically frozen in winter. The difference in climate is reflected in differences in site productivity, which broadly follows climate gradients in Sweden (Bergh et al., 2005).
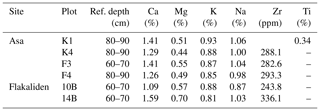
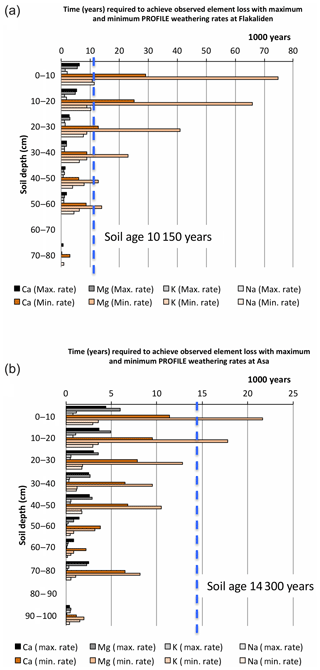
The soils at Asa and Flakaliden differ in age due to differences in the time since deglaciation (Table 1), from approximately 14 300 years at Asa and 10 150 years at Flakaliden (estimated from Fredén, 2009). The soil type at both sites is udic Spodosol, with a more humus horizon overlying glacial till derived from felsic bedrock. The soil texture is classified as sandy loam. The transition between the B and C horizons is mostly located at 50 cm depth at Flakaliden and 50–60 cm depth at Asa. The natural ground vegetation at Flakaliden is dominated by Vaccinium myrtillus (L.) and V. vitis-idaea (L.) dwarf-shrubs, lichens and mosses (Kellner, 1993; Strengbom et al., 2011). The ground vegetation at Asa is dominated by Deschampsia flexuosa, (L.) and mosses (Strengbom et al., 2011; Hedwall et al., 2013).
2.2 Soil sampling and analyses of geochemistry and mineralogy
A detailed description of soil sampling, geochemical analyses and determination of mineralogy can be found in Casetou-Gustafson et al. (2018). The procedures are summarised below. Sampling was performed in untreated control plots (K1 and K4 at Asa and 10B and 14B at Flakaliden) and fertilised (F) plots (F3 and F4 at Asa and 15A and 11B at Flakaliden) in October 2013 (Flakaliden) and March 2014 (Asa), in the border zone of four plots at each site. One intact soil core per plot at Flakaliden and in plot K1 at Asa were extracted using a rotary drill (17 cm inner diameter). In plots K4, F3 and F4 at Asa, soil samples were instead taken from 1 m deep manually dug soil pits, due to inaccessible terrain for the rotary drill machinery. Maximum soil depth was shallower at Flakaliden (70–90 cm) than at Asa (90–100 cm). The volume of stones and boulders was determined for each plot at the two study sites using the penetration method described by Viro (1952) to a maximum depth of 30 cm and by applying the fitted function described by Stendahl et al. (2009). Mean stone and bolder content was higher at Flakaliden (39 % vol) than at Asa (28 % vol).
Soil samples were taken from each 10 cm soil horizon. Prior to chemical analysis, these samples were dried at 30–40 ∘C and sieved to < 2 mm. Analysis of particle size distribution was performed by wet sieving and sedimentation (pipette method) in accordance with ISO 11277. Geochemical analyses were conducted by ALS Scandinavia AB and comprised of inductively coupled plasma mass spectrometry (ICP-MS) on HNO3 extracts of fused samples that were milled and ignited (1000 ∘C) prior to fusion with LiBO2.
Quantitative soil mineralogy was determined with the X-ray powder diffraction (XRPD) technique (Hillier 1999, 2003). Samples for measurement of XRPD patterns were prepared by spray-drying slurries of soil samples (< 2 mm) micronised in ethanol. A full pattern fitting approach was used for quantitative mineralogical analysis of the diffraction data (Omotoso et al., 2006). This fitting process involved the modelling of the measured diffraction pattern as a weighted sum of previously measured and verified standard reference patterns of the identified mineral components. The determination of chemical compositions of various minerals present in the soils was conducted by electron microprobe analysis (EMPA) of mineral grains subsampled from the sifted (< 2 mm) soil samples. Mineralogical composition of the soils is given in the Supplement (Table S1 in the Supplement).
2.3 Historical weathering determined with the depletion method
2.3.1 Method description
The depletion method (Table 2), as defined by Marshall and Haseman (1943) and Brimhall et al. (1991), estimates the accumulated mass loss since soil formation (last deglaciation for our sites) as a function of loss of a mobile (weatherable) element and enrichment of an immobile (weathering resistant) element according to the following general function introduced by Olsson and Melkerud (1989) and based on the same theories as the mass transfer function described in Brimhall et al. (1991):
where W denotes loss of the ith element (g m−2), X denotes mobile element concentrations (0 %), Zr denotes immobile element concentrations (%), w and c denote a weathered soil horizon and the assumed unweathered reference horizon, respectively, d is horizon thickness (m), and ρ is bulk density (g m−3). Zirconium is commonly used as the immobile element due to the inert nature of the mineral zircon (ZrSiO4), although Ti is sometimes used due to the resistance of the Ti-containing minerals anatase and rutile (TiO2) to weathering (Olsson and Melkerud, 1989). The unweathered reference horizon is located in the C horizon and has X-to-Zr ratios that are assumed to represent pristine conditions of the presently weathered horizons above it. In the weathered horizons, X-to-Zr ratios are smaller; that is, Zr is enriched compared with the mobile elements (i.e. the base cations). The method is based on the assumptions that Zr, hosted in zircon, was uniformly distributed throughout the soil profile at the time of deglaciation, that weathering only occurs above the reference horizon and that zircon does not weather. The latter implies that Zr concentrations and Zr ∕ base cation ratios are constant below the reference horizon. The reference depths for different base cations compared with Zr, which were used as the depths of immobile element concentrations, are shown in Table 3. The Zr ∕ base cation ratio (Fig. S1 in the Supplement) was used to help select the reference soil horizon as it highlights heterogeneities in parent material with depth. In cases of heterogeneities in the profile, the reference horizon was chosen above this heterogeneity. This choice was precluded for soil profile 11B, where Zr concentrations and Zr ∕ base cation ratios peaked directly below the B horizon (i.e. at 50–60 cm).
Table 2A short description of characteristics of the three different approaches that are used in the study to estimate base cation release rates at the pedon scale using a harmonised set of input data. The difference between methods reflect expected differences due to different timescales, conceptual differences, assumptions about weathering kinetics and pedogenesis.

2.3.2 Application
Prior to calculating base cation weathering rates with the depletion method, fractional volume change Vp was calculated according to White et al. (1996) in order to assess if there were any large volume changes (collapse) in the mineral soil with implications for which depth the weathering should be calculated to. Similar to White et al. (1996), it was assumed that values close to zero indicate no volumetric change, which was the case below 30–40 cm of soil depth at both sites (Table S2). The homogeneity of the parent material was also evaluated (Fig. 2) using the criterion that the ratio of Ti to Zr should be more or less constant with depth in an originally homogeneous material. Use of the ratio of two immobile elements to establish uniformity of parent material has been suggested previously (Sudom and St. Arnaud, 1971; Starr et al., 2014). The homogeneity criterion was not met using Zr in plot K1 at Asa (i.e. the Zr concentrations decreased towards the soil surface; Fig. 2); here Ti was used as the immobile element instead. Furthermore, the plots 15A and 11B at Flakaliden had to be eliminated from the calculations, because relatively large variability in both the Zr and Ti gradients was observed. These large heterogeneities led to an overall gain of base cations in the rooting zone, which is opposite to what would be expected (i.e. that losses and gains can occur at specific soil depths due to eluviation and illuviation processes in podzolic soils). For this reason, soil profiles 15A and 11B were eliminated from further consideration in calculations of historical weathering rates using the depletion method. Thus, apart from heterogeneities, transportation processes (eluviation and illuviation), and/or erratic Zr or Ti gradients could lead to “negative” weathering, i.e. leading to a calculated relative accumulation of elements. Such negative values were not considered in the calculation of historical weathering losses.
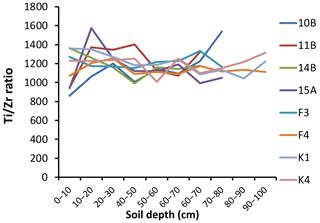
Figure 2Ratios of titanium (Ti) to zirconium (Zr) by concentration in the soil at Asa (K1, K4, F3, F4) and Flakaliden (10B, 11B, 14B, 15A).
Bulk density was estimated for each soil horizon except in some plots where density measurements could not be made below a certain soil depth. Bulk density in these cases was estimated using an exponential model for total organic carbon (TOC) and bulk density (BD, g cm−3) based on our own data. For Asa (soil horizons F3: 70–90 cm; F4: 0–10, 30–40, 50–60, 60–70, 70–80, 80–90, 90–100 cm; and K4: 70–80, 80–90, 90–100 cm), the following function was used:
where x is TOC content (percentage of dry matter). For Flakaliden (soil horizons 14B: 80–90 cm; 10B: 60–70 cm; and 11B: 40–70 cm), the function used was
2.4 The PROFILE model
2.4.1 Model description
The steady-state weathering of soil profiles was estimated using the biogeochemical PROFILE model (Table 2), where weathering of the ith base cation (Wprofile, i) is described by long-term mineral dissolution kinetics at the interface of wetted mineral surfaces and the soil solution. PROFILE is a multilayer model, where parameters are specified for each soil layer based on field measurements and estimation methods (Warfvinge and Sverdrup, 1995).
2.4.2 PROFILE parameter estimation
A detailed description of the application of the PROFILE model to the soils and sites in the present study can be found in Casetou-Gustafson et al. (2019a). The parameters used are listed in Table 4a, b.
Table 4(a) Site parameters used in the PROFILE model. (b) Soil* parameters used in the PROFILE model.
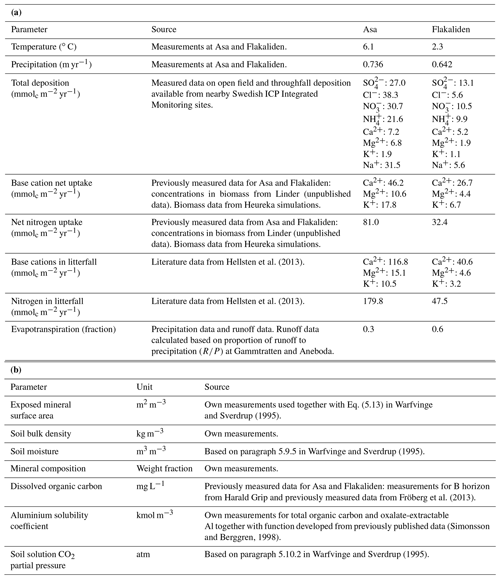
* Physical and chemical input data specific to the soil horizon are given in the Supplement (Tables S3).
Exposed mineral surface areas were estimated from soil bulk density and texture data using the algorithm specified in Warfvinge and Sverdrup (1995). Volumetric soil water content for each soil profile in Flakaliden and Asa was estimated to be 0.25 m3 m−3 according to the moisture classification scheme described in Warfvinge and Sverdrup (1995) (Table S3).
The aluminium (Al) solubility coefficient, a soil chemical parameter needed for solution equilibrium reactions, was defined as log{Al3+} + 3 pH. It was estimated by applying a function developed from previously published data (Simonsson and Berggren, 1998) and existing total carbon and oxalate-extractable Al measurements for the sites (Casetou-Gustafson et al., 2018) (Table S3). For partial CO2 pressure in the soil, the default value of Warfvinge and Sverdrup (1995) was used. Data on measured dissolved organic carbon (DOC) in the soil solution at 50 cm depth were available for plots K4 and K1 at Asa and plots 10B and 14B at Flakaliden, and these values were also applied for deeper soil horizons. Shallower horizons (0–50 cm) were characterised by higher DOC values, based on previous findings (Fröberg et al., 2006, 2013) and the DOC classification scheme in Warfvinge and Sverdrup (1995) (Table S3).
Site-specific parameters used were evapotranspiration, temperature, atmospheric deposition, precipitation, runoff and nutrient uptake in biomass (Table 4a). Mean evapotranspiration per site was estimated from mean annual precipitation and runoff data, using a general water balance equation.
Total deposition was calculated using deposition data from two sites of the Swedish ICP Integrated Monitoring catchments, Aneboda (for Asa) and Gammtratten (for Flakaliden) (Löfgren et al., 2011). Na was used as a tracer ion in order to distinguish canopy exchange from dry deposition for Ca, Mg and K. Dry deposition for Na and Cl was calculated as the difference between wet and throughfall deposition. As outlined in Zetterberg et al. (2016), wet deposition for all elements was calculated by correcting bulk deposition for dry deposition using the ratio of wet-only to bulk deposition. Wet deposition was estimated based on the contribution of dry deposition to bulk deposition, for both base cations and anions, using dry deposition factors from Karlsson et al. (2011, 2013). Finally, total deposition for all elements was calculated from the sum of dry and wet deposition.
Net base cation and nitrogen uptake in aboveground tree biomass (i.e. bark, stem wood, living and dead branches, needles) was estimated as mean accumulation rate over a 100-year rotation period in Flakaliden and a 73-year rotation period in Asa. These calculations were based on Heureka simulations using the StandWise application (Wikström et al., 2011) for biomass estimates, in combination with measured nutrient concentrations in aboveground biomass as described in Sect. 2.5.4 below (Linder, unpublished data).
2.4.3 PROFILE sensitivity analysis
The sensitivity of PROFILE to changes in soil physical and mineralogical input was analysed, to test to what extent the depth gradients of weathering rates as predicted by PROFILE were affected primarily by soil physical properties or by soil mineralogy. Independent PROFILE runs were performed, after replacing horizon-specific input values with soil profile average values regarding (1) soil bulk density and specific exposed mineral surface area (“homogenous soil physics”), (2) soil mineral percentages (“homogenous mineralogy”), or (3) both (“homogenous soil physics and mineralogy”). In each scenario, the squared deviation in weathering rate was calculated for each base cation and horizon, compared to the normal simulation based on horizon-specific inputs for soil physics and soil mineralogy. The sum of squares over base cations and horizons was used as a measure of the overall error caused by the homogenous input data. The ratio of sum of squares, of scenario (1) over (3) and of scenario (2) over (3), was used to estimate the percent contribution of soil physics and soil mineralogy, respectively, to the overall weathering gradients in the soil profile.
2.5 The base cation budget approach
2.5.1 General concepts of the base cation budget approach
The average weathering rate of the ith base cation according to base cation budget, Wbudget, i, over a period of time can be estimated with base cation budgets (Table 2) using the base cation budget approach, which assumes that total deposition (TDi) and weathering are the major sources of mobile and plant-available base cations in the soil and that leaching (Li) and accumulation of base cations in biomass (ΔBi) are the major sinks. A change in the extractable soil stocks of base cations over time (ΔSi) is considered to be a sink if stocks have increased or a source if stocks have been depleted (Simonsson et al., 2015). Each of these terms is measured independently over a specific period of time. Hence,
2.5.2 Atmospheric deposition, TDi
The same estimates of total atmospheric deposition as used in parameter setting of the PROFILE model (Sect. 2.4.2) were used in the base cation budget, Eq. (4).
2.5.3 Changes in exchangeable soil pools, Δ Si
Changes in extractable base cation stocks in the soil were calculated from the difference between two soil samplings, performed in 1986 and 1998 at Flakaliden and in 1988 and 2004 at Asa. The organic horizon was sampled with a 5.6 cm diameter corer, whereas a 2.5 cm diameter corer was used to sample 10 cm sections to 40 cm depth in the mineral soil. For each plot and horizon, 25 cores were combined into one sample.
Exchangeable base cation content in the soil (< 2 mm) for all Flakaliden samples and in Asa for samples from 1988 was determined by extraction of dry samples with 1 M NH4Cl using a percolation method, where 2.5 g of sample was leached with 100 mL of extractant at a rate of 20 mL h−1. The base cations were analysed by atomic absorption spectrophotometry (AAS). For the Asa samples from 2004, batch extraction was performed using the same extractant, and the base cations were determined with ICP. A separate test was conducted to compare the yield of the percolation and batch extraction methods. No consistent difference between the methods was observed.
The amount of fine soil (< 2 mm) per unit area was calculated from the volume of fine earth (< 2 mm) in the soil profiles and the average bulk density of the soil in the 0–10, 10–20 and 20–40 cm horizons. Bulk density and volume proportion of stoniness at Flakaliden were determined from samplings in 1986 in 20 soil profiles (0.5 m × 0.5 m and about 0.5 m deep) outside plots. At Asa, stoniness was determined with the penetration method of Stendahl et al. (2009) and the bulk density of soil < 2 mm was calculated using a pedotransfer function that included soil depth and measured carbon concentrations as variables.
2.5.4 Net uptake in biomass, Δ Bi
Accumulation of base cations in tree biomass, i.e. net uptake of base cations, was calculated as a mean value of control plots over the period 1989–2003, based on increments in aboveground biomass at Asa and Flakaliden for this period and on the concentrations of elements in different tree parts. The increment in aboveground biomass was based on measurements of stem diameter at breast height (DBH) of all individual trees in the plots, and applying DBH data to allometric functions developed for Norway spruce at the sites (Albaugh et al., 2009, 2012). The allometric functions were based on destructive samplings (1987–2003) of 93 and 180 trees at Asa and Flakaliden, respectively. The increment in belowground biomass was estimated from general allometric functions for Norway spruce stumps and roots in Sweden (Marklund, 1988). Since the functions of Marklund (1988) underestimate belowground biomass by 11 %, a factor to correct for this was included (Petersson and Ståhl, 2006). Furthermore, the finest root fraction (≤2 mm), which is not included in the functions of Marklund (1988) and Petersson and Ståhl (2006), was assumed to be 20 % of needle biomass at Asa and 33 % at Flakaliden, respectively, based on data from Helmisaari et al. (2007).
Data on element concentrations in biomass were available from measurements on harvested trees (Sune Linder, unpublished data). At Flakaliden, total element concentrations were analysed in trees sampled for biomass determination in 1992 and 1997. Analyses of needles and branches (dead and live) were conducted on the same tree parts in the biomass sampled in 1993 and 1998. Base cation concentrations in biomass were determined from acid wet digestion in HNO3 and HClO4, followed by determination of elements by ICP-atomic emission spectrophotometry (ICP-AES) (Jobin Yvon JY 70 Plus).
Data on element concentrations in belowground biomass fractions were taken from literature from the Nordic countries (Hellsten et al., 2013). Specifically, data on stump and root biomass of Norway spruce were available for Asa, and data from Svartberget were used for Flakaliden (Table 7 in Hellsten et al., 2013).
2.5.5 Leaching, Li
Base cation leaching was quantified in 6-month intervals from modelled daily runoff multiplied by average element concentrations in soil water collected with tension lysimeters at 50 cm soil depth.
Soil water was collected from five ceramic tension lysimeters (P80) installed at 50 cm depth in each experimental plot. Soil water was collected during frost-free seasons, applying an initial tension of 70 kPa in 250 mL sampling bottles, and left overnight. These soil water samples were pooled by plot. The base cation concentration in the soil solution was determined with ICP-AES. Soil water sampling was performed twice every year, i.e. in the spring and in the autumn, which are the periods of highest water flux so that the most important leaching events were covered. The spring samples were collected soon after the snowmelt, and depending on the weather in a specific year this meant that the yearly spring sampling date varied between the last week of April and the last week of May. The autumn samples were collected when frost risk increased. That meant that the autumn sampling dates varied from year to year, i.e. from the first week in September to mid-November. The seasonal variation in soil water chemistry is shown in Fig. S2.
The drainage flux out of the profile was calculated by the CoupModel (Jansson, 2012). The model was parameterised based on hydraulic soil properties measured at the sites. The model was run with hourly mean values of locally measured climate variables (precipitation, global radiation, wind speed, air temperature and humidity), and model outcomes were tested against tensiometer data; i.e. tensiometer readings at 15, 30 and 45 cm depth once every 2 weeks were used for model calibration. The parameters were then adjusted slightly to obtain good agreement between measured and calculated soil water content. Annual precipitation varied considerably during the period 1990–2002, ranging from 906 to 504 mm at Flakaliden (mean 649 mm) and from 888 to 575 mm at Asa (mean 736 mm). Annual evapotranspiration increased by about 50 mm at both sites, during the period 1987–2003 at Flakaliden and 1990–2002 at Asa, due to the increment in tree leaf area. Monthly means and standard deviation of drainage (mm) at 50 cm depth in the soil of control plots at Asa during 1990–2004 and at Flakaliden during 1988–2004 are shown in Fig. S3.
2.5.6 Assessment of data quality in base cation budget
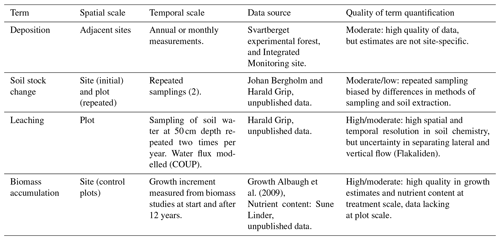
The precision and accuracy of a base cation budget estimate of Wbudget, i, was determined by the quality of estimates of each individual term in Eq. (3), in proportion to the magnitude of each term (Simonsson et al., 2015). Significant uncertainty in the estimate of a quantitatively important term will therefore dominate the overall uncertainty in estimates of Wbudget. Firstly, the quality of data for each term in Eq. (3) was assessed based on the spatial and temporal scales of measurements and the quality of measurements (Table 5). Using these criteria, we consider the estimates of deposition, leaching and accumulation in biomass to be of moderate to high quality. The measurements of changes in extractable soil pools were of lower quality because extraction methods were not identical for samples collected in 1986–1988 and 1998–2004, which would cause significant uncertainty if soil changes were an important part of the element budget. To partly overcome this uncertainty, we used the estimates obtained by PROFILE (Wprofile, i) and the depletion method (Wdepletion, i) in additional base cation budget calculations where the change in soil was determined from the base cation budget. These additional base cation budget estimates, which are conceptually analogous to the regional mass balances presented by Akselsson et al. (2007), were also used to place the PROFILE and depletion method estimates of Wi in the context of other base cation fluxes at the ecosystem scale.
2.6 Statistical analyses
Site mean values and standard error (SE) of Wdepletion and Wprofile were calculated based on the four (or two) soil profiles studied at each site. For Wbudget an average based on the four control plots at each site as well as a combined standard uncertainty were calculated. The latter was partly based on standard errors derived from plotwise replicated data of the present experiments (for leaching and changes in exchangeable soil pools, SE(Li) and SE(ΔSi), respectively), partly on standard uncertainties (u) derived from Simonsson et al. (2015), where replicated data were missing in the present study (for accumulation in biomass and total deposition, u(ΔBi) and u(TDi), respectively). Because total deposition and bioaccumulation differed substantially from those in the study of Simonsson et al. (2015), relative standard uncertainties were derived from that study and multiplied with the average deposition and bioaccumulation rates at Asa and Flakaliden, respectively, to yield realistic standard uncertainties for the present sites. For the weathering rate of the ith base cation according to Eq. (4), a combined standard uncertainty (uc) was calculated as
Confidence intervals were calculated by multiplying the combined standard uncertainties with a coverage factor of 3.
3.1 Depletion method estimates of historical weathering rates
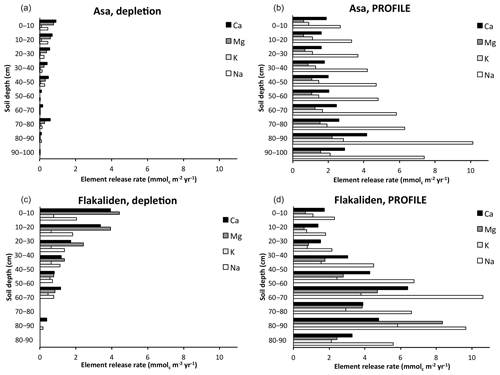
At both Asa and Flakaliden, historical weathering rates estimated with the depletion method (Wdepletion) were highest in the upper soil horizons and showed a gradual decrease down to the reference depth, which was defined at 60–70 cm at Flakaliden and for most plots at 80–90 cm at Asa (Fig. 3). Flakaliden had a higher historical annual weathering rate to 90 cm soil depth, 37.8 mmolc m−2 yr−1, than Asa, 12.8 mmolc m−2 yr−1; the corresponding value for 0–50 cm depth was 34.1 mmolc m−2 yr−1 at Flakaliden and 10.5 mmolc m−2 yr−1 at Asa. The gradients with depth showed that Wdepletion increased towards the surface, although this trend was more pronounced at Flakaliden than at Asa. At Flakaliden, Wdepletion was highest for Mg, followed by Ca, Na and K (Figs. 3 and 4); at Asa, it was highest for Ca, closely followed by Mg, Na and K (Figs. 3 and 4).
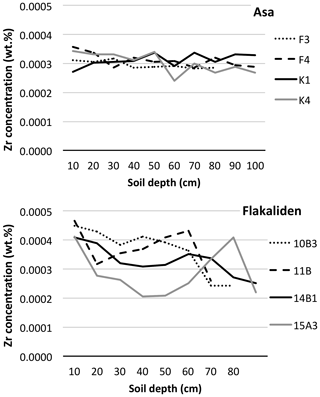
Figure 3Zirconium (Zr) gradient in the soil at Asa (K1, K4, F3, F4) and Flakaliden (10B, 11B, 14B, 15A).
3.2 PROFILE model estimates of steady-state weathering rates
The steady-state weathering rate estimated by the PROFILE model (Wprofile) differed from the historical rate with respect to all three test criteria, i.e. (1) total weathering rate in the 0–50 cm soil horizon, (2) variation in weathering with depth and (3) ranking order of base cations (Figs. 3 and 4). Firstly, regarding base cation weathering rate in the upper 50 cm of the mineral soil, Wprofile estimates for Asa and Flakaliden (Asa: 37.1 mmolc m−2 yr−1, Flakaliden: 42.7 mmolc m−2 yr−1) were around 3.5- and 1.3-fold higher than Wdepletion estimates, respectively. Secondly, the total modelled base cation weathering rate for the soil profile down to 90 cm was around 7-fold higher than the rate estimated using the depletion method at Asa (89.4 mmolc m−2 yr−1) and 3.4-fold higher at Flakaliden (127.6 mmolc m−2 yr−1). Unlike the historical weathering based on the depletion method, PROFILE predicted that weathering rates increased with soil depth at both sites. At Flakaliden, high contents of K- and Mg-bearing tri-octahedral mica (Casetou-Gustafson et al., 2018) gave rise to particularly high weathering rates at 70–80 cm. Thirdly, in contrast to Wdepletion, Wprofile was largest for Na at both sites, followed by Ca. However, Wprofile was larger for K than for Mg at Asa, while the reverse was true at Flakaliden.
The sensitivity analysis of the PROFILE model using homogeneous soil physical and/or mineralogical properties demonstrated that the variations in soil physical properties (i.e. soil bulk density and specific exposed mineral surface area) with depth had a greater influence than mineralogy on the observed change in Wprofile with soil depth. In terms of the ratios of sums of squares, the homogenous soil physics scenario (1) produced 75 % or more of the error obtained with homogenous soil physics and mineralogy (scenario (3)) leaving a mere 25 % or less to the homogenous mineralogy of scenario (2); see also Figs. S4 and S5. The soil physical inputs that were most important for PROFILE weathering rates are indicated in Figs. S4 and S5. There was a strong linear and positive relationship between exposed mineral surface area and Wprofile for all elements at both sites, with R2 values ranging from 0.65 to 0.89 (Fig. S6). The relationship between bulk density and Wprofile was also strong and showed the same linear response, although R2 values were lower, 0.40–0.70 (Fig. S7).
3.3 Base cation budget estimates of current weathering rates
A comparison of weathering rates estimated by base cation budgets (Wbudget), Wprofile and Wdepletion, was made for the 0–50 cm soil horizon. For most elements, Wbudget in the 0–50 cm horizon was higher, or much higher, than Wprofile (Fig. 5). Compared with the PROFILE model estimates, the base cation budget estimates of weathering were 6- to 7-fold higher for Ca, Mg and K weathering at Asa and about 2- to 3-fold higher for Ca, Mg and K at Flakaliden. At Asa, the sum of base cations was on average 13-fold and 3.6-fold larger than Wdepletion and Wprofile, respectively. The closest resemblance between methods was found between Wdepletion and Wbudget for Na. The budget calculations suggested that weathering was a dominant source of K and Mg, but contributed a somewhat smaller proportion of Ca (61 % at Asa and 43 % at Flakaliden).
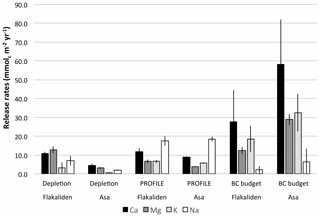
Figure 5Site mean values and standard errors (SE) of weathering rates (mmolc m−2 yr−1) for Ca, Mg, K and Na determined with the depletion method, the PROFILE model and the base cation budget method for the 0–50 cm horizon at Asa and Flakaliden. For the weathering rates based on the depletion method and the PROFILE model, error bars represent the SE calculated based on four soil profiles at each study site, except for Flakaliden, where the depletion method was only applied in two soil profiles. For weathering rates based on the base cation budget approach, SE bars were calculated from combined standard uncertainties, which are based on SE derived from plotwise replicated data of the present experiments (for leaching and changes in exchangeable soil pools) and on standard uncertainties derived from Simonsson et al. (2015), where replicated data were missing in the present study (for accumulation in biomass and total deposition).
As for the fluxes (terms) of the base cation budget, Na showed patterns different from those of K, Mg and Ca (Fig. 6). For Na, uptake in biomass was negligible and leaching was the dominant sink. For K, Mg and Ca, accumulation in biomass was the dominant sink. Loss by leaching was negligible for K but significant for Mg and Na. Deposition generally represented only a small input, except for Na at Asa. The measured decreases in soil stocks of exchangeable base cations indicated that a change in this pool was a particularly important source of Ca. There were minor increases in exchangeable stocks for Na, K and Mg at Asa. Compared to Na and Mg, the combined uncertainty of Wbudget was larger for Ca and K, with both dominated by the bioaccumulation term in Eq. (4), than for Na and Mg (Table 6). In relation to the mean Wbudget, the combined uncertainty was of the same order of magnitude for Na, about half for Ca, one-third for K and lower for Mg.
Table 6Standard errors and standard uncertainties (mmolc m−2 yr−1) for the terms in the base cation budget, Eq. (4). Combined standard uncertainty, plot average value and confidence interval for the weathering rate of base cation i derived from base cation budgets W budget, i (mmolc m−2 yr−1).
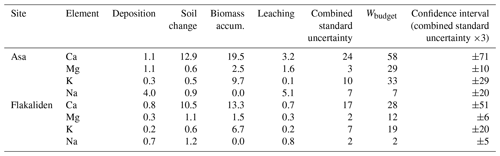
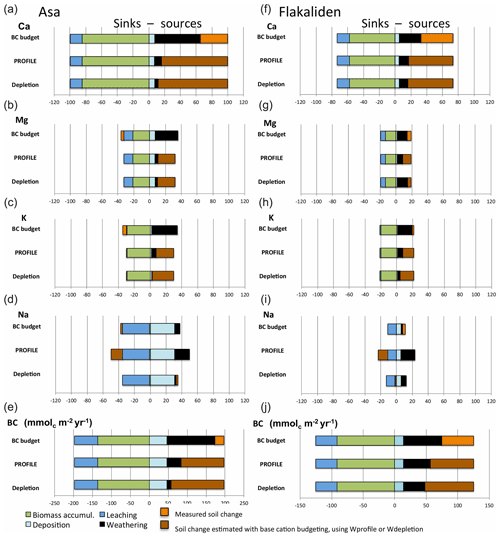
Figure 6Sinks (left) and sources (right) of base cations (BC) in ecosystem net fluxes at Asa and Flakaliden. The soil is a net source of soil BC if soil base cation stocks decrease and a net sink if they increase. “BC budget” denotes current base cation weathering rate (Wbudget) estimated with the BC budget method, including measured changes in soil exchangeable BC stocks; “PROFILE” denotes soil exchangeable pools estimated from BC budget using PROFILE estimates of BC weathering rate; “Depletion” denotes soil exchangeable pools estimated from BC budget using estimates of historical weathering rate by the depletion method. “Measured soil change” and “Base cation budget estimated soil change” indicate that Eq. (4) was used to estimate weathering rate or the soil change, respectively.
By using the weathering estimates obtained with PROFILE and the depletion method in the base cation budget equation, Eq. (4), in combination with measured estimates of deposition, leaching and uptake in biomass, alternative soil balances were estimated (Fig. 6). Since the base cation budget method predicted much higher weathering rates than the other methods, a balance of sources and sinks consequently required more marked decreases in exchangeable soil stocks for K, Ca and Mg when weathering rates were based on PROFILE or the depletion method. Furthermore, as a consequence of the substantially higher Wprofile for Na, the PROFILE-based base cation budget suggested substantial increases in exchangeable Na stocks.
In spite of the fact that this study was well harmonised at the spatial scale and originated from sites with similar soil parent material, our comparison of three approaches to estimate weathering rates showed significant discrepancies between them. Discrepancies were demonstrated for all three test criteria: the sum of weathering rates in the 0–50 cm horizon, the depth gradient of weathering within this horizon and the element rank order of weathering rates. In the following, the discrepancies between the depletion method and the PROFILE method are first analysed because all three test criteria can be applied.
4.1 First test: lower weathering rates with the depletion method compared to PROFILE
Modelled (Wprofile) and historical (Wdepletion) base cation weathering rates were within the range of recently published data for similar forest sites on podzolised glacial till (Stendahl et al., 2013). However, the historical weathering rates at Asa were similar to the lowest historical weathering rate observed by Stendahl et al. (2013), and the historical weathering rates for Flakaliden were similar to their highest rates, at least with regard to Ca and Mg. The overall Wprofile in the 0–50 cm depth was higher than Wdepletion for Na and K. Similarly, high ratios of Wprofile∕Wdepletion were found at the catchment scale by Augustin et al. (2016). At the pedon scale, Stendahl et al. (2013) found Wprofile∕Wdepletion ratios of on average 2.7 for 16 Swedish study sites (with average max. and min. ratios of 7.9 and 0.4, respectively); this ratio was larger than the one found for Flakaliden in our study (1.5) and lower than the one found for Asa (5.1). Similar to Flakaliden, low ratios have been reported for the Lake Gårdsjön site situated in southwestern Sweden (Sverdrup et al., 1998; Stendahl et al., 2013). An exception to the general trend of higher steady-state PROFILE weathering rates compared to historical rates calculated by the depletion method was found for Mg at the Flakaliden site, where Wdepletion was 1.9-fold greater than Wprofile in the upper mineral soil, but only at Flakaliden. This exception with regard to Mg was also found by Stendahl et al. (2013) for all of their 16 study sites.
The observed discrepancy between Wprofile and Wdepletion has both conceptual and random origin, where the conceptual origin is due to the different temporal scales. In contrast to the observed discrepancies referred to above, several studies have concluded that the average historical weathering rate should generally be higher than the present weathering rate since soil development involves loss of easily weatherable minerals and ageing of mineral surfaces (Bain et al., 1993; Taylor and Blum, 1995; White et al., 1996). In a study using the Historic-SAFE model, applied to the Lake Gårdsjön catchment in southwestern Sweden, Sverdrup et al. (1998) predicted a decline in weathering rates due to assumed disappearance of fine particles and loss of minerals. Their results suggested an increase in weathering rates from deglaciation 12 000 years BP towards a peak at 9000 years BP, followed by a gradual decrease to below initial levels.
The particularly low Wdepletion at Asa was largely attributed to a weakly developed depth gradient of Zr in the soil (Fig. 3). This observation probably has a random rather than a conceptual origin, because it might have been the result of soil mixing by different means. Mechanical soil scarification was carried out at both Asa and Flakaliden prior to planting of the present stand, which would at least have caused partial mixing or inversion of surficial soil horizons. In addition, clearance cairns of unknown age were found in the experimental area at Asa, indicating small-scale agriculture in the past. Moreover, if burrowing earthworms were abundant in the past, they might have produced soil mixing in the upper soil horizons (Taylor et al., 2019), resulting in a disturbed Zr gradient and in low estimates of historical weathering in the rooting zone (Whitfield et al., 2011). High or near-neutral soil pH and deciduous litter can promote high population densities of burrowing earthworms following forest clearing and agriculture; and we note that partly deciduous vegetation dominated at Asa until only 1000–2000 years BP, with species such as Corylus avellana (L.), Betula spp., Quercus spp. and Tilia spp. (Greisman et al., 2009).
Apart from disturbances, natural heterogeneity in texture or mineralogy probably influenced the estimate of Wdepletion at the study sites, i.e. biases of random nature. At Flakaliden, it was reasoned that heterogeneous Zr gradients (Fig. 3) and Zr ∕ base cation ratios (Fig. S1) disqualified two soil profiles from further analysis, which would have otherwise indicated unreasonable net gains of elements in the rooting zone (0–50 cm) (i.e. for soil profile 15A for all elements and for soil profile 11B with regard to Na and K). Whitfield et al. (2011) used the same argument for excluding single profiles from their calculations, emphasising that overall gains in the rooting zone are not expected without external additions of base cations to the soil profiles. Several alternative reasons could have contributed to the observed peaks of Zr in the B–C horizons at Flakaliden, such as local heterogeneities of the deposited till, which was suggested by the unstable Ti∕Zr ratio in soil profiles 15A and 11B. However, the observed peaks in the Ti∕Zr gradients were only explained by irregularities in Ti gradients (i.e. increases in the Ti∕Zr ratio indicate that Ti concentrations are increasing), and the latter has to be treated carefully since in cases where both Zr and Ti show inconsistent patterns with soil depth the Ti∕Zr ratio will still be uniform and hereby overshadows heterogeneities observed with soil depth for both elements (Figs. 2, 3). Thus, heterogeneities in Zr gradients observed in the B–C horizons can be attributed to local heterogeneities of the parent material irrespective of whether the Ti∕Zr gradients are uniform at these depths.
Regardless of errors in the Zr gradients, both Wdepletion and Wprofile showed more marked gradients with soil depth at Flakaliden compared to Asa. This could be expected based on the more well-developed podzol profile at Flakaliden. It has been postulated that the formation of podzols is enhanced by long duration and great depth of snow cover (Jauhiainen, 1973; Schaetzl and Isard, 1996), which would imply that soil formation had progressed further at Flakaliden than at Asa (Lundström et al., 2000). At Flakaliden, the average mass loss of Ca and Mg was 4.0-fold larger in the E horizon than in the B horizon, which is similar to findings by Olsson and Melkerud (2000) of a 5-fold higher ratio between losses of base cations in the E compared with the B horizon.
4.2 Second test: PROFILE and depletion method produce different weathering gradients in the soil
Our second test, postulating similarity between Wdepletion and Wprofile concerning the weathering rate gradient with soil depth, was not fulfilled. This discrepancy was basically of conceptual nature. We may imagine a front of intense weathering moving downward through the soil profile over the millennia. Each horizon would undergo an episode, limited in time, of intense weathering followed by slower weathering in the ageing material. The sensitivity test performed with PROFILE revealed that the model output was only a little affected by the differences in mineralogy between horizons. Therefore, if processes are correctly modelled with PROFILE, the notion of a weathering front should primarily be associated with changes in bulk density and exposed mineral surface area, as also suggested by the positive correlation between Wprofile and exposed mineral surface area and bulk density (Figs. S6–S7) and by the findings of Jönsson et al. (1995).
The increase in weathering rate with soil depth simulated by PROFILE is obviously in contrast with the classic notion of weathering rates being highest in the A or E horizon of podzolised soils (Tamm, 1931). To test whether the high Wprofile values could be reconciled with the observed historical weathering, the hypothetical time needed for the PROFILE weathering rates to accomplish the element losses determined with the depletion method was calculated. This showed that the highest weathering rate, presently prevailing at approximately 80 cm (Asa) or 60 cm (Flakaliden) depth according to PROFILE (Fig. 4), would cause the observed depletion losses within less than half of the soil age (“max rates” in Fig. 7), potentially in concert with the concept of a weathering front. However, the calculation also showed that the present minimum weathering rate, presently simulated for the topmost one to three horizons (Fig. 4), would often result in a more severe base cation depletion within less than the postglacial period than observed by the depletion method (“min rates” in Fig. 7), particularly at Flakaliden, and also for K and Na at Asa. Hence, even considering the concept of a possible weathering front, there appears to be a positive bias in Wprofile at the investigated sites.
4.3 Third test: depletion method and PROFILE resulted in different element rank order
The weathering rates of PROFILE may also be criticised based on discrepancies in the ranking order of the weathering of elements, compared to historical weathering; this is our third test criterion. At both sites, PROFILE predicted the highest steady-state weathering for Na at both sites. However, historical weathering at Asa was greatest for Ca among the base cation elements, whilst Mg was the most abundant element released at Flakaliden. The latter was also found by Olsson and Melkerud (2000), who reported the same ranking order of individual base cation weathering (i.e. Mg > Ca > Na > K) for other sites in northern Sweden. At the mineralogical level, Casetou-Gustafson et al. (2019a) demonstrate that K-feldspar was the dominant source of all steady-state PROFILE weathering of K, and previous results from similar soils suggest that the dissolution rate for K-feldspar is too high compared with mica. For example, Thompson and Ukrainczyk (2002) described differences in the plant availability of K via weathering from these two mineral groups. In addition, Simonsson et al. (2016) found that, although K-feldspar contained approximately 90 % of the bulk K in the soil, 25 %–50 % of the weathering of K had occurred in mica. Furthermore, and in more general terms, Hodson and Langan (1999) suggested that the PROFILE model overestimates weathering rates because it does not consider the decrease in mineral reactivity that has taken place over time and because it assumes that all mineral surface areas are reactive. Therefore, PROFILE can be expected to overestimate base cation weathering rates, an error that can be attributed to a combination of conceptual (conditions or processes inaccurately represented in model) and random (lack of relevant field data) sources.
4.4 Weathering in a base cation budget perspective
The base cation budget approach consistently resulted in much higher weathering rates than PROFILE and the depletion method for all base cations except Na. However, as was shown by the large combined uncertainties given in Table 6, base cation budget estimates of weathering are associated with substantial uncertainties from different sources. In general, significant uncertainties in the element budget of ecosystems are common (Yanai et al., 2010), and similarly large uncertainties associated with estimates of Wbudget were observed by Simonsson et al. (2015) for the Skogaby site in southwestern Sweden, a Norway spruce site of similar stand age and soil conditions as Asa. Accounting for all sources of uncertainty, they found that the 95 % confidence interval in estimates of base cation weathering was 2.6 times the mean (33 mmolc m−2 yr−1).
Despite the considerable uncertainties in Wbudget estimates, the base cation budget approach showed that accumulation in biomass was a dominant sink for all base cation elements except Na, in line with findings of Nykvist (2000) for two Norway spruce sites in Sweden and the findings of Simonsson et al. (2015). However, this contrasts other studies, which assumed no change in soil and tree biomass stocks of base cations over time (e.g. Sverdrup et al., 1998). The higher estimated weathering rate at Asa reflected the higher productivity and nutrient demand of the stand at this site (Bergh et al., 1999), which has resulted in 1.4-fold greater accumulation of base cations in biomass than at Flakaliden.
Calcium and Mg uptake in forest trees is considered to be more or less passive flow driven by transpiration fluxes, whereas K uptake is an energy-demanding active process (Nieves-Cordones et al., 2014). Considering that Na was the dominant base cation in the soil solution at 50 cm soil depth (Fig. 6), the negligible accumulation of Na in tree biomass suggests that Na uptake in trees is physiologically blocked. Low concentrations of Na seem to be a general feature of terrestrial plants in boreal forests, in contrast to aquatic plants, which explains why the latter are considered important Na sources for large herbivores like moose (Ohlson and Staaland, 2001). Thus, as in agreement with findings by Taylor and Velbel (1991) and Velbel (1995) for other types of forest ecosystems, the negligible Na accumulation in tree biomass and the particularly low deposition at Flakaliden simplify the Na budget to include only three major counterbalancing fluxes: weathering, deposition and leaching. Because Wdepletion and Wbudget of Na were fairly similar, and were much lower than Wprofile, our results provide additional support for the claim that the PROFILE model produced consistently too high Na weathering.
Accumulation in biomass was the dominant sink for Ca, Mg and K, and this term in the BC budget was considered to be of moderate to high quality (Table 5). The changes observed in extractable Ca stocks in the soil were considered more uncertain (Table 5), but they are consistent with observations over 22 years of aggrading Norway spruce forests by Zetterberg et al. (2016), who reported exchangeable Ca depletion rates of 5–11 and 23–39 mmolc m−2 yr−1 for sites in southwestern and northern Sweden, respectively. The higher value for the northern site reflected higher Ca saturation in the soil. The corresponding values for Asa and Flakaliden were larger, but of similar magnitude (34.5 and 40.5 mmolc m−2 yr−1, respectively). Brandtberg and Olsson (2012) studied the same sites as Zetterberg et al. (2016) over a 10-year period and found a general minor increase in exchangeable K soil stocks and a substantial decrease in the Ca stocks, a result very similar to the findings of the present study.
When an independent estimate of current weathering rate (Wprofile) is introduced in the budget (Fig. 6) the high rate of accumulation in biomass is not explained by the combination of measured (TD, ΔS) and modelled (Wprofile) sources or sinks (L). This result suggests that forest trees have access to additional sources of Ca, Mg and K, not measured or captured by our study. We can only speculate about the nature of such sources: it is possible that depletion of ammonium-chloride-exchangeable base cations underestimates the plant-available phases of BC in the soil. Using extraction media other than NH4Cl may have revealed additional sources from oxalates (Rosenstock et al., 2019b). Additional BC release from decomposing roots, stumps and residues from the felling of the former stand was probably neglected because of difficulties including coarse wood in soil sampling. It is also possible that the assumption made that no base cation uptake takes place below 50 cm in the soil was wrong. If trees can take up base cations from deeper soil horizons (e.g. Callesen et al., 2016; Brantley et al., 2017), the discrepancy in weathering rates between the two methods would be reduced since PROFILE predicted higher weathering rates with increasing depth. Furthermore, although biological processes are represented in PROFILE, the model fails to capture biological feedback mechanisms in their entirety, in particular feedbacks generated by plant uptake and mycorrhiza (Finlay et al., 2009, 2019; Sverdrup, 2009; Smits and Wallander, 2017; Akselsson et al., 2019; Rosenstock et al., 2019a).
A general observation from our comparison of three conceptually different methods was that weathering rate estimates were lower with the depletion method than the PROFILE model for the 0–50 cm soil horizon and that the highest weathering rates were estimated by the BC budget approach. In sharp contrast to the historic weathering estimated by the depletion method, the current steady-state weathering by PROFILE increased with increasing soil depth.
The Na weathering rate was an important exception from the general finding as PROFILE estimated a much higher weathering rate for Na than the other methods, which produced similar weathering rates for Na. This indicated that the high weathering rate of Ca, Mg and K by the budget method was at large an effect of high nutrient demand and uptake rate of these elements in the aggrading forest stands. Hence, weathering rates of Ca, Mg and K by the budget method were in our case most likely overestimated. An implication of this conclusion is that forest trees probably have access to additional sources of nutrient base cations, not measured or captured by our study.
Another implication of the higher weathering rate for Na by PROFILE compared to the other methods is that the model may have overestimated release rates of Na, and probably also of K. This conclusion was based on differences between historical and steady-state estimates regarding the rank order of elements and the fact that even the lowest PROFILE weathering rates were too high compared with observed depletions of Na and K. A possible cause of the fact that K weathering rates were overestimated by the PROFILE method was incorrect parameters for the weathering of K-bearing minerals in the model, which should be accounted for in future PROFILE-based weathering estimates.
The depletion method resulted in generally lower weathering rates at Asa than at Flakaliden, whereas the PROFILE estimates for the sites were more similar, indicating that historical weathering estimated by the depletion method was probably underestimated at Asa. This was an effect of the weakly developed and possibly erratic Zr gradients in the soil at Asa, which could have been caused by natural and anthropogenic disturbances. Future studies based on the depletion method should ensure that the Zr gradient with depth shows a net enrichment of Zr towards the soil surface. This condition was not fulfilled for soil profiles at the Asa site. Another important outcome of the study was to show that within-site variations in Zr gradients can be large, as was the case at Flakaliden for two soil profiles.
| Mineralogy | The identity and stoichiometry of minerals present in a certain geographical unit, a particular site (site-specific mineralogy) or a larger geographical province (regional mineralogy). |
|---|---|
| Quantitative mineralogy ormineral composition | Quantitative information (wt %) on the abundance of specific minerals in the soil. |
| Weathering rate | Weathering of a mineral resulting in release of base cations per unit of area per unit of time. |
| Wdepletion | Historical weathering rate based on calculation of loss of mobile elements since last deglaciation. |
| Wprofile | Steady-state weathering rate estimated using the PROFILE model. |
| Wbudget | Current weathering rate based on base cation budget calculations. |
Data on geochemistry and mineralogical compositions are available in the supplement of Casetou-Gustafson et al. (2018, https://doi.org/10.1016/j.geoderma.2017.09.004). BC budget data are available at https://doi.org/10.6084/m9.figshare.11357786 (Casetou-Gustafson et al., 2019b).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-17-281-2020-supplement.
SCG, BAO, MS and JS designed the study and performed data treatment and analyses. HG and SL contributed with data from long-term experiments. SCG prepared the paper with contributions and assistance from BAO, SH, MS, JS, HG and SL.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Quantifying weathering rates for sustainable forestry (BG/SOIL inter-journal SI)”. It is not associated with a conference.
We thank Cecilia Akselsson for her contribution to the study design, PROFILE model development and valuable comments on earlier versions of the manuscript.
This research has been supported by the Swedish Research Council for Environment, Agricultural Sciences and Spatial Planning (FORMAS) (grant no. 212-2011-1691) and the Swedish Energy Agency (grant no. p36151-1). Stephen Hillier acknowledges financial support of the Scottish Government’s Rural and Environment Science and Analytical Services Division (RESAS).
This paper was edited by Nobuhito Ohte and reviewed by Micheal Velbel and four anonymous referees.
Achat, D.L., Deleuze, C., Landmann, G., Pousse, N., Ranger, J., and Augusto, L.: Quantifying consequences of removing harvesting residues on forest soils and tree growth – A meta-analysis, Forest Ecol. Manag., 348, 124–141, 2015.
Akselsson, C., Westling, O., Sverdrup, H., Holmqvist, J., Thelin, G., Uggla, E., and Malm, G.: Impact of harvest intensity on long-term base cation budgets in Swedish forest soils, Water Air Soil Poll., 7, 201–210, 2007.
Akselsson, C., Belyazid, S., Stendahl, J., Finlay, R., Olsson, B. A., Erlandsson Lampa, M., Wallander, H., Gustafsson, J. P., and Bishop, K.: Weathering rates in Swedish forest soils, Biogeosciences, 16, 4429–4450, https://doi.org/10.5194/bg-16-4429-2019, 2019.
Albaugh, T. J., Bergh, J., Lundmark, T., Nilsson, U., Stape, J. L., Allen, H. L., and Linder, S.: Do biological expansion factors adequately estimate stand-scale aboveground component biomass for Norway spruce?, Forest Ecol. Manag., 258, 2628–2637, 2009.
Albaugh, T. J., Bergh, J., Lundmark, T., Nilsson, U., Stape, J. L., Allen, H. L., and Linder, S.: Corrigendum to “Do biological expansion factors adequately estimate stand-scale aboveground component biomass for Norway spruce?”, Forest Ecol. Manag., 270, p. 314, 2012.
Augustin, F., Houle, D., Gagnon, C., and Courchesne, F.: Evaluation of three methods for estimating the weathering rates of base cations in forested catchments, Catena, 144, 1–10, 2016.
Bailey, S. W., Buso, D. C., and Likens, G. E.: Implications of sodium mass balance for interpreting the calcium cycle of a forested ecosystem, Ecology, 84, 471–484, 2003.
Bain, D. C., Mellor, A., Robertson-Rintoul, M., and Buckland, S.: Variations in weathering processes and rates with time in a chronosequence of soils from Glen Feshie, Scotland, Geoderma, 57, 275–293, 1993.
Bain, D. C., Mellor, A., Wilson, M., and Duthie, D.: Chemical and mineralogical weathering rates and processes in an upland granitic till catchment in Scotland, Water Air Soil Poll., 73, 11–27, 1994.
Bergh, J., Linder, S., Lundmark, T., and Elfving, B.: The effect of water and nutrient availability on the productivity of Norway spruce in northern and southern Sweden, Forest Ecol. Manag., 119, 51–62, 1999.
Bergh, J., Linder, S., and Bergström, J.: Potential production of Norway spruce in Sweden, Forest Ecol. Manag., 204, 1–10, 2005.
Binkley, D. and Högberg, P.: Tamm review: revisiting the influence of nitrogen deposition on Swedish forests, Forest Ecol. Manag., 368, 222–239, 2016.
Boyle, J. R., Phillips, J. J., and Ek, A. R.: “Whole tree” harvesting: Nutrient budget evaluation, J. Forestry Res., 71, 760–762, 1973.
Brandtberg, P.-O. and Olsson, B. A.: Changes in the effects of whole-tree harvesting on soil chemistry during 10 years of stand development, Forest Ecol. Manag., 277, 150–162, 2012.
Brantley, S. L., Eissenstat, D. M., Marshall, J. A., Godsey, S. E., Balogh-Brunstad, Z., Karwan, D. L., Papuga, S. A., Roering, J., Dawson, T. E., Evaristo, J., Chadwick, O., McDonnell, J. J., and Weathers, K. C.: Reviews and syntheses: on the roles trees play in building and plumbing the critical zone, Biogeosciences, 14, 5115–5142, https://doi.org/10.5194/bg-14-5115-2017, 2017.
Brimhall, G. H., Ford, C., Bratt, J., Taylor, G., and Warin, O.: Quantitative geochemical approach to pedogenesis: importance of parent material reduction, volumetric expansion, and eolian influx in lateritization, Geoderma, 51, 51–91, 1991.
Callesen, I., Harrison, R., Stupak, I., Hatten, J., Raulund-Rasmussen, K., Boyle, J., Clarke, N., and Zabrowski, D.: Carbon storage and nutrient mobilization from soil minerals by deep roots and rhizospheres, Forest Ecol. Manag., 359, 322–331, 2016.
Casetou-Gustafson, S., Hillier, S., Akselsson, C., Simonsson, M., Stendahl, J., and Olsson, B. A.: Comparison of measured (XRPD) and modeled (A2M) soil mineralogies: A study of some Swedish forest soils in the context of weathering rate predictions, Geoderma, 310, 77–88, 2018.
Casetou-Gustafson, S., Akselsson, C., Hillier, S., and Olsson, B. A.: The importance of mineral determinations to PROFILE base cation weathering release rates: a case study, Biogeosciences, 16, 1903–1920, https://doi.org/10.5194/bg-16-1903-2019, 2019a.
Casetou-Gustafson, S., Olsson, B. A., Grip, H., Hillier, S., Linder, S., Simonsson, M., and Stendahl, J.: Current, steady-state and historical weathering rates of base cations at two forest sites in northern and southern Sweden: A comparison of three methods, figshare, https://doi.org/10.6084/m9.figshare.11357786.v1, 2019b.
Chadwick, O. A., Brimhall, G. H., and Hendricks, D. M.: From a black to a gray box – a mass balance interpretation of pedogenesis, Geomorphology, 3, 369–390, 1990.
De Jong, J., Akselsson, C., Egnell, G., Löfgren, S., and Olsson, B.A.: Realizing the energy potential of forest biomass in Sweden – how much is environmentally sustainable?, Forest Ecol. Manag., 383, 3–16, 2017.
Erlandsson Lampa, M., Sverdrup, H. U., Bishop, K. H., Belyazid, S., Ameli, A., and Köhler, S. J.: Catchment export of base cations: Improved mineral dissolution kinetics influence the role of water transit time, SOIL Discuss., https://doi.org/10.5194/soil-2019-3, in review, 2019.
Finlay, R., Wallander, H., Smits, M., Holmström, S., Van Hees, P., Lian, B., and Rosling, A.: The role of fungi in biogenic weathering in boreal forest soils, Fungal Biol. Rev., 23, 101–106, 2009.
Finlay, R. D., Mahmood, S., Rosenstock, N., Bolou-Bi, E. B., Köhler, S. J., Fahad, Z., Rosling, A., Wallander, H., Belyazid, S., Bishop, K., and Lian, B.: Biological weathering and its consequences at different spatial levels – from nanoscale to global scale, Biogeosciences Discuss., https://doi.org/10.5194/bg-2019-41, in review, 2019.
Fredén, C.: The National Atlas of Sweden, Geology, 3rd Edn., SNA Publishing House, Stockholm, Sweden, 208 pp., 2009.
Fröberg, M., Berggren, D., Bergkvist, B., Bryant, C., and Mulder, J.: Concentration and Fluxes of Dissolved 795 Organic Carbon (DOC) in Three Norway Spruce Stands along a Climatic Gradient in 796 Sweden, Biogeochemistry, 77, 1–23, 2006.
Fröberg, M., Grip, H., Tipping, E., Svensson, M., Strömgren, M., and Kleja, D. B.: Long-term effects of experimental fertilization and soil warming on dissolved organic matter leaching from a spruce forest in Northern Sweden, Geoderma, 200, 172–179, 2013.
Futter, M., Klaminder, J., Lucas, R., Laudon, H., and Köhler, S.: Uncertainty in silicate mineral weathering rate estimates: source partitioning and policy implications, Environ Res. Lett., 7, 024025, https://doi.org/10.1088/1748-9326/7/2/024025, 2012.
Garrels, R. M. and Mackenzie, F. T.: Origin of the chemical compositions of some springs and lakes, in: Equilibrium Concepts in Natural Water Systems, Advances in Chemistry Series, edited by: Stumm, W., Am. Chem. Soc., 67, 222–242, 1967.
Greisman, A. and Gaillard, M. J.: The role of climate variability and fire in early and mid Holocene forest dynamics of southern Sweden, J. Quartenary Sci., 24, 593–611, 2009.
Grennfelt, P. and Hov, Ø.: Regional air pollution at a turning point, Ambio, 34, 2–10, 2005.
Harden, J. W.: Soils developed in granitic alluvium near Merced, California, Geological Survey Bulletin (USA) 1590 – A, Soil Chronosequences in the Western United States, Government Printing Office, Washington DC, USA, A1–A65, 1987.
Hedin, L. O., Granat, L., Likens, G. E., Buishand, T. A., Galloway, J. N., Butler, T. J., and Rodhe, H.: Steep declines in atmospheric base cations in regions of Europe and North America, Nature, 367, 351–354, 1994.
Hedwall, P. O., Grip, H., Linder, S., Lövdahl, L., Nilsson, U., and Bergh, J.: Effects of clear-cutting and slash removal on soil water chemistry and forest-floor vegetation in a nutrient optimised Norway spruce stand, Silva Fenn., 47, 933, https://doi.org/10.14214/sf.933, 2013.
Hellsten, S., Helmisaari, H. S., Melin, Y., Skovsgaard, J. P., Kaakinen, S., Kukkola, M., Saarsalmi, A., Petersson, H., and Akselsson, C.: Nutrient concentrations in stumps and coarse roots of Norway spruce, Scots pine and silver birch in Sweden, Finland and Denmark, Forest Ecol. Manag., 290, 40–48, 2013.
Helmisaari, H.-S., Derome, J., Nöjd, P., and Kukkola, M.: Fine root biomass in relation to site and stand characteristics in Norway spruce and Scots pine stands, Tree Physiol., 27, 1493–1504, 2007.
Hillier, S.: Use of an air brush to spray dry samples for X-ray powder diffraction, Clay Miner., 34, 127–127, 1999.
Hillier, S.: Quantitative analysis of clay and other minerals in sandstones by X-ray powder diffraction (XRPD), in: Clay Mineral Cements in Sandstones, edited by: Worden, R. and Morad, S., International Association of Sedimentologists, Special Publication, John Wiley and Sons Ltd, Oxford, UK, 34, 213–251, 2003.
Hodson, M. E., Langan, S. J., and Wilson, M. J.: A sensitivity analysis of the PROFILE model in relation to the calculation of soil weathering rates, Appl. Geochem., 11, 835–844, 1996.
Hodson, M. E. and Langan, S. J.: The influence of soil age on calculated mineral weathering rates, Appl. Geochem., 14, 387–394, 1999.
Iwald, J., Löfgren, S., Stendahl, J., and Karltun, E.,: Acidifying effect of removal of tree stumps and logging residues as compared to atmospheric deposition, Forest Ecol. Manag., 290, 49–58, 2013.
Jansson, P.-E.: CoupModel: model use, calibration, and validation, Trans. Am. Soc. Agr. Eng., 55, 1337–1344, 2012.
Jauhiainen, E.: Age and degree of podzolization of sand soils on the coastal plain of northwest Finland, Comm. Biol., 68, 1–32, 1973.
Jönsson, C., Warfvinge, P., and Sverdrup, H.: Uncertainty in predicting weathering rate and environmental stress factors with the PROFILE model, Water Air Soil Poll., 81, 1–23, 1995.
Karlsson, P. E., Ferm, M., Hultberg, H., Hellsten, S., Akselsson, C., and Pihl Karlsson, G.: Totaldeposition av kväve till skog, IVL Swedish Environmental Research Institute, Stockholm, Sweden, Report B1952, 37 pp., 2011.
Karlsson, P. E., Ferm, M., Hultberg, H., Hellsten, S., Akselsson, C., and Pihl Karlsson, G.: Totaldeposition av baskatjoner till skog, IVL Swedish Environmental Research Institute, Stockholm, Sweden, Report B2058, 64 pp., 2013.
Kellner, O.: Effects of fertilization on forest flora and vegetation, Ph.D. thesis, Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science, Uppsala University, Sweden, 464, 32 pp., 1993.
Klaminder, J., Lucas, R., Futter, M., Bishop, K., Köhler, S., Egnell, G., and Laudon, H.: Silicate mineral weathering rate estimates: Are they precise enough to be useful when predicting the recovery of nutrient pools after harvesting?, Forest Ecol. Manag., 261, 1–9, 2011.
Kolka, R. K., Grigal, D., and Nater, E.: Forest soil mineral weathering rates: use of multiple approaches, Geoderma, 73, 1–21, 1996.
Koseva, I. S., Watmough, S. A., and Aherne, J.: Estimating base cation weathering rates in Canadian forest soils using a simple texture-based model, Biogeochemistry, 101, 183–196, 2010.
Lidskog, R. and Sundqvist, G.: The role of science in environmental regimes: The case of LRTAP, Eur. J. Internat. Rel., 8, 77–101, 2002.
Likens, G. E. and Bormann, F. H.: Acid rain: a serious regional environmental problem, Science, 184, 1176–1179, 1974.
Likens, G. E., Driscoll, C. T., Buso, D. C., Siccama, T. G., Johnson, C. E., Lovett, G. M., Fahey, T. J., Reiners, W. A., Ryan, D. F., Martin, C. W., and Bailey, S. W.: The biogeochemistry of calcium at Hubbard Brook, Biogeochemistry, 41, 89–173, 1998.
Linder, S.: Foliar analysis for detecting and correcting nutrient imbalances in Norway spruce, Ecol. Bull., 44, 178–190, 1995.
Löfgren, S., Aastrup, M., Bringmark, L., Hultberg, H., Lewin-Pihlblad, L., Lundin, L., Karlsson, G. P., and Thunholm, B.: Recovery of soil water, groundwater, and streamwater from acidification at the Swedish Integrated Monitoring catchments, Ambio, 40, 836–856, 2011.
Lundström, U., Van Breemen, N., Bain, D., Van Hees, P., Giesler, R., Gustafsson, J. P., Ilvesniemi, H., Karltun, E., Melkerud, P.-A., and Olsson, M.: Advances in understanding the podzolization process resulting from a multidisciplinary study of three coniferous forest soils in the Nordic Countries, Geoderma, 94, 335–353, 2000.
Marklund, L. G.: Biomass functions for pine, spruce and birch in Sweden, Department of Forest Survey, Swedish University of Agricultural Sciences, Umeå, Sweden, Report 45, 1–73, 1988.
Marshall, C. and Haseman, J.: The quantitative evaluation of soil formation and development by heavy mineral studies: A grundy silt loam profile 1, Soil Sci. Soc. Am. J., 7, 448–453, 1943.
Nieves-Cordones, M., Alemán, F., Martínez, V., and Rubio, F.: K+ uptake in plant roots. The systems involved, their regulation and parallels in other organisms, J. Plant Physiol., 171, 688–695, 2014.
Nilsson, S. I. and Tyler, G.: Acidification-induced chemical changes of foret soils during recent decades – a review, in: Effects of acid deposition andtroposhereic ozone on forest ecosystems in Sweden, edited by: Staaf, H. and Tyler, G., Ecol. Bull., 44, 54–64, 1995.
Nilsson, S. I., Miller, H. G., and Miller, J. D.: Forest growth as a possible cause of soil and water acidification – an examination of the concepts, Oikos, 39, 40–49, 1982.
Nykvist, N.: Effects of clearfelling, slash removal and prescribed burning on amounts of plant nutrients in biomass and soil, Studia Forestalia Suecia, 210, 1–43, 2000.
Ohlson, M. and Staaland, H.: Mineral diversity in wild plants: benefits and bane for moose, Oikos, 94, 442–454, 2001.
Olsson, B. A., Bengtsson, J., and Lundkvist, H.: Effects of different forest harvest intensities on the pools of exchangeable cations in coniferous forest soils, Forest Ecol. Manag., 84, 135–147, 1996.
Olsson, M. and Melkerud, P.-A.: Chemical and mineralogical changes during genesis of a Podzol from till in southern Sweden, Geoderma, 45, 267–287, 1989.
Olsson, M. T. and Melkerud, P.-A.: Weathering in three podzolized pedons on glacial deposits in northern Sweden and central Finland, Geoderma, 94, 149–161, 2000.
Omotoso, O., McCarty, D. K., Hillier, S., and Kleeberg, R.: Some successful approaches to quantitative mineral analysis as revealed by the 3rd Reynolds Cup contest, Clay Clay Miner., 54, 748–760, 2006.
Ouimet, R. and Duchesne, L.: Base cation mineral weathering and total release rates from soils in three calibrated forest watersheds on the Canadian Boreal Shield, Can. J. Soil Sci., 85, 245–260, 2005.
Paré, D., Rochon, P., and Brais, S.: Assessing the geocchemical balance of managed boreal forests, Ecol. Indicators, 1, 293–311, 2002.
Petersson, H. and Ståhl, G.: Functions for below-ground biomass of Pinus sylvestris, Picea abies, Betula pendula and Betula pubescens in Sweden, Scand. J. For. Res., 21, 84–93, 2006.
Phelan, J., Belyazid, S., Kurz, D., Guthrie, S., Cajka, J., Sverdrup, H., and Waite, R.: Estimation of soil base cation weathering rates with the PROFILE model to etermine critical loads of acidity for forested ecosystems in Pennsylvania, USA: Pilot application of a potential national methodology, Water Air Soil Pollut., 225, 2109, https://doi.org/10.1007/s11270-014-2109-4, 2014.
Ranius, T., Hämäläinen, A., Egnell, G., Olsson, B., Eklöf, K., Stendahl, J., Rudolphi, J., Sténs, A., and Felton, A.: The effects of logging residue extraction for energy on ecosystem services and biodiversity: A synthesis, J. Environ. Manage., 209, 409–425, 2018.
Reuss, J. O. and Johnson, D. W.: Acid Deposition and the Acidification of Soils and Waters. Ecological Studies 59, Springer Science+Business Media, New York, 119 pp., ISBN 978-4419-8536-1, 1986.
Rosenstock, N. P., van Hees, P. A. W., Fransson, P. M. A., Finlay, R. D., and Rosling, A.: Biological enhancement of mineral weathering by Pinus sylvestris seedlings – effects of plants, ectomycorrhizal fungi, and elevated CO2, Biogeosciences, 16, 3637–3649, https://doi.org/10.5194/bg-16-3637-2019, 2019a.
Rosenstock, N. P., Stendahl, J., van der Heijden, G., Lundin, L., McGivney, E., Bishop, K., and Löfgren, S.: Base cations in the soil bank. Non-exchangeable pools may sustain centuries of net loss to forestry and leaching, Soil, 5, 351–366, https://doi.org/10.5194/soil-5-351-2019, 2019.
Ryan, M. G.: Three decades of research at Flakaliden advancing whole-tree physiology, forest ecosystem and global change research, Tree Physiol., 33, 1123–1131, 2013.
Schaetzl, R. J. and Isard, S. A.: Regional-scale relationships between climate and strength of podzolization in the Great Lakes region, North America, Catena, 28, 47–69, 1996.
Schützel, H., Kutschke, D., and Wildner, G.: Zur Problematik der Genese der Grauen Gneise des Sächsischen Erzgebirges (Zirkonstatistische Untersuchungen), Freiberger Forschungshefte, C 159, Mineralogie, 1–65, 1963.
Sigurdsson, B. D., Medhurst, J. L., Wallin, G., Eggertsson, O., and Linder, S.: Growth of mature boreal Norway spruce was not affected by elevated [CO2] and/or air temperature unless nutrient availability was improved, Tree Physiol., 33, 1192–1205, 2013.
Simonsson, M. and Berggren, D.: Aluminium solubility related to secondary solid phases in upper B horizons with spodic characteristics, Eur. J. Soil Sci., 49, 317–326, 1998.
Simonsson, M., Bergholm, J., Olsson, B. A., von Brömssen, C., and Öborn, I.: Estimating weathering rates using base cation budgets in a Norway spruce stand on podzolised soil: analysis of fluxes and uncertainties, Forest Ecol. Manag., 340, 135–152, 2015.
Simonsson, M., Bergholm, J., Lemarchand, D., and Hillier, S.: Mineralogy and biogeochemistry of potassium in the Skogaby experimental forest, southwest Sweden: pools, fluxes and K/Rb ratios in soil and biomass, Biogeochemistry, 131, 77–102, 2016.
Smits, M. M. and Wallander, H.: Role of mycorrhizal symbiosis in mineral weathering and nutrient mining from soil parent material, in: Mycorrhizal Mediation of Soil: Fertility, Structure, and Carbon Storage, edited by: Johnson, N. C., Gehring, C., and Jansa, J., Elsevier, United States, 35–46, 2017.
Starr, M., Lindroos, A.-J., and Ukonmaanaho, L.: Weathering release rates of base cations from soils within a boreal forested catchment: variation and comparison to deposition, litterfall and leaching fluxes, Environ. Earth Sci., 72, 5101–5111, 2014.
Stendahl, J., Lundin, L., and Nilsson, T.: The stone and boulder content of Swedish forest soils, Catena, 77, 285–291, 2009.
Stendahl, J., Akselsson, C., Melkerud, P.-A., and Belyazid, S.: Pedon-scale silicate weathering: comparison of the PROFILE model and the depletion method at 16 forest sites in Sweden, Geoderma, 211, 65–74, 2013.
Strengbom, J., Dahlberg, A., Larsson, A., Lindelow, A., Sandström, J., Widenfalk, O., and Gustafsson, L.: Introducing intensively managed spruce plantations in Swedish forest landscapes will impair biodiversity decline, Forests, 2, 610–630, 2011.
Sudom, M. and St. Arnaud, R.: Use of quartz, zirconium and titanium as indices in pedological studies, Can. J. Soil Sci., 51, 385–396, 1971.
Sverdrup, H.: Chemical weathering of soil minerals and the role of biological processes, Fungal Biol. Rev., 23, 94–100, 2009.
Sverdrup, H. and de Vries, W., Calculating critical loads for acidity with the simple mass-balance method, Water Air Soil Pollut., 72, 143–162, 1994.
Sverdrup, H. and Rosén, K.: Long-term base cation mass balances for Swedish forests and the concept of sustainability, Forest Ecol. Manag., 110, 221–236, 1998.
Sverdrup, H., Warfvinge, P., Frogner, T., Håøya, A. O., Johansson, M., and Andersen, B.: Critical loads of acidity in the Nordic countries, Ambio, 21, 348–355, 1992.
Sverdrup, H., Warfvinge, P., and Wickman, T.: Estimating the weathering rate at Gårdsjon using different methods, in: Experimental Reversal of Rain Effects: Gardsjon Roof Project, edited by: Hultberg, H. and Skeffington, R., John Wiley & Sons Ltd, Chichester, UK, 231–249, 1998.
Tamm, O.: Studier över jordmånstyper och deras förhållande till markens hydrologi i nordsvenska skogsterränger barrskogsområdet, Reports of the Swedish Institute of Experimental Forestry, 26, 163–355, 1931 (in Swedish).
Taylor, A. and Blum, J. D.: Relation between soil age and silicate weathering rates determined from the chemical evolution of a glacial chronosequence, Geology, 23, 979–982, 1995.
Taylor, A., Lenoir, L., Vegerfors, B., and Persson, T.: Ant and earthworm bioturbation in cold-temperate ecosystems, Ecosystems, 22, 981–994, https://doi.org/10.1007/s10021-018-0317-2, 2019.
Taylor, A. B. and Velbel, M. A.: Geochemical mass balance and weathering rates in forested watersheds of the southern Blue Ridge, II. Effects of botanical uptake terms, in: Weathering and Soils, edited by: Pavich, M. J., Geoderma, 51, 29–50, 1991.
Thiffault, E., Hannam, K. D., Paré, D., Titus, B. D., Hazlett, P. W., Maynard D. G., and Brais, S.: Effects of forest biomass harvesting on soil productivity in boreal and temperate forests – A review, Environ. Rev. 19, 278–309, 2011.
Thompson, M. L. and Ukrainczyk, L.: Micas, Soil mineralogy with environmental applications, in: Soil Mineralogy with Environmental Applications, edited by: Dixon, J. B. and Schulze, D. G., Soil Science Society of America Inc., Madison, 431–466, 2002.
Van Der Salm, C.: Assessment of the regional variation in weathering rates of loess and clay soils in the Netherlands, Water Air Soil Poll., 131, 217–243, 2001.
Velbel, M. A.: Geochemical mass balances and weathering rates in forested watersheds of the southern Blue Ridge, Am. J. Sci., 285, 904–930, 1985.
Velbel, M. A.: Interaction of ecosystem processes and weathering, in: Solute Modelling in Catchment Systems, edited by: Trudgill, S., John Wiley & Sons, 193–209, 1995.
Velbel, M. A. and Price, J. R.: Solute geochemical mass-balances and mineral weathering rates in small watersheds: methodology, recent advances and futures directions, Appl. Geochem., 22, 1682–1700, 2007.
Viro, P.: Kivisyyden maarittamisesta, Summary: On the determination of stoniness, Commun. Inst. For. Fenn., 40, 1–23, 1952.
Warfvinge, P. and Sverdrup, H.: Critical Loads of Acidity to Swedish Forest Soils: Methods, Data and Results, Reports in Ecology and Environmental Engineering, Dpt. of Chemical Engineering II, Lund University, Lund, Sweden, 1–104, 1995.
White, A. F., Blum, A. E., Schulz, M. S., Bullen, T. D., Harden, J. W., and Peterson, M. L.: Chemical weathering rates of a soil chronosequence on granitic alluvium: I. Quantification of mineralogical and surface area changes and calculation of primary silicate reaction rates, Geochim. Cosmochim. Ac., 60, 2533–2550, 1996.
Whitfield, C., Watmough, S., Aherne, J., and Dillon, P.: A comparison of weathering rates for acid-sensitive catchments in Nova Scotia, Canada and their impact on critical load calculations, Geoderma, 136, 899–911, 2006.
Whitfield, C. J. and Watmough, S. A.: A regional approach for mineral soil weathering estimation and critical load assessment in boreal Saskatchewan, Can. Sci. Total Environ., 437, 165–172, 2012.
Whitfield, C. J., Watmough, S. A., and Aherne, J.: Evaluation of elemental depletion weathering rate estimation methods on acid-sensitive soils of north-eastern Alberta, Canada, Geoderma, 166, 189–197, 2011.
Wikström, P., Edenius, L., Elfving, B., Eriksson, L. O., Lämås, T., Sonesson, J., Öhman, K., Wallerman, J., Waller, C., and Klintebäck, F.: The Heureka forestry decision support system: an overview, Math. Comput. For. Nat. Res. Sci., 3, 87–94, 2011.
Yanai, R. D., Battles, J. J., Richardson, A. D., Blodgett, C. A., Wood, D. M., and Rastetter, E. B.: Estimating uncertainty in ecosystem budget calculations, Ecosystems, 13, 239–248, 2010.
Zetterberg, T., Olsson, B. A., Löfgren, S., von Brömssen, C., and Brandtberg, P. O.: The effect of harvest intensity on long-term calcium dynamics in soil and soil solution at three coniferous sites in Sweden, Forest Ecol. Manag., 302, 280–294, 2013.
Zetterberg, T., Olsson, B. A., Löfgren, S., Hyvönen, R., and Brandtberg, P. O.: Long-term soil calcium depletion after conventional and whole-tree harvest, Forest Ecol. Manag., 369, 102–115, 2016.