the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Tropical tree height and crown allometries for the Barro Colorado Nature Monument, Panama: a comparison of alternative hierarchical models incorporating interspecific variation in relation to life history traits
Helene C. Muller-Landau
S. Joseph Wright
Stephanie A. Bohlman
Stephen W. Pacala
Tree allometric relationships are widely employed for estimating forest biomass and production and are basic building blocks of dynamic vegetation models. In tropical forests, allometric relationships are often modeled by fitting scale-invariant power functions to pooled data from multiple species, an approach that fails to capture changes in scaling during ontogeny and physical limits to maximum tree size and that ignores interspecific differences in allometry. Here, we analyzed allometric relationships of tree height (9884 individuals) and crown area (2425) with trunk diameter for 162 species from the Barro Colorado Nature Monument, Panama. We fit nonlinear, hierarchical models informed by species traits – wood density, mean sapling growth, or sapling mortality – and assessed the performance of three alternative functional forms: the scale-invariant power function and the saturating Weibull and generalized Michaelis–Menten (gMM) functions. The relationship of tree height with trunk diameter was best fit by a saturating gMM model in which variation in allometric parameters was related to interspecific differences in sapling growth rates, a measure of regeneration light demand. Light-demanding species attained taller heights at comparatively smaller diameters as juveniles and had shorter asymptotic heights at larger diameters as adults. The relationship of crown area with trunk diameter was best fit by a power function model incorporating a weak positive relationship between crown area and species-specific wood density. The use of saturating functional forms and the incorporation of functional traits in tree allometric models is a promising approach for improving estimates of forest biomass and productivity. Our results provide an improved basis for parameterizing tropical plant functional types in vegetation models.
- Article
(3041 KB) -
Supplement
(5021 KB) - BibTeX
- EndNote
Allometric scaling describes how plant morphology and performance vary as a function of size, patterns that are ultimately due to size-dependent physical constraints and selective pressures (Niklas, 1994). Allometric relationships show high predictive ability and are widely employed for estimating forest carbon biomass and primary production from forest inventory data (e.g., Chave et al., 2014; Goodman et al., 2014). Allometric functions constitute building blocks of more complex, mechanistic forest models, including the vegetation modules of state-of-the art Earth system models (e.g., Weng et al., 2015). These functions provide a basic template for modeling carbon allocation and tree growth (Pacala et al., 1996), and differences in allometric parameters can be used to represent different species or plant functional types (PFTs, Prentice et al., 1992). However, allometric relationships of tropical trees remain poorly documented when compared to temperate and boreal forest ecosystems (Houghton, 2005; Hunter et al., 2013), even though tropical forests account for a disproportionate share of forest carbon stocks and fluxes (∼50 % of the terrestrial carbon sink and ∼33 % of annual NPP; Chapin, 2011; Pan et al., 2013). Alternative choices of tree allometric equations contribute to the wide variability in biomass and productivity estimates in the literature and to the large uncertainty surrounding the response of these ecosystems to warmer and dryer climates (Bonan, 2008).
Power functions are widely used to describe allometric scaling of tree height and crown area with trunk diameter, despite the known limitations of their underlying assumption of scale invariance of tree morphology (Shinozaki et al., 1964a, b; Niklas, 1994). The adoption of power function scaling is particularly problematic at both extremes of the tree size range (Enquist and Bentley, 2012). Power functions fail to capture the allometries of the smallest and largest individuals, generally underestimating dimensions of seedlings and saplings and overestimating the size of large trees (e.g., Fayolle et al., 2016; Ledo et al., 2016). This suggests the need for alternative functional forms to represent life history heterogeneity and the physical constraints that set maximum tree sizes (Koch et al., 2004; Bonan, 2008; Goodman et al., 2014; Mensah et al., 2018). Indeed, the inclusion of a saturating relationship for tree scaling has proved important in reproducing realistic dynamics in vegetation models (Weng et al., 2015).
Allometric studies of tropical trees have highlighted differences in growth and morphology that define distinct life history strategies (Clark and Clark, 1992; Poorter et al., 2006). These differences contribute to species coexistence and play a key role in successional trajectories (Wright, 2002; Chazdon, 2014; Falster et al., 2017). Approaches pooling data across species inherently fail to recognize species heterogeneity in allometric scaling and limit the potential to identify and define plant functional groups. Pooling data across species also tends to over-represent locally abundant species, unless appropriate methods like hierarchical models are employed to account for unbalanced sampling. Species differ systematically in allometric relationships, suggesting that these differences reflect underlying interspecific variation in life history, physiology, morphology, and/or phylogeny (Westoby et al., 2002; Adler et al., 2014). Hierarchical approaches based on functional traits can provide a useful approach for capturing this interspecific variation in tree allometry (Dietze et al., 2008; Iida et al., 2011). Several studies have found regeneration light requirements and/or wood density to be related to tree height and/or crown size across species, suggesting that these are good candidates for inclusion in a hierarchical model (Poorter et al., 2006; Wright et al., 2010; Iida et al., 2012, 2014; Loubota Panzou et al., 2018).
Here, we present a quantitative approach for characterizing allometric relationships for tree height and crown area and their interspecific variation in tropical forests and apply it to a large dataset for a single site. Our overall objective was to develop models informed by functional traits to capture interspecific variation in the allometric scaling of tropical trees and provide a better template for the estimation and modeling of forest biomass and ecosystem fluxes. We address three specific questions: (i) how is interspecific variability in allometric scaling of tree height and crown area in this forest related to tree species functional traits, in particular wood density and measures of shade tolerance? (ii) How do power functions compare with various asymptotic functions in representing these species-specific allometric relationships? (iii) How does the choice of alternative tree height scaling functions affect the estimation of aboveground biomass? To answer these questions, we fitted allometric models whose parameters were related to species-specific functional traits under a Bayesian hierarchical framework, taking advantage of long-term, high-quality data from Barro Colorado, Panama. This approach allowed us to characterize different sources of variability, from individual species to the community level, and to simultaneously assess the relative merits of different functional forms.
2.1 Study site
The Barro Colorado Nature Monument is a protected area in central Panama consisting of Barro Colorado Island (BCI) and peninsulas on the surrounding mainland (Leigh, 1999). The vegetation is tropical moist forest. Annual rainfall averages 2657 mm (years 1926 to 2017), with a 4-month dry season from approximately mid-December to mid-April (Paton, 2018). The forest dynamics plot on BCI is a 50 ha area (1000 m × 500 m) in which all tree stems with trunk diameter of at least 1 cm have been measured, mapped, tagged, and identified to species in regular censuses since the early 1980s (Hubbell, 1983; Condit, 1998; Leigh, 1999; Hubbell et al., 1999, 2005). The plot is mostly old-growth forest of 400 years or older (Piperno, 1990), with the exception of a small area of secondary forest that is ∼127–137 years old in the central part of the northern edge of the plot (Mascaro et al., 2011). The Gigante peninsula on the nearby mainland is covered by secondary forest ranging from 100 to perhaps 300 years old (Denslow and Guzman, 2000; Wright et al., 2011).
2.2 Tree measurements
The allometric data consist of measurements of trunk diameter at 1.3 m height or above buttresses, D (cm), tree height, H (m), and crown area, C (m2). We used a compilation of seven datasets collected in the BCI 50 ha plot and one dataset from old-growth forests on the adjacent Gigante peninsula (see Table S1 in Section S1 of the Supplement for further details). The datasets cover different size classes and combine measurements made with different, albeit standard, methods. Depending on the dataset and tree size, tree heights were measured with a telescoping pole (smaller trees only), with a laser rangefinder using the sine or tangent method (Larjavaara and Muller-Landau, 2013), or from the difference between a model obtained from photogrammetry (of the ground) and that obtained from airborne lidar (only fully sun-exposed trees). Crown areas were from ground-based measurements of crown radii or from delimiting fully sun-exposed crowns in high-resolution aerial photos. We included only species with at least five individual measurements of either H or C and those that have data for the three trait covariates (see below), which resulted in a pool of 162 species, including 9884 trees for height allometries and 2425 trees for crown area allometries.
2.3 Species traits
We considered three species-level covariates to assess whether functional traits can explain interspecific variability in allometric scaling: the structural trait of wood density and two demographically based indicators of shade tolerance. Species-specific wood density values (dry matter weight per unit of fresh volume; g cm−3) – technically wood specific gravity (Williamson and Wiemann, 2010) – were based on measurements taken in central Panama (Wright et al., 2010). The two shade-tolerance indicators were the rates of mean sapling diameter growth and of sapling mortality estimated by Condit et al. (2006) on BCI using the 5-year census data between 1982 and 2005. Sapling relative growth rates (% yr−1) were based on diameter increments for individuals between 10 and 49 mm in diameter at the initial census. Annual mortality rates (% yr−1) were also based on the monitoring of tagged individuals but included saplings with diameters between 10 and 99 mm (Condit et al., 2006). For both growth and mortality, the rates are weighted averages of means for each census interval, weighting by the number of records in a census interval.
2.4 Statistical analyses
We adopted a hierarchical Bayesian (HB) approach to analyze allometric relationships of tree height and crown area with trunk diameter (Dietze et al., 2008; Price et al., 2009; Iida et al., 2011). The HB approach provides several advantages over classic analytical frameworks (Cressie et al., 2009; Gelman, 2014), starting with the easy accommodation of complex data structures and process models. In the current context, the HB framework allowed us to simultaneously estimate (i) community-level allometries that best represent an average species in the community, (ii) species-specific allometries that capture interspecific variation, and (iii) general relationships of species-specific allometric parameters to functional traits. The estimation of general relationships is improved by properly weighting species-specific estimates, whereas species-level estimates for rare species benefit from borrowing strength from the community-level relationship. The latter aspect reduces the negative impact of outlying observations and allows inference for data-poor species, of which there are many in hyperdiverse ecosystems like tropical forests. Another important advantage of the HB approach is that it can easily handle nonlinear models, allowing us to extend the analysis beyond power functions (which are typically fitted through linear regressions on log-transformed data; Mascaro et al., 2014) to other functional relationships. Finally, the HB approach allowed us to assess the relationships of functional traits to tree allometries by explicitly modeling species-specific allometric parameters as functions of species traits.
2.4.1 Model specification
Bayesian hierarchical models have three components (Cressie et al., 2009): (i) a data model linking model predictions with observed data, (ii) a process model providing a mathematical description of the mechanisms underlying the patterns of interest, and (iii) a parameter model that incorporates prior information about parameter values available before the analysis.
For the data model, we assumed a Gaussian likelihood for the natural logarithm of the response variable, ys[i], which was either tree height (H, m) or crown area (C, m2) for each individual i in species s:
the where the process model, f (⋅), predicts expected natural log tree height or crown area from observed trunk diameter, D (cm), and the vector of species-specific parameters, Θs={asbsks}. The standard deviation σν captures deviations between model predictions and observed data.
We considered three functional forms of varying complexity for the process model, representing alternative hypotheses about allometric scaling. Our simplest model was the power function model, which presumes scale invariance of tree morphology with trunk diameter. We also tested two models that are nonlinear in the logarithmic scale, thereby allowing for a curvature in scaling (Thomas, 1996): a generalized Michaelis–Menten (gMM) and a rescaled Weibull function (the cumulative Weibull distribution rescaled to extend from 0 to a rather than 0 to 1). We chose the two saturating functions because they are always nondecreasing and allow for finite constraints on maximum tree dimensions, with both equations featuring a saturating relationship between tree dimensions and trunk size. The equations for all three models are as follows:
Preliminary analyses evaluated additional saturating functional forms, including the Gompertz and logistic forms, and found that they produced inferior fits, in agreement with previous studies of tree height and crown area (Feldpausch et al., 2011; Banin et al., 2012; Ledo et al., 2016).
We evaluated the effect of functional traits by adding an additional layer to the process model to accommodate interspecific differences in model parameters. Each allometric parameter θ (i.e., a, b, or k in Eqs. 2, 3, or 4) was modeled as a univariate linear function of one of the three traits, Ts (i.e., wood density, sapling mortality rate, or sapling growth rate):
Deviations from the linear relationships were assumed to follow a normal distribution with a community-level standard deviation σθ. Each covariate was centered and scaled to mean zero and unit variance before the analysis. As a consequence, the intercept of the linear relationship between parameter values and species-specific traits, αθ, provides an estimate of the across-species mean, while the slope βθ gives the expected effect of an increase of 1 standard deviation for each covariate (Gelman, 2014). We compared models including individual functional traits with models lacking covariates, that is, models in which variation among allometric scaling parameters is assumed to be random (i.e., equivalent to setting βθ to zero). We refer to models incorporating relationships between allometric parameters and species traits as “trait models”. Because each allometric parameter was a linear function of a trait, the trait models had twice the number of community-level parameters as corresponding models lacking covariates. Our trait models each featured a single trait (all parameters in a trait model depended on the same trait).
The model was completed with the specification of uninformative prior distributions in the parameter model. We assumed independent normal priors for the community-level parameters (α, β), with means of 0 and variances of 100. We also assumed that the species-level parameters in Θs were independently normally distributed (assuming a multivariate normal instead and thus allowing for correlations among a, b, and k did not significantly alter the main results). We assumed half-Cauchy prior distributions with a scale parameter set to 2.5 for the observation variance ( and for the across-species variances of the parameters of the allometric models (.The model ignored measurement errors in trunk diameter and in trait data.
2.4.2 Model selection and inference
For both tree height and crown area, model selection and inference involved the assessment of 12 different model formulations resulting from all combinations of the three process models (power, generalized Michaelis–Menten, and Weibull), and the four possibilities for functional traits (wood density, sapling growth, sapling mortality, or the “no trait” models featuring only random variability in allometric parameters across species). Alternative models were fitted using Markov chain Monte Carlo (MCMC) methods (Gelman, 2014). Inference was based on 5000 posterior samples following 10 000 burn-in iterations for four parallel chains, which allowed us to check convergence using the potential scale reduction statistic together with estimates of effective sample size (Gelman and Rubin, 1992). Based on the posterior distribution of the deviance (specifically, the expectation of the log pointwise predictive density – ELP), we calculated the Watanabe (2013) information criterion (WAIC) to rank alternative models in terms of a balance between predictive ability and model complexity (Hooten and Hobbs, 2015). Models were fitted in Stan (Stan Development Team, 2016), a statistical software package to conduct Bayesian analyses (code provided in Sect. S2 in the Supplement).
Posterior samples were used for characterizing the distributions of parameters and to project estimation uncertainty to model-based estimates. We report central, 90 % posterior intervals both for parameter estimates and for model-based predictions of tree height and crown area for selected trunk diameter values. We further provide unbiased community-level models for estimating (untransformed) height and crown area from trunk diameter. These models were corrected for the bias introduced by back transformation of log-transformed predictions; the correction involves multiplying predicted values by , where σν is the residual standard deviation of the fitted model for the log-transformed variable (Sprugel, 1983).
2.4.3 Implications for biomass estimates
Finally, we derived estimates of oven-dry aboveground biomass, AGB (kilograms dry mass), from measured trunk diameters and our estimated heights. We used a general tropical tree allometric model that assumed a linear scaling of AGB with tree height (Eq. 5 in Chave et al., 2014):
where ρ is wood density (g cm−3), D (cm) is trunk diameter, and H (m) is tree height. We first compared individual tree AGB estimates based on measured tree heights with the corresponding AGB estimated using community-level, model-based predictions of tree height from alternative functional forms (i.e., power vs. gMM) and evaluated how these differences varied with tree diameter. Then, we estimated total AGB in the 50 ha plot by summing individual tree estimates of AGB, using individual D measurements from the 2010 census (Hubbell et al., 2005) and model-estimated heights. In the plot-level analyses, we explored the impact of species-specific differences in height allometric scaling by comparing AGB estimates based alternatively on community- or species-level height predictions for both power and gMM functions. For species-specific height predictions, we used fitted species-specific parameters (including species random effects) for the 162 species included in the main analysis and community-level predictions for other species. For those species for which species-specific wood densities were not available, we used the average over species for which values were available (ρ=0.5304 g cm−3; Wright et al., 2010). We computed 90 % credible intervals for each AGB estimate based on 5000 samples from the posterior distributions of all parameters of the corresponding allometric models.
Trees in our dataset varied over 3 orders of magnitude in trunk diameter (0.33–247.70 cm), 2 orders of magnitude in tree height (0.55–57.40 m), and 5 orders of magnitude in crown area (0.0039–1404.2 m2). The tallest species was Dipteryx oleifera (maximum height 57.4 m), and the largest crown area was found in Ceiba pentandra (1404 m2). Among big trees (D > 80 cm), Guazuma ulmifolia presented the shortest tree (28.2 m), and Poulsenia armata presented the smallest crown area (179 m2). Observations were unevenly distributed across species, largely in parallel with the variation in abundance, with a median of 34 trees per species for tree height and 7 for crown area and a range of 5–674 trees per species for tree height and 3–139 for crown area. The hierarchical models accounted for this unbalanced design and provided reasonable fits in all species for all model combinations, with no apparent pattern remaining in the residuals (Figs. S1–S2 in the Supplement; Table 1). The goodness of fit was high for all candidate models, with coefficients of determination (r2) between 0.909 and 0.943. Differences in fits resulted nonetheless in a clear ranking among alternative models according to the WAIC (Table 1).
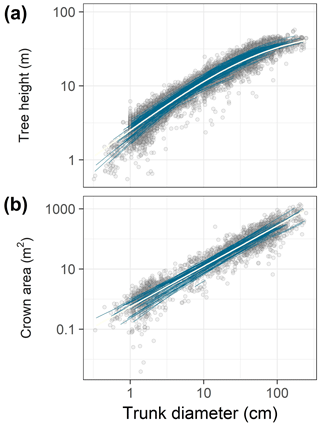
Figure 1Data (points) and best-fit allometric relationships (lines) for tree height (a) and crown area (b) in relation to trunk diameter. In each panel, blue lines correspond to species-specific fits, and the white line to the community-averaged model, both from the best hierarchical model (Tables 1 and 2). The best model for tree height was based on a generalized Michaelis–Menten function (a), whereas the best model for crown area included a power function (b). Note the log scales on all axes.
Table 1Summary of the results of the model selection procedure. We ranked models based on Watanabe's (2013) widely applicable information criterion (WAIC), a measure used to identify models with a good balance between predictive power as represented by the expectation of the log pointwise predictive density (ELP) and model complexity as represented by the estimated effective number of parameters (pWAIC). For each model, we report the difference in WAIC from the best model, ΔWAIC. We derived model weights, wi, based on WAIC values to aid in the interpretation of the model selection procedure (Burnham and Anderson, 2002). Models with the lowest WAIC and with ΔWAIC < 2 are highlighted in boldface.
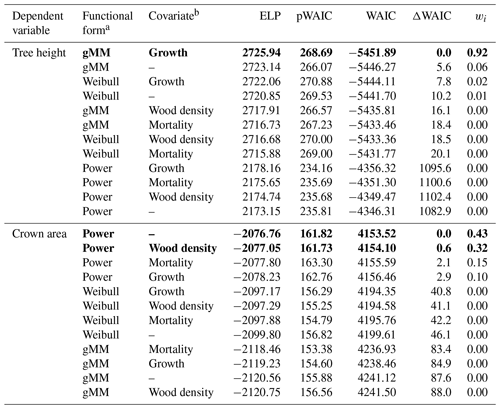
a gMM refers to the generalized Michaelis–Menten. b Growth refers to the log mean sapling relative growth rate, mortality to the log mean sapling mortality rate, and wood density to the wood specific gravity (see Methods).
3.1 Tree height allometry
The best tree height model combined a generalized Michaelis–Menten (gMM) function with species-specific parameters modeled as a linear function of sapling growth rates (Fig. 1a). At the community level, the best model for predicting tree height, H (m), from trunk diameter, D (cm), in the absence of species-level covariates was
This equation incorporates the bias correction for the back transformation from log H based on the estimate of σν=0.181 [0.179, 0.183]90 %. The parameter values with their 90 % posterior central intervals are asymptote before bias correction, exponent , and half-saturation parameter .
Table 2Posterior estimates of the parameters of the best hierarchical models for tree height and crown area allometries (see Table 1). Table entries correspond to the mean and 90 % posterior central intervals for the community-level parameters of each allometric function (see Eqs. 2–4 in Methods). Tree height allometry was best described by a generalized Michaelis–Menten (gMM) model including the effect of the natural logarithm of sapling growth rate (growth). The scaling of crown area was best described by a power law function, with similar performance between a model with no covariates and one with parameters varying depending on species wood density (Table 1). Covariates were centered and scaled before the analysis to ease comparisons of effects (natural logarithm of sapling growth rate (% yr−1); mean (SD) =1.01 (0.65); wood density mean (SD) =0.56 (0.14) g cm−3). The standard error, σν, of the best models were 0.181 (0.179, 0.183), 0.549 (0.536, 0.563), and 0.550 (0.536, 0.562) for tree height and the two models for crown area, including wood density or no covariate, respectively.
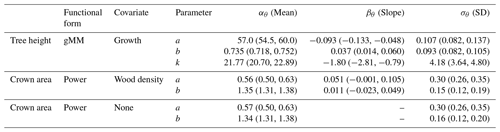
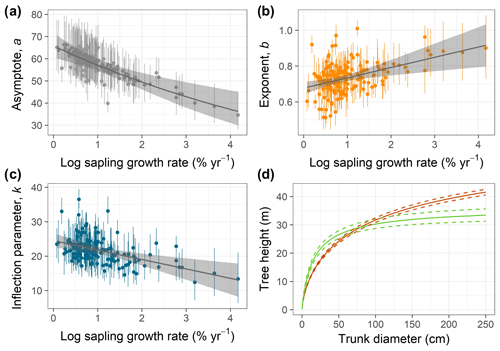
Figure 2(a–c) Relationships of species-specific tree height allometry parameters with log-transformed mean sapling relative growth rate in the best-fit hierarchical model, which incorporated the generalized Michaelis–Menten function (Eq. 3). Points show median posterior estimates for each species, with vertical bars indicating 90 % posterior central intervals. The thick grey line depicts the fitted relationship across species, and the shaded envelope encloses the 90 % posterior interval. (d) Illustration of interspecific differences in tree height scaling in the fitted model, with the red line showing predictions for the lowest sapling growth rate (very high shade tolerance) and the green line showing the highest sapling growth rate (very low shade tolerance), together with their 90 % credible intervals (dashed lines).
Individual species showed considerable variation in their height allometries; this variation was explained to a large extent by the sapling growth rate (Fig. 2). Parameters a and k declined with sapling growth rate, while b increased (Fig. 2; r2=0.42, 0.14, and 0.16 for relationships of the natural logarithm of sapling relative growth rate with a,b, and k, respectively). As a consequence, fast-growing species attain taller heights at small diameters but have shorter asymptotic heights compared with slow-growing species (Fig. 2d). The second-best model included a generalized Michaelis–Menten function and no covariates but was significantly worse in WAIC (ΔWAIC =5.6). The third-best model, which incorporated a Weibull function and interspecific variation in sapling growth rates (Table 1), produced the same results qualitatively as the best model. In general, all the saturating models (Weibull or gMM), regardless of covariate or not, had similar expectations of the log pointwise predictive density (ΔELP < 10), whereas the power function models did much worse (ΔELP > 500, ΔWAIC > 1000).
3.2 Crown area allometry
The allometric scaling of crown area with trunk diameter showed no sign of saturation, thus the power function model provided superior fits (Fig. 1b). At the community level, the best model for predicting crown area, C (m2), from trunk diameter, D (cm), in the absence of information on species-level covariates was
This equation incorporates the bias correction for the back transformation from log C based on . The parameter values with their 90 % posterior central intervals are coefficient before bias correction and exponent . This model does not have an asymptote. For the maximum trunk diameter in our dataset, Dmax=250 cm, we would expect a crown area close to m2, corresponding to a crown radius of 18.5 m. Although the best model did not include a covariate, the model including wood density provided a competitive fit (ΔWAIC =0.6, Table 1), with a slight positive relationship between the intercept and wood density (Fig. 3; r2=0.02 and 0.01 for the relationships presented). This suggests that species with high wood densities tend to have slightly broader crowns at all trunk sizes.
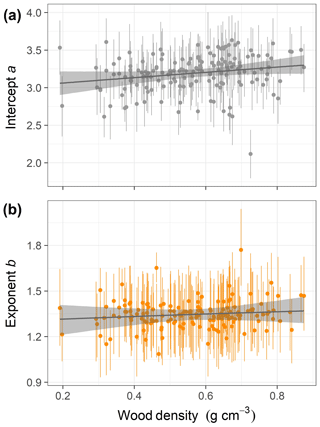
Figure 3Relationships of species-specific crown area allometry parameters with wood density in the second-best hierarchical model, which incorporated a power function (the best model included no covariates; Table 1). Points show median posterior estimates for each individual species, with vertical bars indicating 90 % posterior central intervals. The thick grey line depicts the fitted relationship across species, while the shaded envelope encloses the 90 % posterior interval.
3.3 Consequences for AGB estimates
Individual tree aboveground biomass (AGB) estimates based on the community-average power model (H=3.02D0.56; Table S2) were strongly upwardly biased for large trees relative to estimates based on measured heights, whereas AGB estimates based on the gMM height model were unbiased (Fig. 4). Individual-level AGB estimates calculated using tree height predictions based on the power model exceeded those based on the gMM model by ever larger proportions at larger trunk diameters, with an overestimate of 10 % at D=66 cm [52, 80]90 % that increases up to 59 % [51, 67]90 % at D=250 cm (Fig. 4). This difference in individual-level AGB estimates for large trees translated into substantial differences for whole-plot AGB. Estimates of whole-plot AGB in trees with D≥ 1 cm using the community-average power model were 12.3 % larger than those using the better-supported community-average gMM model (283 vs. 252 Mg dry matter ha−1; Table 3). The incorporation of information about species identity reduces the difference between the models, with the power model estimate exceeding the gMM model estimate by only 4.5 % (276 vs. 264 Mg ha−1). As expected, deviations between estimates based on the power and the gMM models were more pronounced for larger diameter classes (Table 3).
Table 3Posterior mean estimates (with their 90 % credible intervals) of total aboveground biomass density (Mg dry mass ha−1) in the 50 ha plot on Barro Colorado Island (BCI) under alternative tree height scaling relationships. To estimate AGB, the height of each tree in the plot was predicted based on community- or species-level allometric models for the generalized Michaelis–Menten and power functions, together with the height-based biomass allometry equation from Chave et al. (2014); see methods for further details.
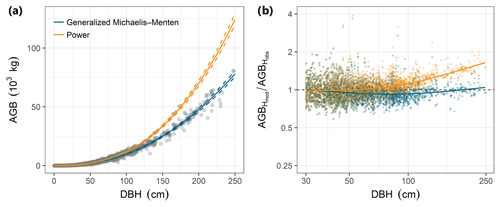
Figure 4Comparison of estimates of individual tree aboveground biomass (AGB, kilograms of dry matter) as a function of trunk diameter (DBH) for the power function (orange) and the generalized Michaelis–Menten (blue) tree height allometric models. (a) AGB estimates based on observed tree heights (grey points) were compared with those based on height predicted from community-level power function (orange lines) or generalized Michaelis–Menten (blue lines) models. The lines are predictions from the allometric models and are based on simulations of the posterior distribution (solid and dashed lines correspond to the median and 90 % posterior central interval, respectively) of the community-level, across-species relationships. (b) Relative error for estimates of AGB based on model predictions of tree height (AGBHmod) compared with estimates derived from height observations (AGBHobs), for trees with DBH > 30 cm (the full range is shown in Fig. S3). Modeled tree heights were from community-level models fitted with either the power function (orange dots) or generalized Michaelis–Menten function (blue dots). The lines are LOESS smoothers that illustrate the overall departures of each model from perfect prediction (i.e., AGBHmod∕ AGBHobs ratio equal to unity) as a function of DBH. All AGB estimates in (a) and (b) were based on biomass allometry (Eq. 6; Chave et al., 2014) and used the average value of wood density across species (ρ=0.5304 g cm−3; data from Wright et al., 2010) to highlight variation related to the height allometry.
Tree allometric relationships are widely employed to estimate forest biomass and production and are the basic building blocks guiding the development and validation of dynamic vegetation models. In tropical forests, the high diversity of tree species makes it difficult to collect sufficient data for characterizing species-specific allometric scaling relationships for any substantial fraction of the flora. Here, we applied Bayesian hierarchical models to a large dataset of tree morphology and functional traits to estimate species-specific allometric relationships for the scaling of tree height and crown area with trunk diameter and evaluate associations with functional traits.
4.1 Tree height allometry
Our analysis supported a saturating relationship between tree height and trunk diameter, consistent with theory (Falster and Westoby, 2003; Niklas, 2007) and with previous studies in tropical forests (Thomas, 1996; Bullock, 2000; Banin et al., 2012; Feldpausch et al., 2012; Molto et al., 2014; Fayolle et al., 2016; Ledo et al., 2016) and other forest biomes (e.g., Canham et al., 1994). The deceleration of height with respect to trunk diameter has been explained by multiple (mutually compatible) mechanisms including mechanical resistance (e.g., McMahon, 1973), growth and hydraulic constraints (e.g., Niklas and Spatz, 2004), and asymmetric competition for light (e.g., Iwasa et al., 1985; Bohlman and O'Brien, 2006; Falster and Westoby, 2003). Past work suggests that mechanical resistance to self or wind loading cannot explain tree height allometries, as trees are generally much shorter for a given diameter than the limits based on mechanical constraints (Niklas, 2007). Metabolic theories based on hydraulic constraints predict a constant logarithmic scaling between tree height and trunk diameter, with an exponent close to 2∕3 (Niklas and Spatz, 2004; West et al., 2009), which is inconsistent with our results that show that the community-level power function exponents differ significantly from 2∕3 and that the data diverge strongly from a power function.
Interspecific variation in tree height scaling parameters was associated with sapling growth rates, which suggests a tendency for shade tolerance and allometric strategies to be aligned in this community (Wright et al., 2010). At one extreme are the fast-growing, light-demanding tree species that are taller at small stem diameters; at the other extreme, slow-growing, shade-tolerant species are taller at larger diameters (Bohlman and O'Brien, 2006), with larger asymptotic heights (parameter a). This does not mean that shade-tolerant species tend to have larger maximum heights, because maximum heights depend on maximum diameters and are often much less than asymptotic heights for small-statured species (Fig. S1). The differences in allometric parameters should be interpreted in terms of differences in trajectories, especially at small diameters, where light-demanding species take greater risks by growing taller for a given diameter. In general, shade tolerance, and maximum height are largely independent axes of variation among tropical tree species (Bohlman and Pacala, 2012; Rüger et al., 2018) and may if anything tend to be negatively correlated across species (Poorter et al., 2006; Wright et al., 2010; Loubota Panzou et al., 2018). Our results quantify how variation in shade tolerance aligns with differences in height trajectories and thus in the parameters of saturating height allometric functions, thereby providing a basis for defining plant functional types representative of different gap-successional stages in tropical forests (Thomas, 1996; Falster et al., 2017).
4.2 Crown area allometry
Crown area and trunk diameter presented a scale-invariant relationship, with no indication of saturation even for the largest trees in our dataset. As a consequence, the model selection procedure favored power function models with estimates of the community-level exponent close to 4∕3 (. This result is consistent with previous analyses across large scale environmental gradients reporting allometric exponents for crown area between 1.21 and 1.36 (Bohlman and O'Brien, 2006; Muller-Landau et al., 2006; Heineman et al., 2011; Antin et al., 2013; Blanchard et al., 2016). This large-scale consistency in community-level relationships emerges despite local variation among species (e.g., the exponent b ranged between 1.09 and 1.77 across species, Table S2). Modeling studies show that community-level crown area allometric parameters crucially determine the scaling of tree growth and mortality and the parameters of tree size distributions (Muller-Landau et al., 2006; Farrior et al., 2016). The fitted community-level crown area exponent is consistent with predictions of 4∕3 scaling by elastic similarity models describing mechanical resistance to wind (McMahon, 1973) as well as by metabolic models invoking design constraints in transportation networks (West et al., 2009).
Our finding of high interspecific variation in the allometric scaling of crown geometry is consistent with previous studies (Iida et al., 2012; Lines et al., 2012; Blanchard et al., 2016). This interspecific variation has been linked to local differentiation and niche partitioning into canopy layers (Clark et al., 2008; Bohlman and Pacala, 2012). For instance, the crowns of subcanopy trees are wider than those of tall-statured trees on BCI (Bohlman and O'Brien, 2006). Our analysis of crown area favored an allometric model lacking trait influences on species-specific parameters, although the model featuring a weak positive relationship between the intercept of the power function and the average wood density of each species also received considerable support. The estimated relationship of crown area to wood density is consistent with the theory that high wood density enables more efficient horizontal crown expansion (Anten and Schieving, 2010) and with previous results for BCI (Francis et al., 2017) and Pasoh, Malaysia (Iida et al., 2012; Francis et al., 2017). However, overall wood density explains relatively little of the extensive interspecific variation in crown area allometries. Processes like crown plasticity in response to competition (Thomas, 1996; Poorter et al., 2008) and other traits may explain additional variation in crown geometry; for example, Loubota Panzou et al. (2018) found that wind-dispersed species had taller heights and larger crown dimensions.
4.3 Implications for forest biomass estimation
Allometric models for individual trees remain the preferred method to estimate forest biomass and production at the stand level from plot data (Chave et al., 2014; Brienen et al., 2015) and provide a basic template to model carbon allocation, tree growth, and tree competition in dynamic vegetation models. Whereas many biomass models incorporate only individual trunk diameter (Brown, 1997) and species wood density (Brown et al., 1989), current state-of-the-art models typically include estimates of tree height as well (e.g., Chave et al., 2014). Crown dimensions have also been incorporated in some models (Goodman et al., 2014; Ploton et al., 2016), although Fayolle et al. (2018) found a minor role of either crown or height dimensions on biomass estimates. Inclusion of height and/or crown dimensions in tree biomass models reduces errors in biomass estimates, especially for large trees, which contribute disproportionately to forest biomass and function (Lindenmayer et al., 2012).
Our results confirm the importance for biomass estimation of accounting for saturation in height–diameter allometries (Feldpausch et al., 2011; Molto et al., 2014; Fayolle et al., 2016). If heights are not directly measured, any estimates of heights should be based on fitting saturating height functions to datasets with sufficient data for large trees to accurately capture the saturating component (Sullivan et al., 2018). The use of power function fits for heights leads to substantial overestimates of biomass of large trees, which translates to substantial overestimates of stand-level biomass.
The considerable heterogeneity among species in both tree height and crown area allometries presents another opportunity for improving estimates of tree biomass. The use of average allometric models that ignore changes in species composition can result in biased estimates of total biomass, reflecting the underlying nonlinearities of these relationships. At the same time, it is clearly impractical to develop species-specific allometries for every tropical tree species. The use of hierarchical models based on functional or demographic traits provides a manageable option for incorporating and accounting for the diversity of allometric scaling relationships in biomass models. Ideally, such hierarchical models would be grounded in a mechanistic understanding of underlying trade-offs on trait diversity (Falster et al., 2017).
4.4 Conclusions and directions for future research
Despite growing evidence highlighting the deceleration in diameter–tree height scaling (e.g., Thomas, 1996; Bullock, 2000; Banin et al., 2012; Ledo et al., 2016), the power function remains the most commonly used model of tree height allometry in tropical forests (e.g., Antin et al., 2013; Goodman et al., 2014; Blanchard et al., 2016; Mensah et al., 2018). Even studies featuring saturating relationships often fix the exponent of the gMM or Weibull functions to unity (e.g., Banin et al., 2012; Ledo et al., 2016; Fayolle et al., 2016; Molto et al., 2014), a value that our results show is inconsistent with data. Our results favored the gMM function over the modified three-parameter Weibull previously proposed by Thomas (1996), suggesting that it provides the required level of flexibility to accommodate changes in tree height scaling during ontogeny. Three-parameter saturating models clearly outperform two-parameter power functions in large datasets containing data on many large individuals; however, the advantage in fit of the saturating models is often insufficient to compensate for the penalty of an extra parameter in the many cases in which smaller datasets or those with data for few larger individuals are analyzed in isolation (Thomas, 1996; Iida et al., 2011; Goodman et al., 2014). We recommend that future analyses of small datasets on tropical tree allometries be conducted in a Bayesian framework in which prior data for larger datasets informs the choice of functional forms (i.e., restriction to saturating functions) and informs prior distributions on parameter values. Future studies can take advantage of our data, code, and results to constrain inferences on tree allometry using informative priors (e.g., Ellison, 2004).
Our analysis of crown allometric scaling involved an unusually large dataset, yet remained limited by sample size, measurement difficulties, and failure to address other dimensions of crown size such as crown depth. The crown area dataset was only one-fifth the size of our tree height dataset, and only 1/14 of the trees had trunk diameters greater than 100 cm. For ground-based data, which constituted the vast majority of our dataset, measurements of crown dimensions are more complicated and time-consuming than those of height, and we expect them to have higher measurement error. Aerial and even satellite imagery increasingly offers an alternative for precisely and accurately measuring crown areas of fully sun-exposed trees, an alternative we took advantage of here. However, these methods do not enable crown area estimates for subcanopy trees (but see e.g., Paris et al., 2016; Shendryk et al., 2016), which differ systematically in their crown allometries. Finally, we evaluated only crown area, even though crown depth and crown shape are also important for the estimation of tree biomass (Goodman et al., 2014; Ploton et al., 2016) and for characterizing tree species life history strategies (Canham et al., 1994; Bohlman and O'Brien, 2006; Poorter et al., 2006). Despite these limitations, our analysis consistently favored models of crown area vs. trunk diameter without saturation and suggested a weak effect of species differences in wood density on the considerable interspecific variability in the scaling of crown size.
Future allometric studies should address additional individual-level, species-level, and site-level covariates of tree allometry and develop improved models of their influences. Interspecific variation in allometry may be more fully explained by incorporating better measures of shade tolerance and additional traits such as seed dispersal mode, leaf habit (deciduous or evergreen) and maximum stature (e.g., Poorter et al., 2003, 2006; Loubota Panzou et al., 2018). Interindividual variation in allometry depends not only on species identity but also on environmental conditions, biogeographic region, and competitive neighborhood. Previous studies show that tropical tree height allometries vary with climate (Chave et al., 2014; Mensah et al., 2018), topography (Ferry et al., 2010; Marshall et al., 2012), edaphic conditions (Aiba and Kitayama, 1999; Feldpausch et al., 2011), canopy position (Thomas, 1996; O'Brien et al., 1995; Poorter et al., 2006), and light exposure (Rüger et al., 2012). Ideally, these factors would be incorporated not in a purely phenomenological manner but would be informed by mechanistic models of underlying trade-offs and alternative strategies (Dybzinski et al., 2011; Farrior et al., 2013).
Tree allometric functions are critical components of forest biomass estimates and of mechanistic models of forest structure and dynamics. Forest size structure and biomass in vegetation models are highly sensitive to allometry parameters and functional forms (Farrior et al., 2016; Weng et al., 2017). Our results confirm that allometric models for tropical trees should incorporate saturating functions for tree height and interspecific variation in scaling parameters. In our analyses of data for over 10 000 tropical trees, tree height presented a saturating relationship with trunk diameter that was well captured by the three-parameter generalized Michaelis–Menten or Weibull functions, whereas power function models exhibited systematic biases in tree height predictions, especially for large trees. In contrast, our somewhat smaller dataset for crown area exhibited a constant scaling with stem size, consistent with a power function. We observed extensive interspecific variability in allometric scaling, with shade tolerance explaining considerable variation in height parameters and wood density weakly related to crown area parameters. The relationship of tree allometric parameters with functional and demographic traits can provide a basis for the incorporation of compositional effects into estimates of forest biomass and production, including through the improved parameterization of tropical plant functional types in vegetation models.
All the data used in this study are available at Dryad through the data package Martínez Cano et al. (2019) (https://doi.org/10.5061/dryad.85k53v8; last access: 7 February 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-16-847-2019-supplement.
HCML and SWP conceived the study. HCML, SJW and SAB contributed data and expertise. IMC programmed the Bayesian models and led the analyses. IMC and HCML drafted an initial version of the paper. All authors discussed the results and revised the paper.
The authors declare that they have no conflict of interest.
The BCI forest dynamics research project was founded by Steven P. Hubbell and
Robin B. Foster, was sustained for many years by Richard Condit, and is now
managed by Stuart Davies, Suzanne Lao, and Rolando Perez under the ForestGEO
program of the Smithsonian Tropical Research in Panama. Numerous
organizations have provided funding, principally the US National Science
Foundation, and hundreds of field workers have contributed. Data on tree
morphology have been gathered through several dedicated projects, and we
gratefully acknowledge the contributions of Pablo Ramos, Paulino Villareal,
Sean Thomas, Sean O'Brien, Peter Spiro, and
Jonathan Dandois. Isabel Martínez Cano, was supported by the Carbon
Mitigation Initiative at Princeton University.
Edited by: Kirsten Thonicke
Reviewed by:
Nicolas Picard, Adeline Fayolle, and one anonymous referee
Adler, P. B., Salguero-Gómez, R., Compagnoni, A., Hsu, J. S., Ray-Mukherjee, J., Mbeau-Ache, C., and Franco, M: Functional traits explain variation in plant life history strategies, P. Natl. Acad. Sci. USA, 111, 740–745, https://doi.org/10.1073/pnas.1315179111, 2014.
Aiba, S.-I. and Kitayama, K.: Structure, composition and species diversity in an altitude-substrate matrix of rain forest tree communities on Mount Kinabalu, Borneo, Plant Ecol., 140, 139–157, https://doi.org/10.1023/a:1009710618040, 1999.
Anten, N. P. R. and Schieving, F.: The Role of Wood Mass Density and Mechanical Constraints in the Economy of Tree Architecture, Am. Nat., 175, 250–260, https://doi.org/10.1086/649581, 2010.
Antin, C., Pélissier, R., Vincent, G., and Couteron, P: Crown allometries are less responsive than stem allometry to tree size and habitat variations in an Indian monsoon forest, Trees, 27, 1485–1495, https://doi.org/10.1007/s00468-013-0896-7, 2013.
Banin, L., Feldpausch, T. R., Phillips, O. L., Baker, T. R., Lloyd, J., Affum-Baffoe, K., Arets, E. J. M. M., Berry, N. J., Bradford, M., Brienen, R. J. W., Davies, S., Drescher, M., Higuchi, N., Hilbert, D. W., Hladik, A., Iida, Y., Salim, K. A., Kassim, A. R., King, D. A., Lopez-Gonzalez, G., Metcalfe, D., Nilus, R., Peh, K. S. H., Reitsma, J. M., Sonké, B., Taedoumg, H., Tan, S., White, L., Wöll, H., and Lewis, S. L: What controls tropical forest architecture? Testing environmental, structural and floristic drivers, Global Ecol. Biogeogr., 21, 1179–1190, https://doi.org/10.1111/j.1466-8238.2012.00778.x, 2012.
Hubbell, S. P., Condit, R., and Foster, R. B.:Barro Colorado Forest Census Plot Data, http://ctfs.si.edu/webatlas/datasets/bci (last access: 20 January 2018), 2005.
Blanchard, E., Birnbaum, P., Ibanez, T., Boutreux, T., Antin, C., Ploton, P., Vincent, G., Pouteau, R., Vandrot, H., Hequet, V., Barbier, N., Droissart, V., Sonké, B., Texier, N., Kamdem, N. G., Zebaze, D., Libalah, M., and Couteron, P: Contrasted allometries between stem diameter, crown area, and tree height in five tropical biogeographic areas, Trees, 30, 1953–1968, https://doi.org/10.1007/s00468-016-1424-3, 2016.
Bohlman, S. and O'Brien, S.: Allometry, Adult Stature and Regeneration Requirement of 65 Tree Species on Barro Colorado Island, Panama, J. Trop. Ecol., 22, 123–136, 2006.
Bohlman, S. and Pacala, S.: A forest structure model that determines crown layers and partitions growth and mortality rates for landscape-scale applications of tropical forests, J. Ecol., 100, 508–518, https://doi.org/10.1111/j.1365-2745.2011.01935.x, 2012.
Bonan, G. B.: Ecological Climatology, Concepts and Applications, 2nd Edition, Cambridge University Press, New York, USA, 2008.
Brienen, R. J. W., Phillips, O. L., Feldpausch, T. R., Gloor, E., Baker, T. R., Lloyd, J., Lopez-Gonzalez, G., Monteagudo-Mendoza, A., Malhi, Y., Lewis, S. L., Vásquez Martinez, R., Alexiades, M., Álvarez Dávila, E., Alvarez-Loayza, P., Andrade, A., Aragão, L. E. O. C., Araujo-Murakami, A., Arets, E. J. M. M., Arroyo, L., Aymard C, G. A., Bánki, O. S., Baraloto, C., Barroso, J., Bonal, D., Boot, R. G. A., Camargo, J. L. C., Castilho, C. V., Chama, V., Chao, K. J., Chave, J., Comiskey, J. A., Cornejo Valverde, F., da Costa, L., de Oliveira, E. A., Di Fiore, A., Erwin, T. L., Fauset, S., Forsthofer, M., Galbraith, D. R., Grahame, E. S., Groot, N., Hérault, B., Higuchi, N., Honorio Coronado, E. N., Keeling, H., Killeen, T. J., Laurance, W. F., Laurance, S., Licona, J., Magnussen, W. E., Marimon, B. S., Marimon-Junior, B. H., Mendoza, C., Neill, D. A., Nogueira, E. M., Núñez, P., Pallqui Camacho, N. C., Parada, A., Pardo-Molina, G., Peacock, J., Peña-Claros, M., Pickavance, G. C., Pitman, N. C. A., Poorter, L., Prieto, A., Quesada, C. A., Ramírez, F., Ramírez-Angulo, H., Restrepo, Z., Roopsind, A., Rudas, A., Salomão, R. P., Schwarz, M., Silva, N., Silva-Espejo, J. E., Silveira, M., Stropp, J., Talbot, J., ter Steege, H., Teran-Aguilar, J., Terborgh, J., Thomas-Caesar, R., Toledo, M., Torello-Raventos, M., Umetsu, R. K., van der Heijden, G. M. F., van der Hout, P., Guimarães Vieira, I. C., Vieira, S. A., Vilanova, E., Vos, V. A., and Zagt, R. J: Long-term decline of the Amazon carbon sink, Nature, 519, 344–348, https://doi.org/10.1038/nature14283, 2015.
Brown, S.: Estimating Biomass and Biomass Change of Tropical Forests: A Primer, FAO – Forestry Paper 134, Food and Agriculture Organization, Rome, Italy, 1997.
Brown, S., Gillespie, A. J. R., and Lugo, A. E.: Biomass Estimation Methods for Tropical Forests with Applications to Forest Inventory Data, For. Sci., 35, 881–902, https://academic.oup.com/forestscience/article-abstract/35/4/881/4642515?redirectedFrom=PDF, 1989.
Bullock, S. H.: Developmental Patterns of Tree Dimensions in a Neotropical Deciduous Forest, Biotropica, 32, 42–52, 2000.
Burnham, K. P. and Anderson, D. R.: Model selection and multimodel inference: a practical information-theoretic approach, 2nd ed., Springer, New York, USA, 2002.
Canham, C. D., Finzi, A. C., Pacala, S. W., and Burbank, D. H.: Causes and consequences of resource heterogeneity in forests: interspecific variation in light transmission by canopy trees, Can. J. Forest Res., 24, 337–349, https://doi.org/10.1139/x94-046, 1994.
Chapin III, F. S., Matson, P. A., and Vitousek, P.: Principles of terrestrial ecosystem ecology, Springer, New York, USA, 2011.
Chave, J., Réjou-Méchain, M., Búrquez, A., Chidumayo, E., Colgan, M. S., Delitti, W. B. C., Duque, A., Eid, T., Fearnside, P. M., Goodman, R. C., Henry, M., Martínez-Yrízar, A., Mugasha, W. A., Muller-Landau, H. C., Mencuccini, M., Nelson, B. W., Ngomanda, A., Nogueira, E. M., Ortiz-Malavassi, E., Pélissier, R., Ploton, P., Ryan, C. M., Saldarriaga, J. G., and Vieilledent, G.: Improved allometric models to estimate the aboveground biomass of tropical trees, Global Change Biol., 20, 3177–3190, https://doi.org/10.1111/gcb.12629, 2014.
Chazdon, R. L.: Second Growth, The Promise of Tropical Forest Regeneration in an Age of Deforestation, The University of Chicago Press, Chicago, USA, 2014.
Clark, D. A. and Clark, D. B.: Life History Diversity of Canopy and Emergent Trees in a Neotropical Rain Forest, Ecol. Monogr., 62, 315–344, https://doi.org/10.2307/2937114, 1992.
Clark, D. B., Olivas, P. C., Oberbauer, S. F., Clark, D. A., and Ryan, M. G.: First direct landscape-scale measurement of tropical rain forest Leaf Area Index, a key driver of global primary productivity, Ecol. Lett., 11, 163–172, https://doi.org/10.1111/j.1461-0248.2007.01134.x, 2008.
Condit, R.: Ecological Implications of Changes in Drought Patterns: Shifts in Forest Composition in Panama, Clim. Change, 39, 413–427, https://doi.org/10.1023/a:1005395806800, 1998.
Condit, R., Ashton, P., Bunyavejchewin, S., Dattaraja, H. S., Davies, S., Esufali, S., Ewango, C., Foster, R., Gunatilleke, I. A. U. N., Gunatilleke, C. V. S., Hall, P., Harms, K. E., Hart, T., Hernandez, C., Hubbell, S., Itoh, A., Kiratiprayoon, S., LaFrankie, J., de Lao, S. L., Makana, J.-R., Noor, M. N. S., Kassim, A. R., Russo, S., Sukumar, R., Samper, C., Suresh, H. S., Tan, S., Thomas, S., Valencia, R., Vallejo, M., Villa, G., and Zillio, T: The Importance of Demographic Niches to Tree Diversity, Science, 313, 98–101, https://doi.org/10.1126/science.1124712, 2006.
Cressie, N., Calder, C. A., Clark, J. S., Hoef, J. M. V., and Wikle, C. K.: Accounting for uncertainty in ecological analysis: the strengths and limitations of hierarchical statistical modeling, Ecol. Appl., 19, 553–570, https://doi.org/10.1890/07-0744.1, 2009.
Denslow, J. S. and Guzman G., S.: Variation in stand structure, light and seedling abundance across a tropical moist forest chronosequence, Panama, J. Veg. Sci., 11, 201–212, https://doi.org/10.2307/3236800, 2000.
Dietze, M. C., Wolosin, M. S., and Clark, J. S.: Capturing diversity and interspecific variability in allometries: A hierarchical approach, Forest Ecol. Manag., 256, 1939–1948, https://doi.org/10.1016/j.foreco.2008.07.034, 2008.
Dybzinski, R., Farrior, C., Wolf, A., Reich, P. B., and Pacala, S. W.: Evolutionarily Stable Strategy Carbon Allocation to Foliage, Wood, and Fine Roots in Trees Competing for Light and Nitrogen: An Analytically Tractable, Individual-Based Model and Quantitative Comparisons to Data, Am. Nat., 177, 153–166, https://doi.org/10.1086/657992, 2011.
Ellison, A. M.: Bayesian inference in ecology, Ecol. Lett., 7, 509–520, https://doi.org/10.1111/j.1461-0248.2004.00603.x, 2004.
Enquist, B. J. and Bentley, L. P.: Land Plants: New Theoretical Directions and Empirical Prospects, in: Metabolic Ecology: A Scaling Approach, edited by: Sibly, R. M., Brown, J. H., and Kodric-Brown, A., John Wiley & Sons, Ltd, Chichester, UK, 2012.
Falster, D. S. and Westoby, M.: Plant height and evolutionary games, Trends Ecol. Evol., 18, 337–343, https://doi.org/10.1016/S0169-5347(03)00061-2, 2003.
Falster, D. S., Brännström, Å., Westoby, M., and Dieckmann, U.: Multitrait successional forest dynamics enable diverse competitive coexistence, P. Natl. Acad. Sci. USA, 114, E2719–E2728, https://doi.org/10.1073/pnas.1610206114, 2017.
Farrior, C. E., Dybzinski, R., Levin, S. A., and Pacala, S. W.: Competition for Water and Light in Closed-Canopy Forests: A Tractable Model of Carbon Allocation with Implications for Carbon Sinks, Am. Nat., 181, 314–330, https://doi.org/10.1086/669153, 2013.
Farrior, C. E., Bohlman, S. A., Hubbell, S., and Pacala, S. W.: Dominance of the suppressed: Power-law size structure in tropical forests, Science, 351, 155–157, https://doi.org/10.1126/science.aad0592, 2016.
Fayolle, A., Loubota Panzou, G. J., Drouet, T., Swaine, M. D., Bauwens, S., Vleminckx, J., Biwole, A., Lejeune, P., and Doucet, J.-L.: Taller trees, denser stands and greater biomass in semi-deciduous than in evergreen lowland central African forests, Forest Ecol. Manag., 374, 42–50, https://doi.org/10.1016/j.foreco.2016.04.033, 2016.
Fayolle, A., Ngomanda, A., Mbasi, M., Barbier, N., Bocko, Y., Boyemba, F., Couteron, P., Fonton, N., Kamdem, N., Katembo, J., Kondaoule, H. J., Loumeto, J., Maïdou, H. M., Mankou, G., Mengui, T., Mofack II, G., Moundounga, C., Moundounga, Q., Nguimbous, L., Nsue Nchama, N., Obiang, D., Ondo Meye Asue, F., Picard, N., Rossi, V., Senguela, Y.-P., Sonké, B., Viard, L., Yongo, O. D., Zapfack, L., and Medjibe, V. P.: A regional allometry for the Congo basin forests based on the largest ever destructive sampling, Forest Ecol. Manag., 430, 228–240, https://doi.org/10.1016/j.foreco.2018.07.030, 2018.
Feldpausch, T. R., Banin, L., Phillips, O. L., Baker, T. R., Lewis, S. L., Quesada, C. A., Affum-Baffoe, K., Arets, E. J. M. M., Berry, N. J., Bird, M., Brondizio, E. S., de Camargo, P., Chave, J., Djagbletey, G., Domingues, T. F., Drescher, M., Fearnside, P. M., França, M. B., Fyllas, N. M., Lopez-Gonzalez, G., Hladik, A., Higuchi, N., Hunter, M. O., Iida, Y., Salim, K. A., Kassim, A. R., Keller, M., Kemp, J., King, D. A., Lovett, J. C., Marimon, B. S., Marimon-Junior, B. H., Lenza, E., Marshall, A. R., Metcalfe, D. J., Mitchard, E. T. A., Moran, E. F., Nelson, B. W., Nilus, R., Nogueira, E. M., Palace, M., Patiño, S., Peh, K. S.-H., Raventos, M. T., Reitsma, J. M., Saiz, G., Schrodt, F., Sonk'e, B., Taedoumg, H. E., Tan, S., White, L., WÖll, H., and Lloyd, J.: Height-diameter allometry of tropical forest trees, Biogeosciences, 8, 1081–1106, https://doi.org/10.5194/bg-8-1081-2011, 2011.
Feldpausch, T. R., Lloyd, J., Lewis, S. L., Brienen, R. J. W., Gloor, M., Monteagudo Mendoza, A., Lopez-Gonzalez, G., Banin, L., Abu Salim, K., Affum-Baffoe, K., Alexiades, M., Almeida, S., Amaral, I., Andrade, A., Aragão, L. E. O. C., Araujo Murakami, A., Arets, E. J. M. M., Arroyo, L., Aymard C., G. A., Baker, T. R., Bánki, O. S., Berry, N. J., Cardozo, N., Chave, J., Comiskey, J. A., Alvarez, E., de Oliveira, A., Di Fiore, A., Djagbletey, G., Domingues, T. F., Erwin, T. L., Fearnside, P. M., França, M. B., Freitas, M. A., Higuchi, N., E. Honorio C., Iida, Y., Jiménez, E., Kassim, A. R., Killeen, T. J., Laurance, W. F., Lovett, J. C., Malhi, Y., Marimon, B. S., Marimon-Junior, B. H., Lenza, E., Marshall, A. R., Mendoza, C., Metcalfe, D. J., Mitchard, E. T. A., Neill, D. A., Nelson, B. W., Nilus, R., Nogueira, E. M., Parada, A., Peh, K. S.-H., Pena Cruz, A., Peñuela, M. C., Pitman, N. C. A., Prieto, A., Quesada, C. A., Ramírez, F., Ramírez-Angulo, H., Reitsma, J. M., Rudas, A., Saiz, G., Salomão, R. P., Schwarz, M., Silva, N., Silva-Espejo, J. E., Silveira, M., Sonké, B., Stropp, J., Taedoumg, H. E., Tan, S., ter Steege, H., Terborgh, J., Torello-Raventos, M., van der Heijden, G. M. F., Vásquez, R., Vilanova, E., Vos, V. A., White, L., Willcock, S., Woell, H., and Phillips, O. L.: Tree height integrated into pantropical forest biomass estimates, Biogeosciences, 9, 3381–3403, https://doi.org/10.5194/bg-9-3381-2012, 2012.
Ferry, B., Morneau, F., Bontemps, J. D., Blanc, L., and Freycon, V.: Higher treefall rates on slopes and waterlogged soils result in lower stand biomass and productivity in a tropical rain forest, J. Ecol., 98, 106–116, https://doi.org/10.1111/j.1365-2745.2009.01604.x, 2010.
Francis, E. J., Muller-Landau, H. C., Wright, S. J., Visser, M. D., Iida, Y., Fletcher, C., Hubbell, S. P., Kassim, A. R., and Kerkhoff, A.: Quantifying the role of wood density in explaining interspecific variation in growth of tropical trees, Global. Ecol. Biogeogr., 26, 1078–1087, https://doi.org/10.1111/geb.12604, 2017.
Gelman, A. and Rubin, D. B.: Inference from Iterative Simulation Using Multiple Sequences, Statist. Sci., 7, 457–472, https://doi.org/10.1214/ss/1177011136, 1992.
Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. D., Vehtari, A., and Rubin, D. B.: Bayesian Data Analysis, 3rd ed., Chapman & Hall/CRC Texts in Statistical Science, CRC Press, Boca Raton, FL, USA, 2014.
Goodman, R. C., Phillips, O. L., and Baker, T. R.: The importance of crown dimensions to improve tropical tree biomass estimates, Ecol. Appl., 24, 680–698, https://doi.org/10.1890/13-0070.1, 2014.
Heineman, K. D., Jensen, E., Shapland, A., Bogenrief, B., Tan, S., Rebarber, R., and Russo, S. E.: The effects of belowground resources on aboveground allometric growth in Bornean tree species, Forest Ecol. Manag., 261, 1820–1832, https://doi.org/10.1016/j.foreco.2011.02.005, 2011.
Hooten, M. B. and Hobbs, N. T.: A guide to Bayesian model selection for ecologists, Ecol. Monogr., 85, 3–28, https://doi.org/10.1890/14-0661.1, 2015.
Houghton, R. A.: Aboveground Forest Biomass and the Global Carbon Balance, Global Change Biol., 11, 945–958, https://doi.org/10.1111/j.1365-2486.2005.00955.x, 2005.
Hubbell, S. P., Foster, R. B., O'Brien, S. T., Harms, K. E., Condit, R., Wechsler, B., Wright, S. J., and de Lao, S. L: Light-Gap Disturbances, Recruitment Limitation, and Tree Diversity in a Neotropical Forest, Science, 283, 554–557, https://doi.org/10.1126/science.283.5401.554, 1999.
Hunter, M. O., Keller, M., Victoria, D., and Morton, D. C.: Tree height and tropical forest biomass estimation, Biogeosciences, 10, 8385–8399, https://doi.org/10.5194/bg-10-8385-2013, 2013.
Iida, Y., Kohyama, T. S., Kubo, T., Kassim, A. R., Poorter, L., Sterck, F., and Potts, M. D.: Tree architecture and life-history strategies across 200 co-occurring tropical tree species, Funct. Ecol., 25, 1260–1268, https://doi.org/10.1111/j.1365-2435.2011.01884.x, 2011.
Iida, Y., Poorter, L., Sterck, F. J., Kassim, A. R., Kubo, T., Potts, M. D., and Kohyama, T. S.: Wood density explains architectural differentiation across 145 co-occurring tropical tree species, Funct. Ecol., 26, 274–282, https://doi.org/10.1111/j.1365-2435.2011.01921.x, 2012.
Iida, Y., Poorter, L., Sterck, F., Kassim, A. R., Potts, M. D., Kubo, T., and Kohyama, T. S.: Linking size-dependent growth and mortality with architectural traits across 145 co-occurring tropical tree species, Ecology, 95, 353–363, https://doi.org/10.1890/11-2173.1, 2014.
Iwasa, Y., Cohen, D., and Leon, J. A.: Tree height and crown shape, as results of competitive games, J. Theor. Biol., 112, 279–297, https://doi.org/10.1016/S0022-5193(85)80288-5, 1985.
Koch, G. W., Sillett, S. C., Jennings, G. M., and Davis, S. D.: The limits to tree height, Nature, 428, 851–854, https://doi.org/10.1038/nature02417, 2004.
Larjavaara, M. and Muller-Landau, H. C.: Measuring tree height: a quantitative comparison of two common field methods in a moist tropical forest, Methods Ecol. Evol., 4, 793–801, https://doi.org/10.1111/2041-210X.12071, 2013.
Ledo, A., Cornulier, T., Illian, J. B., Iida, Y., Kassim, A. R., and Burslem, D. F. R. P.: Re-evaluation of individual diameter: height allometric models to improve biomass estimation of tropical trees, Ecol. Appl., 26, 2376–2382, https://doi.org/10.1002/eap.1450, 2016.
Leigh, E. G.: Tropical Forest Ecology: A View from Barro Colorado Island, Oxford University Press, New York, USA, 1999.
Lindenmayer, D. B., Laurance, W. F., and Franklin, J. F.: Global Decline in Large Old Trees, Science, 338, 1305–1306, https://doi.org/10.1126/science.1231070, 2012.
Lines, E. R., Zavala, M. A., Purves, D. W., and Coomes, D. A.: Predictable changes in aboveground allometry of trees along gradients of temperature, aridity and competition, Global Ecol. Biogeogr., 21, 1017–1028, https://doi.org/10.1111/j.1466-8238.2011.00746.x, 2012.
Loubota Panzou, G. J., Ligot, G., Gourlet-Fleury, S., Doucet, J.-L., Forni, E., Loumeto, J.-J., and Fayolle, A.: Architectural differences associated with functional traits among 45 coexisting tree species in Central Africa, Funct. Ecol., 32, 2583–2593, https://doi.org/10.1111/1365-2435.13198, 2018.
Marshall, A. R., Willcock, S., Platts, P. J., Lovett, J. C., Balmford, A., Burgess, N. D., Latham, J. E., Munishi, P. K. T., Salter, R., Shirima, D. D., and Lewis, S. L.: Measuring and modelling above-ground carbon and tree allometry along a tropical elevation gradient, Biol. Conserv., 154, 20–33, https://doi.org/10.1016/j.biocon.2012.03.017, 2012.
Martínez Cano, I., Muller-Landau, H. C., Wright, S. J., Bohlman, S. A., and Pacala, S. W.: Data from: Tropical tree height and crown allometries for the Barro Colorado Natural Monument, Panama: a comparison of alternative hierarchical models incorporating interspecific variation in relation to life history traits, Dryad Digital Repository, https://doi.org/10.5061/dryad.85k53v8, 2019.
Mascaro, J., Asner, G. P., Muller-Landau, H. C., van Breugel, M., Hall, J., and Dahlin, K.: Controls over aboveground forest carbon density on Barro Colorado Island, Panama, Biogeosciences, 8, 1615–1629, https://doi.org/10.5194/bg-8-1615-2011, 2011.
Mascaro, J., Litton, C. M., Hughes, R. F., Uowolo, A., and Schnitzer, S. A.: Is logarithmic transformation necessary in allometry? Ten, one-hundred, one-thousand-times yes, Biol. J. Linn. Soc., 111, 230–233, https://doi.org/10.1111/bij.12177, 2014.
McMahon, T.: Size and Shape in Biology: Elastic criteria impose limits on biological proportions, and consequently on metabolic rates, Science, 179, 1201–1204, https://doi.org/10.1126/science.179.4079.1201, 1973.
Mensah, S., Pienaar, O. L., Kunneke, A., du Toit, B., Seydack, A., Uhl, E., Pretzsch, H., and Seifert, T.: Height – Diameter allometry in South Africa's indigenous high forests: Assessing generic models performance and function forms, Forest Ecol. Manag., 410, 1–11, https://doi.org/10.1016/j.foreco.2017.12.030, 2018.
Molto, Q., Hérault, B., Boreux, J.-J., Daullet, M., Rousteau, A., and Rossi, V.: Predicting tree heights for biomass estimates in tropical forests – a test from French Guiana, Biogeosciences, 11, 3121–3130, https://doi.org/10.5194/bg-11-3121-2014, 2014.
Muller-Landau, H. C., Condit, R. S., Chave, J., Thomas, S. C., Bohlman, S. A., Bunyavejchewin, S., Davies, S., Foster, R., Gunatilleke, S., Gunatilleke, N., Harms, K. E., Hart, T., Hubbell, S. P., Itoh, A., Kassim, A. R., LaFrankie, J. V., Lee, H. S., Losos, E., Makana, J. R., Ohkubo, T., Sukumar, R., Sun, I. F., Supardi, M. N. N., Tan, S., Thompson, J., Valencia, R., Muñoz, G. V., Wills, C., Yamakura, T., Chuyong, G., Dattaraja, H. S., Esufali, S., Hall, P., Hernandez, C., Kenfack, D., Kiratiprayoon, S., Suresh, H. S., Thomas, D., Vallejo, M. I., and Ashton, P.: Testing metabolic ecology theory for allometric scaling of tree size, growth and mortality in tropical forests, Ecol. Lett., 9, 575–588, https://doi.org/10.1111/j.1461-0248.2006.00904.x, 2006.
Niklas, K. J.: Plant Allometry: The Scaling of Form and Process, University of Chicago Press, Chicago, USA, 1994.
Niklas, K. J.: Maximum plant height and the biophysical factors that limit it, Tree Physiol., 27, 433–440, https://doi.org/10.1093/treephys/27.3.433, 2007.
Niklas, K. J. and Spatz, H.-C.: Growth and hydraulic (not mechanical) constraints govern the scaling of tree height and mass, P. Natl. Acad. Sci. USA, 101, 15661–15663, https://doi.org/10.1073/pnas.0405857101, 2004.
O'Brien, S. T., Hubbell, S. P., Spiro, P., Condit, R., and Foster, R. B.: Diameter, Height, Crown, and Age Relationship in Eight Neotropical Tree Species, Ecology, 76, 1926–1939, https://doi.org/10.2307/1940724, 1995.
Pacala, S. W., Canham, C. D., Saponara, J., Silander, J. A., Kobe, R. K., and Ribbens, E.: Forest Models Defined by Field Measurements: Estimation, Error Analysis and Dynamics, Ecol. Monogr., 66, 1–43, https://doi.org/10.2307/2963479, 1996.
Pan, Y., Birdsey, R. A., Phillips, O. L., and Jackson, R. B.: The Structure, Distribution, and Biomass of the World's Forests, Annu. Rev. Ecol. Evol. S., 44, 593–622, https://doi.org/10.1146/annurev-ecolsys-110512-135914, 2013.
Paris, C., Valduga, D., and Bruzzone, L.: A Hierarchical Approach to Three-Dimensional Segmentation of LiDAR Data at Single-Tree Level in a Multilayered Forest, IEEE T. Geosci. Remote Sens., 54, 4190–4203, https://doi.org/10.1109/TGRS.2016.2538203, 2016.
Paton, S.: 2017 Meteorological and Hydrological Summary for Barro Colorado Island, Smithsonian Tropical Research Institute, Panama, 41 pp., 2018.
Piperno, D. R.: Fitolitos, arquelogía y cambios prehistóricos de la vegetación en un lote de cincuenta hectáreas de la Isla de Barro Colorado, in: Ecología de Un Bosque Tropical: Ciclo Estacionales Y Cambios de Largo Plazo, edited by: Leigh, E. G., Rand, A. S., and Windsor, D. M., 1990.
Ploton, P., Barbier, N., Takoudjou Momo, S., Réjou-Méchain, M., Boyemba Bosela, F., Chuyong, G., Dauby, G., Droissart, V., Fayolle, A., Goodman, R. C., Henry, M., Kamdem, N. G., Mukirania, J. K., Kenfack, D., Libalah, M., Ngomanda, A., Rossi, V., Sonké, B., Texier, N., Thomas, D., Zebaze, D., Couteron, P., Berger, U., and Pélissier, R.: Closing a gap in tropical forest biomass estimation: taking crown mass variation into account in pantropical allometries, Biogeosciences, 13, 1571–1585, https://doi.org/10.5194/bg-13-1571-2016, 2016.
Poorter, L., Bongers, F., Sterck, F. J., and Wöll, H.: Arquitecture of 53 rain forest tree species differing in adult stature and shade tolerance, Ecology, 84, 602–608, https://doi.org/10.1890/0012-9658(2003)084[0602:AORFTS]2.0.CO;2, 2003.
Poorter, L., Bongers, L., and Bongers, F.: Architecture of 54 moist-forest tree species: traits, trade-offs, and functional groups, Ecology, 87, 1289–1301, https://doi.org/10.1890/0012-9658(2006)87[1289:AOMTST]2.0.CO;2, 2006.
Poorter, L., Hawthorne, W., Bongers, F., and Sheil, D.: Maximum size distributions in tropical forest communities: relationships with rainfall and disturbance, J. Ecol., 96, 495–504, https://doi.org/10.1111/j.1365-2745.2008.01366.x, 2008.
Prentice, I. C., Cramer, W., Harrison, S. P., Leemans, R., Monserud, R. A., and Solomon, A. M.: A global biome model based on plant physiology and dominance, soil properties and climate, J. Biogeogr., 19, 117–134, 1992.
Price, C. A., Ogle, K., White, E. P., and Weitz, J. S.: Evaluating scaling models in biology using hierarchical Bayesian approaches, Ecol. Lett., 12, 641–651, https://doi.org/10.1111/j.1461-0248.2009.01316.x, 2009.
Rüger, N., Wirth, C., Wright, S. J., and Condit, R.: Functional traits explain light and size response of growth rates in tropical tree species, Ecology, 93, 2626–2636, https://doi.org/10.1890/12-0622.1, 2012.
Rüger, N., Comita, L. S., Condit, R., Purves, D., Rosenbaum, B., Visser, M. D., Wright, S. J., and Wirth, C.: Beyond the fast–slow continuum: demographic dimensions structuring a tropical tree community, Ecol. Lett., 21, 1075–1084, https://doi.org/10.1111/ele.12974, 2018.
Shendryk, I., Broich, M., Tulbure, M. G., and Alexandrov, S. V.: Bottom-up delineation of individual trees from full-waveform airborne laser scans in a structurally complex eucalypt forest, Remote Sens. Environ., 173, 69–83, https://doi.org/10.1016/j.rse.2015.11.008, 2016.
Shinozaki, K., Yoda, K., Hozumi, K., and Kira, T.: A quantitative analysis of plant form - The pipe model theory II. Further evidence of the theory and its application in forest ecology, Jpn. J. Ecol., 14, 133–139, 1964a.
Shinozaki, K., Yoda, K., Hozumi, K., and Kira, T.: A quantitative analysis of plant form – The pipe model theory I. Basic analyses, Jpn. J. Ecol., 14, 97–105, 1964b.
Sprugel, D. G.: Correcting for Bias in Log-Transformed Allometric Equations, Ecology, 64, 209–210, https://doi.org/10.2307/1937343, 1983.
Stan Development Team: The R Interface to Stan, Version 2.10.1.: http://mc-stan.org/ (last access: February 2018), 2016.
Sullivan, M. J. P., Lewis, S. L., Hubau, W., Qie, L., Baker, T. R., Banin, L. F., Chave, J., Cuni-Sanchez, A., Feldpausch, T. R., Lopez-Gonzalez, G., Arets, E., Ashton, P., Bastin, J. F., Berry, N. J., Bogaert, J., Boot, R., Brearley, F. Q., Brienen, R., Burslem, D. F. R. P., Canniere, C., Chudomelová, M., Dančák, M., Ewango, C., Hédl, R., Lloyd, J., Makana, J. R., Malhi, Y., Marimon, B. S., Junior, B. H. M., Metali, F., Moore, S., Nagy, L., Vargas, P. N., Pendry, C. A., Ramírez-Angulo, H., Reitsma, J., Rutishauser, E., Salim, K. A., Sonké, B., Sukri, R. S., Sunderland, T., Svátek, M., Umunay, P. M., Martinez, R. V., Vernimmen, R. R. E., Torre, E. V., Vleminckx, J., Vos, V., and Phillips, O. L.: Field methods for sampling tree height for tropical forest biomass estimation, Methods Ecol. Evol., 9, 1179–1189, https://doi.org/10.1111/2041-210X.12962, 2018.
Thomas, S. C.: Asymptotic height as a predictor of growth and allometric characteristics in malaysian rain forest trees, Am. J. Bot., 83, 556–566, https://doi.org/10.1002/j.1537-2197.1996.tb12739.x, 1996.
Watanabe, S. A.: Widely Applicable Bayesian Information Criterion, J. Mach. Learn. Res., 14, 867–897, 2013.
Weng, E., Farrior, C. E., Dybzinski, R., and Pacala, S. W.: Predicting vegetation type through physiological and environmental interactions with leaf traits: evergreen and deciduous forests in an earth system modeling framework, Global Change Biol., 23, 2482–2498, https://doi.org/10.1111/gcb.13542, 2017.
Weng, E. S., Malyshev, S., Lichstein, J. W., Farrior, C. E., Dybzinski, R., Zhang, T., Shevliakova, E., and Pacala, S. W.: Scaling from individual trees to forests in an Earth system modeling framework using a mathematically tractable model of height-structured competition, Biogeosciences, 12, 2655–2694, https://doi.org/10.5194/bg-12-2655-2015, 2015.
West, G. B., Enquist, B. J., and Brown, J. H.: A general quantitative theory of forest structure and dynamics, P. Natl. Acad. Sci. USA, 106, 7040–7045, https://doi.org/10.1073/pnas.0812294106, 2009.
Westoby, M., Falster, D. S., Moles, A. T., Vesk, P. A., and Wright, I. J.: Plant Ecological Strategies: Some Leading Dimensions of Variation Between Species, Annu. Rev. Ecol. Syst., 33, 125–159, https://doi.org/10.1146/annurev.ecolsys.33.010802.150452, 2002.
Williamson, G. B. and Wiemann, M. C.: Measuring wood specific gravity… Correctly, Am. J. Bot., 97, 519–524, https://doi.org/10.3732/ajb.0900243, 2010.
Wright, J. S.: Plant diversity in tropical forests: a review of mechanisms of species coexistence, Oecologia, 130, 1–14, https://doi.org/10.1007/s004420100809, 2002.
Wright, S. J., Kitajima, K., Kraft, N. J. B., Reich, P. B., Wright, I. J., Bunker, D. E., Condit, R., Dalling, J. W., Davies, S. J., Díaz, S., Engelbrecht, B. M. J., Harms, K. E., Hubbell, S. P., Marks, C. O., Ruiz-Jaen, M. C., Salvador, C. M., and Zanne, A. E.: Functional traits and the growth–mortality trade-off in tropical trees, Ecology, 91, 3664–3674, https://doi.org/10.1890/09-2335.1, 2010.
Wright, S. J., Yavitt, J. B., Wurzburger, N., Turner, B. L., Tanner, E. V. J., Sayer, E. J., Santiago, L. S., Kaspari, M., Hedin, L. O., Harms, K. E., Garcia, M. N., and Corre, M. D.: Potassium, phosphorus, or nitrogen limit root allocation, tree growth, or litter production in a lowland tropical forest, Ecology, 92, 1616–1625, https://doi.org/10.1890/10-1558.1, 2011.





