the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Competition alters predicted forest carbon cycle responses to nitrogen availability and elevated CO2: simulations using an explicitly competitive, game-theoretic vegetation demographic model
Ray Dybzinski
Caroline E. Farrior
Stephen W. Pacala
Competition is a major driver of carbon allocation to different plant tissues (e.g., wood, leaves, fine roots), and allocation, in turn, shapes vegetation structure. To improve their modeling of the terrestrial carbon cycle, many Earth system models now incorporate vegetation demographic models (VDMs) that explicitly simulate the processes of individual-based competition for light and soil resources. Here, in order to understand how these competition processes affect predictions of the terrestrial carbon cycle, we simulate forest responses to elevated atmospheric CO2 concentration [CO2] along a nitrogen availability gradient, using a VDM that allows us to compare fixed allocation strategies vs. competitively optimal allocation strategies. Our results show that competitive and fixed strategies predict opposite fractional allocation to fine roots and wood, though they predict similar changes in total net primary production (NPP) along the nitrogen gradient. The competitively optimal allocation strategy predicts decreasing fine root and increasing wood allocation with increasing nitrogen, whereas the fixed strategy predicts the opposite. Although simulated plant biomass at equilibrium increases with nitrogen due to increases in photosynthesis for both allocation strategies, the increase in biomass with nitrogen is much steeper for competitively optimal allocation due to its increased allocation to wood. The qualitatively opposite fractional allocation to fine roots and wood of the two strategies also impacts the effects of elevated [CO2] on plant biomass. Whereas the fixed allocation strategy predicts an increase in plant biomass under elevated [CO2] that is approximately independent of nitrogen availability, competition leads to higher plant biomass response to elevated [CO2] with increasing nitrogen availability. Our results indicate that the VDMs that explicitly include the effects of competition for light and soil resources on allocation may generate significantly different ecosystem-level predictions of carbon storage than those that use fixed strategies.
- Article
(3949 KB) -
Supplement
(2482 KB) - BibTeX
- EndNote
Allocation of assimilated carbon to different plant tissues is a fundamental aspect of plant growth and profoundly affects terrestrial ecosystem biogeochemical cycles (Cannell and Dewar, 1994; Lacointe, 2000). Ecologically, allocation represents an evolutionarily honed “strategy” of plants that use limited resources and compete with other individuals and consequently drives successional dynamics and vegetation structure (De Kauwe et al., 2014; DeAngelis et al., 2012; Haverd et al., 2016; Tilman, 1988). Biogeochemically, allocation links plant physiological processes, such as photosynthesis and respiration, to biogeochemical cycles and carbon storage of ecosystems (Bloom et al., 2016; De Kauwe et al., 2014). Thus, correctly modeling allocation patterns is critical for correctly predicting terrestrial carbon cycles and Earth system dynamics.
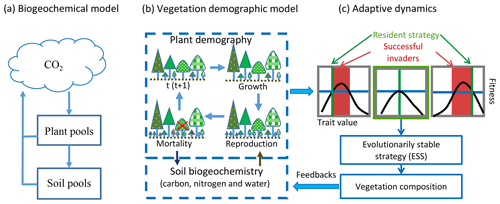
In current Earth system models (ESMs), the terrestrial carbon cycle is usually simulated by pool-based compartment models that simulate ecosystem biogeochemical cycles as lumped pools and fluxes of plant tissues and soil organic matter (Fig. 1a) (Emanuel and Killough, 1984; Eriksson, 1971; Parton et al., 1987; Randerson et al., 1997; Sitch et al., 2003). In these models, the dynamics of carbon can be described by a linear system of equations (Koven et al., 2015; Luo et al., 2001; Luo and Weng, 2011; Sierra and Mueller, 2015; Xia et al., 2013):
where X is a vector of ecosystem carbon pools, U is carbon input (i.e., gross primary production, GPP), B is the vector of allocation parameters to autotrophic respiration and plant carbon pools (e.g., leaves, stems and fine roots), and A is a matrix of carbon transfer and turnover. In this system, carbon dynamics are defined by carbon input (U), allocation (B), and residence time and transfer coefficients (A). The allocation schemes (B) are thus embedded in a linear system, or quasi-linear system if the allocation parameters in B are a function of carbon input (U) or plant carbon pools (X).
The modeling of allocation in this system (i.e., the parameters in vector B) is usually based on plant allometry, biomass partitioning and resource limitation (De Kauwe et al., 2014; Montané et al., 2017). The allocation parameters are either fixed ratios to leaves, stems and roots, which may vary among plant functional types (e.g., CENTURY, Parton et al., 1987; TEM, Raich et al., 1991; CASA, Randerson et al., 1997), or are responsive to climate and soil conditions as a way to phenomenologically mimic the shifts in allocation that are empirically observed or hypothesized (e.g., CTEM, Arora and Boer, 2005; ORCHIDEE, Krinner et al., 2005; LPJ, Sitch et al., 2003). These modeling approaches either assume that vegetation is equilibrated (fixed ratios) or average the responses of plant types to changes in environmental conditions as a collective behavior. Thus, the carbon dynamics in these models can be constrained by selecting appropriate parameters of allocation, turnover rates and transfer coefficients to fit the observations (Friend et al., 2007; Hoffman et al., 2017; Keenan et al., 2013).
To predict transient changes in vegetation structure and composition in response to climate change, vegetation demographic models (VDMs) that are able to simulate transient population dynamics are being incorporated into ESMs (Fisher et al., 2018; Scheiter and Higgins, 2009). Generally, VDMs explicitly simulate demographic processes, such as plant reproduction, growth and mortality, to generate the dynamics of populations (Fig. 1b). To speed computations and minimize complexity, groups of individuals are usually modeled as cohorts. With multiple cohorts and plant functional types (PFTs), VDMs can bring plant functional diversity and adaptive dynamics into the system when explicitly simulating individual-based competition for different resources and vegetation succession and thus predict dominant plant trait changes with environmental conditions and ecosystem development (Scheiter et al., 2013; Scheiter and Higgins, 2009; Weng et al., 2015).
The combinations of plant traits represent the competition strategies at different stages of ecosystem development. Evolutionarily, a strategy that can outcompete all other strategies in the environment created by itself will be dominant. This strategy is called an evolutionarily stable strategy or a competitively optimal strategy (McGill and Brown, 2007). In VDMs, competitively optimal strategies can therefore be reasonably predicted based on the costs and benefits of different strategies (i.e., combinations of plant traits) through their effects on demographic processes (i.e., fitness) and ecosystem biogeochemical cycles (Fig. 1c) (e.g., Farrior et al., 2015; Weng et al., 2015).
The dynamics of plant traits can substantially change predictions of ecosystem biogeochemical dynamics since they change the key parameters of vegetation physiological processes and soil organic matter decomposition (e.g., Dybzinski et al., 2015; Farrior et al., 2015; Weng et al., 2017). Therefore, the key parameters that are used to estimate carbon dynamics in the linear system model (Eq. 1), such as allocation (B) and residence times in different carbon pools (matrix A, which includes coefficients of carbon transfer and turnover time) become functions of competition strategies that vary with environment and carbon input. In addition, the turnover of vegetation carbon pools becomes a function of allocation, leaf longevity, fine root turnover and tree mortality rates, which change with vegetation succession and the most competitive plant traits. These changes make the system nonlinear and can lead to large biases within the framework of the compartmental pool-based models as represented by Eq. (1) (Sierra et al., 2017; Sierra and Mueller, 2015). Because of the high complexity associated with demographic and competition processes, the model predictions are usually sensitive to the parameters in these processes and are of high uncertainty (e.g., Pappas et al., 2016).
In contrast to their implementation in the more complicated VDMs discussed above, models of competitively dominant plant strategies using much simpler model structures and assumptions can sometimes be solved analytically (Dybzinski et al., 2011, 2015; Farrior et al., 2013, 2015). Although simplified, such models can pinpoint the key processes that improve the predictive power of simulation models (Dybzinski et al., 2011; Farrior et al., 2013, 2015), allowing them to help researchers formulate model processes and understand the simulated ecosystem dynamics in ESMs. For example, the analytical model derived by Farrior et al. (2013) that links interactions between ecosystem carbon storage, allocation and water stress at elevated atmospheric CO2 concentration [CO2] sheds light on the otherwise inscrutable processes leading to varied soil water dynamics in a land model coupled with an VDM (Weng et al., 2015). Recognizing the benefit, Weng et al. (2017) included both a simplified analytical model and a more complicated VDM to understand competitively optimal leaf mass per area, competition between evergreen and deciduous plant functional types, and the resulting successional patterns.
In this study, we use a stand-alone simulator derived from the LM3-PPA model (Weng et al., 2017, 2015) to show how forests respond to elevated [CO2] and nitrogen availability via different competitively optimal allocation strategies. The demographic processes of this model have been coupled into the land model of the Geophysical Fluid Dynamical Laboratory's Earth System Model (Shevliakova et al., 2009; Weng et al., 2015) and are being added to NASA Goddard Institute for Space Study's Earth system model, ModelE (Schmidt et al., 2014). Using this model, we simulate the shifts in competitively optimal allocation strategies in response to elevated [CO2] at different nitrogen levels based on insights from the analytical model derived by Dybzinski et al. (2015). Dybzinski et al. (2015)'s model predicts that increases in carbon storage at elevated [CO2] relative to storage at ambient [CO2] are largely independent of total nitrogen because of an increasing shift in carbon allocation from long-lived, low-nitrogen wood to short-lived, high-nitrogen fine roots under elevated [CO2] with increasing nitrogen availability. Here, we analyze the simulated ecosystem carbon cycle variables (gross and net primary production, allocation, and biomass) of separate monoculture and polyculture model runs. In the monoculture runs, ecosystem properties are the result of the prescribed allocation strategies of a given PFT. In the polyculture runs, competition between the different allocation strategies results in succession and the eventual dominance of the most competitive allocation strategy for a given nitrogen availability and [CO2] level. Since everything else in the model is identical, we are able to compare the predictions of single fixed strategies with competitively optimal allocation strategies by comparing the ecosystem properties of these two types of runs.
2.1 BiomeE model overview
We used a stand-alone ecosystem simulator (Biome Ecological strategy simulator, BiomeE) to conduct simulation experiments. BiomeE is derived from the version of LM3-PPA used in Weng et al. (2017), and its code is available at Github (https://github.com/wengensheng/BiomeESS, last access: 27 November 2019). In this version, we simplified the processes of energy transfer and soil water dynamics of LM3-PPA (Weng et al., 2015) but still retained the key features of plant physiology and individual-based competition for light, soil water and, via the decomposition of soil organic matter, nitrogen (Fig. 2 and Supplement I for details). In this model, individual trees are represented as sets of cohorts of similarly sized trees and are arranged in different vertical canopy layers according to their height and crown area following the rules of the perfect plasticity approximation (PPA) model (Strigul et al., 2008). Sunlight is partitioned into these canopy layers according to Beer's law. Thus, a key parameter for light competition, critical height, is defined; all the trees above this context-dependent height get full sunlight and all trees below this height are shaded by the upper-layer trees.
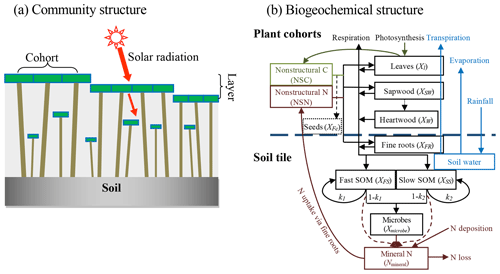
Figure 2Structure of BiomeE. (a) Vegetation structure: trees organize their crowns into canopy layers according to both their height and their crown area following the rules of the PPA model, which mechanistically models light competition. (b) Biogeochemical structure and compartmental pools. The green, brown and black lines are the flows of carbon, nitrogen, and coupled carbon and nitrogen, respectively. The green box is for carbon only. The brown boxes are nitrogen pools. The black boxes are for both carbon and nitrogen pools, where X can be C (carbon) and N (nitrogen). The C:N ratios of leaves, fine roots, seeds and microbes are fixed. The C:N ratios of woody tissues, fast soil organic matter (SOM) and slow SOM are flexible. Only one tree's C and N pools are shown in this figure. The blue box and arrows are for water storage in soil and fluxes of rainfall, evaporation and transpiration. The model can have multiple cohorts of trees, which share the same pool structure. The dashed line separates the aboveground and belowground processes.
Each tree consists of seven pools: leaves, fine roots, sapwood, heartwood, fecundity (seeds), and nonstructural carbohydrates and nitrogen (NSC and NSN, respectively) (Fig. 2b). The carbon and nitrogen in plant pools enter the soil pools with the mortality of individual trees and the turnover of leaves and fine roots. There are three soil organic matter (SOM) pools for carbon and nitrogen: fast turnover, slow turnover and microbial pools, along with a mineral nitrogen pool for mineralized nitrogen in soil. The simulation of SOM decomposition and nitrogen mineralization is based on the models of Gerber et al. (2010) and Manzoni et al. (2010) and described in detail in Weng et al. (2017). The decomposition rate of a SOM pool is determined by the basal turnover rate together with soil temperature and moisture. The nitrogen mineralization rate is a function of decomposition rate and the C:N ratio of the SOM. Microbes must consume more carbon in the high C:N ratio SOM pools to get enough nitrogen and must release excessive nitrogen in the low C:N ratio SOM pools to get enough carbon for energy (Weng et al., 2017).
Plant growth and reproduction are driven by the carbon assimilation of leaves via photosynthesis, which is in turn dependent on water and nitrogen uptake by fine roots. The photosynthesis model is identical to that of LM3-PPA (Weng et al., 2015), which is a simplified version of Leuning model (Leuning et al., 1995). This model first calculates photosynthesis rate, stomatal conductance and water demand of the leaves of each tree (cohort) in the absence of soil water limitation. Then, it calculates available water supply as a function of fine root surface area and soil water content. The demand-based assimilation rate and stomatal conductance are adjusted if soil water supply is less than plant water demand. Soil water content is calculated based on the fluxes of precipitation, soil surface evaporation and plant water update (transpiration) in three layers of soil to a depth of 2 m (see Supplement I for details).
Assimilated carbon enters into the NSC pool and is subsequently used for respiration, growth and reproduction. Empirical allometric equations relate woody biomass (including coarse roots, bole and branches), crown area and stem diameter. The individual-level dimensions of a tree, i.e., height (Z), biomass (S) and crown area (ACR), are given by empirical allometries (Dybzinski et al., 2011; Farrior et al., 2013):
where Z is tree height, D is tree diameter, S is total woody biomass carbon (including bole, coarse roots and branches) of a tree, αc and αZ are PFT-specific constants, θc=1.5 and θZ=0.5 (Farrior et al., 2013) (although they could be made PFT-specific if necessary), π is the circular constant, Λ is a PFT-specific taper constant, and ρW is PFT-specific wood density (kg C m−3) (Table 1).
We set targets for leaf (L∗), fine root (FR∗) and sapwood cross-sectional area () that govern plant allocation of nonstructural carbon and nitrogen during growth. These targets are related by the following equations based on the assumption of the pipe model (Shinozaki et al., 1964):
where , FR∗(D) and are the targets of leaf mass (kg C per tree), fine root biomass (kg C per tree) and sapwood cross-sectional area (m2/tree), respectively, at tree diameter D; l∗ is the target leaf area per unit crown area of a given PFT; ACR(D) is the crown area of a tree with diameter D; σ is PFT-specific leaf mass per unit area (LMA); p(t) is a PFT-specific function ranging from zero to one that governs leaf phenology (Weng et al., 2015); φRL is the target ratio of total root surface area to the total leaf area; γ is specific root area; and αCSA is an empirical constant (the ratio of sapwood cross-sectional area to target leaf area). The phenology function p(t) takes values 0 (nongrowing season) or 1 (growing season) following the phenology model of LM3-PPA (Weng et al., 2015). The onset of a growing season is controlled by two variables, growing degree days (GDDs) and a weighted mean daily temperature (Tpheno), while the end of a growing season is controlled by Tpheno (see Supplement I for details of the phenology model).
2.1.1 Nitrogen uptake
The rate of nitrogen uptake (U, ) from the soil mineral nitrogen pool is an asymptotically increasing function of fine root biomass density (CFR,total, kg C m−2), following McMurtrie et al. (2012)
where Nmineral is the mineral nitrogen in soil (g N m−2), fU,max is the maximum rate of nitrogen absorption per hour when CFR,total approaches infinity, and KFR is a shape parameter (kg C m−2) at which the nitrogen uptake rate is half of the parameter fU,max. The nitrogen uptake rate of an individual tree (Utree, ) is calculated as follows:
where, CFR,tree is the fine root biomass of a tree (kg C tree−1). The nitrogen absorbed by roots enters into the NSN pool and then is allocated to plant tissues through plant growth.
2.1.2 Allocation and plant growth
The partitioning of carbon and nitrogen into the plant pools (, leaves, fine roots and sapwood) is limited by the allometric equations, targets of leaves, fine roots and sapwood cross-sectional area, and the stoichiometry (i.e., C:N ratios) of these plant tissues. At a daily time step, the model calculates the amount of carbon and nitrogen that are available for growth according to the total NSC and NSN and current leaf and fine root biomass. Basically, the available NSC (GC) is the summation of a small fraction (f1) of the total NSC in an individual plant and the differences between the targets of leaf and fine roots and their current biomass capped by a larger fraction (f2) of NSC (Eq. 6a). The available NSN (GN) is analogous to that of the NSC and meets approximately the stoichiometrical requirement of plant tissues (Eq. 6b).
where L∗ and FR∗ are the targets of leaves and fine roots, respectively (see Eq. 3); L and FR are current leaf and fine roots biomass, respectively; and and are nitrogen of leaves and fine roots at their targets according to their target C:N ratios. The parameter f1 is the fraction of NSC (or NSN) for normal growth after leaves and fine roots approach their targets, and f2 caps the maximum daily availability of NSC (or NSN) during the period of leaf flush at the beginning of a growing season. The parameter f1 is much smaller than f2. We let and f2=0.02 in this study.
The allocation of the available NSC (i.e., GC) to wood (GW), leaves (GL), fine roots (GFR) and seeds (GF) follows the equations below (Eq. 7). These equations describe the mass growth of plant tissues with nitrogen effects on the carbon allocation between high-nitrogen tissues and low-nitrogen tissues (wood) for maximizing leaves and fine roots growth (GL and GFR, respectively), optimizing carbon usage at given nitrogen supply (GN) and keeping the tissues at their target C:N ratios.
where CNL,0, CNFR,0, CNF,0, and CNW,0 are the target C:N ratios of leaves, fine roots, seeds, and sapwood, respectively; γ is specific root area (m2 kg C−1); σ is leaf mass per unit area (kg C m−2); fLFR,max is the maximum fraction of GC for leaves and fine roots (0.85 in this study); v is the fraction of left carbon for seeds (0.1 in this study); and rS∕D is a nitrogen-limiting factor ranging from 0 (no nitrogen for leaves, fine roots and seeds) to 1 (nitrogen available for full growth of leaves, fine roots and seeds). The parameter rS∕D controls the allocation of GC and GN to the four plant pools (Eq. 7a). It can be analytically solved as follows (Eqs. 8 and 9).
where N′ is defined as the potential nitrogen demand for plant growth at 1 (i.e., no nitrogen limitation),
when (), there is no nitrogen limitation, all the GC will be used for plant growth and the allocation follows the rules of the carbon only model (Eq. 7d–f as ). The excessive nitrogen () will be returned to the NSN pool (as if they were never taken out). When (i.e., ), all GC and GN will be used in new tissue growth; however, the leaves and fine roots cannot reach their targets at this step (i.e. they are down-regulated). When (), all the GN will be allocated to sapwood and the excessive carbon () will be returned to NSC pool. This is a very rare case since a low GN leads to low leaf growth, reducing GC before the case happens. Therefore, in most cases, Eq. (7a) is . Overall, this strategy down-regulates leaf production under low nitrogen conditions while making use of assimilated carbon in height-structured competition for light.
Allocation to wood tissues (GW) drives the growth of tree diameter, height and crown area and thus increases the targets of leaves and fine roots (Eq. 3). By differentiating the stem biomass allometry in Eq. (2) with respect to time, using the fact that dS∕dt equals the carbon allocated for wood growth (GW), we have the diameter growth:
This equation transforms the mass growth to structural changes in tree architecture. With an updated tree diameter, we can calculate the new tree height and crown area using allometry equations (Eq. 2) and targets of leaf and fine root biomass (Eq. 3) for the next growth step.
Overall, this is a flexible allocation scheme and still follows the major assumptions in the previous version of LM3-PPA (Weng et al., 2015, 2017). This allocation scheme prioritizes the allocation to leaves and fine roots, maintains a minimum growth rate of stems, and keeps the constant area ratio of fine roots to leaves. Based on these allocation rules, the average allocation of carbon and nitrogen to leaves, fine roots and wood over a growing season are governed by the targets for the leaf area per unit crown area (i.e., crown leaf area index, l∗) and fine root area per unit leaf area (φRL). Since the crown leaf area index, l∗, is fixed in this study, φRL is the key parameter determining the relative allocation of carbon to fine roots and stems. A high φRL means a high relative allocation to fine roots and therefore low relative allocation to stems and vice versa. Note that here ϕRL is fixed for each PFT and will remain so for all the model runs.
The process of choosing a context-dependent competitively dominant φRL will take place after finding the fitness of each φRL in monoculture and in competition with other PFTs (, different values of φRL). The competitively optimal strategy is the one that can successfully exclude all others in the processes of competition and succession, but it is not necessarily the one that maximizes production in monoculture. For example, each φRL creates an environment of light profile and soil nitrogen in its monoculture. Other φRL PFTs may have higher fitness in this environment than the one that creates it. Only the competitively dominant strategy has the highest fitness in the environment it creates (Fig. 1c).
2.2 Site and data
Data pertaining to vegetation, climate and soil at Harvard Forest (Aber et al., 1993; Hibbs, 1983; Urbanski et al., 2007) were used to design the plant functional types (PFTs) and ecosystem nitrogen levels used in the simulation experiments, to drive the model and to calibrate model parameters. Harvard Forest is located in Massachusetts, USA (42.54∘, −72.17∘). The climate of Harvard Forest is cool temperate with an annual precipitation of 1050 mm, distributed fairly evenly throughout the year. The annual mean temperature is 8.5 ∘C with a high monthly mean temperature of 20 ∘C in July and a low of −7 ∘C in January. The soils are mainly sandy loam with an average depth of around 1 m and are moderately well drained in most areas. In forest sites, soil carbon is around 8 kg C m−2 and nitrogen 300 g N m−2 (Compton and Boone, 2000). The vegetation is deciduous broadleaf (mixed) forest with its major species being red oak (Quercus rubra), red maple (Acer rubrum), black birch (Betula lenta), white pine (Pinus strobus) and hemlock (Tsuga canadensis) (Compton and Boone, 2000; Savage et al., 2013). The data used to drive our model runs are gap-filled hourly meteorological data at Harvard Forest from 1991 to 2006, obtained from North American Carbon Program (NACP) site-level synthesis datasets (Barr et al., 2013).
2.3 Simulation experiments
We set two atmospheric CO2 concentration ([CO2]) levels, 380 and 580 ppm, and eight ecosystem total nitrogen levels (ranging from 114.5 to 552 g N m−2 at the interval of 62.5 g N m−2) by assigning the initial content of the slow SOM pool for our simulation experiments (Table 2). This range covers the soil nitrogen contents across the plots at Harvard Forest with different species compositions and land-use history (200–300 g N m−2) (Compton and Boone, 2000; Melillo et al., 2011) and represents the range from infertile to fertile soils in temperate forests (Post et al., 1985; Yang et al., 2011). The nitrogen cycles through the plant and soil pools and is redistributed among them via plant demographic processes, soil carbon transfers and plant uptake. In all the simulation experiments, we assume the ecosystem has no nitrogen inputs and no outputs for convenience since we already have eight total nitrogen levels to represent the consequences of different nitrogen input and output processes at an equilibrium state. The PFTs were based on an evergreen needle-leaved tree PFT with different leaf to fine root area ratios, φRL, in the range from 1 to 8 (Table 2). Simply stated, the PFTs we investigate only differ in parameter φRL.
We define the model runs started with only one fixed-φRL PFT as “monoculture runs”, although the actual allocation of carbon to different plant tissues varies with [CO2] and ecosystem nitrogen availability. The model runs started with multiple PFTs are called “polyculture runs” (eight PFTs with different φRL at the beginning, although many are driven to extinction during a given model run). We conducted one set of monoculture runs and two sets of polyculture runs (Table 2).
In the monoculture runs, we run the full combinations of eight PFTs with root/leaf area ratios (φRL) from 1 to 8, eight ecosystem total nitrogen levels and two CO2 concentrations (380 and 580 ppm) (Table 2). For the eight PFTs, only those with φRL≤6 survived at ambient [CO2] (380 ppm) because the carbon assimilated by leaves could not meet the demand by plant tissues at φRL>6. The monoculture runs are for exploring the model predictions of gross primary production (GPP), net primary production (NPP), and allocation and biomass at equilibrium with fixed φRL at different total nitrogen levels.
In polyculture run I, we used the same PFTs as in those monoculture runs, where their φRL varied from 1 to 8 at the interval of 1.0 and the ecosystem total nitrogen levels were the same as those used in the monoculture runs (Table 2). This set of polyculture runs was used to explore successional patterns at both ambient and elevated [CO2] (380 and 580 ppm, respectively). However, this set of model runs could not show the details of equilibrium plant biomass and allocation patterns along the nitrogen gradient because of the large intervals between the φRL values.
To achieve greater resolution in our competition predictions, we designed the polyculture run II using a dynamic PFT combination scheme, according to the ranges of φRL obtained from the polyculture run I that could survive at a particular nitrogen level at both CO2 concentrations. For each nitrogen level, we set eight PFTs with φRL that varied in a range 3.5 (e.g., ) at the interval of 0.5, starting with the highest φRL of 8.0 at the lowest N level (114.5 g N m−2) and decreasing 0.5 per level of increase in ecosystem total N. We used i=1, 2, …, 8 to denote the eight N levels from 114.5 to 552 g N m−2. The φRL of the eight PFTs at each level were 5.0–0.5i, 5.5–0.5i, …, 8.5–0.5i (Table 2). For example, at the nitrogen of 114.5 g N m−2 (i=1), the φRL of the eight PFTs were 4.5, 5.0, …, 8.0 and at 177 g N m−2 (i=2) they were 4.0, 4.5, …, 7.5.
For both monoculture and polyculture runs, visual inspection indicated that stands had reached equilibrium after ∼1200 years. To be conservative, we present equilibrium data by averaging model properties between years 1400 and 1800. We compared simulated equilibrium GPP, NPP, allocation (both absolute amount of carbon and fractions of the total NPP) and plant biomass of the polyculture run II with those from the monoculture runs. We used the results from one PFT (φRL=4) to highlight the differences of plant responses with competitively optimal allocation strategies obtained from the polyculture run II.
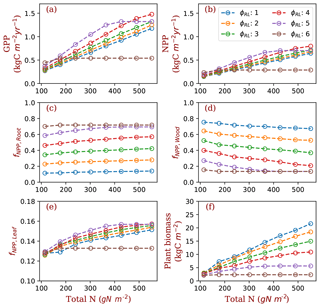
Figure 3GPP, NPP, allocation and plant biomass at equilibrium state simulated by monoculture runs. GPP: gross primary production; NPP: net primary production; fNPP,x: the fraction of NPP allocated to x, where x is root (fine roots), leaf (leaves in crown) or wood (including tree trunk, stems and coarse roots). The data are from the averages of the model run years from 1400 and 1800. Each model run is initiated with one PFT with a fixed ratio of fine root area to leaf area (φRL).
In the monoculture runs, GPP and NPP increase by a factor of 3 along the gradient of nitrogen used in this study (114.5–552 g N m−2) at both ambient (Fig. 3) and elevated [CO2] (Fig. S1 in the Supplement). The magnitude of differences in GPP and NPP due to differences in fixed allocation within a given nitrogen level is comparable to the magnitude of differences in GPP and NPP due to nitrogen level within a given fixed allocation strategy (Fig. 3a and b) when φRL is in the range that allows plants to grow normally (1–5 in the case of ambient [CO2]). As prescribed by the definition of φRL, allocation of NPP to fine roots increases with φRL in monoculture runs (Fig. 3c). As a consequence, allocation of NPP to wood decreases as φRL increases (Fig. 3d). Allocation to leaves does not change much with φRL (Fig. 3e, note differences in scale). Correspondingly, plant biomass at equilibrium decreases with φRL (Fig. 3f). The effects of nitrogen on the allocation of carbon to fine roots and wood follow our allocation model assumptions because more carbon is allocated to low-nitrogen woody tissues in our model when nitrogen is limited. However, the amplitude of changes in GPP and NPP induced by nitrogen availability is lower than the amplitude of changes resulting from different values of φRL in the monoculture runs.
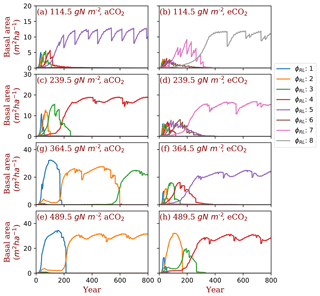
Figure 4Successional patterns of polyculture run I at ambient and elevated [CO2] concentrations. φRL is the fixed ratio of fine root area to leaf area of a particular strategy.
We used two sets of polyculture runs to look for the φRL that is closest to competitively optimal. In the polyculture run I, where φRL ranges from 1 to 8 at all nitrogen levels, the winning strategy (φRL) increases from 5 to 2 as the total nitrogen increases from 114.5 to 489.5 g N m−2 at ambient [CO2] (380 ppm) (Fig. 4a, c, g, e). Elevated [CO2] (580 ppm) shifts the winning strategy to higher (φRL) at all the total nitrogen levels. As shown in Fig. 4, the winning strategy shifts from φRL=5 to φRL=8 at 114.5 g N m−2 and from φRL=2 to φRL=4 at 489.5 g N m−2. In some situations (e.g., Fig. 4g and Figs. S2 and S3), it takes a long time for the most competitive PFTs to out-compete the previously dominant PFTs because of the sequential replacement of dominant PFTs during the course of succession and the slow growth rate of trees in understory.
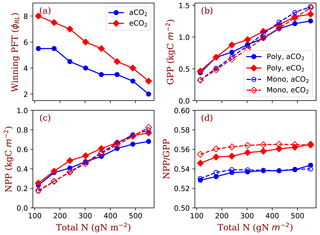
Figure 5Winning PFTs (φRL, a) in polyculture run II and equilibrium gross primary production (GPP, b), net primary production (NPP, c) and carbon use efficiency (NPP∕GPP, d) at two CO2 concentrations (aCO2: 380 ppm; eCO2: 580 ppm). The closed symbols with solid lines represent polyculture runs. The open symbols with dashed lines represent monoculture runs (only φRL=4 shown in this figure). φRL is the fixed ratio of fine root area to leaf area of a particular strategy.
Based on the shifts of the winning φRL from ambient [CO2] to elevated [CO2] at the eight nitrogen levels, we designed the polyculture run II with a high resolution of φRL and calculated their GPP, NPP, allocation and plant biomass at equilibrium state. The of φRL of the winning PFTs decreases from 5.5 to 2 at ambient [CO2] and from 8.0 to 3.0 at elevated [CO2] as total nitrogen increases from 114.5 to 552.0 g N m−2. The equilibrium GPP and NPP increase with total nitrogen at values similar to those of the monoculture runs (Fig. 5b and c). However, the CO2 stimulation of NPP increases with total nitrogen in the polyculture runs more than it is in the monoculture runs. Elevated [CO2] increases carbon use efficiency (defined as the ratio of NPP to GPP in this study, NPP∕GPP) in both the monoculture and polyculture runs (Fig. 5d). Also, the dependence of NPP:GPP ratio on nitrogen is higher in the polyculture runs than it is in the monoculture runs (Fig. 5c).
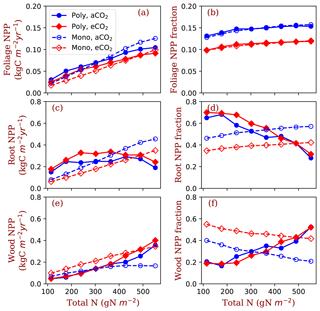
Figure 6Allocation to leaves, fine roots and wood tissues of the competition and monoculture runs at the eight total nitrogen levels and two CO2 concentrations (aCO2: 380 ppm; eCO2: 580 ppm). Panels (a), (c) and (e) show the NPP allocated to the tissues and panels (b), (d) and (f) show the fractions of the allocation in total NPP. The closed symbols with solid lines represent polyculture runs (Poly). The open symbols with dashed lines represent monoculture runs (only φRL=4 is shown in this figure, Mono). φRL is the fixed ratio of fine root area to leaf area of a particular strategy.
Allocation of NPP to leaves increases with nitrogen in all conditions, i.e. both competition and monoculture at both ambient [CO2] and elevated [CO2] (Fig. 6a). Foliage NPP is similar in these four model runs when nitrogen is low. At high nitrogen (>400 g N m−2), polyculture runs have higher foliage NPP than the monoculture runs generally. Allocation to leaves is relatively stable across the nitrogen gradient at the two [CO2] levels (Fig. 6b). The fraction of NPP allocated to leaves changes little with nitrogen (Fig. 6b) and it is universally higher at ambient [CO2] than it is at elevated [CO2].
Fine root NPP does not significantly change with ecosystem total nitrogen in polyculture runs, whereas it increases monotonically with increasing nitrogen in monoculture runs (Fig. 6c). Elevated [CO2] increases fine root allocation at low nitrogen in polyculture runs but decreases root allocation irrespective of nitrogen in monoculture runs (Fig. 6c). The fraction of NPP allocated to fine roots decreases with nitrogen at both CO2 concentrations in polyculture runs, but it increases slightly in monoculture runs (Fig. 6d). In monoculture runs, elevated [CO2] reduces the fraction of NPP allocated to fine roots at all nitrogen levels. In polyculture runs, fractional allocation to fine roots increases at elevated [CO2] when nitrogen is low (e.g., 114.5–302 g N m−2) and decreases at elevated [CO2] when nitrogen is high (e.g., 364–552 g N m−2).
In the reverse of the fine root response, NPP allocation to woody tissues increases with total nitrogen in both competition and monoculture runs (Fig. 6e). In polyculture runs, the fraction of allocation to woody tissues decreases at elevated [CO2] when ecosystem total nitrogen is low (e.g., 114–245 g N m−2) and increases at elevated [CO2] when ecosystem total nitrogen is high (e.g., 302–552 g N m−2).
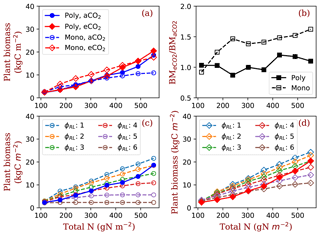
Figure 7Plant biomass responses to elevated [CO2] and nitrogen. Panel (a) shows the equilibrium plant biomass (means of simulated plant biomass from model run year 1400 to 1800) in polyculture runs and monoculture runs (only φRL=4 is shown as an example). Panel (b) shows the ratio of simulated plant biomass at elevated [CO2] to ambient [CO2] for both competition and monoculture runs. Panels (c) and (d) show the comparisons with monoculture runs with φRL increasing from 1 to 6 at ambient (c) and elevated [CO2] (d). The closed symbols with solid lines represent polyculture runs. The open symbols with dashed lines represent monoculture runs (φRL ranges from 1 to 6). φRL is the fixed ratio of fine root area to leaf area of a particular strategy. aCO2: 380 ppm; eCO2: 580 ppm.
As a result of the changes in competitively optimal φRL, plant biomass increases dramatically with ecosystem total nitrogen in polyculture runs compared with that in monoculture runs (Fig. 7a). The effects of elevated [CO2] on plant biomass increase with nitrogen in polyculture runs but are constant overall in monoculture runs (Fig. 7b). Compared with the full spread of monoculture runs with φRL ranging from 1 to 6, polyculture runs have high root allocation at low nitrogen and low root allocation at high nitrogen due to changes in the dominant competitive allocation strategy, which amplifies plant biomass responses to elevated [CO2] with increasing nitrogen (Fig. 7c and d).
Our simulations show that the predicted responses of individual plants to elevated [CO2] can be significantly changed by explicit inclusion of competition processes. Here, the major tradeoff for light- and N-limited trees is the relative allocation between stems and fine roots (Dybzinski et al., 2011). Although the wood allocation (and thus carbon sequestration potential) of every PFT used in this study increases under elevated [CO2] at all nitrogen levels (e.g., Fig. 6e, dashed lines), only those PFTs that allocate more to fine roots (with lower carbon sequestration potential) can survive competition under elevated [CO2] (Fig. 6c, solid lines). Put together, explicit inclusion of competition processes reduces the expected increase in biomass (and thus carbon sequestration potential) under elevated [CO2] compared with simulations that do not include competition processes (Fig. 7b).
Since there is a lack of direct observations or experiments to quantitatively validate the long-term patterns predicted by our model, we did not calibrate it to fit observations at Harvard Forest. In the following section, we analyze the model processes in detail and validate our modeling approach by comparing the general patterns from observations and experiments with model predictions. These comparisons also shed light on the modeling of allocation and vegetation responses to elevated [CO2].
4.1 Mechanisms of game-theoretic allocation modeling and simulation results validation
In our model, the allocation of carbon and nitrogen within an individual tree is based on allometric scaling (Eq. 2), functional relationships (Eq. 3) and optimization of resource usage (Eq. 7). Generally, the allometric scaling relationships define the maximum leaf and fine root surface area at a given tree size and the functional relationships define the ratios of leaf area to sapwood cross-sectional area and fine root surface area. These rules are commonly used in ecosystem models (Franklin et al., 2012) and have been shown to generate reasonable predictions (De Kauwe et al., 2014; Valentine and Mäkelä, 2012). These rules implicitly define the priority of allocation to leaves and fine roots but allow for structurally unlimited stem growth when resources (carbon and nitrogen in this study) are available (i.e., the remainder goes to stems after leaf and fine root growth) and NSC is not accumulated exaggeratedly when ecosystem nitrogen is limited (Fig. S6).
We used a tuning parameter, maximum leaf and fine root allocation, fLFR,max, to constrain the maximum allocation to leaves and fine roots in order to maintain a minimum growth rate of wood in years of low productivity. This is consistent with wood growth patterns in temperate trees, where new wood tissues must be continuously produced (especially early in the growing season) to maintain the functions of tree trunks and branches (Cuny et al., 2012; Michelot et al., 2012; Plomion et al., 2001). This parameter does not change the fact that leaves and fine roots are the priority in allocation, since allocation ratios to stems are around 0.4–0.7 in temperate forests (Curtis et al., 2002; Litton et al., 2007). With a value of 0.85, parameter fLFR,max seldom affects the overall carbon allocation ratios of leaves, fine roots and stems. If (i.e., the highest priority for leaf and fine root growth), simulated trunk radial growth would have unreasonably high interannual variation because leaf and fine root growth would use all carbon to approach to their targets, leaving nothing for stems in some years of low productivity.
The simulation of competition for light and soil resources is based on two fundamental mechanisms: (1) competition for light is based on the height of trees according to the PPA model, which assumes trees have perfectly plastic crown to capture light via stem (trunk) and branch phototropism (Strigul et al., 2008), and (2) individual soil N uptake is linearly dependent on the fine root surface area of an individual tree relative to that of its neighbors (Dybzinski et al., 2019; McMurtrie et al., 2012; Weng et al., 2017). These two mechanisms define an allocation tradeoff between wood and fine roots for carbon and nitrogen investment in different CO2 concentrations and nitrogen environments. Including explicit competition for these resources to determine the dominant strategies results in very different predicted allocation patterns – and thus ecosystem level responses – than those of strategies in the absence of competition. For example, fractional wood allocation increases with increasing nitrogen availability under competitive allocation but decreases – the opposite qualitative response – under a fixed strategy (Fig. 6f). Consequently, equilibrium plant biomass is predicted to increase much more with increasing nitrogen availability under a competitive strategy (Fig. 4c, d). In nature, the effects of competition on dominant plant traits may occur through species replacement or community assembly (akin to the mechanism in our model) (e.g., Douma et al., 2012), but it may also occur through adaptive plastic responses or in-place subpopulation evolution of ecotypes (Grams and Andersen, 2007; McNickle and Dybzinski, 2013; Smith et al., 2013).
Generally, the predictions from competitively optimal allocation strategies predicted by our model can be found in large-scale forest censuses and site-level experiments, such as that (1) high-nitrogen environments (i.e., productive environments) favor high wood allocation and low root allocation (Litton et al., 2003; Poorter et al., 2012), (2) elevated [CO2] increases root allocation (Drake et al., 2011; Iversen, 2010; Jackson et al., 2009; Nie et al., 2013; Smith et al., 2013), (3) low nitrogen availability limits vegetation biomass responses to elevated [CO2] as a result of high root allocation or root exudation (Jiang et al., 2019a; Norby and Zak, 2011), and (4) increases in vegetation biomass at elevated [CO2] are largely due to high wood allocation (Norby and Zak, 2011; Walker et al., 2019). These predictions emerge from the fundamental assumptions of our model without tuning parameters to fit the data, providing some confidence in the robustness of our approach.
The literature on experimental responses of plant community to elevated [CO2] shows that the responses vary with site characteristics, forest composition, stand age, plant physiological responses and soil microbial feedbacks (Norby and Zak, 2011; Terrer et al., 2016, 2018). For example, in the Duke Free Air CO2 Enhancement (FACE) experiment, where the major trees are loblolly pine (Pinus taeda), increases in root production at elevated [CO2] stimulated increased nitrogen supply that allowed the forest to sustain higher productivity (Drake et al., 2011). However, in the Oak Ridge FACE, where the major trees are sweetgum (Liquidambar styraciflua), increased fine-root production under elevated [CO2] did not result in increased net nitrogen mineralization and increases in root production declined after 8 years of CO2 enhancement (Iversen, 2010; Norby and Zak, 2011). In EucFACE (Jiang et al., 2019a), where the major trees are Eucalyptus tereticornis and the soil is infertile, trees significantly increased their root exudation under limited nutrient supplies but had no significant increase in biomass in response to elevated [CO2]. The BangorFACE experiment (Smith et al., 2013) found that interspecific competition (Alnus glutinosa, Betula pendula and Fagus sylvatica) resulted in greater increases in root biomass at elevated [CO2]. Leaf area index (LAI) responses to elevated [CO2] are also highly varied. As summarized by Norby and Zak (2011), low LAI (in this case, open-canopy) sites showed significant increases in LAI and high LAI (in this case, closed-canopy) sites showed low increases or even decreases in LAI. They concluded that LAI in closed-canopy forests is not responsive to elevated [CO2] (Norby et al., 2003; Norby and Zak, 2011).
The nature of developing a model with generic assumptions and balanced processes reduces its capability to predict all of these responses. For example, plants have a variety of physiological mechanisms to deal with excessive carbon supply when plant demand (i.e., “sink”) is relatively low (Fatichi et al., 2019; Körner, 2006), such as down-regulating leaf photosynthesis rate by the accumulated assimilates (Goldschmidt and Huber, 1992) or respiring excessive carbohydrates to regenerate substrates for photosynthesis (Atkin and Macherel, 2009). But these mechanisms are short-term physiological responses (minutes to hours, sometimes days) for plants in situations of temporary nitrogen shortage, high irradiation or drought stress. It is not “economically” sustainable in an infertile environment to maintain highly productive leaves but often suppress their photosynthesis or respire a large portion of their assimilated carbon.
Root exudation is a critical process for plants. It can stimulate soil organic matter decomposition and nitrogen mineralization to facilitate soil nitrogen supply at the expense of carbon (Cheng, 2009; Cheng et al., 2014; Drake et al., 2011; Phillips et al., 2011). The process of root exudation has been adopted by many models to couple with microbial processes in the determination of soil organic matter decomposition (Sulman et al., 2014; Wieder et al., 2014, 2015). Some carbon-only models, e.g., LM3 (Shevliakova et al., 2009), the parent model of this one, and TECO (Luo et al., 2001), incorporate root exudation to put extra carbon into the soil in order to avoid down-regulating canopy photosynthesis or overestimating vegetation biomass, both of which had been tuned against data. However, in a demographic competition model like this one, individual plants cannot reap a reward from root exudation as they do in nature when the microbial activities are not fully coupled and the nitrogen in soil is assumed fully accessible by roots of all individuals. Therefore, root exudation is not a competitive strategy in the system defined by the assumptions of this model.
Since the purpose of this study is to explore long-term ecological strategies in different but relatively stable environments, we did not include these processes, especially since they present additional challenges in balancing the complexity of the tradeoffs between modeled demographic processes and plant traits. However, the lack of these processes does limit the predictions of instantaneous responses to variation in environmental conditions or resource supply and possibly of some long-term vegetation characteristics as well. For example, our model predicts reduced LAI under nitrogen limitation (Fig. S7) based on first principles, but it is incidentally the only mechanism that reduces the whole-canopy photosynthesis rate in our model. There are mechanisms that increase nitrogen use efficiency at the expense of carbon by increasing LMA and therefore leaf longevity to maintain high LAI and high canopy-level photosynthesis rates (Aerts, 1995, 1999; Aerts and Chapin, 1999; Givnish, 2002). We did not include these mechanisms in our simulations, although they are well developed in this model (Weng et al., 2017), because we wished to focus on the strategy of allocation. The clear descriptions of our model's assumptions, its traceable processes, and inclusion of the tradeoffs involved in aboveground and belowground competition provide a useful benchmark from which to incorporate additional mechanisms and tradeoffs.
4.2 Root over-proliferation vs. wood allocation
The allocation strategy that maximizes site vegetation biomass allocates very little to fine roots (Figs. 3 and S1). In contrast, the competitively optimal strategy allocates more carbon to fine roots, termed “fine-root over-proliferation” in the literature (Gersani et al., 2001; McNickle and Dybzinski, 2013; O'Brien et al., 2005). It is the result of a competitive “arms race”: while increasing fine root area under elevated [CO2] does not result in more nitrogen for an individual, failing to do so would cede some of that individual's nitrogen to its neighbors. Because most nitrogen uptake is via mass flow and diffusion (Oyewole et al., 2017) and because both of these mechanisms depend on sink strength, individuals with relatively greater fine root mass than their neighbors take a greater share of nitrogen, as was recently demonstrated empirically (Dybzinski et al., 2019; Kulmatiski et al., 2017). Thus, fine roots may over-proliferate for competitive reasons relative to lower optimal fine root mass in the hypothetical absence of an evolutionary history of competition (Craine, 2006; McNickle and Dybzinski, 2013). This may also explain why root C:N ratio is highly variable (Dybzinski et al., 2015; Luo et al., 2006; Nie et al., 2013): a high density of fine roots in soil may be more important than the high absorption ability of a single root in competing for soil nitrogen in the usually low mineral nitrogen soils.
Root over-proliferation is still controversial in experiments. For example, Gersani et al. (2001) and O'Brien et al. (2005) found that competing plants generated more roots than those growing in isolation, whereas McNickle and Brown (2014) found that competing plants generated comparable roots to those growing in isolation. Compared to modeled roots, real roots are far more adaptive and complex at modifying their growth patterns in response to soil nutrient and water dynamics (Hodge, 2009). The root growth strategies in response to competition also vary with species (Belter and Cahill, 2015). The mechanisms of self-recognition of inter- and intra-roots can also lead to varied behavior of root growth (Chen et al., 2012). However, all of the aforementioned studies considered only plastic root over-proliferation, where individuals produce more roots in the presence of other individuals than they do in isolation, analogous to stem elongation of crowded seedlings (Dudley and Schmitt, 1996). A portion of root over-proliferation may also be fixed, analogous to trees that still grow tall even when grown in isolation. Dybzinski et al. (2019) showed that plant community nitrogen uptake rate was independent of fine root mass in seedlings of numerous species, suggesting a high degree of fixed fine root over-proliferation. To improve root competition models, more detailed experiments that control root growth should be conducted to quantify the marginal benefits of roots in isolated, monoculture and polyculture environments.
At high soil nitrogen, height-structured competition for light (also a game-theoretic response, Falster and Westoby, 2003; Givnish, 1982) prevails and trees with greater relative allocation to trunks prevail. The balance between these two competitive priorities (fine roots vs. stems) can be observed in our model predictions as a shift from fine root allocation to wood allocation as soil nitrogen increases. The increases in the critical height (i.e. the context-dependent height of the shortest tree in canopy layer in the PPA) from low nitrogen to high nitrogen indicates a shift from the importance of competition for soil nitrogen to the importance of competition for light as ecosystem nitrogen increases (Fig. S8). Because the most competitive type shifts from high fine root allocation to low fine root allocation as ecosystem total nitrogen increases, increases in NPP and plant biomass across the nitrogen gradient are greater than the increases in NPP and plant biomass assuming allocation strategies in the absence of competition (Fig. 3). This greatly reduces the carbon cost of belowground competition as ecosystem total nitrogen increases. The decrease in the fraction of NPP allocated to leaves at elevated [CO2] (Fig. 6b) occurs because of increases in total NPP and nearly constant absolute NPP allocation to foliage (Fig. 6a).
4.3 Model complexity and uncertainty
Compared with the conventional pool-based vegetation models that use pools and fluxes to represent plant demographic processes at a land simulation unit (e.g., grid or patch), VDMs add two more layers of complexity. The first is the inclusion of stochastic birth and mortality processes of individuals (i.e., demographic processes). These processes allow the models to predict population dynamics and transient vegetation structure, such as size-structured distribution and crown organization (e.g., Moorcroft et al., 2001; Strigul et al., 2008). With changes in vegetation structure, allocation and mortality rates can change, generating a different carbon storage accumulation curve compared with those predicted by pool-based models where vegetation structure is not explicitly represented (e.g., Weng et al., 2015). The second is the simulated shift in dominant plant traits during succession due to the shifting of competitive outcomes among different PFTs, which changes the allocation between fast- and slow-turnover pools and thus the parameters of allocation and the residence time of carbon in the ecosystem.
Together, these mechanisms may alter long-term predictions of the terrestrial carbon cycle due to changes in PFT-based parameters (Dybzinski et al., 2011; Farrior et al., 2013; Weng et al., 2015). As described in the Introduction, current pool-based models can be described by a linear system of equations characterized by the key parameters of allocation, residence time and transfer coefficients (Eq. 1) with the rigid assumption of unchangeable plant types (Luo et al., 2012; Xia et al., 2013). In VDMs, however, allocation, residence time, leaf traits, phenology, mortality, plant forms and their responses to climate change are all strategies of competition whose success varies with the environmental conditions and the traits of the individuals they are competing against.
Many tradeoffs between plant traits can shift in response to environmental and biotic changes, limiting the applicability of varying a single trait, as we have in this study. For example, allocation, leaf traits, mycorrhizal types and nitrogen fixation can all change with ecosystem nitrogen availability (Menge et al., 2017; Ordoñez et al., 2009; Phillips et al., 2013; Vitousek et al., 2013). The unrealistic effects of model simplification can be corrected by adding important tradeoffs that are missing. For example, the positive feedback between root allocation and SOM decomposition plays a role in mitigating the effects of tragedies of the commons of root over-proliferation (e.g., Gersani et al., 2001; Zea-Cabrera et al., 2006). High root allocation increases the decomposition rate of SOM and the supply of mineral nitrogen because of the high turnover rate of root litter, which favors a strategy of high wood allocation and reduces the competitive optimal fine root allocation. This negative feedback indicates that the model structure is flexible and that we can incorporate correct mechanisms step by step to improve model prediction skills. Testing single strategies is still a necessary step to improving our understanding of the system and prediction skills of the models, though it could lead to unrealistic responses sometimes.
We found that model predictions can differ significantly in response to seemingly small variations in basic assumptions or quantitative relationships. For example, our model predicts that the ratio of plant biomass under elevated [CO2] relative to plant biomass under ambient [CO2] should increase with increasing nitrogen due to the shift of carbon allocation from fine roots to woody tissues. In contrast, the analytic model of Dybzinski et al. (2015) predicts that the ratio of plant biomass under elevated [CO2] relative to plant biomass under ambient [CO2] should be largely independent of total nitrogen because of an increasing shift in carbon allocation from long-lived, low-nitrogen wood to short-lived, high-nitrogen fine roots under elevated [CO2] and with increasing nitrogen. This significant difference between these two predictions traces back to differences in how fine root stoichiometry is handled in the two models. In the model of Dybzinski et al. (2015), the fine root C:N ratio is flexible and the marginal nitrogen uptake capacity per unit of carbon allocated to fine roots depends on its nitrogen concentration. Like the model presented here, the model of Dybzinski et al. (2015) predicts decreasing fine root mass with increasing nitrogen availability. Unlike the model presented here (which has constant fine root nitrogen concentration), the model of Dybzinski et al. (2015) predicts increasing fine root nitrogen concentration with increasing nitrogen availability. As a result, there is less nitrogen to allocate to wood as nitrogen increases in the model of Dybzinski et al. (2015) than there is in the model presented here. These countervailing factors even out the ratio of plant biomass under elevated [CO2] relative to plant biomass under ambient [CO2] across the nitrogen gradient in Dybzinski et al. (2015), whereas their absence amplifies this ratio with increasing nitrogen in the model presented here. Our ability to diagnose and understand this discrepancy highlights the utility of deploying closely related analytical and simulation models (Weng et al., 2017).
We conducted simulations only at one site for the purpose of exploring the general patterns of competitively optimal allocation strategies and their responses to elevated [CO2] at different nitrogen availabilities. We can speculate about shifts in the competitively optimal allocation strategy in different forest biomes by considering the effects of temperature on soil nitrogen supply via the SOM's decomposition rate and its positive effect on net nitrogen mineralization. For example, the SOM decomposition rate is usually high in warm regions and low in cold regions (Davidson and Janssens, 2006) assuming there are no water limitations and SOM is equilibrated with carbon input. According to our model, allocation to roots is high in low nitrogen supply conditions (cold regions) and low in high nitrogen supply conditions (warm regions). This pattern can be found from temperate to boreal forest zones (Cairns et al., 1997; Gower et al., 2001; Reich et al., 2014; Zadworny et al., 2016). Temperature also alters NPP, i.e., carbon supply: as temperature goes down, NPP decreases and nitrogen demand decreases, alleviating nitrogen limitation and leading to shifts of allocation to stems. Therefore, the differences in temperature effects on photosynthesis and SOM decomposition will determine competitive allocation strategy. Since SOM decomposition is more sensitive to temperature than gross primary production is at long-temporal and large spatial scales (Beer et al., 2010; Carey et al., 2016; Crowther et al., 2016), our model suggests that allocation will shift to wood in a warming world. Whether the carbon stored in that wood is enough to offset the carbon released from increasing soil respiration is a critical question.
Water is also a critical factor affecting allocation and its responses to elevated [CO2]. Low soil moisture usually leads to high allocation to roots (Poorter et al., 2012). Elevated CO2 can reduce transpiration (as found in our study as well, Figs. S9–S11) and therefore increase soil moisture, resulting in increases in allocation to stems and aboveground biomass (Walker et al., 2019). A game-theoretic modeling study using the PPA framework shows that the competitively optimal allocation strategy shifts to high wood allocation at elevated [CO2] in environments with water limitation (Farrior et al., 2015). This is the opposite of the elevated [CO2] effects on allocation in nitrogen-limited environments as simulated in this study. According to field experiments, fine root allocation is more responsive to nitrogen changes than it is to soil moisture changes (Canham et al., 1996; Poorter et al., 2012). Poorter et al. (2012) attribute the mechanisms to the optimal strategies in response to the relative stable nitrogen supply and stochastic water input in soil. The vertical distribution of roots and the contributions of roots in different layers to water and nitrogen uptake also suggest that the uptake of soil nutrients are dominant in shaping root system architecture (Chapman et al., 2012; Morris et al., 2017), though root growth and turnover are flexible and sensitive to nitrogen and water supply (Deak and Malamy, 2005; Linkohr et al., 2002; Pregitzer et al., 1993).
4.4 Common principles for allocation modeling and implications
As shown in model intercomparison studies, the mechanisms of modeling allocation differ very much, leading to high variation in their predictions (e.g., De Kauwe et al., 2014). Calibrating model parameters to fit data may not increase model predictive skill because data are often also highly variable. Franklin et al. (2012) suggest that in order to build realistic and predictive allocation models, we should correctly identify and implement fundamental principles. Our model predicts similar patterns to those predicted by the model of Valentine and Mäkelä (2012), which has very different processes of plant growth and allocation. However, these two models share fundamental principles, including (1) evolutionary or competitive optimization, (2) capped leaves and fine roots at given tree sizes, (3) structurally unlimited stem allocation (i.e., optimizing carbon use) because the woody tissues can serve as unlimited sink for surplus carbon, and (4) height–structure competition for light and root-mass-based competition for soil resources. Principles 2 and 3 are commonly used in models (De Kauwe et al., 2014; Jiang et al., 2019b). However, the different rules of implementing them (e.g., allometric equation, functional relationships, etc.) lead to highly varied predictions (as shown in De Kauwe et al., 2014), though model formulations may be very similar.
In competitively optimal models, such as this study and also Valentine and Mäkelä (2012), the competition processes generate similar emergent patterns by selecting those that can survive in competition, regardless of the details of those differences. The competition processes also make the details of allocation settings for a single PFT and their direct responses to elevated [CO2] less important because competition processes will select out the most competitive strategy from diverse strategies in response to changes in [CO2] and nitrogen. Our study and that of Valentine and Mäkelä (2012) posit a fundamental tradeoff between light competition and nitrogen competition via allocation based on insights gained from simpler models (e.g., Dybzinski et al., 2015; Mäkelä et al., 2008) for predicting allocation as an emergent property of competition. One advantage of building a model in this way is that the vegetation dynamics are predicted from first principles, rather than based on the correlations between vegetation properties and environmental conditions. With these first principles, the models can produce reasonable predictions, though the details of physiological and demographic processes vary among models.
For vegetation models designed to predict the effects of climate change, the important operational distinction is that the fundamental rules cannot or will not change as climate changes. Nor, presumably, will the underlying ecological and evolutionary processes change as climate changes. The emergent properties can change as climate changes, however, and the models built on the “scale-appropriate” unbreakable constraints and ecological and evolutionary processes will be able to accurately predict changes in emergent ecosystem properties (Weng et al., 2017). In our opinion, the scientific effort to build better models is better served by understanding unrealistic predictions than by “fixing” them with unreliable mechanisms when there is a lack of data or theory to make them consistent with observations. Validating assumptions and initial responses are critical, and the long-term responses can be validated via spatial patterns.
This modeling approach also demands improvement in model validation and benchmarking systems (Collier et al., 2018; Hoffman et al., 2017). As shown in this study, allocation responses to elevated CO2 at different nitrogen levels in monoculture runs are opposite to those in competitive allocation runs. For example, in monoculture runs, elevated [CO2] increases wood allocation and decreases fine root allocation at low nitrogen; whereas in competitive allocation runs elevated [CO2] leads to low wood allocation and high fine root allocation. Simply calibrating our model against short-term observational data may improve the agreement with observations but would not change the model's predictions because the model's predictions emerge from its fundamental assumptions.
Our study illustrates that including the competition processes for light and soil resources in a game-theoretic vegetation demographic model can substantially change the prediction of the contribution of ecosystems to the global carbon cycle. Allowing the model to explicitly track the competitive allocation strategies can generate significantly different ecosystem-level predictions (e.g., biomass and ecosystem carbon storage) than those of strategies in the absence of explicit competition. Building such a model requires differentiating between the unbreakable tradeoffs of plant traits and ecological processes from the emergent properties of ecosystems. Drawing on insights from closely related analytical models to develop and understand more complicated simulation models seems, to us, indispensable. Evaluating these models also requires an updated model benchmarking system that includes the metrics of competitive plant traits during the development of ecosystems and their responses to global change factors.
The model codes, simulated data and Python scripts used in this study are available from Github (https://github.com/wengensheng/BiomeE-Allocation, last access: 27 November 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-16-4577-2019-supplement.
All authors contributed to model design, results explanation and manuscript writing. EW and RD initially designed the simulation experiments. EW coded the model and implemented model runs and data analysis.
The authors declare that they have no conflict of interest.
The authors thank Benjamin Stocker, Martin De Kauwe and other two anonymous referees for their insightful comments that greatly improved this paper. We also thank the USDA Forest Service Northern Research Station, Carbon Mitigation Initiative at Princeton University, and the University of Texas at Austin for their support. Earth system modeling at GISS is supported by the NASA Modeling, Analysis, and Prediction Program, and resources supporting this work were provided by the NASA High‐End Computing Program through the NASA Center for Climate Simulation (NCCS) at Goddard Space Flight Center.
This research has been supported by the NASA Modeling, Analysis, and Prediction Program.
This paper was edited by Sönke Zaehle and reviewed by Benjamin Stocker, Martin De Kauwe and two anonymous referees.
Aber, J. D., Magill, A., Boone, R., Melillo, J. M., and Steudler, P.: Plant and Soil Responses to Chronic Nitrogen Additions at the Harvard Forest, Massachusetts, Ecol. Appl., 3, 156–166, https://doi.org/10.2307/1941798, 1993.
Aerts, R.: The advantages of being evergreen, Trends Ecol. Evol., 10, 402–407, https://doi.org/10.1016/S0169-5347(00)89156-9, 1995.
Aerts, R.: Interspecific competition in natural plant communities: mechanisms, trade-offs and plant-soil feedbacks, J. Exp. Bot., 50, 29–37, https://doi.org/10.1093/jxb/50.330.29, 1999.
Aerts, R. and Chapin, F. S.: The Mineral Nutrition of Wild Plants Revisited: A Re-evaluation of Processes and Patterns, in: Advances in Ecological Research, edited by: Fitter, A. H. and Raffaelli, D. G., 30, 1–67, Academic Press, Cambridge, MA, USA, 1999.
Arora, V. K. and Boer, G. J.: A parameterization of leaf phenology for the terrestrial ecosystem component of climate models, Global Chang. Biol., 11, 39–59, https://doi.org/10.1111/j.1365-2486.2004.00890.x, 2005.
Atkin, O. K. and Macherel, D.: The crucial role of plant mitochondria in orchestrating drought tolerance, Ann. Bot., 103, 581–597, https://doi.org/10.1093/aob/mcn094, 2009.
Barr, A. G., Ricciu, D. M., Schaefer, K., Richarson, A., Agarwal, D., Thornton, P. E., Davis, K., Jackson, B., Cook, R. B., Hollinger, D. Y., Van Ingen, C., Amiro, B., Andrews, A., Arain, M. A., Baldocchi, D., Black, T. A., Bolstad, P., Curtis, P., Desai, A., Dragoni, D., Flanagan, L., Gu, L., Katul, G., Law, B. E., Lafleur, P. M., Margolis, H., Matamala, R., Meyers, T., McCaughey, J. H., Monson, R., Munger, J. W., Oechel, W., Oren, R., Roulet, N. T., Torn, M., and Verma, S. B.: NACP Site: Tower Meteorology, Flux Observations with Uncertainty, and Ancillary Data, ORNL DAAC, Oak Ridge, Tennessee, USA, https://doi.org/10.3334/ornldaac/1178, 2013.
Beer, C., Reichstein, M., Tomelleri, E., Ciais, P., Jung, M., Carvalhais, N., Rodenbeck, C., Arain, M. A., Baldocchi, D., Bonan, G. B., Bondeau, A., Cescatti, A., Lasslop, G., Lindroth, A., Lomas, M., Luyssaert, S., Margolis, H., Oleson, K. W., Roupsard, O., Veenendaal, E., Viovy, N., Williams, C., Woodward, F. I., and Papale, D.: Terrestrial Gross Carbon Dioxide Uptake: Global Distribution and Covariation with Climate, Science, 329, 834–838, https://doi.org/10.1126/science.1184984, 2010.
Belter, P. R. and Cahill, J. F.: Disentangling root system responses to neighbours: identification of novel root behavioural strategies, AoB Plants, 7, plv059, https://doi.org/10.1093/aobpla/plv059, 2015.
Bloom, A. A., Exbrayat, J.-F., van der Velde, I. R., Feng, L., and Williams, M.: The decadal state of the terrestrial carbon cycle: Global retrievals of terrestrial carbon allocation, pools, and residence times, P. Natl. Acad. Sci. USA, 113, 1285–1290, https://doi.org/10.1073/pnas.1515160113, 2016.
Cairns, M. A., Brown, S., Helmer, E. H., and Baumgardner, G. A.: Root biomass allocation in the world's upland forests, Oecologia, 111, 1–11, https://doi.org/10.1007/s004420050201, 1997.
Canham, C. D., Berkowitz, A. R., Kelly, V. R., Lovett, G. M., Ollinger, S. V., and Schnurr, J.: Biomass allocation and multiple resource limitation in tree seedlings, Can. J. For. Res., 26, 1521–1530, https://doi.org/10.1139/x26-171, 1996.
Cannell, M. G. R. and Dewar, R. C.: Carbon Allocation in Trees: a Review of Concepts for Modelling, in: Advances in Ecological Research, 25, 59–104, Academic Press, Cambridge, MA, USA, 1994.
Carey, J. C., Tang, J., Templer, P. H., Kroeger, K. D., Crowther, T. W., Burton, A. J., Dukes, J. S., Emmett, B., Frey, S. D., Heskel, M. A., Jiang, L., Machmuller, M. B., Mohan, J., Panetta, A. M., Reich, P. B., Reinsch, S., Wang, X., Allison, S. D., Bamminger, C., Bridgham, S., Collins, S. L., de Dato, G., Eddy, W. C., Enquist, B. J., Estiarte, M., Harte, J., Henderson, A., Johnson, B. R., Larsen, K. S., Luo, Y., Marhan, S., Melillo, J. M., Peñuelas, J., Pfeifer-Meister, L., Poll, C., Rastetter, E., Reinmann, A. B., Reynolds, L. L., Schmidt, I. K., Shaver, G. R., Strong, A. L., Suseela, V., and Tietema, A.: Temperature response of soil respiration largely unaltered with experimental warming, P. Natl. Acad. Sci. USA, 113, 13797–13802, https://doi.org/10.1073/pnas.1605365113, 2016.
Chapman, N., Miller, A. J., Lindsey, K., and Whalley, W. R.: Roots, water, and nutrient acquisition: let's get physical, Trends Plant Sci., 17, 701–710, https://doi.org/10.1016/j.tplants.2012.08.001, 2012.
Chen, B. J. W., During, H. J., and Anten, N. P. R.: Detect thy neighbor: Identity recognition at the root level in plants, Plant Sci., 195, 157–167, https://doi.org/10.1016/j.plantsci.2012.07.006, 2012.
Cheng, W.: Rhizosphere priming effect: Its functional relationships with microbial turnover, evapotranspiration, and C-N budgets, Soil Biol. Biochem., 41, 1795–1801, https://doi.org/10.1016/j.soilbio.2008.04.018, 2009.
Cheng, W., Parton, W. J., Gonzalez-Meler, M. A., Phillips, R., Asao, S., McNickle, G. G., Brzostek, E., and Jastrow, J. D.: Synthesis and modeling perspectives of rhizosphere priming, New Phytol., 201, 31–44, https://doi.org/10.1111/nph.12440, 2014.
Collier, N., Hoffman, F. M., Lawrence, D. M., Keppel-Aleks, G., Koven, C. D., Riley, W. J., Mu, M., and Randerson, J. T.: The International Land Model Benchmarking (ILAMB) System: Design, Theory, and Implementation, J. Adv. Model Earth Sy., 10, 2731–2754, https://doi.org/10.1029/2018MS001354, 2018.
Compton, J. E. and Boone, R. D.: Long-Term Impacts of Agriculture on Soil Carbon and Nitrogen in New England Forests, Ecology, 81, 2314, https://doi.org/10.2307/177117, 2000.
Craine, J. M.: Competition for Nutrients and Optimal Root Allocation, Plant Soil, 285, 171–185, https://doi.org/10.1007/s11104-006-9002-x, 2006.
Crowther, T. W., Todd-Brown, K. E. O., Rowe, C. W., Wieder, W. R., Carey, J. C., Machmuller, M. B., Snoek, B. L., Fang, S., Zhou, G., Allison, S. D., Blair, J. M., Bridgham, S. D., Burton, A. J., Carrillo, Y., Reich, P. B., Clark, J. S., Classen, A. T., Dijkstra, F. A., Elberling, B., Emmett, B. A., Estiarte, M., Frey, S. D., Guo, J., Harte, J., Jiang, L., Johnson, B. R., Kröel-Dulay, G., Larsen, K. S., Laudon, H., Lavallee, J. M., Luo, Y., Lupascu, M., Ma, L. N., Marhan, S., Michelsen, A., Mohan, J., Niu, S., Pendall, E., Peñuelas, J., Pfeifer-Meister, L., Poll, C., Reinsch, S., Reynolds, L. L., Schmidt, I. K., Sistla, S., Sokol, N. W., Templer, P. H., Treseder, K. K., Welker, J. M., and Bradford, M. A.: Quantifying global soil carbon losses in response to warming, Nature, 540, 104–108, https://doi.org/10.1038/nature20150, 2016.
Cuny, H. E., Rathgeber, C. B. K., Lebourgeois, F., Fortin, M., and Fournier, M.: Life strategies in intra-annual dynamics of wood formation: example of three conifer species in a temperate forest in north-east France, Tree Physiol., 32, 612–625, https://doi.org/10.1093/treephys/tps039, 2012.
Curtis, P. S., Hanson, P. J., Bolstad, P., Barford, C., Randolph, J. C., Schmid, H. P., and Wilson, K. B.: Biometric and eddy-covariance based estimates of annual carbon storage in five eastern North American deciduous forests, Agric. Forest Meteorol., 113, 3–19, https://doi.org/10.1016/S0168-1923(02)00099-0, 2002.
Davidson, E. A. and Janssens, I. A.: Temperature sensitivity of soil carbon decomposition and feedbacks to climate change, Nature, 440, 165–173, https://doi.org/10.1038/nature04514, 2006.
Deak, K. I. and Malamy, J.: Osmotic regulation of root system architecture, Plant J., 43, 17–28, https://doi.org/10.1111/j.1365-313X.2005.02425.x, 2005.
DeAngelis, D. L., Ju, S., Liu, R., Bryant, J. P., and Gourley, S. A.: Plant allocation of carbon to defense as a function of herbivory, light and nutrient availability, Theor. Ecol., 5, 445–456, https://doi.org/10.1007/s12080-011-0135-z, 2012.
De Kauwe, M. G., Medlyn, B. E., Zaehle, S., Walker, A. P., Dietze, M. C., Wang, Y.-P., Luo, Y., Jain, A. K., El-Masri, B., Hickler, T., Wårlind, D., Weng, E., Parton, W. J., Thornton, P. E., Wang, S., Prentice, I. C., Asao, S., Smith, B., McCarthy, H. R., Iversen, C. M., Hanson, P. J., Warren, J. M., Oren, R., and Norby, R. J.: Where does the carbon go? A model-data intercomparison of vegetation carbon allocation and turnover processes at two temperate forest free-air CO2 enrichment sites, New Phytol., 203, 883–899, https://doi.org/10.1111/nph.12847, 2014.
Douma, J. C., de Haan, M. W. A., Aerts, R., Witte, J.-P. M., and van Bodegom, P. M.: Succession-induced trait shifts across a wide range of NW European ecosystems are driven by light and modulated by initial abiotic conditions: Trait shifts during succession, J. Ecol., 100, 366–380, https://doi.org/10.1111/j.1365-2745.2011.01932.x, 2012.
Drake, J. E., Gallet-Budynek, A., Hofmockel, K. S., Bernhardt, E. S., Billings, S. A., Jackson, R. B., Johnsen, K. S., Lichter, J., McCarthy, H. R., McCormack, M. L., Moore, D. J. P., Oren, R., Palmroth, S., Phillips, R. P., Pippen, J. S., Pritchard, S. G., Treseder, K. K., Schlesinger, W. H., DeLucia, E. H., and Finzi, A. C.: Increases in the flux of carbon belowground stimulate nitrogen uptake and sustain the long-term enhancement of forest productivity under elevated CO2, Ecol. Lett., 14, 349–357, https://doi.org/10.1111/j.1461-0248.2011.01593.x, 2011.
Dudley, S. A. and Schmitt, J.: Testing the adaptive plasticity hypothesis: density-dependent selection on manipulated stem length in Impatiens capensis, J. Ecol., 147, 445–465, https://doi.org/10.1086/285860, 1996.
Dybzinski, R., Farrior, C., Wolf, A., Reich, P. B., and Pacala, S. W.: Evolutionarily Stable Strategy Carbon Allocation to Foliage, Wood, and Fine Roots in Trees Competing for Light and Nitrogen: An Analytically Tractable, Individual-Based Model and Quantitative Comparisons to Data, Am. Nat., 177, 153–166, https://doi.org/10.1086/657992, 2011.
Dybzinski, R., Farrior, C. E., and Pacala, S. W.: Increased forest carbon storage with increased atmospheric CO2 despite nitrogen limitation: a game-theoretic allocation model for trees in competition for nitrogen and light, Global Change Biol., 21, 1182–1196, https://doi.org/10.1111/gcb.12783, 2015.
Dybzinski, R., Kelvakis, A., McCabe, J., Panock, S., Anuchitlertchon, K., Vasarhelyi, L., Luke McCormack, M., McNickle, G. G., Poorter, H., Trinder, C., and Farrior, C. E.: How are nitrogen availability, fine-root mass, and nitrogen uptake related empirically? Implications for models and theory, Global Change Biol., 25, 885–899, https://doi.org/10.1111/gcb.14541, 2019.
Emanuel, W. R. and Killough, G. G.: Modeling terrestrial ecosystems in the global carbon cycle with Shifts in carbon storage capacity by land-use change, Ecology, 65, 970–983, https://doi.org/10.2307/1938069, 1984.
Eriksson, E.: Compartment Models and Reservoir Theory, Annu. Rev. Ecol. Syst., 2, 67–84, https://doi.org/10.1146/annurev.es.02.110171.000435, 1971.
Falster, D. and Westoby, M.: Plant height and evolutionary games, Trends Ecol. Evol., 18, 337–343, https://doi.org/10.1016/S0169-5347(03)00061-2, 2003.
Farrior, C. E., Dybzinski, R., Levin, S. A., and Pacala, S. W.: Competition for Water and Light in Closed-Canopy Forests: A Tractable Model of Carbon Allocation with Implications for Carbon Sinks, J. Ecol., 181, 314–330, https://doi.org/10.1086/669153, 2013.
Farrior, C. E., Rodriguez-Iturbe, I., Dybzinski, R., Levin, S. A., and Pacala, S. W.: Decreased water limitation under elevated CO2 amplifies potential for forest carbon sinks, P. Natl. Acad. Sci. USA, 112, 7213–7218, https://doi.org/10.1073/pnas.1506262112, 2015.
Fatichi, S., Pappas, C., Zscheischler, J., and Leuzinger, S.: Modelling carbon sources and sinks in terrestrial vegetation, New Phytol., 221, 652–668, https://doi.org/10.1111/nph.15451, 2019.
Fisher, R. A., Koven, C. D., Anderegg, W. R. L., Christoffersen, B. O., Dietze, M. C., Farrior, C. E., Holm, J. A., Hurtt, G. C., Knox, R. G., Lawrence, P. J., Lichstein, J. W., Longo, M., Matheny, A. M., Medvigy, D., Muller-Landau, H. C., Powell, T. L., Serbin, S. P., Sato, H., Shuman, J. K., Smith, B., Trugman, A. T., Viskari, T., Verbeeck, H., Weng, E., Xu, C., Xu, X., Zhang, T., and Moorcroft, P. R.: Vegetation demographics in Earth System Models: A review of progress and priorities, Global Change Biol., 24, 35–54, https://doi.org/10.1111/gcb.13910, 2018.
Franklin, O., Johansson, J., Dewar, R. C., Dieckmann, U., McMurtrie, R. E., Brannstrom, A., and Dybzinski, R.: Modeling carbon allocation in trees: a search for principles, Tree Physiol., 32, 648–666, https://doi.org/10.1093/treephys/tpr138, 2012.
Friend, A. D., Arneth, A., Kiang, N. Y., Lomas, M., Ogee, J., Roedenbeckk, C., Running, S. W., Santaren, J.-D., Sitch, S., Viovy, N., Woodward, F. I., and Zaehle, S.: FLUXNET and modelling the global carbon cycle, Global Change Biol., 13, 610–633, https://doi.org/10.1111/j.1365-2486.2006.01223.x, 2007.
Gerber, S., Hedin, L. O., Oppenheimer, M., Pacala, S. W., and Shevliakova, E.: Nitrogen cycling and feedbacks in a global dynamic land model, Global Biogeochem. Cycles, 24, https://doi.org/10.1029/2008GB003336, 2010.
Gersani, M., Brown, J. S., O'Brien, E. E., Maina, G. M., and Abramsky, Z.: Tragedy of the commons as a result of root competition, J. Ecol., 89, 660–669, https://doi.org/10.1046/j.0022-0477.2001.00609.x, 2001.
Givnish, T.: Adaptive significance of evergreen vs. deciduous leaves: solving the triple paradox, Silva Fenn., 36, 703–743, https://doi.org/10.14214/sf.535, 2002.
Givnish, T. J.: On the Adaptive Significance of Leaf Height in Forest Herbs, J. Ecol., 120, 353–381, https://doi.org/10.1086/283995, 1982.
Goldschmidt, E. E. and Huber, S. C.: Regulation of Photosynthesis by End-Product Accumulation in Leaves of Plants Storing Starch, Sucrose, and Hexose Sugars, Plant Physiol., 99, 1443–1448, https://doi.org/10.1104/pp.99.4.1443, 1992.
Gower, S. T., Krankina, O., Olson, R. J., Apps, M., Linder, S., and Wang, C.: Net Primary Production and Carbon Allocation Patterns of Boreal Forest Ecosystems, Ecol. Appl., 11, 1395–1411, https://doi.org/10.1890/1051-0761(2001)011[1395:NPPACA]2.0.CO;2, 2001.
Grams, T. E. E. and Andersen, C. P.: Competition for Resources in Trees: Physiological Versus Morphological Plasticity, in: Progress in Botany, edited by: Esser, K., Löttge, U., Beyschlag, W., and Murata, J., pp. 356–381, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007.
Haverd, V., Smith, B., Raupach, M., Briggs, P., Nieradzik, L., Beringer, J., Hutley, L., Trudinger, C. M., and Cleverly, J.: Coupling carbon allocation with leaf and root phenology predicts tree–grass partitioning along a savanna rainfall gradient, Biogeosciences, 13, 761–779, https://doi.org/10.5194/bg-13-761-2016, 2016.
Hibbs, D. E.: Forty Years of Forest Succession in Central New England, Ecology, 64, 1394–1401, https://doi.org/10.2307/1937493, 1983.
Hodge, A.: Root decisions, Plant Cell Environ., 32, 628–640, https://doi.org/10.1111/j.1365-3040.2008.01891.x, 2009.
Hoffman, F. M., Koven, C. D., Keppel-Aleks, G., Lawrence, D. M., Riley, W. J., Randerson, J. T., Ahlström, A., Abramowitz, G., Baldocchi, D. D., Best, M. J., Bond-Lamberty, B., De Kauwe, M. G., Denning, A. S., Desai, A. R., Eyring, V., Fisher, J. B., Fisher, R. A., Gleckler, P. J., Huang, M., Hugelius, G., Jain, A. K., Kiang, N. Y., Kim, H., Koster, R. D., Kumar, S. V., Li, H., Luo, Y., Mao, J., McDowell, N. G., Mishra, U., Moorcroft, P. R., Pau, G. S. H., Ricciuto, D. M., Schaefer, K., Schwalm, C. R., Serbin, S. P., Shevliakova, E., Slater, A. G., Tang, J., Williams, M., Xia, J., Xu, C., Joseph, R., and Koch, D.: 2016 International Land Model Benchmarking (ILAMB) Workshop Report, USDOE Office of Science, Washington, D.C., 2017.
Iversen, C. M.: Digging deeper: fine-root responses to rising atmospheric CO2 concentration in forested ecosystems, New Phytol., 186, 346–357, https://doi.org/10.1111/j.1469-8137.2009.03122.x, 2010.
Jackson, R. B., Cook, C. W., Pippen, J. S., and Palmer, S. M.: Increased belowground biomass and soil CO2 fluxes after a decade of carbon dioxide enrichment in a warm-temperate forest, Ecology, 90, 3352–3366, https://doi.org/10.1890/08-1609.1, 2009.
Jenkins, J. C., Chojnacky, D. C., Heath, L. S., and Birdsey, R. A.: National-Scale Biomass Estimators for United States Tree Species, Forest Sci., 49, 12–35, https://doi.org/10.1093/forestscience/49.1.12, 2003.
Jiang, M., Medlyn, B. E., Drake, J. E., Duursma, R. A., Anderson, I. C., Barton, C. V. M., Boer, M. M., Carrillo, Y., Castañeda-Gómez, L., Collins, L., Crous, K. Y., De Kauwe, M. G., Emmerson, K. M., Facey, S. L., Gherlenda, A. N., Gimeno, T. E., Hasegawa, S., Johnson, S. N., Macdonald, C. A., Mahmud, K., Moore, B. D., Nazaries, L., Nielsen, U. N., Noh, N. J., Ochoa-Hueso, R., Pathare, V. S., Pendall, E., Pineiro, J., Powell, J. R., Power, S. A., Reich, P. B., Renchon, A. A., Riegler, M., Rymer, P., Salomón, R. L., Singh, B. K., Smith, B., Tjoelker, M. G., Walker, J. K. M., Wujeska-Klause, A., Yang, J., Zaehle, S., and Ellsworth, D. S.: The fate of carbon in a mature forest under carbon dioxide enrichment, BioRxiv, https://doi.org/10.1101/696898, 2019a.
Jiang, M., Zaehle, S., De Kauwe, M. G., Walker, A. P., Caldararu, S., Ellsworth, D. S., and Medlyn, B. E.: The quasi-equilibrium framework revisited: analyzing long-term CO2 enrichment responses in plant–soil models, Geosci. Model Dev., 12, 2069–2089, https://doi.org/10.5194/gmd-12-2069-2019, 2019b.
Keenan, T. F., Davidson, E. A., Munger, J. W., and Richardson, A. D.: Rate my data: quantifying the value of ecological data for the development of models of the terrestrial carbon cycle, Ecol. Appl., 23, 273–286, https://doi.org/10.1890/12-0747.1, 2013.
Körner, C.: Plant CO2 responses: an issue of definition, time and resource supply, New Phytol, 172, 393–411, https://doi.org/10.1111/j.1469-8137.2006.01886.x, 2006.
Koven, C. D., Chambers, J. Q., Georgiou, K., Knox, R., Negron-Juarez, R., Riley, W. J., Arora, V. K., Brovkin, V., Friedlingstein, P., and Jones, C. D.: Controls on terrestrial carbon feedbacks by productivity versus turnover in the CMIP5 Earth System Models, Biogeosciences, 12, 5211–5228, https://doi.org/10.5194/bg-12-5211-2015, 2015.
Krinner, G., Viovy, N., de Noblet-Ducoudré, N., Ogée, J., Polcher, J., Friedlingstein, P., Ciais, P., Sitch, S., and Prentice, I. C.: A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system, Global Biogeochem. Cycles, 19, GB1015, https://doi.org/10.1029/2003GB002199, 2005.
Kulmatiski, A., Adler, P. B., Stark, J. M., and Tredennick, A. T.: Water and nitrogen uptake are better associated with resource availability than root biomass, Ecosphere, 8, e01738, https://doi.org/10.1002/ecs2.1738, 2017.
Lacointe, A.: Carbon allocation among tree organs: A review of basic processes and representation in functional-structural tree models, Ann. For. Sci., 57, 521–533, https://doi.org/10.1051/forest:2000139, 2000.
Leuning, R., Kelliher, F. M., Pury, D. G. G., and Schulze, E.-D.: Leaf nitrogen, photosynthesis, conductance and transpiration: scaling from leaves to canopies, Plant Cell Environ, 18, 1183–1200, https://doi.org/10.1111/j.1365-3040.1995.tb00628.x, 1995.
Linkohr, B. I., Williamson, L. C., Fitter, A. H., and Leyser, H. M. O.: Nitrate and phosphate availability and distribution have different effects on root system architecture of Arabidopsis, Plant J., 29, 751–760, https://doi.org/10.1046/j.1365-313X.2002.01251.x, 2002.
Litton, C., Ryan, M., Knight, D., and Stahl, P.: Soil-surface carbon dioxide efflux and microbial biomass in relation to tree density 13 years after a stand replacing fire in a lodgepole pine ecosystem, Global Change Biol., 9, 680–696, https://doi.org/10.1046/j.1365-2486.2003.00626.x, 2003.
Litton, C. M., Raich, J. W., and Ryan, M. G.: Carbon allocation in forest ecosystems, Global Change Biol., 13, 2089–2109, https://doi.org/10.1111/j.1365-2486.2007.01420.x, 2007.
Luo, Y. and Weng, E.: Dynamic disequilibrium of the terrestrial carbon cycle under global change, Trends Ecol. Evol., 26, 96–104, https://doi.org/10.1016/j.tree.2010.11.003, 2011.
Luo, Y., Hui, D., and Zhang, D.: Elevated CO2 stimulates net accumulations of carbon and nitrogen in land ecosystems: a meta-analysis, Ecology, 87, 53–63, 2006.
Luo, Y. Q., Wu, L. H., Andrews, J. A., White, L., Matamala, R., Schafer, K. V. R., and Schlesinger, W. H.: Elevated CO2 differentiates ecosystem carbon processes: Deconvolution analysis of Duke Forest FACE data, Ecol. Monogr., 71, 357–376, https://doi.org/10.1890/0012-9615(2001)071[0357:ECDECP]2.0.CO;2, 2001.
Luo, Y. Q., Randerson, J. T., Abramowitz, G., Bacour, C., Blyth, E., Carvalhais, N., Ciais, P., Dalmonech, D., Fisher, J. B., Fisher, R., Friedlingstein, P., Hibbard, K., Hoffman, F., Huntzinger, D., Jones, C. D., Koven, C., Lawrence, D., Li, D. J., Mahecha, M., Niu, S. L., Norby, R., Piao, S. L., Qi, X., Peylin, P., Prentice, I. C., Riley, W., Reichstein, M., Schwalm, C., Wang, Y. P., Xia, J. Y., Zaehle, S., and Zhou, X. H.: A framework for benchmarking land models, Biogeosciences, 9, 3857–3874, https://doi.org/10.5194/bg-9-3857-2012, 2012.
Magill, A. H., Aber, J. D., Currie, W. S., Nadelhoffer, K. J., Martin, M. E., McDowell, W. H., Melillo, J. M., and Steudler, P.: Ecosystem response to 15 years of chronic nitrogen additions at the Harvard Forest LTER, Massachusetts, USA, For. Ecol. Manage., 196, 7–28, https://doi.org/10.1016/j.foreco.2004.03.033, 2004.
Mäkelä, A., Valentine, H. T., and Helmisaari, H.-S.: Optimal co-allocation of carbon and nitrogen in a forest stand at steady state, New Phytol., 180, 114–123, https://doi.org/10.1111/j.1469-8137.2008.02558.x, 2008.
Manzoni, S., Trofymow, J. A., Jackson, R. B., and Porporato, A.: Stoichiometric controls on carbon, nitrogen, and phosphorus dynamics in decomposing litter, Ecol. Monogr., 80, 89–106, 2010.
Martin, A. R., Gezahegn, S., and Thomas, S. C.: Variation in carbon and nitrogen concentration among major woody tissue types in temperate trees, Can. J. For. Res., 45, 744–757, https://doi.org/10.1139/cjfr-2015-0024, 2015.
McDowell, N., Barnard, H., Bond, B., Hinckley, T., Hubbard, R., Ishii, H., Köstner, B., Magnani, F., Marshall, J., Meinzer, F., Phillips, N., Ryan, M., and Whitehead, D.: The relationship between tree height and leaf area: sapwood area ratio, Oecologia, 132, 12–20, https://doi.org/10.1007/s00442-002-0904-x, 2002.
McGill, B. J. and Brown, J. S.: Evolutionary Game Theory and Adaptive Dynamics of Continuous Traits, Annu. Rev. Ecol. Evol. Syst., 38, 403–435, https://doi.org/10.1146/annurev.ecolsys.36.091704.175517, 2007.
McMurtrie, R. E., Iversen, C. M., Dewar, R. C., Medlyn, B. E., Näsholm, T., Pepper, D. A., and Norby, R. J.: Plant root distributions and nitrogen uptake predicted by a hypothesis of optimal root foraging, Ecol. Evol., 2, 1235–1250, https://doi.org/10.1002/ece3.266, 2012.
McNickle, G. G. and Brown, J. S.: An ideal free distribution explains the root production of plants that do not engage in a tragedy of the commons game, edited by: Schwinning, S., J. Ecol., 102, 963–971, https://doi.org/10.1111/1365-2745.12259, 2014.
McNickle, G. G. and Dybzinski, R.: Game theory and plant ecology, edited by: Klironomos, J., Ecol. Lett., 16, 545–555, https://doi.org/10.1111/ele.12071, 2013.
Melillo, J. M., Butler, S., Johnson, J., Mohan, J., Steudler, P., Lux, H., Burrows, E., Bowles, F., Smith, R., Scott, L., Vario, C., Hill, T., Burton, A., Zhou, Y.-M., and Tang, J.: Soil warming, carbon-nitrogen interactions, and forest carbon budgets, P. Natl. Acad. Sci. USA, 108, 9508–9512, https://doi.org/10.1073/pnas.1018189108, 2011.
Menge, D. N. L., Batterman, S. A., Hedin, L. O., Liao, W., Pacala, S. W., and Taylor, B. N.: Why are nitrogen-fixing trees rare at higher compared to lower latitudes?, Ecology, 98, 3127–3140, https://doi.org/10.1002/ecy.2034, 2017.
Michelot, A., Simard, S., Rathgeber, C., Dufrene, E., and Damesin, C.: Comparing the intra-annual wood formation of three European species (Fagus sylvatica, Quercus petraea and Pinus sylvestris) as related to leaf phenology and non-structural carbohydrate dynamics, Tree Physiol., 32, 1033–1045, https://doi.org/10.1093/treephys/tps052, 2012.
Montané, F., Fox, A. M., Arellano, A. F., MacBean, N., Alexander, M. R., Dye, A., Bishop, D. A., Trouet, V., Babst, F., Hessl, A. E., Pederson, N., Blanken, P. D., Bohrer, G., Gough, C. M., Litvak, M. E., Novick, K. A., Phillips, R. P., Wood, J. D., and Moore, D. J. P.: Evaluating the effect of alternative carbon allocation schemes in a land surface model (CLM4.5) on carbon fluxes, pools, and turnover in temperate forests, Geosci. Model Dev., 10, 3499–3517, https://doi.org/10.5194/gmd-10-3499-2017, 2017.
Moorcroft, P. R., Hurtt, G. C., and Pacala, S. W.: A method for scaling vegetation dynamics: The ecosystem demography model (ED), Ecol. Monogr., 71, 557–585, https://doi.org/10.1890/0012-9615(2001)071[0557:AMFSVD]2.0.CO;2, 2001.
Morris, E. C., Griffiths, M., Golebiowska, A., Mairhofer, S., Burr-Hersey, J., Goh, T., Wangenheim, D. von, Atkinson, B., Sturrock, C. J., Lynch, J. P., Vissenberg, K., Ritz, K., Wells, D. M., Mooney, S. J., and Bennett, M. J.: Shaping 3D Root System Architecture, Curr. Biol., 27, R919–R930, https://doi.org/10.1016/j.cub.2017.06.043, 2017.
Nie, M., Lu, M., Bell, J., Raut, S., and Pendall, E.: Altered root traits due to elevated CO2: a meta-analysis: Root traits at elevated CO2, Glob. Ecol. Biogeogr., 22, 1095–1105, https://doi.org/10.1111/geb.12062, 2013.
Norby, R. J. and Zak, D. R.: Ecological Lessons from Free-Air CO2 Enrichment (FACE) Experiments, Annu. Rev. Ecol. Evol. Syst., 42, 181–203, https://doi.org/10.1146/annurev-ecolsys-102209-144647, 2011.
Norby, R. J., Sholtis, J. D., Gunderson, C. A., and Jawdy, S. S.: Leaf dynamics of a deciduous forest canopy: no response to elevated CO2, Oecologia, 136, 574–584, https://doi.org/10.1007/s00442-003-1296-2, 2003.
O'Brien, E. E., Gersani, M., and Brown, J. S.: Root proliferation and seed yield in response to spatial heterogeneity of below-ground competition, New Phytol., 168, 401–412, https://doi.org/10.1111/j.1469-8137.2005.01520.x, 2005.
Ordoñez, J. C., van Bodegom, P. M., Witte, J.-P. M., Wright, I. J., Reich, P. B., and Aerts, R.: A global study of relationships between leaf traits, climate and soil measures of nutrient fertility, Glob. Ecol. Biogeogr., 18, 137–149, https://doi.org/10.1111/j.1466-8238.2008.00441.x, 2009.
Oyewole, O. A., Inselsbacher, E., Näsholm, T., and Jämtgård, S.: Incorporating mass flow strongly promotes N flux rates in boreal forest soils, Soil Biol. Biochem., 114, 263–269, https://doi.org/10.1016/j.soilbio.2017.07.021, 2017.
Pappas, C., Fatichi, S., and Burlando, P.: Modeling terrestrial carbon and water dynamics across climatic gradients: does plant trait diversity matter?, New Phytol., 209, 137–151, https://doi.org/10.1111/nph.13590, 2016.
Parton, W., Schimel, D., Cole, C., and Ojima, D.: Analysis of factors controlling soil organic matter levels in Great Plains grasslands, Soil Sci. Soc. Am. J., 51, 1173–1179, https://doi.org/10.2136/sssaj1987.03615995005100050015x, 1987.
Phillips, R. P., Finzi, A. C., and Bernhardt, E. S.: Enhanced root exudation induces microbial feedbacks to N cycling in a pine forest under long-term CO2 fumigation, Ecol. Lett., 14, 187–194, https://doi.org/10.1111/j.1461-0248.2010.01570.x, 2011.
Phillips, R. P., Brzostek, E., and Midgley, M. G.: The mycorrhizal-associated nutrient economy: a new framework for predicting carbon-nutrient couplings in temperate forests, New Phytol., 199, 41–51, https://doi.org/10.1111/nph.12221, 2013.
Plomion, C., Leprovost, G., and Stokes, A.: Wood Formation in Trees, Plant Physiol., 127, 1513–1523, https://doi.org/10.1104/pp.010816, 2001.
Poorter, H., Niklas, K. J., Reich, P. B., Oleksyn, J., Poot, P., and Mommer, L.: Biomass allocation to leaves, stems and roots: meta-analyses of interspecific variation and environmental control: Tansley review, New Phytol., 193, 30–50, https://doi.org/10.1111/j.1469-8137.2011.03952.x, 2012.
Post, W. M., Pastor, J., Zinke, P. J., and Stangenberger, A. G.: Global patterns of soil nitrogen storage, Nature, 317, 613–616, https://doi.org/10.1038/317613a0, 1985.
Pregitzer, K. S., Hendrick, R. L., and Fogel, R.: The demography of fine roots in response to patches of water and nitrogen, New Phytol., 125, 575–580, https://doi.org/10.1111/j.1469-8137.1993.tb03905.x, 1993.
Pregitzer, K. S., DeForest, J. L., Burton, A. J., Allen, M. F., Ruess, R. W., and Hendrick, R. L.: Fine Root Architecture of Nine North American Trees, Ecol. Monogr., 72, 293, https://doi.org/10.2307/3100029, 2002.
Raich, J., Rastetter, E. B., Melillo, J. M., Kicklighter, D. W., Steudler, P. A., Peterson, B. J., Grace, A., Moore, B., and Vorosmary, C. J.: Potential Net Primary Productivity in South America: Application of a Global Model, Ecol. Appl., 1, 399–429, https://doi.org/10.2307/1941899, 1991.
Randerson, J., Thompson, M., Conway, T., Fung, I., and Field, C.: The contribution of terrestrial sources and sinks to trends in the seasonal cycle of atmospheric carbon dioxide, Global Biogeochem. Cycles, 11, 535–560, https://doi.org/10.1029/97GB02268, 1997.
Reich, P. B., Luo, Y., Bradford, J. B., Poorter, H., Perry, C. H., and Oleksyn, J.: Temperature drives global patterns in forest biomass distribution in leaves, stems, and roots, P. Natl. Acad. Sci. USA, 111, 13721–13726, https://doi.org/10.1073/pnas.1216053111, 2014.
Savage, K. E., Parton, W. J., Davidson, E. A., Trumbore, S. E., and Frey, S. D.: Long-term changes in forest carbon under temperature and nitrogen amendments in a temperate northern hardwood forest, Global Change Biol., 19, 2389–2400, https://doi.org/10.1111/gcb.12224, 2013.
Scheiter, S. and Higgins, S. I.: Impacts of climate change on the vegetation of Africa: an adaptive dynamic vegetation modelling approach, Global Change Biol., 15, 2224–2246, https://doi.org/10.1111/j.1365-2486.2008.01838.x, 2009.
Scheiter, S., Langan, L., and Higgins, S. I.: Next-generation dynamic global vegetation models: learning from community ecology, New Phytol., 198, 957–969, https://doi.org/10.1111/nph.12210, 2013.
Schmidt, G. A., Kelley, M., Nazarenko, L., Ruedy, R., Russell, G. L., Aleinov, I., Bauer, M., Bauer, S. E., Bhat, M. K., Bleck, R., Canuto, V., Chen, Y.-H., Cheng, Y., Clune, T. L., Del Genio, A., de Fainchtein, R., Faluvegi, G., Hansen, J. E., Healy, R. J., Kiang, N. Y., Koch, D., Lacis, A. A., LeGrande, A. N., Lerner, J., Lo, K. K., Matthews, E. E., Menon, S., Miller, R. L., Oinas, V., Oloso, A. O., Perlwitz, J. P., Puma, M. J., Putman, W. M., Rind, D., Romanou, A., Sato, M., Shindell, D. T., Sun, S., Syed, R. A., Tausnev, N., Tsigaridis, K., Unger, N., Voulgarakis, A., Yao, M.-S., and Zhang, J.: Configuration and assessment of the GISS ModelE2 contributions to the CMIP5 archive, J. Adv. Model Earth Sy., 6, 141–184, https://doi.org/10.1002/2013MS000265, 2014.
Shevliakova, E., Pacala, S. W., Malyshev, S., Hurtt, G. C., Milly, P. C. D., Caspersen, J. P., Sentman, L. T., Fisk, J. P., Wirth, C., and Crevoisier, C.: Carbon cycling under 300 years of land use change: Importance of the secondary vegetation sink, Global Biogeochem. Cycles, 23, GB2022, https://doi.org/10.1029/2007GB003176, 2009.
Shinozaki, K., Yoda, K., Hozumi, K., and Kira, T.: A quantitative analysis of plant form – the pipe model theory. I. Basic analyses, Jap. J. Ecol., 14, 97–105, 1964.
Sierra, C. A. and Mueller, M.: A general mathematical framework for representing soil organic matter dynamics, Ecol. Monogr., 85, 505–524, https://doi.org/10.1890/15-0361.1, 2015.
Sierra, C. A., Muller, M., Metzler, H., Manzoni, S., and Trumbore, S. E.: The muddle of ages, turnover, transit, and residence times in the carbon cycle, Global Change Biol., 23, 1763–1773, https://doi.org/10.1111/gcb.13556, 2017.
Sitch, S., Smith, B., Prentice, I. C., Arneth, A., Bondeau, A., Cramer, W., Kaplan, J. O., Levis, S., Lucht, W., Sykes, M. T., Thonicke, K., and Venevsky, S.: Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model, Global Change Biol., 9, 161–185, https://doi.org/10.1046/j.1365-2486.2003.00569.x, 2003.
Smith, A. R., Lukac, M., Bambrick, M., Miglietta, F., and Godbold, D. L.: Tree species diversity interacts with elevated CO2 to induce a greater root system response, Global Change Biol., 19, 217–228, https://doi.org/10.1111/gcb.12039, 2013.
Soriano, D., Orozco-Segovia, A., Márquez-Guzmán, J., Kitajima, K., Gamboa-de Buen, A., and Huante, P.: Seed reserve composition in 19 tree species of a tropical deciduous forest in Mexico and its relationship to seed germination and seedling growth, Ann. Bot., 107, 939–951, https://doi.org/10.1093/aob/mcr041, 2011.
Strigul, N., Pristinski, D., Purves, D., Dushoff, J., and Pacala, S.: Scaling from trees to forests: tractable macroscopic equations for forest dynamics, Ecol. Monogr., 78, 523–545, https://doi.org/10.1890/08-0082.1, 2008.
Sulman, B. N., Phillips, R. P., Oishi, A. C., Shevliakova, E., and Pacala, S. W.: Microbe-driven turnover offsets mineral-mediated storage of soil carbon under elevated CO2, Nat. Clim. Change, 4, 1099–1102, https://doi.org/10.1038/NCLIMATE2436, 2014.
Terrer, C., Vicca, S., Hungate, B. A., Phillips, R. P., and Prentice, I. C.: Mycorrhizal association as a primary control of the CO2 fertilization effect, Science, 353, 72–74, https://doi.org/10.1126/science.aaf4610, 2016.
Terrer, C., Vicca, S., Stocker, B. D., Hungate, B. A., Phillips, R. P., Reich, P. B., Finzi, A. C., and Prentice, I. C.: Ecosystem responses to elevated CO2 governed by plant-soil interactions and the cost of nitrogen acquisition, New Phytol., 217, 507–522, https://doi.org/10.1111/nph.14872, 2018.
Tilman, D.: Plant strategies and the dynamics and structure of plant communities, Princeton University Press, Princeton, N.J., 1988.
Urbanski, S., Barford, C., Wofsy, S., Kucharik, C., Pyle, E., Budney, J., McKain, K., Fitzjarrald, D., Czikowsky, M., and Munger, J. W.: Factors controlling CO2 exchange on timescales from hourly to decadal at Harvard Forest, J. Geophys. Res.-Biogeo., 112, G02020, https://doi.org/10.1029/2006JG000293, 2007.
Valentine, H. T. and Mäkelä, A.: Modeling forest stand dynamics from optimal balances of carbon and nitrogen, New Phytol., 194, 961–971, https://doi.org/10.1111/j.1469-8137.2012.04123.x, 2012.
Vitousek, P. M., Menge, D. N. L., Reed, S. C., and Cleveland, C. C.: Biological nitrogen fixation: rates, patterns and ecological controls in terrestrial ecosystems, Philos. Trans. R. Soc. B, 368, 20130119, https://doi.org/10.1098/rstb.2013.0119, 2013.
Walker, A. P., De Kauwe, M. G., Medlyn, B. E., Zaehle, S., Iversen, C. M., Asao, S., Guenet, B., Harper, A., Hickler, T., Hungate, B. A., Jain, A. K., Luo, Y., Lu, X., Lu, M., Luus, K., Megonigal, J. P., Oren, R., Ryan, E., Shu, S., Talhelm, A., Wang, Y.-P., Warren, J. M., Werner, C., Xia, J., Yang, B., Zak, D. R., and Norby, R. J.: Decadal biomass increment in early secondary succession woody ecosystems is increased by CO2 enrichment, Nat. Commun., 10, 454, https://doi.org/10.1038/s41467-019-08348-1, 2019.
Weng, E., Farrior, C. E., Dybzinski, R., and Pacala, S. W.: Predicting vegetation type through physiological and environmental interactions with leaf traits: evergreen and deciduous forests in an earth system modeling framework, Global Change Biol., 23, 2482–2498, https://doi.org/10.1111/gcb.13542, 2017.
Weng, E. S., Malyshev, S., Lichstein, J. W., Farrior, C. E., Dybzinski, R., Zhang, T., Shevliakova, E., and Pacala, S. W.: Scaling from individual trees to forests in an Earth system modeling framework using a mathematically tractable model of height-structured competition, Biogeosciences, 12, 2655–2694, https://doi.org/10.5194/bg-12-2655-2015, 2015.
Wieder, W. R., Grandy, A. S., Kallenbach, C. M., and Bonan, G. B.: Integrating microbial physiology and physio-chemical principles in soils with the MIcrobial-MIneral Carbon Stabilization (MIMICS) model, Biogeosciences, 11, 3899–3917, https://doi.org/10.5194/bg-11-3899-2014, 2014.
Wieder, W. R., Allison, S. D., Davidson, E. A., Georgiou, K., Hararuk, O., He, Y., Hopkins, F., Luo, Y., Smith, M. J., Sulman, B., Todd-Brown, K., Wang, Y.-P., Xia, J., and Xu, X.: Explicitly representing soil microbial processes in Earth system models, Global Biogeochem. Cycles, 29, 1782–1800, https://doi.org/10.1002/2015GB005188, 2015.
Wright, I., Reich, P., Westoby, M., Ackerly, D., Baruch, Z., Bongers, F., Cavender-Bares, J., Chapin, T., Cornelissen, J., Diemer, M., Flexas, J., Garnier, E., Groom, P., Gulias, J., Hikosaka, K., Lamont, B., Lee, T., Lee, W., Lusk, C., Midgley, J., Navas, M., Niinemets, U., Oleksyn, J., Osada, N., Poorter, H., Poot, P., Prior, L., Pyankov, V., Roumet, C., Thomas, S., Tjoelker, M., Veneklaas, E., and Villar, R.: The worldwide leaf economics spectrum, Nature, 428, 821–827, https://doi.org/10.1038/nature02403, 2004.
Xia, J., Luo, Y., Wang, Y.-P., and Hararuk, O.: Traceable components of terrestrial carbon storage capacity in biogeochemical models, Global Change Biol., 19, 2104–2116, https://doi.org/10.1111/gcb.12172, 2013.
Yang, Y., Luo, Y., and Finzi, A. C.: Carbon and nitrogen dynamics during forest stand development: a global synthesis, New Phytol., 190, 977–989, https://doi.org/10.1111/j.1469-8137.2011.03645.x, 2011.
Zadworny, M., McCormack, M. L., Mucha, J., Reich, P. B., and Oleksyn, J.: Scots pine fine roots adjust along a 2000-km latitudinal climatic gradient, New Phytol., 212, 389–399, https://doi.org/10.1111/nph.14048, 2016.
Zea-Cabrera, E., Iwasa, Y., Levin, S., and Rodríguez-Iturbe, I.: Tragedy of the commons in plant water use, Water Resour. Res., 42, W06D02, https://doi.org/10.1029/2005WR004514, 2006.