the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Gas exchange estimates in the Peruvian upwelling regime biased by multi-day near-surface stratification
Annette Kock
Damian L. Arévalo-Martínez
Marcus Dengler
Peter Brandt
Hermann W. Bange
The coastal upwelling regime off Peru in December 2012 showed considerable vertical concentration gradients of dissolved nitrous oxide (N2O) across the top few meters of the ocean. The gradients were predominantly downward, i.e., concentrations decreased toward the surface. Ignoring these gradients causes a systematic error in regionally integrated gas exchange estimates, when using observed concentrations at several meters below the surface as input for bulk flux parameterizations – as is routinely practiced. Here we propose that multi-day near-surface stratification events are responsible for the observed near-surface N2O gradients, and that the gradients induce the strongest bias in gas exchange estimates at winds of about 3 to 6 m s−1. Glider hydrographic time series reveal that events of multi-day near-surface stratification are a common feature in the study region. In the same way as shorter events of near-surface stratification (e.g., the diurnal warm layer cycle), they preferentially exist under calm to moderate wind conditions, suppress turbulent mixing, and thus lead to isolation of the top layer from the waters below (surface trapping). Our observational data in combination with a simple gas-transfer model of the surface trapping mechanism show that multi-day near-surface stratification can produce near-surface N2O gradients comparable to observations. They further indicate that N2O gradients created by diurnal or shorter stratification cycles are weaker and do not substantially impact bulk emission estimates. Quantitatively, we estimate that the integrated bias for the entire Peruvian upwelling region in December 2012 represents an overestimation of the total N2O emission by about a third, if concentrations at 5 or 10 m depth are used as surrogate for bulk water N2O concentration. Locally, gradients exist which would lead to emission rates overestimated by a factor of two or more. As the Peruvian upwelling region is an N2O source of global importance, and other strong N2O source regions could tend to develop multi-day near-surface stratification as well, the bias resulting from multi-day near-surface stratification may also impact global oceanic N2O emission estimates.
This study develops its results and conclusions for the exemplary case of dissolved nitrous oxide (N2O), but many aspects will also be valid for other dissolved gases, particularly for gases with similar solubility in seawater. Oceanic upwelling regimes have been increasingly recognized as strong emitters of N2O, particularly if they are in the vicinity of oxygen-deficient waters (Codispoti et al., 1992; Bange et al., 1996; Nevison et al., 2004; Naqvi et al., 2010; Arévalo-Martínez et al., 2015). N2O is of global importance mainly after its emission to the atmosphere, due to its strong global warming potential (Wang et al., 1976; Myhre et al., 2013) and its involvement in the depletion of stratospheric ozone (Hahn and Crutzen, 1982; Ravishankara et al., 2009). Although oceanic N2O emissions very likely constitute a major fraction of the atmospheric N2O budget, they are not well constrained (Ciais et al., 2013). This is particularly the case for upwelling regions (Nevison et al., 2004; Naqvi et al., 2010). In order to better quantify oceanic N2O emissions, there have been several studies, e.g., with a global perspective (Elkins et al., 1978; Nevison et al., 1995; Suntharalingam and Sarmiento, 2000; Bianchi et al., 2012), and with particular focus on upwelling regions (Law and Owens, 1990; Nevison et al., 2004; Cornejo et al., 2007; Naqvi et al., 2010; Kock et al., 2012; Arévalo-Martínez et al., 2015) because of their anticipated role as emission hotspots. The causes of strong N2O emissions in upwelling regimes are the transport of intermediate and central waters with accumulated N2O toward the surface, and the usually locally enhanced biological production and remineralization. The elevated biological activity also includes microorganisms participating in the nitrogen cycle, which can provide an additional local N2O source (Nevison et al., 2004). The local N2O source can intensify tremendously under low oxygen conditions. Particularly strong net accumulation of N2O is observed at locations in the periphery of anoxic waters (Codispoti and Christensen, 1985; Codispoti et al., 1992; Naqvi et al., 2010; Ji et al., 2015; Kock et al., 2016). This is probably due to three interacting effects of the particular oxygen conditions here: (i) enhanced N2O production by nitrifiers and denitrifiers both working increasingly imperfectly when about to pass the oxygen limits of their respective metabolism (Codispoti et al., 1992; Babbin et al., 2015), (ii) co-existence of oxidative and reductive metabolic pathways that would exclude each other in higher or lower oxygen conditions (Kalvelage et al., 2011; Lam and Kuypers, 2011) thus enabling a fast nitrogen turnover (Ward et al., 1989) including a fast N2O turnover (Codispoti and Christensen, 1985; Babbin et al., 2015), and (iii) sharp oxygen gradients and strong short-term variations of ambient oxygen conditions which guarantee that the oxygen level of optimum N2O production is met at some fraction of time (Naqvi et al., 2000). The Peruvian upwelling regime intersects a pronounced oxygen minimum zone (OMZ) with a large anoxic volume fraction and a typically sharp oxycline and thus offers ideal conditions for such peripheral hotspot N2O production (Kock et al., 2016).
To date, most studies that estimate regional oceanic N2O emissions from observations are based on dissolved N2O concentrations some meters below the surface (e.g., Law and Owens, 1990; Weiss et al., 1992; Rees et al., 1997; Rhee et al., 2009; Kock et al., 2012; Farías et al., 2015; Arévalo-Martínez et al., 2015, 2017). Similarly, air–sea gas exchange estimates of other gas species are also often based on measurements some meters below the surface, or “near-surface” measurements. Usually the chosen sample depths lie within the top 10 m of the water column. Thus, for the course of this paper we define the near-surface layer to be the top 10 m range, even if usually “near-surface” is a qualitative label for the upper few meters, without fixed limits. The measured concentrations are then used to calculate local air–sea gas exchange according to
The flux density Φ across the surface is determined by the concentration difference between water and air (Δc) and a transfer velocity (kw). Δc is assumed to be well described by a measured concentration somewhere in the near-surface layer (cns) and the concentration at the immediate water surface in equilibrium with the atmosphere (ceq, controlled by atmospheric mole fraction and solubility). Thus it is assumed that Φ is well estimated by
This measurement strategy is inspired by the formulation of bulk flux parameterizations, with
requiring the concentration in the “bulk water” (cbulk) instead of cns. The term “bulk” suggests constancy of properties across a not-too-thin layer. cbulk is conventionally understood as the concentration within a layer of homogeneous concentration that immediately adjoins to the viscous boundary layer (Garbe et al., 2014). As this paper focuses on near-surface concentration gradients, we do not want to assume the guaranteed existence of a homogeneous layer down to a certain depth. Nevertheless, we keep the term cbulk for the concentration below the viscous boundary layer, even for the limiting case of an infinitesimally thin homogeneous layer. kw in Eq. (2) is assumed to be identical to kw in Eq. (3). This includes the assumptions that (i) either concentrations are expected to be homogeneous from measurement depth up to the bulk level, so that cns=cbulk everywhere, or (ii) cns and cbulk are expected to differ unsystematically in space and time, so that treating measurements as if cns=cbulk would not result in a systematic error in regionally averaged Φ.
Here we challenge these assumptions by showing that N2O gradients exist in the topmost meters of the Peruvian upwelling region, which are both considerable and systematic. The observed gradients are predominantly downward, i.e., N2O concentrations decrease toward the surface. This evokes a principal systematic measurement issue when assuming cns=cbulk (the “Δc sampling issue” with the use of bulk flux parameterizations). We propose a process, namely the formation of multi-day near-surface stratification, to be responsible for substantial N2O gradients in conditions typical for upwelling regions, and further support this by observations and simple model calculations. Finally, we estimate the total emission bias for the Peruvian upwelling region in December 2012.
This study was initially motivated by an apparent mismatch between N2O emission and N2O supply to the mixed layer in the Mauritanian upwelling region (Kock et al., 2012). One of several hypotheses to reconcile this was to assume that the mismatch is caused by overestimated emissions due to the Δc sampling issue in downward near-surface N2O gradients. Could – in principle – very shallow stratified layers that were encountered before in upwelling regions account for substantial vertical N2O gradients and overestimated emission rates? Temporal near-surface stratification above the seasonal pycnocline has been observed over the last few decades (e.g., Stommel and Woodcock, 1951; Bruce and Firing, 1974; Soloviev and Vershinsky, 1982). Observations mainly from the open ocean revealed a diurnal cycle of near-surface temperature which is associated with the buildup of shallow stratification during daytime and its destruction during nighttime. This picture has become more and more detailed, as time series of high-resolution profiles in the undisturbed surface ocean have become available, from buoys (Prytherch et al., 2013; Wenegrat and McPhaden, 2015) and a free-rising profiler (Sutherland et al., 2014, 2016). The buildup of near-surface stratification is due to solar differential heating of the top few meters of the ocean, with high insolation and weak wind as important prerequisites for strong effects (e.g., Soloviev and Lukas, 1997; Gentemann et al., 2008). This diurnal cycle of near-surface temperature and stratification (“diurnal warm layer cycle”) has been extensively modeled and observed (e.g., Imberger, 1985; Price et al., 1986; Fairall et al., 1996a; Gentemann et al., 2003, 2009; Prytherch et al., 2013; Wenegrat and McPhaden, 2015; Sutherland et al., 2016). The strong stratification dampens turbulence and isolates a surface homogeneous layer from the water below (“surface trapping” of Price et al., 1986; “capping layer” of McNeil and Merlivat, 1996; Soloviev and Lukas, 1997), such that vertical gradients of any water property can develop if supply–source and loss–sink terms differ between above and below the isolating interface. For dissolved gases, vertical gradients in the top meters due to surface trapping had been predicted (McNeil and Merlivat, 1996) and later were indeed observed for oxygen and carbon dioxide (Soloviev et al., 2002; Calleja et al., 2013; Miller et al., 2019). Vertical concentration gradients due to surface trapping cause an additional bias in gas exchange estimates, independent of issues with solubility estimates which are caused by temperature gradients and which have been studied to quantify CO2 exchange bias in particular (e.g., Ward et al., 2004; Woolf et al., 2016). Concerning the surface trapping, the studies of Soloviev et al. (2002) and Calleja et al. (2013) showed that vertical concentration differences in oxygen and carbon dioxide exist across the top meters of several open-ocean regions, albeit with little average effect on gas exchange estimates. Miller et al. (2019) found CO2 concentration gradients across the top meters of the Arctic ocean, and diagnosed substantial errors in CO2 exchange estimates if sampling below the surface layer. This may be rather a case of a very shallow seasonal mixed layer than a case of temporal surface trapping, but still underlines the practical importance of near-surface stratification and the Δc sampling issue. In coastal upwelling regions, there have been no reports of near-surface gas gradients so far. However, the conditions here for near-surface stratification and gradients should be more favorable than in the oligotrophic open ocean, because of stronger near-surface light absorption in the chlorophyll-enriched water, and because of the tendency of wind decreasing toward the coast (Chavez and Messié, 2009).
Typically, it is assumed that the near-surface stratification that has formed during daytime is completely eroded during nighttime through convective and shear-driven mixing, generating a diurnal cycle of near-surface stratification. Night survival of near-surface stratification would prolong the surface trapping tremendously, more than just by the additional night hours, because the preexisting stratification on the following morning eases surface trapping of heat during the following daylight insolation. It thus amplifies and stabilizes near-surface stratification in a positive feedback, and makes it more unlikely that this stratification is destroyed before the following evening. Such events extending beyond the diurnal timescale have not been explicitly investigated before, but hints for their existence can be found in reported observations of Stommel and Woodcock (1951), Stramma et al. (1986), and Prytherch et al. (2013). Multi-day near-surface stratification showed up prominently during our field observations in the Peruvian upwelling region and will be discussed as major factor responsible for substantial vertical gas gradients in Sect. 4. The Peruvian upwelling region was chosen as a suitable study site because very high N2O concentrations had been found here already before the campaign in 2012–2013 (Nevison et al., 2003; Kock et al., 2016), which then expectedly cause large vertical concentration differences that should be more easily detected with statistical significance than elsewhere.
2.1 Data overview
In the context of a ship-based survey campaign from December 2012 to February 2013 in the Peruvian upwelling region, the Meteor cruise 91 (M91, carried out within the scope of BMBF project SOPRAN, Surface Ocean PRocesses in the ANthropocene, http://sopran.pangaea.de/, last access: 28 May 2019) in December 2012 was dedicated to studying biogeochemistry and emissions of various climate-relevant atmospheric trace gases. It yielded several observational parameters that serve this study's purpose to explore the magnitude, causes, and impacts of near-surface N2O concentration gradients. The data set is complemented by near-surface hydrographic time series from a campaign using several ocean gliders during the subsequent Meteor cruises M92 and M93, carried out as part of the German collaborative research center SFB754, https://www.sfb754.de/ (last access: 28 May 2019) (Dengler and Krahmann, 2017a, b; Kanzow and Krahmann, 2017a, b, c, d, e, 2018). For cruise reports see Bange (2013), Lavik (2013), and Sommer et al. (2014). On most of the ship stations during the December 2012 cruise, simultaneous profiles of conductivity–temperature–depth–oxygen (CTD−O2, Krahmann and Bange, 2016) and discrete samples of N2O (Kock and Bange, 2016) were collected (Fig. 1). These data were used to estimate the near-surface vertical N2O gradient, the stratification between 10 and 5 m, the thickness of the top layer (see Sect. 2.2.3), and the depth of the OMZ upper boundary – here defined by a 20 µmol kg−1 oxygen threshold. The latter served to approximately locate the periphery to anoxic conditions, with a sharp oxygen gradient and with expected strong local N2O production, henceforth referred to as the “oxygen interface”. Four vertically high resolution N2O profiles of the top 10 m were measured from a drifting Zodiac positioned at least 1 km away from the research vessel (Fig. 1). The Zodiac sampling aimed at identifying near-surface N2O gradients not affected by ship-induced turbulence. The top 1 m was sampled by a submersible centrifugal pump with radial intake, providing water at a rate of about 0.5 L min−1. For the water column from 1 to 10 m a manually triggered 5 L Niskin bottle was used, accompanied by a MicroCat to record pressure, temperature, and salinity.
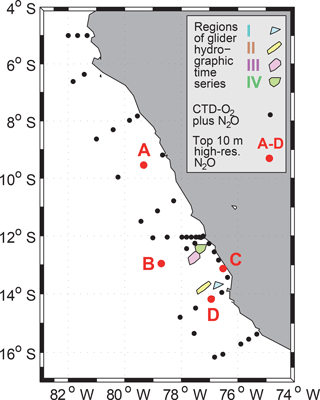
Figure 1Locations of sample stations and glider time series off the coast of Peru, December 2012 to February 2013. Black dots: simultaneous CTD−O2 and N2O sampling, comprising 5 and 10 m depth samples, during M91 (3–23 December 2012). Red dots: Zodiac-based high-resolution N2O profiles of topmost 10 m; A: 8 December 2012 at 16:30 local time; B: 13 December 2012 at 10:00 local time; C: 16 December 2012 at 14:30 local time; D: 17 December 2012 at 14:00 local time. Colored areas: regions where time series of glider near-surface hydrography were obtained; I: 10 days from 17 to 27 February 2013; II: 22 days from 23 January to 22 February 2013; III: 31 days from 15 January to 15 February 2013; IV: 37 days from 11 January to 17 February 2013.
During December 2012, N2O concentrations at 5.5 m were measured continuously from the ship's moon pool and are used in this study to complement the Zodiac high-resolution N2O profiles. In order to estimate N2O 5.5 m concentrations on the station, only values obtained near the station were considered when the vessel was steaming, to avoid disturbances of the water column by the ship's maneuvering and dynamic positioning. The water temperature at the thermosalinograph intake at the ship's hull (at 3 m depth) together with the vertical displacement of the intake was used to create an along-track time series of estimated near-surface stratification, in order to explore the link between strong near-surface stratification events and N2O gradients. Further, a campaign with seven gliders in January and February 2013 (Thomsen et al., 2016) provided undisturbed near-surface hydrographic data with high temporal coverage for four local areas (Fig. 1). For these areas which are characterized by different wind conditions and different distances to land, 1 h resolution time series of stratification in the top 12 m could be composed. These time series served to estimate the occurrence and characteristics of multi-day near-surface stratification, and to force a simple one-dimensional gas-transfer model of the top 12 m of the water column, aimed at producing time series of N2O distribution and outgassing for different stratifications and wind conditions.
2.2 Sample and data processing
2.2.1 N2O concentrations
For the discrete N2O measurements, 20 mL water samples were taken (three replicates per depth during CTD−O2 casts, six replicates per depth during high-resolution profiles). Following Kock et al. (2016), the samples were analyzed on board by gas chromatography with an electron capture detector (GC-ECD) after bringing a helium headspace to static equilibrium. The measurement uncertainty was estimated for each profile separately, from the distribution of residuals around the average profile, and lay typically in the range of 0.5 to 1 nmol kg−1 (95 % level) for the high-resolution profiles and in the range of 0.5 to 4 nmol kg−1 (95 % level) for the CTD profiles. N2O was also measured from a continuous seawater supply (pumped from 5.5 m depth) with a cavity enhanced absorption spectrometer coupled to a seawater and gas equilibrator (Arévalo-Martínez et al., 2013). The response time of the equilibrator was 2.5 min (translating to a space scale of 750 m at a ship speed of 10 knots). The accuracy of 3 min averages is < 0.5 nmol kg−1. A possible instrument drift, which is typically lower than 1 % per week, was corrected by a 6-hourly calibration of the measurement system (Arévalo-Martínez et al., 2013).
2.2.2 CTD−O2
Salinity, temperature, and oxygen profiles were obtained from a lowered SeaBird 911plus CTD with dual conductivity and temperature sensors, plus added membrane-type oxygen sensors. Salinity was calibrated against water samples analyzed with a Guildline AutoSal salinometer. Oxygen was calibrated against water samples using a Winkler titration stand. No further calibration of temperature sensors was performed. Accuracies are 0.002 K in temperature, 0.002 in salinity, and 1 µmol kg−1 in oxygen for concentrations ≥5 µmol kg−1. We also used temperature profiles derived from a microstructure probe which was equipped with a Pt100 temperature sensor and a thermistor. The gliders carried unpumped CTDs that required a special treatment. Following Thomsen et al. (2016), the flow through their conductivity cells was derived from a glider flight model, a thermal lag hysteresis correction was applied, and derived temperature and salinity values were further calibrated against shipboard CTD data from stations close to the glider position. Accuracy (rms) is 0.01 K in temperature and 0.01 in salinity.
2.2.3 Thickness of the top layer
We will use the term “top layer” (TL) to refer to that layer which ranges from the ocean surface down to a layer of strong stratification, and whose interior is characterized by a relatively weak stratification or even homogeneity. In extreme cases when strong stratification extends to the surface, a TL will not exist. Using a new term instead of “mixed layer” or “mixing layer” avoids misunderstandings, as the varieties of definitions and criteria for the latter terms are ample: sometimes the TL might rather match the mixed layer, and sometimes the TL might better match a temporal mixing layer within the mixed layer. We use the top layer to describe the layer of trapped water, and its thickness or “top-layer depth” (TLD) to describe the depth below which turbulent mixing is suppressed. Therefore we define the TLD based on a criterion relevant for the trapping process. The TLD is at the transition from the TL to the layer of suppressed mixing, and matches the “trapping depth” of Price et al. (1986), Fairall et al. (1996a), and Prytherch et al. (2013), who considered surface trapping by the diurnal warm layer cycle. Reported criteria are based on the argument that the trapping depth is set by self-regulation between the competing effects of stratification and shear instability and comes to sit where the gradient Richardson number (Ri) is about critical (Price et al., 1986; Fairall et al., 1996a; Prytherch et al., 2013; Soloviev and Lukas, 2014). Reported Ri criteria are 0.25 and 0.65, typical shear at trapping depth is 0.5 to s−1 (Prytherch et al., 2013) or s−1 (Wenegrat and McPhaden, 2015), both derived from observations of diurnal warm layers. These values correspond to an N2 range of 10−5 to 10−4 s−2 and match the N2 range at trapping depth observed by Wenegrat and McPhaden (2015). We define TLD as the minimum depth where s−2, in order not to underestimate the trapping depth, and not to overestimate the resulting effects. Calculating TLD this way requires reliable density profiles up to the surface, which are provided by the glider hydrographic surveys during January–February 2013. In contrast, the shipboard CTD profiles taken in December 2012 are much less reliable in the top 10 m, because the ship's engines and maneuvering before and during CTD stations causes overturns and turbulence. This is also the reason why shipboard CTD data usually do not show near-surface density gradients of the same strength as we found in the glider data. Due to the lack of reliable density data, for the ship CTD data we use an auxiliary but more robust criterion. It is based on the temperature difference to the surface and was originally intended for mixed layer detection; cf. Schlundt et al. (2014). The temperature profiles from the shipboard CTD were complemented by collocated temperature profiles from the microstructure probe to reduce uncertainty. To reduce the effect of ship-induced turbulence and under the assumption that any unstable stratification is artificially generated, the measured temperatures of the top 10 m were sorted, with the highest temperatures at the surface. The depth criterion applied is a density increase compared to the surface which is equivalent to a temperature decrease of 0.5 ∘C, while salinity is kept constant (Schlundt et al., 2014). This alternative top-layer thickness estimate will be referred to as surface layer depth, to illustrate that it is methodically different from TLD.
2.2.4 Estimate of stratification at 3 m depth
We used the water temperature measured at the thermosalinograph inlet near the ship's bow at nominal 3 m depth, and the vertical movement of the inlet position relative to the water column, in order to derive estimates of the stratification at about 3 m depth while the ship was cruising. This was inspired by the strategy of scanning the near-surface range with bow-mounted sensors by Soloviev and Lukas (1997). As the actual wave height and phase time series are unknown, the inlet position is calculated relative to the mean sea level, defined as average water level relative to the ship in the immediate vicinity of the ship. The vertical distance of the inlet relative to the mean sea level was estimated by rotating the vector of distance of the inlet relative to the ship's center of mass – first rotating around the ship's pitch axis, then around the ship's roll axis, resulting in
with as inlet position relative to the center of mass in ship coordinates, x positive to bow, y positive to starboard, z positive up, ρ roll angle positive for starboard down, π pitch angle positive for bow up, and dcom∕sealevel distance of center of mass to sea level. Heave is not part of the transformation because it is assumed that the ship's center of mass moves only negligibly relative to the mean sea level. The transformation is further only approximate because vertical displacement of the water column at 3 m from wave orbitals or a possible correlation of dinlet∕sealevel and actual sea level at the inlet position could not be taken into account. As the time series of recorded data of temperature and vertical position are not reliably synchronous, the vertical temperature gradient is estimated by the square root of the temperature variance divided by the square root of the vertical distance variance. The used variances are variances of residuals relative to a 200 s low pass. The entire procedure assumes that the temperature variance is dominated by the vertical temperature gradient. However, horizontal temperature variability on short scales, vertical movements of the water column, and sensor noise add to temperature variance. The salinity required to convert the temperature gradient into stratification is taken from the thermosalinograph record, using the average salinity during the respective time bin, i.e., assuming a vertical salinity gradient of zero. After having calculated N2 at 3 m depth for the entire cruise, we find an apparent lower limit for N2 of about 10−5 s−2, which is probably caused by the temperature variance which is not due to the vertical temperature gradient. The derived N2 time series is not used quantitatively due to the described limitations, but allows spatiotemporal variations in near-surface stratification to be qualitatively identified.
2.2.5 Wind speed at 10 m and cloud radiation
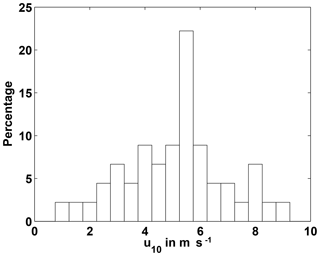
Wind speed at 10 m height was needed to estimate gas exchange fluxes. The 10 m wind speed during the ship cruise was derived by converting the wind speed measured at 34 m height at the ship using the COARE algorithm for non-neutral atmospheric conditions (Fairall et al., 1996b). The 10 m wind is the wind speed that exerts the same wind stress on the water surface as the measured 34 m wind, under the measured atmospheric conditions. In order to account for the integrated effect of the varying wind in the gas exchange estimates, wind speed was rms averaged using a cutoff radius in time and space of 6 h and 5 nm, respectively, around the time and position of N2O sampling. The averaging scales had been chosen after inspecting the continuous N2O record for typical spatial scales of variability during cruising and for typical scales of temporal variability at the station. Averaging was quadratic in order to estimate an effective wind speed that induces the same transfer velocity as the integrated time series of varying transfer velocities, acknowledging that transfer velocities can be well described as proportional to wind speed squared in the lower to medium wind speed range (Garbe et al., 2014), a range that was encountered during most of the cruise (Fig. 2). For the glider time series we used (1) daily wind fields from Metop/ASCAT scatterometer retrievals (http://cersat.ifremer.fr, last access: 28 May 2019; Bentamy and Croize-Fillon, 2012) that were interpolated to the positions of the gliders, and (2) wind speed from collocated ship records (distance <0.3∘) that was allocated to parts of the glider hydrographic time series, i.e., only when the ship was nearby. For the latter positions, the long wave radiation (LWR) attributable to cloud cover was also calculated, from incoming LWR minus clear-sky LWR. These ship-based observations of wind and cloud-caused LWR will serve to investigate conditions for multi-day near-surface stratification, but due to the gaps in the data they cannot serve to force the N2O gas-transfer model of Sect. 2.2.7.
2.2.6 N2O flux densities by air–sea gas exchange, and relative flux error
In order to estimate the N2O flux density (nmol m−2 s−1) from or to the ocean, the bulk flux parameterization of Nightingale et al. (2000) was used with a Schmidt number exponent of . The transfer velocity here only depends on wind speed with a quadratic law, and is of medium range within the multitude of transfer velocity parameterizations (Garbe et al., 2014). We also calculate a relative flux error (similar to Soloviev et al., 2002) which quantifies the bias that emerges when the flux density is not calculated based on a proper bulk concentration but instead on a differing concentration somewhere in the near-surface layer:
with Φbulk the flux density based on bulk concentration cbulk, Φns the flux density based on concentration cns, and ceq the concentration in equilibrium with the atmosphere. ceq was calculated following Weiss and Price (1980), using an N2O mole fraction in dry air of 325 ppb. R can be interpreted as the overestimation percentage of the gas exchange rate if the estimate is based on a concentration cns. The advantage of this relative measure of bias is that it shows the impact of the Δc sampling issue in a clear way independent of the actual value of the transfer velocity and its issues, and abstracting from the actual concentration level of the local N2O profile. Certainly, transfer velocities and N2O concentrations will have to be taken into account when estimating the integrated effect of near-surface stratification on regional emission rates.
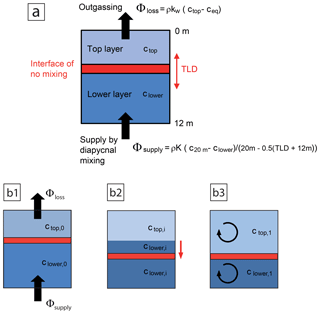
Figure 3(a) The one-dimensional gas-transfer model to simulate the surface trapping mechanism. The interface of complete mixing inhibition shifts up and down according to the high-resolution time series of observed TLD without instantaneously affecting local N2O concentrations. Vertical N2O transport is achieved by mixing within the two layers after the shifting interface has left a portion of clower water in the top layer, or vice versa. Panels (b1–b3) demonstrate the processing sequence during a model time step. (b1) For the duration of the time step, supply flux and outgassing flux change ctop and clower, resulting in intermediate concentrations ctop,i and clower,i. (b2) After the time step, the TLD is shifted, in the example to a greater depth. (b3) Instantaneous linear mixing within the new top and lower layers results in concentrations ctop,1 and clower,1, which serve as start values for the next model time step.
2.2.7 One-dimensional gas-transfer model of the surface trapping mechanism
Here we investigate whether the observed vertical near-surface N2O gradients can principally be caused by near-surface stratification alone. Further, we want to compare the impact of multi-day near-surface stratification versus the impact of just diurnal episodes of near-surface stratification. For these purposes, a model is used which simulates the surface trapping mechanism in a straightforward and simplified manner by vertical one-dimensional transport processes (Fig. 3). The model represents the top 12 m of the water column and takes into account N2O supply from below, air–sea gas exchange at the surface, and the suppressed mixing that is caused by a thin near-surface stratified layer. That thin stratified layer is simplified to be an interface of complete mixing inhibition, which divides the water column into two separate layers. The two layers (top layer and lower layer) are idealized to be each immediately and completely mixed. The interface of complete mixing inhibition represents the TLD and can shift up and down in the water column, independent of water movements. That means that the top and lower layers can change thicknesses and entrain water of each other, which leads to the exchange of N2O between the layers (Fig. 3b1–b3). For our purposes, the model needs to be constrained by realistic fluxes and high-resolution time series of TLD data, representative for the conditions in the Peruvian upwelling regime. In particular the TLD time series require attention, as on the one hand locating the TLD needs undisturbed high-resolution information on the top meters of the water column, and on the other hand the temporal resolution must be fine enough to catch the principal TLD shifts through the hours of the day. In particular the expected TLD maximum in the morning and the TLD minimum in the afternoon should be reliably resolved. We use observational data from four locations in the upwelling regime (regions I, II, III, IV in Fig. 1). The locations represent different grades of near-surface stratification, from domination by diurnal episodes to domination by multi-day events. The corresponding four time series of TLD are obtained from glider hydrographic near-surface profiles in January–February 2013 (see Sects. 2.1, 2.2.2, and Thomsen et al., 2016), as they represent undisturbed near-surface data of high spatiotemporal resolution. Time series of hourly density profiles in the top 12 m were assembled from shorter time series of different gliders that were passing through regions I to IV. The density time series were then low-pass-filtered (12 h half power, 3 h cut off) to remove density changes that are only caused by vertical movements of the water column due to internal waves and would otherwise cause spurious exchange between the two layers. TLD was determined as the shallowest depth where stratification was stronger than N2 = 10−4 s−2 (see Sect. 2.2.3). Air–sea gas exchange was calculated via the Nightingale et al. (2000) parameterization from the actual simulated N2O concentration of the top layer, from ceq based on surface temperature and salinity of the glider hydrographic data, and from transfer velocity calculated from wind speed (see Sect. 2.2.5). N2O supply from below was determined based on the assumptions that observed N2O concentrations at 20 m depth can be treated as steady-state and thus are understood as constant boundary values, and that N2O transport into the lower layer is by turbulent mixing. Actual 20 m concentrations were taken from discrete N2O profiles of December 2012 that were both near regions I to IV and situated at land distances that corresponded to those of region I to IV. Chosen values were 50, 30, 40, and 60 nmol kg−1, respectively. The supply flux density was then calculated as N2O with ρ water density, K vertical exchange coefficient, and ∇ N2O vertical gradient of N2O concentration. The N2O gradient is the difference between 20 m concentration and the concentration in the lower layer, divided by the distance between 20 m and the temporary center depth of the lower layer. In order to get an estimate of the range of the vertical exchange coefficient K, K was determined from microstructure measurements at stations where strong shallow stratification between two weakly stratified layers was clearly present. There, vertically averaged K was determined for the depth range from below the TLD down to 20 m. For details of K estimation from velocity microstructure see Fischer et al. (2013). The observed K values ranged from 10−5 m2 s−1 to near 10−2 m2 s−1 with median 10−4 m2 s−1 and mean 10−3 m2 s−1. After having chosen a value for K and which region (I to IV) was to be simulated, the model is forced by cyclic application of according wind and TLD time series until cyclic equilibrium. As a result, the model produces time series of N2O concentration vs. depth, so that time series of measurement bias R vs. depth can be obtained and compared to observations.
The four off-ship high-resolution N2O profiles (A to D) that were unaffected by ship-induced stirring show that near-surface N2O gradients do generally exist in the Peruvian upwelling region (Fig. 4). The N2O gradients, which are of variable strength but all downward or zero, are located below a thin homogeneous top layer of 1 to 5 m thickness. The N2O gradients strengthen with decreasing distance to the coastline and weakening winds. They are very similar in shape to the corresponding density profiles, i.e., a stronger N2O gradient is also associated with stronger stratification.
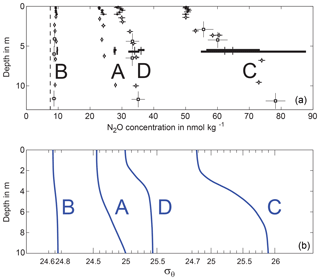
Figure 4N2O and density profiles at the off-ship high-resolution stations A to D, complemented by shipboard observations at adjacent positions and times. For positions and times of station A to D see Fig. 1. Distances to land – B: 106 nm; A: 48 nm; D: 36 nm; C: 7 nm. 95 % limits of 10 m wind distribution in meters per second (m s−1): B [4.3 6.6], A [3.1 6.0], D [2.6 5.9], C [3.3 5.4]. (a) N2O measurements with 95 % confidence limits from measurement uncertainty; black dots in top 1 m: samples from centrifugal pump off-ship; black circles below 1 m: samples from Niskin bottles off-ship; black squares: samples from shipboard CTD; thick black lines: 95 % limits of distribution of continuous ship samples during approach and departure of the station, median values are marked. (b) Density profiles derived from MicroCat temperature and conductivity profiles at stations A to D.
Discrete N2O samples from the closest shipboard CTD profiles are consistent with the off-ship profiles, despite some distance in space and time. The N2O data – taken while approaching or leaving a station – are from a distinctly larger distance in space and time than the discrete N2O samples and vary more, though still match the general pattern. Particularly at site C the data based on continuous sampling span the entire concentration range of the top 10 m of the off-ship high-resolution profile. The consistency of off-ship, discrete, and mean N2O concentrations from continuous sampling suggests larger regions of at least some nautical miles' extent to be basically horizontally homogeneous in the top 10 m, while the variability of the continuous N2O concentrations particularly at site C suggests that vertical motions (most likely due to internal waves) are superposed, transferring water from different nominal depths to the sample inlet at 5.5 m. Such variability is not visible in the discrete N2O samples of profile C, because these were projected onto the mean density profile which was observed during the off-ship sampling. So profile C does explicitly not show variability caused by internal wave motion, which was strong in the top meters at that site.
In order to further explore the spatial distribution and the conditions that lead to near-surface N2O gradients, the data set was complemented by the topmost ship-based N2O samples collected during December 2012. By taking into account these data, we accept the enhanced uncertainty in allocating N2O concentrations to depths which arises from ship-induced disturbances in the top 10 m of the water column. On the other hand we have shown a consistent behavior of off-ship and shipboard N2O samples at sites A to D. The ship-based data allow the N2O difference between about 5 and 10 m depth to be examined. This provides a data set of 45 near-surface N2O gradient estimates, as plotted in Fig. 5a as a function of distance to land. The encountered N2O gradients are mostly downward, i.e., negative with the convention of the z axis pointing upward, but occasional upward (positive) gradients occur very close to the coast. Far off the coast, gradients are mostly insignificant. The compilation shows that even stronger N2O gradients exist than observed at the off-ship high-resolution stations and suggests a zoning into neutral (“no”) gradients off 60 nm, downward gradients between 60 and 6 nm, and upward gradients inland of 6 nm. These zone limits are peculiar for the sampling depth between 5 and 10 m and would probably take different values for gradients at other sampling depths. Note that the profiles' behavior at depths shallower than 5 m is unknown here, so we cannot exclude that profiles of upward gradient between 5 and 10 m still exhibit a downward gradient in the top meters. Note as well that the high-resolution profiles tended to not exhibit their strongest gradients between 10 and 5 m, suggesting that stronger gradients than those shown in Fig. 5a may exist. The single occurrence of a strong N2O gradient 70 nm offshore coincides with a shallower mixed layer and less oxygen below the mixed layer than expected at that open-ocean location. The sea surface temperature field at the time of sampling shows a filament reaching from the coast to the station position. Those aspects suggest that coastal water with a downward N2O gradient has been transported to the open ocean.
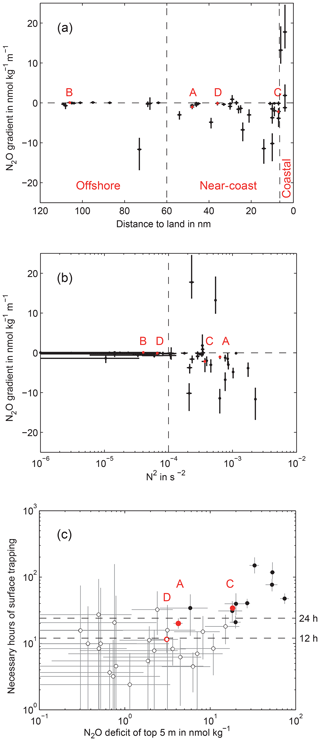
Figure 5Characteristics of shallow N2O gradients derived from shipboard samples. The N2O gradient is calculated from bottle samples at about 5 m and about 10 m depth; negative gradients are defined as concentration decreasing with vertical coordinate z or increasing with depth. Error bars are 95 % confidence limits based on measurement uncertainty. Red symbols are high-resolution stations A to D (see Figs. 1 and 4). (a) N2O gradient vs. distance to land, calculated as shortest distance to coast. Dashed vertical lines separate three zones (offshore, near-coast, coastal), dominated by neutral, downward, and upward gradients, respectively. (b) N2O gradient vs. buoyancy frequency squared, N2, calculated from densities of the corresponding N2O bottle samples. The dashed vertical line at N2=10−4 s−2 marks the approximate threshold below which no strong N2O gradients occur. (c) N2O deficit vs. estimated necessary time span of surface trapping, N2O deficit is concentration difference between 10 and 5 m; hours of isolation are the time needed to deplete a 5 m water column from the 10 m concentration down to the 5 m concentration. Filled circles are stations where the necessary isolation time includes minimum one entire night, even for the lower confidence limit. Open circles are stations where night mixing cannot be excluded. Station B showed no negative gradient and is not part of the plot.
Elevated N2O gradients (downward and upward) are confined to strong stratification (Fig. 5b), with a threshold buoyancy frequency of about N2 = 10−4 s−2. Following the arguments in Sect. 2.2.3 that during surface trapping the trapped top layer is isolated from waters below by already somewhat weaker stratifications of N2 between 10−5 and 10−4 s−2, this indicates that the strong N2O gradients are associated with surface trapping.
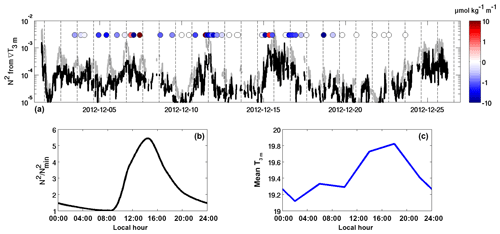
Figure 6(a) Observed near-surface N2O gradients vs. stratification at 3 m, in December 2012. Grey line: N2 at 3 m estimated from hull temperature variance and ship motion variance; data gaps are during ship stations. Diurnal periodicity is visible most days. Black line: same with mean diurnal cycle subtracted, by that mimicking the expected minimum nighttime stratification at each location. Colored dots: N2O gradient between about 10 and 5 m depth from ship-based discrete sampling. Dashed lines mark 15:00 h local time. (b) Mean diurnal cycle of stratification at 3 m, relative to minimum nighttime stratification . (c) Mean diurnal cycle of temperature at 3 m.
A question to address here is how much time would be needed to form the observed N2O gradients by surface trapping and air–sea gas exchange. The shipboard discrete N2O data allow a rough estimate for the majority of profiles with significant gradients, namely the downward ones, with 5 m concentration < 10 m concentration (Fig. 5c). The calculation assumes an initially homogeneous N2O distribution in the upper 10 m. Then, the top 5 m are trapped and get depleted by air–sea gas exchange, until the observed 5 m concentrations are reached. Horizontal N2O transport and N2O supply from below are not accounted for. Thus, the N2O concentration difference between 5 and 10 m is an N2O deficit that developed during the hours of isolation of the top 5 m, assuming the wind conditions encountered during station sampling. Taking into account that we expect the top 5 m to exhibit a downward or neutral gradient (cf. Fig. 4), the N2O deficit calculated in this simple approach is actually expected to be a lower bound to the real amount of N2O that has been emitted. Together with the assumption of no-N2O supply from below, the calculated time spans represent an underestimate of the necessary duration of surface trapping. The strongest quarter of N2O gradients in Fig. 5c needs isolation periods of distinctly more than 24 h, i.e., multi-day near-surface stratification, and there are some other strong gradients with isolation periods shorter than 24 h that nevertheless still comprise the entire previous night. Profiles of upward gradient between 10 and 5 m will be discussed in Sect. 4.3.
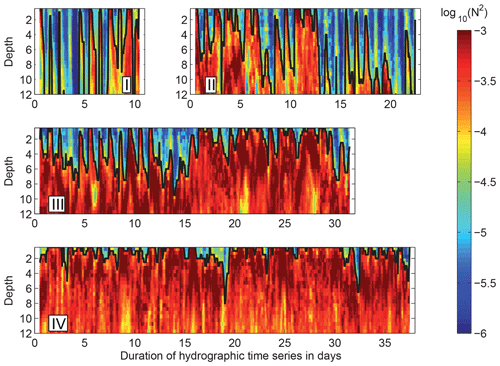
Figure 7Near-surface stratification in composite glider hydrographic time series, sorted by increasing grade of persistence, from that dominated by the diurnal cycle to that dominated by multi-day events. I, II, III, IV: regions of glider time series (Fig. 1). Black line: minimum depth of s−2, as base of the top layer (TLD, Sect. 2.2.3). Time series are composites of different, partly overlapping glider sections in respective regions. All four time series are from January–February 2013; their exact dates can be obtained from Fig. 1. N2 processed in 0.5 m vertical bins, after low-pass-filtering the hydrographic time series (half power k = (12 h)−1, cutoff (3 h)−1) to eliminate spurious variations of TLD caused by internal wave vertical motions.
The suggestion that multi-day near-surface stratification exists and is not rare, and that it is associated with the strongest near-surface N2O gradients, is further supported by additional observations. Figure 6 aligns the shipborne along-track time series of estimated N2 at 3 m depth during December 2012 with the observed N2O gradients. The time series of 3 m stratification shows a distinct diurnal cycle with maximum stratification around 15:00 local time. We aimed to subtract that diurnal cycle of near-surface stratification, in order to mimic a time series of the local nighttime N2 minimum, and in this way detect locations where near-surface stratification probably survived the previous night and can be called multi-day near-surface stratification. Interestingly, the diurnal cycle is much better removed in logarithmic space than in linear space; so we calculated a mean diurnal cycle of log10 N2, scaled it with an offset such that the minimum of (log10 N2 + offset) equals zero, and then subtracted this scaled mean diurnal cycle from the time series of log10 N2. The nonlinearity of the diurnal evolution of near-surface stratification might be due to the fact that preexisting stratification will suppress turbulent mixing and increasingly promote surface trapping of heat during the daytime, thus acting to self-perpetuate. The presence of surface trapping is also revealed by the mean diurnal cycle of temperature at 3 m (Fig. 6), with a mean amplitude of 0.6 K. Figure 6 shows that the strongest N2O gradients come in three clusters (i.e., around 5, 10, and 15 December, respectively), and they are associated with minimum nighttime stratification on the order of N2 = 10−4 s−2, which is strong enough to assume surface trapping (Sect. 2.2.3). The clusters suggest the existence of larger regions of multi-day near-surface stratification that have been crossed during the cruise. Direct observational evidence for multi-day near-surface stratification in the form of stratification time series in fixed regions comes from four local hydrographic time series obtained during the glider campaign in January–February 2013 (Fig. 7). The time series in regions I to IV (see Fig. 1) show different grades of persistence of near-surface stratification, ranging from a classic diurnal warm layer periodicity with regular nighttime mixing (I) to a strong stratification layer not retreating deeper than 2 m from the surface for several days in a row (IV). Conditions that promote the occurrence of multi-day near-surface stratification were examined for the glider data on nights when glider positions and ship positions were collocated (distance ≤0.3∘ in latitude and longitude), so that wind speed and long wave radiation from clouds could be assigned to thicknesses of the homogeneous top layer (Fig. 8). The data show that at low to moderate wind (0 to 6 m s−1) it is possible to find near-surface stratification persisting all night, the main prerequisite of multi-day near-surface stratification. Below wind speeds of 3 to 4 m s−1 multi-day near-surface stratification even seems certain. Additional cloud cover supports the persistence of near-surface stratification. Unfortunately the glider time series could not be accompanied by N2O measurements, so that a co-occurrence of the glider-observed periods of multi-day near-surface stratification with a progressing formation of strong N2O gradients can only be tested in a modeling framework. We use the 1-D gas-transfer model introduced in Sect. 2.2.7, simulating within its simple setup the surface trapping mechanism and the formation of N2O gradients. The model is forced with the glider time series of TLD and with ASCAT daily winds. Figure 9 shows N2O distributions as a function of depth which result from the model runs with applied forcings of region I to IV, displayed as distributions of relative flux error R or flux overestimation (Sect. 2.2.6). R is insensitive to the actual N2O supply from below, both for the range of assumed 20 m concentrations and for the range of vertical turbulent diffusivity from 10−5 to 10−2 m2 s−1. This insensitivity is plausible, because R can be expressed as , (cns−cbulk) is proportional to the N2O flux from the lower layer (with cns) to the top layer (with cbulk), (cbulk−ceq) is proportional to the N2O flux from the top layer to the atmosphere, and in the model equilibrium both fluxes are equal on average. This way, expressed as R, modeled N2O gradients can be advantageously compared to observed gradients without considering the magnitude of supply flux. It is just the impact of surface trapping on gradient formation that is compared between model and observed N2O profiles. The results in Fig. 9 show that the model produces distributions of R that comprise the observed R of the high-resolution N2O profiles; i.e., the observed N2O gradients during December 2012 are within the range that was modeled in accordance with observed surface trapping scenarios. An increase in the number of multi-day events in the TLD time series I to IV leads to increasingly higher R values; i.e., increasingly stronger N2O gradients are expected on average.
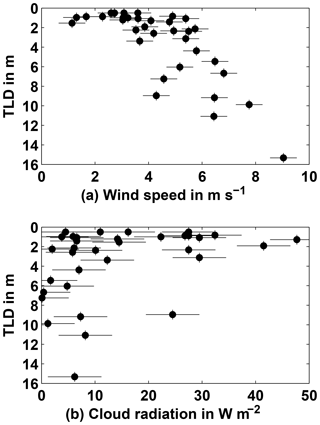
Figure 8Influence of wind speed (a) and cloud radiation (b) on nighttime near-surface stratification. Night TLD is the night average from glider hydrographic time series (Fig. 7). Wind speed is the night rms average of ship wind from collocated positions (distance ≤0.3∘ lat. and long.), converted to 10 m wind under non-neutral conditions using the COARE algorithm. Cloud radiation is the night average of long wave radiation minus clear-sky long wave radiation.
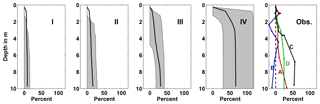
Figure 9Modeled and observed N2O profiles, expressed as relative flux error R (Sect. 2.2.6), i.e., equivalent to overestimation of air–sea gas exchange flux if using N2O at depth instead of bulk N2O in bulk flux parameterizations. I, II, III, IV: distributions of R in runs of 1-D transport model (Sect. 2.2.7), forced by time series of TLD from respective glider time series, and by ASCAT wind speed. Thin lines/grey shading: 95 % limits of temporal distribution of flux overestimation at each depth. Thick lines: mean flux overestimation. OBS: flux overestimation of observed high-resolution profiles at sites A to D.
4.1 The role of multi-day near-surface stratification for near-surface gas gradients
We will argue here that multi-day persistence of near-surface stratification is able to explain the formation of strong near-surface gas gradients, and furthermore that it is unlikely to achieve strong gas gradients through near-surface stratification on shorter timescales. The basic linkage of near-surface stratification and vertical gradients of any property in the near-surface ocean has been established (particularly plainly stated by Soloviev and Lukas, 2014) and is attributed to turbulence suppression in the temporally stratified layer, i.e., to surface trapping. However, studies dealing with consequences of near-surface stratification generally focus on short timescales, usually on the diurnal warm layer cycle (Soloviev et al., 2002; Kawai and Wada, 2007; Gentemann et al., 2009; Wenegrat and McPhaden, 2015). Prytherch et al. (2013) mention the possibility of preexisting stratification at sunrise (i.e., incomplete erosion of stratification during the night and longer timescales of near-surface stratification are implied), and observe subsequent amplification of surface warming, but they do not explore further consequences. Our database and results allow the view to be extended to the multi-day timescale. In this respect our results show, firstly, that multi-day near-surface stratification in the Peruvian upwelling region is not rare, lasts up to several nights in a row, and that remaining stratification at sunrise is strong of order N2=10−4 s−2 and more (Fig. 7). Conditions which support the endurance of stratification through the night and thus multi-day timescales are basically the same as those that promote near-surface stratification on shorter timescales, that is, low wind energy input and low heat loss (Fig. 8). Secondly, observations show that the absolute near-surface N2O gradient is positively related to the strength of near-surface stratification (Figs. 4, 5b), such that the observation that multi-day stratification is abundant and strong results in the expectation of associated abundant and strong N2O gradients. Thirdly, the duration of near-surface stratification can also be directly related to the strength of near-surface N2O gradients. This is indicated by three lines of observations and analyses. (i) During the cruise in December 2012, clusters of multi-day stratification coincided with clusters of the strongest N2O gradients (Fig. 6). (ii) When estimating necessary trapping times to produce observed N2O gradients (Fig. 5c), the strongest quarter of gradients can only be caused by multi-day trapping. (iii) When on the other hand estimating N2O gradients caused by observed trapping conditions (process model with observed TLD time series; Fig. 9), strong gradients become more and more likely with more frequent occurrences of multi-day stratification events.
Until here, the line of evidence supports the hypothesis that multi-day near-surface stratification can explain strong near-surface N2O gradients. To go beyond this, Figs. 5c and 9 and also the results of Soloviev et al. (2002) suggest that substantial gas gradients are not only made possible by but even need trapping times beyond the typical up to 12 h of the diurnal warm layer cycle. “Substantial” is unfortunately vague here, because the strength of gradients cannot be directly compared between the figures. Figure 9 indicates that region I which is dominated by the diurnal cycle is good for a typical R of 10 %, while region IV, which is dominated by multi-day near-surface stratification, exhibits R of 50 % to 100 %. The transition between diurnal and multi-day stratification cycles may be seen in regions II and III with R about 30 %. This is in line with Soloviev et al. (2002), who find a maximum R of 30 % in their investigation of gas gradients caused by the diurnal warm layer cycle. For the gradients of Fig. 5c, information on concentrations above 5 m depth is lacking, so R cannot be calculated. However, we can still roughly estimate R by using the concentration at 5 m for cbulk, and using the concentration at 10 m for cns, as is done in Fig. 10. This results in a threshold for R of 30 % to 50 %, above which gradients can only be achieved by multi-day near-surface trapping. Overall, these three independent estimates indicate that near-surface stratification at diurnal timescale can only account for gradients worth R=30 % or less.
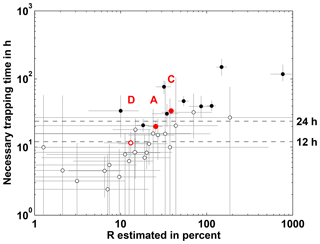
Figure 10Necessary trapping time to explain observed differences between N2O concentrations at 5 and 10 m, as a function of R. Depletion of the top 5 m layer by air–sea gas exchange due to observed wind is assumed. Due to the sparse resolution of N2O profiles at ship stations, R is estimated by setting cbulk=c5 m and cns=c10 m.
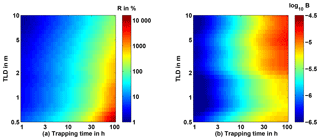
Figure 11Gas exchange overestimation R as a measure of relative gas exchange bias (a) and specific flux bias B as a measure of absolute gas exchange bias (b), both as a function of trapping time Ttrap and top-layer depth TLD. Based on corresponding values of wind speed u10 and TLD as observed during the glider mission (Fig. 8), the field of R(Ttrap,TLD) has been interpolated and smoothed by a Gaussian algorithm. A complete shutdown of N2O supply to the TL from below is assumed, as is air–sea gas exchange transfer velocity following Nightingale et al. (2000).
Can we understand better why the trapping time seems to play such an important role for gradients? Other factors such as TLD and wind speed are involved in the effectiveness of the surface trapping mechanism, but it seems they only occur in combinations which lead to necessary trapping times on multi-day scales in order to cause substantial N2O gradients. To gain some insight, we examine the formation of downward N2O gradients in a very simplified setting and work out the time and TLD dependence of relative emission bias R (as a measure for gradient strength). An initially homogeneous water column of concentration c0, which becomes stratified at the depth TLD at time t0=0, is assumed. The stratification immediately causes a complete shutdown of N2O supply from below, such that only gas exchange with the atmosphere acts and diminishes the concentration cTL in the TL. In the following we will call this simplified process model the “shutdown model”. The difference to the 1-D gas-transfer model of Sect. 2.2.7 is the lack of vertical movement of the TLD, which would permit N2O supply from below through entrainment. Using a bulk parameterization, the outgassing flux density will be , and the change in top-layer concentration with time . The solution is , such that
The decisive timescale here is and the necessary trapping time to reach a certain R is
For kw we choose the transfer velocity of Nightingale et al. (2000), which after scaling to the N2O Schmidt number is a function of wind speed u10 only: . To estimate trapping times Ttrap as a function of R and TLD, we use TLD from glider observations, and corresponding u10 from nearby ship time series, which were already employed to investigate the conditions for multi-day stratification (Fig. 8). Displaying R as a function of Ttrap and TLD (Fig. 11a) shows that TLD has an effect, but R proves to be more sensitive to changes in Ttrap than in TLD, within the observed range of values. This can be explained by the relation of TLD and kw (or u10): weaker wind which tends to accompany thinner TL leads to a reduction in gas exchange so that gradient formation is only weakly intensified with decreasing TLD. However, for very thin TL with TLD ≤0.5 m, trapping on a diurnal timescale might produce R>30 %. Unfortunately, this is outside of our observational evidence.
So far we evaluated the strength of gas gradients in terms of relative flux overestimation R. If we want to evaluate the absolute impact of gas gradients on gas flux estimates, the transfer velocity and the actual gas concentration have to be accounted for as well. Keeping the shutdown model that was introduced just above, and defining the absolute flux bias ΔΦ as the difference between the flux estimate based on concentration c0 and the flux estimate based on concentration cTL, we get
and using the definition of R (Eq. 5) to eliminate cTL,
As there is no data for c0 to accompany the relation between kw and TLD, ΔΦ itself cannot be calculated, but we will examine the term
which can be interpreted as a specific absolute flux bias per unit supersaturation. Comparing B for different conditions means assuming that c0 is independent of the conditions, while TLD and cTL react to wind speed and trapping time. Figure 11b shows that B is practically independent of TLD. This means that the enhancing effect on B of a stronger gas gradient, which comes with a thinner TL, is fully compensated for by the diminishing effect on B of the lower total gas transfer due to the lower wind speed which enabled the thinner TL in the first place.
Thus we may conclude from this subsection that (i) the trapping time is decisive for the formation of gas gradients of high impact on gas exchange estimates (Fig. 11), and building on this, (ii) multi-day near-surface stratification can explain the observed gas gradients (Figs. 7 and 9), while (iii) substantial flux bias is not to be expected from near-surface stratification at diurnal or shorter timescales (Figs. 9, 10, and 11).
4.2 Moderate wind speed causes strongest gas exchange bias
Further using the shutdown model of Sect. 4.1, the timescale as a function of wind speed u10 (Fig. 12a) suggests that there exists an optimum wind range for gas gradient formation. Gas gradients that cause a particular relative gas exchange bias R are reached after a trapping time that is proportional to the timescale (see Eq. 7) and can thus be achieved in the shortest time for moderate wind speeds between about 3 and 6 m s−1. That means that the strongest near-surface gradients are most likely to be observed in this wind speed range. For wind below 3 m s−1, gas exchange weakens while TLD remains about constant (see Fig. 8). For wind above 6 m s−1, a more than proportional TLD increase outweighs the effect of increased gas exchange.
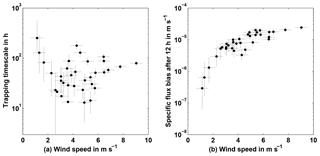
Figure 12Trapping timescale (a measure of trapping needed to reach a certain R) as a function of wind speed u10 (a), and specific flux bias for R after 12 hours of trapping as a function of wind speed u10 (b). The shape of B(u10) is very robust to varying trapping times. R and B are based on the relation between wind speed u10 and TLD as observed during the glider mission (Fig. 8). A complete shutdown of N2O supply to the TL from below is assumed, as is transfer velocity following Nightingale et al. (2000).
In order to examine the absolute gas exchange bias, Fig. 12b shows the wind speed dependence of specific flux bias B, as introduced in Sect. 4.1. B depends on trapping time, but the functional shape of B(u10) proves to be independent of Ttrap (at least up to Ttrap=48 h), such that different Ttrap mainly causes a factor in B or a constant offset in log10 B. We arbitrarily chose Ttrap=12 h to produce Fig. 12b. Again, the moderate wind range of 3 to 6 m s−1 stands out. This time, for wind below 3 m s−1, low R and low air–sea gas exchange both mutually act to diminish flux bias. For wind above 6 m s−1, B is admittedly high, but practically the gas gradient is no longer a measurement issue, as TLD becomes greater than 5 to 10 m (see Fig. 8), and routine near-surface measurements now happen within the TL.
4.3 Spatial pattern of N2O gradients in the Peruvian upwelling region
The previous insights lead us to propose an explanation for the observed distribution of near-surface N2O gradients in the Peruvian upwelling region, particularly the qualitative zonation seen in Fig. 5a. There are several parameters in the upwelling region which are related to the distance to the coastline (Fig. 13). Wind speed slows down toward the coast and sets favorable conditions for enhanced near-surface stratification and reduced top-layer thickness near the coast. The favorable wind speed range for gas gradient formation of 3 to 6 m s−1 (Sect. 4.2) is covered more and more frequently toward the coast. The oxygen interface is shoaling toward the coast, due to upwelling and more intense biological production, and subsequently more intense oxygen consumption at depth (Pennington et al., 2006). It reaches extremely shallow depths of about 10 m depth near coast, which, however, is not unusual (Hamersley et al., 2007; Gutiérrez et al., 2008). The oxygen interface is connected to peripheral hotspot production of N2O and therefore we expect to find a shoaling N2O source when approaching the coast. Even if N2O production by nitrification is probably inhibited by light (Ward, 2008), we consider the local conditions favorable to sustain a shallow N2O source near the coast: denitrification and nighttime nitrification can intensely produce N2O in a near-surface oxygen interface that exists below the TLD for multi-day periods. During daytime we observed very high chlorophyll content such that light absorption at 5 to 10 m depth may have been strong enough to even allow for shallow daytime nitrification. Figure 13 shows that the depth of the shallowest local N2O maximum and the depth of the oxygen interface coincide, although with large variability superposed. This leads us to generally link the N2O maximum to the oxygen interface and peripheral hotspot N2O production, a conclusion also made by Ji et al. (2015) after investigating the metabolic activity of N2O-producing microorganisms. This linkage is why we fit the shoaling of the oxygen interface and the shoaling of the N2O maximum by the same line. Altogether the previous considerations lead to the following scheme of processes affecting the pattern of N2O concentration: (i) accumulation of N2O is favored below the TLD, because N2O is produced below the TLD and at the same time surface trapping slows down N2O loss toward the TL; (ii) N2O diminishes toward the surface, because in the TL it is reduced by gas exchange; (iii) N2O below the oxygen interface diminishes toward the deep due to an increasing influence of active N2O loss processes toward the anoxic part of the OMZ. The resulting principal shape of the N2O profile is characterized by a local N2O maximum below the TLD at about the oxygen interface depth, and it shoals toward the coast because TLD and oxygen interface both shoal. Further the N2O maximum becomes more intense due to enhanced N2O production and more effective surface trapping toward the coast. A compilation of more and past N2O measurements off Peru (Kock et al., 2016) confirms this first-order scheme.
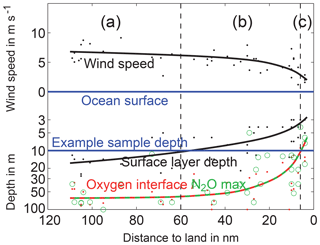
Figure 13Observed distributions of wind speed, surface layer depth, oxygen interface depth, and depth of maximum N2O vs. distance to land in December 2012. Surface layer depth is an estimate of TLD from ship data (Sect. 2.2.3). N2O max is the depth of shallowest local N2O maximum. Dots and circles are observations, lines represent schematic drawings. A constant sampling at 10 m (blue line) would intersect the TLD curve and the oxygen interface curve at two critical points with different distance to land (dashed vertical lines). The tilt of the layers leads to a perceived horizontal zonation of vertical N2O gradients (cf. Fig. 5a): (a) offshore zone, (b) near-coastal zone, (c) coastal zone.
Accepting this principal spatial structure, the horizontal zonation of observed N2O gradients (Fig. 5a) is immediately plausible as a consequence of scanning the tilted N2O field at a constant sampling depth. The two critical points are the land distance where the top-layer depth becomes shallower than the sampling depth, and the land distance where even the oxygen interface becomes shallower than the sampling depth (Fig. 13). These critical points limit and define three zones: the offshore zone with no observed gradient when sampling above the top-layer depth because N2O should be homogeneous within the TL, the near-coastal zone with downward gradient when sampling between top-layer depth and oxygen interface or N2O maximum, and the coastal zone with upward gradient when sampling below the oxygen interface or N2O maximum. Arguments in the literature are for a lower oxygen threshold of maximum N2O production than the 20 µmol kg−1 we use, e.g., < 10 µmol kg−1 (Ji et al., 2015). In any case, both 10 and 20 µmol kg−1 oxygen isosurfaces are mostly positioned very close to the sharp oxycline – often beyond the practical uncertainty of which depth exactly the sampled water is from – and with standard CTD instrumentation and Winkler calibration, oxygen concentrations far above 5 µmol kg−1 are preferable due to reduced uncertainty. So 20 µmol kg−1 is a practical choice to mark the approximate position of the oxygen interface.
The fraction of profiles in the coastal zone which show upward gradients at 5 to 10 m depth seems particularly interesting, because they are very high in N2O at 5 m and thus could be very important for the total N2O emission of an upwelling region. However, the behavior of N2O above 5 m is unknown. An N2O reduction toward the surface from a shallow subsurface maximum is likely, because the occurrences of upward gradient profiles were under low wind conditions with very stable near-surface stratification, so that long-duration surface trapping can be expected. The encountered wind speed of generally below 3 m s−1 would though suggest that very long trapping times are necessary to produce strong downward gradients. In analogy to the process understanding of the downward gradient profiles farther offshore, the upward gradient profiles might be seen as an expression of local N2O production at the shallow oxygen interface. In this case a very strong and very shallow production is suggested to occur in a high productivity environment less than 5 m from the surface. However, while some upward gradient profiles indeed show a coincidence of highest measured N2O concentration at the depth of the oxygen interface, others are higher still above the oxygen interface, at oxygen levels larger than 100 µmol kg−1. Kock et al. (2016) found that maximum N2O concentrations near the coast were indeed uncorrelated to the oxygen level. They discuss this to be an expression of strong time variability of oxygen conditions, i.e., the patchiness in the N2O distribution was suggested to be due to different oxygen histories, including some events of high N2O production at near-anoxic level with resulting high N2O concentrations which are still captured after mixing with water of higher oxygen level. This explanation would still leave surface trapping plus (transient) peripheral hotspot production as dominant processes in the near coast zone. However, it cannot be ruled out that other processes are involved as well.
4.4 Impact of near-surface N2O gradients on bias of total emission estimate
The impact of near-surface stratification on gas exchange seemed low so far, according to the rare studies. A study on oxygen gradients and fluxes in the open ocean during the GasEx98 project (Soloviev et al., 2002) found weak gas gradients (average systematic oxygen flux overestimation of 4 % across the top 4 m, with peak maxima of 30 % in calm conditions). A study on oxygen and CO2 near-surface gradients in different open-ocean regions (Calleja et al., 2013) found large variability of upward and downward near-surface gas gradients in the top 8 m, which, however, was unsystematic with the mean gradient not significantly different from zero (their Fig. 2). However, the present study with its different conditions (upwelling region instead of open ocean, tendency toward multi-day surface trapping, a gas which is basically biologically inactive in the near-surface layer) suggests a higher impact on gas exchange. We find stronger gas flux overestimations R of median 12 %, mean 37 %, a 95 % interval of [−40 % 180 %] and a maximum of 770 % across the depth range from 10 to 5 m from ship-based profiles, and the N2O gradients are systematically downward with the exception of the coastal zone (Fig. 5a). As the observed near-surface N2O gradients are both strong and systematic, we expect a non-negligible bias on N2O emission estimates for the entire Peruvian upwelling region. Assuming that the conclusions of the previous subsections are valid and that measurements are representative, and building on model results, we will estimate the total emission bias in the following, if relying on bulk flux parameterizations and sampling at 10 to 5 m depth.
For this purpose, N2O fluxes at the stations were calculated using the Nightingale bulk flux formulation, from 10 m measurements, 5 m measurements, and “true” bulk concentrations, using collocated shipborne wind speeds (see Sect. 2.2.5). The “true” bulk concentrations are the main issue here, and, apart from the measured values of the 4 high-resolution profiles, have to be estimated. For this purpose we take advantage of common features of profiles in the three zones (Figs. 5a, 13) and assume that near-surface gradients in each zone obey common distributions, which we estimate from the model results (Fig. 9) and the high-resolution profiles (Fig. 4). For the offshore zone we assume no multi-day stratification, as found in region I and in high-resolution profile B, and choose a normal distribution for R with mean zero and standard deviation 0.1, i.e., N(0, 10 %). For the near-coastal zone we use regions II to IV and high-resolution profiles A, C, and D, which are all from the zone of downward gradients, and choose N(40 %, 20 %) as R for 10 m concentrations and N(30 %, 20 %) as R for 5 m concentrations. The coastal zone is particularly uncertain, as we have no observations for the behavior of the upward-gradient profiles near the surface. Therefore, three alternative assumptions are compared. (i) The upward-gradient profiles could continue with a downward gradient above 5 m, and we choose R=60 %, which is the maximum R directly observed. (ii) The upward-gradient profiles could show constant concentration from 5 m up to the surface. And (iii) the upward-gradient profiles could continue with still upward gradient up to the surface. According to the assumptions above, expected distributions of bulk concentrations are then calculated for the three zones, and the total bias of emission estimates is calculated for the two cases of either using 10 m concentrations or 5 m concentrations instead of bulk concentrations (Table 1). Area weights are 0.5, 0.45, and 0.05 for offshore, near-coastal, and coastal zone, respectively, because of their land distance ranges of 120 to 60, 60 to 6, and 6 to 0 nm. The result is quite robust to the alternatives in the coastal zone, and to the choice of 10 or 5 m concentrations: total emission bias R is 20 % to 25 % overestimation for the region encompassing all three zones. If confining the bias estimation to the near-coastal and coastal zones where gradients are found within the top 10 m, we can give a more general number for expected bias through near-surface gradients, as 20 % to 35 % overestimation. We see that the offshore zone has a low impact on bias due to the absence of an N2O gradient on average and low N2O supersaturations causing low emissions. The coastal zone has a low impact due to its small area and low wind speed, causing low emissions. The near-coastal zone with systematic downward gradients and moderate wind dominates the total bias like it dominates the total emissions.
Table 1Estimated average emission rates of N2O for December 2012 in different zones of the Peruvian upwelling region. Comparison between fluxes calculated from 10 m, 5 m, and surface (bulk) concentrations.
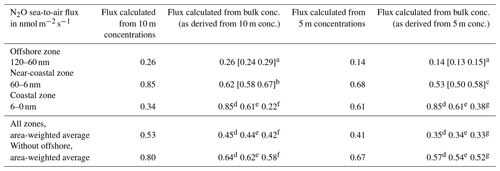
a 95 % confidence interval, based on the estimated range of flux overestimation in the offshore zone of −10 % to 10 %.
b 95 % confidence interval, based on the estimated range of flux overestimation in the near-coastal zone of 20 % to 60 % relative to 10 m depth.
c 95 % confidence interval, based on the estimated range of flux overestimation in the near-coastal zone of 10 % to 50 % relative to 5 m depth.
d Estimated surface concentration in the coastal zone is based on the assumption that the concentration gradient continues to the surface.
e Estimated surface concentration in the coastal zone is based on the assumption that the concentration is constant from 5 m upwards.
f Estimated surface concentration in the coastal zone is based on a flux overestimation of 60 % relative to 10 m depth.
g Estimated surface concentration in the coastal zone is based on a flux
overestimation of 60 % relative to 5 m depth.
Note that this total bias is rather a conservative estimate, as we ignored extreme values of model runs and ship-based profiles, which suggest that downward gradients equivalent to R > 100 % may exist. Further we took into account the possibility that profiles from the coastal zone with upward gradients might even continue with increasing concentration up to the surface.
Our database is representative only for December 2012 to February 2013, and also the N2O field and emissions are not yet well constrained for other seasons and years. While the N2O emissions in other seasons could principally be surveyed, predictions of a future trend remain largely uncertain. The latter is mainly due to partly competing effects of expected increased wind speed and expected increased stratification and leads to uncertain predictions of the future development of the nitrogen cycle in coastal upwelling regimes (Capone and Hutchins, 2013), and the N2O formation, which depends sensitively on complex boundary conditions. However, we may speculate about the seasonal and future bias associated with the Δc sampling issue. We know that the wind speed during the entire year is higher than in December to February (Echevin et al., 2008), and it is expected to increase in the future (Capone and Hutchins, 2013). Referring to our discussed results, the bias is most effective in the wind speed range between 3 and 6 m s−1 (Fig. 12) and is practically absent beyond 6 m s−1, as the TLD will most probably lie below the sampling depth (Fig. 8). When taking into account the observed wind distribution (Fig. 6), and assuming a shift of the distribution to higher wind speeds, the wind range between 3 and 6 m s−1 will be less and less abundant, and the probability of finding strong biases in the region will be reduced. So we expect less impact of the Δc sampling issue for the seasons outside December to February, and also less impact in a future scenario characterized by increased winds.
We studied near-surface stratification and the formation of near-surface gas gradients to obtain a consistent process picture of the air–sea gas exchange in the Peruvian upwelling region. We found that the peculiar setting composed of moderate wind conditions, subsequent near-surface stratification, and surface trapping, in combination with strong local N2O production, lead to the formation of near-surface N2O gradients that are both strong and systematic. Thus, routine gas exchange estimates via bulk flux parameterizations, which are based on concentration measurements at several meters below the surface, overestimate the region's N2O outgassing by about a third. With this, the sampling issue with the use of bulk flux parameterizations (Δc sampling issue) is brought back into discussion, as the bias of inferred gas exchange for the Peruvian upwelling region is an order of magnitude larger compared to results obtained by Soloviev et al. (2002) for the open ocean. Our observations combined with simple model calculations showed that the duration of near-surface stratification is the dominant factor influencing the strength of near-surface gas gradients. In particular the abundant multi-day near-surface stratification observed in the Peruvian upwelling region can explain the observed gas gradients, while near-surface stratification on diurnal or shorter timescales only has a minor impact. The multi-day timescale of surface trapping events has not found much attention yet. Usually near-surface stratification is assumed to be destroyed during nighttime, resulting in a diurnal warm layer cycle without memory beyond the diurnal cycle.
The impact of near-surface N2O gradients on emission estimates may even be of global relevance, because the global pattern of high N2O emission regions correlates with regions tending to surface trapping due to moderate wind. The Peruvian upwelling region alone is a large player in global oceanic N2O emissions, with an estimated share of 5 % to 20 % (Arévalo-Martínez et al., 2015), and other oceanic N2O hotspots like coastal and equatorial upwelling regimes may also show favorable conditions for near-surface gradients. Arguably other uncertainties in gas exchange estimates may be equal to or larger than the Δc sampling issue, e.g., transfer velocity parameterization uncertainties under low wind conditions (Garbe et al., 2014) or in the presence of surfactants (Tsai and Liu, 2003; Frew et al., 2004; Salter et al., 2011; Krall et al., 2014). But the systematic bias in N2O emissions identified here can prospectively be eliminated by simpler means, be it by parameterization or changes in routine measurement strategy. So it deserves some effort to be understood better and be eliminated. As a result of this study, an “educated screening” of the oceans for regions with expected strong near-surface gas gradients could enclose two criteria: near-surface stratification s−2 and wind speed at 10 m between 3 and 6 m s−1. The findings also bring up open questions including what causes the extreme N2O near-surface distribution close to the coast. High-resolution measurements here could help to clarify the existence, strength, and conditions of a near-surface N2O source, and also contribute to better parameterization of gas exchange under low wind conditions. The air–sea gas exchange of other gases might be affected in other ways by near-surface stratification. Gradients of photochemically produced substances with their main source near the surface may be much stronger than those of N2O. Inferred fluxes of biologically active gases (O2, CO2) might even be altered in sign regionally.
The data sets used are stored on the Kiel Ocean Science Information System (OSIS, 2019, https://portal.geomar.de/kdmi, datamanagement@geomar.de) and can be accessed upon request. According to the SFB 754 data policy (https://www.sfb754.de/de/data, last access: 28 May 2019), all data associated with this publication were published at a world data center (https://www.pangaea.de/, last access: 28 May 2019) when the paper was published. They have been described and cited in Sect. 2.1 of this paper. The N2O data presented here are archived in MEMENTO (2019, https://memento.geomar.de/de) and can be accessed upon request.
TF and AK conceived the study, which was encouraged, discussed, and made possible through the constructive contributions of MD, PB, DLAM, and HWB. AK and DLAM provided N2O measurements. TF wrote the paper with contributions from all authors.
The authors declare that they have no conflict of interest.
We highly appreciate the support of the RV Meteor crew and scientific crew, and in particular thank Rudi Link and Andreas Pinck for constructing the near-surface water sampling equipment, Tina Baustian and Matthias Krüger who conducted oxygen and salinity measurements, and Gerd Krahmann for the final postprocessing of glider CTD and ship CTD data. The German Federal Ministry of Education and Research (BMBF) supported this study as part of the SOPRAN project (grant no. FKZ 03F0611A and 03F0662A). The German Science Foundation (DFG) provided support as part of Sonderforschungsbereich SFB754 “Climate Biogeochemistry Interactions in the Tropical Ocean” and as part of cooperative project FOR1740. Damian L. Arévalo-Martínez received financial support from the EU FP7 project InGOS (grant agreement 284274). The daily wind fields from Metop/ASCAT scatterometer retrievals were obtained from the Centre de Recherche et d'Exploitation Satellitaire (CERSAT), at IFREMER, Plouzané (France). We thank the Peruvian authorities for permitting us to conduct the study in their territorial waters.
The article processing charges for this open-access publication were covered by a Research Centre of the Helmholtz Association.
This paper was edited by S. Wajih A. Naqvi and reviewed by Jorge Vasquez and one anonymous referee.
Arévalo-Martínez, D. L., Beyer, M., Krumbholz, M., Piller, I., Kock, A., Steinhoff, T., Körtzinger, A., and Bange, H. W.: A new method for continuous measurements of oceanic and atmospheric N2O, CO and CO2: performance of off-axis integrated cavity output spectroscopy (OA-ICOS) coupled to non-dispersive infrared detection (NDIR), Ocean Sci., 9, 1071–1087, https://doi.org/10.5194/os-9-1071-2013, 2013. a, b
Arévalo-Martínez, D. L., Kock, A., Löscher, C. R., Schmitz, R. A., and Bange, H. W.: Massive nitrous oxide emissions from the tropical South Pacific Ocean, Nat. Geosci., 8, 530–535, https://doi.org/10.1038/NGEO2469, 2015. a, b, c, d
Arévalo-Martínez, D. L., Kock, A., Steinhoff, T., Brandt, P., Dengler, M., Fischer, T., Körtzinger, A., and Bange, H. W.: Nitrous oxide during the onset of the Atlantic cold tongue, J. Geophys. Res., 122, 171–184, https://doi.org/10.1002/2016JC012238, 2017. a
Babbin, A. R., Bianchi, D., Jayakumar, A., and Ward, B. B.: Rapid nitrous oxide cycling in the suboxic ocean, Science, 348, 1127–1129, https://doi.org/10.1126/science.aaa8380, 2015. a, b
Bange, H. W., Rapsomanikis, S., and Andreae, M. O.: Nitrous oxide in coastal waters, Global Biogeochem. Cy., 10, 197–207, https://doi.org/10.1029/95GB03834, 1996. a
Bange, H. W.: Surface Ocean–Lower Atmosphere Study (SOLAS) in the upwelling region off Peru – Cruise No. M91 – December 01–December 26 2012 – Callao (Peru) – Callao (Peru). METEOR-Berichte, M91, 69 pp., DFG-Senatskommission für Ozeanographie, https://doi.org/10.2312/cr_m91, 2013. a
Bentamy, A. and Croize-Fillon, D.: Gridded surface wind fields from Metop/ASCAT measurements, Int. J. Remote Sens., 33, 1729–1754, https://doi.org/10.1080/01431161.2011.600348, 2012. a
Bianchi, D., Dunne, J. P., Sarmiento, J. L., and Galbraith, E. D.: Data-based estimates of suboxia, denitrification, and N2O production in the ocean and their sensitivities to dissolved O2, Global Biogeochem. Cy., 26, GB2009, https://doi.org/10.1029/2011GB004209, 2012. a
Bruce, J. G. and Firing, E.: Temperature measurements in the upper 10 m with modified expendable bathythermograph probes, J. Geophys. Res., 79, 4110–4111, https://doi.org/10.1029/JC079i027p04110, 1974. a
Calleja, M. Ll., Duarte, C. M., Álvarez, M., Vaquer-Sunyer, R., Agustí, S., and Herndl, G. J.: Prevalence of strong vertical CO2 and O2 variability in the top meters of the ocean, Global Biogeochem. Cy., 27, 941–949, https://doi.org/10.1002/gbc.20081, 2013. a, b, c
Capone, D. G. and Hutchins, D. A.: Microbial biogeochemistry of coastal upwelling regimes in a changing ocean, Nat. Geosci., 6, 711–717, https://doi.org/10.1038/NGEO1916, 2013. a, b
Chavez, F. P. and Messié, M.: A comparison of eastern boundary upwelling ecosystems, Prog. Oceanogr., 83, 80–96, https://doi.org/10.1016/j.pocean.2009.07.032, 2009. a
Ciais, P., Sabine, C., Bala, G., Bopp, L., Brovkin, V., Canadell, J., Chhabra, A., DeFries, R., Galloway, J., Heimann, M., Jones, C., Le Quéré, C., Myneni, R. B., Piao, S., and Thornton, P.: Carbon and other biogeochemical cycles, in: Climate Change 2013: The physical science basis. Contribution of working group I to the fifth assessment report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK, and New York, NY, USA, 2013. a
Codispoti, L. A. and Christensen, J. P.: Nitrification, denitrification and nitrous oxide cycling in the eastern tropical South Pacific ocean, Mar. Chem., 16, 277–300, https://doi.org/10.1016/0304-4203(85)90051-9, 1985. a, b
Codispoti, L. A., Elkins, J. W., Yoshinari, T., Friederich, G. E., Sakamoto, C. M., Packard, T. T.: On the nitrous oxide flux from productive regions that contain low oxygen waters, in: Oceanography of the Indian Ocean, edited by: Desai, B. N., Oxford-IBH, New Delhi, India, 271–284, 1992. a, b, c
Cornejo, M., Farías, L., and Gallegos, M.: Seasonal cycle of N2O vertical distribution and air–sea fluxes over the continental shelf waters off central Chile (36∘ S), Prog. Oceanogr., 75, 383–395, https://doi.org/10.1016/j.pocean.2007.08.018, 2007. a
Dengler, M. and Krahmann, G.: Physical oceanography from glider mission ifm03_depl08, PANGAEA, https://doi.org/10.1594/PANGAEA.884278, 2017a. a
Dengler, M. and Krahmann, G.: Physical oceanography from glider mission ifm10_depl03, PANGAEA, https://doi.org/10.1594/PANGAEA.884279, 2017b. a
Echevin, V., Aumont, O., Ledesma, J., and Flores, G.: The seasonal cycle of surface chlorophyll in the Peruvian upwelling system: A modelling study, Prog. Oceanogr., 79, 167–176, https://doi.org/10.1016/j.pocean.2008.10.026, 2008. a
Elkins, J. W., Wofsy, S. C., McElroy, M. B., Kolb, C. E., and Kaplan, W. A.: Aquatic sources and sinks for nitrous oxide, Nature, 275, 602–606, https://doi.org/10.1038/275602a0, 1978. a
Fairall, C. W., Bradley, E. F., Godfrey, J. S., Wick, G. A., Edson, J. B., and Young, G. S.: Cool-skin and warm-layer effects on sea surface temperature, J. Geophys. Res., 101, 1295–1308, https://doi.org/10.1029/95JC03190, 1996a. a, b, c
Fairall, C. W., Bradley, E. F., Rogers, D. P., Edson, J. B., and Young, G. S.: Bulk parameterization of air-sea fluxes for Tropical Ocean-Global Atmosphere Coupled-Ocean Atmosphere Response Experiment, J. Geophys. Res., 101, 3747–3764, https://doi.org/10.1029/95JC03205, 1996b. a
Farías, L., Besoain, V., and García-Loyola, S.: Presence of nitrous oxide hotspots in the coastal upwelling area off central Chile: an analysis of temporal variability based on ten years of a biogeochemical time series, Environ. Res. Lett., 10, 044017, https://doi.org/10.1088/1748-9326/10/4/044017, 2015. a
Fischer, T., Banyte, D., Brandt, P., Dengler, M., Krahmann, G., Tanhua, T., and Visbeck, M.: Diapycnal oxygen supply to the tropical North Atlantic oxygen minimum zone, Biogeosciences, 10, 5079–5093, https://doi.org/10.5194/bg-10-5079-2013, 2013. a
Frew, N. M., Bock, E. J., Schimpf, U., Hara, T., Haussecker, H., Edson, J. B., McGillis, W. R., Nelson, R. K., McKenna, S. P., Uz, B. M., and Jähne, B.: Air-sea gas transfer: its dependence on wind stress, smallscale roughness, and surface films, J. Geophys. Res., 109, C08S17, https://doi.org/10.1029/2003JC002131, 2004. a
Garbe, C. S., Rutgersson, A., Boutin, J., deLeeuw, G., Delille, B., Fairall, C. W., Gruber, N., Hare, J., Ho, D. T., Johnson, M. T., Nightingale, P. D., Pettersson, H., Piskozub, J., Sahlée, E., Tsai, W., Ward, B., Woolf, D. K., and Zappa, C. J.: Transfer across the air-sea interface, in: Ocean-atmosphere interactions of gases and particles, edited by: Liss, P. S. and Johnson, M. T., Springer Earth System Sciences, Heidelberg, New York, Dordrecht, London, https://doi.org/10.1007/978-3-642-25643-1_2, 2014. a, b, c, d
Gentemann, C. L., Donlon, C. J., Stuart-Menteth, A., and Wentz, F. J.: Diurnal signals in satellite sea surface temperature measurements, Geophys. Res. Lett., 30, 1140, https://doi.org/10.1029/2002GL016291, 2003. a
Gentemann, C. L., Minnett, P. J., LeBorgne, P., and Merchant, C. J.: Multi-satellite measurements of large diurnal warming events, Geophys. Res. Lett., 35, L22602, https://doi.org/10.1029/2008GL035730, 2008. a
Gentemann, C. L., Minnett, P. J., and Ward, B.: Profiles of ocean surface heating (POSH): A new model of upper ocean diurnal warming, J. Geophys. Res., 114, C07017, https://doi.org/10.1029/2008JC004825, 2009. a, b
Gutiérrez, D., Enriquez, E., Purca, S., Quipuzcoa, L., Marquina, R., Flores, G., and Graco, M.: Oxygenation episodes on the continental shelf of central Peru: Remote forcing and benthic ecosystem response, Prog. Oceanogr., 79, 177–189, https://doi.org/10.1016/j.pocean.2008.10.025, 2008. a
Hahn, J. and Crutzen, P. J.: The role of fixed nitrogen in atmospheric photochemistry, Philos. T. R. Soc. B, 296, 521–541, 1982. a
Hamersley, M. R., Lavik, G., Woebken, D., Rattray, J. E., Lam, P., Hopmans, E. C., Sinninghe Damsté, J. S., Krüger, S., Graco, M., Gutiérrez, D., and Kuypers, M. M. M.: Anaerobic ammonium oxidation in the Peruvian oxygen minimum zone, Limnol. Oceanogr., 52, 923–933, https://doi.org/10.4319/lo.2007.52.3.0923, 2007. a
Imberger, J.: The diurnal mixed layer, Limnol. Oceanogr., 30, 737–770, https://doi.org/10.4319/lo.1985.30.4.0737, 1985. a
Ji, Q., Babbin, A. R., Jayakumar, A., Oleynik, S., and Ward, B. B.: Nitrous oxide production by nitrification and denitrification in the eastern tropical South Pacific oxygen minimum zone, Geophys. Res. Lett., 42, 10755–10764, https://doi.org/10.1002/2015GL066853, 2015. a, b, c
Kalvelage, T., Jensen, M. M., Contreras, S., Revsbach, N. P., Lam, P., Günter, M., LaRoche, J., Lavik, G., and Kuypers, M. M. M.: Oxygen sensitivity of anammox and coupled N-cycle processes in oxygen minimum zones, PLOS ONE, 6, e29299, https://doi.org/10.1371/journal.pone.0029299, 2011. a
Kanzow, T. and Krahmann, G.: Physical oceanography from glider mission ifm06_depl02, PANGAEA, https://doi.org/10.1594/PANGAEA.884284, 2017a. a
Kanzow, T. and Krahmann, G.: Physical oceanography from glider mission ifm07_depl08, PANGAEA, https://doi.org/10.1594/PANGAEA.884286, 2017b. a
Kanzow, T. and Krahmann, G.: Physical oceanography from glider mission ifm08_depl05, PANGAEA, https://doi.org/10.1594/PANGAEA.884281, 2017c. a
Kanzow, T. and Krahmann, G.: Physical oceanography from glider mission ifm11_depl04, PANGAEA, https://doi.org/10.1594/PANGAEA.884282, 2017d. a
Kanzow, T. and Krahmann, G.: Physical oceanography from glider mission ifm12_depl01, PANGAEA, https://doi.org/10.1594/PANGAEA.884283, 2017e. a
Kanzow, T. and Krahmann, G.: Physical oceanography from glider mission ifm03_depl09, PANGAEA, https://doi.org/10.1594/PANGAEA.887703, 2018. a
Kawai, Y. and Wada, A.: Diurnal sea surface temperature variation and its impact on the atmosphere and ocean: a review, J.Oceanogr., 63, 721–744, https://doi.org/10.1007/s10872-007-0063-0, 2007. a
Kock, A., Schafstall, J., Dengler, M., Brandt, P., and Bange, H. W.: Sea-to-air and diapycnal nitrous oxide fluxes in the eastern tropical North Atlantic Ocean, Biogeosciences, 9, 957–964, https://doi.org/10.5194/bg-9-957-2012, 2012. a, b, c
Kock, A., Arévalo-Martínez, D. L., Löscher, C. R., and Bange, H. W.: Extreme N2O accumulation in the coastal oxygen minimum zone off Peru, Biogeosciences, 13, 827–840, https://doi.org/10.5194/bg-13-827-2016, 2016. a, b, c, d, e, f
Kock, A. and Bange, H. W.: Nitrous oxide measured on water bottle samples during METEOR cruise M91, PANGAEA, https://doi.org/10.1594/PANGAEA.858178, 2016. a
Krahmann, G. and Bange, H. W.: Physical oceanography during METEOR cruise M91, PANGAEA, https://doi.org/10.1594/PANGAEA.858090, 2016. a
Krall, K. E., Schneider-Zapp, K., Reith, S., Kiefhaber, D., and Jähne, B.: Air-sea gas exchange under nature-like surfactant influence in the lab, 7th SOPRAN Annual Meeting, Zenodo, https://doi.org/10.5281/zenodo.10900, 2014. a
Lam, P. and Kuypers, M. M. M.: Microbial nitrogen cycling processes in oxygen minimum zones, Ann. Rev. Mar. Sci., 3, 317–345, https://doi.org/10.1146/annurev-marine-120709-142814, 2011. a
Lavik, G.: Short cruise report Meteor cruise M93 – Callao (Peru) – Balboa (Panama) – February 7–March 9 2013, 15 pp., https://www.ldf.uni-hamburg.de/meteor/wochenberichte/wochenberichte-meteor/m90-m93/m93-scr.pdf (last access: 4. May 2016), 2013. a
Law, C. S. and Owens, N. J. P.: Significant flux of atmospheric nitrous oxide from the northwest Indian Ocean, Nature, 346, 826–828, https://doi.org/10.1038/346826a0, 1990. a, b
McNeil, C. L. and Merlivat, L.: The warm oceanic surface layer: Implications for CO2 fluxes and surface gas measurements, Geophys. Res. Lett., 23, 3575–3578, https://doi.org/10.1029/96GL03426, 1996. a, b
MEMENTO: N2O data, available at: https://memento.geomar.de/de, last access: 16 May 2019. a
Miller, L. A., Burgers, T. M., Burt, W. J., Granskog, M. A., and Papakyriakou, T. N.: Air-sea CO2 flux estimates in stratified Arctic coastal waters: How wrong can we be?, Geophys. Res. Lett., 46, https://doi.org/10.1029/2018GL080099, 2019. a, b
Myhre, G., Shindell, D., Bréon, F.-M., Collins, W., Fuglestvedt, J., Huang, J., Koch, D., Lamarque, J.-F., Lee, D., Mendoza, B., Nakajima, T., Robock, A., Stephens, G., Takemura, T., and Zhang, H.: Anthropogenic and natural radiative forcing, in: Climate Change 2013: The physical science basis. Contribution of working group I to the fifth assessment report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK, and New York, NY, USA, 2013. a
Naqvi, S. W. A., Jayakumar, D. A., Narvekar, P. V., Naik, H., Sarma, V. V. S. S., D'Souza, W., Joseph, S., and George, M. D.: Increased marine production of N2O due to intensifying anoxia on the Indian continental shelf, Nature, 408, 346–349, https://doi.org/10.1038/35042551, 2000. a
Naqvi, S. W. A., Bange, H. W., Farías, L., Monteiro, P. M. S., Scranton, M. I., and Zhang, J.: Marine hypoxia/anoxia as a source of CH4 and N2O, Biogeosciences, 7, 2159–2190, https://doi.org/10.5194/bg-7-2159-2010, 2010. a, b, c, d
Nevison, C. D., Weiss, R. F., and Erickson, D. J.: Global oceanic emissions of nitrous oxide, J. Geophys. Res., 100, 15809–15820, https://doi.org/10.1029/95JC00684, 1995. a
Nevison, C., Butler, J. H., and Elkins, J. W.: Global distribution of N2O and the delta N2O-AOU yield in the subsurface ocean, Global Biogeochem. Cy., 17, 1119, https://doi.org/10.1029/2003GB002068, 2003. a
Nevison, C. D., Lueker, T. J., and Weiss, R. F.: Quantifying the nitrous oxide source from coastal upwelling, Global Biogeochem. Cy., 18, GB1018, https://doi.org/10.1029/2003GB002110, 2004. a, b, c, d
Nightingale, P. D., Malin, G., Law, C. S., Watson, A. J., Liss, P. S., Liddicoat, M. I., Boutin, J., and Upstill-Goddard, R. C.: In situ evaluation of air-sea gas exchange parameterizations using novel conservative and volatile tracers, Global Biogeochem. Cy., 14, 373–387, https://doi.org/10.1029/1999GB900091, 2000. a, b, c, d, e
OSIS: data of GEOMAR expeditions and experiments, available at: https://portal.geomar.de/kdmi, last access: 16 May 2019. a
Pennington, J. T., Mahoney, K. L., Kuwahara, V. S., Kolber, D. D., Calienes, R., and Chavez, F. P.: Primary production in the eastern tropical Pacific: A review, Prog. Oceanogr., 69, 285–317, https://doi.org/10.1016/j.pocean.2006.03.012, 2006. a
Price, J. F., Weller, R. A., and Pinkel, R.: Diurnal cycling: Observations and models of the upper ocean response to diurnal heating, cooling, and wind mixing, J. Geophys. Res., 91, 8411–8427, https://doi.org/10.1029/JC091iC07p08411, 1986. a, b, c, d
Prytherch, J., Farrar, J. T., and Weller, R. A.: Moored surface buoy observations of the diurnal warm layer, J. Geophys. Res., 118, 4553–4569, https://doi.org/10.1002/jgrc.20360, 2013. a, b, c, d, e, f, g
Ravishankara, A. R., Daniel, J. S., and Portmann, R. W.: Nitrous oxide (N2O): The dominant ozone-depleting substance emitted in the 21st century, Science, 326, 123–125, https://doi.org/10.1126/science.1176985, 2009. a
Rees, A. P., Owens, N. J. P., and Upstill-Goddard, R. C.: Nitrous oxide in the Bellingshausen Sea and Drake Passage, J. Geophys. Res., 102, 3383–3391, https://doi.org/10.1029/96JC03350, 1997. a
Rhee, T. S., Kettle, A. J., and Andreae, M. O.: Methane and nitrous oxide emissions from the ocean: A reassessment using basin-wide observations in the Atlantic, J. Geophys. Res., 114, D12304, https://doi.org/10.1029/2008JD011662, 2009. a
Salter, M. E., Upstill-Goddard, R. C., Nightingale, P. D., Archer, S. D., Blomquist, B., Ho, D. T., Huebert, B., Schlosser, P., and Yang, M.: Impact of an artificial surfactant release on air-sea gas fluxes during Deep Ocean Gas Exchange Experiment II, J. Geophys. Res., 116, C11016, https://doi.org/10.1029/2011JC007023, 2011. a
Schlundt, M., Brandt, P., Dengler, M., Hummels, R., Fischer, T., Bumke, K., Krahmann, G., and Karstensen, J.: Mixed layer heat and salinity budgets during the onset of the 2011 Atlantic cold tongue, J. Geophys. Res.-Oceans, 119, 7882–7910, https://doi.org/10.1002/2014JC010021, 2014. a, b
Soloviev, A. V. and Vershinsky, N. V.: The vertical structure of the thin surface layer of the ocean under conditions of low wind speed, Deep Sea Res., 29, 1437–1449, https://doi.org/10.1016/0198-0149(82)90035-8, 1982. a
Soloviev, A. and Lukas, R.: Observation of large diurnal warming events in the near-surface layer of the western equatorial Pacific warm pool, Deep-Sea Res. Pt. I, 44, 1055–1076, https://doi.org/10.1016/S0967-0637(96)00124-0, 1997. a, b, c
Soloviev, A., Edson, J., McGillis, W., Schluessel, P., and Wanninkhof, R.: Fine thermohaline structure and gas-exchange in the near-surface layer of the ocean during GasEx-98, in: Gas transfer at water surfaces, edited by: Donelan, M. A., Drennan, W. M., Saltzman, E. S., and Wanninkhof, R., AGU Geophysical Monograph 127, Washington DC, USA, 2002. a, b, c, d, e, f, g, h
Soloviev, A. and Lukas, R.: The near-surface layer of the ocean, 2nd edition, Springer, Dordrecht, the Netherlands, 2014. a, b
Sommer, S., Dengler, M., and Treude, T.: Benthic element cycling, fluxes and transport of solutes across the benthic boundary layer in the Peruvian oxygen minimum zone, (SFB 754) – Cruise No. M92 – January 05–February 03 2013 – Callao (Peru) – Callao (Peru), METEOR-Berichte, M92, 55 pp., DFG-Senatskommission für Ozeanographie, https://doi.org/10.2312/cr_m92, 2014. a
Stommel, H. and Woodcock, A. H.: Diurnal heating of the surface of the Gulf of Mexico in the spring of 1942, Transactions of the American Geophysical Union, 32, 565–571, 1951. a, b
Stramma, L., Cornillon, P., Weller, R. A., Price, J. F., and Briscoe, M. G.: Large diurnal sea surface temperature variability: satellite and in situ measurements, J. Phys. Oceanogr., 16, 827–837, https://doi.org/10.1175/1520-0485(1986)016<0827:LDSSTV>2.0.CO;2, 1986. a
Suntharalingam, P. and Sarmiento, J. L.: Factors governing the oceanic nitrous oxide distribution: Simulations with an ocean general circulation model, Global Biogeochem. Cy., 14, 429–454, https://doi.org/10.1029/1999GB900032, 2000. a
Sutherland, G., Reverdin, G., Marié, L., and Ward, B.: Mixed and mixing layer depths in the ocean surface boundary layer under conditions of diurnal stratification, Geophys. Res. Lett., 41, 8469–8476, https://doi.org/10.1002/2014GL061939, 2014. a
Sutherland, G., Marié, L., Reverdin, G., Christensen, K. H., Broström, G., and Ward, B.: Enhanced turbulence associated with the diurnal jet in the ocean surface boundary layer, J. Phys. Oceanogr., 46, 3051–3067, https://doi.org/10.1175/JPO-D-15-0172.1, 2016. a, b
Thomsen, S., Kanzow, T., Krahmann, G., Greatbatch, R. J., Dengler, M., and Lavik, G.: The formation of a subsurface anticyclonic eddy in the Peru-Chile Undercurrent and its impact on the near-coastal salinity, oxygen, and nutrient distributions, J. Geophys. Res., 121, 476–501, https://doi.org/10.1002/2015JC010878, 2016. a, b, c
Tsai, W. and Liu, K.: An assessment of the effect of sea-surface surfactant on global atmosphere-ocean CO2 flux, J. Geophys. Res., 108, 3127, https://doi.org/10.1029/2000JC000740, 2003. a
Wang, W. C., Yung, Y. L., Lacis, A. A., Mo, T., and Hansen, J. E.: Greenhouse effects due to man-made perturbations of trace gases, Science, 194, 685–690, 1976. a
Ward, B., Wanninkhof, R., McGillis, W. R., Jessup, A. T., DeGrandpre, M. D., Hare, J. E., and Edson, J. B.: Biases in the air-sea flux of CO2 resulting from ocean surface temperature gradients, J. Geophys. Res., 109, C08S08, https://doi.org/10.1029/2003JC001800, 2004. a
Ward, B. B., Glover, H. E., and Lipschultz, F.: Chemoautotrophic activity and nitrification in the oxygen minimum zone off Peru, Deep-Sea Res. Pt. A, 36, 1031–1051, https://doi.org/10.1016/0198-0149(89)90076-9, 1989. a
Ward, B. B.: Chapter 5 – Nitrification in marine systems, in: Nitrogen in the marine environment, Academic Press, San Diego, CA, USA, 2nd ed., 199–261, https://doi.org/10.1016/B978-0-12-372522-6.00005-0, 2008. a
Weiss, R. F. and Price, B. A.: Nitrous oxide solubility in water and seawater, Mar. Chem., 8, 347–359, 1980. a
Weiss, R. F., Van Woy, F. A., and Salameh, P. K.: Surface water and atmospheric carbon dioxide and nitrous oxide observations by shipboard automated gas chromatography: Results from expeditions between 1977 and 1990, Rep. ORNL/CDIAC-59, NDP-044, Oak Ridge Nat. Lab., Oak Ridge, TN, USA, 1992. a
Wenegrat, J. O. and McPhaden, M. J.: Dynamics of the surface layer diurnal cycle in the equatorial Atlantic Ocean (0∘, 23∘ W), J. Geophys. Res., 120, 563–581, https://doi.org/10.1002/2014JC010504, 2015. a, b, c, d, e
Woolf, D. K., Land, P. E., Shutler, J. D., Goddijn-Murphy, L. M., and Donlon, C. J.: On the calculation of air-sea fluxes of CO2 in the presence of temperature and salinity gradients, J. Geophys. Res.-Oceans, 121, 1229–1248, https://doi.org/10.1002/2015JC011427, 2016. a