the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Underestimation of denitrification rates from field application of the 15N gas flux method and its correction by gas diffusion modelling
Martin Maier
Dominika Lewicka-Szczebak
Jan-Reent Köster
Nicolas Ruoss
Common methods for measuring soil denitrification in situ include monitoring the accumulation of 15N-labelled N2 and N2O evolved from 15N-labelled soil nitrate pool in closed chambers that are placed on the soil surface. Gas diffusion is considered to be the main transport process in the soil. Because accumulation of gases within the chamber decreases concentration gradients between soil and the chamber over time, the surface efflux of gases decreases as well, and gas production rates are underestimated if calculated from chamber concentrations without consideration of this mechanism. Moreover, concentration gradients to the non-labelled subsoil exist, inevitably causing downward diffusion of 15N-labelled denitrification products. A numerical 3-D model for simulating gas diffusion in soil was used in order to determine the significance of this source of error. Results show that subsoil diffusion of 15N-labelled N2 and N2O – and thus potential underestimation of denitrification derived from chamber fluxes – increases with chamber deployment time as well as with increasing soil gas diffusivity. Simulations based on the range of typical soil gas diffusivities of unsaturated soils showed that the fraction of N2 and N2O evolved from 15N-labelled that is not emitted at the soil surface during 1 h chamber closing is always significant, with values up to >50 % of total production. This is due to accumulation in the pore space of the 15N-labelled soil and diffusive flux to the unlabelled subsoil. Empirical coefficients to calculate denitrification from surface fluxes were derived by modelling multiple scenarios with varying soil water content. Modelling several theoretical experimental set-ups showed that the fraction of produced gases that are retained in soil can be lowered by lowering the depth of 15N labelling and/or increasing the length of the confining cylinder.
Field experiments with arable silt loam soil for measuring denitrification with the 15N gas flux method were conducted to obtain direct evidence for the incomplete surface emission of gaseous denitrification products. We compared surface fluxes of 15N2 and 15N2O from 15N-labelled micro-plots confined by cylinders using the closed-chamber method with cylinders open or closed at the bottom, finding 37 % higher surface fluxes with the bottom closed. Modelling fluxes of this experiment confirmed this effect, however with a higher increase in surface flux of 89 %.
From our model and experimental results we conclude that field surface fluxes of 15N-labelled N2 and N2O severely underestimate denitrification rates if calculated from chamber accumulation only. The extent of this underestimation increases with closure time. Underestimation also occurs during laboratory incubations in closed systems due to pore space accumulation of 15N-labelled N2 and N2O. Due to this bias in past denitrification measurements, denitrification in soils might be more relevant than assumed to date.
Corrected denitrification rates can be obtained by estimating subsurface flux and storage with our model. The observed deviation between experimental and modelled subsurface flux revealed the need for refined model evaluation, which must include assessment of the spatial variability in diffusivity and production and the spatial dimension of the chamber.
- Article
(761 KB) -
Supplement
(328 KB) - BibTeX
- EndNote
N2O reduction to N2 is the last step of microbial denitrification, i.e. anoxic reduction of nitrate () to N2 with the intermediates , NO and N2O (Müller and Clough, 2014). Commonly applied analytical techniques enable us to quantitatively analyse only the intermediate product of this process, N2O, but not the final product, N2. The challenge of quantifying denitrification rates is largely due to the difficulty in measuring N2 production due to its spatial and temporal heterogeneity and the high N2 background of the atmosphere (Groffman et al., 2006). There are three principles to overcome the latter problem: (i) adding that is highly enriched in 15N and monitoring 15N-labelled denitrification products (15N gas flux method; e.g. Siegel et al., 1982), (ii) adding acetylene to block N2O reductase quantitatively and estimating total denitrification from N2O production (acetylene inhibition technique, e.g. Felber et al., 2012), and (iii) measuring denitrification gases during incubation of soils in the absence of atmospheric N2 using gas-tight containers and artificial helium–oxygen atmosphere (HeO2 method; Scholefield et al., 1997; Butterbach-Bahl et al., 2002). Each of these methods to quantify denitrification rates in soils has various limitations with respect to potential analytical bias, applicability at different experimental scales and the necessity of expensive instrumentation that is not available for routine studies. Today the acetylene inhibition technique is considered to be unsuitable for quantifying N2 fluxes under natural atmosphere, since its main limitation (among several others; e.g. Saggar et al., 2013) is the catalytic decomposition of NO in the presence of O2 (Bollmann and Conrad, 1997a, b). This results in unpredictable underestimation of gross N2O production (Nadeem et al., 2013). The 15N gas flux method requires homogenous 15N labelling of the soil (Mulvaney and Vandenheuvel, 1988). Moreover, under natural atmosphere this method is not sensitive enough to detect small N2 fluxes (Lewicka-Szczebak et al., 2013). Direct measurement of N2 fluxes using the HeO2 method is not subject to the problems associated with 15N-based methods (Butterbach-Bahl et al., 2013), but the need for sophisticated gas-tight incubation systems limits its use to laboratory incubations only. Consequently, the 15N gas flux method is the only method that is potentially applicable in field conditions.
Denitrification in ecosystems is complexly controlled by interaction of labile C, abundance and community structure of denitrifiers, pore structure, soil and root respiration, and mineral N dynamics (Müller and Clough, 2014). It is difficult to keep conditions in the lab identical to the field, where some conditions dynamically change due to climatic factors but especially due to the activity of plants. Hence, field measurements are indispensable for reliable determination of denitrification in ecosystems.
When chamber methods are used to determine soil gas fluxes to the atmosphere, a certain fraction of the produced gas is not emitted at the surface but remains in the soil (Parkin et al., 2012). This is because the accumulation of gases in the closed chamber decreases concentration gradients between soil and chamber atmosphere, causing lowering of surface fluxes with increasing chamber deployment time (Healy et al., 1996). This effect has been addressed in numerous studies (Venterea et al., 2009; Healy et al., 1996; Sahoo et al., 2010). To correct bias from this effect, several approaches have been developed and compared (Parkin et al., 2012). Denitrification estimates based on measurements of N2 and N2O surface fluxes could also be biased by this effect. This was suggested for the acetylene inhibition technique in the field (Mahmood et al., 1998) and also for the 15N gas flux method (Sgouridis et al., 2016). However, to our knowledge the magnitude in possible underestimation of denitrification rates has not been investigated until now. It can be expected that diffusive loss of 15N-labelled gases to the subsoil is even more relevant than the respective loss of non-labelled soil gases. This is due to the fact that the production of CO2 and trace gases in soil is ubiquitous, whereas the formation of 15N-labelled denitrification products is limited to the soil volume amended with 15N-labelled .
Estimating bias from the diffusive loss of 15N-labelled gases could be done by modelling. Previously, denitrification in subsoil was quantified by fitting measured and modelled steady-state concentration of 15N2+15N2O (Well and Myrold, 2002). Modelling diffusive fluxes of 15N2+15N2O produced in 15N-labelled surface soil based on measured surface flux and diffusivity could be used to estimate its accumulation in pore space and diffusive loss to the subsoil. This could be used to quantify denitrification from the sum of surface flux, subsoil flux and storage within the 15N-labelled soil volume.
Our objectives were thus to determine the significance of the fraction of 15N-labelled denitrification products produced in 15N-labelled soil in the field that is not emitted at the soil surface. This was done experimentally and by diffusion modelling. Moreover, we aimed to develop a procedure for determining denitrification rates from surface flux data. We hypothesized that (i) a significant fraction of 15N-labelled denitrification products is not emitted at the soil surface; (ii) this fraction depends on diffusivity, chamber deployment time and depth of 15N labelling; and (iii) diffusive loss of 15N-labelled gases to the subsoil is more relevant than accumulation in the pore space of the 15N-labelled soil.
2.1 Principles of the 15N gas flux method and gas flux dynamics following 15N tracer application
The 15N gas flux method consists of quantifying N2 and/or N2O emitted from 15N-labelled nitrate applied to soil in order to quantify fluxes from microbial denitrification (Mulvaney, 1988; Stevens et al., 1993), where N2 and N2O are formed from the combination of two NO precursor molecules. To quantify denitrification, experimental soil is typically confined by cylinders installed to a certain depth. These micro-plots are amended with 15N-labelled nitrate either by surface application of the fertilizer (Kulkarni et al., 2014) or by injecting fertilizer solution using needles to achieve homogenous labelling (Sgouridis et al., 2016; Buchen et al., 2016). Emitted 15N-labelled gases are collected in chambers, fitted to be gas tight on top of the cylinders, typically for periods of 1 h or longer. Soil-derived gases mix with background air inside the closed chambers. N2 and N2O fluxes from the labelled are calculated from the abundance of N2 and N2O isotopologues (i.e. molecular species that differ in the number of isotopic substitutions; Coplen, 2011) in the gas accumulating in the chamber.
In order to measure denitrification in arable soil, depth of confinement, and also of labelling, typically includes the ap horizon of the soil, i.e. usually depth of tillage. In this horizon, most denitrification activity is assumed due to its content in soil organic matter, undecomposed plant litter, organic root exudates, root respiration and fertilizer application to the surface (Groffman et al., 2009).
To keep our modelling as simple as possible we assume a simplified process dynamics where in terms of N transformation, only nitrate reduction by microbial denitrification occurs, with N2 and N2O as emitted products.
The bias in determining denitrification rates from the accumulation of 15N2 and 15N2O is illustrated by a conceptual model (Figs. 1 and 2a, b). After closing a chamber on top of the 15N-labelled soil, the timing and magnitude of 15(N2+N2O) fluxes depend on the chamber volume, on denitrification rates of the 15N-labelled soil, and on gas diffusivity within and around this soil (Fig. 1).
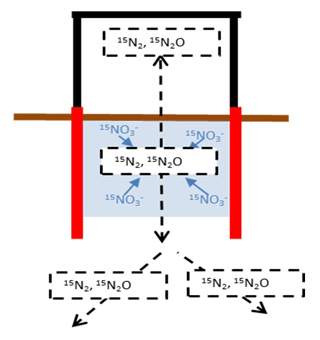
Figure 1Conceptual model describing the dynamics of diffusive fluxes (black dotted arrows) of 15N-labelled gaseous denitrification products evolved in a 15N-labelled soil volume (shaded area) that is confined by a cylinder with open bottom to the subsoil but temporarily closed from above with a flux chamber to collect emitted gases.
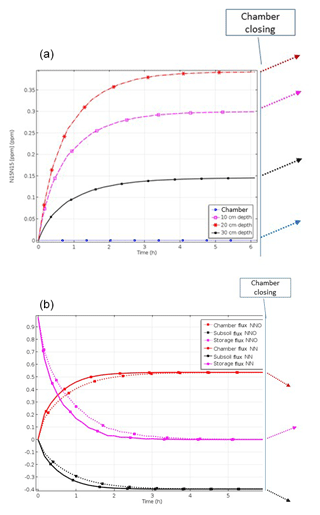
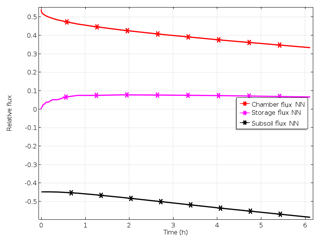
Figure 2(a) Increase in pore space concentrations of N2 evolved from the 15N-labelled pool after start of denitrification, with open chamber when production of 15N-labelled N2 and N2O starts at constant rates, leading to accumulation of 15N-labelled gases and thus build-up of concentration gradients to the surface and to the subsoil. Concentration trends following chamber closure are shown as dotted lines. (b) Time course of relative fluxes of N2 and N2O evolved from the 15N-labelled pool after start of denitrification, with open chamber showing increasing surface and subsoil fluxes while the storage flux decreases until steady state is reached. Trends of fluxes following chamber closure are shown as dotted lines.
We define the fluxes of 15N-labelled gases as relative fluxes in relation to the production of these gases as follows.
-
The surface flux is the flux of 15N-labelled gases to the atmosphere at the soil surface, either into the free atmosphere or into a closed flux chamber. Relative surface flux is the ratio between the surface flux rate and production rate.
-
Relative subsoil flux is the flux rate of 15N-labelled gases at the lower boundary of the 15N-labelled soil in relation to the production rate. Subsoil flux occurs always in the downward direction and is thus expressed as negative flux.
-
Accumulation of 15N-labelled gases within the 15N-labelled soil is referred to as storage flux, which is the increase in the concentration of accumulated 15N-labelled gases. Relative storage flux is thus storage flux rate in relation to the production rate.
Assuming constancy of denitrification rates and gas diffusivity, the dynamics in concentration and gaseous fluxes would establish the following.
-
Following 15N labelling, production of 15N-labelled N2 and N2O would start at constant rates.
-
Before closing the chamber, the upper soil boundary is the free atmosphere, where gas exchange is fast enough to preclude 15N accumulation above the soil surface.
-
Production leads to accumulation of 15N-labelled gases and thus to a build-up of concentration gradients to the surface and to the subsoil (Fig. 2a), which causes increasing surface and subsoil fluxes while the storage flux decreases (Fig. 2b).
-
After a certain time, the steady state is reached, where all fluxes reach constancy.
-
Closing the chamber changes the upper boundary, since chamber concentration increases due to surface flux (Fig. 2a). Consequently, subsoil and storage flux are rising again, whereas surface flux is decreasing.
If diffusivity and volume of 15N-labelled soil are known and constancy of parameters is long enough to achieve the steady state before closing the chamber, then the relative surface flux can be determined by modelling production and diffusion with an open chamber until the steady state and during the subsequent phase of chamber closing. Production can thus be calculated from modelled relative surface flux and the measured surface flux rate.
2.2 Numerical finite element modelling of soil gas transport
2.2.1 Conceptual model of the experimental set-up
Numerical finite element modelling (FEM) was used for simulating gas transport during the chamber measurements (COMSOL Multiphysics, Version 5.2, COMSOL Inc., Burlington, Massachusetts, US) to estimate surface and subsurface fluxes of 15N-labelled N2 and N2O. A conceptual 3-D model was built based on geometry and properties of the experimental set-up, meaning soil and the cylinder containing the labelled , the atmosphere and the chamber. We assumed a soil pore matrix consisting of two soil layers with homogenous properties each (total pore volume, soil water content and soil gas diffusivity) into which a gas-impermeable cylinder of 15 cm diameter and 35 cm length was vertically installed to a depth of 30 cm. The soil within the cylinder was assumed to be homogenously distributed and labelled with 50 at. % 15N to homogeneously produce the isotopologues of N2 and N2O (14N14N, 15N14N, 15N15N, 14N14NO, 15N14NO and 15N15NO), while the surrounding soil did not produce any of these gas species. The latter assumption is a simplification to reduce modelling effort, since all of the isotopologues are produced to some extent also from non-labelled N sources outside the 15N-labelled soil volume. However, due to the high 15N enrichment in the labelled soil, the abundance of 15N14N is 69 times higher in the 15N pool derived fluxes, and the abundance of 15N15N is even 18 600 times higher, compared to natural abundance of 15N. Hence, fluxes from non-labelled N pools would not significantly affect the model result. A cylinder-shaped gas-impermeable cover chamber 20 cm height in total was used to temporarily close the base cylinder to measure soil gas fluxes. The model assumes that the chamber atmosphere is always homogeneously mixed and that production is constant within the 15N-labelled soil volume. The cylinder was always assumed to be open at the bottom unless differently specified.
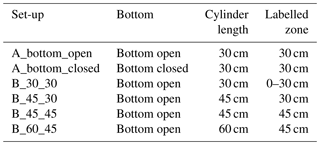
Two different experimental set-ups were modelled and used in the field. The first experimental set-up (A_bottom_open) is described by the conceptual model above and includes an open bottom cylinder containing the labelled . In the second set-up (A_bottom_closed), the lower end of the cylinder was sealed so that gases could only be emitted via the surface. This was represented by an additional impermeable thin layer (Table 1).
2.2.2 Gas transport modelling
Molecular gas diffusion was assumed to be the only transport mechanism in the soil. The left and right side and the bottom of the modelled domain were defined as impermeable (Neumann boundary condition). The upper boundary of the atmospheric layer was set to atmospheric gas concentrations as the Dirichlet boundary condition and acts therefore as a sink for the gases produced. To increase computational efficiency, a 2-D axisymmetric modelling approach was chosen, since the cylinder and the chamber were round objects. The modelled volume was set to sufficiently large volume with a soil depth of 1.0 m and a diameter of 1.0 m to ensure that the dimension of the modelled area does not affect the modelling outcome within the cylinder and chamber area.
Gas transport was modelled for all isotopologues of N2 and N2O. Diffusivity in free air (D0) was set to 0.193 cm2 s−1 for 14N14N and 0.137 cm2 s−1 for 14N14NO according to Marrero and Mason (1972). Diffusivity in free air of 15N14N (0.1913 cm2 s−1), 15N15N (0.1896 cm2 s−1), 15N14NO (0.1364 cm2 s−1) and 15N15NO (0.1358 cm2 s−1) were derived based on their mass, following Jost (1960). The relative diffusion coefficient in soil DS∕D0 accounts for the reduced diffusivity in a porous system. DS∕D0 was calculated using the diffusion model of Millington (1959; ), where the air-filled pore volume E was calculated as the difference of the total pore volume (TP) of the soil and the volumetric soil water content (SWC), and TP was derived from bulk density. The free atmosphere was assumed to be a well-mixed single layer, and the effective diffusivity was set to 40×D0 so that the concentration in the atmosphere was kept stable.
2.3 Modelling set-ups and scenarios
Different experimental set-ups and scenarios were modelled with the lower end of the cylinder being sealed or open (A_bottom_closed; A_bottom_open), describing the field set-up that was actually used (Table 1). Also further theoretical set-ups have been modelled to evaluate the effect of the dimension of the cylinder and labelled zone (B scenarios).
2.3.1 Time until steady state after labelling
Time-dependent modelling of the open chamber set-up was performed to assess the time that is needed after the initiation of the system, i.e. after adding labelled , until the production and transport of the N2O and N2 isotopologues reach a steady-state concentration distribution within the soil cylinder and the surrounding soil (Fig. 2a and b). This represents the minimum time to be waited after the label application before the first chamber measurement.
2.3.2 Modelling chamber measurements
To model chamber measurement, two modelling steps were run. In a first modelling step, steady-state concentration distributions assuming steady denitrification were modelled for the open chamber. The resulting concentration distributions were then used in a second modelling step as input for time step 0 for the time-dependent modelling of the closed chamber (Fig. 2a and b). This approach was used for all modelling scenarios.
2.3.3 Modelling the effect of soil moisture
Parameter sweeps were conducted for the set-ups used in the field (A_bottom_open and A_ bottom_ closed; Table 1) to assess the theoretical effect of soil moisture, pore volumes and production rates. This was done to account for these transport-related effects in the calculation of the flux measurements. For all parameter combinations a new model was calculated.
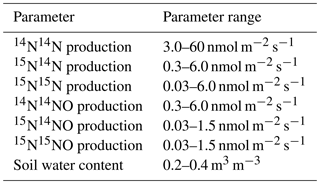
Total pore volume was set to 0.51 m3 m−3 for the parameter sweep which corresponds to a bulk soil density of 1.30 g cm−3. The soil water contents used for the parameter sweep were 0.2, 0.3, 0.35 and 0.4 m3 m−3 and corresponded to a range of DS∕D0 of 0.053–0.210. The production rates of the gas species used for the parameter sweep were chosen (Table 2) so that the outcome of the parameter sweep models covered the range of the observed concentration of the respective species.
The output of the parameter sweeps of scenario A_ bottom_open and scenario A_bottom closed included combinations of soil water content, production rates of the soil core, chamber concentrations, and fluxes into the chamber and into the subsoil of the respective gas species. This dataset allowed for linking the gas concentration in the chamber after 2 h at a given soil moisture with the respective production rate. Non-linear functions were fitted to the dataset (PROC NLIN, SAS 9.2, SAS Institute Inc., Cary, North Carolina, USA) so that the original production of a gas species could be directly calculated from the concentration after 2 h of the respective gas, the total pore volume and the soil moisture. Instead of soil water content, the soil gas diffusion coefficient DS was used as a factor, which allowed deriving a single functional relationship for all gas species for each scenario. This procedure was chosen as an efficient alternative to inverse modelling of individual datasets as described in Laemmel et al. (2019).
Four additional theoretical experimental set-ups were modelled to assess the effect of the soil cylinder length and the length of the labelled zone within the cylinder (B-scenarios, Table 1). For these set-ups the same soil parameters were used as for the field scenarios. To assess the effect of soil moisture, the model was run at soil water contents of 0.24, 0.34 and 0.44 m3 m−3 .
Underestimation of gas production was quantified as the difference between the production (Pi) and the mean surface efflux during the chamber closure (mean Effluxi), divided by . The mean surface efflux during the chamber closure corresponds to a linear approach, e.g. the flux is calculated using the initial and final gas concentration. Subsoil loss was quantified as mean subsoil flux at the lower end of the core during the chamber closure divided by Pi.
2.4 Field measurements
Experiments were part of a field campaign to measure N2O fluxes and denitrification in an arable soil cropped with maize. The soil was a Haplic Luvisol developed in loess (silty loam texture with 83±3 % silt, 15±3 % clay and 2±0.5 % sand), with a pH of 6.7±0.1 (in CaCl2), a total organic carbon content of 1.24±0.18 % (TOC) and a total nitrogen content of 0.16±0.02 % N in the 0–30 cm topsoil layer. Experiments were conducted between 30 May and 4 June 2016.
Four aluminium cylinders of 35 cm length and tapered at the lower end were driven into the soil to 30 cm depth, thus leaving the upper end 5 cm above the soil surface. 15N labelling was conducted on 30 May, as described previously (Buchen et al., 2016). Soil columns were fertilized with 15N-labelled KNO3 (70 at. % 15N) at 10 mg N kg−1, resulting in a fertilizer equivalent of 45 kg N ha−1. The tracer was dissolved in distilled water and then applied by injections via 12 equidistant steel capillaries. Defined volumes were injected at 2.5, 7.5, 12.5, 17.5, 22.5 and 27.5 cm depth using a peristaltic pump (Ismatec BVP, Wertheim, Germany) to achieve homogenous labelling at 0 to 30 cm depth. Fluxes of N2O were determined using the closed-chamber method (Hutchinson and Mosier, 1981) with opaque PVC chambers with a volume of 4.42 dm3 (diameter 1.5 dm; height 2 dm). At each sampling date, chambers were closed and sealed to be air tight with rubber bands for 120 min. Headspace sampling for gas chromatography (GC) analysis was performed in evacuated screw-cap Exetainers (12 mL) in a sampling interval of 0, 20, 40 and 60 min using a 30 mL syringe; 120 min after closing, duplicate headspace samples were taken for GC and isotope-ratio mass spectrometry (IRMS) analysis. Flux measurements were conducted daily, but only the final date of this measurement campaign (4 June) was used to evaluate the extent of diffusive loss of 15N-labelled N2 and N2O to the subsoil. This was done by comparing conventional flux measurements with cylinders open to the subsoil or with cylinders closed at the bottom. For the latter, cylinders were carefully removed from the surrounding soil. Soil material extending below the lower end of the cylinders was cut off with a knife. Bottom ends were sealed with plastic foil that was fixed to the outer cylinder wall with adhesive tape. Finally, sealed cylinders were put back to their original position in the surrounding soil in order to keep temperature within the cylinders identical to the surrounding soil. Chambers were fitted on the cylinders again for 120 min. Samples were collected from the chambers as in the conventional flux measurement. Between measurements with an open and closed bottom, cylinders remained open at the top for 120 min to allow equilibration of soil air with the free atmosphere and thus to release accumulated 15N2 and 15N2O.
2.5 Analysis
2.5.1 Soil analyses
Soil water content was determined by weight loss after 24 h drying at 110 ∘C. Soil and were extracted in 0.01 M CaCl2 solution (1:10 ratio) by shaking at room temperature for 1 h, and and NH concentrations were determined colourimetrically with an automated analyser (Skalar Analytical B.V., Breda, the Netherlands).
2.5.2 Isotopic analysis of NO3
15N abundances of () were measured according to the procedure described in Eschenbach et al. (2017). was reduced to NO by vanadium(III) chloride (VCl3). 15N measurement of produced NO was done with a quadrupole mass spectrometer (GAM 200, InProcess, Bremen, Germany).
2.5.3 Total N2O
Samples were analysed using an Agilent 7890A gas chromatograph (Agilent Technologies, Santa Clara, CA, USA) equipped with a pulsed discharge detector (VICI, V-D-3-I-7890-220). Precision, as given by the standard deviation (1σ of four standard gas mixtures), was typically 1.5 %.
2.5.4 Isotopic analysis of N2 and N2O
Gas samples were analysed for m∕z 28 (14N14N), m∕z 29 (14N15N) and m∕z 30 (15N15N) of N2 using a modified GasBench II preparation system coupled to an IRMS (MAT 253, Thermo Fisher Scientific, Bremen, Germany) according to Lewicka-Szczebak et al. (2013). This system allows a simultaneous determination of mass ratios 29R (29 / 28) and 30R (30 / 28) of three separated gas species (N2, N2+N2O and N2O), all measured as N2 gas after N2O reduction in a Cu oven. For each of the analysed gas species, the fraction originating from the 15N-labelled pool with respect to total N in the gas sample (fp) and the 15N enrichment of the 15N-labelled N pool (ap) producing N2O () or N2+N2O () was calculated after Spott et al. (2006), as described in Lewicka-Szczebak et al. (2017). The residual fraction of N2O remaining after N2O reduction to N2 () is given by the ratio . Typical repeatability of 29R and 30R (1σ of three replicate measurements) was for both values.
2.6 Statistics
Results of flux measurements with the bottom open or bottom closed were compared by a paired t test. Fluxes were log-transformed, which is a common prerequisite for analysing denitrification data due to its skewed distribution (Folorunso and Rolston, 1984). The measured additional N2+N2O flux was compared with the modelled value with a one-sample t test. Multiple regression analysis was conducted to derive a model of N2+N2O production. t tests and regression analysis were conducted with WinSTAT (R. Fitch Software, Bad Krozingen, Germany) and SAS (SAS Institute, Heidelberg, Germany), respectively.
3.1 Modelling
3.1.1 Surface and subsurface fluxes before and after chamber closure
Modelling results of Scenario A_bottom_open (imitating the field set-up) demonstrated 3-D spatial distribution of gas concentrations and the resulting diffusive fluxes with the highest concentrations in the centre of the 15N-labelled soil volume with an open chamber at the steady state (Figs. 2a, S1 in the Supplement). The time until the steady state after the onset of 15(N2+N2O) production increased with decreasing gas diffusivity and increasing soil moisture. For soil water content (SWC) of 0.34 g g−1, it was approximately 3 h (Fig. 2a). Soil air concentration of 15(N2+N2O) at the steady state also increased with SWC (data not shown).
Chamber closing leads to an increase in maximum concentrations (Fig. S1) and also to lowering of surface fluxes (Figs. 3 and 4).
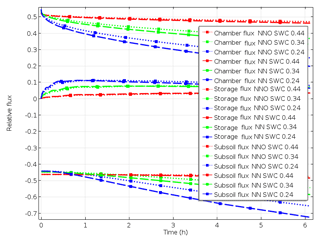
Figure 4Relative fluxes following chamber closing with different water contents in scenario A_bottom_open (surface flux, storage flux and subsoil flux starting at positive values, at zero and at negative values, respectively).
After chamber closing, surface flux decreases continuously while subsurface flux increases, and the storage flux initially increases before gradually decreasing. This shows that the lowering of surface flux with the increasing time of chamber closing results from increasing subsoil flux but also from further accumulation of denitrification products in pore space. While surface flux is largest among all fluxes at chamber closing, it is exceeded by subsoil flux after about 1 h. With increasing SWC, and thus decreasing diffusivity, the change in fluxes with time is lowering (Fig. 4). The highest relative subsoil fluxes are thus obtained at the lowest SWC. For N2O, the decrease in surface flux is slightly lower compared to N2 (Fig. 4). The change in relative fluxes is almost identical for the different isotopologues of N2 and N2O (only shown for N2 in Fig. S3).
To understand the effect of the labelling design, modelled fluxes of scenario B_30_30, B_45_30, B_ 45_45 and B_60_45 were compared. With decreasing depth of 15N labelling, surface flux during the first hours after chamber closing increases, since fewer denitrification products accumulate or are lost to the subsoil. This is evident by comparing fluxes obtained with 30 and 45 cm depth of confined 15N-labelled soil (Fig. 5). Increasing cylinder length below the depth of labelled soil, e.g. if the length of the cylinder extends 15 cm below the 30 or 45 cm deep labelled soil, yields an increase in surface flux and slight decrease in subsoil flux due to more accumulation of 15N-labelled gases below the 15N-labelled soil. Hence, underestimation of production based on surface flux is more severe with deeper labelling but lowers if the depth of confinement is increased.
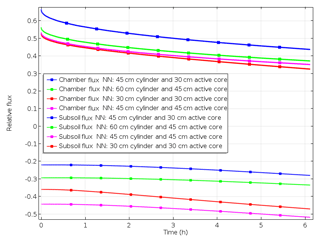
Figure 5Impact of the depth of the active core (representing depth of 15N labelling) and/or length of cylinder on relative surface and subsurface fluxes (scenarios B_30_30, B_ 45_ 30, B_45_45 and B_60_45.
Modelled underestimation of N2 production derived from chamber accumulation is summarized in Table 3. Depending on diffusivity, depth of 15N labelling and depth of confinement, underestimation ranges between 28 % and 71 %. Possible deviations of these estimates that would result from errors in the determination of diffusivity can be seen by comparing the modelled underestimation at a different SWC, giving a range of, for example, 51 % to 61 % for the B_30_30 scenario with 2 h closure.
Table 3Underestimation of N2 production by chamber measurements using linear regression over time, and mean subsoil loss of N2 produced within the 15N-labelled soil. Underestimation and subsoil loss are relative to production rates of the labelled core.
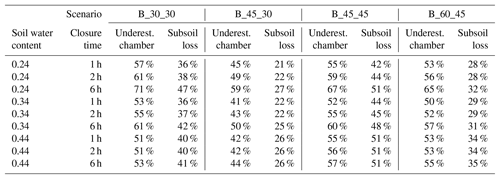
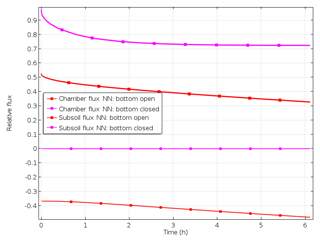
If diffusion to the subsoil was omitted, e.g. by closing the bottom of cylinders in the field or during laboratory incubations, soil air concentrations and surface fluxes increase (Fig. 6). When comparing values with and without omitted subsoil diffusion, relative surface flux 2 h after closure was 0.75 and 0.4, respectively. But with the bottom closed, surface flux was still significantly lower than production due to continuing pore space accumulation (relative storage flux of 0.25 after 2 h).
3.1.2 Determination of denitrification rates based on chamber concentration
We conducted several runs using the field scenarios A_bottom_open and A_bottom_closed to generate a dataset that allowed the parameterization of functions that describe the relation of the concentration reached after 2 h of chamber closure and the production within the labelled soil volume. This was done to allow a comparison of modelled data with the field measurements (Table 5). Moreover, we hereby give an example how denitrification rates can be calculated using empirical equations and thus without the need to run the 3-D model for each data evaluation.
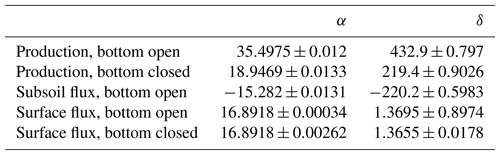
We obtained the following equation to calculate the production of each gas species of interest (x=14N14N, 14N15N, 15N15N, 14N14NO, 14N15NO or 15N15NO) based on chamber concentration after a certain time of closure:
where Px is the production for the respective gas species (L ha−1 d−1), Cx is concentration in parts per million, Ds is the apparent gas diffusion coefficient (cm2 s−1), and α and δ are fit parameters.
3.2 Field measurement
3.2.1 Soil moisture, mineral N and bulk density
Average –N was 16 mg N kg−1 without significant trends with depth and without significant differences between cylinders (Table S1 in the Supplement). –N was highest in 0 to 10 cm depth (1.8 mg N kg−1) and <1 mg N kg−1 below 10 cm depth. The average 15N atomic fraction of extracted (15a) was 0.15, but values increased with depth in all cylinders, where 20–30 cm averages (0.2) were more than twice the 0–10 cm depth (0.09). Bulk density ranged between 1.48 and 1.52, with the highest values at 10 to 20 cm depth. Water-filled pore space (WFPS) was higher at 0 to 10 cm depth (72 %) than at 10 to 30 cm depth (60 % to 62 %), with similar depth trends in all cylinders.
3.2.2 Field fluxes
The comparison between surface flux with or without closing the cylinder bottom was conducted on 4 June 2016, with the chamber closing at 10:40 (bottom open) and 14:40 (bottom closed; CET – Central European Time; all times listed in CET). Mean surface flux of N2+N2O with the bottom open was 589 g N ha−1 d−1 (Table 4) and was thus in between the fluxes observed during preceding 2 d (460±161 g N ha−1 d−1 on 2 June at 18:50; 657±206 g N ha−1 d−1 on 3 June at 11:00). This shows that denitrification rates were quite stable over several days and that denitrification was a significant N loss, probably due to the coincidence of high soil moisture and content (Table S1). The residual fraction of N2O remaining after N2O reduction to N2 () was 0.15 on average (Table S2), showing that N2 dominated N2+N2O fluxes. Mean 15a values for each cylinder were somewhat variable (0.09 to 0.18). Means of 15a (Table S1) and of the 15N enrichment of the labelled N pool producing N2O (; Table S2) were in close agreement (0.15 and 0.16, respectively).
Table 4Coefficients for the calculation of denitrification rates using Eq. (1) based on chamber concentrations for 2 h chamber closing time, 30 cm depth of 15N labelling, chamber height of 15, 15 cm diameter and assuming subsoil diffusivity identical to diffusivity of the 15N-labelled soil. Coefficients α and δ were derived by regression analysis of modelled concentration (R2>0.999).
Comparing N2+N2O surface fluxes when the cylinders were open or closed at the bottom resulted in significantly (P<0.05) higher surface fluxes when closed (Table 5), which was evident for each of the replicate micro-plots (Table S2). Because bottom-closed measurement was conducted as soon as possible immediately after the bottom-open measurement, i.e. after venting of the cylinders with chambers open for 2 h and thus 4 h after bottom-open measurements, we assumed that denitrification rates had not changed significantly and that the increase in surface fluxes was due to bottom closing.
Table 5N2+N2O fluxes of field experiments with 2 h chamber closing with and without closed bottom in comparison with modelled data.

The values of bottom-open and bottom-closed measurements exactly coincided. Conversely, the N2O residual fraction () of individual cylinders differed inconsistently, since values of bottom-closed measurements were higher in replicates 1 and 4 but were lower in replicates 2 and 3.
3.3 Comparison of modelled and measured surface flux
The ability of the model to predict the time pattern of gas accumulation was evaluated by comparing measured and simulated values. Model runs using the Ds values calculated from measured moisture and bulk density data of the field experiment assuming an open or closed bottom yielded relative surface fluxes of 0.47 and 0.88, respectively (Table 5). The additional surface flux with the bottom closed was thus quite relevant according to both model and measurement. However, the magnitude of the modelled additional flux (88 %) was more than twice, and thus significantly higher (P<0.001) than, the measured value. Using Eq. (1) and N2+N2O concentration in the chamber measured in the field with the open cylinder bottom and using respective coefficients of Table 1 resulted in N2+N2O production of 1055 g N ha−1 d−1. The modelled subsurface flux with the bottom open was almost half of the N2+N2O production. Modelled accumulation of N2+N2O in the pore space of the 15N-labelled soil was higher with the bottom closed (relative storage flux of 0.12) compared to bottom open (relative storage flux of 0.10). Evaluation of N2 and N2O fluxes individually yielded results similar to N2+N2O fluxes (data not shown).
4.1 Field study
Our comparison between 15(N2+N2O) fluxes from 15N-labelled micro-plots with and without closing the bottom of the cylinders supplied for the first time direct evidence for the underestimation of 15(N2+N2O) production due to diffusive loss to the subsoil, as suggested earlier (Mahmood et al., 1998; Sgouridis et al., 2016). In view of the poor sensitivity of the 15N gas flux method in the field under ambient atmosphere (Well et al., 2018), a prerequisite for this proof was the occurrence of sufficiently high and relatively stable denitrification rates. These conditions were given in our experiment due to the coincidence of high soil moisture and –N during the experimental period. Considering the relatively low variation of denitrification rates during the 2 d preceding the comparison, we conclude that the increase in surface fluxes after closing of the cylinder bottom was mainly due to the exclusion of diffusive loss to the subsoil.
While the increase in 15(N2+N2O) surface flux after bottom closing was comparable among the four replicates, this was not the case for the N2O flux and , which both exhibited considerable variabilities. showed larger deviation probably because the N2O reduction to N2 is not only sensitive to N2O concentration in pore space but also to changes in control factors like temperature, O2, and labile C (Müller and Clough, 2014). We suspect that the latter factors were somewhat variable within the replicates and that their interaction with N2O concentration leads to the observed variability in . The apparent sensitivity of to bottom closing shows that care should be taken when interpreting N2O reduction to N2 from determined in closed laboratory systems. Apart from our observations, an effect of bottom closure on N2O reduction is to be expected, since the resulting increased pore space N2O concentration would favour N2O reduction. This effect would thus lead to overestimation of N2O reduction when extrapolating results to the field.
4.2 Estimating production of N2 and N2O based on surface fluxes and diffusion modelling
Modelling diffusive fluxes of N2 and N2O evolved from 15N-labelled soil showed that denitrification rates are underestimated by more than 50 % when only surface fluxes are taken into account, which has been general practice in the past (Sgouridis et al., 2016, and references therein). Modelling also confirmed that in contrast to our hypothesis, not only is subsoil flux a relevant fraction of 15(N2+N2O) production but it is also the increasing accumulation during chamber closing. Several authors increased the chamber deployment time of 40 to 60 min, as is common for N2O flux measurement (Parkin et al., 2012), e.g. to 2 h (Tauchnitz et al., 2015; Buchen et al., 2016) or even 24 h (Sgouridis et al., 2016). This was done to increase 15N2+N2O concentration in the chamber and thus to improve the detection limit for denitrification at a given IRMS precision. Because surface fluxes lower with deployment time, it is clear that the underestimation of surface flux based denitrification rates is also increasing.
For laboratory studies with the 15N gas flux method using closed incubation systems, our findings on 15N2 and 15N2O accumulation in pore space are quite relevant. Closing incubation vessels for a limited time and estimating denitrification from headspace concentration (e.g. Meyer et al., 2010; Siegel et al., 1982) inevitably lead to underestimation of denitrification rates. Experimental evidence for this underestimation was obtained by destroying pore structure at final sampling to homogenize headspace and pore space (Harter et al., 2016). Because the fraction of denitrification products accumulated in pore space increases with decreasing diffusivity, the problem is most severe for water-saturated soils. While this was previously solved by homogenizing headspace and pore space before sampling (Well and Myrold, 1999), other studies with water-saturated substrates did not take accumulated gases into account (e.g. Nielsen, 1992).
Our results show that extending chamber deployment time is not a good strategy for improving the detection limit for denitrification. This is because the fraction of gaseous denitrification products that is not emitted at the soil surface is increasing with time. Although we can now estimate this fraction with our model, uncertainties of the modelled data lead to increasing uncertainty in denitrification estimates with chamber deployment time. Another way to improve detection is to lower the N2 background concentration in the field by flushing chambers with an N2-depleted gas matrix (Well et al., 2018). Due to the good sensitivity of that method, chamber deployment could be kept at 1 h. Principally, our modelling approach could also determine the subsurface flux and pore space accumulation for that method but will have to be adapted to take diffusion dynamics in the N2-depleted gas matrix into account.
Because the flux dynamics of gaseous denitrification products in the soil were not taken into account in past field flux and certain laboratory studies, we assume that numerous studies underestimated denitrification significantly. It can thus be concluded that soil denitrification is probably even more relevant than assumed today.
Our model approach is suitable for estimating pore space accumulation and subsoil diffusion of denitrification products. It thus allows us to determine production based on surface fluxes in field flux studies but also in closed laboratory incubations. Principally, it could also be used to correct previously published data if necessary information on diffusivity and pore space were available. For experiments with the same dimensions and bulk density as those assumed in our regression model, it is also possible to calculate production from surface flux using the parameters of Table 4. Principally, the regression approach offers an easy way to derive production without the need to run the 3-D model. But to obtain a general solution that would fit any experimental conditions in terms of bulk density, depth of labelling, chamber design and deployment time, it will be necessary to conduct multiple model runs, which was beyond the scope of this paper.
Our approach includes several factors of uncertainty. A prerequisite for precise quantification is the knowledge of the vertical distribution in activity and diffusivity. Moreover, we have to assume the steady state, which is never perfectly realized due to temporal change of diffusivity and denitrification rates, e.g. following precipitation and thus decreasing diffusivity, increasing moisture, changing the labelled volume. Finally, we did not yet take into account water-phase transport. But this has some relevance due to low diffusivity in the water phase. The impact of water-phase transport should be largest for N2O due to its high solubility in water, yet gas diffusivity of N2O in water is more than 3 orders of magnitude lower than in air (Rabot et al., 2018). For CO2, which has also a high solubility in water, the contribution of the aqueous phase to diffusive fluxes is negligible when the ratio of air-filled porosity and total pore space is greater than 0.12 (Jassal et al., 2004). But since denitrification occurs often in soil near water saturation, water-phase dynamics might be another explanation for the deviations between the ratios determined with the bottom open and bottom closed.
The general agreement between measured and modelled increase in surface flux after closing the cylinder bottom can be seen as a first proof of our concept to quantify denitrification rates using surface fluxes and modelling. Reasons for the observed deviations between experimental and model results can be manifold. In view of the aforementioned factors of uncertainty, these could include imperfect estimation of Ds by the empirical model (Millington, 1959), spatial variability of diffusivity (Kühne et al., 2012; Lange et al., 2009; Maier et al., 2017; Maier and Schack-Kirchner, 2014; Marrero and Mason, 1972) within the 10 cm layers for which Ds was determined, spatial variability of denitrification rates (Groffman et al., 2009) and an incomplete steady state. Further reasons could be the production of 15N2 and 15N2O from possible leached below the confined soil cores and a possible shift in denitrification rates during the 6 h between the two experiments with the bottom open and bottom closed. A quantitative evaluation of the model by 15N gas flux experiments would be quite challenging, since it would mean assessing all aforementioned uncertain factors and including heterogeneity in the modelling. Future attempts are therefore necessary to improve model evaluation and check how our approach will perform under heterogenic conditions. But despite these uncertainties, the general agreement of model and measurements shows that our approach leads to improved denitrification estimates.
Which progress in flux estimation is obtained in view of incomplete knowledge on parameters, and could incorrect parameter estimation lead to augmented bias? Even uncertain estimates of subsoil fluxes would improve the outcome of the 15N gas flux method in comparison with current practice (i.e. without taking subsoil diffusion and storage into account), as it would lower the bias in estimating denitrification rates. We can exclude that our approach would increase total bias in estimating denitrification through incorrect determination of diffusivity. A larger overestimation of subsoil diffusion or storage could only occur at high soil gas diffusivity, which means in dry highly porous soils (Table 3). But these conditions are less relevant for our approach, since denitrification is inhibited at high diffusivity. Taking into account the uncertainty in subsoil diffusion modelling, we demonstrate that worst-case scenarios would still improve estimates compared to previous practice: the scenario with 30 cm depth of labelling and confinement of labelled soil (B_30_30) yields 51 % and 61 % underestimation for the highest and lowest modelled water content, respectively. Our approach would thus overestimate production by up to 10 %, whereas production derived from surface flux only would underestimate the true production at least by 51 %. Between soil water contents of 0.34 and 0.44, our overestimation would be only 2 % (i.e. 53 %–51 %). Consequently, potential bias of our correction approach arising from errors in determination of diffusivity would be quite small under conditions favouring denitrification. Under drier conditions, errors would still be much smaller compared to the errors from neglecting subsurface fluxes. The moderate impact of diffusivity also shows that spatial heterogeneity of diffusivity (Kühne et al., 2012) would not have a large impact and its assessment would not have to be prioritized.
While it was beyond the scope of this study to evaluate uncertainty in detail, future work should follow up on this in order to explore the achievable accuracy in estimating subsoil flux and storage under given conditions. This should include modelling water-phase transport, depth of labelling, and the impact of spatial and temporal variability in diffusivity and denitrification rates. Moreover, controlled experiments would be needed to validate model results as far as possible.
Measurements and production–diffusion modelling showed that field surface fluxes of 15N-labelled N2 and N2O emitted from 15N-labelled soil severely underestimate denitrification due to subsoil flux and accumulation in pore space. The extent of underestimation increases with chamber deployment time. Soil denitrification has thus been underestimated in many previous studies using the 15N gas flux method without taking subsoil flux and accumulation in pore space into account. While production–diffusion modelling is a promising tool for estimating subsoil flux and storage flux, the observed deviations between experimental and modelled subsoil flux reveal the need for refined model evaluation. To enable correction of previously published data, further model parameterization work should cover all soil and land use types.
Data from measurements and modelling are available upon request from the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-16-2233-2019-supplement.
RW designed the overall concept. RW and DLS designed the field experiments, and DLS and NR carried them out. MM developed the model code and performed the simulations. RW prepared the paper, with contributions from JRK, DLS and MM.
The authors declare that they have no conflict of interest.
We thank Frank Hegewald for technical support in experiments, Martina Heuer and Jennifer Ehe for stable isotope analysis, Kerstin Gilke and Andrea Oehns-Rittgerod for analysis by GC, and Roland Fuß for support in statistical analyses. We further thank the supplying of an experimental field site by the Faculty of Agriculture, South Westphalia University of Applied Sciences. We are grateful to two anonymous referees for their constructive feedback.
This research has been supported by the Deutsche Forschungsgemeinschaft (grants LE 3367/1-1 and research unit 2337: “Denitrification in Agricultural Soils: Integrated Control and Modeling at Various Scales (DASIM)”).
This paper was edited by Ivonne Trebs and reviewed by two anonymous referees.
Bollmann, A. and Conrad, R.: Enhancement by acetylene of the decomposition of nitric oxide in soil, Soil Biol. Biochem., 29, 1057–1066, https://doi.org/10.1016/s0038-0717(97)00006-0, 1997a.
Bollmann, A. and Conrad, R.: Acetylene blockage technique leads to underestimation of denitrification rates in oxic soils due to scavenging of intermediate nitric oxide, Soil Biol. Biochem., 29, 1067–1077, https://doi.org/10.1016/s0038-0717(97)00007-2, 1997b.
Buchen, C., Lewicka-Szczebak, D., Fuss, R., Helfrich, M., Flessa, H., and Well, R.: Fluxes of N2 and N2O and contributing processes in summer after grassland renewal and grassland conversion to maize cropping on a Plaggic Anthrosol and a Histic Gleysol, Soil Biol. Biochem., 101, 6–19, https://doi.org/10.1016/j.soilbio.2016.06.028, 2016.
Butterbach-Bahl, K., Willibald, G., and Papen, H.: Soil core method for direct simultaneous determination of N-2 and N2O emissions from forest soils, Plant Soil, 240, 105–116, https://doi.org/10.1023/a:1015870518723, 2002.
Butterbach-Bahl, K., Baggs, E. M., Dannenmann, M., Kiese, R., and Zechmeister-Boltenstern, S.: Nitrous oxide emissions from soils: how well do we understand the processes and their controls?, Philos. T. R. Soc. B, 368, 23713120, https://doi.org/10.1098/rstb.2013.0122, 2013.
Coplen, T. B.: Guidelines and recommended terms for expression of stable-isotope-ratio and gas-ratio measurement results, Rapid Commun. Mass Sp., 25, 2538–2560, https://doi.org/10.1002/rcm.5129, 2011.
Eschenbach, W., Lewicka-Szczebak, D., Stange, C. F., Dyckmans, J., and Well, R.: Measuring N-15 Abundance and Concentration of Aqueous Nitrate, Nitrite, and Ammonium by Membrane Inlet Quadrupole Mass Spectrometry, Anal. Chem., 89, 6077–6082, https://doi.org/10.1021/acs.analchem.7b00724, 2017.
Felber, R., Conen, F., Flechard, C. R., and Neftel, A.: Theoretical and practical limitations of the acetylene inhibition technique to determine total denitrification losses, Biogeosciences, 9, 4125–4138, https://doi.org/10.5194/bg-9-4125-2012, 2012.
Folorunso, O. and Rolston, D.: Spatial variability of field-measured denitrification gas fluxes, Soil Sci. Soc. Am. J., 48, 1214–1219, 1984.
Groffman, P., Butterbach-Bahl, K., Fulweiler, R. W., Gold, A. J., Morse, J. L., Stander, E. K., Tague, C., Tonitto, C., and Vidon, P.: Challenges to incorporating spatially and temporally explicit phenomena (hotspots and hot moments) in denitriWcation models, Biogeochemistry, 93, 49–77, 2009.
Groffman, P. M., Altabet, M. A., Böhlke, J. K., Butterbach-Bahl, K., David, M. B., Firestone, M. K., Giblin, A. E., Kana, T. M., Nielsen, L. P., and Voytek, M. A.: Methods for measuring denitrification diverse approaches to a difficult problem, Ecol. Appl., 16, 2091–2122, 2006.
Harter, J., Guzman-Bustamante, I., Kuehfuss, S., Ruser, R., Well, R., Spott, O., Kappler, A., and Behrens, S.: Gas entrapment and microbial N2O reduction reduce N2O emissions from a biochar-amended sandy clay loam soil, Sci. Rep.-UK, 6, 39574, https://doi.org/10.1038/srep39574, 2016.
Healy, R. W., Striegl, R. G., Russell, T. F., Hutchinson, G. L., and Livingston, G. P.: Numerical evaluation of static-chamber measurements of soil-atmosphere gas exchange: Identification of physical processes, Soil Sci. Soc. Am. J., 60, 740–747, https://doi.org/10.2136/sssaj1996.03615995006000030009x, 1996.
Hutchinson, G. and Mosier, A.: Improved soil cover method for field measurement of nitrous oxide fluxes, Soil Sci. Soc. Am. J., 45, 311–316, 1981.
Jassal, R. S., Black, T. A., Drewitt, G. B., Novak, M. D., Gaumont-Guay, D., and Nesic, Z.: A model of the production and transport of CO2 in soil: predicting soil CO2 concentrations and CO2 efflux from a forest floor, Agr. Forest Meteorol., 124, 219–236, https://doi.org/10.1016/j.agrformet.2004.01.013, 2004.
Jost, W.: Diffusion in Solids, Liquids and Gases, Academic, San Diego, Calif., 558 pp., 1960.
Kühne, A., Schack-Kirchner, H., and Hildebrand, E. E.: Gas diffusivity in soils compared to ideal isotropic porous media, J. Plant Nutr. Soil. Sc., 175, 34–45, https://doi.org/10.1002/jpln.201000438, 2012.
Kulkarni, M. V., Burgin, A. J., Groffman, P. M., and Yavitt, J. B.: Direct flux and N-15 tracer methods for measuring denitrification in forest soils, Biogeochemistry, 117, 359–373, 2014.
Laemmel, T., Mohr, M., Longdoz, B., Schack-Kirchner, H., Lang, F., Schindler, D., and Maier, M.: From above the forest into the soil – how wind affects soil gas transport through air pressure fluctuations, Agr. Forest Meteorol., 265, 424–434, 2019.
Lange, S. F., Allaire, S. E., and Rolston, D. E.: Soil-gas diffusivity in large soil monoliths, Eur. J. Soil Sci., 60, 1065–1077, https://doi.org/10.1111/j.1365-2389.2009.01172.x, 2009.
Lewicka-Szczebak, D., Well, R., Giesemann, A., Rohe, L., and Wolf, U.: An enhanced technique for automated determination of N-15 signatures of N2, (N2+N2O) and N2O in gas samples, Rapid Commun. Mass Sp., 27, 1548–1558, https://doi.org/10.1002/Rcm.6605, 2013.
Lewicka-Szczebak, D., Augustin, J., Giesemann, A., and Well, R.: Quantifying N2O reduction to N2 based on N2O isotopocules – validation with independent methods (helium incubation and 15N gas flux method), Biogeosciences, 14, 711–732, https://doi.org/10.5194/bg-14-711-2017, 2017.
Mahmood, T., Malik, K. A., Shamsi, S. R. A., and Sajjad, M. I.: Denitrification and total N losses from an irrigated sandy-clay loam under maize-wheat cropping system, Plant Soil, 199, 239–250, https://doi.org/10.1023/a:1004335132617, 1998.
Maier, M. and Schack-Kirchner, H.: Using the gradient method to determine soil gas flux: A review, Agr. Forest Meteorol., 192, 78–95, https://doi.org/10.1016/j.agrformet.2014.03.006, 2014.
Maier, M., Paulus, S., Nicolai, C., Stutz, K. P., and Nauer, P. A.: Drivers of Plot-Scale Variability of CH4 Consumption in a Well-Aerated Pine Forest Soil, Forests, 8, 193, https://doi.org/10.3390/f8060193, 2017.
Marrero, T. R. and Mason, E. A.: Gaseous Diffusion Coefficients, J. Phys. Chem. Ref. Data, 1, https://doi.org/10.1063/1.3253094, 1972.
Meyer, A., Bergmann, J., Butterbach-Bahl, K., and Bruggemann, N.: A new 15N tracer method to determine N turnover and denitrification of Pseudomonas stutzeri, Isot. Environ. Healt. S., 46, 409–421, https://doi.org/10.1080/10256016.2010.528840, 2010.
Millington, R. J.: Gas diffusion in porous media, Science, 130, 100–102, 1959.
Müller, C. and Clough, T. J.: Advances in understanding nitrogen flows and transformations: gaps and research pathways, J. Agr. Sci., 152, S34–S44, https://doi.org/10.1017/s0021859613000610, 2014.
Mulvaney, R. L.: Evaluation of N-15 tracer techniques for direct measurement of denitrification in soil. 3. Laboratory studies, Soil Sci. Soc. Am. J., 52, 1327–1332, https://doi.org/10.2136/sssaj1988.03615995005200050022x, 1988.
Mulvaney, R. L. and Vandenheuvel, R. M.: Evaluation of N-15 tracer techniques for direct measurement of denitrification in soil. 4. Field studies, Soil Sci. Soc. Am. J., 52, 1332–1337, https://doi.org/10.2136/sssaj1988.03615995005200050023x, 1988.
Nadeem, S., Dörsch, P., and Bakken, L. R.: Autoxidation and acetylene-accelerated oxidation of NO in a 2-phase system: Implications for the expression of denitrification in ex situ experiments, Soil Biol. Biochem., 57, 606–614, https://doi.org/10.1016/j.soilbio.2012.10.007, 2013.
Nielsen, L. P.: Denitrification in sediment determined from nitrogen isotope pairing, Fems Microbiol. Ecol., 86, 357–362, https://doi.org/10.1111/j.1574-6968.1992.tb04828.x, 1992.
Parkin, T. B., Venterea, R. T., and Hargreaves, S. K.: Calculating the Detection Limits of Chamber-based Soil Greenhouse Gas Flux Measurements, J. Environ. Qual., 41, 705–715, https://doi.org/10.2134/jeq2011.0394, 2012.
Rabot, E., Wiesmeier, M., Schluter, S., and Vogel, H. J.: Soil structure as an indicator of soil functions: A review, Geoderma, 314, 122–137, https://doi.org/10.1016/j.geoderma.2017.11.009, 2018.
Saggar, S., Jha, N., Deslippe, J., Bolan, N. S., Luo, J., Giltrap, D. L., Kim, D. G., Zaman, M., and Tillman, R. W.: Denitrification and N2O:N2 production in temperate grasslands: Processes, measurements, modelling and mitigating negative impacts, Sci. Total Environ., 465, 173–195, https://doi.org/10.1016/j.scitotenv.2012.11.050, 2013.
Sahoo, B. K. and Mayya, Y. S.: Two dimensional diffusion theory of trace gas emission into soil chambers for flux measurements, Agr. Forest Meteorol., 150, 1211–1224, https://doi.org/10.1016/j.agrformet.2010.05.009, 2010.
Scholefield, D., Hawkins, J. M. B., and Jackson, S. M.: Use of a flowing helium atmosphere incubation technique to measure the effects of denitrification controls applied to intact cores of a clay soil, Soil Biol. Biochem., 29, 1337–1344, https://doi.org/10.1016/s0038-0717(97)00059-x, 1997.
Sgouridis, F., Stott, A., and Ullah, S.: Application of the 15N gas-flux method for measuring in situ N2 and N2O fluxes due to denitrification in natural and semi-natural terrestrial ecosystems and comparison with the acetylene inhibition technique, Biogeosciences, 13, 1821–1835, https://doi.org/10.5194/bg-13-1821-2016, 2016.
Siegel, R. S., Hauck, R. D., and Kurtz, L. T.: Determination of 30N2 and application to measurement of N2 evolution during denitrification, Soil Sci. Soc. Am. J., 46, 68–74, 1982.
Spott, O., Russow, R., Apelt, B., and Stange, C. F.: A N-15-aided artificial atmosphere gas flow technique for online determination of soil N-2 release using the zeolite Kostrolith SX6 (R), Rapid Commun. Mass Sp., 20, 3267–3274, https://doi.org/10.1002/rcm.2722, 2006.
Stevens, R. J., Laughlin, R. J., Atkins, G. J., and Prosser, S. J.: Automated determination of nitrogen-15-labelled dinitrogen and nitrous – oxide by mass-spectrometry, Soil Sci. Soc. Am. J., 57, 981–988, https://doi.org/10.2136/sssaj1993.03615995005700040017x, 1993.
Tauchnitz, N., Spott, O., Russow, R., Bernsdorf, S., Glaser, B., and Meissner, R.: Release of nitrous oxide and dinitrogen from a transition bog under drained and rewetted conditions due to denitrification: results from a N-15 nitrate-bromide double-tracer study, Isot. Environ. Healt S., 51, 300–321, https://doi.org/10.1080/10256016.2015.1011634, 2015.
Venterea, R. T., Spokas, K. A., and Baker, J. M.: Accuracy and Precision Analysis of Chamber-Based Nitrous Oxide Gas Flux Estimates, Soil Sci. Soc. Am. J., 73, 1087–1093, https://doi.org/10.2136/sssaj2008.0307, 2009.
Well, R. and Myrold, D. D.: Laboratory evaluation of a new method for in situ measurement of denitrification in water-saturated soils, Soil Biol. Biochem., 31, 1109–1119, 1999.
Well, R. and Myrold, D. D.: A proposed method for measuring subsoil denitrification in situ, Soil Sci. Soc. Am. J., 66, 507–518, 2002.
Well, R., Burkart, S., Giesemann, A., Grosz, B., Köster, J. R., and Lewicka-Szczebak, D.: Improvement of the 15N gas flux method for in situ measurement of soil denitrification and its product stoichiometry, Rapid Commun. Mass Sp., 33, 437–448, https://doi.org/10.1002/rcm.8363, 2018.