the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A trait-based modelling approach to planktonic foraminifera ecology
Maria Grigoratou
Fanny M. Monteiro
Daniela N. Schmidt
Jamie D. Wilson
Ben A. Ward
Andy Ridgwell
Despite the important role of planktonic foraminifera in regulating the ocean carbonate production and their unrivalled value in reconstructing paleoenvironments, our knowledge on their ecology is limited. A variety of observational techniques such as plankton tows, sediment traps and experiments have contributed to our understanding of foraminifera ecology. But, fundamental questions around costs and benefits of calcification and the effect of nutrients, temperature and ecosystem structure on these organisms remain unanswered. To tackle these questions, we take a novel mechanistic approach to study planktonic foraminifera ecology based on trait theory. We develop a zero-dimensional (0-D) trait-based model to account for the biomass of prolocular (20 µm) and adult (160 µm) stages of non-spinose foraminifera species and investigate their potential interactions with phytoplankton and other zooplankton under different temperature and nutrient regimes. Building on the costs and benefits of calcification, we model two ecosystem structures to explore the effect of resource competition and temperature on planktonic foraminifera biomass. By constraining the model results with ocean biomass estimations of planktonic foraminifera, we estimate that the energetic cost of calcification could be about 10 %–50 % and 10 %–40 % for prolocular and adult stages respectively. Our result suggest that the shell provides protection against processes other than predation (e.g. pathogen invasion). We propose that the low standing biomass of planktonic foraminifera plays a key role in their survival from predation, along with their shell protection. Our model suggests a shift from temperature as a main regulator of foraminifera biomass in the early developmental stage to resource competition for adult biomass.
Planktonic foraminifera as a group comprise 50 holoplanktonic heterotrophic protozoans (Kučera, 2007). They are the most widely used zooplankton group to reconstruct past marine environments, with proxies devised that are based on their abundance, assemblage composition and/or physio-geochemical characteristic of their shell (e.g. Schmidt et al., 2003; Schiebel and Hemleben, 2005). They are also the most important calcifying zooplankton group, supplying between 23 % and 55 % of the total marine planktonic carbonate production (Schiebel, 2002) and hence are a key contributor to the composition of marine sediments (Schiebel and Hemleben, 2005).
In contrast to their high abundances in sediments, they tend to grow at very low abundance in the ocean and never dominate the zooplankton community, representing less than 5 % of total microprotozooplankton abundance (Beers and Stewart, 1971). Based on plankton tow observations, abundances range from 1 ind. m−3 in blue waters to 20–50 ind. m−3 in oligo- and mesotrophic waters (Schiebel and Hemleben, 2005) and >1000 ind. m−3 in polar regions (Carstens et al., 1997). Their global biomass in the water column has been estimated to be between 0.002 and 0.0009 Pg C and their contribution to global plankton biomass to be ∼0.04 % (Buitenhuis et al., 2013).
Despite their importance in paleooceanography and modern biochemical oceanography, our knowledge of planktonic foraminifera's physiology, development and ecology is limited to a few observations. Planktonic foraminifera are difficult to grow in culture, and it has been impossible to grow a next generation (Hemleben et al., 1989). Consequently, information regarding the intra-species and inter-species competition, as well as a mechanistic understanding of their physiology through their whole life cycle, is missing.
Trait-based approaches can be useful for improving our knowledge of planktonic foraminifera ecology as they can address fundamental questions around the cost of growth across developmental stages, their position in the global food webs and calcification. Trait-based approaches provide mechanistic understanding of individuals, populations or ecosystems, as they describe these systems from first principles by defining individuals' key traits (e.g. size, feeding, reproduction) and associated trade-offs like energetic needs and predation risks (e.g. Litchman and Klausmeier, 2008; Litchman et al., 2013; Barton et al., 2013; Hébert et al., 2017; Kiørboe et al., 2018b). For example, body size is considered a master trait for plankton, impacting many physiological and ecological aspects such as metabolic rates (e.g. growth), diet, abundance, biomass and reproduction (e.g. Litchman et al., 2013).
Several traits and trade-offs have been identified for planktonic foraminifera, summarized in Fig. 1. The size of planktonic foraminifera can be regarded as a “master” trait and can be used as an indicator for environmental conditions that are optimal for growth (e.g. Caron et al., 1982; Schmidt et al., 2004a). Planktonic foraminifera development is divided into five stages, defined based on shell size and wall structure: prolocular, juvenile, neanic, adult and terminal (gametogenesis) (Brummer et al., 1986, 1987). Their shell diameter ranges from about 10 µm for the prolocular life stage to more than 1250 µm for the adult under optimal conditions (Schmidt et al., 2004a). Planktonic foraminifera are considered to reach the adult stage and subsequently be sexually mature when their shell size reaches around 100 µm (Brummer et al., 1986; Caromel et al., 2016). Shell size increases from low to high latitudes (Schmidt et al., 2003, 2004b) and is related to reproductive success (gametogenesis), as bigger individuals release more gametes (e.g. Caron and Bé, 1984; Hemleben et al., 1989). Temperature and food availability are suggested to be the main environmental factors which regulate their size (e.g. Anderson et al., 1979; Spero et al., 1991; Caron et al., 1982; Schmidt et al., 2004a), but a mechanistic understanding of the response of shell size to temperature and food is missing.
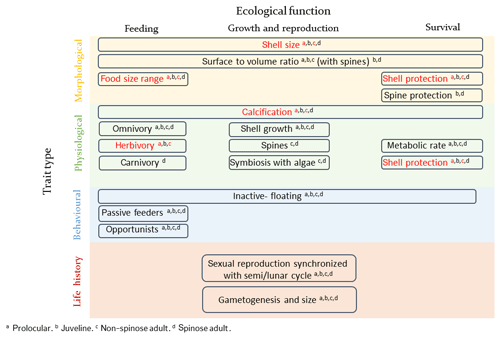
Figure 1Schematic presentation of planktonic foraminifera traits and trade-offs. The examined traits of the present study are shown in red. The presentation of planktonic foraminifera's traits was inspired from the topology of zooplankton traits proposed by Litchman et al. (2013).
Calcification is another important trait of planktonic foraminifera, relative to shell size, but the costs and benefits of possessing a shell and the nature of the associated trade-off are not well understood. Paleorecords indicate changes in size (Schmidt et al., 2004a), thickness (Barker and Elderfield, 2002) and morphology of planktonic foraminifera shell as responses to changing climates (Malmgren and Kennet, 1981; Norris, 1991). Determining the cost and benefit of producing a shell is fundamental to quantifying the influence of climate change on planktonic foraminifera ecology, distribution and carbonate production in the past, present and future.
The feeding strategies of planktonic foraminifera are also an important trait as they are crucial for survival and influence plankton community ecology. Planktonic foraminifera are inactive organisms and passive feeders. They do not detect their prey but encounter them while drifting, using a rhizopodial network which extends from their body (e.g. Anderson and Bé, 1976). As planktonic foraminifera are typically collected for experimental work at sizes >60 µm and subsequently grown as individuals, information regarding the feeding behaviour of the early (prolocular and juvenile) life stages, the cost and benefits of being inactive passive feeders and interactions with other plankton is missing. It has been suggested that at the prolocular stage all species are herbivorous (Hemleben et al., 1989) and subsequently widen their food sources. Field and laboratory observations suggest that spinose species use their spines, which start growing during the neanic stage, to capture and control active zooplankton prey, that are often larger than themselves (e.g. Anderson et al., 1979; Spindler et al., 1984). Spinose species tend to be either omnivorous or carnivorous (Schiebel and Hemleben, 2017) and many have developed a symbiotic relationship with photosynthesizing algae (Schiebel and Hemleben, 2017) which allows them to be successful in oligotrophic areas. It has been speculated that the higher abundance of spinose species compared to the non-spinose is the result of their carnivory as oligotrophic areas are characterized by relative low phytoplankton concentration but relative high abundance of copepods (Schiebel et al., 2004; Moriarty and O'Brien, 2013). Non-spinose species are often omnivorous and herbivorous (Anderson et al., 1979; Hemleben and Auras, 1984), with the ability to catch and feed on small zooplankton or dead organic matter resulting in their maximum abundance in high-productivity regions (Schiebel and Hemleben, 2017).
Trait-based models can supplement the physiological and ecological understanding of foraminifera gained in the field and cultures (Fig. 1) to improve our understanding of planktonic foraminifera ecology. Trait-based models have been successfully applied to phytoplankton (e.g. Follows et al., 2007; Litchman and Klausmeier, 2008; Monteiro et al., 2016) with little development and application on zooplankton (e.g. Banas, 2011; Maps et al., 2011; Ward et al., 2012, 2014; Banas et al., 2016). However, until now, only species-specific ecological models have been developed to study the ecology of modern planktonic foraminifera species: Žarić et al. (2006) (from now on Žarić06), PLAFOM (Fraile et al., 2008, 2009) and FORAMCLIM (Lombard et al., 2011; Roy et al., 2015). Žarić06 developed an empirical model which relates the global fluxes of 18 species of planktonic foraminifera to environmental conditions based on observations. PLAFOM models field observations to predict the influence of temperature (Fraile et al., 2008) and food availability (Fraile et al., 2009) on the global biogeography of five species. FORAMCLIM represents eight species of planktonic foraminifera and studies the influence of temperature, food availability, light and climate change on growth rates and global distribution. These models provide important insights into the interaction between planktonic foraminifera and their habitat. Their main limitation is that they are based on empirical (Žarić et al., 2006; Fraile, 2008, 2009) or laboratory data (Lombard et al., 2011; Roy et al., 2015) and their application is thus species-specific and limited to specific environmental ranges (Roy et al., 2015).
Here, we describe the first trait-based generic model of planktonic foraminifera using body size, calcification and feeding behaviour as key traits to investigate the mechanisms behind planktonic foraminifera ecology. We focus on modelling non-symbiotic non-spinose species because these species are predominantly herbivorous throughout their whole life and do not develop spines and algal symbionts, all of which increase complexity and are not sufficiently constrained by basic physiological data. Our trait-based planktonic foraminifera model was derived from the size-structured plankton models of Ward et al. (2012, 2014) which use cell and body size as the ecophysiological trait to study the phytoplankton–zooplankton food web. We investigate the energetic costs and benefits of calcification and their feeding behaviour and resource competition with other zooplankters, as well as the environmental controls on two different developmental stages. Model results assess and quantify the biotic and abiotic factors influencing their physiology and ecology and the interactions of planktonic foraminifera with phytoplankton and other zooplankton, as well as their environment.
2.1 Model structure
Our model represents a chemostat experiment in a zero-dimensional (0-D) setting. It accounts for one source of nutrients (here defined as nitrates, ) and 51 generic phytoplankton (autotrophs) and zooplankton (heterotrophs) size classes from pico- to mesoplankton (Sieburth et al., 1978).
The nutrient availability (N) depends on the input nutrient concentration (No) interpreted as either a nutrient-rich vertical source of nutrient (typical of high-productivity regions) or a less-rich horizontally advective nutrient source (typical of oligotrophic gyres), dilution rate κ and phytoplankton uptake (Eq. 1).
We investigated a range of No values (0–5 mmol N m−3) to account for a range of different nutrient regimes, from oligotrophic to eutrophic (Ward et al., 2014).
Plankton populations are modelled in terms of nitrogen biomass (B) with the rate of change of biomass described by
where Pgrowth,j represents the phytoplankton growth (Eq. A2), the zooplankton grazing (Eq. A3), the plankton losses due to zooplankton grazing and mj the plankton background mortality (Table 1). Phytoplankton growth (Pgrowth,j) depends on limitation from light, temperature and nutrient availability, following a Monod response (Appendix A, Eq. A2). Zooplankton grazing is controlled by the biomass and size of the prey and is described through a Holling type II response with a prey refuge (Eq. A3).
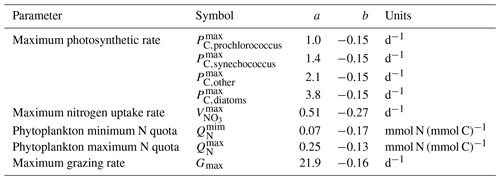
Table 1Model parameters (Ward et al., 2014 and references with in).

a Value for the food chain. b−e Values for the food web. b Zooplankton and prolocular stage of planktonic foraminifera. c Adult stage of planktonic foraminifera for meso- and eutrophic ecosystems. d, e Adult stage of planktonic foraminifera for oligotrophic ecosystem of 20 and 30 ∘C respectively.
We assumed that the terms of plankton mortality and zooplankton sloppy feeding (prey which is lost from the predator during feeding; Lampert, 1978) are exported out of the chemostat. There is no nutrient recycling in the model. The model parameters and symbols are defined in Tables 1 and 2, and a more detailed description of the model and plankton growth is available in Appendix A.
2.2 Complexity of the ecosystem structure
We modelled two simplified ecosystems: a simple food chain and a more complex food web (Fig. 2). In the simple food chain model, zooplankton were herbivorous size-specialist predators feeding on one prey size group. In order to examine the grazing pressure of a specialist predator on planktonic foraminifera, we made an exception by defining one zooplankton group to be omnivorous, capable of consuming only planktonic foraminifera, and one phytoplankton group with the same size as planktonic foraminifera. Resource competition occurred mostly at the phytoplankton level. In zooplankton, the only competition was between individual planktonic foraminifera and with zooplankton of the same size group (Fig. 2a). This simple representation of the marine ecosystem allowed us to better understand the model behaviour and the top-down and bottom-up controls on foraminifera while testing the grazing pressure of a specialist predator on planktonic foraminifera.
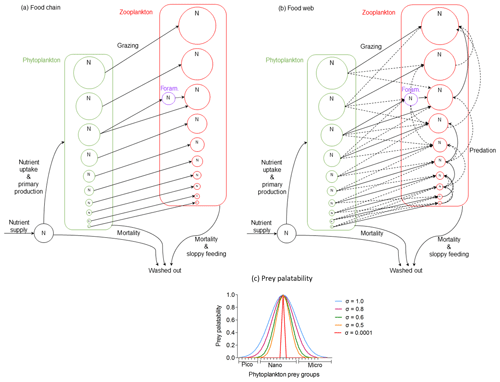
Figure 2Schematic description of the two model versions of the size trait-based model of planktonic foraminifera: (a) food chain and (b) food web (adopted with permission from Ward et al., 2012). Note that the figure does not present the accurate position of the planktonic foraminifera size group ran in the model but a generic position to illustrate how they interact with the rest of the plankton community. (c) Illustration of the prey palatability of one herbivorous predator (160 µm size) with phytoplankton prey groups. Size specialist predator (present in the food chain version) is characterized by standard deviation (σ) equal to 0.0001. Size generalist predator (present in the food web version) is characterized by σ≥0.5.
In the food web model, resource competition occurred at both phytoplankton and zooplankton levels. Zooplankton predators were size-generalist omnivorous predators able to consume more than one prey (Fig. 2b). This more complex version helped us to better understand how the herbivorous non-spinose planktonic foraminifera can compete with other omnivorous zooplankters and handle multiple predation pressure. The food web model has a more realistic representation of the plankton community in terms of the set-up. This is because it better represents the predator–prey interactions between phytoplankton and zooplankton communities than the food chain model, but these dynamic interactions within the groups are more challenging to disentangle (Banas, 2011; Ward et al., 2014). With the two versions of the model we were able to examine how the resource competition within the plankton community, as well as predation, influences different life stages of planktonic foraminifera.
The switch from the food chain to food web version was implemented through predators' grazing kernel, which dictates the relative palatability of potential prey (Fig. 2c, Eq. 3). In this parameterization, the prey palatability () expresses the likelihood of a predator to eat a prey (Eq. 3) and it depends on the optimum predator : prey length ratio (θopt), the log size ratio of each predator with each prey () and the standard deviation (σ) which shows the width of size prey preference and defines how specialist or generalist the predator can be (Fig. 3).
We assumed a 10:1 predator : prey length ratio as the optimum size for zooplankton to feed upon, as is often observed for zooplankton (Kiørboe, 2008). Prey with a size ratio equal to this optimum therefore had the highest prey palatability of this particular predator. For the food chain model, predators could only consume one prey group that was exactly 10 times smaller than themselves (σ=0.0001). In the food web model, we allowed zooplankton to be more generalist predators and feed on prey of size around this optimum ratio but with a smaller palatability to acknowledge that zooplankton can feed on prey of a wider size range (Kiørboe, 2008) (σ=0.5). When considering generalist planktonic foraminifera (food web model), we tested a range of different grazing kernels (σ=0.5–1.0). This is because the model results showed that being more generalist than other zooplankton groups is a condition for planktonic foraminifera to survive.
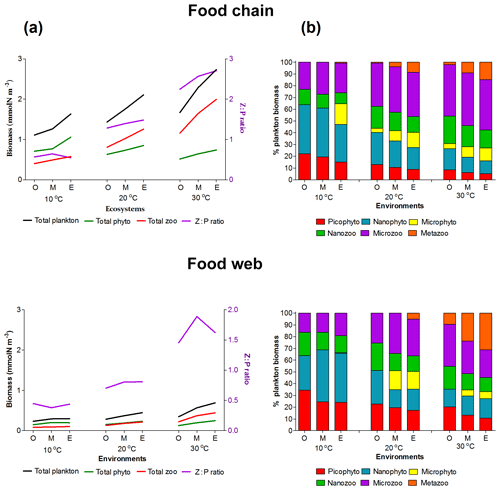
Figure 3Plankton total biomass and group diversity for all environments (O: oligotrophic, M: mesotrophic and E: eutrophic environments). (a) Right axis: biomass of phytoplankton (green line), zooplankton (red line) and total plankton (black line) (mmol Nm−3). Left axis: zooplankton : phytoplankton biomass ratio (purple line). (b) Relative (%) biomass of phytoplankton and zooplankton size groups.
2.3 Adding planktonic foraminifera to the model
We explored the potential ecological controls on planktonic foraminifera ecology by means of a series of ensembles of model experiments (Table 3). Each individual ensemble was designed to explore a wide range of potential parameter value combinations of growth, predation and background mortality rates and hence different trade-off assumptions and growth conditions. The ensembles were repeated for different potential assumed ecological structures and life stages (prolocular and adult) of planktonic foraminifera. We applied a series of “plausibility” filters on the model results to derive a series of subsets of experiments that we analyse in detail and discuss the implications of.
Table 3Summary of studied traits and environmental conditions for the non-spinose planktonic foraminifera. O: oligotrophic, M: mesotrophic, E: eutrophic regions.
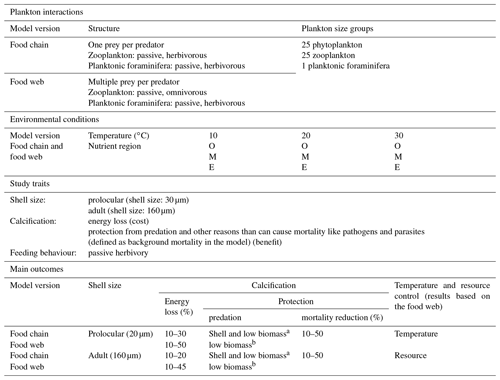
a The model showed that both shell and low biomass are important for protection from predation. b The results showed that low biomass is more important than shell for protection from predation.
2.3.1 Planktonic foraminifera biomass
We estimated that the contribution of the prolocular and adult stage of non-spinose planktonic foraminifera to zooplankton biomass ranges from 0.007 % to 0.09 % based on the studies by Schiebel and Movellan (2012) and Buitenhuis et al. (2013). According to Schiebel and Movellan (2012), adults with a shell size fraction of 150–200 µm contribute 12.4 % in total planktonic foraminifera biomass in the North Hemisphere. Buitenhuis et al. (2013) estimated that the contribution of planktonic foraminifera to micro- and mesozooplankton biomass (Pg C) ranges from 0.05 % to 0.08 %, based on the data from Schiebel and Movellan (2012). To compare our modelled biomass to observations from Schiebel and Movellan (2012) and Buitenhuis et al. (2013), we converted Pg C and µg C to mmol N m−3, using the carbon molecular weight (12 g C mol−1) and a C:N Redfield stoichiometry of 6.625. We assumed that non-spinose species represent 50 % of the samples of Schiebel and Movellan (2012) and there is no correlation between the species and the size fractions, to estimate that the relative biomass of the non-spinose planktonic foraminifera 150–200 µm size fraction to micro- and mesozooplankton biomass ranges from 0.02 % (5×103 mmol N m−3) to 0.03 % (1×104 mmol N m−3).
Due to the lack of data, we presumed that the prolocular biomass is similar to the adult biomass. To include sampling errors, methods' bias for estimating the contribution of planktonic foraminifera to global zooplankton biomass due to their low biomass (Buitenhuis et al., 2013) and a global biomass representation of early stages, we extended the biomass range to be from 0.007 % to 0.09 % based on the suggestion by Schiebel and Movellan (2012) that biomass of early stages can be up to 3 times higher than adults with size <125 µm. Model simulations for which planktonic foraminifera relative biomass was within the observed range of 0.007 % to 0.09 % are referred to here as “low biomass” simulations.
2.3.2 Calcification
With the model we tested basic hypotheses to investigate the trade-offs of shell size and calcification and the effect of resource competition on planktonic foraminifera biomass for two life stages, prolocular (20 µm) and the adult (160 µm). Each life stage was modelled independently. As the costs and benefits of foraminifera's calcification are not experimentally known, we added a calcifying zooplankton type in the model with an associated trade-off for calcification, following the Monteiro et al. (2016) representation of a calcifying phytoplankton type (coccolithophore). To model non-spinose planktonic foraminifera, we used the same parameterization and equations as for zooplankton, hypothesizing that the main cost for shell development is energy loss and the main benefit of calcification is protection. Preliminary experiments showed that the background mortality (m) had to be decreased to keep planktonic foraminifera biomass within the low biomass range defined, following suggestions that planktonic foraminifera can use their shell as a protection against more than just predation (Armstrong and Brasier, 2005).
To estimate the cost and benefit of calcification, we ran a sensitivity analysis by decreasing planktonic foraminifera maximum grazing (Gmax) and background mortality (m) rate from 5 % to 95 % and 0 % to 95 % (in 5 % steps) respectively, to represent calcification's energy loss and benefit. Studies have shown that zooplankton metabolic rate and biomass can vary with temperature (Ikeda, 1985), but the reasons behind the correlation between habitat and mortality rate are still not very well understood (Aksnes and Ohman, 1996). There are currently no quantitative estimates of the energetic cost and benefits of calcification in planktonic foraminifera. Hence, we selected as most likely (herein denoted as “plausible” simulations) the simulations that had a range of reductions of Gmax and m smaller than 40 % throughout all tested environments (e.g. 10 %–50 % or 20 %–60 % reduction). This is a way to account for the non-unlimited plasticity of an organism.
In the end, to quantify the benefit of predation protection, we chose a number of simulations to examine different predation pressures on planktonic foraminifera by decreasing the grazing term () (Eq. A3) by 100 % (no grazing pressure on planktonic foraminifera), 75 %, 50 %, 25 % and 0 % (no protection from grazing pressure) of its initial value.
2.4 Model set-up and numerical simulations
We set up a series of experiment ensembles to systematically test traits and trade-offs for nine different environmental combinations, with three input nutrient concentrations (No=1, 2.5 and 5 mmol N m−3) to represent oligo-, meso- and eutrophic environments respectively and three water temperatures (10, 20, 30 ∘C) (Table 3). Each ensemble comprises a series of model experiments that explore a wide range of potential parameter value combinations of growth, predation and background mortality rates in different environmental conditions (temperature and nutrient concentrations). The ensemble set-up is then repeated for two life stages of planktonic foraminifera (prolocular and adult) using both the food chain and the food web model.
Every individual experiment was initialized with the concentration of all plankton groups set to 0.0001 mmol N m−3 and run for 10 000 days (∼27 years). For the food chain, the experiments reached steady state (biomass ±0.01 mmol N m−3). In the food web version, the majority of the experiments reached an oscillatory steady state close to an equilibrium, which was still present after running the model for more than 270 years (results not shown). This oscillatory behaviour is a common feature in ecosystem models (e.g. Baird et al., 2010), especially of planktonic communities (e.g. Petrovskii and Malchow, 1999; Petrovskii et al., 2001; Banas et al., 2011).
We present the absolute and relative biomass of planktonic foraminifera from all tested scenarios of calcification costs and benefits in Grigoratou et al. (2019, https://doi.org/10.5281/zenodo.2631905) based on the last 1000 days of the simulations. From 921 (500 for the food chain and 421 for the food web) tested simulations, 9.5 % (88 simulations) were within the low biomass criterion. From the low biomass simulations, 75 % (64 simulations) cover the conditions of the plausible criterion. Due to the low number of plausible simulations (<4) per environment (Figs. 4–7, Grigoratou et al., 2019), we were not able to perform statistical analysis, and instead we provided ranges of values for costs and benefits of calcification in non-spinose planktonic foraminifera for each life stage. We ran 100 simulations for both stages and model versions to examine different predation on planktonic foraminifera.
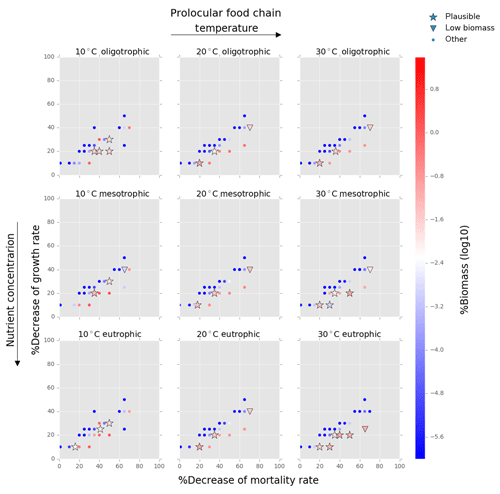
Figure 4Results from the food chain model for the calcification cost (reduction of growth) and benefit (reduction of mortality rate) for the prolocular life stage of planktonic foraminifera. Legend shows “other” for total tested simulations, low biomass for simulations for which their biomass is within the defined range and plausible for the simulations we consider to be as most likely. More details on low biomass and plausible simulations are given in Sect. 2.3, “Adding planktonic foraminifera to the model”.
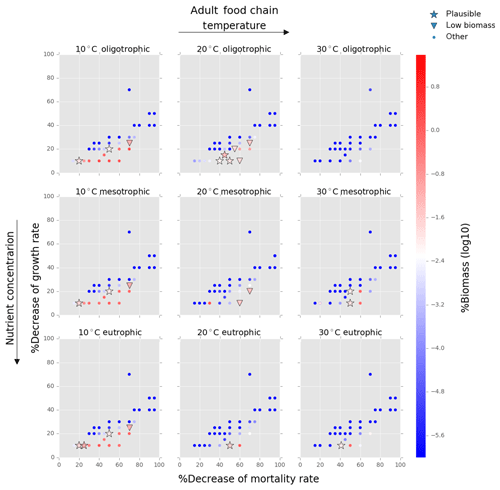
Figure 5Results from the food chain model for the calcification cost (reduction of growth) and benefit (reduction of mortality rate) for the adult life stage of planktonic foraminifera. Legend shows other for total tested simulations, low biomass for simulations for which their biomass is within the defined range and plausible for the simulations we consider to be as most likely. More details on low biomass and plausible simulations are given in Sect. 2.3, “Adding planktonic foraminifera to the model”.
3.1 General plankton distribution at different environments
Both versions of the model showed an increasing diversity and biomass from oligo- to eutrophic environments and from cold to warmer environments (Fig. 3), capturing the main patterns of marine plankton community structure (e.g. Irigoien et al., 2004; Müren et al., 2009; O'Connor et al., 2009). In the food chain version, biomass of phytoplankton and zooplankton increased continuously with the number of coexisting size groups (Fig. B1a in Appendix B). In contrast, the food web version had a patchy distribution of biomass with fewer coexisting groups, equivalent to “winners” of resource competition, and an overall lower biomass than the food chain model (Fig. B1b) in agreement with previous studies (e.g. Armstrong, 1994; Banas et al., 2011).
Picoplankton, nanophytoplankton, nanozooplankton and microzooplankton dominated the plankton biomass at 10 ∘C in both versions (Fig. 3b) as they outcompete the larger cell sizes through resource competition. As the concentration of the incoming nutrients (No) was increased from oligo- to eutrophic, the growth rate and coexistence of phytoplankton groups also increased, leading to a higher grazing pressure of zooplankton, biomass and zooplankton coexistence. In the food chain model, microphytoplankton survived in the eutrophic environment at low temperatures (10 ∘C) and all the nutrient environments at 20 and 30 ∘C. In the food web, microphytoplankton were present in meso- and eutrophic environments at 20 and 30 ∘C. Mesozooplankton were sustained in meso- and eutrophic environments at 20 ∘C for the food chain model, in eutrophic environments at 20 ∘C for the food web model and in all environments at 30 ∘C at both versions of the model (Fig. 3b). Since our model captured the general trends of plankton community through different environments, we used it to investigate the importance of individual traits and trade-offs.
3.2 Planktonic foraminifera ecology
3.2.1 Cost of calcification
We estimated the potential energetic cost of calcification in non-spinose planktonic foraminifera by decreasing their growth rate. In the food chain model, of the 500 simulations, 10.6 % (54 simulations) were within the low biomass and 8 % (39 simulations) within the plausible criteria. The plausible simulations showed a decrease of foraminifera growth rate by 10 % to 30 % for the prolocular stage and 10 % to 20 % for the adult stage (Figs. 4, 5). For the adult stage, we found no plausible simulations for the mesotrophic environment at 20 ∘C due to a high decrease of the background mortality (>60 %) compared with the low reduction (10 %) of their growth rate.
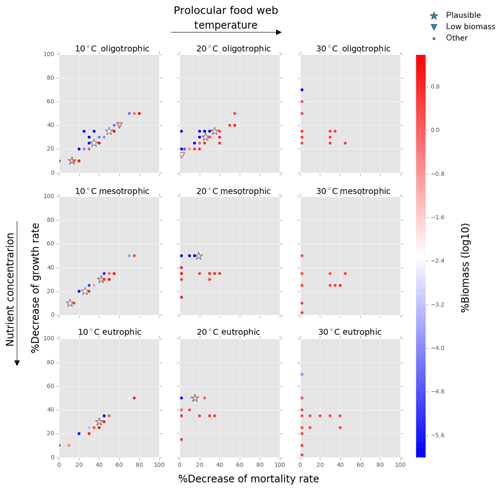
Figure 6Results from the food web model for the calcification cost (reduction of growth) and benefit (reduction of mortality rate) for the prolocular life stage of planktonic foraminifera. Legend shows other for total tested simulations, low biomass for simulations for which their biomass is within the defined range and plausible for the simulations we consider to be as most likely. More details on low biomass and plausible simulations are given in Sect. 2.3, “Adding planktonic foraminifera to the model”. For the meso- and eutrophic environments of 20 ∘C and all environments of 30 ∘C, the pattern of the simulations is more scattered than for the remaining environments. This is because in a range of a 0 % to 50 % reduction on the mortality rate, the relative biomass of planktonic foraminifera was high and outside the observation range. As a further reduction of the mortality rate would result in an additional increase of relative biomass, the sensitivity analysis was not required.
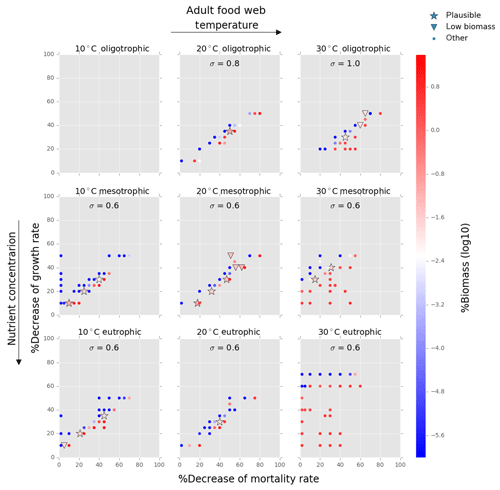
Figure 7Results from the food web model for the calcification cost (reduction of growth) and benefit (reduction of mortality rate) for the adult life stage of planktonic foraminifera. Legend shows other for total tested simulations, low biomass for simulations for which their biomass is within the defined range and plausible for the simulations we consider to be as most likely. More details on low biomass and plausible simulations are given in Sect. 2.3, “Adding planktonic foraminifera to the model”. For all environments of 30 ∘C, the pattern of the simulations is more scattered than for the rest environments. This is because in a range of a 0 % to 50 % reduction on the mortality rate, the relative biomass of planktonic foraminifera in some scenarios was high and outside the observation range. As a further reduction of the mortality rate would result in an additional increase of relative biomass, the sensitivity analysis was not required.
Of the 421 food web simulations, 8 % (34 simulations) were low biomass and 6 % (25 simulations) plausible. The biomass of the prolocular stage increased with temperature and nutrients. The model could not produce any low biomass simulation of early life stages of foraminifera at 30 ∘C as values were significantly too high (1 %–7.3 % of the total zooplankton biomass, Fig. 6). In all environments at 10 ∘C and for oligotrophic environment at 20 ∘C the plausible simulations showed a 10 %–35 % decrease of growth rate. To maintain the prolocular biomass within the defined low biomass range in meso- and eutrophic environments at 20 ∘C, the calcification cost was equal to a 50 % reduction of the growth rate (Fig. 6). The model did not generate results for adults in oligotrophic waters at 10 ∘C as only small zooplankton groups (<63 µm) could survive for that environment. There were no plausible simulations for the eutrophic environment at 30 ∘C, as planktonic foraminifera relative biomass was higher than the defined range (Fig. 7). For all the other environment the cost of calcification for the adult stage ranged from 10 % to 40 % (Fig. 7).
3.2.2 Potential benefits of calcification in planktonic foraminifera
Both versions of the model showed that to maintain planktonic foraminifera within the defined biomass range, the background mortality rate of both prolocular and adult stages had to be reduced by 10 %–50 % (Figs. 4–7). Our results suggest that planktonic foraminifera use their shell not only for predation protection but for other reasons, e.g. against pathogens, like bacteria or viruses and parasites.
Regarding the use of the shell as protection from predation, both model versions showed different results. This is due to different feeding behaviour of zooplankton (specialist vs. generalist) as in both models, predation depends on the feeding behaviour of the predator, prey size and biomass.
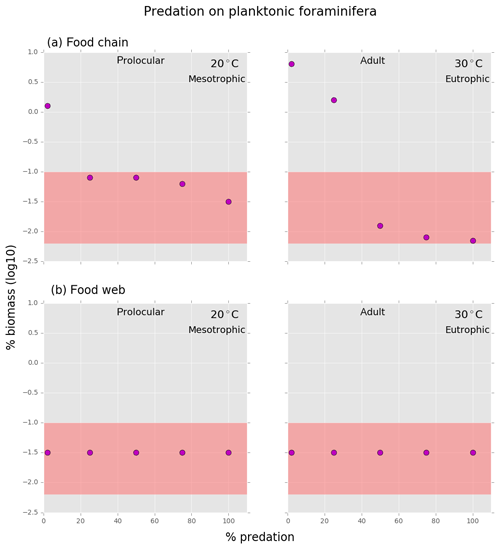
In the food chain model, the foraminifera biomass could be maintained inside the observed range when grazing pressure was reduced by 25 % for the prolocular and 50 % for the adult stage compared to full predation (Fig. B2). Therefore, both low biomass and possession of hard parts are important mechanisms against specialist predators.
Shell protection against predation had no effect on the relative low biomass of foraminifera in the food web model as their biomass remained the same with or without predation at both life stages (Fig. B2). The food web version suggests that low biomass is a more efficient protective mechanism than the shell against a generalist predator. We found that with a combination of higher than observed biomass of planktonic foraminifera and a predation pressure lower than 50 %, planktonic foraminifera became a dominant group with up to 22 % of the total zooplankton biomass, suggesting that the shell has a protective function (results not shown).
3.2.3 Temperature and feeding control amongst different life stages of planktonic foraminifera
We focus on the results of the food web as it considers resource competition between planktonic foraminifera and the rest of zooplankton and simulates the plankton food web better than the food chain. Our model suggested that being herbivorous is a successful strategy for the prolocular stage as their optimum size prey group (≈2–3 µm, as determined by the 10:1 predator : prey size ratio) was present in high abundance in all environments (Fig. 8). Resource competition is therefore not a determinant factor for the prolocular stage. The model results suggest that temperature had a stronger control on this stage, resulting in higher biomass (1 %–7 %) at 30 ∘C (Fig. 6, Grigoratou et al., 2019; https://doi.org/10.5281/zenodo.2631905).
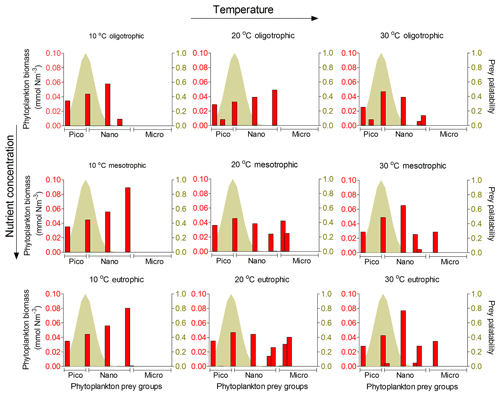
Figure 8Model results of resource competition for the prolocular stage (20 µm) of planktonic foraminifera in the food web version. Left axis (red columns): biomass (mmol N m−3) of phytoplankton size groups. Right axis (coloured shadow): prey palatability of planktonic foraminifera using a σ=0.5. A total of 6 pico- (0.6–2.0 µm), 10 nano- (2.6–20 µm) and 9 microplankton groups (25–160 µm) are included in the model set-up.
Adult foraminifera in the model achieved realistic relative biomass only when they became more generalist feeders by increasing their prey palatability by 20 % (σ=0.6) for meso- and eutrophic conditions and by 80 % (σ=0.8) to 100 % (σ=1.0) in oligotrophic environments (relatively to σ=0.5 for other zooplankton) (Fig. 9). Without this change, adult herbivorous foraminifera in the model were outcompeted by omnivorous predators. To understand if feeding behaviour or the lower growth rate and mortality associated with calcification led them to become more generalists, we switched the feeding behaviour in the model from herbivorous to omnivorous. The results showed that omnivorous planktonic foraminifera did not need to be more generalist than the other zooplankters (results not shown). Resource limitation had therefore an important role in controlling the non-spinose planktonic foraminifera adult stages.
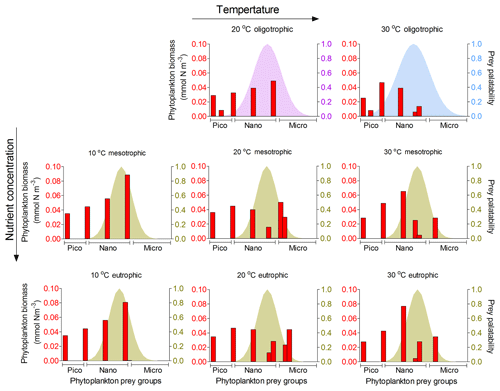
Figure 9Model results of resource competition for the adult stage (20 µm) of planktonic foraminifera in the food web version. Left axis (red columns): biomass (mmol N m−3) of phytoplankton size groups. Right axis (coloured shadow): prey palatability of planktonic foraminifera. For oligotrophic environments, σ=0.8 (violet) and 1 (light blue) for 20 and 30 ∘C, respectively. For all meso- and eutrophic ecosystems σ=0.6. No zooplankton larger than 100 µm and adult stage of planktonic foraminifera survived in the oligotrophic ecosystem at 10 ∘C for the model set-up. A total of 6 pico- (0.6–2.0 µm), 10 nano- (2.6–20 µm) and 9 microplankton groups (25–160 µm) are included in the model set-up.
We developed the first size-based 0-D model of two life stages (one prolocular, 20 µm, and one adult, 160 µm) of planktonic non-spinose foraminifera to investigate the cost and benefits of calcification and feeding behaviours under different environmental conditions (temperature and nutrient). It is important to note that the present model, like other size-structured models, cannot capture the complexity of the plankton community (Banas, 2011) but represents general patterns and encapsulates basic physiological relationships. The model shows that diversity increases from oligo- to eutrophic environments and from cold to warmer environments. The model therefore captures the increase in complexity in planktic ecosystems toward the tropics and eutrophic systems (Irigoien et al., 2004).
In the ocean, phytoplankton biomass and productivity are controlled by nutrient availability, light, temperature and grazing pressure (Irigoien et al., 2004). In oligotrophic areas, nutrient limitation leads to the dominance of small-sized phytoplankton cells as there is not enough energy to sustain larger cells (Menden-Deuer and Kiørboe, 2016). As nutrient availability increases, phytoplankton size diversifies. Zooplankton shows a similar pattern; oligotrophic environments are dominated by small heterotrophs, while the size of the species increases in eutrophic environments (Razouls et al., 2018). Our model captured this general pattern, but it struggled to sustain a high biomass of the largest size groups of microphytoplankton and mesozooplankton, especially in non-eutrophic environments. We suggest that the oversimplification of physiological and behavioural traits, especially for zooplankton, leads to this limitation, as species are represented as spheres with fixed half-saturation (Kzoo) and assimilation efficiency (λ) (more details in Appendix A). Changing the shape of the body from a sphere towards an ellipse for representing metazoans, combined with variable half-saturation, may circumvent this problem. Including motility, an important trait for organisms' survival (e.g. feeding, predation protection) with a strong influence on metabolic rates (e.g. Ikeda, 1985), could also improve model results.
In the present study we tried to quantify the cost and benefit associated with calcification in planktonic foraminifera. Our model suggests a cost of calcification in non-spinose planktonic foraminifera of 10 %–50 % for the early life stages and 10 %–40 % for the adults. This cost is similar to estimates for coccolithophores (∼30 %; Monteiro et al., 2016) and for shell production of marine benthic molluscs (22 %–50 %; Palmer, 1992). While biocalcification evolved in the Precambrian and across many clades, metabolic costs may be comparable as pathways and constraints are similar for a range of organisms (Knoll, 2003). Our model results suggest that planktonic foraminifera calcify for a combination of reasons (e.g. protection from pathogen, parasites and grazers), as suggested by other studies on planktonic foraminifera (Armstrong and Brasier, 2005) and phytoplankton (Hamm et al., 2003; Hamm and Smetacek, 2007; Monteiro et al., 2016). Observations show that bacteria can attack the cytoplasm of unhealthy or dead planktonic foraminifera (Schiebel and Hemleben, 2017). More field and laboratory studies are needed to gain a deeper knowledge on the interaction between planktonic foraminifera and pathogens.
Predation on planktonic foraminifera is still not well understood (Schiebel and Hemleben, 2017). While benthic foraminifera are selectively preyed upon by scaphopods (Murray, 1991), evidence for predation on planktonic foraminifera is limited. It is difficult to detect remains of early developmental states in faecal pellets due to their small size, thin walls and low biomass, resulting in the lack of data (Schiebel and Hemleben, 2017). Shell and spines of adults have been detected in faecal pellets of metazooplankton groups (like salps, copepods, pteropods and euphausiids) and nekton shrimps (Bé et al., 1977; Bradbury et al., 1970; Berger, 1971b). Our results highlight that low biomass is a main mechanism for protection against predation in planktonic foraminifera. The food web model results showed that reducing grazing pressure could be a potential benefit of calcification for planktonic foraminifera if they were to become more abundant. The earliest planktonic foraminifera are thin-shelled and very small (Gradstein et al., 2017), while modern species have more complex morphologies with larger and thicker shells (Schmidt et al., 2004a). While the planktonic ecosystem has become more complex over the last 150 Ma, we speculate that their low abundance and thick shells may have prevented the evolution of a specific predator in contrast to other dominant phytoplankton groups with shells like diatoms (Hamm et al., 2003; Hamm and Smetacek, 2007). As planktonic foraminifera are immotile organisms, it is difficult for predators to sense them (Kiørboe, 2008; Van Someren Gréve et al., 2017). Their thick shell can then act as armour when a grazer reaches them to counterbalance their non-motility. Based on the results of our model and our current knowledge on foraminiferal physiology, we propose that the combination of low abundance and a carbonate shell protects planktonic foraminifera against predation. Planktonic foraminifera are thus high-energy-demand prey: they are hard to find and digest, corroborating earlier suggestions that foraminifera do not have specific predators (Hemleben et al., 1989). We suggest that planktonic foraminifera non-motility is an important behavioural trait to be further tested in order to improve our understanding of grazing protection.
Temperature and food appear to be the main controlling factors of planktonic foraminifera ecology and distribution in the ocean (e.g. Ortiz et al., 1995; Bé and Tolderlund, 1971), corroborated by modelling studies (Žarić et al., 2006; Fraile et al., 2008, 2009; Lombard et al., 2009; Roy et al., 2015). Studies have shown that sea surface temperature (SST) is one of the most important environmental factors of planktonic foraminifera's diversity (Rutherford et al., 1999) and size (Schmidt et al., 2006, 2004a). Field observations (e.g. Bé and Tolderlund, 1971), geochemical analysis (Elderfield and Ganssen, 2000) and culture experiments (Caron et al., 1987a, b) show that adult species have a specific optimum temperature range which controls their size development and abundance (Schmidt et al., 2004a; Žarić et al., 2005; Lombard et al., 2009). In the present study, we use our trait-based model to study planktonic foraminifera as a group of species to investigate the general patterns of the influence of temperature and resource on planktonic foraminifera biomass on both juvenile and adult stages.
We find that temperature is the main limiting factor for the prolocular life stage, since there is no food limitation. Our model provides insights on the importance of resource availability and competition during development, resulting in a switch to generalist herbivory and omnivory diet at adult stages. Food availability impacts planktonic foraminifera ecology (e.g. Ortiz et al., 1995; Schmidt et al., 2004a). Culture experiments highlight that the amount and type of food have a strong influence on growth rate (e.g. Spindler et al., 1984; Anderson et al., 1979), shell size (Bé et al., 1981) and gametogenesis (Caron et al., 1982; Caron and Bé, 1984; Hemleben et al., 1989). The model results support the hypothesis that during early stages planktonic foraminifera have a herbivorous diet. They also indicate that food availability is a key controlling factor of the biomass of non-spinose adult stages that defines their type of feeding strategy for different nutrient concentration environments.
We propose that non-spinose adult planktonic foraminifera are very successful herbivorous predators, capable to prey on different phytoplankton size groups, or that they can be omnivorous and use other food sources like bacteria, detritus and zooplankton. Observations suggest an opportunistic feeding behaviour for non-spinose species. Diatoms are usually considered to be their primary prey (e.g. Spindler et al., 1984; Hemleben et al., 1989), though some can also consume dinoflagellates (e.g. Anderson et al., 1979) and cryophytes, which are either slowly digested or used as symbionts (Hemleben et., 1989). Animal tissues have been found in several non-spinose species (Anderson et al., 1979; Hemleben and Spindler, 1983). Globorotalia menardii, an abundant and the biggest non-spinose species, is suggested to actively control microzooplankton (ciliates) prey (e.g. Hemleben et al., 1977). Culture experiments suggest cannibalism between non-spinose species but never between spinose species (Hemleben et al., 1989). These observations support our results that non-spinose adult species can feed on different types and size of phytoplankton or switch to omnivory when phytoplankton concentrations are rare.
Our model provides important information on how resource competition among planktonic foraminifera and other zooplankters influences the feeding behaviour of different life stages and their distribution. Moreover, the inability of our food web model to sustain adult stages of non-spinose foraminifera in warm oligotrophic regions agrees with observations as planktonic foraminifera are dominated by symbiont-bearing species in these regions (Bé and Tolderlund, 1971). Our model results can provide new perspectives regarding the development of symbiosis as an additional energy source in planktonic foraminifera, and hence adding symbiosis to the model can be a next important step for improving our understanding of planktonic foraminifera ecology.
This study takes a first step towards including planktonic foraminifera ecology as part of the plankton community in a trait-based framework and estimates the energetic cost of calcification and the associated benefits. We find that the energetic cost of calcification varies between 10 % and 30 % in the food chain model for both prolocular and adult stages, between 10 % and 50 % in the food web model for the prolocular stage and between 10 % and 40 % for the adult stage. We consider that both low biomass and the carbonate shell are key elements for protection of planktonic foraminifera from predation. A reduction in mortality by 10 %–50 % suggests that the shell may be more important for pathogens and parasites than against grazing pressure.
Similar to coccolithophores (Monteiro et al., 2016), the costs and benefits of calcification in planktonic foraminifera vary with the environment. In the model, temperature is the dominant factor for the prolocular stage, whereas both temperature and resources are important for the adult. Consequently, the adults are more impacted by resource competition driven by less available food in the optimal size of their prey, resulting in feeding on a wider range of prey size, particularly in oligotrophic environments where food is scarce. We therefore suggest that the adults are generalist herbivorous or omnivorous or use other resources in oligotrophic environments such as symbiosis.
To develop the model further, data on energy allocated to growth, calcification and motility are needed to better understand the physiology and ecology of this important paleoclimate proxy carrier and producer of marine carbonates. Other traits and trade-offs such as feeding mechanism (rhizopodial network, spines), mobility and symbiosis with algae need to be tested in the future and supported by culture experiments.
The code can be found online at https://doi.org/10.5281/zenodo.2631905 (Grigoratou et al., 2019).
Our model represents a chemostat experiment in a zero-dimensional (0-D) setting, with one source of nutrients and 51 generic plankton (autotrophs and heterotrophs) size classes from pico- to mesoplankton (Sieburth et al., 1978).
A1 Plankton size groups
We selected plankton cell sizes in the model so that the volume of each plankton doubles from one class to another similar to Ward et al. (2014). We set up the model to have 6 pico- (0.6–2.0 µm), 10 nano- (2.6–20 µm) and 9 microplankton groups (25–160 µm) for the phytoplankton and 6 nano- (6–20 µm), 10 micro- (26–200 µm) and 9 (250–1600 µm) mesozooplankton groups for the zooplankton. The diagnostic equation for plankton biomass (phytoplankton and zooplankton) is given in Eq. (1) and shows the generic dependence of biomass on nutrient uptake, zooplankton grazing and mortality. The symbols are explained in Tables 1 and 2.
A2 Environmental variables
The model accounts for two environmental variables influencing plankton growth: light and temperature. Light limitation (li) is represented as a fixed parameter set to 0.1 (equivalent to 90 % of light limitation; Ward et al., 2014). The influence of temperature on plankton metabolic rates (γT) is represented by an Arrhenius-like equation (Eq. A1), with (Tref) the reference temperature at which γT=1 is 293.15 K (20 ∘C), (T) the ambient temperature of the water (K) and (R) the temperature sensitivity of plankton growth rate.
We tested three ambient water temperatures (T): 10, 20 and 30 ∘C, characteristic of subpolar, subtropical and tropical regions respectively. Temperature limitation (γT) has a proportionate impact on both phytoplankton and zooplankton growth (Eqs. A2, A3).
A3 Phytoplankton growth
Phytoplankton growth (Pgrowth,j) is size-dependent and described via the Monod equation, assuming there is a balance between the nutrient uptake and growth of phytoplankton (Monod, 1950) (Eq. A2).
Phytoplankton half-saturation (KN) and maximum specific growth rate (μmax) are cell-size-dependent (Table 1). The maximum uptake rate (μmax) has been normalized to 20 ∘C and is a function of the maximum photosynthetic rate (Pmax), the cell volume () and the phytoplankton quota (Tables 1 and 2) (Ward et al., 2014). The maximum photosynthetic rate (Pmax) for each size class of phytoplankton reflects observations of Prochlorococcus for the two first picoplankton groups (0.6 and 0.8 µm) and of Synechococcus for the remaining four picoplankton groups, other eukaryotes for nanoplankton and diatoms for microphytoplankton (Irwin et al., 2006) (Table 2).
A3.1 Zooplankton growth
We used the zooplankton grazing term as has been described in Ward et al. (2012), applied for two different feeding behaviours of zooplankton: specialist (i.e. consume one prey) herbivorous for the food chain and generalist (i.e. consume more than one prey) omnivorous predators for the food web. Zooplankton grazing () is represented using the Holling type II function (Eq. A3). Although most zooplankton have different feeding behaviours in different life stages, Holling type II better illustrates predator–prey relationships of many ambush zooplankton groups in the lab over a long-term period (Kiørboe et al., 2018a).
where Gmax is the maximum grazing rate, γT is temperature limitation, is prey palatability, is the prey's biomass, is the total available biomass for each predator, is the predator's half-saturation constant, Prey refuge is the prey refuge and ΦP,Z is the predator's “switching” between phytoplankton and zooplankton prey.
The maximum prey ingestion rate (Gmax) is size-dependent (Table 2). The prey palatability () expresses the likelihood of a predator to consume the prey (Eq. 3). It depends on the log size ratio of predator : prey length ratio with the optimum predator : prey length ratio (θopt).
The total prey biomass available to each predator () is calculated as a sum of prey biomass weighted by their prey palatability (Eq. A4).
We set the zooplankton half-saturation constant () to 0.1051 mmol N m−3. This value is a conversion of the Ward et al. (2012) value (1 mmol C m−3) from carbon to nitrogen based on the Redfield ratio (106 : 16 mol C : mol N). While observations show evidence of a variable half-saturation constant for zooplankton (e.g. Hansel et al., 1997), there is not enough information to tease apart its value for the different species, so we assumed a constant among our zooplankton groups.
A4 Prey refuge
The predator–prey interactions depend mostly on the predator : prey length ratio (Kiørboe, 2008), the prey's availability and ability to escape predation (e.g. van Someren Gréve et al., 2017; Pančić and Kiørboe, 2018) and the predator's feeding behaviour (Kiørboe et al., 2018a). As immotile phytoplankton species cannot physically escape predation, they use other defence mechanisms, like shell, spines, toxins and colony formation (Pančić and Kiørboe, 2018). We believe that planktonic foraminifera, as immotile organisms, use their shell as a defence mechanism against predators, to balance their inability to escape predation through movement.
In our study we include a prey refuge term which is based on the prey's size and density based on the function of Mayzaud and Poulet (1978) (Eq. A5). The prey refuge term describes how predators' grazing rate changes with prey density and never satiates (Gentleman and Neuheimer, 2008). At high prey density the grazing rate is similar to Holling type I, where it becomes linearly related to the prey availability () (Fig. A1, Eq. A5 in Appendix A). When the prey density is low, the decay constant parameter (Λ) decreases the grazing pressure such that the grazing rate is similar to Holling type III (Fig. A1) (Gentleman et al., 2003). In our model the prey refuge term causes a reduction of grazing pressure on prey with low density (Fig. A1).
The present version of the model does not include the prey's movement and other defence mechanisms because of limited understanding (van Someren Gréve et al., 2017; Almeda et al., 2017). As the main aim of our study is to better understand calcification and the function of shell as a defence mechanism, we removed planktonic foraminifera's prey refuge term, by making the assumption that the lack of prey refuge could balance the cost of their immotility. We are aware that this is a very simply way to represent the trade-offs of immotility, but we chose not to add motility and increase the complexity of the model and the uncertainty of the results, as the costs and benefits of planktonic foraminifera's motility have not been studied yet. Our model can be used as a first step for building a mechanistic understanding, and more studies can follow focusing on planktonic foraminifera's defence mechanisms.
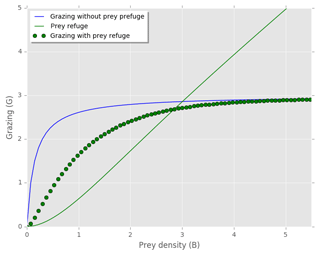
Figure A1Zooplankton grazing on one prey with and without the prey refuge term included. Prey refuge = (Mayzaud and Poulet, 1978). Grazing without prey refuge: . Grazing with prey refuge included: . Temperature limitation (γT), prey palatability (φ) and prey refuge constant (Λ) equal to 1, and .
We ran simulations with and without planktonic foraminifera's prey refuge included (results not shown). For the food chain the prey refuge had a stronger influence than the food web. This is an expected result, as specialist predators (food chain) feed only on specific preys, while generalist ones (food web) can consume multiple prey types and find other sources when the density of one is low. We found that the general trend of our model output does not change, and a reduction on mortality rate is still needed with or without the prey refuge term. In the present study we present the results with the prey refuge excluded (Figs. 4–7, B2).
A5 Zooplankton feeding
Omnivorous zooplankton can consume in parallel more than one phytoplankton and zooplankton prey. The predator can actively choose to feed mostly on phytoplankton (ΦP) or zooplankton (ΦZ) prey, depending on the prey's palatability () and density () weighted in total prey density (Bprey) (Gentleman et al., 2003; Kiørboe, 2008; Ward et al., 2012), so as (Eqs. A6, A7).
A6 Plankton mortality
Phytoplankton has a linear mortality term for both versions of the model. We assumed a size-dependent mortality term for zooplankton in the food chain model due to the absence of predation on zooplankton (Table 1) (Ward et al., 2014). As in the food web model predation on zooplankton exists, we assumed a linear mortality term equal to phytoplankton (Table 1) (Ward et al., 2012).
In Appendix B, we investigate the coexistence of plankton size groups in different nutrient environments (Fig. B1) and the examples of planktonic foraminifera's shell protection against different predation pressures in the food chain and food web (Fig. B2).
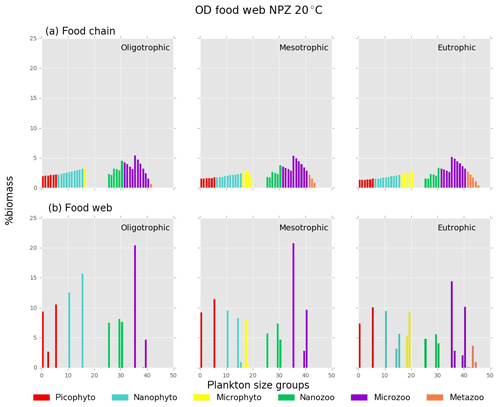
Figure B1Relative biomass (%) of each phyto- and zooplankton group in (a) food chain and (b) food web for oligo-, meso- and eutrophic environments at 20 ∘C.
MG, FMM and DNS designed the study. MG, JDW and BAW developed the model. MG prepared the paper. All authors contributed to writing and editing the final version of the paper.
The authors declare that they have no conflict of interest.
This work was supported by the European Research Council “PALEOGENiE” project (ERC-2013-CoG617313). This work was also supported by NERC (grant number NE/J019062/1) to Fanny M. Monteiro. Daniela N. Schmidt acknowledges support via a Wolfson Merit Award from the Royal Society. We thank the two reviewers for supplying constructive suggestions that helped to improve an earlier version of this paper.
This paper was edited by Stefano Ciavatta and reviewed by Friederike Prowe and Sakina-Dorothée Ayata.
Almeda, R., van Someren Gréve, H., and Kiørboe, T.: Behavior is a major determinant of predation risk zooplankton, Ecosphere, 8, e01668, https://doi.org/10.1002/ecs2.1668, 2017.
Anderson, O. R. and Bé, A. W. H.: A cylochemical fine structure study of phagotrophy in a planktonic foraminifer Hastigerina pelagica (d'Orbigny), Biol. Bull., 151, 437–449, https://doi.org/10.2307/1540498, 1976a.
Anderson, O. R., Spindler, M., Bé, A. W. H., and Hemleben, C.: Trophic activity of planktonic foraminifera, J. Mar. Biol. Assoc. UK, 59, 791–799, https://doi.org/10.1017/S002531540004577X, 1979.
Armstrong, H. A. and Brasier, M. D.: Foraminifera, Microfossils, 2nd Edn., Blackwell Publishing, Oxford, 296 pp., 2005.
Armstrong, R. A.: Grazing limitation and nutrient limitation in marine ecosystems: steady state solutions of an ecosystem model with multiple food chains, Limnol. Oceanogr., 39, 597–608, https://doi.org/10.4319/lo.1994.39.3.0597, 1994.
Aksnes, D. L. and Ohman, D. M.: A vertical life table approach to zooplankton mortality estimation, Limnol. Oceanogr., 41, 1461–1469, 1996.
Baird, M. E.: Limits to prediction in a size-resolved pelagic ecosystem model, J. Plankton Res., 32, 1131–1146, https://doi.org/10.1093/plankt/fbq024, 2010.
Banas, N. S.: Adding complex trophic interactions to a size-spectral plankton model: emergent diversity patterns and limits on predictability, Ecol. Model., 222, 2663–2675, https://doi.org/10.1016/j.ecolmodel.2011.05.018, 2011.
Banas, N. S., Møller, E. F., Nielsen, T. G., and Eisner, L. B.: Copepod Life Strategy and Population Viability in Response to Prey Timing and Temperature: Testing a New Model across Latitude, Time, and the Size Spectrum, Front. Mar. Sci., 3, 225, https://doi.org/10.3389/fmars.2016.00225, 2016.
Barker, S. and Elderfield, H.: Foraminiferal calcification response to glacial-interglacial changes in atmospheric CO2, Science, 297, 833–836, https://doi.org/10.1126/science.1072815, 2002.
Barton, A. D., Pershing, A. J., Litchman, E., Record, N. R., Edwards, K. L., Finkel, Z. F., Kiørboe, T., and Ward, B. A.: The biogeography of marine plankton traits, Ecol. Lett., 16, 522–534, https://doi.org/10.1111/ele.12063, 2013.
Bé, A. W. H. and Tolderlund, D. S.: Distribution and ecology of planktonic foraminifera, in: The Micropaleontology of Oceans, edited by: Funnell, B. M. and Riedel, W. R., 105–150, Cambridge University Press, London, 1971.
Bé, A. W. H., Hemleben, C., Anderson, O. R., Spindler, M., Hacunda, J., Tuntivate-Choy, S.: Laboratory and field observations of living planktonic Foraminifera, Micropaleontology, 23, 155–179, https://doi.org/10.2307/1485330, 1977.
Bé, A. W. H., Caron, D. A., and Anderson, O. R.: Effects of feeding frequency on life processes of the planktonic foraminifer Globigerinoides sacculifer in laboratory culture, J. Mar. Biol. Assoc. UK, 61, 257–277, https://doi.org/10.1017/S002531540004604X, 1981.
Beers, J. R. and Stewart, G. L.: Micro-zooplankters in the plankton communities of the upper waters of the eastern tropical Pacific, Deep-Sea Res., 18, 861–883, https://doi.org/10.1016/0011-7471(71)90061-1, 1971.
Berger, W. H.: Planktonic Foraminifera: sediment production in an oceanic front, J. Foramni. Res., 1, 95–118, https://doi.org/10.2113/gsjfr.1.3.95, 1971b.
Bradbury, M. G., Abbott, D. P., Bovbjerg, R. V., Mariscal, R. N., Fielding, W. C., Barber, R. T., Pearse, V. B., Proctor, S. J., Ogden, J. C., Wourms, J. P., Taylor Jr., L. R., Christofferson, J. G., Christofferson, J. P., McPhearson, R. M., Wynne, M. J., and Stromborg Jr., P. M.: Studies on the fauna associated with the deep scattering layers in the equatorial Indian Ocean, conducted on R/V Te Vega during October and November 1964, in: Proceedings of an International Symposium on Biological Sound Scattering in the Ocean, 31 March–2 April 1970, edited by: Farquhar, G. B., 409–452, Airlie House Conference Center, Warrenton, Virginia, 1970.
Brummer, G. J. A., Hemleben, C., and Spindler, M.: Planktonic foraminiferal ontogeny and new perspectives for micropaleontology, Nature, 39, 50–52, https://doi.org/10.1038/319050a0, 1986.
Brummer, G. J. A., Hemleben, C., and Spindler, M.: Ontogeny of extant spinose planktonic foraminifera (Globigerinidae): A concept exemplified by Globigerinoides sacculifer (Brady) and G. Ruber (d'Orbigny), Mar. Micropaleontol., 12, 357–381, https://doi.org/10.1016/0377-8398(87)90028-4, 1987.
Buitenhuis, E. T., Vogt, M., Moriarty, R., Bednaršek, N., Doney, S. C., Leblanc, K., Le Quéré, C., Luo, Y.-W., O'Brien, C., O'Brien, T., Peloquin, J., Schiebel, R., and Swan, C.: MAREDAT: towards a world atlas of MARine Ecosystem DATa, Earth Syst. Sci. Data, 5, 227–239, https://doi.org/10.5194/essd-5-227-2013, 2013.
Caromel, A. G. M., Schmidt, D. N., Fletcher, I., and Rayfield, E. J.: Morphological Change During The Ontogeny Of The Planktic Foraminifera, J. Micropalaeontol., 35, 2–19, https://doi.org/10.1144/jmpaleo2014-017, 2016.
Caron, D. A. and Bé, A. W. H.: Predicted and observed feeding rates of the spinose planktonic foraminifer Globigerinoides sacculifer, Bullets of Marine Science, 35, 1–10, 1984.
Caron, D. A., Bé, A. W. H., and Anderson, O. R.: Effects of variations in light intensity on life processes of the planktonic foraminifer Globigerinoides sacculifer in laboratory culture, J. Mar. Biol. Assoc. UK, 62, 435–452, https://doi.org/10.1017/S0025315400057374, 1982.
Caron, D. A., Faber, W. W. J., and Bé, A. W. H.: Effects of temperature and salinity on the growth and survival of the planktonic foraminifer Globigerinoides sacculifer, J. Mar. Biol. Assoc. UK, 67, 323–342, https://doi.org/10.1017/S0025315400026643, 1987a.
Caron, D. A., Faber, W. W., and Bé, A. W. H.: Growth of the spinose planktonic foraminifer Orbulina universa in laboratory culture and the effect of temperature on the life processes, J. Mar. Biol. Assoc. UK, 67, 343–358, https://doi.org/10.1017/S0025315400026655, 1987b.
Carstens, J., Hebbeln, D., and Wefer, G.: Distribution of planktic foraminifera at the ice margin in the Arctic (Fram Strait), Mar. Micropaleontol., 29, 257–269, https://doi.org/10.1016/S0377-8398(96)00014-X, 1997.
Elderfield, H. and Ganssen, G. M.: Past temperature and δ18O of surface ocean waters inferred from foraminiferal Mg∕Ca ratios, Nature, 405, 442–445, https://doi.org/10.1038/35013033, 2000.
Follows, M. J., Dutkiewicz, S., Grant, S., and Chisholm, S. W.: Emergent biogeography of microbial communities in a model ocean, Science, 315, 1843–1846, https://doi.org/10.1126/science.1138544, 2007.
Fraile, I., Schulz, M., Mulitza, S., and Kucera, M.: Predicting the global distribution of planktonic foraminifera using a dynamic ecosystem model, Biogeosciences, 5, 891–911, https://doi.org/10.5194/bg-5-891-2008, 2008.
Fraile, I., Schulz, M., Mulitza, S., Merkel, U., Prange, M., and Paul, A.: Modelling the seasonal distribution of planktonic foraminifera during the Last Glacial Maximum, Paleogeography, 24, PA2216, https://doi.org/10.1029/2008PA001686, 2009.
Gentleman, W. C. and Neuheimer, A. B.: Functional responses and ecosystem dynamics: How clearance rates explain the influence of satiation, food-limitation and acclimation, J. Plankton Res., 30, 1215–1231, https://doi.org/10.1093/plankt/fbn078, 2008.
Gentleman, W. C., Leising, A., Frost, B., Strom, S., and Murray, J.: Functional responses for zooplankton feeding on multiple resources: A review of assumptions and biological dynamics, Deep-Sea Res. Pt. II, 50, 2847–2875, https://doi.org/10.1016/j.dsr2.2003.07.001, 2003.
Gradstein, F., Gale, A., Kopaevich, L., Waskowska, A., Grigelis, A., and Glinskikh, L.: The planktonic foraminifera of the Jurassic. Part I: material and taxonomy, Swiss J. Palaeontol., 136, 187–257, https://doi.org/10.1007/s13358-017-0131-z, 2017.
Grigoratou, M., Monteiro, F. M., Schmidt, D. N., Wilson, J. D., Ward, B. A., and Ridgwell, A.: Grigoratouetal2019_Biogeosciences_SM: First release of Grigoratou et al 2019 NPZF model, Zenodo, https://doi.org/10.5281/zenodo.2631905, 2019.
Hamm, C. and Smetacek, V.: Armor: Whey, When, and How, Evolution of Primary Producers in the Sea, edited by: Falkowsi, P. and Knoll, A. H., Academic Press, Burlington, California, London, 2007.
Hamm, C., Merkel, R., Springer, O., Jurkojc, P., Marer, C., Prechtel, K., and Smetacek, V.: Architecture and material properties of diatom shell provide effective mechanical protection, Nature, 421, 81–843, https://doi.org/10.1038/nature01416, 2003.
Hansen, P. J., Bjørnsen, P. K., and Hansen, B. W.: Zooplankton grazing and growth: Scaling with the 2–2000-mm body size range, Limnol. Oceanogr., 42, 678–704, 1997.
Hébert, M. P., Beisner, B. E., and Maranger, R.: Linking zooplankton communities to ecosystem functioning: Toward an effect-Trait framework, J. Plankton Res., 39, 3–12, https://doi.org/10.1093/plankt/fbw068, 2017.
Hemleben, C. and Auras, A.: Variations in the calcite dissolution pattern on the Barbados ridge complex al Sites 541 and 543, Deep Sea Drilling Project Leg 78A, in: Initial Reports of the Deep Sea Drilling Project, Leg 78, Washington (U.S. Govt. Printing Office), edited by: Biju-Duval, B. and Moore, J. C, et al., 471–497, https://doi.org/10.2973/dsdp.proc.78a.124.1984, 1984.
Hemleben, C. and Spindler, M.: Recent advances in research on living planktonic foraminifera, Utrecht Micropal. Bull., 30, 141–170, 1983.
Hemleben, C., Bé, A. W. H., Anderson, O. R., and Tunlivate, S.: Test morphology, organic layers and chamber formation of the planktonic foraminifer Globorotalia menardii (d'Orbigny), J. Foramin. Res., 7, 1–25, https://doi.org/10.2113/gsjfr.7.1.1, 1977.
Hemleben, C., Spindler, M., and Anderson, O. R.: Modern Planktonic Foraminifera, Chapter 6: Collecting and Culture Methods, p. 42, Chapter 6: Trophic Activity and Nutrition, 112–127, 134–136, Springer Verlag, New York, 1989.
Ikeda, T.: Metabolic rates of epipelagic marine zooplankton as a function of body and temperature, Mar. Biol., 85, 1–11, https://doi.org/10.1007/BF00396409, 1985.
Irigoien, X., Huisman, J., and Harris, R. P.: Global biodiversity patterns of marine phytoplankton and zooplankton, Nature, 429, 863–867, https://doi.org/10.1038/nature02593, 2004.
Irwin, A. J., Finkel, Z. V., Schofield, O. M. E., and Falkowski, P. G.: Scaling up from nutrient physiology to the size-structure of phytoplankton communities, J. Plankton Res., 28, 459–471, https://doi.org/10.1093/plankt/fbi148, 2006.
Kiørboe, T.: A mechanistic approach to plankton ecology, Chapter 4: Particle Encounter by Advection, 75–82, Chapter 6, Zooplankton Feeding Rates and Bioenergetics, 107–114, Princeton University Press, 2008.
Kiørboe, T., Saiz, E., Tiselius, P., and Andersen, K. H.: Adaptive feeding behaviour and functional responses in zooplankton, Limnol. Oceanogr., 63, 308–321, https://doi.org/10.1002/lno.10632, 2018a.
Kiørboe, T., Visser, A., and Andersen, K. H.: A trait-based approach to ocean ecology, ICES J. Mar. Sci., 75, 1849–1863, https://doi.org/10.1093/icesjms/fsy090, 2018b.
Knoll, A. H.: Biomineralization and Evolutionary History, Rev. Mineral. Geochem., 54, 329–356, https://doi.org/10.2113/0540329, 2003.
Kučera, M.: Planktonic Foraminifera as tracers of past ocean environments, in: Proxies in Late Cenozoic Paleoceanography, edited by: Hillaire-Marcel, C. and de Vernal, A., Elsevier, Amsterdam, 213–262, https://doi.org/10.1016/S1572-5480(07)01011-1, 2007.
Lampert, W.: Release of dissolved organic carbon by grazing zooplankton, Limnol. Oceanogr., 23, 831–834, https://doi.org/10.4319/lo.1978.23.4.0831, 1978.
Litchman, E. and Klausmeier, C. A.: Trait-Based Community Ecology of Phytoplankton, Annu. Rev. Ecol. Evol. S., 39, 615–639, https://doi.org/10.1146/annurev.ecolsys.39.110707.173549, 2008.
Litchman, E., Ohman M. D., and Kiørboe T.: Trait-based approaches to zooplankton communities, J. Plankton Res., 3, 473–484, https://doi.org/10.1093/plankt/fbt019, 2013.
Lombard, F., Labeyrie, L., Michel, E., Spero, H. J., and Lea, D. W.: Modelling the temperature dependent growth rates of planktic foraminifera, Mar. Micropaleontol., 70, 1–7, https://doi.org/10.1016/j.marmicro.2008.09.004, 2009.
Lombard, F., Labeyrie, L., Michel, E., Bopp, L., Cortijo, E., Retailleau, S., Howa, H., and Jorissen, F.: Modelling planktic foraminifer growth and distribution using an ecophysiological multi-species approach, Biogeosciences, 8, 853–873, https://doi.org/10.5194/bg-8-853-2011, 2011.
Malmgren, B. A. and Kennett, J. P.: Phyletic gradualism in a Late Cenozoic planktonic foraminiferal lineage; DSDP Site 284, southwest Pacific, Paleobiology, 7, 230–240, 1981.
Maps, F., Pershing, A. J., and Record, N. R.: A generalized approach for simulating growth and development in diverse marine copepod species, ICES J. Mar. Sci., 69, 370–379, https://doi.org/10.1093/icesjms/fsr182, 2011.
Mayzaud, P. and Poulet, S. A.: The importance of the time factor in the response of zooplankton to varying concentrations of naturally occuring particulate matter, Limnol. Oceanogr., 23, 1144–1154, https://doi.org/10.4319/lo.1978.23.6.1144, 1978.
Menden-Deuer, S. and Kiørboe, T.: Small bugs with a big impact: linking plankton ecology with ecosystem processes, J. Plankton Ecol., 38, 1036–1043, https://doi.org/10.1093/plankt/fbw049, 2016.
Monod, J.: La technique de culture continue, théorie et applications, Ann. l'Instit. Pasteur (Paris), 79, 390–410, 1950.
Monteiro, M. F., Bach, L. T., Brownlee, C., Bown, P., Rickaby, R. E. M., Poulton, A. J., Tyrrell, T., Beaufort, L., Dutkiewicz, S., Gibbs, S., Gutowska, M. A., Lee, R., Riebesell, U., Young, J., and Ridgwell, A.: Why marine phytoplankton calcify, Science Advances, 2, 1–14, e1501822, https://doi.org/10.1126/sciadv.1501822, 2016.
Moriarty, R. and O'Brien, T. D.: Distribution of mesozooplankton biomass in the global ocean, Earth Syst. Sci. Data, 5, 45–55, https://doi.org/10.5194/essd-5-45-2013, 2013.
Müren, U., Berglund, J., Samuelsson, K., and Andersson, A.: Potential effects of elevated sea-water temperature on pelagic food webs, Hydrobiologia 545, 153–166, https://doi.org/10.1007/s10750-005-2742-4, 2009.
Murray, J. W.: Ecology and Palaeoecology of Benthic Foraminifera, Longman, Harlow, 397 pp., 1991.
Norris, R. D.: Biased extinction and evolutionary trends, Paleobiology, 17, 388–399, https://doi.org/10.1017/S0094837300010721, 1991.
O'Connor, M. I., Piehler, M. F., Leech, D. M., Anton, A., and Bruno, J. F.: Warming and Resource Availability Shift Food Web Structure and Metabolism, PLoS Biol., 7, 1–6, https://doi.org/10.1371/annotation/73c277f8-421a-4843-9171-403be1a014c7, 2009.
Ortiz, J. D., Mix, A. C., and Collier, R. W.: Environmental control of living symbiotic and asymbiotic planktonic foraminifera in the California Current, Paleoceanography, 10, 987–1009, https://doi.org/10.1029/95PA02088, 1995.
Palmer, A. R.: Calcification in marine molluscs: how costly is it?, P. Natl. Acad. Sci. USA, 89, 1379–1382, https://doi.org/10.1073/pnas.89.4.1379, 1992.
Pančić, M. and Kiørboe, T.: Phytoplankton defence mechanisms: traits and trade-offs, Biol. Rev., 93, 1269–1303, https://doi.org/10.1111/brv.12395, 2018.
Petrovskii, S. V. and Malchow, H.: A minimal model of pattern formation in a prey predator system, Math. Comput. Model., 29, 49–63, 1999.
Petrovskii, S. V., Kawasaki, K., Takasu, F., and Shigesada, N.: Diffusive waves, dynamical stabilization and spatio-temporal chaos in a community of three competitive species, Jpn. J. Ind. Appl. Math., 18, 459–481, https://doi.org/10.1007/BF03168586, 2001.
Razouls, C., de Bovée, F., Kouwenberg, J., and Desreumaux, N.: 2005–2018, Diversity and Geographic Distribution of Marine Planktonic Copepods, Sorbonne Université, CNRS, available at: http://copepodes.obs-banyuls.fr/en (last access: 10 November 2018), 2018.
Roy, T., Lombard, F., Bopp, L., and Gehlen, M.: Projected impacts of climate change and ocean acidification on the global biogeography of planktonic Foraminifera, Biogeosciences, 12, 2873–2889, https://doi.org/10.5194/bg-12-2873-2015, 2015.
Rutherford, S., Hondt, S. D., and Prell, W.: Environmental controls on the geographic distribution of zooplankton diversity, Nature, 400, 749–753, https://doi.org/10.1038/23449, 1999.
Schiebel, R.: Planktic foraminiferal sedimentation and the marine calcite budget, Global Biogeochem. Cy., 16, 1–21, https://doi.org/10.1029/2001GB001459, 2002.
Schiebel, R. and Hemleben, C.: Modern planktic foraminifera, Palaeont. Z., 79, 135–148, https://doi.org/10.1007/BF03021758, 2005.
Schiebel, R. and Hemleben, C.: Planktic Foraminifers in the Modern Ocean, Chapter 4: Nutrition, Symbionts, and Predators, p. 154, Chapter 7: Ecology, 209–220, Springer-Verlag, Berlin Heidelberg, https://doi.org/10.1007/978-3-662-50297-6, 2017.
Schiebel, R. and Movellan, A.: First-order estimate of the planktic foraminifer biomass in the modern ocean, Earth Syst. Sci. Data, 4, 75–89, https://doi.org/10.5194/essd-4-75-2012, 2012.
Schiebel, R., Zeltner, A., Treppke, U. F., Waniek, J. J., Bollmann, J., Rixen, T., and Hemleben, C.: Distribution of diatoms, coccolithophores and planktic foraminifers along a trophic gradient during SW monsoon in the Arabian Sea, Mar. Micropaleontol., 51, 345–371, https://doi.org/10.1016/j.marmicro.2004.02.001, 2004.
Schmidt, D. N., Renaud, S., and Bollmann, J.: Response of planktic foraminiferal size to late Quaternary climate change, Paleoceanography, 18, 1039, https://doi.org/10.1029/2002PA000831, 2003.
Schmidt, D. N., Renaud, S., Bollmann, J., Schiebel, R., and Thierstein, H. R.: Size distribution of Holocene planktic foraminifer assemblages: Biogeography, ecology and adaptation, Mar. Micropaleontol., 50, 319–338, https://doi.org/10.1016/S0377-8398(03)00098-7, 2004a.
Schmidt, D. N., Thierstein, H. R., Bollmann, J., and Schiebel, R.: Abiotic forcing of plankton evolution in the Cenozoic, Science, 303, 207–210, https://doi.org/10.1126/science.1090592, 2004b.
Schmidt, D. N., Lazarus, D., Young, J. R., and Kucera, M.: Biogeography and evolution of body size in marine plankton, Earth Sci. Rev., 78, 239–266 https://doi.org/10.1016/j.earscirev.2006.05.004, 2006.
Sieburth, J. M. N., Smatacek, V., and Lenz, J.: Pelagic ecosystem structure: heterotrophic compartments of the plankton and their relationship to plankton size fractions, Limnol. Oceanogr., 23, 1256–1263, https://doi.org/10.4319/lo.1978.23.6.1256, 1978.
Spero, H. J., Lerche, I., and Williams D. F.: Opening the carbon isotope “vital effect” box. 2. Quantitative model for interpreting foraminiferal carbon isotope data, Paleoceanography, 6, 639–655, https://doi.org/10.1029/91PA02022, 1991.
Spindler, M., Hemleben, C., Salomons, J. B., and Smit, L. P.: Feeding behaviour of some planktonic foraminifers in laboratory cultures, J. Foramin. Res., 14, 237–249, https://doi.org/10.2113/gsjfr.14.4.237, 1984.
van Someren Gréve, H., Almeda, R., and Kiørboe, T.: Motile behavior and predation risk in planktonic copepods, Limnol. Oceanogr., 62, 1810–1824, https://doi.org/10.1002/lno.10535, 2017.
Ward, B. A., Dutkiewicz, S., Jahn, O., and Follows, M. J.: A size-structured food-web model for the global ocean, Limnol. Oceanogr., 57, 1877–1891, https://doi.org/10.4319/lo.2012.57.6.1877, 2012.
Ward, B. A., Dutkiewicz, S., and Follows, J. M.: Modelling spatial and temporal patterns in size-structured marine plankton communities: top–down and bottom–up controls, J. Plankton Res., 36, 31–47, https://doi.org/10.1093/plankt/fbt097, 2014.
Žarić, S., Schulz, M., and Mulitza, S.: Global prediction of planktic foraminiferal fluxes from hydrographic and productivity data, Biogeosciences, 3, 187–207, https://doi.org/10.5194/bg-3-187-2006, 2006.