the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Silicon isotopes of deep sea sponges: new insights into biomineralisation and skeletal structure
Lucie Cassarino
Christopher D. Coath
Joana R. Xavier
Katharine R. Hendry
The silicon isotopic composition (δ30Si) of deep sea sponges' skeletal element – spicules – reflects the silicic acid (DSi) concentration of their surrounding water and can be used as natural archives of bottom water nutrients. In order to reconstruct the past silica cycle robustly, it is essential to better constrain the mechanisms of biosilicification, which are not yet well understood. Here, we show that the apparent isotopic fractionation (δ30Si) during spicule formation in deep sea sponges from the equatorial Atlantic ranges from −6.74 ‰ to −1.50 ‰ in relatively low DSi concentrations (15 to 35 µM). The wide range in isotopic composition highlights the potential difference in silicification mechanism between the two major classes, Demospongiae and Hexactinellida. We find the anomalies in the isotopic fractionation correlate with skeletal morphology, whereby fused framework structures, characterised by secondary silicification, exhibit extremely light δ30Si signatures compared with previous studies. Our results provide insight into the processes involved during silica deposition and indicate that reliable reconstructions of past DSi can only be obtained using silicon isotope ratios derived from sponges with certain spicule types.
1.1 Introduction to the Porifera world
Sponges (phylum Porifera) are one of the most primitive metazoans and have likely occupied ocean sea floors since the Precambrian period as indicated by molecular fossil records from the end of the Marinoan glaciation 635 Myr ago (Love et al., 2009) and Mongolian silica spicules dating from 545 million years ago (Antcliffe et al., 2014). Sponges are obligate sessile organisms, most of which are efficient filter feeders, capable of filtering 99 % of the particles from water pumped through their internal body structure (Strehlow et al., 2017, and references therein). Most sponges secrete minerals such as calcite, aragonite and/or silica to build a complex and strong skeletal framework composed of elements called spicules, providing protection and the maximum of contact between cells and their surrounding water (Uriz et al., 2003). Of the biomineralising sponges, 92 % of living species produce silica, compared to 8 % that produce calcium carbonate skeletons (Hooper and Van Soest, 2002), but this ratio may have varied in the past due to changes in paleo-ocean chemistry (Montanez, 2002) because sponges rely on the ion chemistry of their surrounding water to build their skeleton.
Three classes of sponges in the phylum Porifera, Homoscleromorpha, Demospongiae and Hexactinellida, produce their spicules made of bio-silica (amorphous silica) through the incorporation and deposition of hydrated silica (SiO2 ⋅ nH2O), a process referred to as biosilicification (e.g. Uriz, 2006; Otzen, 2012). The spicules may represent up to 70 %–90 % of the body (dry weight) depending on the species (e.g Sandford, 2003; Maldonado et al., 2012). Demosponges and hexactinellids differ in their body structure and spicule shape and size, which are both highly variable. Siliceous spicules can be subdivided into megascleres (up to and beyond 300 µm) and microscleres (up to 50 µm) and are generally categorised by their size and their role in the skeletal framework (Uriz et al., 2003).
Demospongiae is the largest class of the phylum Porifera (Van Soest et al., 2012). Species within this class harbour monaxonic and/or tetraxonic megascleres with various shapes, as well as various types of microscleres, which compose their skeletal structure. Both mega- and microscleres are loose and unfused but joined by spongin (collagen protein) (Uriz, 2006). Demospongiae have a cellular organisation, i.e composed of cells that form tissues, which themselves form organs, which form an organism.
Hexactinellida, commonly called glass sponges, exhibit a wide range of body structures, such as tubular, cup-shaped and branching (Ereskovsky, 2010). The spicules of hexactinellid sponges are characterised by hexactins (three axes with regular angles), which can lose or gain rays, resulting in a wide range of shape and structure (Ereskovsky, 2010). One distinctive feature of the Hexactinellida class is that their spicules can be loose, partially or totally fused, or even cemented by a secondary silica layer and or junction (Uriz et al., 2003). One key feature that distinguishes between Demospongiae and Hexactinellida is that Hexactinellida are characterised by a syncytial organisation, i.e. tissue composed of cells without an individual plasma membrane (Leys and Lauzon, 1998; Maldonado and Riesgo, 2007).
Sponges have recently roused interest and are increasingly recognised as a key component of the marine silicon cycle (Tréguer and De La Rocha, 2013; Maldonado et al., 2005). They live on the sea floor at most latitudes and depths (De La Rocha, 2003; Wille et al., 2010; Maldonado and Riesgo, 2007; Maldonado et al., 2012) and may be considered a large living standing stock of silica in the oceans (Maldonado et al., 2010). Because of their relatively low growth rate and their inability to move, they are sensitive to change of their environment and because an individual sponge can live decades or centuries (Pansini and Pronzato, 1990; Leys and Lauzon, 1998) they can record information over long time periods (Jochum et al., 2017).
1.2 Silicon isotope and deep sea sponges
The silicon isotopic composition of biogenic silica (δ30BSi) has been introduced to study the past nutrient utilisation by De La Rocha et al. (1997) and since has been used to study the silicon cycle Hendry et al. (e.g 2016); Fontorbe et al. (e.g 2017). Silicon is composed of three stable isotopes, 28Si, 29Si and 30Si, with relative abundances of approximatively 92.23 %, 4.67 % and 3.10 % respectively (De Bièvre and Taylor, 1993). Silicon isotopic abundances in samples (SMP) are expressed as δ29Si or δ30Si with the abundance ratio, 29Si ∕ 28Si or 30Si ∕ 28Si respectively, and measured relative to the reference standard (NBS28). The results presented in this study are expressed as per mille to be consistent with the International Union of Pure and Applied Chemistry (IUPAC) nomenclature, i.e.
The δ30Si signature of deep sea sponges has been highlighted as a potential paleoceanographic proxy for silicic acid DSi concentration (De La Rocha, 2003; Hendry et al., 2010; Wille et al., 2010; Hendry and Robinson, 2012). The asymptotic relationship between DSi concentration and δ30Si signature of sponge spicules (δ30SiSpicules) is the result of the preferential incorporation of the lighter isotope (Wille et al., 2010; De La Rocha, 2003; Hendry et al., 2011). There is also a significant correlation between the apparent fractionation factor, δ30Si (δ30SiSpicules − δ30SiDSi), and the ambient DSi concentration (Hendry and Robinson, 2012). The relationship between δ30SiSpicules and DSi concentration is not yet understood, but a simple biological model suggests that the fractionation factor could arise during sponge uptake, polymerisation and efflux (Wille et al., 2010; Hendry and Robinson, 2012). Thus, δ30SiSpicules is a potential proxy to quantify ocean changes in Si cycling with a larger spatial range and timescales than diatoms (De La Rocha, 2003; Fontorbe et al., 2017). Furthermore, the dissolution rate of sponge spicules is lower than that of diatoms' frustules (Maldonado et al., 2005), which may result in a better preservation. A calibration of modern sponge specimens and core-top spicules from different oceans shows that the core-top specimens are not affected by post-depositional dissolution or even early diagenesis (Hendry and Robinson, 2012), which are both potential concerns when dealing with the chemistry of reactive biogenic opal (Ragueneau et al., 2001; De La Rocha et al., 2011).
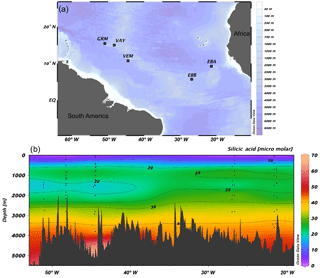
Figure 1(a) JC094 sampling stations from the equatorial Atlantic. From east to west: EBA (Carter Seamount), EBB (Knipovich Seamount), VEM (Vema Fracture Zone), VAY (Vayda Seamount) and GRM (Gramberg Seamount). Cross section of DSi concentration in micromolar along the JC094 transect. Dots representing the sampling depth of stations, from east to west: EBA, EBB, VEM, VAY and GRM.
Despite the great potential of sponges as archives of past ocean Si cycling, there are still a number of outstanding questions relating to Si isotopic fractionation. Does Si isotopic fractionation remain constant during sponge growth? Can we trace DSi concentration over time by analysing δ30Si sections of sponge skeleton? At what stage during biomineralisation does the Si isotopic fractionation occur, and does it vary with spicule morphology? Here, some of these questions are going to be addressed by investigating δ30Si of modern deep sea sponges collected from the equatorial Atlantic.
2.1 Sample collection
Sponge samples were collected by a remotely operated vehicle (ROV) at five stations, EBA, EBB, VEM, VAY and GRM, between 298 and 2985 m (Fig. 1) aboard the RRS James Cook on the TROPICS cruise (JC094), a west–east cross section in the equatorial Atlantic between ∼5 and ∼15∘ N, from 13 October to 30 November 2013. Seawater samples were sampled using Niskin bottles attached to CTD rosette system and occasionally by a ROV at each station. Whilst the best attempts were made to spatially match the sponge and water samples, it was not always possible to collect precisely co-located sponge and seawater samples. The δ30SiDSi values are reported in Table (Appendix) and, for each sponge specimen, the closest seawater sample is used to calculate Δ30Si.
The sponge specimens were sampled as either large individual sponges or smaller individuals encrusted on other organisms such as corals. Subsamples were dried for transportation to the UK. Preliminary assignment of the specimens to the classes Demospongiae and Hexactinellida was carried out onboard using binocular and petrological microscopes. Identifications to lower taxonomic ranks, combining morphological and molecular methods, are underway and will be published in a separate paper.
2.2 Sponge spicule cleaning procedure and Si pre-concentration from seawater
For δ30SiSpicules, organic matter (OM) was removed using hydrogen peroxide (H2O2, 30 % reagent grade). Subsamples of dry sponge specimens were transferred into 50 mL Eppendorf tubes, covered with H2O2 (30 % reagent grade) for 24 h at room temperature and then heated for 3 h with new H2O2 (30 % reagent grade) at 85 ∘C. The samples were rinsed with 18.2 MΩ Milli-Q water and heated for a further 3 h with fresh H2O2, before a final Milli-Q rinse. Samples were transferred into clean Teflon vials to undergo further cleaning, three times in concentrated (16 N) in-house Teflon-distilled HNO3, rinsing between each stage with Milli-Q water. If remaining, lithogenic material was removed by hand before further cleaning steps. A subsample was taken and weighed before going through a final cleaning step. The subsample was covered with HNO3 (16 N Romil) and dried down at 120∘C. When the spicules were dried, each sample was dissolved in 0.4 M NaOH (Analar) at 100 ∘C for 3 days, following published protocols (Ragueneau et al., 2005; Cardinal et al., 2007; Hendry and Robinson, 2012). Samples were acidified with 8 N HNO3 and diluted with Milli-Q water to reach a pH of 2–3. This cleaning procedure followed the technique in Hendry et al. (2010) and Hendry and Robinson (2012).
Prior to isotopic analysis of seawater, Si was pre-concentrated using the MAGIC method (magnesium-induced co-precipitation) of Karl and Tien (1992) with Reynolds et al. (2006) modifications. Brucite was precipitated overnight by the addition of 1.2 % v∕v 1 M NaOH. After centrifugation (3000 g force for 3 min) the supernatant was transferred and 1 % v∕v 1 M NaOH was added and left overnight in order to extract any residual silicon. The two precipitates were combined and rinsed with 0.001 M NaOH solution to remove remaining salt matrix before a final separation by centrifugation. Finally the precipitate, Mg(OH)2, was dissolved by adding 8 N HNO3, resulting in a pH range of 1–3. The yield recovery of Si is equivalent to 92.1 %.
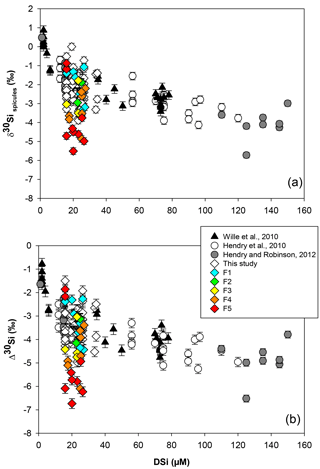
Figure 2Sponge calibration data from Hendry et al. (2010) (Drake Passage and Scotia Sea), Wille et al. (2010) (Antarctica, Tasmania and New Zealand), Hendry and Robinson (2012) (North Atlantic, west Antarctic Peninsula, Woods Hole and North Pacific), and data from this study (equatorial Atlantic, JC094). (a) Silicon isotopic composition of the spicules (δ30SiSpicules) and (b) deep sea sponges' apparent Si isotopic fractionation (δ30Si) against DSi concentration. Error bars for this study show 2 SD, ± 0.13 for δ30SiSpicules and ± 0.17 for δ30Si. NB: core-top samples from Hendry and Robinson (2012) are not included.
2.3 Analytical procedures
For δ30Si analysis, pre-treated spicules and seawater samples were purified through cation ion exchange chromatography (Bio-Rad AG50W X12, 200–400 mesh in H+ form). Analysis of δ30SiSpicules and δ30SiDSi was carried out by multi-collector inductively coupled plasma mass spectrometry (MC-ICP-MS, Finnigan Neptune s/n 1002) at the Bristol Isotope Group facilities, University of Bristol. All sample analyses were repeated at least twice and followed the typical standard-sample bracketing and Mg doping methods from Cardinal et al. (2003) with the best intensity match possible between samples and bracketing standards. Measurement of secondary standards LMG-08 and Diatomite give δ30Si values of ‰ (2 SD, n = 173) and 1.23±0.15 ‰ (2 SD, n = 41) respectively. The external reproducibility of Si isotope measurements is ± 0.13 ‰ and ± 0.17 ‰ (2 SD, degrees of freedom = 212) for δ29Si and δ30Si respectively, for which the analytical scatter for both standards has been pooled (Steele et al., 2012). For comparison, Hendry et al. (2011) and Reynolds et al. (2007) report δ30Si = ‰ and δ30Si = 1.26 ± 0.20 ‰ for LMG-08 and Diatomite respectively. The new seawater standard ALOHA deep was analysed as an additional quality check and yielded values within error of those obtained during an interlaboratory study (Grasse et al., 2017): ALOHA deep: δ30Si = 1.08± 0.12 ‰ and δ29Si = 0.58± 0.12 ‰ (2 SD, n = 4). The δ29Si and δ30Si of all seawater and sponge samples are consistent with the kinetic mass fractionation law (Reynolds et al., 2007); i.e. δ29Si vs. δ30Si has a slope of 0.516 (SE = 0.002, n = 362, r2 = 0.995). The results are reported relative to the standard NBS28 (Eq. 1).
2.4 Scanning electron microscope images
Scanning electron microscope (SEM) images of sponge spicules have been carried out at the University of Bristol on a Hitachi S-3700N SEM. Clean spicules were sputter-coated with 10 nm of gold. The instrument operated at an acceleration voltage of 15 kV in second electron image mode.
3.1 δ30Si of deep sea sponges
Data from the equatorial Atlantic exhibit δ30SiSpicules from −5.51 to (2 SD) and δ30Si from −6.74 to (2 SD) (Fig. 2, a and b respectively), representing the greatest δ30Si observed in sponges to date (Hendry et al., 2010; Wille et al., 2010; Hendry and Robinson, 2012). Detailed results are presented in Table in the Appendix. The results have been added to the existing calibration from Hendry et al. (2010), Wille et al. (2010), and Hendry and Robinson (2012) (Fig. 2), showing that our new data are largely consistent with the existing calibration. However, a number of specimens deviate from the published calibration and record unusually light isotopic signatures.
3.2 Degrees of spicule fusion
The SEM images from all sponges showing a δ30Si larger than −5 ‰ and from 20 other samples chosen randomly within a lower δ30Si range () have highlighted a variety of spicule shapes and degrees of skeletal fusion. In the bulk of sponge samples two groups can be identified: sponges with loose spicules with δ30SiSpicules following the published calibration curve and sponges with fused spicules with δ30SiSpicules deviating from the published calibration curve.
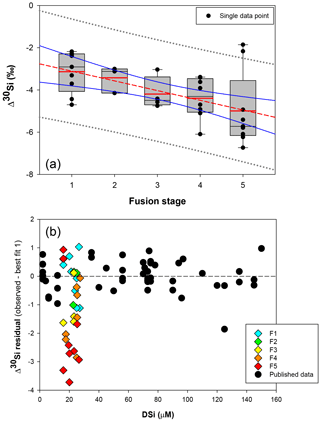
Figure 4(a) Box plot showing the apparent Si isotopic fractionation δ30Si by sponges as a function of spicule fusion degree: 1 for loose spicules (F1), 2 for net-like (F2), 3 for additional silica coating (F3), 4 for dictyonal framework (F4) and 5 for dense dictyonal framework (F5). Red lines in the box plots are the mean of each population and black is the median. The boxes define the 25th and the 75th percentiles and the error bars are the 10th and 90th percentiles. Black circles show a single sample for each of the fusion stages and the red dashed line shows the significant linear relationship between δ30Si and the fusion stage of the spicule (n = 33, p<0.0011). The blue lines represent the 95 % confidence band and the grey short dashed lines the 95 % prediction band. Data plotted here correspond to the samples from the equatorial Atlantic with an identified fusion stage, i.e. coloured diamond of (b), and so occupy a very narrow range of DSi. (b) δ30Si residual of samples with an identified fusion stage compared to the published calibration (best fit 1).
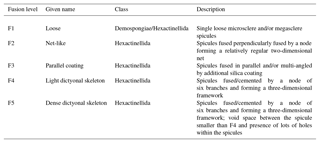
Further, the SEM images of spicules with various δ30SiSpicules signatures reveal five levels of fusion, defined here as F1, F2, F3, F4 and F5. Level F1 represents loose spicules, F2 spicules fused by a node (netlike feature), F3 loose spicules fused in parallel with additional silica coating, F4 light dictyonal skeleton and F5 dense dictyonal skeleton; see Fig. 3 for SEM image examples and Table 1 for a detailed description of the fusion degree from F1 to F5. It is observed that δ30SiSpicules and δ30Si show an enrichment in light isotopes with a higher degree of spicule fusion (see Fig. 4).
Table 1Criteria of the five levels of sponge spicule fusion. See Fig. 3 for the corresponding picture.
4.1 δ30Si fractionation by deep sea sponges
The new data presented here, from the equatorial Atlantic, show to date the largest range of δ30SiSpicules signatures and δ30Si for a small range in DSi concentration (15 to 35 µM). As δ30Si larger than −5 ‰ for this DSi range deviates from the published calibration curve, particular attention has been paid to these samples in order to understand the factors causing this large Si isotopic fractionation. SEM images show that these specimens have a common feature: a fused dictyonal framework skeleton. The following discussion introduces in more detail the fractionation of Si isotopes by sponges and the hypotheses relating to the large δ30Si values from the dictyonal skeleton.
Previous studies tracking the δ30Si of sponge silica have shown a non-linear relationship between δ30SiSpicules signatures and DSi concentration (Wille et al., 2010; Hendry and Robinson, 2012). The Si isotopic fractionation by sponges can be expressed with either δ30Si or εf notation. Here δ30Si is defined by the difference between δ30SiSpicules and δ30SiDSi, which describes the observed apparent Si isotopic fractionation by sponges, whereas εf is the result from the biological model from Wille et al. (2010) (Eq. 2). Published data have shown δ30Si varying from −0.77 ‰ to −6.52 ‰ (Fig. 2b), which follow a non-linear relationship and cannot be described by a diatom-like Rayleigh fractionation (characterised by a constant fractionation factor during DSi utilisation) because isotopic fractionation during the uptake of DSi by sponges is variable, increasing with DSi concentration. Wille et al. (2010) proposed a model following Milligan et al. (2004), which suggests that Si isotopic fractionation in marine sponges is mainly controlled by Si uptake. Reincke and Barthel (1997) first investigated the formation of BSi (i.e. silicification) in cultured sponges by regeneration of sponge pieces and, more recently, Si uptake has been investigated in culture using whole sponges collected at sea that were then transferred to a controlled environment (Maldonado et al., 2011; López-Acosta et al., 2016, 2018). Despite the different set-up and species chosen for each experiment, all culture experiments carried out to date suggest that the silicification in sponges is controlled by enzymatic processes, exhibiting Michaelis–Menten enzyme kinetics, and is dependent on substrate concentration, here DSi. From the close resemblance of the DSi and δ30SiSpicules relationship and the growth rate kinetics, Wille et al. (2010) proposed a model from which δ30Si is fractionated during the uptake phase and internal spicule formation. The related fractionation of Si isotopes is expressed as εf (Eq. 2), with DSi concentration being the main factor influencing δ30SiSpicules.
where εtI is the Si isotopic fractionation during Si uptake, εp is the Si isotopic fractionation during polymerisation, εE is the Si isotopic fractionation during the efflux, Vmax,P and Vmax,I are the maximum polymerisation and incorporation rates respectively, Km,P and Km,I are the half saturation constant of polymerisation and incorporation respectively, and DSi is the silicic acid concentration of the surrounding water.
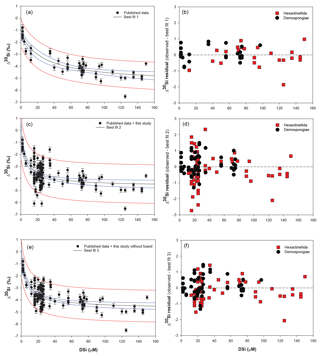
Figure 5Plots of the best-fit model (left) and the corresponding δ30Si residual (right) of Hexactinellida (red squares) and Demospongiae (black circles). (a) Best fit (δ30Si = −5.39(0.4) + 111.51(11.3) ∕ (26.87(11.2) + DSi)) and (b) residual from Hendry and Robinson (2012), Wille et al. (2010), and Hendry et al. (2010) data. (c) Best fit (δ30Si = −4.69(0.2) + 30.89(2.7) ∕ (7.29(2.7) + DSi)) and (d) residual from Hendry and Robinson (2012), Wille et al. (2010), and Hendry et al. (2010) with the equatorial Atlantic data (JC094). (e) Best fit (δ30Si = −4.71(0.18) + 34.25(2.6) ∕ (8.29(2.6) + DSi)) and (f) residual from Hendry and Robinson (2012), Wille et al. (2010), and Hendry et al. (2010) with the equatorial Atlantic (JC094) without the fused spicules (F2 to F5). For best-fit model plots, black lines show the best-fit regression, blue lines the 95 % confidence interval and red lines the 95 % prediction interval, and for the best-fit equation, the numbers in parentheses are the standard error. NB, best fits 2 and 3 and their corresponding residual tests were calculated only with identified sponge samples, which results in discrepancies between Figs. 2b and 6.
Hendry and Robinson (2012) applied this model to a wide range of modern sponges from different ocean basins showing that the temperature, one of the factors controlling enzymatic processes, does not affect the relationship between δ30Si and DSi concentration, which supports DSi concentration being the main factor controlling Si isotopic fractionation. Despite the small range of seawater temperature in this study, our data show no relationship between δ30Si and temperature (Fig. A1 in Appendix). However, here a group of sponges from the equatorial Atlantic exhibit a different relationship between δ30Si and DSi concentration with a very large apparent fractionation, , at low concentration (15 to 35 µM). Figure 4a shows the variability in δ30Si for each fusion stage and that the fusion degree of the spicules appears to affect δ30Si. Furthermore Fig. 4b shows the δ30Si residual of the same samples against the previous published calibration (Hendry et al., 2010; Wille et al., 2010; Hendry and Robinson, 2012), which suggests that processes other than silicic acid concentration are involved in the fractionation of Si isotopes.
Dictyonal framework skeletons, F4 and F5, only belong to the Hexactinellida class, which could suggest that the two classes have a different Si isotopic fractionation due to their different silicification mechanism (Maldonado and Riesgo, 2007). The δ30SiSpicules average signature of the two siliceous sponge families from the compiled data presented in Fig. 2 (Hendry and Robinson, 2012, Wille et al., 2010, Hendry et al., 2010, with the equatorial Atlantic data (JC094)) show that the Hexactinellida class is significantly lighter than Demospongiae, with δ30SiSpicules = ‰ (CI (confidence interval) of the mean) and ‰ (CI of mean) respectively. However, it is important to take into consideration the environmental conditions of growth because δ30SiSpicules depends on the δ30Si and DSi concentration of seawater and the two groups live at different depth ranges and nutrient conditions. To eliminate the influence of these two parameters and resolve whether or not Demospongiae and Hexactinellida fractionate Si isotopes in different ways, a δ30Si residual has been calculated: δ30Si residual = Δ30SiObserved − Δ30SiSpiculesbestfit. Three best fits have been calculated assuming the hyperbolic relationship between DSi and δ30Si (Hendry and Robinson, 2012) to deconvolve the influence of fused skeleton. Equations (3), (4) and (5) correspond to the best-fit curves (number in parentheses are the standard error) in Fig. 5, for
-
the previous compilation from Hendry and Robinson (2012), Wille et al. (2010) and Hendry et al. (2010),
-
the previous compilation from Hendry and Robinson (2012), Wille et al. (2010) and Hendry et al. (2010) with this study data,
-
the previous compilation from Hendry and Robinson (2012), Wille et al. (2010) with Hendry et al. (2010) with this study without the dictyonal skeleton,
Figure 5b, d, and f show δ30Si residual results of each class, calculated from the best fit (Fig. 5a, c, e, respectively) with the compilation (a) of published data (Hendry and Robinson, 2012; Wille et al., 2010; Hendry et al., 2010), (b) of published and all JC094 data, and (c) of published and JC094 data without the fused spicules (F1 to F5). Only the samples with class identification are include in the three residual results. The results of these residual tests show that there is no disparity between the two classes even with the incorporation of the dictyonal framework (Fig. 5b, d, f). The residual test, however, highlights that hexactinellids have a tendency to live in water with a higher DSi concentration compared to demosponges, which supports the idea that the Si isotopic fractionation is driven by DSi concentration. Furthermore, when data from all JC094 data are incorporated into the published calibration curve (Fig. 5c), the dictyonal framework (F4 and F5) is not included in the 95 % confidence limits (red lines). This observation illustrates that sponges with fused spicules, in particular dictyonal frameworks F4 and F5, cannot yet be used as a robust proxy for ocean chemistry.
The question still remains as to what controls the large δ30Si observed for sponges with complex dictyonal framework skeletons. Two main hypotheses are proposed and discussed in order to deconvolve δ30SiSpicules and fusion type.
4.2 Spicule composition: a control of δ30Si?
The primary hypothesis concerns the structure of the spicule itself. Recently He et al. (2016) have shown, using chemical modelling, that there is an extremely large Si isotopic fractionation of −9.1 ‰ at 25 ∘C between hyper-coordinated organosilicon complexes and DSi. This paper has raised the idea that the organic content inside the spicule itself could impact the fractionation of Si isotopes during biosilicification.
A spicule is composed of hydrated amorphous silica (SiO2)2−5: H2O with Si and O up to 75 % and more, and 6 %–13 % of water, with some traces of other elements (Sandford, 2003; Schröder et al., 2008) and organic molecules (Uriz et al., 2003). Biosilicification is mediated by enzymes such as silicatein during the formation of the spicule, during which silica layers are deposited around an organic axial filament containing the mature silicatein (Cha et al., 1999; Müller et al., 2008; Wang et al., 2012a). The spicule formation starts with an immature spicule inside a sclerocyte, and Si is supplied by internal vesicules, the silicasomes. The immature spicule is extruded by evagination from the sclerocyte, resulting in an axial elongation. In the extracellular space the elongated immature spicule is in contact with silicatein and galectin (protein with structural function), which mediate the deposition of silica released from external silicasome vesicules (Müller et al., 2013). One major difference between hexactinellids and demosponges is that the spicules in demosponges fuse their silica and organic layers, constituting the primary spicule, when extruded from the sclerocyte (Müller et al., 2008; Wang et al., 2011, 2012a) while the concentric silica layers could remain separated with thin organic layers in hexactinellids (Aizenberg, 2005; Müller et al., 2009; Wang et al., 2012b).
Thermal analysis showed that the hexactinellid Scolymastra joubini spicules are composed of 15 % OM compared to demosponges with 10 % (Croce et al., 2004). Furthermore, SDS-PAGE analysis of Hexactinellid Euplectella aspergillum has shown that the proteins of its axial filament have higher molecular weights than those isolated in demosponges (Weaver and Morse, 2003), which supports the difference in organic content between the two classes. The larger Si isotopic fractionation of sponges with a dictyonal framework could be a result of a much greater number of organosilicon complexes within the structure. Indeed, Weaver et al. (2007) showed using a SEM that the internal skeletal structure of the hexactinellid sponge E. aspergillum is comprised of small spicules that are embedded in a silica matrix surrounding a larger spicule (Fig. B1a, in the Appendix). The structural dictyonal framework consists then of multiple layers of silica–organic composite (Fig. B1c and d).
Nevertheless, results from the residual tests (Fig. 5) show that there is no significant difference in δ30Si between Hexactinellida and Demospongiae despite the difference in their spicule composition. This suggests that the large δ30Si value in sponges that display a dictyonal framework is not solely a result of the differences in organic composition of the spicules but could also be controlled by the enzymes that mediate silica deposition.
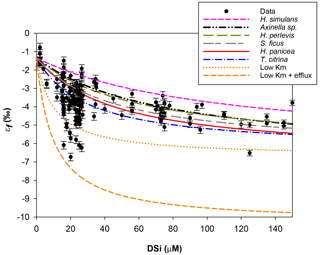
Figure 6Michaelis–Menten kinetic model of Si isotopic fractionation (Eq. 2) for six parameterisations (see Table 2). Black circles are all previously published and JC094 data. Sponge species from top to bottom are as follows. Pink: εf from Haliclona simulans kinetic parameters (López-Acosta et al., 2018); black: εf from Axinella sp. (Maldonado et al., 2011); green: εf from Hymeniacidon perlevis (López-Acosta et al., 2016); grey: εf from Suberites ficus (López-Acosta et al., 2018); red: εf from Halichondria panicea (Reincke and Barthel, 1997); blue: εf from Tethya citrina (López-Acosta et al., 2016). The following curves are experimental tests. Orange: Vmax,p of López-Acosta et al. (2016) T. citrina sp. and Km (10 µM), with εE as 1.39 (dotted) or 5 ‰ (dashed).
4.3 An enzymatic control of δ30Si?
The second hypothesis relates to the growth rate kinetics of the sponges. As proposed by Wille et al. (2010) the fractionation of Si isotopes by sponges, εf, can be expressed by Eq. (2). The Si isotopic fractionation by sponges is assumed to occur during Si uptake and during internal spicule formation with spicule formation being a function of Si influx and efflux from the sclerocyte (Milligan et al., 2004). The efflux is the difference between Si incorporated into the sclerocyte and Si used to form the spicule (i.e. polymerisation) Wille et al. (2010, and references therein). To date, only Reincke and Barthel (1997), Maldonado et al. (2011), López-Acosta et al. (2016), and López-Acosta et al. (2018) have cultured sponges to investigate the Michaelis–Menten enzyme kinetics of sponges. In this section, εf has been modelled using Km,P and Vmax,p values from these four sponge culture experiments, which summarised in Table 2.
López-Acosta et al. (2018)Maldonado et al. (2011)López-Acosta et al. (2016)López-Acosta et al. (2018)Reincke and Barthel (1997)López-Acosta et al. (2016)Table 2Summary of Michaelis–Menten enzyme kinetic parameters of sponges used to model εf (Fig. 6) following Eq. (2) with Vmax,p the the maximum polymerisation rates and Km,P the half saturation constant of polymerisation.
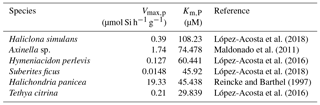
In order to compare the effect of the kinetic parameters on Si isotopic fractionation following the Wille et al. (2010) model (Eq. 2), the six simulations have been undertaken with a constant value for εp−εE corresponding to −5.39 ‰. εp − εE was calculated from the hyperbolic relationship between DSi and δ30Si following Eq. (3) for each sponge species from the culture studies. Vmax,I and εtI are the constant values defined by the minimum misfit function described in Wille et al. (2010), with Vmax,I = 120 µmol Si h−1 g−1 and εtI = −1.34 ‰.
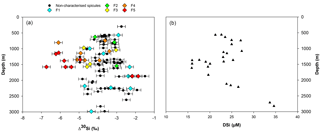
Figure 7(a) Apparent Si isotopic fractionation (δ30Si) by sponges against depth from this study. Coloured diamonds represent the degree of fusion from loose spicules (blue), net-like (green), additional silica coating (yellow), dictyonal framework (orange) and dense dictyonal framework (red). (b) DSi concentration in the equatorial Atlantic from EBA, EBB, VEM, VAY and GRM.
Figure 6 shows the results of εf simulated from the six kinetic parameters detailed above and in Table 2. The results of this simulation show lighter εf from Haliclona simulans to Tethya citrina. This observation coincides with the Km,P values of each species for which Km,P of Haliclona simulans is the highest and Km,P of Tethya citrina is the smallest (Table 2). The Km,P value illustrates the affinity of an enzyme with a substrate; i.e. the smaller the Km,P value, the higher the affinity between the substrate (DSi) concentration and the enzyme. In other words, Km,P informs on the binding efficiency between the substrate and the enzyme sites and is used as an indicator of competitiveness among species. The comparison of the six species suggests that the lower the Km,P, the larger the εf and εf values calculated from López-Acosta et al. (2016). T. citrina sp. is related to Tethya citrina sp., which has the lowest Km,P value, showing a high affinity for DSi compared to the five other species. Unfortunately, to date there are no published culture studies related to the class Hexactinellida but it is likely that their Km,P values show a higher affinity with DSi due to their high requirements for silicon.
In López-Acosta et al. (2016), Tethya citrina is more silicified than Hymeniacidon perlevis and has a 2 times higher Vmax,p and 3 times lower Km,P. Dictyonal frameworks display very dense skeletons compared to the demosponges made of loose spicules. Here, the hypothesis made is that the affinity between the enzyme and DSi is higher for sponges with a dictyonal framework, which means that their Km,P value is likely to be lower. The simulation of Si isotopic fractionation has been made using the T. citrina sp. kinetic parameters, except Km,P, which has been reduced to 10 µM. Results of this simulation are referred to as low Km in Fig. 6. It is clear that the reduction of the half saturation constant (Km,P) value has a major impact on the Si isotopic fractionation, with larger Si isotopic fractionation specifically for the low concentration, for which DSi = 20–30 µM (Fig. 6). However, the very large δ30Si of −6.74 ‰ for DSi = 20.05 µM could be modelled by decreasing Km,P to 1 µM. Whilst this value of Km,P is low, and potentially not biologically plausible, more research is required in order to constrain enzymatic control in hexactinellid biomineralisation. However, a low Km value suggests that the sponges need only a small amount of substrate (DSi) to grow, which means that sponges with a low Km are likely to grow in seawater with a low DSi concentration. When plotted against depth, the dictyonal framework skeletons, level F5, are located between 1100 and 1800 m (see Fig. 7) corresponding to a regional minimum in DSi concentration as shown in Figs. 1b and 7b. This observation reinforces the hypothesis that the kinetic parameter Km,P is involved in Si isotopic fractionation. However, to successfully model the highest δ30Si (−6.74 ‰) we must also investigate the potential impact of efflux on Si isotopic fractionation.
Biosilicification in sponges results in the condensation of DSi into BSi controlled by silicifying enzymes, such as silicatein (Cha et al., 1999; Müller et al., 2008), which interacts with other enzymes and proteins, for example galectin and collagen (Krasko et al., 2000; Müller et al., 2013), to form their spicule. The bonding reactions made by silicatein during spicule formation appear to be reversible. For example, the spicule formation of the Demospongiae Suberites domuncula and Geodia cydonium is the result of anabolic reactions (bonds being created) via silicatein and catabolic reactions (breaking of bonds) via silicase (Müller et al., 2008). This dynamic feedback regulates the internal cell DSi concentration (Wang et al., 2012b), which could suggest that the efflux from the sclerocyte is more important than previously thought. To test this hypothesis, εf has been simulated with Km = 10 µM (same as low Km,P presented earlier) and by increasing the δ30Si fractionation from the efflux of Si from the sclerocyte, εE, to 5 ‰. The result presented in Fig. 6 (referred to as low Km + efflux) shows that the largest observed δ30Si value of −6.74 ‰ can be modelled by increasing εE. Our results highlight the possibility that sponges that grow in a low-DSi environment are “tuned” to take up DSi rapidly into their sclerocytes, releasing any excess via efflux processes. Whilst further work is required to understand sponge biomineralisation, our results show the potential for Si isotopes as a tool to investigate cellular uptake and silicification processes.
4.4 Comparison with previous studies
The new data set of this study shows a wide range of δ30Si values for a small range of DSi concentrations compared to previous studies (Fig. 2) (Hendry and Robinson, 2012; Wille et al., 2010; Hendry et al., 2010). Here spicule shape, in particular the fusion stage, and δ30Si have been investigated and are closely related, and high fusion stages show very large δ30Si values, which deviate from the existing calibration. Why has this relationship between spicule fusion and δ30Si not been observed in previous studies? This new data set is composed of 103 samples of which 15 deviate from the calibration and display a dictyonal skeleton. Previous studies are based on fewer samples and all the hexactinellid specimens have been found, except for one, in high-DSi environments (higher than 45 µM) (Hendry and Robinson, 2012; Wille et al., 2010; Hendry et al., 2010). As the spicules in Hexactinellida can be loose, partially or totally fused, or even cemented by secondary silica (Uriz et al., 2003), it is likely that previous studies only analysed samples with loose spicules (equivalent to F1 here). Furthermore, Hendry and Robinson (2012) published one sample with δ30Si = −6.52 ‰ for DSi = 125 µM (Fig. 2). This sample also displayed a fused skeleton but at this date the large fractionation was attributed to the lack of constraint on ambient seawater δ30Si.
Marine sponges are potential geochemical archives of present and past oceanic silicon cycling. Through a simple kinetic model it is possible to predict δ30Si fractionation of modern sponges, which support the use of Si isotopes in the reconstruction of past silicic acid concentration of bottom waters. However, the data presented here illustrate that the proxy has its limits. The skeleton type and, in particular, the level of fusion of the skeleton lattice impacts the Si isotopic fractionation significantly. Sponges displaying a dictyonal framework do not fit the asymptotic relationship with DSi observed in previous studies. This divergence has also been observed for a carnivorous sponge (Hendry et al., 2015) for which it is suggested that the Si isotopic fractionation is associated with a specific hypersilicified spicule type (desma). Here, we suggest that the organic template responsible for spicule formation, the organic matter content that differs between the two major classes, could influence the Si isotopic fractionation. However, residual tests have shown that there is no significant difference between Hexactinellida and Demospongiae when differences in habitat and nutrient conditions are taken into consideration. Yet, this study shows a strong relationship between enzyme kinetic parameters (Km) and εf, with low Km related to lighter Si isotopic fractionation, which suggests that Si isotopic fractionation is dependent on the equilibrium between molecules and bonding interactions mediated by catabolic and anabolic reactions in the process of biomineralisation. As yet, sponge biomineralisation processes are not fully understood and further work is required to understand the specific pathways involved, especially in the case of the hexactinellids.
The data that support the findings of this study are available from the corresponding author, L. Cassarino, upon reasonable request.
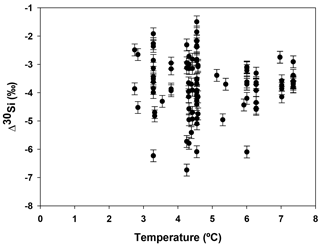
Figure A1Apparent Si isotopic fractionation (δ30Si) of deep sea sponges from the equatorial Atlantic against the ambient seawater temperature.
Table A1Location details and isotopic signature (δ30Si) and apparent Si isotopic fractionation (δ30Si) of deep sea sponges from the equatorial Atlantic. Taxonomic rank of sample starts with the class (Hexact. for Hexactinellida and Demosp. for Demospongiae), the order and finally the family. δ30Sispicule and δ29Sispicule are the Si isotopic signatures of the spicules, δ30SiDSi is the Si isotopic signature of seawater, δ30Si is the apparent Si isotopic fractionation by deep sea sponges and fusion is the fusion stage defined from SEM images (see Table 1 for details). Reproducibility, 2 SD, is based upon measurements of standards (see Sect. 2.3) and corresponds to 0.13 ‰ for δ30Sispicule, 0.11 ‰ for δ30SiDSi and 0.17 ‰ for δ30Si.
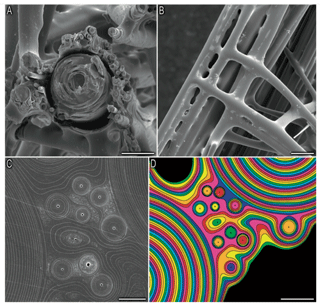
Figure B1Picture from Weaver et al. (2007). Organisational details of the consolidation silica matrix. (a) Cross section of the skeletal lattice showing a large spicule surrounded by small spicules, scale bar: 50 µm. (b) External view of the skeletal lattice, scale bar: 100 µm. Panels (c) and (d) show a polished cross section showing that the cement of the skeletal lattice is made of multiple layers, scale bar: 10 and 20 µm respectively.
Samples and sample images are available at the University of Bristol; for further detail contact Katharine R. Hendry, email address: k.hendry@bristol.ac.uk
LC conducted the analysis, created the figures and wrote the paper. CDC helped conduct the isotopic analysis. KRH conducted the fieldwork and conceived the study. JRX identified the samples. All authors have reviewed the paper.
The authors declare that they have no conflict of interest.
We acknowledge the science team and the crew of JC094 and Laura Robinson for
cruise organisation. We would also like to thank Paul Curnow for constructive
comments, Stuart Kearns for his SEM training and assistance, and
Maria López-Acosta for her help. Finally, the funding from the Royal
Society (grant code RG130386) and from the European Research Council is acknowledged.
Joana R. Xavier received support from the European Union's Horizon 2020
research and innovation program through the SponGES project (grant agreement
no. 679849).
Edited by: Jack Middelburg
Reviewed by: Jill Sutton and two anonymous referees
Aizenberg, J.: Skeleton of Euplectella sp.: Structural Hierarchy from the Nanoscale to the Macroscale, Science, 309, 275–278, https://doi.org/10.1126/science.1112255, 2005. a
Antcliffe, J. B., Callow, R. H., and Brasier, M. D.: Giving the early fossil record of sponges a squeeze, Biol. Rev., 89, 972–1004, https://doi.org/10.1111/brv.12090, 2014. a
Cardinal, D., Alleman, L. Y., de Jong, J., Ziegler, K., and Andre, L.: Isotopic composition of silicon measured by multicollector plasma source mass spectrometry in dry plasma mode, J. Anal. Atom. Spectrom., 18, 213–218, https://doi.org/10.1039/b210109b, 2003. a
Cardinal, D., Savoye, N., Trull, T. W., Dehairs, F., Kopczynska, E. E., Fripiat, F., Tison, J. L., and André, L.: Silicon isotopes in spring Southern Ocean diatoms: Large zonal changes despite homogeneity among size fractions, Mar. Chem., 106, 46–62, https://doi.org/10.1016/j.marchem.2006.04.006, 2007. a
Cha, J. N., Shimizu, K., Zhou, Y., Christiansen, S. C., Chmelka, B. F., Stucky, G. D., and Morse, D. E.: Silicatein filaments and subunits from a marine sponge direct the polymerization of silica and silicones in vitro, P. Natl. Acad. Sci. USA, 96, 361–365, https://doi.org/10.1073/pnas.96.2.361, 1999. a, b
Croce, G., Frache, A., Milanesio, M., Marchese, L., Causà, M., Viterbo, D., Barbaglia, A., Bolis, V., Bavestrello, G., Cerrano, C., Benatti, U., Pozzolini, M., Giovine, M., and Amenitsch, H.: Structural Characterization of Siliceous Spicules from Marine Sponges, Biophys. J., 86, 526–534, https://doi.org/10.1016/S0006-3495(04)74131-4, 2004. a
De Bièvre, P. and Taylor, P. D. P.: Table of the isotopic compositions of the elements, Int. J. Mass Spectrom., 123, 149–166, https://doi.org/10.1016/0168-1176(93)87009-H, 1993. a
De La Rocha, C. L.: Silicon isotope fractionation by marine sponges and the reconstruction of the silicon isotope composition of ancient deep water, Geol. Soc. Am. Bull., 31, 423–426, https://doi.org/10.1130/0091-7613(2003)031<0423:SIFBMS>2.0.CO;2, 2003. a, b, c, d
De La Rocha, C. L., Brzezinski, M. A., and DeNiro, M. J.: Fractionation of silicon isotopes by marine diatoms during biogenic silica formation, Geochim. Cosmochim. Ac., 61, 5051–5056, https://doi.org/10.1016/s0016-7037(97)00300-1, 1997. a
De La Rocha, C. L., Bescont, P., Croguennoc, A., and Ponzevera, E.: The silicon isotopic composition of surface waters in the Atlantic and Indian sectors of the Southern Ocean, Geochim. Cosmochim. Ac., 75, 5283–5295, https://doi.org/10.1016/j.gca.2011.06.028, 2011. a
Ereskovsky, A. V.: Development of Sponges from the Class Hexactinellida Schmidt, 1870, in: The Comparative Embryology of Sponges, Springer, Chap. 2, 37–46, https://doi.org/10.1007/978-90-481-8575-7, 2010. a, b
Fontorbe, G., Frings, P. J., De La Rocha, C. L., Hendry, K. R., Carstensen, J., and Conley, D. J.: Enrichment of dissolved silica in the deep equatorial Pacific during the Eocene-Oligocene, Paleoceanography, 32, 848–863, https://doi.org/10.1002/2017PA003090, 2017. a, b
Grasse, P., Brzezinski, M. A., Cardinal, D., de Souza, G. F., Andersson, P. S., Closset, I., Cao, Z., Dai, M., Ehlert, C., Estrade, N., François, R., Frank, M., Jiang, G., Jones, J. L., Kooijman, E., Liu, Q., Lu, D., Pahnke, K., Ponzevera, E., Schmitt, M., Sun, X., Sutton, J. N., Thil, F., Weis, D., Wetzel, F., Zhang, A., Zhang, J., and Zhang, Z.: GEOTRACES inter-calibration of the stable silicon isotope composition of dissolved silicic acid in seawater, J. Anal. At. Spectrom., 32, 562–578, 2017. a
He, H.-t., Zhang, S., Zhu, C., and Liu, Y.: Equilibrium and kinetic Si isotope fractionation factors and their implications for Si isotope distributions in the Earth's surface environments, Acta Geochimica, 35, 15–24, https://doi.org/10.1007/s11631-015-0079-x, 2016. a
Hendry, K. R. and Robinson, L. F.: The relationship between silicon isotope fractionation in sponges and silicic acid concentration: Modern and core-top studies of biogenic opal, Geochim. Cosmochim. Ac., 81, 1–12, https://doi.org/10.1016/j.gca.2011.12.010, 2012. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y
Hendry, K. R., Georg, B. R., Rickaby, R. E. M., Robinson, L. F., and Halliday, A. N.: Deep ocean nutrients during the Last Glacial Maximum deduced from sponge silicon isotopic compositions, Earth Planet. Sc. Lett., 292, 290–300, https://doi.org/10.1016/j.epsl.2010.02.005, 2010. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p
Hendry, K. R., Leng, M. J., Robinson, L. F., Sloane, H. J., Blusztjan, J., Rickaby, R. E. M., Georg, B. R., and Halliday, A. N.: Silicon isotopes in Antarctic sponges: an interlaboratory comparison, Antarct. Sci., 23, 34–42, 2011. a, b
Hendry, K. R., Swann, G. E. A., Leng, M. J., Sloane, H. J., Goodwin, C., Berman, J., and Maldonado, M.: Technical Note: Silica stable isotopes and silicification in a carnivorous sponge Asbestopluma sp., Biogeosciences, 12, 3489–3498, https://doi.org/10.5194/bg-12-3489-2015, 2015. a
Hendry, K. R., Gong, X., Knorr, G., Pike, J., and Hall, I. R.: Deglacial diatom production in the tropical North Atlantic driven by enhanced silicic acid supply, Earth Planet. Sc. Lett., 438, 122–129, 2016. a
Hooper, J. N. a. and Van Soest, R. W.: Systema Porifera. A Guide to the Classification of Sponges, Plenum, 1, 1–1707, https://doi.org/10.1007/978-1-4615-0747-5_1, 2002. a
Jochum, K. P., Schuessler, J. A., Wang, X.-H., Stoll, B., Weis, U., Müller, W. E. G., Haug, G. H., Andreae, M. O., and Froelich, P. N.: Whole-Ocean Changes in Silica and Ge/Si Ratios During the Last Deglacial Deduced From Long-Lived Giant Glass Sponges, Geophys. Res. Lett., 44, 11555–11564, 2017. a
Karl, D. M. and Tien, G.: Magic: A sensitive and precise method for measuring dissolved phosphorus in aquatic environments, Limnol. Oceanogr., 37, 105–116, https://doi.org/10.4319/lo.1992.37.1.0105, 1992. a
Krasko, A., Lorenz, B., Batel, R., Schröder, H. C., Müller, I. M., and Müller, W. E. G.: Expression of silicatein and collagen genes in the marine sponge Suberites domuncula is controlled by silicate and myotrophin, Eur. J. Biochem., 267, 4878–4887, 2000. a
Leys, S. P. and Lauzon, N. R.: Hexactinellid sponge ecology: growth rates and seasonality in deep water sponges, J. Exp. Mar. Biol. Ecol., 230, 111–129, https://doi.org/10.1016/S0022-0981(98)00088-4, 1998. a, b
López-Acosta, M., Leynaert, A., and Maldonado, M.: Silicon consumption in two shallow-water sponges with contrasting biological features, Limnol. Oceanogr., 61, 2139–2150, 2016. a, b, c, d, e, f, g, h, i
López-Acosta, M., Leynaert, A., Grall, J., and Maldonado, M.: Silicon consumption kinetics by marine sponges: An assessment of their role at the ecosystem level, Limnol. Oceanogr., 63, 1–15, https://doi.org/10.1002/lno.10956, 2018. a, b, c, d, e, f
Love, G. D., Grosjean, E., Stalvies, C., Fike, D. A., Grotzinger, J. P., Bradley, A. S., Kelly, A. E., Bhatia, M., Meredith, W., Snape, C. E., Bowring, S. A., Condon, D. J., and Summons, R. E.: Fossil steroids record the appearance of Demospongiae during the Cryogenian period, Nature, 457, 718–721, 2009. a
Maldonado, M. and Riesgo, A.: Intra-epithelial spicules in a homosclerophorid sponge, Cell Tissue Res., 328, 639–650, 2007. a, b, c
Maldonado, M., Carmona, M. C., Velásquez, Z., Puig, A., Cruzado, A., López, A., and Young, C. M.: Siliceous sponges as a silicon sink: An overlooked aspect of benthopelagic coupling in the marine silicon cycle, Limnol. Oceanogr., 50, 799–809, 2005. a, b
Maldonado, M., Riesgo, A., Bucci, A., and Tzlerb, K. R.: Revisiting silicon budgets at a tropical continental shelf: Silica standing stocks in sponges surpass those in diatoms, Limnol. Oceanogr., 55, 2001–2010, 2010. a
Maldonado, M., Navarro, L., Grasa, A., Gonzalez, A., and Vaquerizo, I.: Silicon uptake by sponges: a twist to understanding nutrient cycling on continental margins, Sci. Rep., 1, 1–30, 2011. a, b, c, d
Maldonado, M., Ribes, M., and van Duyl, F. C.: Nutrient Fluxes Through Sponges, Adv. Mar. Biol., 62, 113–182, 2012. a, b
Milligan, A. J., Varela, D. E., Brzezinski, M. a., and Morel, F. M. M.: Dynamics of silicon metabolism and silicon isotopic discrimination in a marine diatomas a function of pCO2, Limnol. Oceanogr., 49, 322–329, 2004. a, b
Montanez, I. P.: Biological skeletal carbonate records changes in major-ion chemistry of paleo-oceans, P. Natl. Acad. Sci. USA, 99, 15852–15854, https://doi.org/10.1073/pnas.262659599, 2002. a
Müller, W. E. G., Schloßmacher, U., Wang, X., Boreiko, A., Brandt, D., Wolf, S. E., Tremel, W., and Schröder, H. C.: Poly(silicate)-metabolizing silicatein in siliceous spicules and silicasomes of demosponges comprises dual enzymatic activities (silica polymerase and silica esterase), FEBS J., 275, 362–370, 2008. a, b, c, d
Müller, W. E. G., Wang, X., Burghard, Z., Bill, J., Krasko, A., Boreiko, A., Schloßmacher, U., Schröder, H. C., and Wiens, M.: Bio-sintering processes in hexactinellid sponges: Fusion of bio-silica in giant basal spicules from Monorhaphis chuni, J. Struct. Biol., 168, 548–561, 2009. a
Müller, W. E. G., Schröder, H. C., Burghard, Z., Pisignano, D., and Wang, X.: Silicateins-A Novel Paradigm in Bioinorganic Chemistry: Enzymatic Synthesis of Inorganic Polymeric Silica, Chemistry-Eur. J., 19, 5790–5804, 2013. a, b
Otzen, D.: The Role of Proteins in Biosilicification, Scientifica, 2012, 1–22, 2012. a
Pansini, M. and Pronzato, R.: Observation on the dynamics of a mediterranean sponge community, New Perspectives in Sponge Biology, 404–415, 1990. a
Ragueneau, O., Gallinari, M., Corrin, L., Grandel, S., Hall, P., Hauvespre, A., Lampitt, R., Rickert, D., Stahl, H., Tengberg, A., and Witbaard, R.: The benthic silica cycle in the Northeast Atlantic: annual mass balance, seasonality, and importance of non-steady-state processes for the early diagenesis of biogenic opal in deep-sea sediments, Prog. Oceanogr., 50, 171–200, 2001. a
Ragueneau, O., Savoye, N., Del Amo, Y., Cotten, J., Tardiveau, B., and Leynaert, A.: A new method for the measurement of biogenic silica in suspended matter of coastal waters: using Si:Al ratios to correct for the mineral interference, Cont. Shelf Res., 25, 697–710, 2005. a
Reincke, T. and Barthel, D.: Silica uptake kinetics of Halichondria panicea in Kiel Bight, Mar. Biol., 129, 591–593, 1997. a, b, c, d
Reynolds, B. C., Frank, M., and Halliday, A. N.: Silicon isotope fractionation during nutrient utilization in the North Pacific, Earth Planet. Sc. Lett., 244, 431–443, https://doi.org/10.1016/j.epsl.2006.02.002, 2006. a
Reynolds, B. C., Aggarwal, J., André, L., Baxter, D., Beucher, C. P., Brzezinski, M. A., Engström, E., Georg, B. R., Land, M., Leng, M. J., Opfergelt, S., Rodushkin, I., Sloane, H. J., van den Boorn, S. H. J. M., Vroon, P. Z., and Cardinal, D.: An inter-laboratory comparison of Si isotope reference materials, J. Anal. Atom. Spectrom., 22, 561–568, https://doi.org/10.1039/B616755A, 2007. a, b
Sandford, F.: Physical and chemical analysis of the siliceous skeletons in six sponges of two groups (Demospongiae and Hexactinellida), Microsc. Res. Techniq., 62, 336–355, https://doi.org/10.1002/jemt.10400, 2003. a, b
Schröder, H. C., Wang, X., Tremel, W., Ushijima, H., and Müller, W. E. G.: Biofabrication of biosilica-glass by living organisms, Nat. Prod. Rep., 25, 455–474, 2008. a
Steele, R. C., Coath, C. D., Regelous, M., Russell, S., and Elliott, T.: Neutron-poor nickel isotope anomalies in meteorites, Astrophys. J., 758, 1–21, https://doi.org/10.1088/0004-637X/758/1/59, 2012. a
Strehlow, B. W., Pineda, M.-c., Duckworth, A., Kendrick, G. A., Renton, M., Azmi, M., Wahab, A., Webster, N. S., and Clode, P. L.: Sediment tolerance mechanisms identified in sponges using advanced imaging techniques, PEER J., 5:e3904, 1–26, https://doi.org/10.7717/peerj.3904, 2017. a
Tréguer, P. J. and De La Rocha, C. L.: The World Ocean Silica Cycle, Annu. Rev. Mar. Sci., 5, 477–501, 2013. a
Uriz, M.-J.: Mineral skeletogenesis in sponges, Can. J. Zool., 84, 322–356, https://doi.org/10.1139/z06-032, 2006. a, b
Uriz, M.-J., Turon, X., Becerro, M. A., and Agell, G.: Siliceous spicules and skeleton frameworks in sponges: Origin, diversity, ultrastructural patterns, and biological functions, Microsc. Res. Techniq., 62, 279–299, 2003. a, b, c, d, e
Van Soest, R. W., Boury-Esnault, N., Vacelet, J., Dohrmann, M., Erpenbeck, D., De Voogd, N. J., Santodomingo, N., Vanhoorne, B., Kelly, M., and Hooper, J. N.: Global diversity of sponges (Porifera), PLoS ONE, 7, 1–23, https://doi.org/10.1371/journal.pone.0035105, 2012. a
Wang, X., Wiens, M., Schroder, H. C., Jochum, K. P., Schlossmacher, U., Gotz, H., Duschner, H., and Muller, W. E. G.: Circumferential spicule growth by pericellular silica deposition in the hexactinellid sponge Monorhaphis chuni, J. Exp. Biol., 214, 2047–2056, 2011. a
Wang, X., Schloßmacher, U., Wiens, M., Batel, R., Schröder, H. C., and Müller, W. E. G.: Silicateins, silicatein interactors and cellular interplay in sponge skeletogenesis: formation of glass fiber-like spicules, FEBS J., 279, 1721–1736, 2012a. a, b
Wang, X., Schröder, H. C., Wang, K., Kaandorp, J. A., and Müller, W. E. G.: Genetic, biological and structural hierarchies during sponge spicule formation: from soft sol-gels to solid 3D silica composite structures, Soft Matter, 8, 9489–9714, 2012b. a, b
Weaver, J. C. and Morse, D. E.: Molecular biology of demosponge axial filaments and their roles in biosilicification, Microsc. Res. Techniq., 62, 356–367, 2003. a
Weaver, J. C., Aizenberg, J., Fantner, G. E., Kisailus, D., Woesz, A., Allen, P., Fields, K., Porter, M. J., Zok, F. W., Hansma, P. K., Fratzl, P., and Morse, D. E.: Hierarchical assembly of the siliceous skeletal lattice of the hexactinellid sponge Euplectella aspergillum, J. Struct. Biol., 158, 93–106, https://doi.org/10.1016/j.jsb.2006.10.027, 2007. a, b
Wille, M., Sutton, J. N., Ellwood, M. J., Sambridge, M., Maher, W., Eggins, S., and Kelly, M.: Silicon isotopic fractionation in marine sponges: A new model for understanding silicon isotopic variations in sponges, Earth Planet. Sc. Lett., 292, 281–289, https://doi.org/10.1016/j.epsl.2010.01.036, 2010. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z






