2.1 Datasets used for algorithm development and validation

In situ concentrations of DMS and DMSPt (nM) and chlorophyll a (Chl, mg m⁻³), accompanied by ancillary data (bottom depth, temperature, salinity, wind speed), were downloaded from the global sea-surface DMS database. The latter was complemented with additional in situ datasets recently obtained by the authors' teams. After quality control, the database had 41 304, 3700 and 9182 measurements for in situ DMS, DMSPt and Chl, respectively, with 3637 DMS–DMSPt and 8141 DMS–Chl pairs.The in situ database was extended with geophysical and biogeochemical parameters, including satellite retrievals collocated in time and space (“matchups”) and gridded climatological datasets, following Galí et al. (2015; see below). Detailed information regarding data sources, quality control and processing can be found in the Supplement and in Tables S1–S3.

We performed satellite matchups using SeaWiFS (1997–2010) and MODIS-Aqua (2003–2012) retrievals of remotely sensed Chl (mg m⁻³), vertical attenuation coefficient at 490 nm (Kd490, m⁻¹), particulate inorganic carbon (PIC, mol m⁻³) and daily photosynthetically available radiation at the sea surface (PAR, $\mathrm{mol}\mathrm{photons}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$). To maximize the amount of available matchups, and after verifying the consistency between the two sensors, we produced merged variables by averaging SeaWiFS and MODIS-Aqua matchups. We employed a hierarchical search procedure whereby the matchup criteria were progressively relaxed from 1 to 8 days and from single-pixel to 5×5 pixel bins (Sect. S2 in the Supplement). These merged variables are hereafter designated with the SAT subscript (e.g., Chl_SAT). Daily sea-surface temperature (SST_SAT, ^∘C) from the AVHRR sensors was also matched to the database.

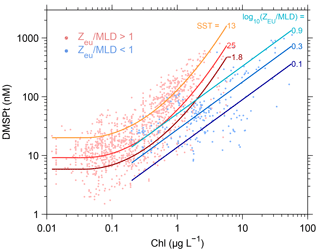
Figure 1Relationship between DMS, DMSPt and PAR across oceanic biomes and data availability. (a) DMS vs. DMSPt. (b) DMS ∕ DMSPt ratio vs. mean daily irradiance (PAR) at the sea surface. (c) Longhurst biogeochemical provinces and biomes. (d) In situ DMS data counts in $\mathrm{5}{}^{\circ }\times \mathrm{5}{}^{\circ }$ latitude–longitude bins; stippling indicates bins with measurements available for 3 or more months. In (a, b) small grey dots represent individual data points and large colored dots represent the median in a given Longhurst biogeochemical province and month and the corresponding interquartile ranges. Province–month medians are colored by biome following the map in (c), which also shows the amount of DMS–DMSPt–PAR measurements available in each biome. In (a–c), the R² and n (data counts) outside and inside parentheses correspond to non-binned data and province–month (MLongh) binned data, respectively. Regression lines in (a, b), calculated with MLongh binned data, are only illustrative.

Download

The database was further extended with monthly climatological data: daily PAR from SeaWiFS (1997–2010 average); mixed layer depth (MLD, in meters) from the monthly MIMOC climatology (Schmidtko et al., 2013); bottom depth from the General Bathymetric Chart of the Oceans (GEBCO08); and sea-surface nitrate and phosphate concentrations (µM) from the World Ocean Atlas 2009 (WOA09). Nutricline depths were calculated from WOA09 vertical profiles as the depth where nitrate and phosphate first exceeded 1 and 0.4 µM, respectively. Nutricline depth estimations were robust to changes of ±50 % in these concentration thresholds.

The mean daily PAR in the upper mixed layer (PAR_MLD) was calculated as

When satellite matchups were not available (before September 1997), we used climatological PAR from SeaWiFS (1997–2010 average) in order to increase the temporal coverage of the PAR_SAT and PAR_MLD variables. Statistical analyses done with climatological or matchup PAR_SAT gave very similar results. This procedure was not followed with other variables (Chl, PIC, Kd490) that show wider interannual variations.

2.2 Statistical analyses and data binning schemes

All statistical analyses were conducted using (i) non-binned data; (ii) data binned by month and $\mathrm{5}{}^{\circ }\times \mathrm{5}{}^{\circ }$ latitude–longitude bins (M5×5); and (iii) data binned by month and the 56 Longhurst biogeochemical provinces (designated MLongh; Longhurst, 2010). Data binning eliminates low-frequency variation (“noise”) below a given space or timescale. MLongh binned data were further aggregated into six biomes: two Polar biomes (Arctic and Antarctic), two mid-latitude Westerlies biomes (Northern and Southern hemispheres), one Trades biome (tropical latitudes) and one global Coastal biome (Fig. 1c). Variables with a right-skewed approximate lognormal distribution entered statistical analyses after log ₁₀ transformation: DMS, DMSPt, DMS ∕ DMSPt ratio, Chl, nitrate and phosphate concentrations. To further account for non-normality, we conducted statistical explorations using both bin means and bin medians.

To develop the DMS algorithm we analyzed the relationship between DMS, the DMS ∕ DMSPt ratio and environmental variables (listed in Table 1). After an exploratory analysis based on the calculation of Pearson correlation coefficients (Table 1), we built several regression models where DMS was estimated as a function of in situ DMSPt concentration and additional variables (Tables 2 and S4). We added one variable at a time in order of decreasing data availability, and significant terms were selected using stepwise regression with entrance and removal p values set at 0.001 and 0.005, respectively. The logic for adding one variable at a time, rather than building a single initial model with all the predictor variables, is that the size (N) of the data subset used for model fitting decreases rapidly when variables with sparse coverage are combined. Each set of initial predictors was tested across the three degrees of data binning described above and three degrees of model complexity: linear without interactions, linear with interactions and quadratic with interactions. This 3×3 nested structure provided a stringent test for the robustness of a given regression model. Improvements in model performance were assessed based on the increase in adjusted r squared, $R_{\text{adj}}^{\mathrm{2}}$, and the decrease in root-mean-square error (RMSE) and the Akaike information criterion (AIC).

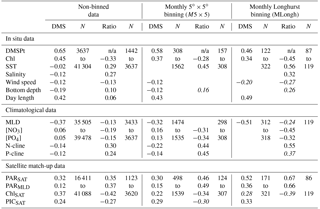
Table 1Correlation analysis (Pearson's r) for different data binning levels. Pearson's r with p value <0.01 are not shown; values in italic are $\mathrm{0.0001}<p<\mathrm{0.01}$; n/a: not applicable. “Ratio” refers to log ₁₀(DMS ∕ DMSPt). DMS, DMSPt, Chl, MLD, [NO₃] and [PO₄] were log ₁₀ transformed; Pearson's r calculated on log ₁₀-transformed variables were higher than those calculated on the same non-transformed variables, and similar in magnitude to Spearman's rank correlations. Bottom and nutricline depth values are shown as positive values (deeper is bigger). See the text for other acronyms.

Download Print Version | Download XLSX

Regression models were further optimized for global and regional domains using the bootstrap method followed by nonlinear optimization as described in Sect. S4. Selected models were then validated using an independent data subset composed of in situ DMS measurements and their satellite matchups (described in Sect. 3.1.3) and evaluated using a wide array of skill metrics (following Galí et al., 2015): R², RMSE, mean absolute percentage error (MAPE), percentage bias and the slope of major axis (type II) linear regression between observations and model estimates (Slope_MA). All analyses were carried out using MATLAB R2013b.

2.3 Algorithm implementation

The newly developed DMS_SAT algorithm (Fig. 2) was implemented to produce (i) a monthly global DMS climatology and (ii) several regional time series with 8-day resolution for the period 2003–2016. Further details and data sources can be found in Sect. S5 and Table S2.

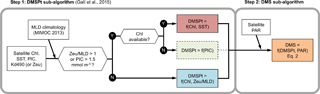
Figure 2Scheme of the DMS_SAT algorithm. The algorithm proceeds in two steps: the DMSPt sub-algorithm (described by Galí et al., 2015 see Appendix A) and the DMS sub-algorithm (this study). Dashed lines mark the PIC-based equation of the DMSPt sub-algorithm, which in practice is not used when gap-free satellite Chl fields are used as input.

Download

Global DMS_SAT fields were computed using ocean color data from SeaWiFS (1997–2010 monthly climatology, 1∕12^∘ grid), SST from AVHRR and the MIMOC monthly MLD climatology. We used SeaWiFS data to maximize the temporal overlap between the satellite-based DMS_SAT climatology and the in situ data used to produce the L11 climatology, which span the period 1972–2010. Note, however, that DMSPt_SAT climatologies derived from SeaWiFS and MODIS-Aqua are extremely similar (Galí et al., 2015). We established a reference DMS_SAT run where Chl_SAT was computed with a band-ratio algorithm (OC4-OCI standard NASA algorithm) and the euphotic layer depth (Zeu_SAT) was computed as the 1 % penetration depth of 490 nm radiation (${\text{Zeu}}_{\text{SAT}}=\mathrm{4.6}/\text{Kd}\mathrm{490}$). The impact of this choice was evaluated with sensitivity tests where Chl_SAT and Zeu_SAT were calculated with the semi-analytical algorithms of Garver–Siegel–Maritorena (GSM; Maritorena et al., 2002) and Lee et al. (2007), respectively, which are more appropriate in optically complex waters. Observation gaps caused by low solar elevation at high latitudes in winter were left blank. Global monthly DMS_SAT fields were averaged onto 1 and 5^∘ grids for mapping and comparison to other DMS climatologies: the interpolated L11 climatology (Lana et al., 2011), and the climatologies derived with the empirical algorithms of Simó and Dachs (2002; SD02) and Vallina and Simó (2007b; VS07). The procedures used to calculate these datasets are briefly described in Sect. 3.2.

Regional DMS_SAT time series between 2003 and 2016 were computed using daily MODIS-Aqua data (4.64 km) combined with the MIMOC MLD climatology. As done for the global implementation, we produced DMS_SAT fields using both band-ratio and semi-analytical bio-optical products. We also performed a test comparing DMSPt_SAT obtained with the MIMOC MLD climatology vs. model-derived MLD time series, showing little DMSPt_SAT sensitivity (Fig. S1 in the Supplement). Since non-climatological satellite data contain gaps caused by cloudiness, we applied a binning and gap-filling procedure to obtain full coverage, such that the final regional time series had a resolution of 8 days and 27.8 km. We produced DMS_SAT time series for the Bermuda Atlantic Time-series Study (BATS) station (31^∘40^′ N, 64^∘10^′ W) and for the Northern Hemisphere at latitudes >45^∘ N. The latter dataset was then sampled at selected North Atlantic sites and at the Ocean Station P (OSP) in the NE Pacific (50^∘ N, 145^∘ W). Satellite time series were compared to the L11 climatology and to in situ DMS and DMSPt. These in situ data, kindly provided by the BATS (Levine et al., 2016) and OSP (https://www.waterproperties.ca/linep/, last access: 29 November 2017) teams, were not used in algorithm development.

3.1 Development and validation of the DMS sub-algorithm

3.1.1 Statistical exploration

We analyzed the correlation between potential predictor variables and log ₁₀(DMS) or log ₁₀(DMS∕DMSPt) (Table 1). This analysis systematically showed that (i) DMSPt was the best correlate of DMS (r=0.46 to 0.65), and (ii) surface PAR_SAT and mean PAR in the mixed layer (PAR_MLD) were the best correlates of the DMS ∕ DMSPt ratio (r=0.35 to 0.67). These correlation patterns remained across different binning levels, suggesting that DMS can be estimated, to first order, by the concentration of its phytoplanktonic precursor compound and by the PAR-dependent enhancement of DMSPt-to-DMS conversion. It is also noteworthy that the correlation between day length and the DMS ∕ DMSPt ratio was weak or non-significant. This supports the causal relationship between PAR and the DMS ∕ DMSPt ratio and discards other factors that might follow synchronous seasonal cycles.

Table 2Summary of fitted model coefficients and goodness-of-fit statistics. Different sets of coefficients were obtained by fitting the model ${\log }_{\mathrm{10}}\text{DMS}=\mathit{\alpha }+\mathit{\beta }$ log ₁₀DMSPt+γPAR to observed DMS, DMSPt and PAR_SAT after applying different binning schemes. Equations (2f) and (2h) were derived using a different optimization procedure, applied to the global MLongh binned dataset and to the BATS station local dataset. The models implemented to calculate a global DMS climatology are denoted in italic, regional or local time series in bold.

Download Print Version | Download XLSX

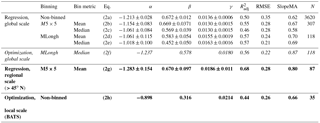
Guided by the correlation patterns, we established a base regression model expressed by the equation:

$$\begin{array}{}\text{(2)}& {\log }_{\mathrm{10}}\text{DMS}=\mathit{\alpha }+\mathit{\beta }{\log }_{\mathrm{10}}\text{DMSPt}+\mathit{\gamma }\text{PAR}.\end{array}$$

This model explained between 50 and 57 % of log ₁₀(DMS) variance with an increasing level of data binning, and the corresponding RMSE ranged between 0.35 and 0.21 (Table 2).

We assessed whether the base model could be significantly improved by adding predictor variables and/or increasing model complexity. We started by adding a variable X to a linear model without interactions of the form ${\log }_{\mathrm{10}}\text{DMS}=\mathit{\alpha }+\mathit{\beta }{\log }_{\mathrm{10}}\text{DMSPt}+\mathit{\gamma }\text{PAR}+\mathit{\delta }X$. Variable X was chosen among those showing higher correlations to either DMS or the DMS ∕ DMSPt ratio: SST, nitrate concentration, nitracline depth, salinity, wind speed and PIC_SAT (Table 1). Although this analysis led us to discard additional predictor variables, its results are briefly described below and compiled in Table S4 for the sake of completeness. With non-binned data, all the additional variables entered regression models with significant coefficients, but only salinity, wind speed and PIC_SAT produced significant decreases in RMSE and AIC. With MLongh binned data, only SST and PIC_SAT entered with significant coefficients. Yet none of the additional variables improved simultaneously the R² adj, RMSE and AIC skill metrics with respect to the base model. Increasing model complexity through addition of interaction and quadratic terms, or by adding a fourth variable, generally resulted in minor improvements or erratic changes in model performance (results not shown). Invariably, DMSPt and PAR were the only variables with highly significant coefficients ($p\ll {\mathrm{10}}^{-\mathrm{10}}$) regardless of the binning scheme or the inclusion of additional variables.

As a corollary, the use of PAR_MLD instead of PAR_SAT slightly degraded model skill (Table S4). Although PAR_MLD is a priori a more realistic metric of light exposure, it is possible that the use of climatological MLD degraded the PAR_MLD estimates. Another potential explanation is the episodic nature of oceanic vertical mixing, which requires the distinction between the actively mixing layer, which is defined by higher turbulence than in the ocean interior, and the mixed layer, here termed MLD and defined by the vertical homogeneity of regular temperature–salinity profiles (Brainerd and Gregg, 1995; Sutherland et al., 2014). This distinction implies that, on occasion, mean light exposure at the sea surface is better approximated by surface PAR_SAT than by PAR_MLD. After these considerations we excluded PAR_MLD from our algorithm, and focused on optimizing Eq. (2).

Finally, note that PAR_SAT is used in our algorithm both as a direct driver of DMS cycling processes and as a proxy for UVR-driven processes (e.g., Archer et al., 2010; Galí et al., 2013; Royer et al., 2016). For obvious astronomical reasons, incident PAR and UVR are strongly correlated. Attenuation of PAR and UVR in the atmosphere, first, and in seawater, afterwards, also covary (Kirk, 2011), so that plankton UVR exposure is to first order well correlated to PAR.

3.1.2 Implications of the model structure

Here we analyze the physical and biogeochemical meaning of Eq. (2) coefficients in view of their optimization for diagnostic purposes (3.1.3).

• The intercept (α) acts to adjust the magnitude of DMS concentrations by a fixed proportion everywhere; e.g., increasing α by log ₁₀(1.10) would raise estimated DMS concentrations by 10 % globally.

• The log ₁₀DMSPt coefficient (β) expresses the nonlinear relationship between DMS and DMSPt. Fitted β is smaller than 1 regardless of the binning applied. For a constant PAR, this implies that DMS increases more slowly than DMSPt (Fig. 3a) and that the DMS ∕ DMSPt ratio decreases nonlinearly and approaches an horizontal asymptote as DMSPt increases (Fig. 3a). This behavior implicitly represents the change in DMSPt-to-DMS conversion efficiency depending on the biomass and structure of the microbial plankton community.

• The PAR coefficient (γ) expresses the DMSPt-independent modulation of DMS concentration. Fitted γ is larger than 0, meaning that the PAR sensitivity increases exponentially with PAR, regardless of DMSPt (Fig. 3b). Incident PAR is positively correlated to shallow mixing at the global scale, and to seawater transparency at low latitudes (but not at high latitudes). Thus, nonlinear PAR sensitivity possibly embodies the enhancement of sunlight exposure by shallow mixing and deeper PAR (and UVR) penetration. In summary, γ represents stress-driven DMS production.

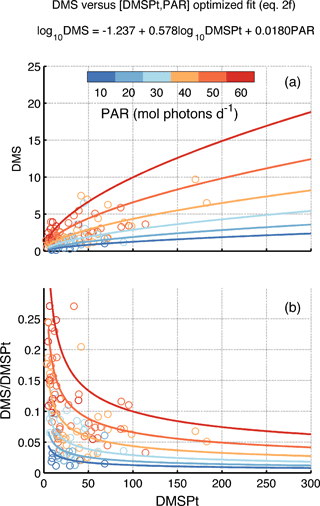
Figure 3Relationship between DMS, DMSPt and PAR as represented in the DMS_SAT algorithm. (a) DMS vs. DMSPt and (b) DMS ∕ DMSPt ratio vs. DMSPt, as a function of PAR. Colored circles represent the medians of in situ data binned by Longhurst province and month, and lines correspond to the model predictions. PAR levels are indicated in the color bar.

Download

In biogeochemical terms, Eq. (2) implies maximal DMS ∕ DMSPt ratios when/where low DMSPt and high PAR co-occur. In biogeographic terms (Fig. 1), highest DMS ∕ DMSPt ratios are found in oligotrophic areas of the Trades biome, where low DMSPt concentrations prevail (<20 nM). Low DMSPt concentrations are also found in winter at high latitudes in deeply mixed waters, but the corresponding low irradiance results in DMS ∕ DMSPt < 0.05. At the high DMSPt concentrations that occur at high latitudes in summer (>100 nM), the DMS ∕ DMSPt ratio is generally <0.1.

As shown in Table 2, Eq. (2) coefficients change systematically as the binning spatial scale increases. To further explore the interrelationship between the model coefficients, we used the bootstrap method to produce 10⁵ sets of regression coefficients for the MLongh dataset. The scatter plots between α, β and γ resulting from the 10⁵ bootstrapped regressions confirmed that covariation between the coefficients is non-random, such that fitted β and γ are negatively correlated to α (Fig. S2). These trade-offs should be kept in mind when optimizing our model for global or regional implementation.

3.1.3 Optimization and validation

By definition, least squares regression minimizes the RMSE, but it has been shown that regression models derived in this way do not necessarily have the best skill (Jolliff et al., 2009). Therefore, we devised an alternative nonlinear optimization procedure (Sect. S4). To obtain realistic solutions, we constrained the optimized coefficients to the confidence intervals derived from the bootstrapped regressions for the MLongh dataset (Fig. S2). The resulting optimal model (Eq. 2f) had higher DMSPt (β) and PAR (γ) coefficients and a smaller intercept (α), and moved the modeled DMS concentration closer to the 1:1 agreement line without degrading either RMSE or R² (Table 2).

We validated the different versions of Eq. (2) (Table 2) by comparing DMS_SAT against in situ DMS using an independent subset of the database. Since the complete DMS algorithm proceeds in two steps (Fig. 2), its validation must take into account uncertainty in variables used as input to the DMSPt_SAT sub-algorithm. Galí et al. (2015) showed that, apart from the inherent algorithm uncertainty, most uncertainty in DMSPt_SAT (RMSE ≤0.3 in log ₁₀ space) results from error in Chl_SAT. Thus, the validation subset was defined according to three criteria: (i) satellite matchup data used as input to the algorithm (Chl_SAT, K_d,490, PAR_SAT and SST_SAT) were available; (ii) in situ DMSPt was not available – thus excluding the data used for model fitting; (iii) in situ DMS and Chl were available. We used in situ Chl concentration to constrain the uncertainty in Chl_SAT used as input to the algorithm. Indeed, this procedure progressively reduced the size of the validation subset as the maximum Chl_SAT error tolerated decreased. Uncertainty arising from PAR_SAT could not be assessed because the current database lacks in situ PAR measurements. Frouin et al. (2003) reported an error of ±15 % (<10 % for weekly and monthly periods), with negligible bias for PAR_SAT, suggesting it is a minor source of uncertainty.

Figure 4a summarizes the validation results for the best-performing regression model (Eq. 2e) and its optimized version (Eq. 2f). Supporting our assumption, DMS_SAT skill metrics improved as the maximum tolerated Chl_SAT RMSE decreased from 0.5 to 0.2 (Fig. 4). With Chl_SAT RMSE smaller than 0.2, the statistics showed erratic behavior owing to reduced sample size. Other skill metrics (not shown in Fig. 4) showed comparable trends.

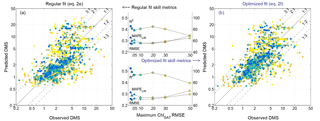
Figure 4Algorithm validation results constrained by the uncertainty in satellite-retrieved Chl. (a) Equation (2e), derived from regular multiple regression; (b) Eq. (2f), obtained through an optimization procedure. The scatter plots compare non-binned data and model estimates, color-coded depending on the maximum tolerated error in Chl_SAT with respect to Chl in situ, as shown in the x axis of the center plots. The center plots show the performance of the DMS algorithm for increasing error in Chl_SAT, evaluated with different skill metrics: the log ₁₀ space R² and RMSE (left y axis) and the linear space MAPE (right y axis). N increases from 86 to 1293 as the tolerated Chl_SAT error increases.

Download

Table 3Relative deviation (“bias”) of the global-scale optimized DMS_SAT algorithm across ocean biomes when evaluated against the in situ database (a and b) and against the L11 monthly climatology (c). Comparison with the in situ database was done using either (a) satellite matchups with Chl_SAT error constrained with respect to in situ Chl or (b) all Chl_SAT matchups, regardless of the availability of in situ Chl. The last column shows a qualitative overall assessment of DMS_SAT bias, based on columns (a–c), classifying the most likely magnitude and sign as small ± (±10 %), moderate (10 to 40 %, either + or −) or large (>40 %, either + or −).

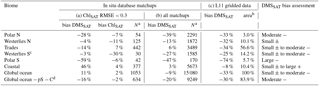
^a For the database comparisons, the amount of data (N) available for validation in a given region depends on the total amount of measurements, the proportion of data points with satellite matchups and, for the constrained case, the fraction of matchups where Chl_SAT has log ₁₀RMSE<0.3 compared to concurrent Chl in situ. Samples with available DMSPt measurements were excluded because they were used in model fitting and optimization.
^b For the global climatology comparison we report the percentage of ocean area, excluding pixels that could not be observed by satellites (high-latitude winter).
^c Samples where DMSPt was measured (not excluded) for this biome due to the small amount of data. Removing them would leave N=13.
^d Global ocean minus Polar S and Coastal biomes.

Download Print Version | Download XLSX

The optimized model coefficients (Eq. 2f) increased R² and reduced RMSE with respect to the regression-derived coefficients, achieving a maximal R² of 0.53 and a minimal RMSE of 0.25 for error-free Chl_SAT (log ₁₀-space non-binned data; Table S5). Corresponding best scores in linear space were R²=0.24 and RMSE =3.4 nM. These linear space statistics might be interpreted as a sign of poor performance, but it should be noted that they were strongly affected by a small fraction of highly biased estimates. Removing the most biased estimates (8 % of points beyond a factor of 3 from real measurements; Fig. 4) increased the linear space R² to 0.42–0.53 and decreased the RMSE to 1.8–2.3 nM across the full range of Chl_SAT error, with MAPE of 34–41 % and relative bias of −1 to 7 %. Altogether, these statistics illustrate the good performance of the DMS_SAT algorithm and the greater robustness of log-space statistics. The global-scale optimized algorithm had a mean-normalized standard deviation of 1.06–1.14 (log ₁₀ space), meaning that the spread of DMS_SAT nearly matched that of in situ DMS concentrations.

Table 4Mean area-weighted DMS concentrations for different climatological datasets and domains. Different results for the DMS_SAT algorithm were obtained using alternative approaches for retrieving chlorophyll a concentration (Chl_SAT) and the euphotic layer depth (Zeu_SAT). Results (based on $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ gridded data) are shown for the global domain, the Longhurst Coastal biome and, within it, areas shallower than 200 m (shelves); n/a: not applicable.

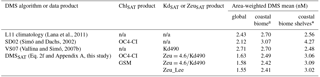
^* The Longhurst Coastal biome represents about 10.4 % of the global ocean area, of which one third is shallower than 200 m (3.5 % of global area).

Download Print Version | Download XLSX

Table 3 summarizes a detailed analysis of algorithm bias in different biomes. When Chl_SAT error was constrained to RMSE <0.3, DMS_SAT showed a global mean bias of 11 % (with a global mean bias of 2 % in Chl_SAT itself). DMS_SAT bias was negligible in the Westerlies biomes and larger than ±10 % in the other biomes, where its sign often matched that of Chl_SAT bias. When DMS_SAT bias was assessed using all available matchups, irrespective of Chl_SAT error, we obtained a global bias of −9 %. In some biomes, the sign and magnitude of DMS_SAT bias changed when Chl_SAT error was not constrained, indicating the influence of input satellite data. Assuming that Chl_SAT matchups (N∼15 000) are a random sample of the database between 1997 and 2012 (N∼24 000), this analysis suggests that global DMS_SAT bias likely ranges between −9 and 11 %.

3.2 Global climatologies

We implemented the global-scale optimized algorithm (Eq. 2f) using the SeaWiFS climatology. As shown in Fig. 5 and 6, DMS concentrations around ∼2.5 nM prevail during the astronomical spring and summer in each hemisphere, decreasing to around 1 nM in fall and <1 nM in winter. The seasonal cycle has wider amplitude at high latitudes and is nearly flat in the tropical oceans (see also Fig. S3). Regional enhancement of DMS concentrations occurs in some coastal and shelf areas, equatorial and eastern boundary upwellings, close to the subtropical front in austral summer (40^∘ S) and in the subpolar North Atlantic in boreal summer (60^∘ N). The global mean area-weighted DMS_SAT concentration is 1.63 nM (median and geometric mean of 1.36 nM). This global mean decreases by less than 5 % when semi-analytical Chl_SAT and Zeu_SAT products are used instead of our reference products, but larger deviations occur in the Coastal biome, particularly in shallow areas, associated with optically complex waters (Table 4).

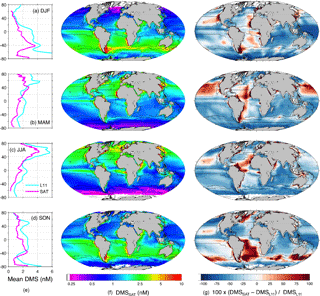
Figure 5Global DMS_SAT concentration fields by season. (a) December–February (DJF); (b) March–May (MAM); (c) June–August (JJA); (d) September–November (SON). Each row contains mean latitudinal profiles for the L11 climatology and DMS_SAT (left); DMS_SAT concentration maps (center); and maps of the percentage difference between DMS_SAT and the L11 climatology (right).

Download

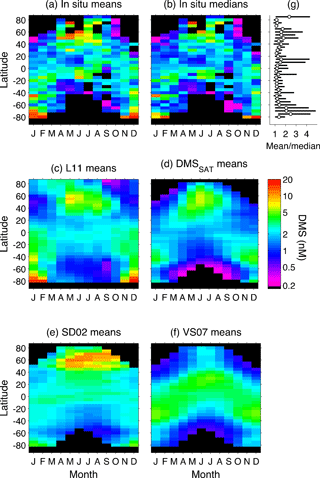
Figure 6Hovmöller diagrams comparing climatological DMS fields (monthly 5^∘ latitude bins). (a) In situ database means, (b) in situ database medians, (c) L11 climatology, (d) DMS_SAT algorithm, (e) SD02 algorithm and (f) VS07 algorithm. Panels (a–f) share the same color scale; the black background indicates no data. Panel (g) shows the average and range of monthly mean∕median ratios (shown in panels a and b) in each latitude band. Geometric means of in situ binned data (b) are similar to bin medians.

Download

3.2.2 Comparison to the SD02 climatology

The SD02 algorithm (Simó and Dachs, 2002) was designed to estimate DMS from MLD and Chl_SAT using two different equations depending on the Chl∕MLD ratio,

$$\begin{array}{}\text{(3a)}& {\displaystyle }& {\displaystyle }\text{DMS}=-\ln \left(\text{MLD}\right)+\mathrm{5.7}\text{Chl}/\text{MLD}<\mathrm{0.02},\text{(3b)}& {\displaystyle }& {\displaystyle }\text{DMS}=\mathrm{55.8}\text{Chl}/\text{MLD}+\mathrm{0.6}\text{Chl}/\text{MLD}\ge \mathrm{0.02},\end{array}$$

such that DMS increases linearly with the Chl∕MLD ratio in stratified productive conditions (e.g., high latitudes in summer) and inversely with MLD in typical oligotrophic conditions.

Validation of SD02 with the same dataset used for DMS_SAT indicates that it explains less variance (log ₁₀ R² of 0.22–0.31) but has similar RMSE and MAPE (Table S5). Globally, DMS_SD02 is characterized by a bimodal distribution (Fig. 7), with an area-weighted mean of 2.12 nM, 13 % lower than DMS_L11 (Table 4). SD02 estimates are in good agreement with the L11 climatology at tropical and temperate latitudes. In the southern Westerlies biome, however, prevailing deep vertical mixing and low Chl cause SD02 to underestimate DMS throughout the productive season (Figs. 6 and S3). Another feature of SD02 is the high DMS concentration in northern polar latitudes through late summer and fall, caused mainly by the shallow MLD due to freshwater-driven stratification. As DMS_SAT, DMS_SD02 suffers from negative bias in the Antarctic biome during the productive season (November through February).

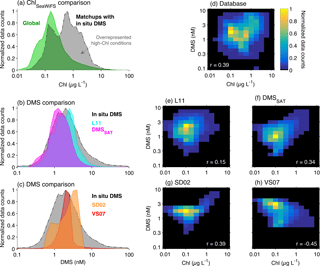
Figure 7Histograms illustrating the relationship between DMS and Chl in the global ocean. (a) Global SeaWiFS 1997–2010 Chl_SAT climatology and SeaWiFS Chl_SAT matchups for the in situ DMS database; (b) Global L11 and DMS_SAT climatologies and in situ DMS database; (c) Global SD02 and VS07 climatologies and in situ DMS database; (d) bivariate histogram of in situ DMS vs. corresponding SeaWiFS Chl_SAT matchups; (e–h) bivariate histograms of the global SeaWiFS Chl_SAT climatology vs. climatological DMS from (e) L11, (d) DMS_SAT, (e) SD02 and (f) VS07 algorithms. In (d–h), the correlation coefficient (Pearson's r) between DMS and Chl in each dataset is super-imprinted in white.

Download

3.3 Regional DMS_SAT time series

We selected different regions to test the DMS_SAT algorithm based on the following criteria: the abundance of in situ data (subpolar North Atlantic), the existence of seasonal and multiannual time series (Ocean Station P and BATS station), and the challenges posed by intra- and interannual variability of phytoplankton and DMS(P) in each region.

3.3.1 Subpolar Atlantic and Pacific

We used MODIS-Aqua data to produce a 14-year DMS_SAT time series (and the corresponding climatology) for the Northern Hemisphere at latitudes >45^∘ N. In this regional implementation we used a different set of coefficients, obtained from regression of M5×5 binned data restricted to latitudes >45^∘ N (Eq. 2g, Table 2). These regional coefficients largely corrected the negative bias observed with globally optimized coefficients. In this case, further optimization did not lead to significant improvement. We then sampled the resulting time series in some representative regions: three rectangles with an area of ∼200 000 km² each, located along the 50–56^∘ N band in the North Atlantic, and the Ocean Station P (OSP, 50^∘ N, 145^∘ W) in the NE Pacific.

Figure 8 shows the seasonal cycles of DMS_SAT, DMSPt_SAT and Chl_SAT in selected North Atlantic areas: (a) the deep waters of the northwest Atlantic drift, (b) the shelf break west of Ireland, and (c) the shallow southern North Sea. We observe good agreement between the 14-year DMS_SAT climatology and the L11 climatology, except in the southern North Sea where DMS_SAT is too high through summer and fall. DMS_SAT reproduces well the east–west variation in the temporal lag between the annual peaks of DMS and Chl, with a lag of up to 4 months in the southern North Sea. The most salient result is however the wide interannual variability of the DMS_SAT seasonal cycles. Estimated DMS_SAT concentrations during the productive season vary by up to 3-fold between years (see variability metrics in Fig. 8), and the annual DMS_SAT peak can occur within a temporal window of 2–3 months. Although years with a major peak in spring–summer are the norm, a second peak in late summer is not unusual. Additional validation supports the good performance of DMS_SAT in the subpolar North Atlantic (Fig. S4), lending credit to satellite-determined variability patterns.

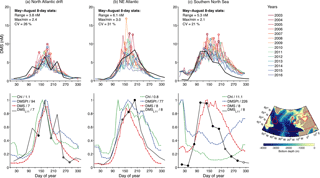
Figure 8Interannual DMS_SAT variability in the subpolar North Atlantic. (a) Northwest Atlantic drift, (b) shelf break west of Ireland, (c) southern North Sea shelf. Top panels show individual years between 2003 and 2016 determined from 8-day MODIS-Aqua data, differentiated by color, and the mean seasonal cycle according to the L11 DMS climatology (black); colored circles mark the peak of each seasonal cycle. Bottom panels show the mean annual cycles of Chl_SAT, DMSPt_SAT, DMS_SAT and the L11 DMS climatology. Each variable is divided by its maximum, shown by the number in the quotient; a common scaling factor is used for DMS_SAT and DMS_L11. Markers on the L11 line indicate the amount of in situ data on which the L11 climatology is based in a given month: no data, i.e., month filled through interpolation (no marker); 1–9 measurements in a single year (empty circles); ≥10 measurements in a single year (crossed circles); and ≥10 measurements distributed in different years (filled black circles). Red polygons on the map show the 3 selected areas and the larger region used for the validation scatter plots (see Fig. S4).

Download

We used the same MODIS-Aqua dataset to analyze the mean seasonal cycle and the interannual variability at OSP (Fig. 9a–c), where DMS has been measured around February, June and August since 1996. DMS_SAT captures in situ DMS concentrations in February and June but suffers from low bias in August. Examination of August measurements during the 2005–2016 period suggests the existence of two regimes: 8 years with in situ DMS of 6.6±1.1 nM, about twice as high as DMS_SAT, and 4 years with in situ DMS of 16.1±4.8 nM, about 6-fold higher than DMS_SAT. Local tuning of Eq. (2) using OSP data could not increase DMS_SAT in August–September without degrading its performance in other months.

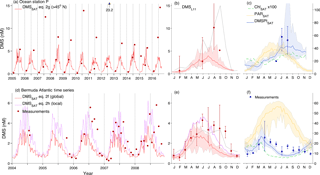
Figure 9DMS_SAT vs. in situ data at long-term research stations. (a–c) Ocean Station P in the northeast Pacific (50^∘ N, 145^∘ W); (d–f) BATS station (31^∘40^′ N, 64^∘10^′ W). (a, d) compare DMS_SAT estimates to in situ measurements; (b, e) compare monthly DMS means (i.e., climatologies) derived from DMS_SAT (2003–2016 MODIS-Aqua data), in situ data (available measurements between 2003–2016) and the L11 climatology; (c, f) show the corresponding Chl_SAT, DMSPt_SAT and PAR_SAT climatologies (2003–2016) and in situ DMSPt. Lines and shaded envelopes show the mean ± range of satellite-derived data; filled circles and error bars show the mean ± range of available in situ data. DMS and DMSPt are in nM units, Chl in µg L⁻¹ and PAR in mol photons ${\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$. In addition to public OSP data (three DMS measurements per year generally available between 2005 and 2016) we show DMSPt data reported in published studies (Asher et al., 2017; Levasseur et al., 2006; Royer et al., 2010). BATS data are comprised of the monthly 2005–2008 time series (Levine et al., 2016) and cruise data from the vicinity of BATS station in July 2004 (Bailey et al., 2008; Gabric et al., 2008).

Download

Finally, note that these time series were calculated using semi-analytical bio-optical products (see section S5). Using the band-ratio Chl algorithm for MODIS (OC3) gave very similar results in deep ocean regions but 70 % higher concentrations in the shallow southern North Sea, possibly due to interference of non-algal materials on OC3 Chl retrieval (data not shown).

4.1 Known sources of error and bias: interpolated climatology vs. DMS_SAT

Global DMS fields estimated by the L11 climatology and by the DMS_SAT algorithm show remarkable geographic differences (Fig. 5), and their mean concentrations differ by a factor of ∼1.5. Particularly, changes in the sign of the DMS_SAT–DMS_L11 anomaly often follow the somewhat artificial boundaries of the Longhurst biogeochemical provinces. As explained below, regional and global biases in L11 arise from the application of objective interpolation procedures to a global dataset characterized by (1) the right-skewed distribution of DMS concentrations (Kettle et al., 1999; Fig. 7), (2) the small amount of monthly data available in many biogeochemical provinces (Fig. 1), (3) the absence of repeat measurements in most oceanic regions (Halloran et al., 2010), (4) the low spatial resolution of most DMS datasets and (5) the preferential sampling of DMS-productive conditions.

A primary drawback for the calculation of interpolated climatologies is the overrepresentation of biologically productive conditions in the sea-surface DMS database. This sampling bias is clearly illustrated by comparing SeaWiFS-retrieved Chl concentration in the global ocean and in the database matchups (Fig. 7a). If we assume that SeaWiFS matchups (N=11 600) represent a random sample of the DMS database (N=41 304), and considering the global positive correlation between Chl and DMS (Fig. 7d), this implies a sampling bias towards high DMS concentrations. The bias is largest when the comparison is restricted to the spring–summer semester of each hemisphere, when the median Chl_SAT is 0.19 in the global SeaWiFS climatology and 0.74 in the DMS database matchups. This is the period when DMS peaks and has more influence on mean annual DMS concentration.

Sampling bias is intertwined with the right-skewed distribution of sea-surface DMS concentrations (Fig. 7b) and the poor spatial resolution of most in situ DMS datasets. Spatial averaging, justified by data scarcity, is appropriate when applied over small or sufficiently homogeneous regions. However, when applied over a large and potentially heterogeneous Longhurst province, it can propagate the sampling bias over the entire province and up to the global scale. As illustrated in Fig. 6g, the mean DMS concentration in M5×5 bins is systematically higher, by 40 % on average, than the corresponding median. Province-level averaging converts the long tail of high in situ DMS concentrations into too-large province means, such that the global mode of DMS_L11 is similar or even higher than that of in situ DMS (Fig. 7b).

The influence of extreme in situ DMS concentrations is maximal in productive regions, where mean∕median ratios of around 4 are observed in M5×5 bins (Fig. 6g). In these regions, sharp productivity gradients and dynamic ecosystem processes complicate the task of sampling DMS through all appropriate scales (Nemcek et al., 2008), suggesting the need to apply finer-scale or dynamic regionalization (Devred et al., 2007) prior to interpolation. Emerging biogeochemical relationships, like that between net community production and DMS observed by Kameyama et al. (2013) in the northeast Pacific, might assist DMS interpolation and determination, but require validation across contrasting regions and relevant scales (Asher et al., 2017). In low-latitude oligotrophic areas where DMS shows reduced spatial variability (Royer et al., 2015), the method used to construct interpolation-based climatologies (Kettle et al., 1999; Lana et al., 2011) seems appropriate regarding spatial resolution.

In the temporal domain, the calculation of interpolated climatologies is complicated by two factors: poor interannual coverage, i.e., the scarcity of DMS measurements repeated in different years in a given region; and poor seasonal coverage, i.e., the scarcity of fully resolved seasonal cycles. Seasonal coverage is limited at the province level (see Table 1 in Lana et al., 2011) and obviously worse in 5^∘ bins (Fig. 1d). Regarding interannual coverage at the MLongh level, 42 % of the province–month bins contain measurements from a single year, 21 % from two years and 37 % from three or more years. Thus, data from one or two years are often assumed representative of the mean ecosystem state in interpolated climatologies, which is probably not the case in regions with wide interannual variability or long-term trends (Vantrepotte and Mélin, 2011). While this does not necessarily bias global DMS fields, it can produce artificial seasonal cycles. For example, L11 suggests the existence of early spring and fall DMS peaks in the North Atlantic drift area, which result from interpolation from neighboring regions (Fig. 8a). In contrast, DMS_SAT suggests these are improbable (spring) or infrequent (fall) features. Another example is found at OSP, where DMS_L11, based on measurements made before 2003, is in poor agreement with measurements made between 2005 and 2016. In February and June, DMS_SAT is in better accordance with in situ DMS data at OSP (Fig. 9a and b).

In summary, caution has to be taken when comparing DMS measurements, their derived climatological products, and independent model estimates that are not collocated in time. This temporal mismatch may partly explain the poor correlation between modeled DMS climatologies, on one hand, and the DMS database and DMS_L11 climatology, on the other (Tesdal et al., 2016). Note that the latter study compared DMS fields binned into monthly $\mathrm{5}{}^{\circ }\times \mathrm{5}{}^{\circ }$ boxes (M5×5), such that 82 % of the bins contained measurements from a single year.

Compared to interpolated climatologies, DMS_SAT provides a robust means to estimate DMS concentrations in sparsely sampled areas because it relies on satellite observations and macroecological relationships. The resulting DMS fields are in better accordance with natural gradients in plankton abundance (biogeography, phenology) and environmental forcing, as long as the models can account for the driving factors, as discussed below.

4.2 Unknown sources of error: how far can we go with remote sensing algorithms?

By testing DMS_SAT in challenging biogeochemical settings (Fig. 9), we identified its main drawback: the failure to reproduce high DMS, and more specifically DMS ∕ DMSPt ratios higher than 0.3, at intermediate PAR levels (Fig. 3), as observed between midsummer and early fall at BATS and OSP in some years. This limitation can hardly be fixed without identifying the underlying biogeochemical processes, which are not necessarily the same in these contrasting biogeochemical regimes. Although this feature is probably not widespread (see Fig. 2 in Lana et al., 2011), its occurrence in emblematic time series stations warrants further discussion.

A common explanation could be the underestimation of irradiance effects, caused by the use of sea-surface PAR_SAT rather than PAR_MLD as DMS predictor variable. For instance, a delay of seasonal mixing, associated with deeper irradiance penetration, could enhance stress-driven DMS production well into fall. Yet examination of the BATS and OSP time series does not support this explanation. At both sites, the summer MLD is stable at about ≤20 m and deepens slowly in late summer (Levine et al., 2016; Steiner et al., 2012), such that PAR_MLD declines faster than sea-surface PAR_SAT (Eq. 1). Thus, using PAR_MLD instead of surface PAR cannot delay the decline of modeled DMS ∕ DMSPt ratios through the summer, and other factors need to be invoked.

In the oligotrophic BATS station, some modeling studies proposed macronutrient limitation of bacteria (Polimene et al., 2011) and also phytoplankton (Belviso et al., 2012) as drivers of the seasonal mismatch between DMSPt and DMS, besides irradiance (Vallina et al., 2008). With this in mind, we tried to factor phosphate and nitrate limitation into our regression models using different variables: nutrient concentrations, nutricline depths (Table S4) and limitation factors estimated according to Michaelis–Menten kinetics (not shown). However, none of the tested variables improved the regression models significantly. Moreover, macronutrient availability (limitation) terms generally entered regression models with positive (negative) coefficients, even when regressions were restricted to oligotrophic low latitudes. This implies that macronutrient limitation of phytoplankton growth globally acts to decrease DMS, offsetting nutrient stress responses that increase DMS. Note also the irregular occurrence of high DMS at the BATS station in late summer in different years (Fig. 9d; Levine et al., 2016), and that a BATS-like seasonality is not observed at other sites with late summer macronutrient limitation (Archer et al., 2009; Belviso et al., 2012; Galí and Simó, 2015; Vila-Costa et al., 2008). Altogether, these observations suggest that regional macronutrient stress responses are difficult to generalize.

Analysis of the OSP time series also yields valuable information because macronutrient concentrations remain at high concentrations in late summer in this iron-limited regime (Harrison et al., 2004). While in situ DMS is accurately estimated by DMS_SAT in February and June, the variable DMS peak occurring around August is strongly underestimated. Previous studies emphasized the role of iron limitation at OSP, which configures phytoplankton communities dominated by high DMSP taxa (Asher et al., 2017; Levasseur et al., 2006; Royer et al., 2010; Steiner et al., 2012). Interestingly, DMSPt_SAT peaks in August at OSP, in phase with the in situ DMS peak and in good accordance with the few available DMSPt measurements (Fig. 9c), even though the DMSPt_SAT sub-algorithm does not explicitly resolve phytoplankton taxonomy (Galí et al., 2015). Therefore, high DMS yields, possibly co-occurring with low DMS removal rate constants (Asher et al., 2017), are required to explain DMS ∕ DMSPt ratios observed at OSP. High DMS yields probably result from a combination of processes, including algal and bacterial DMSP metabolism (Merzouk et al., 2006; Royer et al., 2010) and microzooplankton grazing (Steiner et al., 2012). The striking late summer variability at OSP is presently not captured by biogeochemical models (Steiner et al., 2012) or empirical algorithms, and it remains unanswered whether it simply reflects too low sampling frequency, or it is caused by processes that switch on/off depending on environmental conditions in a given year, or by the variable location of oceanic fronts in response to circulation patterns.

In summary, our analysis indicates that additional factors are needed to better reproduce DMS seasonality in specific regions, where DMS ∕ DMSPt ratios are occasionally higher than the “baseline” established by Eq. (2) (Figs. 3 and 9). Biotic interactions involving phytoplankton, bacteria and microzooplankton, regionally interacting with iron and macronutrient limitation in multiple ways, are good candidates to explain strong deviations from the mean relationship between DMS, DMSPt and irradiance. However, they can hardly be represented in empirical algorithms with our current level of understanding, particularly when interannual changes are considered (Figs. 8 and 9).

From a practical standpoint, tuning the Eq. (2) coefficients is a workable alternative in certain regions (Figs. 8 and 9). If sufficient measurements were available in all oceanic areas, Eq. (2) could perhaps be generalized in a way that allows its coefficients to vary across different biogeochemical regimes, while avoiding geographic discontinuities. The inclusion of additional terms in Eq. (2) lacks strong statistical support when applied globally, at least with the current dataset (Table S4). If posterior analyses supported the addition of new satellite variables, their retrieval uncertainty and its propagation to DMS_SAT should be considered. More obviously, climatological variables such as the WOA nutrient concentrations are not appropriate to produce time series, and their use in remote sensing algorithms should be minimized. The only climatological variable used in our algorithm is MLD, which enters mainly as a categorical variable (Galí et al., 2015), such that DMSPt_SAT is robust to MLD uncertainties (Fig. S1).

The question of the “optimal model complexity” is a pervasive one in biogeochemistry, and the right answer may depend on the purpose of each study. The algorithms tested here showed improved qualitative and quantitative performance with increasing complexity (VS07 < SD02 <DMS_SAT). VS07 failed to capture DMS patterns outside the subtropical band, possibly due to its inability to modulate the DMS–irradiance relationship depending on phytoplankton biomass. Inclusion of phytoplankton biomass-dependent terms in SD02, and of implicit taxonomic information through the embedded DMSPt_SAT sub-algorithm in DMS_SAT, improved algorithm skill in productive regions, where DMS shows wider seasonal cycles and sharper spatial gradients.

More sophisticated approaches may be needed to achieve significant improvements in model skill, but they also suffer from major uncertainties. For example, neural networks were successfully used to estimate DMS in the Arctic (Humphries et al., 2012), but their robustness might be compromised by the small training datasets, the use of climatological variables and the lack of a mechanistic basis. Complex biogeochemical models with satellite data assimilation have strong potential for resolving interannual DMS variations, but reliance on several tens of poorly constrained parameters currently limits their skill (Le Clainche et al., 2010; Galí and Simó, 2015; Tesdal et al., 2016). An approach of intermediate complexity that deserves further exploration is DMS diagnosis based on a simplified steady-state budget equation (Galí and Simó, 2015). Applying empirical parameterizations for the main DMS production and removal pathways, this approach could enhance the flexibility of remote sensing algorithms across a wider range of biogeochemical settings.