the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Landscape analysis of soil methane flux across complex terrain
Kendra E. Kaiser
Brian L. McGlynn
John E. Dore
Relationships between methane (CH4) fluxes and environmental conditions have been extensively explored in saturated soils, while research has been less prevalent in aerated soils because of the relatively small magnitudes of CH4 fluxes that occur in dry soils. Our study builds on previous carbon cycle research at Tenderfoot Creek Experimental Forest, Montana, to identify how environmental conditions reflected by topographic metrics can be leveraged to estimate watershed scale CH4 fluxes from point scale measurements. Here, we measured soil CH4 concentrations and fluxes across a range of landscape positions (7 riparian, 25 upland), utilizing topographic and seasonal (29 May–12 September) gradients to examine the relationships between environmental variables, hydrologic dynamics, and CH4 emission and uptake. Riparian areas emitted small fluxes of CH4 throughout the study (median: 0.186 µg CH4–C m−2 h−1) and uplands increased in sink strength with dry-down of the watershed (median: −22.9 µg CH4–C m−2 h−1). Locations with volumetric water content (VWC) below 38 % were methane sinks, and uptake increased with decreasing VWC. Above 43 % VWC, net CH4 efflux occurred, and at intermediate VWC net fluxes were near zero. Riparian sites had near-neutral cumulative seasonal flux, and cumulative uptake of CH4 in the uplands was significantly related to topographic indices. These relationships were used to model the net seasonal CH4 flux of the upper Stringer Creek watershed (−1.75 kg CH4–C ha−1). This spatially distributed estimate was 111 % larger than that obtained by simply extrapolating the mean CH4 flux to the entire watershed area. Our results highlight the importance of quantifying the space–time variability of net CH4 fluxes as predicted by the frequency distribution of landscape positions when assessing watershed scale greenhouse gas balances.
Considerable effort has been directed to the study of carbon dioxide (CO2) fluxes in a variety of diverse terrestrial ecosystems using both spatially distributed chamber measurements and eddy covariance methods (e.g., Lavigne et al., 1997; Sotta et al., 2004; Webster et al., 2008; Riveros-Iregui and McGlynn, 2009; Allaire et al., 2012). However, challenges associated with measuring upland methane (CH4) fluxes (Denmead, 2008; Wolf et al., 2011) have made similar studies less prevalent, despite CH4 being a more potent greenhouse gas (GHG) than CO2. Global CH4 emissions have increased by 47 % since 1970 (IPCC, 2014), and though the soil CH4 sink is significantly smaller than its chemical oxidation in the atmosphere, the uncertainty in the size of the soil CH4 sink is on par with the annual atmospheric CH4 growth rate (Kirschke et al., 2013). Despite progress in our understanding of CH4 dynamics in saturated soils, assessing the variability of CH4 fluxes in aerated soils and exploring how landscape structure influences CH4 fluxes and watershed CH4 budgets have been limited. Topography can create predictable physical redistribution of resources across a landscape, suggesting that these patterns (e.g., soil moisture: Western et al., 1999; temperature: Urban et al., 2000; Emanuel et al., 2010; soil organic matter and nutrients: Creed et al., 2002; Mengistu et al., 2014) could produce observable landscape patterns in soil C fluxes (Webster et al., 2008; Riveros-Iregui and McGlynn, 2009; Pacific et al., 2011).
Net soil CH4 flux can be highly variable in space and time, particularly because microbial production and consumption of CH4 can occur simultaneously in the soil profile. Methane is predominantly consumed in aerated upland soils and produced in saturated or nearly saturated riparian soils. Methanogenesis occurs under anoxic conditions and at low redox potential through two major microbial pathways (CO2 reduction and acetate fermentation) (Hanson and Hanson, 1996; Le Mer et al., 2001). Under aerobic conditions, methanotrophic bacteria oxidize CH4 to CO2, but anaerobic oxidation of methane (AOM) can also occur in a variety of environments, including forest soils (e.g., Blazewicz et al., 2012; Gauthier et al., 2015). The interactions of local thermodynamics and environmental conditions – including soil moisture, temperature, substrate availability, pH, and oxygen status – have made it difficult to determine the most influential parameters across ecosystems (e.g., temperate forest, desert: Luo et al., 2013). In addition, the environmental factors that create the observed heterogeneity of CH4 fluxes can be influenced by the spatial scale of analysis. For example, the microbial dynamics that drive CH4 cycling are influenced by small-scale (centimeter) environmental conditions (e.g., substrate availability and redox state) (Born et al., 1990; Conrad, 1996). However, at larger scales these environmental conditions can be heavily influenced by physical processes such as landscape scale (kilometer) hydrology (Burt and Pinay, 2005; Lohse et al., 2009), and at still larger scales (hundreds of kilometers, which we will refer to as “ecosystem scale”) parent material and climate create the setting in which these processes occur (Potter et al., 1996; Tang et al., 2006; Tian et al., 2010).
A spatially explicit understanding of heterogeneity in CH4 fluxes is necessary for appropriate watershed scale budgets (Ullah and Moore, 2011; Bernhardt et al., 2017), particularly in mountainous regions, where the spatial distribution of resources could have a significant influence on the direction and magnitude of CH4 fluxes due to the lateral redistribution of water and substrates caused by convergent and divergent areas of the landscape (Davidson and Swank, 1986; Meixner and Eugster, 1999; Wachinger et al., 2000; von Fischer and Hedin, 2002). Although many studies have quantified the magnitude and variability of CH4 fluxes, they often covered large spatial extents (from transects that are tens of meters to hundreds of kilometers long) which captured significant environmental gradients at those scales, but sampling locations were generally sparse (Del Grosso et al., 2000; Dalal and Allen, 2008; Yu et al., 2008; Teh et al., 2014; Tian et al., 2014). The smaller-scale patterns of CH4 fluxes within these landscapes has not been investigated as thoroughly as ecosystem scale gradients, which could be problematic if those patterns are important for estimating CH4 fluxes (Fiedler and Sommer, 2000; Ullah and Moore, 2011; Nicolini et al., 2013).
Functional landscape elements have proven useful for assessing spatial heterogeneity and influences of scale in hydrology (Wood et al., 1988), ecology (Forman and Godron, 1981), and biogeochemistry (Corre et al., 1996; Reynolds and Wu, 1999). Functional landscape elements and terrain metrics that represent topographically driven hydrologic gradients have been used to analyze and scale biogeochemical cycles (e.g., carbon: Creed et al., 2002; Riveros-Iregui and McGlynn, 2009; Pacific et al., 2011; nitrogen: Hedin et al., 1998b; Creed and Beall, 2009; Duncan et al., 2013; Anderson et al., 2015; phosphorus: Devito et al., 2000; sulfate: Welsch et al., 2004), but limited analogous work has been done for CH4 consumption. The importance of soil moisture in mediating CH4 fluxes has been shown across ecosystems (Smith et al., 2000; von Fischer and Hedin, 2007), but studies of how this influence is related to, or predictable from, landscape characteristics have been limited (Boeckx et al., 1997; Creed et al., 2013). Continuous topographic metrics such as the topographic wetness index (TWI, a surrogate for water accumulation) could represent hydrologic influences on variables relevant for CH4 fluxes (e.g., redox state, diffusivity of CH4 and O2, and substrate availability). Here, we build on previous research from Tenderfoot Creek Experimental Forest (TCEF) that has demonstrated how topographic metrics can represent landscape structure and its influence on hydrologic processes (Jencso et al., 2009; Jencso and McGlynn, 2011) and carbon cycling (Riveros-Iregui and McGlynn, 2009; Pacific et al., 2010, 2011). Our objectives were to determine how locally and distally mediated environmental conditions influence CH4 fluxes, and to estimate the net seasonal CH4 balance of the upper Stringer Creek watershed. Spatially distributed measures of soil moisture, groundwater elevation, and landscape position provide the opportunity to investigate spatial patterns of CH4 fluxes, linking the point scale conditions to watershed scale hydrologic patterns. We suggest these approaches are beneficial for interpolating, scaling, and predicting CH4 dynamics, particularly in complex terrain. We address the following questions to assess spatial and temporal dynamics of CH4 fluxes across this semi-arid, subalpine landscape; examine environmental relationships; and estimate net watershed balances:
-
How do environmental variables relate to CH4 flux across a subalpine watershed through the growing season?
-
How does landscape structure relate to relative magnitude and direction of CH4 fluxes across the landscape?
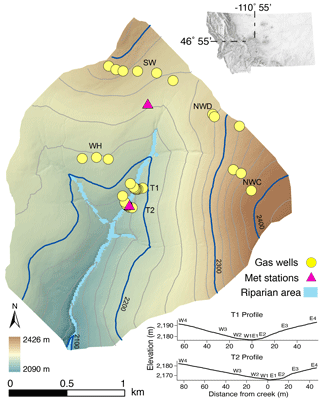
Figure 1Map of upper Stringer Creek watershed (394 ha), located in central Montana, showing sampling locations and meteorological towers. Inset shows profiles of transects T1 and T2, where site number increases away from the creek on the west and east sides.
2.1 Site description
Tenderfoot Creek Experimental Forest (46.55∘ N, 110.52∘ W) is located in the Little Belt Mountains of central Montana (Fig. 1). This study was conducted in the upper Stringer Creek watershed (394 ha; elevation 2090–2425 m), a sub-watershed of TCEF. The gentle to steep gradient slopes (average: 15 %) and the range of aspect and topographic convergence/divergence in upper Stringer Creek are characteristic of the greater Tenderfoot Creek watershed (Jencso et al., 2009).
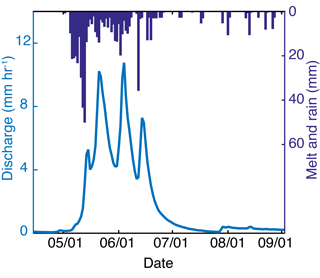
The watershed experiences a continental climate, with 70 % of the 800 mm annual precipitation typically falling as snow from November to May. Growing season length ranges from 45 to 70 days (Schmidt and Friede, 1996), and mean daily summer temperature is 11 ∘C (Farnes et al., 1995). Peak snowmelt typically occurs between mid-May and mid-June, and the driest months occur in the late summer and fall (Fig. 2). Summer precipitation rarely causes significant streamflow response (Nippgen et al., 2011).
The geology of the Stringer Creek watershed is comprised of Flathead sandstone, Wolsey shale, and granite gneiss. Soils are shallow (< 1 m) typic cryocrepts in the uplands and aquic cryobalfs in the riparian areas. The seasonal dry-down of the upland soils vs. the riparian areas (which typically maintain a shallow water table throughout the year; Jencso et al., 2009) reflects the differentiation in soil types. Upland soils have a sandy loam texture but vary in rock and organic matter content across landscape positions.
Plant communities transition from wet riparian meadows in the valley bottom through drier meadows to the upland conifer forest. The vegetation in the riparian area is predominately grasses (Juncus, Carex, Poa) and willows (Salix) with a mixture of wildflowers (Erigeron, Aster). The forest is primarily comprised of lodgepole pine (Pinus contorta) and subalpine fir (Abies lasiocarpa); Englemann spruce (Picea engelmannii) and whitebark pine (Pinus albicaulis) are also common; and grouse whortleberry (Vaccinium scoparium) is dominant in the understory (Mincemoyer and Birdsall, 2006).
2.2 Landscape characterization
Ten-meter and 3 m digital elevation models (DEMs) were constructed by coarsening 1 m2 resolution light detection and ranging (lidar) data. These data were collected in 2005 by the National Center for Airborne Laser Mapping (NCALM). We calculated topographic characteristics that describe both energy availability and relative water availability of each site using DEM landscape analysis methods as described in McGlynn and Seibert (2003). Terrain metrics included in the analysis were aspect (radians), elevation (m), insolation (kWh m−2), slope (%), elevation above the creek (EAC, m), distance from creek (DFC, m), gradient to creek (GTC), upslope accumulated area (UAA, m2), and the TWI (Jencso and McGlynn, 2011; Nippgen et al., 2011). Aspect and position-on-slope effects were calculated using the following vector of covariates (Clark, 1990):
where ϕ is aspect and θ is percent slope. Potential incoming insolation (from 1 May to 1 September) was calculated in the System for Automated Geoscientific Analyses (SAGA) using 1 h increments averaged over 5-day windows (Böhner and Antonic, 2009). UAA is the watershed area contributing to each point in the landscape and was derived using the MD∞ algorithm (Seibert and McGlynn, 2007). TWI has also been used as an approximation for relative wetness and was calculated using the following equation (Beven and Kirkby, 1978):
where a is UAA and θ is local slope. All topographic metrics were assessed for relationships with CH4 and for inclusion in the multivariate model. The riparian area was initially delineated as the area less than 2 m in elevation above the creek using topographically derived flow paths and validated with extensive field surveys (90 transects; Jencso et al., 2010).
We examined the spatial and temporal variability of CH4 fluxes using data collected across a range of landscape positions in the Stringer Creek watershed. Terrain metrics were used to select 32 sampling sites that span a range of slopes, contributing area, and convergence/divergence in the upper Stringer Creek watershed (Fig. 1). Twenty-five sites were distributed across the uplands, and two transects that cross Stringer creek (with three to four riparian sites each) were selected to characterize the riparian and lower hillslope positions and their transition. The transition zone between the riparian area and the uplands is identified hydrologically as the toe slope position where groundwater tables persist longer than in the uplands but not through the growing season as observed in the riparian area. Measurement sites along the two transects that cross the creek are identified by the side of the creek they are on (east/west) and increase in number away from the creek.
2.3 Soil characterization measurements
Soil cores were collected on 8 and 9 July 2012 within 2 m of each gas sampling site for soil analysis. Soil cores were extracted using a 100 cm3 cylinder that was inserted into the soil, and they were laterally excavated from the organic (0–10 cm) and mineral (22.5–27.5 and 47.5–52.5 cm) soil layers (n= 32 sites). The samples were dried and weighed to calculate bulk density and were analyzed for % carbon (C) and % nitrogen (N), ∂13C, and ∂15N (Kansas State Stable Isotope Mass Spectrometry Laboratory, Thermo Finnigan Delta Plus mass spectrometer and CE 1110 elemental analyzer with ConFlo II Universal Interface for C and N analysis of solids; additional details in Nippert et al., 2013). These data were used to calculate total Csoil (mg cm−3), Nsoil (mg cm−3), and molar C : N ratios. Intact soil cores and bulk soil samples were also collected from 0 to 5 cm on 6 and 7 August 2014 to determine porosity, bulk density, mineral bulk density, and organic content for each site. Porosity was determined by measuring the change in weight between fully saturated and oven-dried intact soil cores (n= 18). The bulk samples were used to corroborate bulk density and particle size distribution following standard procedures.
2.4 Environmental measurements
Weekly measurements of environmental variables were collected in conjunction with gas samples at each site from May to September 2013 between 09:00 and 18:00 UTC. Environmental variables that were measured included volumetric soil water content (VWC), soil temperature (12 cm soil thermometer, Reotemp Instrument Corporation, CA, USA), and barometric pressure (Atmospheric Data Center Pro, Brunton, Boulder, CO, USA). VWC was measured three times at each site during each round of sampling using a Hydrosense II portable soil water content meter (12 cm, Campbell Scientific Inc., UT, USA). The mean of the three samples was used for data analysis. We measured real-time water content hourly at individual riparian (T1E1), transition (T1E2), and hillslope (T1E3) sites using water content probes (CSI model 616, Campbell Scientific Inc., UT, USA) that were inserted from 0 to 12 cm in the soil (Fig. 1).
2.5 Hydrological measurements
Groundwater table data were recorded in wells located along the two riparian–hillslope transects to augment the weekly measurements of near-surface soil water content (Fig. 1). Groundwater wells (created from 3.81 cm diameter polyvinyl chloride (PVC), screened from completion depth to within 10 cm of ground surface) were installed along the riparian–hillslope transects (co-located with gas wells). Capacitance rods (±1 mm, Tru Track, Inc., New Zealand) in each well recorded groundwater level every 30 min. Well completion depths (to the soil bedrock interface) ranged from 0.5 to 1 m in the riparian zones and from 0.8 to 1.5 m on the hillslopes. Installation details can be found in Jencso et al. (2009). Groundwater data were also used to evaluate our initial delineation of sites as riparian vs. upland.
2.6 Soil gas measurements and flux calculations
Soil gas wells constructed of 5.25 cm diameter, 15 cm long sections of PVC were installed to sample soil air for concentration measurements of CH4, CO2, and O2 at 5, 20, and 50 cm depths. Gas wells were buried at completion depths of 20 and 50 cm and capped with a size 11 rubber stopper. These gas wells were open at the bottom to equilibrate with soil gas at their respective depths. Shallow gas wells were designed to measure gas concentrations closer to the soil surface; the bottoms were closed with a PVC cap, and screened openings on the sides enabled equilibration with soil gas at 5 cm depth. All gas wells were outfitted with a closed sampling loop made of PVC tubing (4.8 mm inside diameter, Nalgene 180 clear PVC, Nalgene Nunc International, Rochester, NY, USA) that was passed through the rubber stopper and joined above the ground surface by 6–8 mm HDPE tubing connectors (FisherBrand, Fisher Scientific, USA). Thus, the equilibrium volume was the volume of the PVC well plus that of the tubing.
Weekly gas samples were taken from the closed recirculation loop after observed soil CO2 concentration stabilized. Soil CO2 concentration was measured in-line using a Vaisala Carbocap handheld CO2 meter (GM70, measurement range of either 0–20 000 ppmv or 0–50 000 ppmv) adjusted for local temperature and pressure. Soil % O2 was also measured in-line using a handheld Apogee O2 sensor (MO-200, Logan, UT, USA; precision: ±0.1 % O2). Once the CO2 concentration reading stabilized, one gas sample was collected from each depth through a brass Swagelok T fitting with a 9.5 mm Cole-Parmer septum (Vernon, IL, USA) sampling port, using a PrecisionGlide needle (22G1, Becton Dickinson & Co, NJ, USA) and 60 mL Luer-Lok syringe (BD, Franklin Lakes, NJ, USA). Gas samples (∼ 50 mL) were transferred to and stored in 150 mL laminated FlexFoil sample bags (SKC, Eighty Four, PA, USA). Prior to sample collection in the field, sample bags were emptied by vacuum, filled with N2 carrier gas, and evacuated in the lab to avoid sample contamination. This process was done twice for bags that had previously contained gas with concentrations of CH4 considerably higher than ambient. The sampling syringe was cleared between samples and flushed with 10 mL of air from the gas well three times before slowly taking the sample (to avoid creating any vacuum in the gas well). During snowmelt, saturated soils in the riparian area resulted in flooded wells, preventing gas sampling at those time points.
Gas samples were analyzed for CH4 at Montana State University using a Hewlett-Packard 5890 Series II gas chromatograph outfitted with a flame ionization detector (FID). The inlet system used a 10-port injection valve with a 1 cm3 sample loop. The injection valve was configured for backflushing of a precolumn (25 cm × 0.32 cm OD, packed with Porapak T 80/100 mesh) to prevent water vapor from reaching the analytical column. The sample loop temperature (ambient) was monitored using a NIST-traceable electronic thermometer, and barometric pressure was obtained from the Montana State University weather station (operated by Dr. Joseph A. Shaw). Two analytical columns (both 183 cm × 0.32 cm OD, one packed with Chromosorb 102 80/100 mesh and the other with Porapak-Q 80/100 mesh) were used in series for gas separation. The temperatures of the column oven and FID were 55 and 240 ∘C, respectively. The carrier gas was a commercial ultra-high-purity N2, which was further purified through Molecular Sieve 5A, activated charcoal, and an oxygen scrubber. The carrier flow to the FID was maintained at approximately 30 mL min−1. Under these conditions, CH4 eluted to the FID at 1.9 min. A certified 51 ppmv CH4 in air standard (Air Liquide; ±1 % accuracy) was used for instrument calibration, both alone and after dilution into ultra-high-purity N2 carrier gas; the detector response was linear, and the overall analytical precision was better than ±0.05 ppmv.
Methane fluxes were calculated using the gradient method (Fick's first law) and measured soil concentrations at 5 cm (Eq. 3).
where is the flux of CH4 out of the soil (µg CH4- C m−2 h−1), is the CH4 effective diffusivity (m2 h−1), and (d[CH4]) ∕ dz is the CH4 gradient from 0.05 m to the soil surface (µg CH4–C m−4; the distance from the soil surface, z (m), is defined as positive upward). For determination of (d[CH4]) ∕ dz , measured mole fractions of CH4 were converted to mass concentrations assuming ideality of gases and using the measured soil temperature. Although this formulation does not include production or consumption that is occurring between 5 cm and the surface, the CH4 concentration gradient from shallow depths to the surface is typically relatively linear (Koschorreck and Conrad, 1993), suggesting that determining using a linear equation is appropriate. Effective diffusivity was estimated for each sample using an empirical relationship between the measured VWC and the ratio of CH4 diffusivity to its value in free air at measured temperature and barometric pressure (Massman et al., 1998). This relationship (Fig. 3) was established by measuring methane flux and concentrations across a variety of spatial locations (co-located with gas wells) and time points using a LI-COR 8100A infrared gas analyzer with a 20 cm diameter chamber and an in-line sampling port for collecting discrete time-course CH4 samples from the chamber. Our exponential model relating effective CH4 diffusivity to soil water content is mathematically equivalent to an exponential fit of diffusivity to air-filled pore space (Richter et al., 1991) when total porosity is treated as a constant. Our model results were in good agreement with other commonly used physical models of soil gas diffusion for total porosities near 0.6 (Buckingham, 1904; Ghanbarian and Hunt, 2014; Møldrup et al., 2014) and incorporate site-to-site variability due to local VWC. We calculated cumulative seasonal CH4 flux ( for each site by summing the linearly interpolated daily fluxes (29 May–12 September). We believe that this parsimonious approach is appropriate to assess how landscape position influences the relative magnitude of seasonal CH4 fluxes.
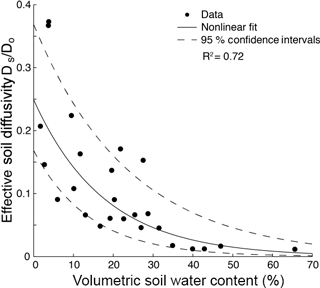
Figure 3Relationship between effective soil diffusivity for methane Ds (expressed relative to its free-air diffusivity Do) and soil water content. This empirical relationship was used to estimate 0–5 cm soil CH4 diffusivity for every sampling event at each site.
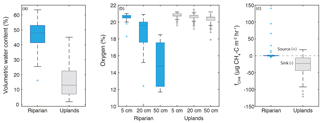
Figure 4(a) Riparian and upland soil water content. (b) Percent oxygen of riparian and upland landscape positions at 5, 20, and 50 cm. (c) Methane flux in riparian and upland landscape positions. Riparian and upland sample sets were significantly different for all sets of data except for the 5 cm O2 data (two-sample t test p < 0.01). Riparian measurements n= 53; upland measurements n= 259. Boxes denote 25th, 50th, and 75th percentiles; whiskers represent maximum and minimum values; and crosses denote outliers (greater than 75th percentile times interquartile range, or less than 25th percentile times interquartile range).
2.7 Statistics and modeling
We used two-sample t tests to test for differences between and environmental variables across riparian and upland locations. We performed linear regression analysis on the upland CH4 fluxes to assess relationships between instantaneous upland and environmental variables using the R Stats Package (R Core Team, 2016). Further linear regression analysis was performed on natural log-transformed cumulative CH4 influx (ln vs. all terrain metrics, soil properties, and each site's average VWC (VWCavg) and temperature (Tavg). We log-transformed the absolute value of to meet linear regression assumptions of homoscedasticity and linearity.
We assessed two sets of predictor variables for multiple-regression modeling: (1) both terrain metrics and local soil measurements (VWCavg, Tavg, and soil properties) and (2) only terrain metrics. We subset the predictor variables to prevent multicollinearity in the final model. If a set of topographic or soil variables had a Pearson's correlation coefficient greater than 0.6 (Dorman et al., 2013), the variable with a lower correlation with ln was removed from the multiple-regression analysis (Fig. A1 and A2). We also assessed the strength of local soil measurements independent of the multiple-regression models to determine which local variables were of most importance. A parameter jack-knife method (Phillips, 2006, 2008) was used to determine the importance of individual variables within each set of data (Fig. A4). We used the Leaps package and the exhaustive search method (Lumley and Miller, 2009) to select the best linear multiple-regression model using terrain metrics and local measurements, and terrain metrics alone in order to create a spatially distributed estimate of ln. Model assessment was based on the adjusted r2 and Bayesian information criterion (BIC; see Sect. 3.5). Given the necessity of using the same dataset to select predictor variables that were used to create the model, we performed a leave-one-out cross validation (LOOCV) using the DAAG package (Maindonald and Braun, 2015) to determine the mean square error of each model.
3.1 Terrain analysis
Terrain analysis was performed using both 3 and 10 m DEMs, and although higher-resolution mapping can be beneficial in some scenarios, the 10 m flow accumulation results have been shown to be more reflective of the lateral transport of water in TCEF and were used in this analysis (Jencso et al., 2009). The slopes in the upper Stringer Creek watershed range from moderate (2 %) to steep (66 %). Sampling sites encompassed the range of aspects in the watershed (72–312∘); however the range of potential incoming solar radiation was relatively narrow over the growing season (1026–1141 kWh m−2). Our site selection spanned a range of landscape hydrologic settings with UAAs ranging from 318 m2 to 10 667 m2 in the uplands, with one site representing a less frequent but much higher UAA (22 981 m2). This site was removed from upland regression analysis due to the strong leverage it had on observed relationships. Riparian sites were not characterized by the 10 m2 DEM due to their relatively small extent (less than the grid size) and challenges associated with discerning between down-hillslope and down-valley flow accumulation. A threshold of 2 m in EAC was used to identify riparian areas (Jencso et al., 2009) and was consistent with field observations for five of seven riparian gas well nests. One site (T2W3), located 40 m away from the creek (4.5 m EAC), was heavily influenced by the large upstream riparian extent and gentle local slope, which resulted in it maintaining a groundwater table and high soil water content throughout the season, characteristic of riparian sites. Alternatively, a sampling site that was located within the EAC delineated riparian area (T2W2 1.5 m EAC, 15 m away) no longer had a groundwater table present by late July and had a steady decline in soil water content, which is characteristic of hillslope locations. The hydrologic dynamics of these sites suggested that their CH4 dynamics could be better characterized by categorizing them based on hydrologic measurements rather than the simple terrain analysis.
3.2 Range and seasonality of environmental variables
Soil molar C : N ratios ranged from 13 to 43 in the shallow soil samples (0–5 cm). Average bulk density was 0.64 g cm−3 at riparian sites (n= 7) and 0.75 g cm−3 in the uplands (n= 25; Table 1). Average soil porosity in the riparian area (0.76; n= 6) was significantly higher (two-sample t test, p < 0.05) than average soil porosity of the uplands (0.65; n= 12) and agreed well with the estimated landscape-average soil porosity of ∼ 0.6 implicated by the exponential VWC–diffusivity relationship (Fig. 3).
Soil temperatures ranged from 0 to 8 ∘C across all sampling sites during the first sampling event on 23 May 2013 and reached the seasonal maximum soil temperature (9–20 ∘C) by mid-July. Soil temperatures declined through August with seasonally intermediate temperatures by 12 September (8–15 ∘C). The average soil temperature in the riparian area (11.5 ∘C) was higher than that of the upland soils (10.6 ∘C), likely due to minimal canopy cover and thus higher insolation in the riparian corridor.
VWC had a strong seasonal pattern and was significantly different between riparian and upland landscape positions (two-sample t test, p < 0.001; Fig. 4a), as shown by real-time water content probes and spatially distributed VWC measurements (Fig. 5). VWC reached a minimum (2–12 % in the uplands and 25–55 % in the riparian area) in late July prior to a sequence of late-season rain events that increased the range of VWC in the uplands to 3–21 % and the riparian area to 29–59 %.
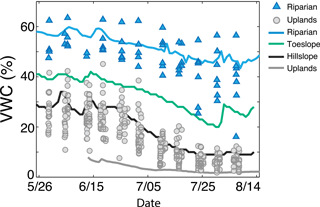
Figure 5Real-time water content sensors (solid lines) that were distributed across landscape positions during the growing season of 2013 show the seasonal dry-down of the landscape, with a muted signal in the riparian area. These high-frequency sensor data corroborate the distributed volumetric water content (VWC) measurements made at every site during discrete sampling (filled symbols). Riparian sites increase in variability throughout the season, and hillslope positions gradually dry down to low soil moisture conditions.
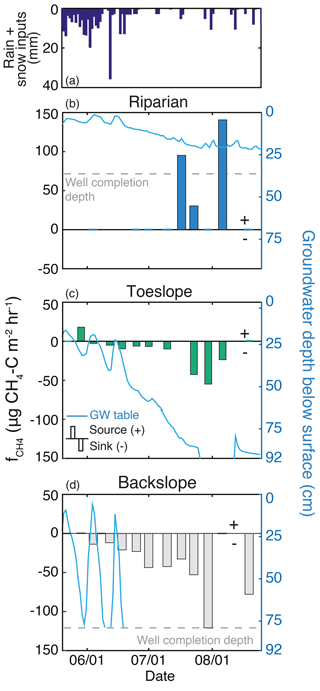
Figure 6Methane dynamics and the seasonal decline of the groundwater (GW) table at three sites located along a riparian–hillslope transect during the 2013 growing season. (a) Rain and snow inputs for the season. (b) The riparian GW table remained in the soil zone throughout the season, and this location (T1E1) was a source of CH4. (c) The toe slope position (T1E2) GW table dropped below the soil zone in late July but recovered after a late-season rain event. Early in the season, this landscape position produced CH4 but gradually increased CH4 uptake as the GW table declined. (d) The backslope (T1E3) GW table dropped below the soil zone in late June and was a CH4 sink the entire season, with maximum uptake at the end of July.
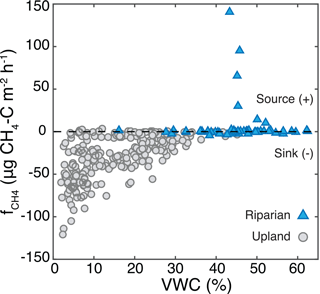
Figure 7Measurements of CH4 flux () and soil water content across all 32 sites for all sampling dates. Magnitude of in the riparian area was not related to VWC, while magnitude and variability of CH4 uptake in the uplands increased with decreasing VWC.
Groundwater (GW) table dynamics can be described by three general responses that were related to proximity to the creek (Fig. 6). Riparian locations maintained a GW table throughout the season, with near-surface saturation during snowmelt, and GW tables 20–50 cm below the soil surface late in the season. GW wells closest to the stream (T1E1 and T1W1) had a water table within 22–25 cm of the surface throughout the season. Toe slope positions (near the strong break in slope on the east side) responded rapidly to snowmelt, and retained a GW table through late July. Wells in this transition zone (e.g., T1E2, Fig. 6c) had variable GW dynamics, which included GW response to the rain events (up to 11 mm) in the first week of August. At another transition location, a well that was influenced by the large local riparian extent and low local gradient (T2W3) maintained a GW table within 70 cm of the surface throughout the season. Upland positions above the break in slope exhibited transient GW tables during peak snowmelt, and by mid- to late June no longer had GW tables present. During snowmelt these wells had a GW table for up to 28 days, and no wells had a GW table after 26 June.
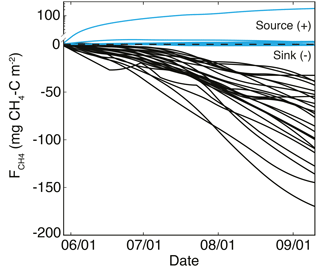
Figure 8Cumulative CH4 flux () for each site, riparian in blue and uplands in black. Most riparian sites were near neutral, with one location being a source; all upland locations were CH4 sinks.
The shallow soil was well oxygenated; in the uplands 5 cm O2 ranged from 19.6 to 21.2 %, and 5 cm riparian O2 ranged from 18.3 to 21.0 % in the soil atmosphere (Fig. 4b). Upland soils were well oxygenated across all sites and depths (19.2–21.5 % O2 at 20 cm, 17.9–21.2 % O2 at 50 cm; Fig. 4b). The only substantial depletion of O2 was in the 20 and 50 cm samples in the riparian area, which ranged from 10.2 to 20.9 % O2 at 20 cm and from 11.7 to 18.5 % O2 at 50 cm (Fig. 4). Median O2 of riparian sites decreased from 20.5 % at 5 cm to 18.2 % at 20 cm and 16.7 % at 50 cm.
Methane fluxes () exhibited a considerable range across the landscape (−121 to 141 µg CH4–C m−2 h−1; Fig. 4, Table 2), with significantly different between the riparian and upland positions (two-sample t test, p < 0.001). Riparian CH4 efflux was generally low, and the upland positions were predominately sinks (Table 2). Upland locations did produce small CH4 fluxes out of the soil (up to 3.5 µg CH4–C m−2 h−1) early in the season.
3.3 Environmental influences on measured CH4 fluxes
Net CH4 uptake was largest in dry soils, and a transition to net emission occurred around 38–43 % VWC (Fig. 7). Upland was significantly correlated with VWC (r2= 0.36, p < 0.001), and the variability in magnitude of CH4 uptake increased with decreasing VWC. Although soil CH4 concentrations were not correlated with VWC, the influence of VWC on diffusivity was associated with a significant relationship between upland and VWC. Maximum efflux occurred at 43 % VWC, and maximum uptake occurred at 4.7 % VWC. At low VWC substantial into the soil occurred. Efflux out of the soil occurred at high VWC (∼ 40–50 %), and near-net-zero was measured through the full range of VWC (1.4–64 %; Fig. 7).
Methane fluxes were not significantly correlated with % O2 at any depth, nor with soil temperature (Fig. A3). CH4 uptake was constrained to samples with 5 cm O2 above 19 % and generally increased with increasing 5 cm % O2, with the largest between 20 and 21 % O2 (i.e., at approximate atmospheric levels). CH4 efflux occurred even when 5 cm O2 was 21 % and up to 19.5 % O2 at 20 cm. The largest (either into or out of the soil) occurred between 8 and 14 ∘C, and declined with higher or lower temperatures.
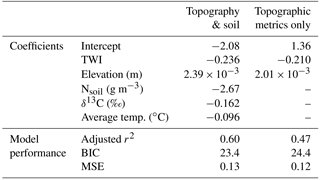
Table 3Coefficients of the parameters used to model cumulative seasonal influx (ln, and statistical measures of model performance (all p < 0.01 ). MSE is the mean square error calculated from the leave-one-out cross validation (Methods Sect. 4.8). TWI is unitless, and aspect is scaled from 0 to 1. Model types are differentiated by the inclusion of soil data to show how the lack of soil data in a spatially distributed estimate of upland ln decreases goodness of model fit.
3.4 Cumulative seasonal CH4 fluxes and relationships to environmental variables and landscape position
Cumulative seasonal CH4 fluxes () ranged from −170 to −33 mg CH4–C m−2 in the uplands and from −0.98 to 3.12 mg CH4–C m−2 in the riparian sites, with one riparian location producing a relatively large of 232 mg CH4–C m−2 (Fig. 8). Rates of upland consumption generally increased through the season and were consistent across sites until July when cumulative fluxes began to diverge (Fig. 8). Although most environmental variables (bulk density, C : N, Csoil, Nsoil, Tavg, ∂13C, and ∂15N) were not significantly correlated with ln, the average VWC of each site was negatively correlated with ln (r2= 0.32, p < 0.01).
We assessed the degree to which terrain metrics were correlated with environmental variables and in order to understand how the characteristics of a given landscape position could influence environmental variables and resulting total seasonal CH4 fluxes (cumulative fluxes). Relationships between ln and terrain metrics were stronger with the 10 m DEM than the 3 m DEM; therefore relationships reported below and remaining analyses were conducted with the 10 m resolution DEM. Cumulative seasonal CH4 influx (ln was regressed against average VWC (VWCavg) and temperature of each site (Tavg), soil characteristics, and each terrain metric (Figs. A1 and A2). We used the strength of these individual relationships to determine which soil variables and terrain metrics to include in the multiple-regression models. If variables were cross-correlated, the variable with a stronger relationship with ln was retained; therefore individual regressions should not be used as independent predictors. Five of the nine terrain metrics evaluated had significant relationships with ln, including elevation, EAC, DFC, TWI, and UAA (Fig. A1). Elevation, DFC, and EAC showed a positive relationship with ln, meaning locations farther away or higher in elevation above the creek (e.g., toward ridges) had higher ln than near-creek sites. UAA and TWI had a negative relationship to ln and were positively related to VWCavg (UAA r2= 0.27, p < 0.01; TWI r2= 0.43, p < 0.001). The negative influence of soil moisture on ln resulted in lower ln in locations with higher TWI or UAA. In summary, both landscape-mediated relative water availability and local VWC explained net uptake of CH4 across the watershed during the 2013 growing season.
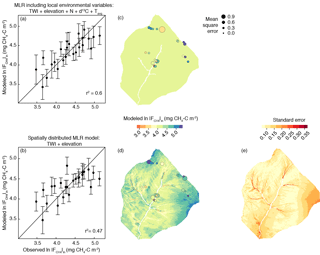
Figure 9Measured cumulative CH4 influx (ln vs. predicted ln for (a) the model that includes soil variables and (b) the model that only used topographic variables. 1:1 lines are shown for reference. The associated adjusted r2 is shown with each model; details on model fit and coefficients are in Table 3. (c) Sampling locations and associated error for the soils model. (d) Map of ln across the upper Stringer Creek watershed showing results from the topographic model. Size of site symbols are scaled to their mean square error, and color is associated with predicted flux shown in (a) and (b). (e) Standard error from the topographic model.
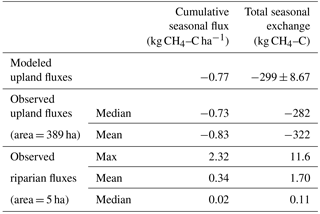
Table 4Modeled and observed seasonal CH4 uptake (separated by landscape element), as well as total areally integrated seasonal CH4 exchange. Observed mean and median of upland bracket the estimated average from the spatially distributed topographic model. Total estimated riparian CH4 effluxes are orders of magnitude smaller than uptake in the uplands.
3.5 Multiple-regression model of cumulative upland CH4 fluxes
Multiple regressions that included soil data explained up to 60 % of the observed variability in ln (Table 3), showing that, albeit not as readily available, the addition of soil variables can improve modeling results. Although these models cannot be extrapolated to the watershed scale, including Nsoil improves the model performance by 12 %, whereas including Tavg and δ13C only improves the model by 3 and 2 %, respectively (Fig. A4).
We created a spatially explicit model of upper Stringer Creek ln using the topographically based model with the best fit (adjusted r2= 0.47, p < 0.001) and lowest BIC (for model selection, where the model with the lowest BIC is preferred; Schwarz, 1978). This model included only TWI and elevation as parameters (Eq. 4, Table 3, Fig. 9). The seasonal CH4 uptake from the spatial model reached up to 2.1 kg CH4–C ha−1, averaged 0.77 kg CH4–C ha−1, and totaled 299 kg CH4–C for the entire upland area (Table 4). We extrapolated the mean, median, and maximum riparian to estimate contributions from riparian area (5 ha), resulting in a range of potential total riparian (Table 4). Even when using the maximum riparian CH4 efflux, the riparian emission offset < 4 % of total upland CH4 influx, highlighting the strong role of upland uptake in the net landscape CH4 balance.
We utilized understanding of watershed hydrology processes at TCEF (Jencso et al., 2009, 2010; Kelleher et al., 2017; Nippgen et al., 2015) to design a sampling campaign which captured CH4 fluxes across environmental gradients that were characterized through topographic analysis, field observation, and hydrological measurements. This approach allowed us to assess environmental influences on CH4 fluxes: at the point scale, we examined the influence of environmental variables on observed CH4 fluxes (); at the intermediate scale, we identified functional landscape elements (riparian, upland, and the transition between them) which related to the direction and persistence of ; and at the landscape scale, we assessed the influence of topographic position on cumulative CH4 fluxes (ln in the uplands. Our observed average (−28.5 ± 25.1 µg CH4–C m−2 h−1, Table 2) was comparable to those of other temperate forests, which range from −333 to 0.75 µg CH4–C m−2 h−1 (mean: 32.9 µg CH4–C m−2 h−1, standard error: 18; Dalal et al., 2008). We used observed relationships between ln and topographic metrics to create multiple-regression models of varying complexity to estimate the total watershed . The average predicted from the spatially distributed model of upland CH4 fluxes was similar to the extrapolated mean of measured . This is partially due to our sampling approach which captured a range of landscape positions found at TCEF. It should be noted that simply extrapolating a mean flux from a measurement site or multiple measurement sites does not capture the frequency distribution of similar landscape positions unless this is built into the sampling scheme (Vidon et al., 2015). Thus, we suggest capturing and/or modeling the spatial variability of landscapes is critical to estimating CH4 consumption or efflux across landscapes.
4.1 How do environmental variables relate to CH4 flux through the growing season, and how does landscape structure relate to relative magnitude and direction of CH4 fluxes across the landscape?
Research on soil–atmosphere CH4 exchange has been conducted across a range of ecosystems (Smith et al., 2000; Castaldi and Fierro, 2005; Dalal and Allen, 2008; Luo et al., 2013), but assessing the spatial and temporal variability of CH4 fluxes at the landscape scale has been limited. Studies focused on CH4 oxidation have shown varied responses to commonly measured environmental variables such as soil moisture and temperature (e.g., Adamsen and King, 1993; Bradford et al., 2001; Price et al., 2004), nutrient variability (e.g., N species: Verchot et al., 2000; dissolved organic carbon: Sullivan et al., 2013). In addition to these physiological constraints, soil structure and texture create the physical landscape at the microbial scale by mediating how quickly soils drain and saturate, directly influencing transport and diffusion of substrates and O2 (Dorr et al., 1993; Czepiel et al., 1995; Ball et al., 1997; von Fischer et al., 2009). Soil nutrient status can be important in understanding the variability of CH4 dynamics between ecosystems or dominant landscape units (Boeckx et al., 1997; Saari et al., 1998) but did not have a significant influence on CH4 uptake at the landscape scale. Although we did not find relationships between soil characteristics and CH4 uptake, small-scale (centimeters to meters) variability in soil structure and organic matter can be particularly relevant in low moisture conditions, where even with similar values of VWC a range of soil moisture conditions (and therefore diffusivity) can occur.
Rates of both soil CH4 production and consumption have been shown to increase with increasing temperature in laboratory studies (Bowden et al., 1998) and in field studies spanning wetlands, rice paddies (Bartlett and Harriss, 1993; Segers, 1998; Meixner and Eugster, 1999; Yvon-Durocher et al., 2014), spruce forests of Germany (Steinkamp et al., 2001), the Mongolian steppe region (Wu et al., 2010), and alpine grasslands (Wei et al., 2014). However, consensus has not been reached on the relationship between CH4 flux and temperature across ecosystems (Luo et al., 2013). In fact, several studies have shown limited temperature influence on daily and seasonal variability of CH4 consumption in upland soils (King and Adamsen, 1992; Del Grosso et al., 2000; Smith et al., 2000; Castaldi and Fierro, 2005; Shrestha et al., 2012; Imer et al., 2013). At TCEF, we did not find a simple relationship between and soil temperature. Early in the growing season, when soils were near saturation due to the recent snowmelt, both low soil temperatures and restricted gas-phase transport were likely limiting . As the season progressed and temperatures increased, the largest range and magnitude of was observed, but these conditions coincided with increased diffusivity due to decreasing soil moisture, making the independent effects difficult to ascertain. These compounding seasonal factors in both riparian and upland settings, and the relatively low range of variability in soil temperature suggest our site is not an ideal location for assessing temperature effects on CH4 fluxes. Given these caveats, our results do agree with findings from a study of temperature and moisture effects on methane consumption across ecosystem types (Luo et al., 2013) which found maximum CH4 uptake corresponded with average soil temperature (Fig. A3).
Depth to groundwater table, VWC, and O2 have been used to estimate soil redox conditions that are essential for methanogenesis (Fiedler and Sommer, 2000; Liptzin et al., 2011). As depth to water table increases, the volume in which oxidation can occur increases, thereby decreasing net CH4 efflux (Moore and Roulet, 1993), yet, similar to Fiedler and Sommer (2000), we found that depth to groundwater table was not sufficient to predict the magnitude of riparian CH4 efflux in these well-drained soils. High VWC is often associated with O2 depletion (Silver et al., 1999), yet we measured near-atmospheric O2 even up to 60 % VWC, similarly to Hall et al. (2012), who suggest that high VWC does not necessarily lead to depleted O2, even when soil water content is above field capacity. Additionally, Teh et al. (2005) show that laboratory experiments varying O2 do not result in significant changes in rates of methanogenesis. Based on these findings, we suggest that using VWC as a proxy for O2 conditions should be done with caution when estimating biogeochemical fluxes reliant on redox conditions, and we highlight the limited support for predictability of the magnitude of CH4 efflux based on O2.
Soil moisture has a strong influence on the microbial populations that drive methane cycling (Conrad, 1996; Potter et al., 1996; Smith et al., 2003; Luo et al., 2013; Du et al., 2015), but the differential response of methanotrophs and methanogens to soil moisture status can make it difficult to find simple relationships between net CH4 flux and VWC. The hydrologic landscape at TCEF is such that the groundwater dynamics are heavily influenced by topography (Jencso et al., 2009, 2010), which creates a range of soil moisture conditions across the uplands and a distinct riparian area that maintains a shallow water table through the growing season (Figs. 5 and 6). We assessed the direction, magnitude, and seasonality of and determined that the patterns created by the soil moisture conditions influencing these fluxes functionally corresponded to riparian, transitional, and upland landscape elements.
Riparian zones are often characterized by high rates of biogeochemical cycling due to organic carbon availability, fluctuating water tables, and correspondingly variable redox conditions. At TCEF, soil in the riparian area is saturated during the snowmelt period, and the hydrologic connection to the uplands provides a downslope pulse of dissolved organic carbon (Pacific et al., 2010). This seasonal input of carbon could lead to increased methanogenesis, yet soil CH4 concentrations remained relatively consistent throughout the growing season (data not shown). Despite this, and the fact that the riparian locations sampled at TCEF maintained a water table throughout the season, these sites often exhibited little to no measurable CH4 flux (Figs. 6, 7). These low CH4 fluxes are consistent with observations from other forest riparian areas, where much of the CH4 produced deeper in the soil is oxidized before reaching the soil surface (humid tropics: Teh et al., 2005; floodplain wetland: Batson et al., 2015; seasonally dry ecosystems: von Fischer and Hedin, 2002; Castaldi et al., 2006; riparian area: Vidon et al., 2015). The few large fluxes observed might be due to limited sampling when gas wells were inundated (potentially missing ebullition events); low temperatures and diffusivity; fluxes of dissolved CH4 through the groundwater to the stream channel (Itoh et al., 2007); recalcitrance of organic matter (Valentine et al., 1994; Updegraff et al., 1995); or lack of sampling of fluxes from riparian vegetation, which can be an important transport process in wetlands (Whiting and Chanton, 1993; Shannon et al., 1996; Bridgham et al., 2013). Given these caveats, 115 samples over 13 weeks of sampling show that, although riparian areas can be locations of high rates of biogeochemical cycling, large net emissions of CH4 were not common among the riparian sites sampled at TCEF.
Transition zones or boundaries between landscape elements can exhibit steep gradients in hydrologic conditions and nutrients (Hedin et al., 1998a). We determined that this was also true for CH4 dynamics, which shifted from CH4 efflux in the saturated soils of the riparian area to CH4 uptake in the aerated soils of the uplands. Distinguishing the general boundary between riparian and upland landscape elements can be tractable using terrain metrics (here, the EAC threshold of 2 m), but accurately capturing the shifting spatial extent of the transition zone through time can be challenging (Creed and Sass, 2011). At TCEF, this required direct measurement of the local groundwater table. The near-net-zero in these transitional sites was a culmination of both CH4 efflux and uptake rather than a consistent intermediate VWC that created near-neutral fluxes throughout the season. We did observe near-zero fluxes in the VWC range of 38–43 %, which are in accordance with VWC thresholds (32–44 %) differentiating net CH4 efflux from net uptake in other upland forests (Sitaula et al., 1995; Luo et al., 2013), but this intermediate VWC is likely a transient state that occurs in some parts of the landscape rather than being characteristic of a landscape position throughout the season. We expect the transition zones could be particularly sensitive to climate variability because the resulting changes in hydrologic dynamics could shift their boundaries and net CH4 flux behavior.
Flux of CH4 into the soil () was strongly mediated by local soil water content (Figs. 7 and A4), resulting in a seasonal pattern of that was reflective of the snowmelt dynamics in this watershed. During and shortly after snowmelt, relatively high upland VWC constrained and even resulted in a few small sources of CH4 (Fig. 6). Low rates of could have been due to the combined effects of restricted diffusion of CH4 (and O2) into the soil, production of CH4 deeper in the soil, and/or low temperatures. As the soil moisture state of the watershed decreased, gas-phase transport of CH4 into the soil increased, microsites of potential methanogenesis decreased, and those combined effects increased CH4 uptake through the growing season (Fig. 6). Previous studies have suggested that there is an optimum water content range for CH4 oxidation, below which methanotrophs become water stressed and consume less CH4 (Adamsen and King, 1993; Torn and Harte, 1996; West and Schmidt, 1998; Dunfield, 2007). Here, we did not find a pronounced decrease in uptake at low water content; in fact, we observed our largest measured influx at an extremely dry site (Fig. 7); we note, however, that this was preceded by a rain event which might have influenced this measurement (Lohse et al., 2009). Net CH4 consumption at low water content has been documented in other systems, most notably in arid environments (savannas: Otter and Scholes, 2000; desert soils: McLain and Martens, 2005; shrublands: Castaldi and Fierro, 2005; in some temperate forests: Castro et al., 1995). At TCEF, the driest sites were not only the locations of the largest measured CH4 uptake, but they also showed the greatest variability in , again highlighting the potential influence of small-scale heterogeneity in soil texture and nutrient status.
4.2 Prediction and scaling of CH4 consumption using terrain analysis
Greenhouse gases have been modeled using a range of frameworks including empirical (data-driven), mechanistic (process-based), and atmospheric inverse modeling (see Blagodatsky and Smith (2012) and Wang et al. (2012) for detailed reviews). Although these modeling efforts have significantly advanced our understanding of GHG dynamics at landscape to regional scales, most of them do not reflect spatial patterns (or variability) in the lateral redistribution of water (Tague and Band, 2001; Groffman, 2012). The spatial patterns of soil properties (Konda et al., 2010), microbial assemblages (Florinsky et al., 2004), and resultant biogeochemistry influenced by landscape position and topography (Creed and Beall, 2009; Riveros-Iregui and McGlynn, 2009; Creed et al., 2013; Anderson et al., 2015) have been investigated and used to scale point observations to the larger landscape in a limited number of studies. Remote sensing and vegetation classification have also been suggested as empirical methods to scale CH4 effluxes from wetlands to larger areas (Bartlett et al., 1992; Bubier et al., 1995; Sun et al., 2013), but similar remotely sensed scaling of soil CH4 uptake is currently lacking.
We used an empirical model based on topographic indices to scale CH4 fluxes from point measurements to the watershed scale. The extensive area of dry uplands consuming CH4 (98 % of watershed area) and low average production from the small riparian area resulted in a watershed net growing season sink up to 299 ± 8 kg CH4–C (0.77 kg CH4–C ha−1). We found higher uncertainty in the near-stream area; this is likely due to the influence of higher TWI in locations that have an EAC above the riparian threshold of 2 m (Fig. 9). These locations might behave more like the transitional areas which are saturated early in the season and no longer have a groundwater table, or saturated conditions, later in the season. These locations highlight two limitations to this methodology: firstly, CH4 flux dynamics in locations that transition between saturated and aerated conditions will not be captured by a regression using static terrain metrics. Secondly, 10 m resolution digital elevation data are insufficient to resolve topographic variability within our small riparian zone, even though the variable contributing area along the riparian zone influences the timing and delivery of nutrients to the riparian area (Jencso et al., 2010; Pacific et al., 2010).
This spatially distributed model (ln ∝ TWI and elevation) estimated a total net seasonal CH4 uptake similar to the CH4 uptake estimated by extrapolating the mean . This might partially be because the model did not capture the highest cumulative fluxes well and had higher standard error in the dry, high-elevation locations (Fig. 9). The high frequency of landscape settings that experience drier conditions represents the disproportionate amount of the landscape which exhibits high net CH4 uptake. Therefore, extrapolating a mean value to the entire watershed can bias estimates across watersheds. The use of central tendency and its effects on estimating GHG fluxes across landscapes was also highlighted with respect to CH4 by Vidon et al. (2015) and has significant implications for our understanding of the contribution of upland landscapes to regional and global CH4 inventories.
Terrain analysis reflects the long-term conditions of a given location relative to its landscape setting. Lower VWC (at the point scale) and relative water availability (as represented by TWI at the landscape scale) corresponded to more CH4 uptake and are the most influential parameters at those respective scales due to their influence on microbial activity and soil diffusivity (Fig. A4). The inclusion of elevation in the model might be due to a combination of factors including its effect on both temperature and incoming insolation, which could lead to higher evapotranspiration and lower soil water content at the high elevations. Elevation could also be capturing the differences in mineral type which result in variable soil chemistry and pH. This could be impacting the soil microbial communities, which have been shown to significantly differ between lower and higher upland soils in the watershed (Du et al., 2015). Our modeling exercise demonstrates soil variables can aid in the explanation of CH4 uptake (particularly at high CH4 uptake) and suggests that we might be conservatively estimating CH4 consumption given the lack of soil parameters in the spatially distributed estimate of CH4 consumption (Eq. 5).
Consistent with previous research on CO2 fluxes at TCEF (Riveros-Iregui and McGlynn, 2009) and other studies (Duncan et al., 2013; Vidon et al., 2014), our regression model results suggest that the topographic redistribution of water and the frequency distribution of relevant functional landscape elements should be considered in scaling exercises. These approaches may better reflect CH4 dynamics in a variety of watersheds, such as locations where the riparian extent is proportionally larger and potentially offsets the upland CH4 sink to a greater degree (Sakabe et al., 2016). Here, even if the maximum from the riparian area were used to estimate net efflux, it would have to comprise over 25 % of the watershed area to offset the net CH4 consumption in the uplands. As noted in a recent review by Bernhardt et al. (2017), it is critically important to perform these scaling exercises to determine the relative influences of point scale measurements on net watershed balances. These results highlight the importance of accounting for the upland CH4 sink, which can significantly offset high rates of methane production in riparian areas.
The strong gradients of water availability at TCEF impose both a direct (local) and indirect (distal/historic) effect on the microbial communities and physical transport processes regulating biogeochemical fluxes. We implemented a sampling design that utilized these hydrologic gradients to study the influence of landscape heterogeneity on watershed CH4 fluxes. We determined that soil moisture was the dominant environmental influence on the direction of net CH4 fluxes, and the magnitude of CH4 uptake in the uplands due to its influence on soil diffusivity. Low nutrient status and limited range in soil temperature could be responsible for the lack of a direct relationship between Csoil, Nsoil, or Tavg and CH4 uptake but likely contribute to the variability in observed CH4 fluxes across the landscape.
Landscape elements can be useful in characterizing areas that behave similarly to net sources or sinks of CH4, but the boundary between elements can shift as the landscape dries down or wets up. Although riparian areas can disproportionally contribute to net landscape biogeochemical fluxes, their area relative to the uplands made them a minor component of the CH4 balance in upper Stringer Creek. Interestingly, there was limited support for a consistent seasonal trend in CH4 effluxes in the riparian area, while the uplands increased in sink strength as the growing season progressed.
The effect of soil moisture on CH4 uptake led to an observable relationship between landscape structure and CH4 flux. We used these relationships to create empirically derived multiple-regression models with spatially distributed parameters. This allowed us to better visualize spatial patterns of fluxes and to extrapolate from measurement locations the watershed scale. This is preferable to the use of central tendency, which does not incorporate the frequency distribution of landscape settings relative to measurement locations. The importance of specific terrain metrics will vary across watersheds, particularly those that are not in water-limited regions. Further research on the applicability of this method in other locations and the use of higher-resolution DEMs to assess spatial variability in the riparian area is needed. These findings contribute to the literature on the importance of spatial heterogeneity, and the lateral redistribution of water, and suggest that we could be significantly underpredicting net watershed CH4 sink strength if we do not account for spatial variability.
Data are publicly available and can be accessed at https://www.hydroshare.org/resource/ (Kaiser et al., 2018).
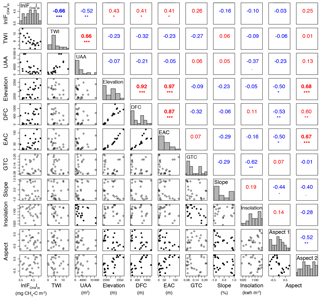
Figure A1All topographic variables included in initial exploratory data analysis. If a set of topographic variables had a Pearson's correlation coefficient greater than 0.6, then the variable with a lower correlation with ln was removed from the analysis. Significance is denoted by asterisks: ( ) < 1, (*) ≤ 0.05, (**) ≤ 0.01, and (***) ≤ 0.001. Blue text indicates negative relationships and red indicates positive relationships. Histograms of each variable run diagonally and separate the correlation coefficients from the bivariate plots. Bivariate plots with filled symbols denote significant relationships. Aspect parameters were calculated in radians using Eq. (1).
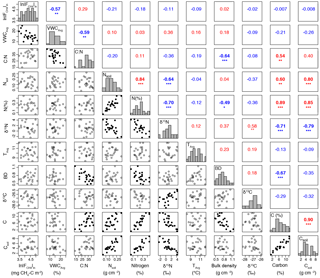
Figure A2All environmental variables considered in the initial exploratory data analysis. If a set of variables had a Pearson's correlation coefficient greater than 0.6, the variable with a lower correlation with ln was removed. Significance is denoted by asterisks: ( ) ≤ 1, (*) ≤ 0.05, (**) ≤ 0.01, and (***) ≤ 0.001. Blue text indicates negative relationships, and red indicates positive relationships. Histograms of each variable run diagonally and separate the correlation coefficients from the bivariate plots. Bivariate plots with filled symbols denote significant relationships.
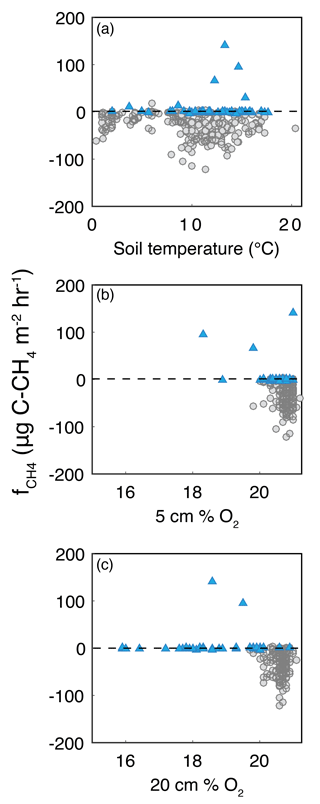
Figure A3Bivariate plots of CH4 flux (fCH4) with (a) soil temperature, (b) 5 cm %O2, and (c) 20 cm % O2. Circles are measurements from upland locations, and triangles are from riparian locations.
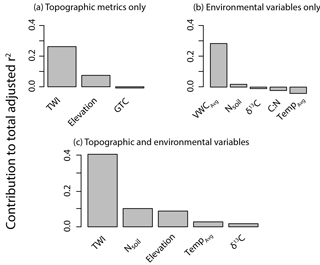
Figure A4Results from the variable jack-knife analysis to determine which variables were the most important from a given parameter set: (a) topographic metrics (in final MLR), (b) soil variables only, and (c) topographic and soil variables (from grouped MLR). Variables included in each set are shown on the x axis. The y axis indicates the contribution to the total adjusted r2 of the model when the variable is included in the model (the larger the number, the more important the variable is to the model, and the higher its relative influence on ln). Given the penalty to the adjusted r2 for additional variables, some variables did not contribute to model performance and were not included in any of the models (e.g., Tavg, C : N).
BLM and JED conceived of the initial project as project principal investigators. The project became a collaborative effort with KEK, who conducted most of the fieldwork. JED led collection of the LI-COR data for the diffusivity relationship and analyzed the gas samples. KEK conducted data analysis and prepared the manuscript with contributions from her advisor (BLM) and revisions from both co-authors.
This work was principally supported by NSF grant 1114392 awarded to John E. Dore and
Brian L. McGlynn and an NSF GRFP fellowship DGE 1644868 awarded to Kendra E. Kaiser. Additional support to John E. Dore from NSF EPSCoR Cooperative
Agreement #EPS-1101342 is gratefully acknowledged. The authors appreciate
logistical collaboration with the USDA Forest Service, particularly Helen Smith
of the Rocky Mountain Research Station and Carol Hatfield of the Lewis and
Clark National Forest. We thank Chris Allen, William Avery, Andrew Birch, Keenan Brame, Mark Burr, Patrick Clay, Tim Covino, Calvin Dore, Helena Dore, Missey Dore, Rob Edwards,
James Irvine,
Kelsey Jencso, Ryan Jones, Liyin Liang, Tracey Lorenzo, Tim McDermott, Alex Michaud, Fabian Nippgen, Sarah Ohlen, Hayden Wilson, Ellie Zignego, and Margaret Zimmer
for field and/or
laboratory assistance, and Dean Urban for his suggestions on how to improve
assessment of model performance. We would particularly like to thank Erin Seybold for her critical contributions in the field and assistance with data
quality control.
Edited by: Edzo Veldkamp
Reviewed by: two anonymous referees
Adamsen, A. P. S. and King, G. M.: Methane consumption in temperate and subarctic forest soils: Rates, vertical zonation, and responses to water and nitrogen, Appl. Environ. Microb., 59, 485–490, 1993.
Allaire, S. E., Lange, S. F., Lafond, J. A., Pelletier, B., Cambouris, A. N., and Dutilleul, P.: Multiscale spatial variability of CO2 emissions and correlations with physico-chemical soil properties, Geoderma, 170, 251–260, https://doi.org/10.1016/j.geoderma.2011.11.019, 2012.
Anderson, T. R., Groffman, P. M., and Walter, M. T.: Using a soil topographic index to distribute denitrification fluxes across a northeastern headwater catchment, J. Hydrol., 522, 123–134, https://doi.org/10.1016/j.jhydrol.2014.12.043, 2015.
Ball, B. C., Dobbie, K. E., Parker, J. P., and Smith, K. A.: The influence of gas transport and porosity on methane oxidation in soils, J. Geophys. Res., 102, 301–308, 1997.
Bartlett, K. B. and Harriss, R. C.: Review and assessment of methane emissions from wetlands, Chemosphere, 26, 261–320, https://doi.org/10.1016/0045-6535(93)90427-7, 1993.
Bartlett, K. B., Crill, P. M., Sass, R. L., Harriss, R. C., and Dise, N. B.: Methane emissions from tundra environments in the Yukon-Kuskokwim Delta, Alaska, J. Geophys. Res., 97, 16645–16660, 1992.
Batson, J., Noe, G. B., Hupp, C. R., Krauss, K. W., Rybicki, N. B., and Schenk, E. R.: Soil greenhouse gas emissions and carbon budgeting in a short-hydroperiod floodplain wetland, J. Geophys. Res.-Biogeo., 120, 77–95, https://doi.org/10.1002/2014JG002817, 2015.
Bernhardt, E. S., Blaszczak, J. R., Ficken, C. D., Fork, M. L., Kaiser, K. E., and Seybold, E. C.: Control Points in Ecosystems: Moving Beyond the Hot Spot Hot Moment Concept, Ecosystems, 20, 665–682, https://doi.org/10.1007/s10021-016-0103-y, 2017.
Beven, K. J. and Kirkby, M. J.: A physically based, variable contributing area model of basin hydrology, Hydrol. Sci. B., 24, 43–69, 1978.
Blagodatsky, S. and Smith, P.: Soil physics meets soil biology: Towards mechanistic prediction of greenhouse gas emissions from soil, Soil Biol. Biochem., 47, 78–92, https://doi.org/10.1016/j.soilbio.2011.12.015, 2012.
Blazewicz, S. J., Petersen, D. G., Waldrop, M. P., and Firestone, M. K.: Anaerobic oxidation of methane in tropical and boreal soils: Ecological significance in terrestrial methane cycling, J. Geophys. Res.-Biogeo., 117, 1–10, https://doi.org/10.1029/2011JG001864, 2012.
Boeckx, P., Van Cleemput, O., and Villaralvo, I.: Methane oxidation in soils with different textures and land use, Nutr. Cycl. Agroecosys., 49, 91–95, https://doi.org/10.1023/A:1009706324386, 1997.
Böhner, J. and Antonic, O.: Land-surface parameters specific to topo-climatology, in: Geomorphometry: Concepts, Software, Applications. Developments in Soil Science, edited by: Hengl, T. and Reuter, H. I., Elsevier, Amsterdam, the Netherlands, 33, 1–28, 2009.
Born, M., Dorr, H., and Levin, I.: Methane consumption in aerated soils of the temperate zone, Tellus, 42B, 2–8, 1990.
Bowden, R. D., Newkirk, K. M., and Rullo, G. M.: Carbon dioxide and methane fluxes by a forest soil under laboratory-controlled moisture and temperature conditions, Soil Biol. Biochem., 30, 1591–1597, https://doi.org/10.1016/S0038-0717(97)00228-9, 1998.
Bradford, M. A., Ineson, P., Wookey, P. A., and Lappin-Scott, H. M.: Role of CH4 oxidation, production and transport in forest soil CH4 flux, Soil Biol. Biochem., 33, 1625–1631, 2001.
Bridgham, S. D., Cadillo-Quiroz, H., Keller, J. K., and Zhuang, Q.: Methane emissions from wetlands: Biogeochemical, microbial, and modeling perspectives from local to global scales, Glob. Change Biol., 19, 1325–1346, https://doi.org/10.1111/gcb.12131, 2013.
Bubier, J. L., Moore, T. R., Bellisario, L., Comer, N. T., and Crill, P. M.: Ecological controls on methane emissions from a northern peatland complex in the zone of discontinuous permafrost, Manitoba, Canada, Global Biogeochem. Cy., 9, 455–470, https://doi.org/10.1029/95GB02379, 1995.
Buckingham, E.: Contributions to our knowledge of the aeration of soils, USDA Soil Bull., 25, 1–52, 1904.
Burt, T. P. and Pinay, G.: Linking hydrology and biogeochemistry in complex landscapes, Prog. Phys. Geog., 29, 297–316, https://doi.org/10.1191/0309133305pp450ra, 2005.
Castaldi, S. and Fierro, A.: Soil-atmosphere methane exchange in undisturbed and burned Mediterranean shrubland of southern Italy, Ecosystems, 8, 182–190, https://doi.org/10.1007/s10021-004-0093-z, 2005.
Castaldi, S., Ermice, A., and Strumia, S.: Fluxes of N2O and CH4 from soils of savannas and seasonally-dry ecosystems, J. Biogeogr., 33, 401–415, https://doi.org/10.1111/j.1365-2699.2005.01447.x, 2006.
Castro, M. S., Steudler, A., Melillo, M., Aber, J. D., and Bowden, R. D.: Factors controlling atmospheric methane consumption by temperate forest soils, Global Biogeochem. Cy., 9, 1–10, 1995.
Clark, J. S.: Fire and Climate Change During the Last 750 Yr in Northwestern Minnesota, Ecol. Monogr., 60, 135–159, 1990.
Conrad, R.: Soil microorganisms as controllers of atmospheric trace gases (H2, CO, CH4, OCS, N2O, and NO), Microbiol. Rev., 60, 609–640, 1996.
Corre, M. D., van Kessel, C., and Pennock, D. J.: Landscape and seasonal patterns of nitrous oxide emissions in a semiarid region, Soil Sci. Soc. Am. J., 60, 1806, https://doi.org/10.2136/sssaj1996.03615995006000060028x, 1996.
Creed, I. F. and Beall, F. D.: Distributed topographic indicators for predicting nitrogen export from headwater catchments, Water Resour. Res., 45, W10407, https://doi.org/10.1029/2008WR007285, 2009.
Creed, I. F. and Sass, G. Z.: Digital terrain analysis approaches for tracking hydrological and biogeochemical pathways and processes in forested landscapes, in: Forest Hydrology and Biogeochemistry: Synthesis of Past Research and Future Directions, edited by: Levia, D. F., Carlyle-Moses, D., and Tanaka, T., 216, 69–100, Springer, the Netherlands, 2011.
Creed, I. F., Trick, C. G., Band, L. E., and Morrison, I. K.: Characterizing the spatial pattern of soil carbon and nitrogen pools in the Turkey Lakes Watershed: A comparison of regression techniques, Water Air Soil Poll., 2, 81–102, 2002.
Creed, I. F., Miller, J., Aldred, D., Adams, J. K., Spitale, S., and Bourbonniere, R. A.: Hydrologic profiling for greenhouse gas effluxes from natural grasslands in the prairie pothole region of Canada, J. Geophys. Res.-Biogeo., 118, 680–697, https://doi.org/10.1002/jgrg.20050, 2013.
Czepiel, P. M., Crill, P. M., and Harriss, R. C.: Environmental factors influencing the variability of methane oxidation in temperate zone soils, J. Geophys. Res., 100, 9359–9364, 1995.
Dalal, R. C. and Allen, D. E.: Greenhouse gas fluxes from natural ecosystems, Aust. J. Bot., 56, 369–407, https://doi.org/10.1071/bt07128, 2008.
Dalal, R. C., Allen, D. E., Livesley, S. J., and Richards, G.: Magnitude and biophysical regulators of methane emission and consumption in the Australian agricultural, forest, and submerged landscapes: a review, Plant Soil, 309, 43–76, https://doi.org/10.1007/s11104-007-9446-7, 2008.
Davidson, E. A. and Swank, W. T.: Environmental parameters regulating gaseous nitrogen losses from two forested ecosystems via nitrification and denitrification, Appl. Environ. Microb., 52, 1287–1292, 1986.
Del Grosso, S. J., Parton, W. J., Mosier, A. R., Ojima, D. S., Potter, C. S., Brumme, R., Dobbie, P. M. C. K., and Smith, K. A.: General CH4 oxidation model and comparisons of CH4 oxidation in natural and managed systems, Global Biogeochem. Cy., 14, 999–1019, 2000.
Denmead, O. T.: Approaches to measuring fluxes of methane and nitrous oxide between landscapes and the atmosphere, Plant Soil, 309, 5–24, https://doi.org/10.1007/s11104-008-9599-z, 2008.
Devito, K. J., Creed, I. F., Rothwell, R. L., and Prepas, E. E.: Landscape controls on phosphorus loading to boreal lakes: implications for the potential impacts of forest harvesting, Can. J. Fish. Aquat. Sci., 57, 1977–1984, https://doi.org/10.1139/cjfas-57-10-1977, 2000.
Dormann, C., Elith, J., Bacher, S., Buchmann, C., Carl, G., Carré, G., García Marquéz, J. R., Gruber, B., Lafourcade, B., Leitão, P. J., Münkemüller, T., Mcclean, C., Osborne, P. E., Reineking, B., Schröder, B., Skidmore, A. K., Zurell, D., and Lautenbach, S.: Collinearity: a review of methods to deal with it and a simulation study evaluating their performance, Ecography, 36, 27–4, https://doi.org/10.1111/j.1600-0587.2012.07348.x, 2013.
Dorr, H., Katruff, L., and Levin, I.: Soil texture parameterization of the methane uptake in aerated soils, Chemosphere, 26, 697–713, 1993.
Du, Z., Riveros-Iregui, D. A., Jones, R. T., McDermott, T. R., Dore, J. E., McGlynn, B. L., Emanuel, R. E., and Li, X.: Landscape position influences microbial composition and function via redistribution of soil water across a watershed, Appl. Environ. Microb., 81, 8457–8468, https://doi.org/10.1128/AEM.02643-15, 2015.
Duncan, J. M., Groffman, P. M., and Band, L. E.: Towards closing the watershed nitrogen budget: Spatial and temporal scaling of denitrification, J. Geophys. Res.-Biogeo., 118, 1105–1119, https://doi.org/10.1002/jgrg.20090, 2013.
Dunfield, P. F.: The soil methane sink, in: Greenhouse Gas Sinks, edited by: Reay, D. S., Hewitt, N. C., Smith, K. A., and Grace, J., 152–170, 2007.
Emanuel, R. E., Epstein, H. E., McGlynn, B. L., Welsch, D. L., Muth, D. J., and D'Odorico, P.: Spatial and temporal controls on watershed ecohydrology in the northern Rocky Mountains, Water Resour. Res., 46, W11553, https://doi.org/10.1029/2009wr008890, 2010.
Farnes, P., Shearer, R. C., Mccaughey, W. W., and Hansen, K. J.: Comparisons of hydrology, geology, and physical characteristics between Tenderfoot Creek Experimental Forest Montana and Coram Experimental Forest Montana, USDA, USFS, Bozeman, MT, USA, 1995.
Fiedler, S. and Sommer, M.: Methane emissions, groundwater levels and redox potentials of common wetland soils in a temperate-humid climate, Global Biogeochem. Cy., 14, 1081–1093, https://doi.org/10.1029/1999GB001255, 2000.
Florinsky, I. V., McMahon, S., and Burton, D. L.: Topographic control of soil microbial activity: A case study of denitrifiers, Geoderma, 119, 33–53, https://doi.org/10.1016/S0016-7061(03)00224-6, 2004.
Forman, R. T. T. and Godron, M.: Patches and structural components for a landscape ecology, Bioscience, 31, 28977–28985, 1981.
Gauthier, M., Bradley, R. L., and Šimek, M.: More evidence that anaerobic oxidation of methane is prevalent in soils: Is it time to upgrade our biogeochemical models?, Soil Biol. Biochem., 80, 167–174, https://doi.org/10.1016/j.soilbio.2014.10.009, 2015.
Ghanbarian, B. and Hunt, A. G.: Universal scaling of gas diffusion in porous media, Water Resour. Res., 50, 2242–2256, 2014.
Groffman, P. M.: Terrestrial denitrification: challenges and opportunities, Ecol. Process., 1, 1–11, https://doi.org/10.1186/2192-1709-1-11, 2012.
Hall, S. J., McDowell, W. H., and Silver, W. L.: When wet gets wetter: Decoupling of moisture, redox biogeochemistry, and greenhouse gas fluxes in a humid tropical forest soil, Ecosystems, 16, 576–589, https://doi.org/10.1007/s10021-012-9631-2, 2012.
Hanson, R. S. and Hanson, T. E.: Methanotrophic bacteria, Microbiol. Rev., 60, 439–471, 1996.
Hedin, L. O., von Fischer, J. C., Ostrom, N. E., Kennedy, B. P., Brown, M. G., and Robertson, G. P.: Thermodynamic constraints on nitrogen transformations and other biogeochemical processes at soil-stream interfaces, Ecology, 79, 684–703, 1998a.
Hedin, L. O., von Fischer, J. C., Ostrom, N. E., Kennedy, B. P., Brown, M. G., and Robertson, G. P.: Thermodynamic contraints on nitrogen transformations and other biogeochemical processes at soil-stream interfaces, Ecology, 79, 684–703, 1998b.
Imer, D., Merbold, L., Eugster, W., and Buchmann, N.: Temporal and spatial variations of soil CO2, CH4 and N2O fluxes at three differently managed grasslands, Biogeosciences, 10, 5931–5945, https://doi.org/10.5194/bg-10-5931-2013, 2013.
IPCC: Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (Core Writing Team, edited by: Pachauri, R. K. and Meyer, L. A.). IPCC, Geneva, Switzerland, 151 pp., 2014.
Itoh, M., Ohte, N., Koba, K., Katsuyama, M., Hayamizu, K., and Tani, M.: Hydrologic effects on methane dynamics in riparian wetlands in a temperate forest catchment, J. Geophys. Res.-Biogeo., 112, G01019, https://doi.org/10.1029/2006JG000240, 2007.
Jencso, K. G. and McGlynn, B. L.: Hierarchical controls on runoff generation: Topographically driven hydrologic connectivity, geology, and vegetation, Water Resour. Res., 47, W11527, https://doi.org/10.1029/2011WR010666, 2011.
Jencso, K. G., McGlynn, B. L., Gooseff, M. N., Wondzell, S. M., Bencala, K. E., and Marshall, L. A.: Hydrologic connectivity between landscapes and streams: Transferring reach- and plot-scale understanding to the catchment scale, Water Resour. Res., 45, 1–16, https://doi.org/10.1029/2008WR007225, 2009.
Jencso, K. G., McGlynn, B. L., Gooseff, M. N., Bencala, K. E., and Wondzell, S. M.: Hillslope hydrologic connectivity controls riparian groundwater turnover: Implications of catchment structure for riparian buffering and stream water sources, Water Resour. Res., 46, W10524, https://doi.org/10.1029/2009wr008818, 2010.
Kaiser, K. E., McGlynn, B. L., and Dore, J. E.: Terrain Metrics, Soil Characteristics, and Seasonal Methane Flux at TCEF, 2013, HydroShare, https://www.hydroshare.org/resource/, last access: 22 May 2018.
Kelleher, C., McGlynn, B., and Wagener, T.: Characterizing and reducing equifinality by constraining a distributed catchment model with regional signatures, local observations, and process understanding, Hydrol. Earth Syst. Sci., 21, 3325–3352, https://doi.org/10.5194/hess-21-3325-2017, 2017.
King, G. M. and Adamsen, A. P. S.: Effects of temperature on methane consumption in a forest soil and in pure cultures of the methanotroph Methylomonas rubra, Appl. Environ. Microb., 58, 2758–2763, 1992.
Kirschke, S., Bousquet, P., Ciais, P., et al.: Three decades of global methane sources and sinks, Nat. Geosci., 6, 813–823, https://doi.org/10.1038/ngeo1955, 2013.
Konda, R., Ohta, S., Ishizuka, S., Heriyanto, J., and Wicaksono, A.: Seasonal changes in the spatial structures of N2O, CO2, and CH4 fluxes from Acacia mangium plantation soils in Indonesia, Soil Biol. Biochem., 42, 1512–1522, https://doi.org/10.1016/j.soilbio.2010.05.022, 2010.
Koschorreck, M. and Conrad, R.: Oxidation of atmospheric methane in soil: Measurements in the field, in soil cores and in soil samples, Global Biogeochem. Cy., 7, 109–121, 1993.
Lavigne, M. B., Ryan, M. G., Anderson, D. E., Baldocchi, D. D., Crill, P. M., Fitzjarrald, D. R., Goulden, M. L., Gower, S. T., Massheder, J. M., McCaughey, J. H., Rayment, M., and Striegl, R. G.: Comparing nocturnal eddy covariance measurements to estimates of ecosystem respiration made by scaling chamber measurements at six coniferous boreal sites, J. Geophys. Res., 102, 28977, https://doi.org/10.1029/97JD01173, 1997.
Le Mer, J., Roger, P., Provence, D., and Luminy, D.: Production, oxidation, emission and consumption of methane by soils: A review, Eur. Soil Biol., 37, 25–50, 2001.
Liptzin, D., Silver, W. L., and Detto, M.: Temporal dynamics in soil oxygen and greenhouse gases in two humid tropical forests, Ecosystems, 14, 171–182, https://doi.org/10.1007/s10021-010-9402-x, 2011.
Lohse, K. A., Brooks, P. D., McIntosh, J. C., Meixner, T., and Huxman, T. E.: Interactions between biogeochemistry and hydrologic systems, Annu. Rev. Env. Resour., 34, 65–96, https://doi.org/10.1146/annurev.environ.33.031207.111141, 2009.
Lumley, T. and Miller, A.: Leaps: Regression subset selection, R package version 2.9, 2009.
Luo, G. J., Kiese, R., Wolf, B., and Butterbach-Bahl, K.: Effects of soil temperature and moisture on methane uptake and nitrous oxide emissions across three different ecosystem types, Biogeosciences, 10, 3205–3219, https://doi.org/10.5194/bg-10-3205-2013, 2013.
Maindonald, J. H. and Braun, W. J.: DAAG: Data Analysis and Graphics Data and Functions, R package version 1.22, https://CRAN.R-project.org/package=DAAG (last access: April 2017), 2015.
Massman, W. J.: A review of the molecular diffusivities of H2O, CO2, CH4, CO, O3, SO2, NH3, N2O, NO, and NO2 in air, O2 and N2 near STP, Atmos. Environ., 32, 1111–1127, 1998.
McGlynn, B. L. and Seibert, J.: Distributed assessment of contributing area and riparian buffering along stream networks, Water Resour. Res., 39, 1082, https://doi.org/10.1029/2002wr001521, 2003.
McLain, J. E. T. and Martens, D. A.: Studies of methane fluxes reveal that desert soils can mitigate global climate change, Southwest Watershed Research Center, USDA Forest Service, Tucson, AZ, USA, 2005.
Meixner, F. X. and Eugster, W.: Effects of landscape pattern and topography on emissions and transport, in: Integrating Hydrology, Ecosystem Dynamics, and Biogeochemistry in Complex Landscapes, edited by: Tenhunen, J. D. and Kabat, P., 143–175, John Wiley & Sons Ltd, Berlin, Germany, 1999.
Mengistu, S. G., Creed, I. F., Webster, K. L., Enanga, E., and Beall, F. D.: Searching for similarity in topographic controls on carbon, nitrogen and phosphorus export from forested headwater catchments, Hydrol. Process., 28, 3201–3216, https://doi.org/10.1002/hyp.9862, 2014.
Mincemoyer, S. A. and Birdsall, J. L.: Vascular flora of the Tenderfoot Creek Experimental Forest, Little Belt Mountains, Montana, Madroño, 53, 211–222, https://doi.org/10.3120/0024-9637(2006)53[211:VFOTTC]2.0.CO;2, 2006.
Møldrup, P., Chamindu, D., Hamamoto, S., Komatsu, T., Kawamoto, K., Rolston, D. E., and de Jonge, L. W.: Structure-dependent water-induced linear reduction model for predicting gas diffusivity and tortuosity in repacked and intact soil, Vadose Zone J., 12, 1–11, 2014.
Moore, T. R. and Roulet, N. T.: Methane flux: Water table relations in northern wetlands, Geophys. Res. Lett., 20, 587–590, 1993.
Nicolini, G., Castaldi, S., Fratini, G., and Valentini R.: A literature overview of micrometeorological CH4 and N2O flux measurements in terrestrial ecosystems, Atmos. Environ., 81, 311–319, https://doi.org/10.1016/j.atmosenv.2013.09.030, 2013.
Nippert, J. B., Ocheltree, T. W., Orozco, G. L., Ratajczak, Z., Ling, B., Skibbe, A. M.: Evidence of physiological decoupling from Grassland ecosystem drivers by an encroaching woody shrub, PLoS ONE, 8, e81630, https://doi.org/10.1371/journal.pone.0081630, 2013.
Nippgen, F., McGlynn, B. L., Marshall, L. A., and Emanuel, R. E.: Landscape structure and climate influences on hydrologic response, Water Resour. Res., 47, W12528, https://doi.org/10.1029/2011WR011161, 2011.
Otter, L. B. and Scholes, M. C.: Methane sources and sinks in a periodically flooded South African savanna, Global Biogeochem. Cy., 14, 97–111, 2000.
Pacific, V. J., Jencso, K. G., and McGlynn, B. L. Variable flushing mechanisms and landscape structure control stream DOC export during snowmelt in a set of nested catchments, Biogeochemistry, 99, 193–211, https://doi.org/10.1007/s10533-009-9401-1, 2010.
Pacific, V. J., McGlynn, B. L., Riveros-Iregui, D. A., Welsch, D. L., and Epstein, H. E.: Landscape structure, groundwater dynamics, and soil water content influence soil respiration across riparian-hillslope transitions in the Tenderfoot Creek Experimental Forest, Montana, Hydrol. Process., 25, 811–827, https://doi.org/10.1002/hyp.7870, 2011.
Paerl, H. W. and Pinckney, J. L.: A Mini-review of microbial consortia: Their roles in aquatic production and biogeochemical cycling, Microb. Ecol., 31, 225–247, 1996.
Phillips, S. J. and Dudik, M.: Modeling of species distributions with maxent: new extensions and a comprehensive evaluation, Ecography, 31, 161–175, https://doi.org/10.1111/j.0906-7590.2008.5203.x, 2008.
Phillips, S. J., Anderson, R. P., and Shapire, R. E.: Maximum entropy modeling of species geographic distribution, Ecol. Model., 190, 231–259, https://doi.org/10.1016/j.ecolmodel.2005.03.026, 2006.
Phillips, S. J. and Dudik, M.: Modeling of species distributions with maxent: new extensions and a comprehensive evaluation, Ecography, 31, 161–175, https://doi.org/10.1111/j.0906-7590.2008.5203.x, 2008.
Potter, C. S. S., Davidson, E. A., Verchot, L. V., Davidsonz, E. A., and Verchotz, L. V.: Estimation of global biogeochemical controls and seasonality in soil methane consumption, Chemosphere, 32, 2219–2246, 1996.
Price, S. J., Kelliher, F. M., Sherlock, R. R., and Tate, K. R.: Environmental and chemical factors regulating methane oxidation in a New Zealand forest soil, Aust. J. Soil Res., 42, 767–776, https://doi.org/10.1071/SR04026, 2004.
R Core Team: R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria, available at: https://www.R-project.org/ (last access: 30 November 2017), 2016.
Reynolds, J. and Wu, J.: Do landscape structural and functional units exist?, in: Integrating Hydrology, Ecosystem Dynamics, and Biogeochemistry in Complex Landscapes, edited by: Tenhunen, J. D. and Kabat, P., 273–296, John Wiley & Sons Ltd., Chichester, UK, 1999.
Richter, J., Kersebaum, K. C., and Willenbockel, I.: Gaseous diffusion reflecting soil structure, Z. Pflanz. Bodenkunde, 154, 13–19, 1991.
Riveros-Iregui, D. A. and McGlynn, B. L.: Landscape structure control on soil CO2 efflux variability in complex terrain: Scaling from point observations to watershed scale fluxes, J. Geophys. Res., 114, G02010, 2009.
Saari, A., Heiskanen, J., and Martikainen, P. J.: Effect of the organic horizon on methane oxidation and uptake in soil of a boreal Scots pine forest, FEMS Microbiol. Ecol., 26, 245–255, https://doi.org/10.1016/S0168-6496(98)00040-3, 1998.
Sakabe, A., Kosugi, Y., Okumi, C., Itoh, M., and Takahashi, K.: Impacts of riparian wetlands on the seasonal variations of watershed-scale methane budget in a temperate monsoonal forest, J. Geophys. Res.-Biogeo., 121, 1717–1732, https://doi.org/10.1002/2015JG003292, 2016.
Schmidt, W. C. and Friede, J. L.: Experimental forests, ranges, and watersheds in the northern Rocky Mountains: A compendium of outdoor laboratories in Utah, Idaho, and Montana, USDS Forest Service, Intermountain Research Station, Logan, UT, USA, 1996.
Schwarz, G.: Estimating the dimension of a model, Ann. Stat., 6, 461–464, 1978.
Segers, R.: Methane production and methane consumption: A review of processes underlying wetland methane fluxes, Biogeochemistry, 41, 23–51, https://doi.org/10.1023/A:1005929032764, 1998.
Seibert, J., and McGlynn, B. L.: A new triangular multiple flow direction algorithm for computing upslope areas from gridded digital elevation models, Water Resour. Res., 43, W04501, https://doi.org/10.1029/2006wr005128, 2007.
Shannon, R. D., White, J. R., Lawson, J. E., and Gilmour, B. S.: Methane efflux from emergent vegetation in peatlands, J. Ecol., 84, 239–246, https://doi.org/10.2307/2261359, 1996.
Shrestha, P. M., Kammann, C., Lenhart, K., Dam, B., and Liesack, W.: Linking activity, composition and seasonal dynamics of atmospheric methane oxidizers in a meadow soil, ISME J., 6, 1115–1126, https://doi.org/10.1038/ismej.2011.179, 2012.
Silver, W. L., Lugo, A. E., and Keller, M.: Soil oxygen availability and biogeochemical cycling along elevation and topographic gradients in Puerto Rico, Biogeochemistry, 44, 301–328, 1999.
Sitaula, B. K., Bakken, L. R., and Abrahamsen, G.: CH4 uptake by temperate forest soil: Effect of N input and soil acidification, Soil Biol. Biochem., 27, 871–880, https://doi.org/10.1016/0038-0717(95)00017-9, 1995.
Smith, K. A., Dobbie, K. E., Ball, B. C., Bakken, L. R., Sitaula, B. K., Hansen, S., Brumme, R., Borken, W., Christensen, S., Priemé, A., Fowler, D., Macdonald, J. A., Skiba, U., Klemedtsson, L., Kasimir-Klemedtsson, A., Degórska, A., and Orlanski, P.: Oxidation of atmospheric methane in Northern European soils, comparison with other ecosystems, and uncertainties in the global terrestrial sink, Glob. Change Biol., 6, 791–803, https://doi.org/10.1046/j.1365-2486.2000.00356.x, 2000.
Smith, K. A., Ball, T., Conen, F., Dobbie, K. E. E., Massheder, J., and Rey, A.: Exchange of greenhouse gases between soil and atmosphere: interactions of soil physical factors and biological processes, Eur. J. Soil Sci., 54, 779–791, https://doi.org/10.1046/j.1351-0754.2003.0567.x, 2003.
Sotta, E. D., Meir, P., Malhi, Y., Nobre, A. D., Hodnett, M., and Grace, J.: Soil CO2 efflux in a tropical forest in the central Amazon, Glob. Change Biol., 10, 601–617, 2004.
Steinkamp, R., Butterbach-Bahl, K., and Papen, H.: Methane oxidation by soils of a N-limited and N-fertilized spruce forest in the Black Forest, Germany., Soil Biol. Biochem., (33), 145–153, 2001.
Sullivan, B. W., Selmants, P. C., and Hart, S. C.: Does dissolved organic carbon regulate biological methane oxidation in semiarid soils?, Glob. Change Biol., 19, 2149–2157, https://doi.org/10.1111/gcb.12201, 2013.
Sun, L., Song, C., Miao, Y., Qiao, T., and Gong, C.: Temporal and spatial variability of methane emissions in a northern temperate marsh, Atmos. Environ., 81, 356–363, https://doi.org/10.1016/j.atmosenv.2013.09.033, 2013.
Tague, C. L. and Band, L. E.: Evaluating explicit and implicit routing for watershed hydro-ecological models of forest hydrology at the small catchment scale, Hydrol. Process., 15, 1415–1440, 2001.
Tang, X., Liu, S., Zhou, G., Zhang, D., and Zhou, C.:, Soil-atmospheric exchange of CO2, CH4, and N2O in three subtropical forest ecosystems in southern China, Glob. Change Biol., 12, 546–560, https://doi.org/10.1111/j.1365-2486.2006.01109.x, 2006.
Teh, Y. A., Silver, W. L., and Conrad, M. E.: Oxygen effects on methane production and oxidation in humid tropical forest soils, Glob. Change Biol., 11, 1283–1297, https://doi.org/10.1111/j.1365-2486.2005.00983.x, 2005.
Teh, Y. A., Diem, T., Jones, S., Huaraca Quispe, L. P., Baggs, E., Morley, N., Richards, M., Smith, P., and Meir, P.: Methane and nitrous oxide fluxes across an elevation gradient in the tropical Peruvian Andes, Biogeosciences, 11, 2325–2339, https://doi.org/10.5194/bg-11-2325-2014, 2014.
Tian, H., Xu, X., Liu, M., Ren, W., Zhang, C., Chen, G., and Lu, C.: Spatial and temporal patterns of CH4 and N2O fluxes in terrestrial ecosystems of North America during 1979–2008: application of a global biogeochemistry model, Biogeosciences, 7, 2673–2694, https://doi.org/10.5194/bg-7-2673-2010, 2010.
Tian, H., Chen, G., Lu, C., Xu, X., Ren, W., Zhang, B., Banger, K., Pan, S., Liu, M., Zhang, C., Bruhwiler, L., and Wofsy, S.: Global methane and nitrous oxide emissions from terrestrial ecosystems due to multiple environmental changes, Ecosyst. Heal. Sustain., 1, 1–20, 2014.
Torn, M. and Harte, J.: Methane consumption by montane soils: implications for positive and negative feedback with climatic change, Biogeochemistry, 32, 53–67, https://doi.org/10.1007/BF00001532, 1996.
Ullah, S. and Moore, T. R.: Biogeochemical controls on methane, nitrous oxide, and carbon dioxide fluxes from deciduous forest soils in eastern Canada, J. Geophys. Res., 116, G03010, https://doi.org/10.1029/2010jg001525, 2011.
Updegraff, K., Pastor, J., Bridgham, S. D., and Johnston, C. A.: Environmental, and substrate controls over carbon and nitrogen mineralization in Northen wetlands, Ecol. Appl., 5, 151–163, https://doi.org/10.2307/1942060, 1995.
Urban, D. L., Miller, C., Halpin, P. N., and Stephenson, N. L.: Forest gradient response in Sierran landscapes: the physical template, Landsc. Ecol., 15, 603–620, 2000.
Valentine, D. W., Holland, E. A., and Schimel, D. S.: Ecosystem and physiological controls over methane production in northern wetlands, J. Geophys. Res., 99, 1563–1571, 1994.
Verchot, L. V., Davidson, E. A., Cattânio, J. H., and Ackerman, I. L.: Land-use change and biogeochemical controls of methane fluxes in soils of eastern Amazonia, Ecosystems, 3, 41–56, https://doi.org/10.1007/s100210000009, 2000.
Vidon, P., Jacinthe, P. A., Liu, X., Fisher, K., and Baker, M.: Hydrobiogeochemical controls on riparian nutrient and greenhouse gas dynamics: 10 years post-restoration, J. Am. Water Resour. As., 50, 639–652, https://doi.org/10.1016/j.jhydrol.2007.05.016, 2014.
Vidon, P., Marchese, S., Welsh, M., and McMillan, S.: Short-term spatial and temporal variability in greenhouse gas fluxes in riparian zones, Environ. Monit. Assess., 187, 503, https://doi.org/10.1007/s10661-015-4717-x, 2015.
von Fischer, J. C. and Hedin, L. O.: Separating methane production and consumption with a field-based isotope pool dilution technique, Global Biogeochem. Cy., 16, 8-1–8-13, https://doi.org/10.1029/2001GB001448, 2002.
von Fischer, J. C. and Hedin, L. O.: Controls on soil methane fluxes: Tests of biophysical mechanisms using stable isotope tracers, Global Biogeochem. Cy., 21, GB2007, https://doi.org/10.1029/2006GB002687, 2007.
von Fischer, J. C., Butters, G., Duchateau, P. C., Thelwell, R. J., and Siller, R.: In situ measures of methanotroph activity in upland soils: A reaction diffusion model and field observation of water stress, J. Geophys. Res.-Biogeo., 114, 1–12, https://doi.org/10.1029/2008JG000731, 2009.
Wachinger, G., Fiedler, S., Zepp, K., Gattinger, A., Sommer, M., and Roth K.: Variability of soil methane production on the micro-scale: spatial association with hot spots of organic material and Archaeal populations, Soil Biol. Biochem., 32, 1121–1130, https://doi.org/10.1016/S0038-0717(00)00024-9, 2000.
Wang, L., Zou, C., Donnell, F. O., Good, S., Franz, T., Miller, G. R., Caylor, K. K., Cable, J. M., and Bond, B.: Characterizing ecohydrological and biogeochemical connectivity across multiple scales: a new conceptual framework, Ecohydrology, 5, 221–233, https://doi.org/10.1002/eco.187, 2012.
Webster, K. L., Creed, I. F., Bourbonnière, R. A. and Beall, F. D.: Controls on the heterogeneity of soil respiration in a tolerant hardwood forest, J. Geophys. Res., 113, G03018, https://doi.org/10.1029/2008JG000706, 2008.
Wei, D., Xu-Ri, Tenzin-Tarchen, Wang, Y., and Wang, Y.: Considerable methane uptake by alpine grasslands despite the cold climate: In situ measurements on the central Tibetan Plateau, 2008–2013, Glob. Change Biol., 21, 777–788, https://doi.org/10.1111/gcb.12690, 2014.
Welsch, D. L., Burns, D. A., and Murdoch, P. S.: Processes affecting the response of sulfate concentrations to clearcutting in a northern hardwood forest, Catskill Mountains, New York, USA, Biogeochemistry, 68, 337–354, https://doi.org/10.1023/B:BIOG.0000031034.48927.1e, 2004.
West, A. E. and Schmidt, S. K.: Wetting stimulates atmospheric CH4 oxidation by alpine soil, FEMS Microbiol. Ecol., 25, 349–353, 1998.
Western, A. W., Grayson, R. B., Blöschl, G., Willgoose, G. R., and McMahon, T. A.: Observed spatial organization of soil moisture and its relation to terrain indices, Water Resour. Res., 35, 797–810, 1999.
Whiting, G. J. and Chanton, J. P.: Primary production control of methane emission from wetlands, Nature, 364, 794–795, https://doi.org/10.1038/364794a0, 1993.
Wolf, B., Chen, W., Brüggemann, N., Zheng, X., Pumpanen, J., and Butterbach-Bahl, K.: Applicability of the soil gradient method for estimating soil-atmosphere CO2, CH4, and N2O fluxes for steppe soils in Inner Mongolia, J. Plant Nutr. Soil Sc., 174, 359–372, https://doi.org/10.1002/jpln.201000150, 2011.
Wood, E. F., Sivapalan, M., Beven, K., and Band, L.: Effects of spatial variability and scale with implications to hydrologic modeling, J. Hydrol., 102, 29–47, 1988.
Wu, X., Yao, Z., Brüggemann, N., Shen, Z. Y., Wolf, B., Dannenmann, M., Zheng, X., and Butterbach-Bahl, K.: Effects of soil moisture and temperature on CO2 and CH4 soil-atmosphere exchange of various land use/cover types in a semi-arid grassland in Inner Mongolia, China, Soil Biol. Biochem., 42, 773–787, https://doi.org/10.1016/j.soilbio.2010.01.013, 2010.
Yu, K., Faulkner, S. P., and Baldwin, M. J.: Effect of hydrological conditions on nitrous oxide, methane, and carbon dioxide dynamics in a bottomland hardwood forest and its implication for soil carbon sequestration, Glob. Change Biol., 14, 798–812, https://doi.org/10.1111/j.1365-2486.2008.01545.x, 2008.
Yvon-Durocher, G., Allen, A. P., Bastviken, D., Conrad, R., Gudasz, C., St-Pierre, A., Thanh-Duc, N., and del Giorgio, P. A.: Methane fluxes show consistent temperature dependence across microbial to ecosystem scales, Nature, 507, 488–491, https://doi.org/10.1038/nature13164, 2014.