the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Use of argon to measure gas exchange in turbulent mountain streams
Robert O. Hall Jr.
Hilary L. Madinger
Gas exchange is a parameter needed in stream metabolism and trace gas emissions models. One way to estimate gas exchange is via measuring the decline of added tracer gases such as sulfur hexafluoride (SF6). Estimates of oxygen (O2) gas exchange derived from SF6 additions require scaling via Schmidt number (Sc) ratio, but this scaling is uncertain under conditions of high gas exchange via bubbles because scaling depends on gas solubility as well as Sc. Because argon (Ar) and O2 have nearly identical Schmidt numbers and solubility, Ar may be a useful tracer gas for estimating stream O2 exchange. Here we compared rates of gas exchange measured via Ar and SF6 for turbulent mountain streams in Wyoming, USA. We measured Ar as the ratio of Ar : N2 using a membrane inlet mass spectrometer (MIMS). Normalizing to N2 confers higher precision than simply measuring [Ar] alone. We consistently enriched streams with Ar from 1 to 18 % of ambient Ar concentration and could estimate gas exchange rate using an exponential decline model. The mean ratio of gas exchange of Ar relative to SF6 was 1.8 (credible interval 1.1 to 2.5) compared to the theoretical estimate 1.35, showing that using SF6 would have underestimated exchange of Ar. Steep streams (slopes 11–12 %) had high rates of gas exchange velocity normalized to Sc=600 (k600, 57–210 m d−1), and slope strongly predicted variation in k600 among all streams. We suggest that Ar is a useful tracer because it is easily measured, requires no scaling assumptions to estimate rates of O2 exchange, and is not an intense greenhouse gas as is SF6. We caution that scaling from rates of either Ar or SF6 gas exchange to CO2 is uncertain due to solubility effects in conditions of bubble-mediated gas transfer.
- Article
(466 KB) -
Supplement
(484 KB) - BibTeX
- EndNote
Air–water gas flux is a key process in aquatic ecosystems because it defines the flow of material between water and the atmosphere. Knowing this flux is needed for questions ranging from global CO2 balance (Raymond et al., 2013) to short-term O2 budgets to estimate ecosystem metabolism (Odum, 1956). Gas flux is the product of air–water gas exchange velocity (k, m d−1) and the relative saturation in water, i.e., , where Cair and Cwater are the concentrations of gas in the air and water and α is the unitless Ostwald solubility coefficient. The gas exchange velocity, k (m d−1), is a central variable for estimating gas flux, and it is much harder to measure than the air–water concentration gradient in gases. k can vary greatly through time and space and thus requires many empirical measurements or robust predictive models to accurately estimate gas exchange.
There are several ways to measure gas exchange in aquatic ecosystems. In places with high rates of primary production and low gas exchange, it is possible to measure gas exchange rates via diel curves of oxygen with time (Hornberger and Kelly, 1975; Holtgrieve et al., 2010; Hall et al., 2016; Appling et al., 2018). Direct measures with domes are practical in low-exchange habitats (Borges et al., 2004; Alin et al., 2011). Tracer gas addition is another effective means of measuring gas exchange across all types of aquatic habitats (Wanninkhof et al., 1990; Wanninkhof, 1992; Cole and Caraco, 1998). Tracer additions are particularly useful because they represent direct measures at spatial scales similar to that of turnover length of gases. Given enough estimates of k, it is then possible to build the theory of gas exchange across time and space (Wanninkhof, 1992; Raymond et al., 2012), e.g., among small high-energy streams. A trade-off with gas exchange measured by tracer gases is that it is necessary to scale exchange rates measured for the tracer gas (e.g., SF6, propane, 3He) with that of gases of ecological interest (e.g., O2, CO2, CH4). This scaling is not always straightforward because high rates of bubble-mediated gas exchange cause scaling to depend on differences in solubility of gases as well as their diffusivity (Asher and Wanninkhof, 1998a, b; Woolf et al., 2007). Thus, an ideal tracer gas would not require scaling if its solubility and diffusivity were similar to the gas of ecological interest. Here we demonstrate the use of argon (Ar) as a tracer gas; Ar has similar solubility and diffusivity to O2, a gas of major biological interest in the context of estimating metabolism in aquatic ecosystems (Odum, 1956; Nicholson et al., 2015; Bernhardt et al., 2018).
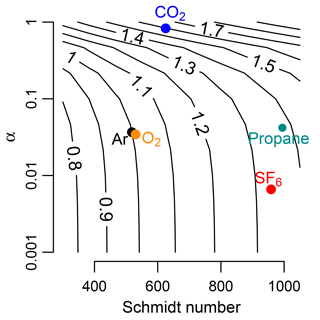
Figure 1Bubble-mediated gas exchange rate (Kb) normalized to that of argon. Temperature was at 20 ∘C. Contours are equivalent to , where Kb,2 varies as a function of solubility and Schmidt number. At low solubilities (α, Ostwald solubility coefficient), scaling among gases depends only on variation of Schmidt number (SF6). As solubility increases, scaling depends on both Schmidt number and α (CO2). O2 is similar to Ar. Propane has similar properties to SF6. Analysis is based on Eq. (13) in Woolf et al. (2007).
In the absence of extensive bubbles, one can scale gas exchange rates between gases based on the ratio of their Schmidt numbers (Sc); Sc is the dimensionless ratio of kinematic viscosity of water (ν) and the diffusion coefficient of the gas (D), i.e., . Given Sc for two gases, scaling gas exchange rates is given by
(Jähne et al., 1987), where n is a coefficient ranging from 0.67 for smooth water to 0.5 for wavy water. When bubbles are present, scaling between gases depends upon solubility of the gases in addition to their diffusivity (Asher and Wanninkhof, 1998b). This bubble effect kb is additive to that of an unbroken surface (ko) such that (Goddijn Murphy et al., 2016). One model for the bubble-mediated component of gas exchange, kb, is given by Eq. (13) in Woolf et al. (2007):
where Qb is the bubble flux and f=1.2. We can compare the ratios of the bubble-mediated component of gas exchange for two gases with varying solubility α1 and α2 as
This model shows that the effect of varying solubility on scaling kb among gases depends on the solubility (Fig. 1). For low-solubility gases such as Ar and SF6, this model predicts only a Schmidt number effect. For more soluble gases, such as CO2, the scaling factor is higher than what would be predicted because of the higher solubility of CO2 (Fig. 1). Here, we test the gas exchange scaling of two sparingly soluble gases, Ar and SF6, in high-energy mountain streams with presumably high rates of bubble-mediated gas exchange.
Argon is promising for measuring gas exchange because it has low background concentrations in water, it is inert, it is cheaply available from welding supply stores, it has similar solubility and diffusivity to O2 (Fig. 1), and it is easily detected using membrane inlet mass spectrometry. We compared Ar to SF6, another commonly used tracer gas that supersedes Ar in detectability but has a higher Schmidt number and lower solubility in addition to being an intense greenhouse gas. Our objectives were as follows.
-
Develop a method to measure gas exchange in streams using Ar tracer additions.
-
Test scaling of Ar to SF6 in turbulent streams with high rates of bubble-mediated gas transfer.
Table 1Site data for streams sampled including average stream width, reach length, solute travel time (t), water velocity v, discharge (Q), average stream depth (), stream slope, and average stream temperature during plateau. Gas exchange parameters kAr600 and a are reported with 95 % credible intervals. We also include the per-time rate of gas exchange, K600 (d−1).

2.1 Sites
We sampled five streams across a gradient of predicted gas exchanges to compare performance of Ar and SF6 as tracers. Streams were headwaters in southeast Wyoming ranging from three mountain streams in Snowy and Laramie ranges (NoName Creek, Pole Creek, and Gold Run); one urban spring stream (Spring Creek); and a low-slope, meadow stream in the Vedauwoo area of the Laramie Range (Blair Creek) (Table 1). The three mountain streams were steep channels with step-pool morphology and presumed high rates of gas exchange.
2.2 Gases and NaCl injection
We added Ar and SF6 gases to each stream and modeled their downstream evasion to estimate their relative exchange rates. Prior to injection, we collected pre-plateau samples at each of six sampling locations and an upstream location. We collected dissolved Ar : N2 samples using a 3.8 cm diameter PVC pipe with an attached outlet tube (3.2 mm ID × 20 cm vinyl tube) at the downstream end. As water flowed through the pipe, we capped the downstream end with a stopper. Lifting from the stream, water flowed through outlet tube to > triple overflow a 12 mL Exetainer vial. These vials were capped immediately without bubbles. We did not use preservative because we analyzed samples within a week and we found no change in concentration of these nearly inert gases in this time period using laboratory tests. We measured specific conductivity using a handheld conductivity sensor or conductivity and temperature using a Onset HOBO conductivity logger and converted the values to specific conductivity at each sampling location. We also recorded the stream temperature using a reference Thermapen (ThermoWorks, American Fork, UT) and barometric pressure in millimeters of mercury (mmHg) using a handheld barometer (Extech, Nashua, NH, USA) to calculate saturated dissolved gas concentrations. We assumed SF6 concentration was 0 before the addition.
Following pre-injection sampling, we simultaneously injected Ar, SF6, and a NaCl solution. We bubbled Ar using a micro bubble ceramic diffuser (Point Four Systems Inc., Coquitlam, BC, Canada) from a compressed Ar tank at a constant bubbling rate ∼ 0.2 m3 h−1. SF6 was bubbled at ∼ 100 mL min−1 through a needle valve attached to a variable area flow meter and to a 30 cm aquarium air stone. Concurrently we injected a NaCl solution at a constant rate using a peristaltic pump. Salt solution flow rates were enough to increase stream conductivity by 20 to 50 µS cm−1. Once the downstream station reached plateau conductivity, we sampled each station for specific conductivity, stream temperature, barometric pressure, and triplicate dissolved gas concentration as for the pre-injection sampling. Additionally, we sampled SF6 by sucking 45 mL of stream water into a 60 mL plastic syringe and adding 15 mL of air. The syringe was shut using a stopcock and shaken for 5 min. The 15 mL of headspace was injected into an evacuated 12 mL Exetainer. We collected three SF6 samples at each station. We collected all samples in an upstream to downstream sequence and we stored these samples at cooler-than-stream temperature to prevent outgassing.
We measured stream physical variables. We estimated stream discharge, Q, based on dilution of the NaCl tracer. Nominal transport time (t) was estimated as the time to reach one half of the plateau concentration of conductivity. Stream velocity (v) was reach length, measured by meter tape, divided by t. We measured the stream mean wetted width at more than eight locations at constant intervals through the sampling reach.
2.3 Ar and N2 analysis
We measured dissolved Ar : N2 in water samples using a membrane inlet mass spectrometer (MIMS) (Bay Instruments Inc., Easton, MD, USA) (Kana et al., 1994). We used a two-point calibration by setting water bath temperatures at ±2 ∘C of the sample collection temperature. Round-bottom flasks in each water bath were equilibrated with the atmosphere by stirring at ∼ 200 rpm. We bracketed groups of 5–10 samples with calibration samples from each water bath. We recorded the currents at m∕z 28 and 40, and their ratio from the mass spectrometer (Kana et al., 1994).
We converted the ratio currents m∕z 40 : m∕z 28 to Ar : N2 ratios. We normalized all Ar measures to N2 because the MIMS is more precise with gas ratios than absolute concentrations. We calculated the Ar : N2 in each of the two standard flasks assuming that they were in equilibrium with the atmosphere at a known temperature and barometric pressure. We estimated saturation concentrations in each flask based on Hamme and Emerson (2004). Unknown Ar : N2 in each sample was calibrated using a linear relationship derived from the Ar : N2 in the two standard flasks. Despite adding Ar to the streams, the amount of Ar was not high relative to ambient Ar. Based on the small enrichment of Ar, we assumed that N2 concentration changed little during the injection due to bubble exchange with Ar. In addition we assumed no biologically driven N2 fluxes. Denitrification would cause a uniform and small increase to the N2 concentration compared to saturation throughout the reach.
2.4 SF6 analysis
We measured SF6 at the Utah State University Aquatic Biogeochemistry Lab using a gas chromatograph (GC) (SRI Instruments, Torrance, CA, USA) with an electron capture detector. We injected 5–20 µL of samples into the GC for analysis. From each measurement, we estimated the relative SF6 concentration as area of the peak divided by injection volume. We assumed no SF6 present in streams naturally and therefore use a pre-plateau value of 0. Blanks showed no SF6.
2.5 Data analysis and inference
We estimated gas exchange rates assuming a first-order decay with distance. Let A represent the excess Ar : N2 and S excess SF6 (measured as peak area × injection volume) in stream water corrected for groundwater inputs. C is specific electrical conductivity (µS cm−1). First, at each site, x, we estimated a groundwater-corrected Ax and Sx as
where “plateau” and “ambient” indicate samples collected during and before the gas and salt additions. We estimated ambient Ar based upon temperature at each site during the collection time of the plateau samples. Measured ambient Ar : N2 accurately matched the calculated ambient but had higher within-site variability due to measurement error; thus, we assumed that ambient Ar : N2 was that estimated based on saturation calculations (see Supplement). We normalized Ax and Sx to that of their upstream-most concentrations, i.e., at the first sampling station below the injection (A0, S0).
We fit exponential decay statistical models to the data
where Kd is the per-length evasion rate of Ar and a is the ratio of exchange rates between Ar and SF6. This model assumes that both Ar and SF6 declined exponentially with distance downstream (x) and that residual errors were normally distributed with a mean of 0 and standard deviations σA for Ar and σS for SF6. Parameters in this model are An0, Sn0, Kd, a, σA, and σS.
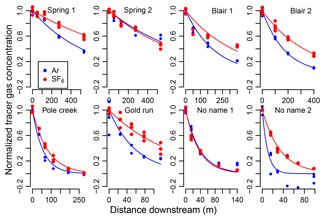
Figure 2Exponential decline of normalized argon and SF6 at each downstream sampling site for each stream shows that rates of decline for SF6 (blue) are lower than that for Ar (red). Points are normalized tracer gas concentrations, Anx and Snx, and lines are exponential model fits (Eq. 6).
We fit these models within a hierarchical Bayesian framework. We were most interested in the value of a, i.e., the ratio of gas exchange for Ar and SF6. For any stream, j, we estimated aj by using partial pooling across additions such that its prior probability was
where amean had a prior distribution of . This distribution had a mean of 1.36, which is the expected ratio of kAr : based on Eq. (1), and a standard deviation of 1 allowing for considerable variation in amean from 1.36. The among-stream variation aj (σa) had a half-normal prior distribution of . Prior probability for Kd was , where −0.1 would be a very high rate of gas exchange. Prior probabilities for An0 and Sn0 were .
We fit this model by simulating the posterior parameter distributions using the program Stan (Stan Development Team, 2018) via the rstan package in R (R Core Team, 2016). Stan uses a Markov chain Monte Carlo (MCMC) method to simulate posterior distributions. For each parameter we ran four MCMC chains with 500 steps for burn-in and 1000 for sampling. We visually checked the chains for convergence and that of the scale reduction factor, , for all parameters.
We converted the per-distance rate to gas exchange of Ar to per-unit time (K, d−1) as , where v is stream velocity (m d−1). Gas exchange velocity (k, m d−1) was calculated as
To facilitate comparison with other studies, we scaled our temperature-specific estimates of k from each stream to k at a Schmidt number of 600 (k600) following Eq. (1) using equations to estimate Sc from Raymond et al. (2012).
We enriched all streams with Ar and estimated gas exchange rates with varying precision. Enriched Ar : N2 at the first station downstream from the addition site averaged 7 % higher than the ambient Ar : N2 (range 1.2 to 18 %). This low enrichment was large enough to easily measure a decline in Ar : N2 to ambient (Fig. 2), but low enough to minimally affect absolute N2 concentration via degassing of N2 if we had, for example, enriched Ar 10-fold. Gas exchange rates, Kd, ranged from 0.00067 to 0.050 m−1 and the 95 % credible interval on these rates averaged 0.42 % (range 36–54 %) of the rate itself. Precision on our Ar : N2 measures was high. The median standard deviation of replicate samples at each station was , corresponding to a coefficient of variation (cv) of 0.09 %. The cv for Ar concentration was 2.5 times higher at 0.23 %, showing that normalizing Ar by N yielded more precise estimates. The coefficient of variation for replicates of SF6 analyses was 5 %, much higher than that for Ar : N2.
Ratios of KAr:KSF6 measured in each injection varied greatly and were higher than the expected ratio of 1.36. These ratios (aj) varied from 0.6 to 3.4 (Table 1) and the mean of the pooled ratio (amean) was 1.8 with a 95 % credible interval, 1.1–2.5. Variation among releases was high, with σa=0.9. The credible interval in a averaged 49 % of a, showing that estimates of SF6 evasion had slightly more uncertainty than that for Kd. This finding is despite the fact that σS was lower than σA, likely because some values of normalized A (Anx) were negative. Negative values of Anx increase σS, but do not necessarily increase uncertainty in the estimate of Kd because the predicted Anx values are always > 0 in an exponential model.
Variability in a led to potential for error in estimating k600 between Ar and SF6. K600 based on SF6 was lower than that for Ar for six of the eight additions (Fig. 3). Deviance from a 1 : 1 line exceeded that of the statistical errors around Kd in the models because the posterior distributions themselves deviated from the 1 : 1 line (Fig. 3).
Gas exchange was high at our steep streams. Gas exchange velocity (k600) ranged from 5.4 to 208 m d−1 and covaried tightly with variation in stream slope (Fig. 4). The k600 from our streams were much higher than most literature values; the four sites with slopes ≥0.05 exceeded 99 % of the values in Raymond et al. (2012). The per-time rate of gas exchange ranged from 28 to 740 d−1 (Table 1).
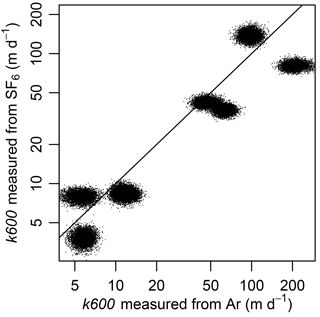
Figure 3k600 measured from SF6 was lower than predicted from k600 measured from argon in six of the eight injections. Each injection is represented by a cloud of points that represents 6000 draws from the posterior distributions of kj and aj, from which we calculated gas exchange velocity (k) following Eq. (8) and converted to k600 using Eq. (1). Line is 1 : 1. Note log-scaled axes.
Despite low enrichment of Ar : N2, we estimated Kd based upon exponential declines of this tracer gas signal. On the surface, one might consider Ar to be a poor tracer gas because it is the third most abundant gas in the atmosphere at 1 % concentration, thus requiring a large increase in concentration to detect a decline. However, because MIMS is highly precise when measuring gas ratios (Kana et al., 1994), it is not necessary to elevate concentrations greatly. This low enrichment has two advantages. One is the practical aspect of not needing to haul a big tank of gas to a remote stream (a 2.2 kg tank lasted us for several additions). The second is that the Ar bubbling stripped little of the N2 from the stream. A potential concern when conducting these experiments is that excess Ar bubbled to the stream will strip N2 as Ar diffuses from bubbles and N2 diffuses in. If this N2 flux is large, one would need to model the concomitant invasion of N2 as well as the evasion of Ar. How much N2 did the Ar strip? We averaged an enrichment of 7 % of ambient Ar concentration with a high of 18 %. This high value corresponds to in an increase in dissolved Ar from 0.476 to 0.561 mg L−1, which is an enrichment of 0.00214 mmol Ar L−1. Assuming a mole for mole exchange with N2 gas, there would be a 0.00214 mmol L−1 decline in N2 from its saturation concentration of 0.455 mmol L−1. This value represents a 0.47 % decline in dissolved N2, a small amount relative to the 18 % increase in Ar.
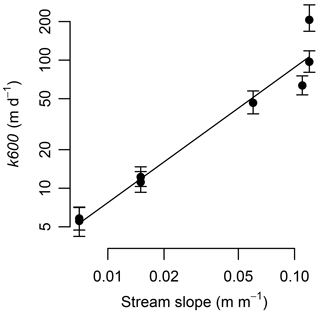
Figure 4Gas exchange velocity increased as a power relationship with stream slope. Equation is . Error bars are the 95 % credible intervals.
However, added Ar must exceed a threshold to have a high enough signal-to-noise ratio to detect a decline in Ar. We suggest at least a 3 % increase in the Ar concentration. Given that measurement error with the MIMS is constant across a range of concentrations, all things equal, higher values of Ar : N2 are better, until such an amount that it is necessary to model concomitant N2 invasion. We did not test the conditions under which we could increase the incorporation rate of Ar into streams, but it seems reasonable to assume that higher Ar flow rate, larger air stones, and deeper pools in which to inject Ar would all increase values of Ar : N2. We used a fine-bubble air stone and suggest that this device greatly facilitated Ar exchange. One needs to be aware of changing temperature between the ambient and during plateau samples. Changing temperature 5 ∘C can cause a 1 % change in Ar : N2; hence, one needs to estimate ambient Ar : N2 during plateau if temperature is changing either by calculating ambient Ar : N2 at sampling temperature or monitoring at an upstream station.
Our estimates of the ratio of (a) were higher than the 1.36 expected based on Schmidt number scaling (Jähne et al., 1987) and the 1.33 based on Eq. (3). This ratio a also varied greatly among injections, such that we had high uncertainty on the actual value of a (Table 1). Thus, there are two problems. One is estimates of Kd for either tracer gas contained substantial error, leading to high variation in estimates of a. The other is that a was inexplicably higher than predicted for both smooth surface and bubble-mediated transfer. Either the theory for scaling in Eqs. (1) and (3) (Woolf et al., 2007; Goddijn Murphy et al., 2016) did not work in our case or we estimated either or with bias. From a theoretical perspective, this question behind a>1.36 is compelling, because if true it complicates models of bubble-mediated gas exchange (Goddijn Murphy et al., 2016). From a practical perspective – where one simply needs to estimate k600 for O2 exchange – this question is less germane given that one could simply use Ar rather than SF6. If one uses tracer estimates for SF6, and our estimate of a was in fact 1.8, then, all else equal, gas exchange will be estimated at times lower than the true value, which we observed for six of the eight injections (Fig. 3). If using these gas exchange rates to estimate metabolism, then estimates of ecosystem respiration will also be 0.75 times too low. This bias in ecosystem respiration may be small relative to the effects of groundwater, probe calibration, and process error (Appling et al., 2018), but this bias adds to the complications in estimating ecosystem respiration from diel O2 data (Demars et al., 2015).
In steep, turbulent streams and rivers, bubbles likely cause most of the gas exchange (Hall et al., 2012), complicating scaling among gases because one must consider variation in solubility as well as variation in Sc. Theory from Woolf et al. (2007) suggests that at low solubilities variation in Sc is all that is needed to scale among gases. Thus, scaling from SF6 to Ar or O2 may be constant as kb approaches Kw. Although we did not assess propane in this study, based on the similarity of propane Sc and α with SF6, it is likely that there is not a strong solubility effect on its rate of kb. For gases with much higher solubility, i.e., CO2, scaling may deviate strongly when bubbles dominate gas exchange (Fig. 1) because bubbles do not reach equilibrium and this scaling depends upon both Sc and solubility. Such streams have high rates of gas exchange and error in estimating k for CO2 that may greatly affect flux estimates in these streams. Thus, we caution using the findings here for estimating CO2 flux in streams with high turbulence. In addition, our subsequent work (Amber J. Ulseth, unpublished data, 2018) will show that it is not possible to predict k600 in highly turbulent stream based on models from low-energy streams and rivers (Raymond et al., 2012). Streams with steep slopes, such as our four steepest streams, have much higher gas exchange than would be predicted from current empirical models (Raymond et al., 2012).
We recommend using Ar as a tracer gas in small streams. Argon is an inert and easily obtained gas that one can precisely measure using MIMS. In addition, Ar is not a greenhouse gas. While SF6 is inert and easily detectable, thus making a potentially ideal tracer, SF6 has 23 500 times the greenhouse forcing of CO2 (Myhre et al., 2013). It is somewhat ironic to study carbon cycling using a tracer gas with that much greenhouse forcing. If one is interested in O2 exchange, then Ar is an optimal tracer because it has nearly the same solubility and diffusivity of O2, thus eliminating the need to scale between gases. Given uncertainty with scaling due to bubbles and the higher-than-predicted scaling ratio (a) found here, scaling from SF6 to O2 is somewhat uncertain. SF6 does hold the advantage as a gas tracer for large streams and rivers. We focused only on small streams here and have not tested this method on larger streams and rivers. One would need to add much more Ar, which is difficult, but possible with larger tanks and air stones. SF6 is so detectable that it is used in very large rivers (Ho et al., 2011). But it may be easier to measure gas exchange in large rivers using diel cycling of O2 in lieu of a tracer (Hall et al., 2016). In fact, with low gas exchange, diel O2 cycling may provide more accurate estimates of k600 than tracer additions that extend for multiple kilometers downstream (Holtgrieve et al., 2015) and with a long time series of diel O2, one can obtain even better estimates of k600 (Appling et al., 2018). The Ar method we present here, however, worked well in small, steep streams where high rates of gas exchange required empirical measurements for accurate estimates of k600.
Code and data for all analyses are available in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-15-3085-2018-supplement.
ROH Jr. and HLM designed the study, conducted fieldwork, measured SF6, and analyzed data. HLM measured Ar : N2. ROH Jr. wrote the first draft of the paper and made the figures.
The authors declare that they have no conflict of interest.
Ina Goodman, Alison Appling, Pavel Garcia, Keli Goodman, Brady Kohler,
Brittany Nordberg, and Rachel Usher assisted with fieldwork. Michelle Baker
and Autumn Slade set us up with their GC and provided food. Financial support
came from National Science Foundation grants EPS-1208909 and EF-1442501.
Amber Ulseth, Tom Battin, Lauren Koenig, Daniel F. McGinnis, and an anonymous
reviewer read and commented on early drafts of this paper. We dedicate this
paper to the memory of Ina Goodman.
Edited by: Tom J. Battin
Reviewed by: D. F. McGinnis and one anonymous referee
Alin, S., Maria de Fátima, F., Salimon, C., Richey, J. E., Holtgrieve, G. W., Krusche, A. V., and Snidvongs, A.: Physical controls on carbon dioxide transfer velocity and flux in low-gradient river systems and implications for regional carbon budgets, J. Geophys. Res.-Biogeosci., 116, G01009, https://doi.org/10.1029/2010JG001398, 2011. a
Appling, A. P., Hall, Jr., R. O., Yackulic, C. B., and Arroita, M.: Overcoming equifinality: Leveraging long time series for stream metabolism estimation, J. Geophys. Res.-Biogeosci., 123, 624–645, https://doi.org/10.1002/2017JG004140, 2018. a, b, c
Asher, W. and Wanninkhof, R.: Transient tracers and air-sea gas transfer, J. Geophys. Res.-Oceans, 103, 15939–15958, 1998a. a
Asher, W. E. and Wanninkhof, R.: The effect of bubble-mediated gas transfer on purposeful dual-gaseous tracer experiments, J. Geophys. Res.-Oceans, 103, 10555–10560, 1998b. a, b
Bernhardt, E., Heffernan, J., Grimm, N., Stanley, E., Harvey, J., Arroita, M., Appling, A., Cohen, M., McDowell, W., Hall, R., Read, J., Roberts, B., Stets, E., and Yackulic, C.: The metabolic regimes of flowing waters, Limnology and Oceanography, 63, s99–s118, https://doi.org/10.1002/lno.10726, 2018. a
Borges, A., Delille, B., Schiettecatte, L., Gazeau, F., Abril, G., and Frankignoulle, M.: Gas transfer velocities of CO2 in three European estuaries (Randers Fjord, Scheldt, and Thames), Limnol. Oceanogr., 49, 1630–1641, 2004. a
Cole, J. J. and Caraco, N. F.: Atmospheric exchange of carbon dioxide in a low-wind oligotrophic lake measured by the addition of SF6, Limnol. Oceanogr., 43, 647–656, 1998. a
Demars, B. O., Thompson, J., and Manson, J. R.: Stream metabolism and the open diel oxygen method: Principles, practice, and perspectives, Limnol. Oceanogr.-Methods, 13, 356–374, 2015. a
Goddijn Murphy, L., Woolf, D. K., Callaghan, A. H., Nightingale, P. D., and Shutler, J. D.: A reconciliation of empirical and mechanistic models of the air-sea gas transfer velocity, J. Geophys. Res.-Oceans, 121, 818–835, 2016. a, b, c
Hall, R. O., Kennedy, T. A., and Rosi-Marshall, E.: Air-water oxygen exchange in a large whitewater river, Limnol. Oceanogr.-Fluids Environ., 2, 1–11, 2012. a
Hall, R. O., Tank, J. L., Baker, M. A., Rosi-Marshall, E. J., and Hotchkiss, E. R.: Metabolism, gas exchange, and carbon spiraling in rivers, Ecosystems, 19, 73–86, 2016. a, b
Hamme, R. and Emerson, S.: The solubility of neon, nitrogen and argon in distilled water and seawater, Deep-Sea Res. Pt. I, 51, 1517–1528, 2004. a
Ho, D. T., Schlosser, P., and Orton, P. M.: On factors controlling air–water gas exchange in a large tidal river, Estuar. Coast., 34, 1103–1116, 2011. a
Holtgrieve, G. W., Schindler, D. E., Branch, T. A., and A'mar, Z. T.: Simultaneous quantification of aquatic ecosystem metabolism and reaeration using a Bayesian statistical model of oxygen dynamics, Limnol. Oceanogr., 55, 1047–1063, 2010. a
Holtgrieve, G. W., Schindler, D. E., and Jankowski, K.: Comment on Demars et al. 2015, “Stream metabolism and the open diel oxygen method: Principles, practice, and perspectives”, Limnol. Oceanogr.-Methods, 14, 110–113, 2015. a
Hornberger, G. M. and Kelly, M. G.: Atmospheric reaeration in a river using productivity analysis, J. Env. Eng.-Div.-ASCE, 101, 729–739, 1975. a
Jähne, B., Münnich, K. O., Bösinger, R., Dutzi, A., Huber, W., and Libner, P.: On the parameters influencing air-water gas exchange, J. Geophys. Res.-Oceans, 92, 1937–1949, 1987. a, b
Kana, T. M., Darkangelo, C., Hunt, M. D., Oldham, J. B., Bennett, G. E., and Cornwell, J. C.: Membrane inlet mass spectrometer for rapid high-precision determination of N2, O2, and Ar in environmental water samples, Anal. Chem., 66, 4166–4170, 1994. a, b, c
Myhre, G., Shindell, D., Bréon, F.-M., Collins, W., Fuglestvedt, J., Huang, J., Koch, D., Lamarque, J.-F., Lee, D., Mendoza, B., Nakajima, T., Robock, A., Stephens, G., Takemura, T., and Zhang, H.: Anthropogenic and natural radiative forcing, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 658–740, Cambridge University Press, 2013. a
Nicholson, D. P., Wilson, S. T., Doney, S. C., and Karl, D. M.: Quantifying subtropical North Pacific gyre mixed layer primary productivity from Seaglider observations of diel oxygen cycles, Geophys. Res. Lett., 42, 4032–4039, 2015. a
Odum, H. T.: Primary production in flowing waters, Limnol. Oceanogr., 1, 102–117, 1956. a, b
Raymond, P., Hartmann, J., Lauerwald, R., Sobek, S., McDonald, C. P., Hoover, M., Butman, D., Striegl, R., Mayorga, E., Humborg, C., Kortelainen, P., Dürr, H., Meybeck, M., Cais, P., and Guth, P.: Global carbon dioxide emissions from inland waters, Nature, 503, 355–359, 2013. a
Raymond, P. A., Zappa, C. J., Butman, D., Bott, T. L., Potter, J., Mulholland, P., Laursen, A. E., McDowell, W. H., and Newbold, D.: Scaling the gas transfer velocity and hydraulic geometry in streams and small rivers, Limnol. Oceanogr.-Fluids Environ., 2, 41–53, 2012. a, b, c, d, e
R Core Team: R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, https://www.R-project.org/, last access: 30 November 2016. a
Stan Development Team: Stan Modeling Language Users Guide and Reference Manual, Version 2.17.0, available at: http://mc-stan.org, last access: 11 May 2018. a
Wanninkhof, R.: Relationship between wind speed and gas exchange, J. Geophys. Res.-Oceans, 97, 7373–7382, 1992. a, b
Wanninkhof, R., Mulholland, P. J., and Elwood, J.: Gas exchange rates for a first-order stream determined with deliberate and natural tracers, Water Resour. Res., 26, 1621–1630, 1990. a
Woolf, D., Leifer, I., Nightingale, P., Rhee, T., Bowyer, P., Caulliez, G., De Leeuw, G., Larsen, S., Liddicoat, M., and Baker, J.: Modelling of bubble-mediated gas transfer: Fundamental principles and a laboratory test, J. Marine Syst., 66, 71–91, 2007. a, b, c, d, e





