the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Nutrient availability and the ultimate control of the biological carbon pump in the western tropical South Pacific Ocean
Thierry Moutin
Thibaut Wagener
Mathieu Caffin
Alain Fumenia
Audrey Gimenez
Melika Baklouti
Pascale Bouruet-Aubertot
Mireille Pujo-Pay
Karine Leblanc
Dominique Lefevre
Sandra Helias Nunige
Nathalie Leblond
Olivier Grosso
Alain de Verneil
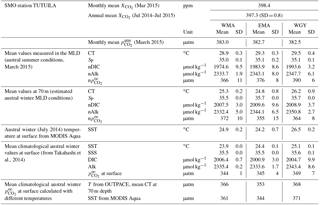
Surface waters (0–200 m) of the western tropical South Pacific (WTSP) were sampled along a longitudinal 4000 km transect (OUTPACE cruise, DOI: 10.17600/15000900) during the austral summer (stratified) period (18 February to 3 April 2015) between the Melanesian Archipelago (MA) and the western part of the SP gyre (WGY). Two distinct areas were considered for the MA, the western MA (WMA), and the eastern MA (EMA). The main carbon (C), nitrogen (N), and phosphorus (P) pools and fluxes provide a basis for the characterization of the expected trend from oligotrophy to ultra-oligotrophy, and the building of first-order budgets at the daily and seasonal timescales (using climatology). Sea surface chlorophyll a well reflected the expected oligotrophic gradient with higher values obtained at WMA, lower values at WGY, and intermediate values at EMA. As expected, the euphotic zone depth, the deep chlorophyll maximum, and nitracline depth deepen from west to east. Nevertheless, phosphaclines and nitraclines did not match. The decoupling between phosphacline and nitracline depths in the MA allows for excess P to be locally provided in the upper water by winter mixing. We found a significant biological “soft tissue” carbon pump in the MA sustained almost exclusively by dinitrogen (N2) fixation and essentially controlled by phosphate availability in this iron-rich environment. The MA appears to be a net sink for atmospheric CO2, while the WGY is in quasi-steady state. We suggest that the necessary excess P, allowing the success of nitrogen fixers and subsequent carbon production and export, is mainly brought to the upper surface by local deep winter convection at an annual timescale rather than by surface circulation. While the origin of the decoupling between phosphacline and nitracline remains uncertain, the direct link between local P upper water enrichment, N2 fixation, and organic carbon production and export, offers a possible shorter timescale than previously thought between N input by N2 fixation and carbon export. The low iron availability in the SP gyre and P availability in the MA during the stratified period may appear as the ultimate control of N input by N2 fixation. Because of the huge volume of water to consider, and because the SP Ocean is the place of intense denitrification in the east (N sink) and N2 fixation in the west (N source), precise seasonal C, N, P, and iron (Fe) budgets would be of prime interest to understand the efficiency, at the present time and in the future, of the oceanic biological carbon pump.
The oceanic biological carbon pump corresponds to the transfer of carbon from the upper surface to the ocean interior by biological processes, greatly influencing atmospheric CO2 concentration and therefore the earth's climate. It is a highly ranked priority in current research in oceanography (Burd et al., 2016). Two biological pumps have been defined (Volk and Hoffert, 1985), the “soft tissue” and “carbonate” pumps associated with organic matter or calcium carbonate processes (e.g., production, export, remineralization or dissolution). The “soft tissue” pump (see Moutin et al., 2017a; their Fig. 1), considering both its intensity and shorter timescales, is by far the larger contributor to the dissolved inorganic carbon gradient between the upper surface and the deep sea. Following climate alteration, the biological “soft tissue” pump begins to deviate from its equilibrium condition, meaning that its influence on atmospheric CO2 change may occur at timescales shorter than previously thought (Sarmiento and Gruber, 2006). Because the strength of the biological carbon pump depends on nutrient availability in the upper ocean, and more particularly on N availability (Falkowski et al., 1998; Tyrell, 1999; Moore et al., 2013), which is in the long term regulated by external input by N2 fixation and internal denitrification (Grüber and Sarmiento, 1997; Codispoti et al., 2001; Deutsch et al., 2001, 2007; Brandes and Devol, 2002; Grüber, 2004; Mahaffey et al., 2005; Codispoti, 2007; Capone and Knapp, 2007; Moutin et al., 2008; Deutsch and Weber, 2012; Landolfi et al., 2013; Jickells et al., 2017), quantitative evaluation of the regulation, interdependence, and patterns of change of these two processes require attention at the present time. It has been suggested earlier that N2 fixation may play a large part in changing atmospheric CO2 inventories (McElroy, 1983), but at long timescales and taking into account major differences in Aeolian iron input (Falkowski, 1997; Broecker and Henderson, 1998). Because N2 fixation may ultimately be controlled by iron availability, and because dust delivery to the ocean is climate sensitive, there may be inextricably linked feedback mechanisms that regulate N2 fixation, atmospheric CO2 concentrations, and dust deposition over relatively long periods (Michaels et al., 2001; Karl, 2014). Although fundamental, the timescales by which N sources and sinks are coupled in the ocean remain uncertain (Falkowski et al., 1998; Brandes and Devol, 2002; Straub et al., 2013). Excess P emerges as a master variable to link them in the modern ocean (Deutsch et al., 2007), as well as from a paleobiogeochemical point of view (Straub et al., 2013). It has been suggested that the recent (since the beginning of the industrial era) increase in production by N2-fixing cyanobacteria may have provided a negative feedback response to rising atmospheric carbon dioxide concentrations (McMahon et al., 2015), although an inverse trend was also proposed (Kim et al., 2017). While the observed changes in N2 fixation and biogeochemical cycling reflect either natural oceanic variability or climate change (Karl et al., 1997; Karl, 2014), the most probable changes for the near future in both N2 fixation and denitrification processes following climate forcing are predicted to be a strengthening control of the carbon cycle by P availability (Moutin et al., 2008).
The western tropical South Pacific (WTSP) is a poorly studied area where large blooms of diazotrophs were previously observed by satellite (Dupouy et al., 2000, 2011), and which has been recently qualified as a hotspot of N2 fixation (Bonnet et al., 2017). It is hypothesized that following the South Equatorial Current (SEC), the N-depleted and P-enriched waters from areas of denitrification located in the east Pacific reach waters with sufficient iron in the west to allow N2 fixation to occur (Moutin et al., 2008; Bonnet et al., 2017). While horizontal advection of waters from the east through the SEC probably supports an active biological pump in the WTSP, local vertical convection may also play a central role.
In addition to the main objective of following the same water mass for several days (de Verneil et al., 2018) by a quasi-Lagrangian experiment (Moutin et al., 2017a) in order to propose daily budgets (Caffin et al., 2018; Knapp et al., 2018), or short term biological trends (Van Wambeke et al., 2018), here we propose to work at larger space and time scales, in complement to the work by Fumenia et al. (2018) showing that N2 fixation in the WTSP may influence the whole South Pacific (SP) Ocean. While many recent works focus on small spatial scales influencing the biological carbon pump (Lévy et al., 2012; Stukel et al., 2017), we found it important to also show results from a larger-scale study in the OUTPACE (Oligotrophy to the UlTra-oligotrophy PACific Experiment) special issue (Moutin et al., 2017b), showing that they are complementary rather than mutually exclusive. Another interest of this study is that we are far from resolving seasonal variations in the main biogeochemical variables in the WTSP, still largely under-sampled compared to the North Pacific and Atlantic. Therefore, the aim of this study is to provide a large spatial (hundreds of kilometers) and temporal (annual) scale study of the main biogeochemical C, N, and P stocks and fluxes in the upper 200 m of the WTSP Ocean from measurements gathered during the stratified period, and to evaluate the main seasonal trends on the basis of estimations of previous winter conditions and climatological analysis.
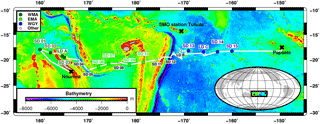
Figure 1Transect of the OUTPACE cruise (18 February–3 April 2015) superimposed on a bathymetry map (GEBCO_2014 grid) of the western tropical South Pacific Ocean. The two types of stations, short duration and long duration, are indicated together with the stations chosen to represent three selected areas: the western Melanesian Archipelago (WMA in dark green), the eastern Melanesian Archipelago (EMA in light green), and the western SP gyre (WGY in blue). SMO station Tutuila (American Samoa; lat. 14.247∘ S, long. 170.564∘ W).
2.1 General method and strategy
2.1.1 Station locations, chronology, CTD measurements, and sample collection
The OUTPACE cruise was carried out between 18 February and 3 April 2015 from Nouméa (New Caledonia) to Papeete (French Polynesia) in the WTSP (Fig. 1). We sampled water along a 4000 km transect from the oligotrophic water of the MA to the clearest ocean waters of the SP gyre (Moutin et al., 2017a) from a SBE 911+ CTD rosette. Euphotic zone depth (EZD) was immediately determined on board from the photosynthetically available radiation (PAR) at depth compared to the sea surface PAR(0+), and used to determine the upper water sampling depths corresponding to 75, 54, 36, 19, 10, 3, 1 (EZD), 0.3, and 0.1 % of PAR(0+). CTD sensors were calibrated and data processed post-cruise using Sea-Bird software in 1 m bins. Conservative temperature, absolute salinity, and potential density were computed using TEOS-10 (McDougall and Barker, 2011). Chlorophyll a (Chl a) in mg m−3 were measured with an Aqua Trak III fluorimeter (Chelsea Technologies Group Ltd.). All samples were collected from 24 12 L Niskin bottles equipped with silicone rubber closures and tubing for measurements (see Sect. 2.2, “Analytical chemical methods”) for stock variables (dissolved oxygen; dissolved inorganic carbon, DIC; total alkalinity, TA; nutrients; Chl a; and particulate and dissolved organic C, N, and P) and fluxes (primary and bacterial production rates; N2 fixation rates; and dissolved inorganic phosphate, DIP, turnover times, TDIP; i.e., the ratio of DIP concentration to DIP uptake).
Table 1General physical and biogeochemical characteristics of the stations investigated along the OUTPACE transect presented in columns: (1) short-duration (SD) or long-duration (LD) station; (2) station number; (3) CTD rosette number; (4) MLD: mixed layer depth (m); (5) EZD: euphotic zone depth (m); (6) Kz: mean 40–200 m vertical eddy diffusivity (m2 d−1); (7) Kz error (m2 d−1); (8) DCMD: deep Chl a maximum depth; (9) DCMC: deep Chl a maximum concentration; i.e., Chl a concentration at the DCMD (mg m−3); (10 and 11) IChl a: integrated (0–70 m) and (0–200 m) Chl a concentration (mg m−2); (12–24) Dx, eDx, Sx, eSx, Nx, and : characteristics of nutriclines (depths in m where NO3 or PO4 reaches zero and slopes in µmol m−4 with associated errors; N: number of samples for the linear relationship; r2: correlation coefficient). QL: quantification limit; nd: no data; nc: not calculated (linear relationship not established); na: nutrient above QL at surface.
2.1.2 Group of stations
For our large-scale study, we considered three areas: the western MA (WMA), the eastern MA (EMA), and the western gyre (WGY) waters. Four 0–200 m CTD casts, mainly devoted to nutrient pool analyses, were considered for each area and correspond to the following stations: SD 1, SD 2, SD 3, and LD A for WMA; SD 6, SD 7, SD 9, and SD 10 for EMA; and SD 13, SD 14, SD 15, and LD C for WGY (Fig. 1, Tables 1 and 2). Therefore, the same number of CTD casts was used to characterize each area. The choice of the stations for each area was essentially geographical, but justified a posteriori by the results. SD 8 was discarded because no nutrient measurements were available. SD 11, SD 12, and LD B were also discarded because a bloom was sampled at LD B, meaning these measurements are outside the scope of this paper, which deals with large-scale spatial and temporal variations. The specificities of the transition area between the MA and WGY waters are presented in another paper of the OUTPACE special issue (de Verneil et al., 2018). WMA, EMA, and WGY will be presented in dark green, light green, and blue, respectively, in close relationship with the expected oligotrophic gradient.
Table 2General physical and biogeochemical characteristics for the three selected areas presented in columns: (1) western Melanesian Archipelago (WMA), eastern Melanesian Archipelago (EMA), and western gyre (WGY) with the corresponding stations chosen; (2) mean or standard deviation (SD); (3) MLD: mixed layer depth (m); (4) EZD: euphotic zone depth (m); (5) Kz: mean 40–200 m vertical eddy diffusivity (m2 d−1); (6) DCMD: deep Chl a maximum depth; (7) DCMC: deep Chl a maximum concentration = Chl a concentration at the DCMD (mg m−3); (8 and 9) IChl a, integrated (0–70 m) and (0–200 m) Chl a concentration (mg m−2); (10–13) Dx, Sx: characteristics of nutriclines (depths in m where NO3 or PO4 reaches zero and slopes in µmol m−4). QL: quantification limit; na: nutrient above QL at surface.

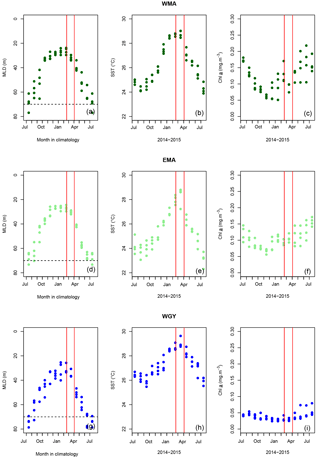
Figure 2Monthly mean mixed layer depth (MLD) against month in climatology (a, d, g), sea surface temperature (SST) (b, e, h), and Chl a (c, f, i) against months from July 2014 to July 2015, respectively, for (a, b, c) the western Melanesian Archipelago (WMA), (d, e, f) the eastern Melanesian Archipelago (EMA) and (g, h, i) the western SP gyre (WGY). The horizontal dashed lines indicate the mixed layer depth of 70 m. The vertical red lines indicate the period of the OUTPACE cruise: 18 February to 3 April 2015.
2.1.3 Mixed layer depths
Mixed layer depth (MLD) was calculated using a threshold temperature of 0.2 ∘C deviation from the reference value at 10 m depth (de Boyer Montegut et al., 2004) from OUTPACE CTD profiles (Table 1). For climatological MLD data (Fig. 2a, d, g), values at each station were extracted from the global climatology at 2∘ resolution proposed by de Boyer Montegut et al. (2004) (downloaded from http://www.ifremer.fr/cerweb/deboyer/mld/Surface_Mixed_Layer_Depth.php, last access: 12 January 2017). The same criterion (threshold temperature deviation of 0.2 ∘C) was used.
2.1.4 Vertical eddy diffusivity measurement
The mean eddy vertical diffusivity Kz between 40 and 200 m was determined for each station from one to several casts undertaken using a using a vertical microstructure VMP-1000 profiler (Bouruet-Aubertot et al., 2018). Briefly, Kz is inferred from the dissipation rate of turbulent kinetic energy, ε, mixing efficiency, γ, and buoyancy frequency, N, according to the Osborn relationship: . Then ε is computed from the microstructure shear measurements (e.g., Xie et al., 2013) and the mixing efficiency is inferred from the Bouffard and Boegman parameterization as a function of turbulence intensity (Bouffard and Boegman, 2013).
2.1.5 Satellite data
Sea surface temperature (SST; Fig. 2b, e, h) and sea surface Chl a (SSChl a; Fig. 2c, f, i) from July 2014 to July 2015 were obtained using processed satellite data provided by the MODIS Aqua mission (downloaded from https://oceandata.sci.gsfc.nasa.gov/, last access: 3 January 2017). The mapped level 3 re-analysis has a 4 km spatial resolution produced at a monthly timescale. For each station, pixels within a rectangle with sides ±0.125∘ longitude and latitude away from the station position were averaged together to produce a single value.
2.1.6 Depth profiles of all discrete variables
All measurements are presented together with their estimated mean concentrations profile (thick line) in Figs. 3, 4, 5, and 6. In order to determine the mean concentrations, the profiles of the variable in question (concentration vs. depth) for all stations included in the group were interpolated between 5 and 200 m with a piecewise cubic hermite interpolating scheme (pchip function in the pracma R package). In case of missing values close to 200 m, the interpolation was stopped at the deepest (above 200 m) point available. The mean profile was estimated from the mean value of the interpolated profiles at every 1-meter depth horizon. For inorganic nutrient concentrations less than the quantification limit (QL; see Sect. 2.2), a zero was indicated to show that a measurement was taken.
Table 3Mean integrated 0–70 m C, N, and P pools (mol m−2) during the OUTPACE cruise (austral summer period) for the three selected areas: western Melanesian Archipelago (WMA), eastern Melanesian Archipelago (EMA), and western gyre (WGY). Dissolved inorganic (DI), dissolved organic (DO), and particulate organic (PO) C, N, and P, respectively.
2.1.7 Normalization
Concentrations normalized by salinity are used to study biological processes independent of variations related to evaporation or precipitation. At global scales, it is common to apply SP = 35 (Millero, 2007). In order to estimate seasonal trends in our specific areas, we normalized to the mean absolute salinity measured at 70 m depth in each area, SA = 35.65 ± 0.04, 35.83 ± 0.04, and 35.91 ± 0.02 g kg−1 for the WMA, EMA, and WGY, respectively. This choice will be further justified hereafter. Important differences in the carbonate system require this normalization to be taken into account, which justifies its use for the other variables, even if changes are relatively small (e.g., for nutrients).
2.1.8 Inventories
Inventories were calculated from the depth profiles of the discrete variables of inorganic and organic C, N, and P dissolved and particulate pools (see Sect. 2.2), measured during the OUTPACE cruise (Table 3) between 0 and 70 m depth. The latter depth corresponded to the average deeper annual MLD obtained using climatology, as explained above and shown in Fig. 2a, d, g. The integrated fluxes were calculated considering the same depths.
2.1.9 Settling particulate matter mass and C, N, and P flux measurements
The settling of particles in the water column outside the upper layer was measured using two PPS5 sediment traps (1 m2 surface collection, Technicap, France), deployed for 4 days at 150 and 330 m at LD A (MA) and LD C (WGY) stations (Fig. 1). The PPS5 traps are covered with baffled lids (sieve 1 cm2) to reduce current shear at the mouth of the trap, but also to prevent large zooplankton and fish from entering the traps. Particle export was recovered in polyethylene flasks screwed on a rotary disk, which automatically changed the flask every 24 h to obtain daily material recovery. The flasks were previously filled with a 2 % (v∕v) buffered solution of formaldehyde (final pH ≈ 8) prepared with in situ deep seawater. A sample of this water is kept to measure dissolved nutrients (phosphate and silicate). Immediately after trap retrieval, samples were stored at 4 ∘C in the dark until they were processed. Back in the laboratory, one part of the sample's supernatant was kept and stored at 4 ∘C to measure dissolved nutrients (phosphate and silicate), and pH was checked on every trap sample. Swimmers (all organisms deemed to have actively entered the trap) were identified under a stereomicroscope and carefully removed with plastic fine-tipped forceps and placed in small vials with some of the reserved trap preservative. The main species removed were copepods, crustaceans (ostracods, euphausiids, amphipods), and pteropods. Microphotographs of each sample were taken. After the swimmers were removed, the whole sample was then rinsed 3 times with ultrapure (Milli-Q) water in order to remove salt and then freeze-dried. Mass particle fluxes were obtained by weighing the freeze-dried sample 5 times. The accuracy of the weighing (and thus of the flux) was 1 % over the whole data series. In this study, swimmers were rinsed and freeze-dried and their dry weight was also determined. Settling particulate matter and swimmers were analyzed separately on an elemental analyzer coupled to an isotope ratio mass spectrometer EA-IRMS (Integra2, Sercon Ltd.) to quantify total C and N. Total P was analyzed as described in Sect. 2.2. The total element measurements for the settling particulate matter were considered to represent the settling particulate organic C, N, and P. The results are presented in Sect. 2.2 (Table 4).
Table 4Sediment trap data. Minimum, maximum, and mean values of particulate matter mass flux and swimmer contents, C, N, and P and Redfield ratio (RR) from particulate matter and swimmers (Zoo). * P calculated from the RR with adding the P measured in the supernatant. Last column: particulate matter mass flux and swimmer content ratio. MA: Melanesian Archipelago, WGY: western SP gyre.

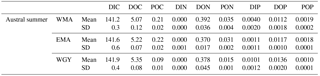
Table 5Molar fraction of CO2 () in dry air measured at SMO station Tutuila (American Samoa; lat. 14.247∘ S, long. 170.564∘ W; see Fig. 1; source: NOAA/ESRL) and derived atmospheric (. Mean values for the carbonate system, measured in the mixed layer depth (MLD) during the OUTPACE cruise (summer conditions), measured at 70 m depth (estimated winter conditions), and NDP-094 climatological data (Takahashi et al., 2014). Oceanic climatological ( are given for different estimations of winter temperature (SST from NDP-094, mean T at 70 m depth from OUTPACE, SST from MODIS Aqua). CT: conservative temperature, Sp: practical salinity, nDIC: normalized dissolved inorganic carbon, nAlk: normalized alkalinity, SST: sea surface temperature; SSS: sea surface salinity. WMA: western Melanesian Archipelago, EMA: eastern Melanesian Archipelago, and WGY: western SP gyre sampled during the OUTPACE cruise.
2.1.10 Ocean–atmosphere CO2 fluxes
The Ocean–atmosphere CO2 fluxes = ) were calculated considering (1) a mean kg of 0.031 ± 0.005 mol m−2 yr−1 µatm−1 (i.e., 85 µmol m−2 d−1 µatm−1) for gas transfer velocity, estimated from the Liss and Melivat (1986) relationship and sea winds derived from satellite measurements (1999–2009). Data came from Boutin et al. (2009; downloaded from http://cersat.ifremer.fr/, last access: 3 March 2017 and extracted on a geographical grid; latitude −17 to −23∘ N, longitude +159 to +211∘ E; one grid was used because no significant differences were obtained in kg for the three areas: WMA, EMA, and WGY), (2) a mean oceanic ( determined for each area during the OUTPACE cruise, and (3) a mean atmospheric ( estimated from the molar fraction of CO2 ( in dry air measured at SMO station Tutuila (American Samoa; lat. 14.247∘ S, long. 170.564∘ W; north of LD B (Fig. 1); NOAA/ESRL – data downloaded from https://doi.org/10.7289/V51834DB, last access: 7 February 2017). A monthly averaged = 398.4 ppm for March 2015 was used, whereas varied from 396.0 to 398.4 ppm from July 2014 to July 2015 at Tutuila with an annual mean of 397.3 ppm. The data were converted to considering 100 % humidity and a total pressure of 1 atm (101 325 Pa), following Weiss and Price (1980), with surface seawater temperature and salinity of each area (Table 5). A total pressure of 101 260 ± 180 Pa was determined considering NCEP-NCAR Reanalysis 1 on the OUTPACE area from July 2014 to July 2015, with no longitudinal trend, justifying the consideration of 1 atm as total pressure for the conversion (downloaded from https://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.html, last access: 19 December 2017).
Table 7Estimated temporal evolution of surface biogeochemical properties between austral winter (up) and summer (below) in µmol L−1 presented in columns: (1) Mean measurements at 70 m depth during OUTPACE were considered to represent the homogeneous upper water column (0–70 m) variables and initial winter conditions (i.e., conditions in July 2014). The summer conditions were those observed during the OUTPACE cruise (March 2015). Δ represents the summer minus winter condition differences. (2) Selected area: western Melanesian Archipelago (WMA), eastern Melanesian Archipelago (EMA), or western gyre (WGY). (3) Mean or standard deviation (SD), (4 to 15) dissolved inorganic (DI), dissolved organic (DO), particulate organic (PO), and total (T) C, N, and P, respectively. All variables were normalized to the mean absolute salinity measured at 70 m depth to discard evolution due to evaporation or precipitation.
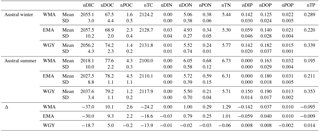
Table 8Estimated temporal evolution of (0–70 m) biogeochemical inventories between austral winter and summer in mmol m−2 presented in columns: (1) Mean measurements at 70 m depth during OUTPACE were considered to represent the homogeneous upper water column (0–70 m) variables and initial winter conditions (i.e., conditions in July 2014). The summer conditions were those observed during the OUTPACE cruise (March 2015). Δ represents the summer minus winter conditions differences. (2) Selected area: western Melanesian Archipelago (WMA), eastern Melanesian Archipelago (EMA), or western gyre (WGY). (3) Mean or standard deviation (SD), (4 to 15) dissolved inorganic (DI), dissolved organic (DO), particulate organic (PO), and total (T) C, N, and P, respectively. All variables were normalized to the mean absolute salinity measured at 70 m depth to discard evolution due to evaporation or precipitation.

2.1.11 Upper layer (0–70 m) daily C, N, and P budgets
Comparative daily C, N, and P budgets of the upper 70 m layer were established for each area (Table 6). Inputs from below associated with vertical turbulent diffusion were calculated using the mean vertical eddy diffusivity, and slopes of nutriclines (Table 2) and DIC gradients calculated between 70 and 200 m using linear regressions (data not shown). The ocean–atmosphere CO2 fluxes were detailed in the previous paragraph. The input of N by N2 fixation was calculated for each area (Table 6) using depth profile sampling and on-deck 24 h 15N2 incubations (Sect. 2.2). The C, N, and P particulate and dissolved organic export were estimated. The method of obtaining particulate export by settling material (Table 4) was described above. Output of dissolved and particulate organic matter by turbulent diffusion was calculated from the mean vertical eddy diffusivity (Table 1) and from gradients estimated with linear regressions (data not shown) between the surface and 70 m depth of DOC-POC (Fig. 5d–g), DON-PON (Fig. 5e–h), and DOP-POP (Fig. 5f–i). When non-significant gradients were obtained, fluxes were nil.
2.1.12 Seasonal variations and upper layer (0–70 m) annual C, N, and P budgets
During OUTPACE, we sampled during the stratified period characterized by minimum MLDs close to 20–40 m (Fig. 2a, d, g), where the largest part of biological fluxes (Fig. 6) occurred. Because the only mechanism able to disrupt this stratification at a large spatial scale is deep water mixing occurring during winter, and more specifically in July in this area (Fig. 2a, d, g), we postulated that conditions at 70 m depth (average depth of wintertime MLD) remained unchanged, or did not significantly change, throughout the year. Considering no large inter-annual differences in winter MLDs, we considered that the mean measurements at 70 m depth during OUTPACE well represented the homogeneous upper water column (0–70 m) variables and initial winter conditions (i.e., conditions in July 2014), allowing us to determine first-order winter to summer seasonal variations (Table 7) and 8-month C, N, and P budgets (Table 8). The dashed lines in Figs. 3, 4, and 5 indicate the upper surface expected values for all variables during the 2014 austral winter, and allow for an evaluation of the temporal variation toward the austral summer season (full lines) in each area.
2.1.13 Surface waters carbonate system climatology
The climatological gridded values proposed in Takahashi et al. (2014), hereafter referred as NDP-094 climatology, were used to validate our estimated values for the carbonate system in the upper surface previous winter conditions (July 2014). The dataset is based on interpolated and calculated TA data (based on regional linear potential alkalinity–salinity relationships) on a 4∘ latitude by 5∘ longitude monthly grid in the reference year 2005. The variable DIC (among others) is calculated from and TA. Data were downloaded from http://cdiac.ess-dive.lbl.gov/ftp/oceans/NDP_094/ (last access: 19 December 2017). Climatological July data centered on 20∘ S were extracted along the cruise transect and 2, 3, and 3 pixels were averaged for comparison in the WMA, EMA, and WGY areas, respectively (Table 5). In order to account for the increase at the earth's surface between 2005 and 2015, a constant offset of 1.5 µatm yr−1 was applied to and a corresponding constant offset of 1 µmol kg−1 yr−1 was also applied to DIC.
2.2 Analytical chemical methods
2.2.1 Oxygen and apparent oxygen utilization (AOU)
Oxygen concentration in the water column was measured with a Seabird SBE43 electrochemical sensor interfaced with the CTD unit. The raw signal was converted to an oxygen concentration with 13 calibration coefficients. The method is based on the Owens and Millard Jr. (1985) algorithm that has been slightly adapted by Seabird in the data treatment software using a hysteresis correction. A new set of calibration coefficients has been determined after the cruise to post-process the whole dataset. Only three coefficients (the oxygen signal slope, the voltage at zero oxygen signal, the pressure correction factor) among the 13 determined by the pre-cruise factory calibration of the sensor were adjusted with the following procedure: the oxygen concentrations measured by Winkler were matched with the signal measured by the sensor at the closing of the Niskin bottles. The three values were fitted by minimizing the sum of the square of the difference between Winkler oxygen and oxygen derived from the sensor signal. Winkler oxygen concentration was measured following the Winkler method (Winkler, 1888), with potentiometric endpoint detection (Oudot et al., 1988) on discrete samples collected with Niskin bottles. For sampling, reagent preparation, and analysis, the recommendations from Langdon (2010) have been carefully followed. The thiosulfate solution was calibrated by titrating it against a potassium iodate certified standard solution of 0.0100N (WAKO). AOU was computed with oxygen concentration at saturation estimated following the algorithm proposed by Garcia and Gordon (1992), considering Benson and Krause values.
2.2.2 TA, DIC, and
Samples for total alkalinity (TA) and dissolved inorganic carbon (DIC) were collected from Niskin bottles in one 500 mL glass flask (Schott Duran) and poisoned directly after collection with HgCl2 (final concentration 20 mg L−1). Samples were stored at 4 ∘C during transport and analyzed 5 months after the end of the cruise at the SNAPO-CO2 (Service National d'Analyse des paramètres Océaniques du CO2, LOCEAN, Paris). TA and DIC were measured on the same sample based on one potentiometric titration in a closed cell (Edmond, 1970). A non-linear curve fitting approach was used to estimate TA and DIC (Dickson, 1981; DOE, 1994). Measurements were calibrated with reference materials (CRM) for oceanic CO2 measurements purchased by the SNAPO-CO2 from Prof. Andrew G. Dickson (Oceanic Carbon Dioxide Quality Control, USA). The reproducibility expressed as the standard deviation of the CRM analysis was 4.6 µmol kg−1 for TA and 4.7 µmol kg−1 for DIC. Moreover, the standard deviation on the analysis of 12 replicates collected at the same depth (25 m) at station LD C was 3.6 µmol kg−1 for TA and 3.7 µmol kg−1 for DIC. The estimation of was made with the SEACARB R package (Gattuso and Lavigne, 2009). The dissociation constants K1 and K2 (for carbonates in seawater) from Lueker et al. (2000) were used. When available, phosphate and silicate concentrations were used in the calculation.
2.2.3 Nutrient, dissolved and particulate C, N, and P pools
Total C, N, and P (TC, TN, TP) in seawater samples may be separated in three pools: the dissolved inorganic C, N, and P pools (DIC, DIN, DIP); the dissolved organic C, N, and P pools (DOC, DON, DOP); and the particulate organic C, N, and P pools (POC, PON, POP). No significant particulate inorganic pools are generally considered in open ocean waters.
Two samples for dissolved inorganic nutrient pool measurements were collected from Niskin bottles in 20 mL polyethylene bottles, and one sample was directly analyzed on board and the other poisoned with 50 µL HgCl2 (20 g L−1) and stored for analysis after the cruise in the laboratory. DIN = [] + [] + [], sum of nitrate, nitrite, and ammonium, respectively. Because [] and [] were negligible compared to [], DIN = []. DIP = [] + [] which are orthophosphates and are also symbolized as PO4. Nitrate, nitrite, and orthophosphate concentrations were determined on a segmented flow analyzer (AAIII HR Seal Analytical) according to Aminot and Kérouel (2007), with a QL of 0.05 µmol L−1. Ammonium was measured by fluorometry (Holmes et al., 1999; Taylor et al., 2007) on a fluorimeter Jasco FP-2020 with a QL of 0.01 µmol L−1.
The dissolved organic pools, DON and DOP, were measured using high-temperature (120 ∘C) persulfate wet-oxidation mineralization (Pujo-Pay and Raimbault, 1994). Samples were collected from Niskin bottles in 100 mL combusted glass bottles and immediately filtered through two pre-combusted (24 h, 450 ∘C) glass fiber filters (Whatman GF/F, 25 mm). Filtered samples were then collected in Teflon vials adjusted at 20 mL for wet oxidation. Nitrate and phosphate formed, corresponding to total dissolved pool (TDN and TDP), and were then determined as previously described for the dissolved inorganic pools. DON and DOP were obtained by the difference between TDN and DIN, and TDP and DIP, respectively. The precision and accuracy of the estimates decreased with increasing depth, as inorganic concentrations became the dominant component in the total dissolved nutrient pools. The limits of quantification were 0.5 and 0.05 µmol L−1 for DON and DOP, respectively. The same pre-filtration was used for dissolved organic carbon (DOC) measurements. Filtered samples were collected into glass pre-combusted ampoules that were sealed immediately after samples were acidified with orthophosphoric acid (H3PO4) and analyzed by high-temperature catalytic oxidation (HTCO; Sugimura and Suzuki, 1988; Cauwet, 1994, 1999) on a Shimadzu TOC-L analyzer. Typical analytical precision is ±0.1–0.5 (SD). Consensus reference materials (http://www.rsmas.miami.edu/groups/biogeochem/CRM.html, last access: 8 May 2018) were injected every 12 to 17 samples to insure stable operating conditions.
The particulate pools (PON, POP) were determined using the same wet oxidation method (Pujo-Pay and Raimbault, 1994). The 1.2 L samples were collected from Niskin bottles in polycarbonate bottles and directly filtered onto a pre-combusted (450 ∘C, 4 h) glass fiber filter (Whatman 47 mm GF/F). Filters were then placed in Teflon vials with 20 mL of ultrapure water (Milli-Q grade) and 2.5 mL of wet oxidation reagent for mineralization. Nitrate and orthophosphates produced were analyzed as described previously. QLs are 0.02 and 0.001 µmol L−1 for PON and POP, respectively. Particulate organic carbon (POC) was measured using a CHN analyzer and the improved analysis proposed by Sharp (1974).
2.2.4 Primary production rates and DIP turnover times
Vertical profiles of DIC uptake (VDIC) and phosphate turnover time (TDIP) were measured once at each station using a dual-labeling method (14C and 33P) considering a 33P period T1∕2 = 25.55 ± 0.05 days (Duhamel et al., 2006). Each sample (150 mL polycarbonate bottle) was inoculated with 10 µCi of 14C carbon (sodium bicarbonate, Perkin Elmer NEC086H005MC; 1 Ci = 3.7×1010 Bq) and 4 µCi of 33P phosphate (H3PO4 in dilute hydrochloric acid, Perkin Elmer NEZ080001MC). The bottles were then placed in blue-screen on-deck incubators representing 75, 54, 36, 19, 10, 2.7, 1, 0.3, and 0.1 % incident PAR (PAR(0+)), https://outpace.mio.univ-amu.fr/spip.php?article135, last access: 8 May 2018) and maintained at constant temperature using a continuous circulation of surface seawater. The same protocol was used for duplicate 150 mL samples, where 150 µL HgCl2 (20 g L−1) had been added as a control for non-biological uptake. After 3 to 24 h (the optimal incubation time was determined from a prior time-series experiment), incubations were stopped by the addition of 150 µL of non-radioactive KH2PO4 (10 mmol L−1) and dark conditions. Filtrations of 50 mL triplicate subsamples were carried out on 25 mm polycarbonate filters (0.2 µm), placed on DIP-saturated support GF/F filters, using a low-vacuum pressure (< 0.2 bar). Filters were not washed with filtered seawater at the end of the filtration, but pressure was briefly increased to 0.6 bar to remove non-cellular 33P radioactivity from the filter. Filters were then placed in low-potassium 6 mL glass scintillation vials (Wheaton) with 500 µL of 0.5 M HCl for 12 h in order to drive off any unincorporated 14C. Then, 6 mL of scintillation liquid (Ultima gold MV, Packard) was added and the radioactivity of the filters measured using a scintillation counter Packard Tri-Carb® 2100TR on board (first count). Initial radioactivity was also measured on 5 replicates for each profile. Samples were then stored until the second count in the laboratory after 33P emission became unmeasurable (12 months). DIC uptake and DIP turnover time were then deduced from the following equations (details in Thingstad et al., 1993; Moutin et al., 2002): TDIP = −Ti ∕ ln(1 − (dpm33P − dpm)∕dpm), where TDIP is DIP turnover time (in days), Ti is the incubation time, dpm33P is the disintegration per minute (dpm) attributable to the 33P activity of the filtered sample, dpm is the dpm attributable to the blank, and dpm is the initial (total) activity of 33P. VDIC = [(dpm14C − dpm)∕dpm] ⋅ [DIC]∕Ti where: VDIC is the C uptake rate (nmol L−1 h−1), dpm14C is the dpm attributable to the 14C activity of the filtered sample, dpm is the dpm attributable to the blank, dpm is the initial (total) activity of 14C added to the sample, [DIC] is the dissolved inorganic carbon concentration of the sample, and Ti is the incubation time. The daily surface photosynthetically available radiation (SPAR) data were used to estimate the daily primary production (PP) values from the PP rates obtained with short time incubation durations using a conversion model (Moutin et al., 1999).
2.2.5 N2 fixation rates
N2 fixation rates were measured using the 15N2 tracer method (Montoya et al., 1996), adapted and precisely described in Bonnet et al. (2018). As for PP measurements, seawater was rapidly collected in triplicates from the Niskin bottles in 2.3 L polycarbonate bottles at six depths (75, 54, 19, 10, 1, and 0.1 % of PAR(0+)). Then 2.5 mL of 15N2 gas (99 atom% 15N, Eurisotop) were injected in each bottle through the septum cap using a gas-tight syringe. All bottles were shaken 20 times to facilitate the 15N2 dissolution and incubated for 24 h from dusk to dusk. To avoid any possible rate underestimation due to equilibration of the 15N2 gas with surrounding seawater, final ™15N enrichment in the N2 pool was quantified for each profile in triplicates at 5 m and at the deep Chl a maximum (DCM). After incubation, 12 mL of each 4.5 L bottle were subsampled in Exetainer vials, fixed with HgCl2, and stored upside down at 4 ∘C in the dark and analyzed onshore within 6 months after the cruise, according to Kana et al. (1994), using a membrane inlet mass spectrometer. Incubation was stopped by gentle filtration of the samples onto pre-combusted (450 ∘C, 4 h) Whatman GF/F filters (25 mm diameter, 0.7 µm nominal porosity). Filters were stored in pre-combusted glass tubes at −20 ∘C during the cruise, then dried at 60 ∘C for 24 h before analysis onshore by an EA-IRMS on an Integra2 (Sercon Ltd.). The detection limit associated with the measurement was 0.14 nmol L−1 d−1. The accuracy of the EA-IRMS system was systematically controlled using International Atomic Energy Agency (IAEA) reference materials, AIEA-N-1 and IAEA-310A. In addition, the natural δ15N of particulate organic N needed for N2 fixation rate calculations was measured in each profile at two depths (surface and DCM).
3.1 General annual trends of MLD, SST, and SSChl a for the three selected areas
MLD against month in the climatology (Fig. 2a, d, g) varied annually from around 70 m depth in July during the austral winter to between 20 and 40 m during the austral summer for the three areas. The OUTPACE cruise from 18 February to 3 April 2015 (red lines) sampled during the stratified period was characterized by minimum MLD and maximum SST (Fig. 2b, e, h). SST varied from 24.2 ± 0.2 to 28.8 ± 0.3, 23.8 ± 0.5 to 28.3 ± 0.7, and 25.9 ± 0.4 to 29.0 ± 0.4 ∘C between July 2014 and July 2015 for WMA, EMA, and WGY, respectively. Mean March 2015 SST of 28.8 ± 0.3, 28.3 ± 0.7, and 29.1 ± 0.4 ∘C are close to the mean conservative temperature measurements measured in the MLD during the OUTPACE cruise of 28.9 ± 0.3, 29.3 ± 0.3, and 29.5 ± 0.4 ∘C for WMA, EMA, and WGY, respectively. The mean conservative temperature measurements at 70 m depth were 25.3 ± 0.3, 24.8 ± 0.9 ∘C, and 26.1 ± 0.9 ∘C for WMA, EMA, and WGY, respectively (Fig. 3a). These values are comparable with the SST measured during the deeper winter mixing in July 2014 of 24.9 ± 0.2, 24.2 ± 0.7, and 26.5 ± 0.2 for WMA, EMA, and WGY, respectively (Table 5). Our hypothesis to consider limited exchanges allowing properties to be conservative at 70 m depth seems reasonable for temperature. Expected seasonal upper surface temperature variations calculated from the differences between temperature at the surface and at 70 m depth were 3.6 ± 0.6, 4.5 ± 1.2, and 3.4 ± 1.3 ∘C for WMA, EMA, and WGY, respectively, agreed relatively well with SST variations observed between July 2014 and March 2015 of 3.9 ± 0.5, 4.2 ± 1.4, and 2.6 ± 0.6 ∘C (Fig. 2b, e, h). Following a similar reasoning, we established a relatively good comparison between Chl a measured at 70 m depth during OUTPACE of 0.217 ± 0.092, 0.091 ± 0.012, and 0.046 ± 0.010 mg m−3 for WMA, EMA, and WGY, respectively (Fig. 3f), and SSChl a obtained during the deeper mixing of 0.173 ± 0.005, 0.121 ± 0.023, and 0.042 ± 0.002 mg m−3 for WMA, EMA, and WGY, respectively (Fig. 2c, f, i). SSChl a well reflected the expected oligotrophic gradient with higher values obtained at WMA, lower values at WGY, and intermediate values at EMA. The increase in SSChl a observed in July seems to be related to the deep mixing during winter. The comparison between measurements at 70 m depth and in the upper mixed layer during OUTPACE may be used as a first approach to characterize surface seasonal changes in physical and biogeochemical properties of upper surface waters (Sect. 4.3).
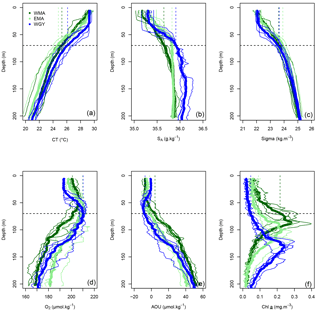
Figure 3Vertical profiles of (a) conservative temperature (CT in ∘C), (b) absolute salinity (SA in g kg−1), (c) potential density (Sigma in kg m−3), (d) dissolved oxygen (O2 in µmol kg−1), (e) apparent oxygen utilization (AOU in µmol kg−1), and (f) Chl a (mg m−3) versus depth (0–200 m) in the three distinct areas sampled during the OUTPACE cruise: the western Melanesian Archipelago (WMA in dark green), the eastern Melanesian Archipelago (EMA in light green), and the western SP gyre (WGY in blue). The horizontal dashed lines indicate the mixed layer depth of 70 m. The vertical dashed lines indicate the upper surface expected values for all variables during the 2014 austral winter.
3.2 General hydrological and biogeochemical conditions allowing for characterization of oligotrophic states of the different upper water masses sampled during OUTPACE
The general hydrological and biogeochemical conditions during OUTPACE provide the means to characterize the oligotrophic states of the different water masses sampled (Table 1). The shallow austral summer MLD varied between 11 and 34 m with a mean of 16.7 m (SD = 6.4 m). The low variation is in agreement with the relatively similar weather conditions and SST along the zonal transect near 20∘ S (Moutin et al., 2017a). The EZD and the DCM depth (DCMD) deepen from west to east, from around 70 m to considerably deeper than 100 m, indicating the higher oligotrophy of the SP gyre water compared to the MA water with shallower nitracline depths. The DCM concentration decreases from west to east, but only slightly, from a maximum of 0.40 mg m−3 to a minimum of 0.25 mg m−3. A better indicator of oligotrophic conditions is the depth of the nitracline () which varied between 46 and 141 m, typical of oligotrophic to ultraoligotrophic areas of the world ocean (Moutin et al., 2012, their Fig. 9). A relative homogeneity of the slopes ( = 47.0 ± 11.5 µmol m−4) was observed (Table 1). Phosphaclines and nitraclines did not match, as shown by the lower observed everywhere. No phosphaclines linked with upper water biological processes were determined in the SP gyre because phosphate concentrations above the QL were measured up to the surface. The , when measurable, was 2.8 ± 1.0 µmol m−4 (Table 1).
The same characteristics are presented for the three areas considered (WMA, EMA, and WGY) in Table 2 by their means and SD. The DCMD (about 10–20 m below the EZD in all areas) increased from 78 ± 10 m in the WMA to 134 ± 14 m in the WGY, with an intermediate value of 104 ± 15 m in EMA. follows the same pattern, with values of 76 ± 10, 100 ± 18, and 116 ± 18 m, respectively, showing a clear relationship between DCMD and (Table 2).
The three areas considered are characterized by similar trends of conservative temperature, absolute salinity, and potential density vs. depth between 0–200 m (Fig. 3a, b, c), i.e., a homogeneity in the mixed layer followed by a drastic change at the base of the mixed layer and a break in slopes around 70 m depth. Temperature increased from the deeper layer to the surface where higher temperature characterized the austral summer heating, while lower salinity above 70 m depth indicate significant fresh water input from rainfall. The deepening of the DCMD from WMA (dark green) to WGY (blue), with an intermediate value for EMA (light green), demonstrates the westward–eastward gradient of increased oligotrophy (Fig. 3f), also reflected by corresponding ( = DDIN, see Sect. 2.2) at similar depths (Fig. 5b). The 0–70 m integrated Chl a decreased considerably from west to east along the transect, from 7.2 ± 2.1 mg m−2 for WMA to 2.0 ± 0.6 mg m−2 for WGY, with an intermediate value of 4.6 ± 0.7 mg m−2 for EMA (Table 2). When integrated over the top 200 m, no difference between Chl a stocks were noticeable with a mean value for the whole dataset of 19.9 ± 2.4 mg m−2.
AOU showed similar patterns in all areas, with a slight decrease from the surface to a minimum between 50 and 70 m, and an increase below 70 m (Fig. 3e). The values close to zero for the first depths indicated saturation or a light super-saturation following classical rapid exchanges with atmospheric oxygen. The AOU values below, and up to, 70 m at both WMA and EMA, and to 100 m depth at WGY, indicated oversaturation. Between 70 and 200 m, almost linear relationships between AOU and depth were observed for all areas.
3.3 C, N, and P pools
The dissolved inorganic (upper), dissolved organic (middle), and particulate organic (below) C, N and P (left to right) pools are represented in Fig. 5. For N and P graphs, a Redfield ratio (RR) of 16 : 1 was systematically applied between N and P axes, allowing for a more direct comparison. DIC in µmol kg−1 (Fig. 4a), nDIC (normalized DIC) in µmol kg−1 (Fig. 4c), and nDIC in µmol L−1 (Fig. 5a) showed linear increasing trends with depth in all areas between 70 and 200 m. The specific variations in nDIC close to the surface will be discussed later. Total alkalinity increased rapidly with depth between 0 and 70 m and was more or less constant down to 200 m (Fig. 4b). Normalized total alkalinity indicated no change in concentration with depth (Fig. 4d), showing that total alkalinity variations were related to fresh water input. Surface was everywhere close to or below the average atmospheric of 383 µatm (Table 5). Nitrate (DIN) was under the QL everywhere in the upper surface down to 70 m (Fig. 5b). Then the increase with depth (nitracline) was almost the same in each area (similar slopes, ) but did not begin at the same depth (), as previously described. Phosphate (DIP) concentrations were considerably higher than nitrate concentrations (considering RR) everywhere except close to the surface at WMA and EMA, where they reached QL. High DIP concentrations around 0.2 µmol L−1 in the upper 70 m were observed at WGY (Fig. 5c). The depletion in DIP was higher in EMA than in WMA (Fig. 5c). DOC, DON, and DOP concentrations were higher close to the surface (Fig. 5d, e, f) and decreased almost linearly with depth down to 200 m with only slight differences between the different areas, particularly for the deeper depth measurements where ∼ 50, 4, and 0.07 µmol L−1 of DOC, DON, and DOP were measured, respectively. The concentration increases at the surface compared to the values at 200 m depth corresponded roughly to around 25, 1.5, and 0.1 µmol L−1 of DOC, DON, and DOP, respectively (in similar proportions to the RR for N and P, but more than 2-fold higher for C). The particulate organic C, N, and P pools showed similar patterns with depth between 70 and 200 m but diverged in the upper layer between the different areas (Fig. 5g, h, i). No significant changes were observed at WGY, while significant increases in concentration close to the surface were observed both in WMA and EMA. The increases in surface water concentrations compared to the value at 200 m depth corresponded roughly to changes around 5, 0.5, and 0.03 µmol L−1 of POC, PON, and POP, respectively (in relatively similar proportions to the RR for C, N, and P).
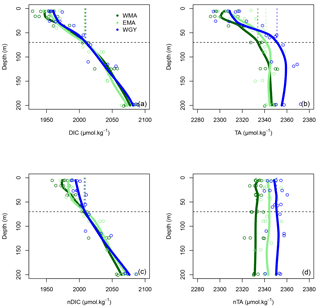
Figure 4Vertical profiles of (a) dissolved inorganic carbon (DIC), (b) total alkalinity (TA), (c) normalized dissolved inorganic carbon (nDIC), and (d) normalized total alkalinity (nTA) against depth (m) for the three distinct areas sampled during the OUTPACE cruise: the western Melanesian Archipelago (WMA in dark green), the eastern Melanesian Archipelago (EMA in light green), and the western SP gyre (WGY in blue). The horizontal dashed lines indicate the mixed layer depth of 70 m. The vertical dashed lines indicate the upper surface expected values for all variables during the 2014 austral winter.
The 0–70 m depth inventories are presented in Table 3. Interestingly, there were very similar C stocks in the three areas, both for the dissolved inorganic and dissolved organic pools. The particulate organic C pool was twice lower in WGY than in the MA. Very similar observations were obtained for all N pools. Nevertheless, DIN stocks were negligible in all areas. DIP stocks were different, and higher in the gyre. The other P pools follow the same pattern as C and N pools, i.e., almost identical in the three areas concerning the dissolved organic pool and twice lower in the gyre for the particulate pool.
3.4 C, N, and P fluxes
Some major fluxes, PP and N2 fixation rates, together with DIP turnover times, are shown Fig. 6. All rates are considerably higher for WMA and EMA than for WGY, where values indicated only slight differences with depth. Conversely, higher PP (Fig. 6a) and N2 fixation (Fig. 6b) rates were measured close to the surface, and rapidly decreased with depth reaching negligible values below 50 m and beyond for WMA and EMA. TDIP values of around 100 days for WGY contrast with lower values for WMA and EMA upper waters close to or even below 2 days (Fig. 6c).
Particulate matter mass flux and swimmer contents collected with sediment traps are presented in Table 4 with C, N, and P partitioning. Wide variability occurs between measurements as shown by the minimum and maximum values obtained. Nevertheless, a mean particulate matter mass flux of 48 mg d−1, 3 times higher in the MA compared to WGY, was obtained, in good agreement with the higher PP rates and biomass in the MA compared to the gyre. Swimmer contents were also highly variable and represent, as a mean, 9.7 (min: 0.7, max: 26.0) times more mass (dry weight) per day than the settling particles in the MA, and 4.4 (min: 1.4, max: 7.1) times for WGY. The mean proportion of C, N, and P in the settling organic matter was 106 : 12.7 : 1.2 for MA and 106 : 16.6 : 0.5 for WGY are in relatively good agreement with the theoretical 106 : 16 : 1 RR. Note that this is also the case for C, N, and P proportions in swimmers both for MA (106 : 15.8 : 0.7) and WGY (106 : 19.9 : 0.7), particularly when P measured in the supernatant was added to the swimmers (see * in Table 4). Otherwise, very low and improbable P contents were found in the swimmers (see the previous column in Table 4).
4.1 A significant biological carbon pump in the WTSP fueled by N2 fixation
We use the surface expected seasonal changes between austral winter and summer in order to draw a first picture of the role of the biological pump in the WTSP. Surface is determined by temperature and salinity changes, and by processes affecting the DIC and alkalinity concentrations, which includes gas exchange, the biological pump, lateral and vertical advection, and mixing (Sarmiento and Grüber, 2006). We will consider that the horizontal spatial scale is large enough to avoid considering lateral advection. Numerical horizontal particle experiments integrating several months of satellite data using Ariane (Rousselet et al., 2018), together with the relative homogeneity of SST along the 4000 km water transect (Moutin et al., 2017a), provides support for this first assumption. Furthermore, we will consider that the influence of salinity changes on the “soft tissue” pump is negligible, as generally considered (Sarmiento and Grüber, 2006).
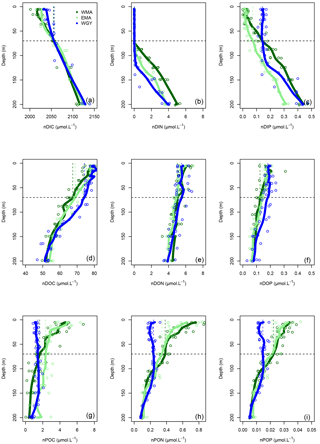
Figure 5Vertical profiles of normalized (n) C, N, and P data against depth (m). Dissolved inorganic (DI), dissolved organic (DO) and particulate organic (PO) C (a, d, g), N (b, e, h), and P (c, f, i), respectively, in µmol L−1, for the three distinct areas sampled during the OUTPACE cruise: the western Melanesian Archipelago (WMA in dark green), the eastern Melanesian Archipelago (EMA in light green), and the western SP gyre (WGY in blue). The horizontal dashed lines indicate the mixed layer depth of 70 m. The vertical dashed lines indicate the upper surface expected values for all variables during the 2014 austral winter.
Upper surface temperature variations between the 2014 austral winter and the 2015 austral summer period were estimated to be 3.6 ± 0.6, 4.5 ± 1.2, and 3.4 ± 1.3 ∘C for WMA, EMA, and WGY, respectively. Estimated winter were 372, 355, and 364 µatm (Table 5). Following the Takahashi et al. (1993) calculation (), considering a closed system with constant DIC and Alk, we estimate an increase in to be +57, +68, and +52 µatm following summer warming for WMA, EMA, and WGY, respectively. The seasonal warming should result in an ∼ 60 µatm increase in , which is not observed for any group of stations; indeed, the differences in were 366 − 372 = −6, 376 − 355 = +21, and 390 − 364 = +26 µatm between winter and summer for WMA, EMA, and WGY, respectively (Table 5). The differences were obtained from normalized DIC and Alk measured during the OUTPACE cruise in the MLD and estimated from the expected normalized winter DIC and Alk. The lower than expected changes suggest that the seasonal variations of due to SST changes are counterbalanced by a seasonal reduction due to DIC and/or Alk changes. We can estimate this term by removing changes due to thermal variation from the observations (), resulting in −63, −47, and −26 µatm for WMA, EMA, and WGY, respectively. The negative signs imply a decrease in DIC or an increase in Alk between winter and summer. When normalized, we do not observe any difference in Alk with depth (Fig. 4d), suggesting that seasonal salinity changes due to high rainfall may explain the small change in Alk observed (Fig. 4b). Therefore, the carbonate pump does not seem to play a significant role in the WTSP, and consequently, we expect a major role of the “soft tissue” pump and thus DIC variations. Considering a Revelle factor γDIC of 9.5, we calculate DIC changes of −35.8, −28.0, and −15.0 µmol kg−1 (ΔDIC = ) necessary to explain the changes in observed. We did indeed observe a decrease in nDIC concentrations of 32.9, 25.7, and 15.3 µmol kg−1 (Table 5) for WMA, EMA, and WGY, respectively (37.0, 30.0, and 18.7 µmol L−1; Table 7, Fig. 5a) between the estimated winter concentration and the mean value measured during the OUTPACE cruise. This may explain the negative sign and the order of magnitude of the DIC changes. This result based on estimated winter values is reinforced by the fact that winter DIC from NDP-094 climatology of 2006.4 ± 0.7, 2000.9 ± 3.0, and 2004.7 ± 9.9 µmol kg−1 are close to our estimates for winter conditions, 2007.5 ± 3.0, 2009.6 ± 9.6, and 2008.9 ± 3.7 µmol kg−1, for WMA, EMA, and WGY, respectively (Table 5). TA also showed good agreement, 2335.4 ± 0.2, 2333.6 ± 1.7, and 2343.4 ± 8.6 µmol kg−1 from the NDP-094 climatology and 2332.4 ± 5.0, 2344.1 ± 6.5, and 2350.8 ± 2.7 µmol kg−1 with our estimates for winter conditions. The differences between climatological and our estimates for winter conditions are wider (Table 5) and can be related to differences in temperature (SST from NDP-094 climatology, SST from MODIS Aqua, and T from our estimates). If are calculated from DIC and Alk (NDP-094 climatology) with SST from MODIS Aqua (361, 344, and 371 µatm) or our estimated temperatures (366, 353, and 368 µatm), the values are close to our estimated winter upper surface (372, 355, and 364 µatm for WMA, EMA, and WGY, respectively) (Table 5). Upper surface estimated DIC seasonal changes may explain why counterintuitive low seasonal changes were obtained despite significant increases in temperature. Therefore, what controls the decrease in nDIC? Is it gas exchange at the air–sea interface, mixing, and/or the biological pump?
Gas exchange may be excluded because surface water ranged from 355 to 390 µatm while the is 383 µatm, with almost no seasonal variations (Table 5). Therefore, surface waters are close to saturation at WGY or under-saturated in the MA all year round and will uptake CO2 from the atmosphere, and as a result DIC should then increase, which was not observed. Thus, our observations are more biological in origin, but there is an inconsistency. The significant decrease in nDIC (Fig. 5a and Table 7), indicating a significant biological soft tissue pump, coincided with no significant changes in nitrate concentration, which were ≤ 0.03 µmol L−1 in all areas (Fig. 5b, Table 7), indicating no or almost no nitrate input by deep winter mixing. Considering the low nitrogen input by upward nitrate turbulent diffusion (see later), we have to consider another nitrogen source, N2 fixation (Fig. 6b), which is really high in the upper water of the WTSP, recently identified as a hotspot for N2 fixation (Bonnet et al., 2017).
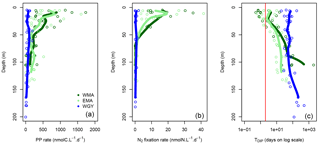
Figure 6Vertical profiles of (a) primary production (PP rate in nmolC L−1 d−1), (b) N2 fixation rate (nmolN L−1 d−1) and dissolved inorganic phosphate turnover times (TDIP in days on log scale) against depth for the three distinct areas sampled during the OUTPACE cruise: the western Melanesian Archipelago (WMA in dark green), the eastern Melanesian Archipelago (EMA in light green), and the western SP gyre (WGY in blue). The vertical red line indicates the critical DIP turnover time of 2 days.
The estimated seasonal nDIC (ΔDIC) variations for the MA waters of 32.9 and 25.7 µmol kg−1 for WMA and EMA, respectively, can be compared to those measured in oceanic gyre time-series sites. They are higher than the ΔDIC ∼ 15 µmol kg−1 observed at the HOT station in the North Pacific subtropical gyre near Hawaii (Dore et al., 2003), and close to the ΔDIC ∼ 30 µmol kg−1 observed at BATS in the subtropical North Atlantic gyre near Bermuda (Bates et al., 2012), where ΔDIC is at least partially attributable to nitrate from below (Sarmiento and Grüber, 2006). Interestingly, the estimated amplitude of surface DIC seasonal change for the MA is only twice lower than the around 50 µmol kg−1 DIC decrease measured between March and April in the North Atlantic (Merlivat et al., 2009), in an area known to experience a large bloom of phytoplankton. The biological “soft tissue” carbon pump, fueled almost exclusively by N2 fixation (see Sect. 4.2), therefore plays a significant role in the WTSP.
4.2 A net sink of atmospheric CO2
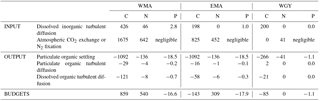
Quantification of the major biogeochemical fluxes on a daily basis allows for certain conclusions to be drawn concerning the upper biogeochemical cycles of C, N, and P (Table 6). C-budgets of the 0–70 m upper layer showed that the MA area appears as a net sink of atmospheric CO2 with a mean atmospheric carbon input in the ocean of 1250 µmol m−2 d−1. Sediment trap POC export was one order of magnitude higher than POC or DOC export by turbulent diffusion, which represented only 7–12 % of the total organic export. Without considering any additional flux, the budget resulted in a surprising daily net accumulation of carbon of 859 µmol m−2 d−1 for WMA, and a quasi-equilibrium for EMA and WGY. Note that the accumulation at WMA resulting in an increase of only several nmol L−1 d−1, is considerably below what we are able to measure at the present time, and longer timescales are thus needed to observe and study the changes (Sect. 4.3).
Averaged integrated PP (IPP) rates were 33.3 ± 12.1, 26.4 ± 16.2, and 6.5 ± 2.4 mmol m−2 d−1, and export by settling and turbulent diffusion (Table 6, in µmol m−2 d−1) represented only 1.2, 1.2, or 0.3 mmol m−2 d−1, for WMA, EMA, and WGY, respectively. The organic matter exported daily compared to IPP represented 3.6, 4.5, and 4.6 %, respectively, in good agreement with previous measurements in oligotrophic areas (Moutin and Raimbault, 2002; Karl et al., 2012), with a high proportion relative to particles settling, 3.3, 4.1, and 4.1 %, rather than turbulent diffusion. Swimmer contents are really high in the sediment traps, considerably above fluxes by settling material (Table 4, last column) and diel vertical migrations of mesozooplankton-micronekton, already observed in the MA (Smeti et al., 2015) and might play a significant role in the transfer of carbon from the upper surface in deeper layers. These organisms spend half of the daytime at depth around 500 m where they loose carbon by respiration.
Except for the WMA area, there were no DIN gradients around 70 m depth and therefore no nitrate input from below by turbulent diffusion (Table 6). Nitrogen input by N2 fixation was by far the largest input of new nitrogen (at least 83 %), and reached values among the highest measured anywhere in the open ocean (Caffin et al., 2018; Knapp et al., 2018). A net daily accumulation of nitrogen is estimated for MA and equilibrium for WGY. Zooplankton diel migrations may also play a significant role in daily N budgets through defecation, excretion, or mortality at depth (Caffin et al., 2018; Valdés et al., 2018). Averaged integrated N2 fixation rates were 0.64 ± 0.21, 0.45 ± 0.27, and 0.04 ± 0.04 mmol N m−2 d−1 for WMA, EMA, and WGY, respectively. The very high N2 fixation rates in the MA, compared to other areas in the world (Bonnet et al., 2017), may provide the new nitrogen required for new PP, creating the necessary decrease in to stimulate CO2 invasion.
The daily P budgets of the 0–70 m upper layer showed losses greater than inputs, in complete contrast to daily C and N budgets showing accumulation in the WMA (Table 6). This observation indicates why this element, compared to carbon and nitrogen, may rapidly become a limiting factor for biological production and specifically of the input of nitrogen by N2 fixation in the MA (Moutin et al., 2008). Nevertheless, the mean particulate P export seemed relatively high (Table 6) and should be considered with caution, considering the huge range of variation, from 0.6 to 68.9 µmol m−2 d−1, for only eight measurements in the MA.
4.3 Estimated seasonal trends of the major biogeochemical stocks and fluxes
As already stated, the dashed lines in Figs. 3, 4, and 5 indicate the upper surface expected values for all variables during the 2014 austral winter, and allow evaluation of the temporal variation toward the 2015 austral summer season (full lines) in each area corresponding to the OUTPACE dataset. The hypothesis allowing this first-order estimation of seasonal variation was presented in Sect. 2.1, validated for SST and Chl a variations in Sect. 3.1, and shown to give good agreement with upper surface DIC expected seasonal changes (Sect. 4.2).
Conservative temperature (Fig. 3a) increased everywhere, but more for WMA and EMA than for WGY, while absolute salinity decreased everywhere. Potential density values were similar in each area at 70 m depth. Similar mean depths of convection were estimated for the three areas (min of 68 m at LD A and max of 73 m at LD C), and justified the mean value of 70 m taken into account for the whole OUTPACE area. The rapid exchange of oxygen between ocean and atmosphere pre-empted significant seasonal changes in the upper surface (Fig. 3d, e). The vertical homogeneous Chl a concentration expected in winter (Fig. 3f) was shown to be in good agreement with climatological SSChl a (Sect. 3.1). Part of the relatively high Chl a concentration estimated in July 2014, specifically in WMA, is probably linked to enhanced vertical winter mixing from the DCM.
The seasonal C, N, and P pool changes may be followed by concentration in Fig. 5 but are easier to discuss as 0–70 m water column inventories (Table 8). As previously indicated, DIC decreased in all areas but more so in the west than in the east (Fig. 5a), following the already described oligotrophic gradient clearly shown both in biomass (Fig. 3f) and in PP (Fig. 6a). The DIC decrease was partially compensated for by the increase in organic concentrations, with the increase in the dissolved concentrations (Fig. 5d) being larger than those of the particulates (Fig. 5g). No increase in the particulate carbon concentration was found for WGY. The decrease in TC (representing the sum of all pools) between winter and summer indicated that 68.1, 61.9, and 68.3 % of ΔDIC were lost from the upper layer, i.e., only 31.9, 38.1, and 31.7 % accumulated in the organic C pools for WMA, EMA, and WGY, respectively (Table 8). Therefore, organic matter accumulation may partly explain why the large input of atmospheric carbon did not result in DIC accumulation in the MA waters. It may partly explain why the total carbon pool decreased so much seasonally. Following the RR, DIN decreases of 236, 198, and 109 mmol m−2 might be expected from the DIC decreases. The DIN decreases were indeed around 0–2 mmol m−2, which is in concordance with very poor DIN replenishment of the upper water column. Conversely, increases of the PON stocks of the same order of magnitude as the RR predicts from POC stocks for WMA and EMA were observed (C : N of 12.0 and 7.3, compared to the RR of C : N ), with a small PON decrease for WGY. The largest increases for the organic pools were for the dissolved phase in all areas (Table 8). DOC accumulation was 3.8 and 8.1 times higher than POC accumulation for WMA and EMA, respectively. Only DOC accumulated at WGY, but with a change twice lower in magnitude than in the MA waters (Table 8). A relatively stronger dissolved organic carbon production compared to particulate production may be observed in oligotrophic areas, depending largely on light and nutrient availabilities (Carlson, 2002). In oligotrophic areas characterized by a low export of particulate organic matter, relatively large dissolved organic matter production, and heterotrophic bacteria often limited by nutrients (Van Wambeke et al., 2002), DOC may accumulate (Copin-Montégut and Avril, 1993; Marañón et al., 2005; Pujo-Pay et al., 2011), which is indeed observed (Fig. 5d). Dissolved organic carbon accumulation reached 391, 445, and 220 mmol m−2 over 8 months (Table 8), which dispersed over 70 m gives a mean 8-month accumulation of 7.0, 7.1, and 3.0 µmol L−1 for the 0–70 m water column. These values, while lower, are of the same order of magnitude of DOC concentration changes observed in the upper mixed layers of 10.1, 9.3, and 5.0 µmol L−1 for WMA, EMA, and WGY, respectively (Fig. 5d, Table 7). Interestingly, the western SP was recently shown as a localized refractory dissolved organic carbon sink (Hansell and Carlson, 2013).
No significant DIN inventory changes were observed, while strong increases in the DON stocks and similar but relatively lower increases were observed for the PON stocks for WMA and EMA (Table 8; Fig. 5e, h). The TN evolution was a net increase in inventories between winter and summer of 49 and 34 mmol m−2 for WMA and EMA, respectively. No significant changes in the N pools were observed at WGY (Table 8, Fig. 5b, e, h). A decrease in DIP stocks was observed in the MA waters between the winter and summer, with no significant change for WGY (Table 8). Following the RR, DIP decreases of 14.7, 12.3, and 6.8 mmol m−2 might be expected from the DIC decreases. The DIP decreases were indeed less, 5.9 and 3.1 mmol m−2 for WMA and EMA, and no decrease was observed at WGY. The DIC decreases are probably only partially related to the DIP decreases in the MA. As for C and N, the highest organic P inventory increases were for the dissolved phase (Fig. 5f, Table 8). Nevertheless, the changes were close to the SD calculated for the mean concentrations and should be considered with caution. As an example, the 1.8 mmol m−2 increase in DOP concentrations for EMA (Table 8) corresponds to the difference between 11.6 ± 1.1 mmol m−2 during winter and 9.8 ± 2.0 mmol m−2 during summer. Note that the SD reported is the maximum SD calculated at each season (Table 8). Small or no decreases in the organic P pools were observed for WGY. Finally, it is clear that seasonal C losses were not compensated by organic carbon accumulation in the 0–70 m layer. Therefore, organic carbon production, which represents by far the largest flux in each area, should be linked with an efficient export from the upper layer, not directly related to RR.
We shall now try to connect the seasonal variations in C, N, and P stocks with the estimated C, N, and P fluxes in order to determine first-order budgets and characterize the main seasonal trends in the WTSP. Our very simple model considers an instantaneous winter mixing followed by 8 months (240 days) of C, N, and P fluxes at the same rates as the mean rates measured during the OUTPACE cruise. All fluxes expressed in mmol m−2 and corresponding to the 8-month period defined (July 2014–March 2015) are summarized in Fig. 7. Accumulation rates are presented inside the boxes and input and output fluxes outside the boxes, with arrows for direction (+ for input, − for output). The X value corresponds to the flux necessary to reach equilibrium in each box. The main question is still how can we explain the large DIC losses in all areas? Even though we obtained (1) a significant DIC input by winter convection and turbulent diffusion, (2) low export of organic matter by settling or turbulent diffusion during the summer period, and (3) a lower than or equal to the meaning a DIC enrichment by atmospheric exchanges, and furthermore (4) no significant input of DIN from below in the 0–70 m upper layer.
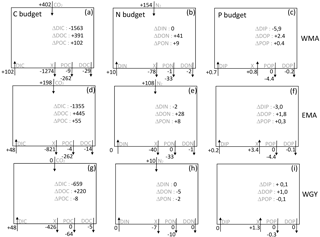
Figure 7C, N, and P estimated budgets in the 0–70 m water column during the 8-month period between deep convection in July 2014 (austral winter) and strong stratification in March 2015 (austral summer) for the three distinct areas sampled during the OUTPACE cruise: the western Melanesian Archipelago (WMA, top), the eastern Melanesian Archipelago (EMA, middle), and the western SP gyre (WGY, bottom). C budgets (a, d, g), N budgets (b, e, h), and P budgets (c, f, i) are shown. Dissolved inorganic (DI), dissolved organic (DO), and particulate organic (PO) C, N, and P fluxes are considered, respectively. Atmospheric exchanges limited to CO2 penetration and N2 fixation are indicated. All fluxes are expressed in mmol m−2 (of elemental C, N, and P, respectively) with arrows indicating direction (input or output). The two numbers for the particulate fluxes correspond to fluxes by turbulent diffusion (above) and particle settling (below). Estimated accumulation rates for the same period are indicated inside the boxes.
The source of new N required to sustain new PP is clearly N2 fixation (Fig. 7b, e, h). Converted to C using the RR of 6.6, new production may represent 12.8, 11.3, and 4.2 % of IPP of 7.94, 6.34, and 1.56 mol m−2 for the 8-month period in the WMA, EMA, and WGY, respectively. New production ≤ 5 % is typical of strong oligotrophic conditions (Moutin and Raimbault, 2002), while above 5 % is related to more productive areas or areas with high N2 fixation rates (Karl et al., 2012). Taking into account the fact that the previous values are for 8 months only, we can estimate annual production rates of 145, 116, and 28 gC m−2 yr−1 for WMA, EMA, and WGY, respectively, close to the average rate of 170 gC m−2 yr−1 reported for the ALOHA station in the North Pacific central gyre (Karl et al., 1996), and to the 86–232 gC m−2 yr−1 range reported for the Mediterranean Sea at the DYFAMED site (Marty and Chiavérini, 2002), known as oligotrophic areas.
Having found the source of new N, several hypotheses may be considered in order to answer the question regarding DIC losses. A first hypothesis is an episodic or seasonal high export of matter considerably different from that measured during the end of the summer season (OUTPACE cruise). We cannot discard this hypothesis specifically because no seasonal data are available at the present time, and also because episodic yet large export fluxes have already been reported in other oligotrophic areas (Böttjer et al., 2017). Nevertheless, the relative constant Chl a concentration during the entire period considered in the upper water column (Fig. 2c, f, i), where most of the production is likely to occur (Fig. 6a), preferentially suggests relatively constant production and therefore export. Furthermore, the C, N, and P proportions of the X fluxes (Fig. 7) in all areas are completely different from RR, even in an opposite sense for P (Fig. 7c, f, i), suggesting that such C fluxes were not directly related to organic matter settling.
A second hypothesis might be in relation to diel vertical migrations of zooplankton-micronekton already described in the MA (Smeti et al., 2015), which may explain significant C losses with proportionally lower N losses and no P losses (Fig. 7). Indeed, mesozooplankton-micronekton feed at night in order to avoid predators and migrate to spend half of the time at around 500 m depth where they respire and lose carbon. Chl a varied only between 0.05 and 0.20 mg m−3 in the MA upper surface, suggesting a strong top-down control by zooplankton able to maintain pigment concentration in a quasi-steady state for many months (Banse, 2013). Zooplankton-micronekton diel vertical migrations, the latter being widespread in the ocean and forming a fundamental component of the biological pump generally overlooked in global models (Bianchi et al., 2013) and well known in the Pacific Ocean (Zhang and Dam, 1998; Al-Mutairi and Landry, 2001; Landry et al., 2011), might explain part of the unexplained ΔDIC observed in the upper surface waters. A third hypothesis might be an underestimation of the settling carbon through methodological issues, mainly concerning the performance of traps (Buesseler et al., 2007) or solubilization (Antia, 2005), which is impossible to take into account without specific measurements. There is in fact no reliable way to separate the swimmers contribution to different elements from that originating from the passive flux (Antia, 2005), and in particular, using formalin, we cannot measure the DOC in the trap supernatant.
Tropical storms, such as Cyclone Pam observed during the OUTPACE cruise (de Verneil et al., 2018), might have an influence on seasonal budgets. Law et al. (2011) reported the effect of such a cyclone in the north Tasman Sea. There was no nitrate entrainment but rather phosphate entrainment due to explicit differences in nitracline and phosphacline depths. This allowed nitrogen fixation to be enhanced in a process close to that we described in our study, albeit in response to physical forcing acting at a smaller spatial scale than winter mixing. During OUTPACE, the strong wind-forcing event Pam entered the southwest Pacific in early March, and a drop in SST and increase in Chl a followed in its wake. The storm did indeed have a fertilizing effect but at relatively short spatial (around Vanuatu islands) and time (around 2 weeks) scales, compared to the larger-scale processes highlighted in the present study.
Mesoscale structures have been previously shown to influence PP (Falkowski et al., 1991; Oschlies and Garçon, 1998; Moutin and Prieur, 2012; Levy et al., 2015). Nevertheless, the mesoscale vertical fluxes due to quasi-geostrophic forcing calculated from satellite data during OUTPACE were weak and acted on a layer displaced from the relevant nutrient reservoirs (de Verneil et al., 2018). The seasonal vertical nutrient input into the photic layer, mainly driven by deep vertical mixing, will be the main influence on annual biological production, whereas summertime mesoscale activity will primarily influence the horizontal spatial distribution of phytoplankton (Rousselet et al., 2018).
4.4 Iron and phosphate availabilities as key factors controlling the N input by N2 fixation and the biological carbon pump in the WTSP
The western SP is known as an iron-rich area (Wells et al., 1999). Iron concentrations measured during the DIAPALIS cruises (http://www.obs-vlfr.fr/proof/vt/op/ec/diapazon/dia.htm, last access: 8 May 2018) near New Caledonia (Martine Rodier, unpublished data in Van den Broeck et al., 2004) were higher than concentrations reported in the sub-tropical North Pacific (Landing and Bruland, 1987), and indicated no clear seasonal variations. Average iron concentrations of 0.57 nmol L−1 were reported in the upper surface waters of the WTSP (Campbell et al., 2005), higher than the ∼ 0.1 nmol L−1 measured in the upper 350 m water column of the SP gyre (Blain et al., 2008) where ferricline depths were located well below nitracline depths (Blain et al., 2008). The Equatorial Undercurrent, which originates near Papua New Guinea, close to New Caledonia, is known to be a source of iron in the SP Ocean (Wells et al., 1999; Ganachaud et al., 2017). Nevertheless, atmospheric deposition fluxes of iron are very low (Duce and Tindale, 1991; Wagener et al., 2008). During OUTPACE, the apparent contradiction between low atmospheric deposition of iron and high surface water iron concentration was resolved. The high iron average concentration within the photic layer in the MA (1.7 nmol L−1) compared to WGY (0.3 nmol L−1) was shown to be related to the influence of hydrothermal sources at shallower depths than commonly associated with volcanic activities (Guieu et al., 2018), confirming the importance of a hydrothermal contribution to the oceanic iron inventory (Tagliabue et al., 2010, 2017; Fitzsimmons et al., 2014). The averaged 0–70 m integrated concentrations were 0.57 ± 0.14, 1.18 ± 1.02, and 0.28 ± 0.03 nM for WMA, EMA, and WGY, respectively. Iron is a major component of the nitrogenase enzyme that catalyzes N2 fixation (Raven, 1988). The high iron concentration likely alleviates the iron limitation of N2 fixation in the WTSP, again considered as a hotspot of N2 fixation (Bonnet et al., 2017).
Phosphate turnover time (TDIP) represents the ratio between natural concentration and uptake by planktonic species (Thingstad et al., 1993) and is considered the most reliable measurement of phosphate availability in the upper ocean waters (Moutin et al., 2008). Phosphate availability in the MA, characterized by DIP < 50 nmol L−1 and TDIP reaching below 2 days, is considerably lower than in the SP gyre, with DIP concentrations above 100 nmol L−1 and TDIP in the order of magnitude of months (Fig. 6c), as already reported (Moutin et al., 2008). Phosphate availability, as well as PP, were shown to follow the same seasonal patterns close to New Caledonia in the MA, suggesting that in this iron-rich area known to sustain high N2 fixation rates, phosphate may appear as a key factor controlling carbon production (Van den Broeck et al., 2004). It was suggested that a seasonal pattern of phosphate availability with higher values (low DIP, high TDIP) related to winter mixing and lower values (higher DIP, lower TDIP) during the stratified period might control Trichodesmium spp. growth and decay in the SP near New Caledonia (Moutin et al., 2005). A TDIP below 2 days was shown to be critical for Trichodesmium spp. growth (Moutin et al., 2005). TDIP below or close to 2 days was measured in the MA upper waters during the OUTPACE cruise (Fig. 6c), and TDIP as low as several hours was measured at LD B station and has been related to the strong biomass and specifically Trichodesmium spp. decline observed at this station (de Verneil et al., 2018). With TDIP around or even below 2 days, the MA appears as a low P area during the stratified period, indicating a probable role of phosphate availability in the control of nitrogen input by the nitrogen fixers. The higher iron availability in the MA is probably the main factor allowing N2 fixation to occur, and phosphate availability the main factor controlling the annual input of N by N2 fixation. A TDIP of 2 days corresponds to the lowest value reported at the ALOHA station in the North Pacific (NP; Table 2 in Moutin et al., 2008), where phosphate availability is considered to play a dominant role in the control of nitrogen fixers (Karl et al., 1997; Karl, 2014). TDIP reached several hours, which is close to the phosphate availability of the Mediterranean Sea or the Sargasso Sea, known for a long time for their phosphate deficiency (Wu et al., 2000; Moutin et al., 2002). While phytoplankton and heterotrophic bacterioplankton may appear N-limited (Van Wambeke et al., 2018; Gimenez et al., 2018), the low availability of phosphate in the upper waters of the WTSP during the stratified period probably controls the biomass of nitrogen fixers and ultimately the input of nitrogen by this process. In a recent mesocosm experiment, high increases in N2 fixation rates, PP rates, and carbon export were obtained after a DIP enrichment of WTSP waters (Berthelot et al., 2015). Nevertheless, several days were necessary to measure significant increases, indicating that regular short-term experiments to establish nutrient limitation as usually operated (Dekaezemacker et al., 2013; Moisander et al., 2012; Moore et al., 2013) may not be relevant in WTSP conditions (Gimenez et al., 2016).
The high DIP and low DIN (excess P or high P*) content of water was suggested as a preliminary condition allowing N2 fixation to occur (Redfield, 1934; Capone and Knapp, 2007; Deutsch et al., 2007), and is a characteristic of surface waters of the SEC flowing from the east to the west in the SP, due to intense denitrification related to one of the main OMZ (oxygen minimum zone) areas in the east Pacific (Codispoti et al., 2001). The alleviation of iron limitation when waters originating from the east reach the WTSP was considered as the main factor explaining the hotspot of N2 fixation observed in the OUTPACE area (Bonnet et al., 2017). The strong nitracline and phosphacline depth differences (Table 1), associated with winter mixing down to around 70 m, allows us to estimate a replenishment of DIP of the order of magnitude of ΔDIP (5.9 mmol m−2 for WMA and 3.0 mmol m−2 for EMA; Fig. 7c, f), far above the vertical input by turbulent diffusion (around 0.7 mmol m−2), together with no DIN replenishment. Alone, these DIP fluxes may support N2 fixation of 94.4 and 48.0 mmol m−2 during this period (following RR), of the order of magnitude of the fluxes of 154 and 108 mmol m−2 calculated for WMA and EMA (Fig. 7b, e), respectively. While horizontal advection of high DIP and low DIN waters from the SP gyre toward the iron-rich WTSP was suggested to create the environmental conditions favorable for diazotroph growth (Moutin et al., 2008; Bonnet et al., 2017), here we suggest that local seasonal winter mixing may also play a significant role in providing excess P to the upper waters, and therefore in controlling nitrogen input by N2 fixation and therefore the associated carbon cycle. Phosphate availability appears, in the iron-rich MA, as the ultimate control of the biological carbon pump. The simulations of the main C, N, and P fluxes at LD A and LD C, using a 1 vertical dimension model with similar physical forcing, strengthen the idea of strong seasonal variations being able to explain the control of N2 fixation and carbon fluxes by the availability of phosphate in the MA and iron at WGY (Gimenez et al., 2018). Iron was hypothesized to prevent N2 fixation at LD C and this allows us to obtain the high DIP concentration observed at LD C.
4.5 Toward reconciliation between simulations and observations?
During the past 10 years, global biogeochemical model simulations suggested relatively high N2 fixation in the SP gyre and low fixation in the western part of the Pacific Ocean (Deutsch et al., 2007; Grüber, 2016), in contradiction with the little data then available. While the decrease in P* toward the center of the gyre observed during the BIOSOPE cruise (eastern tropical South Pacific, ETSP, toward the central gyre 10–30∘ S in latitude) corresponds to the trend observed by Deutsch et al. (2007), N2 fixation in the simulation, with minimum values found on the edge and maximum values found in the center of the gyre, was contrary to our observations (Moutin et al., 2008). The high N2 fixation expected in the ETSP, because “downstream of OMZs, surface waters that initially carry a surplus of phosphorus (because of subsurface denitrification) lose this excess gradually through N2 fixation” (Deutsch et al., 2007), was not confirmed by isotopic budgets (Knapp et al., 2016), suggesting an elusive marine N2 fixation (Grüber, 2016). The discovery of a hotspot of N2 fixation in the whole WTSP covered by the OUTPACE transect and other cruises in the Coral Sea (Bonnet et al., 2017) justifies considering a larger spatial coupling between denitrification and N2 fixation than previously thought (Deutsch et al., 2007). Taking into account the role of iron to allow (or not) N2 fixation to occur seems a necessary basis to reconcile simulations and observations (Dutkiewicz et al., 2012; Monteiro et al., 2011; Weber and Deutsch, 2014). These new modeling studies have identified the WTSP as a unique region with conditions seemingly favorable for significant N2 fixation fluxes (Knapp et al., 2018). Interestingly, the opposite trends between expected N2 fixation and P* observed during the BIOSOPE cruise and possibly attributed to non-Redfieldian processes (Moutin et al., 2008) may be rather due to horizontal advection and isopycnal mixing of water masses originating from the WTSP, and therefore marked by a strong signature of intense N2 fixation (high N* corresponding to low P*; Fumenia et al., 2018), in an opposite sense than the better-known and more widely studied influence of water masses marked by a strong signature of intense denitrification originating from the OMZ (Yoshikawa et al., 2015). Furthermore, the deepening of isopycnals from the eastern to the western SP (Yoshikawa et al., 2015; Fumenia et al., 2018) suggests a deeper (∼ 200 m) influence of excess P waters from the SEC in the MA, deeper than previously hypothesized (Moutin et al., 2008; Bonnet et al., 2017). Because the influence of isopycnal mixing is below the maximum mixing depth estimated in the WTSP (∼ 70 m), the link between N sink in the east and N source in the west implies longer timescales than that associated only with surface circulation. The N budget of the SP Ocean is of prime interest to understand the efficiency, at the present time and in the future, of the oceanic biological carbon pump. Determining the budget requires a precise understanding of the general water mass circulation, which at the present time suffers from a lack of data, specifically during water mass formation (Fumenia et al., 2018).
We found a significant biological soft tissue carbon pump in the WTSP despite no winter replenishment of surface waters by DIN. N2 fixation is the major process introducing the necessary N to sustain the biological soft tissue carbon pump allowing oceanic < in the MA, and therefore significant atmospheric C input. Because of N2 fixation, the WTSP is a significant atmospheric carbon sink.
The upper surface waters of the MA sampled during the stratified period were characterized by a DIP availability close to or below the level required for phosphate sufficiency, which contrasts with observations in the central Pacific gyre at the same latitude. We confirmed the geographical trend of a limitation of N2 fixation in the SP, from a probable iron limitation in the east and central SP Ocean to a P limitation in the west. The limit was clearly shown to be associated with the lower depths of the MA, where sufficient iron was provided to upper surface waters to alleviate iron limitation of N2 fixation, probably by hydrothermal sources at anomalously shallow depths. Extrapolating these data in order to obtain seasonal trends enables us to show that winter vertical mixing, although limited to 70 m depth, may bring sufficient excess P to allow most of the N2 fixation to occur. In addition, more excess P may be locally provided in the upper surface (where N2 fixation was shown to occur predominantly) by winter mixing than by horizontal transport from areas of excess P formation (OMZ). As previously hypothesized (Moutin et al., 2008), the low availability of phosphate in the iron-rich upper waters of the WTSP during the stratified period probably controls the biomass of nitrogen fixers and ultimately the input of nitrogen by this process, and the biological pump. As high nutrient concentrations in high nutrient low chlorophyll (HNLC) areas (Minas et al., 1986) may be considered as the result of an inefficient biological carbon pump (Sarmiento and Grüber, 2006), high phosphate concentrations (and high DIP turnover time) in the SP gyre (Moutin et al., 2008; this study) may be the result of inefficient or nonexistent N2 fixation. Conversely, the low P availability (low concentration and DIP turnover time) in the upper surface of the WTSP is the result of intense N2 fixation. Because iron concentrations are low in the gyre and high in the MA (even during the strongest stratified period), and because of the specific iron needs of diazotrophs, iron availability is the best candidate for preventing nitrogen fixation in the gyre and allowing nitrogen fixation in the MA. Therefore, iron availability and DIP availability may appear as the ultimate controls of biological production and export in the gyre and in the MA, respectively.
The SP Ocean deserves special attention because of its huge volume of water where the N budget is likely to be controlled by N lost in the east (denitrification) and N gain in the west (N2 fixation). Furthermore, both diazotrophy and denitrification are expected to undergo drastic alterations due to climate change (McMahon et al., 2015; Lachkar et al., 2018). Our data suggest that one had better take into account the role of iron and phosphate in global biogeochemical models in order to better reconcile simulations and data, which seems to be the prerequisite to understand at the present time the relationship between N sources and sinks in the SP Ocean. Moreover, it will be of great interest to study future scenarios which consider iron coming from below (hydrothermal sources) in addition to that from above (atmospheric source) in the WTSP and in the whole SP Ocean. Changes in N2 fixation following changes in dust (iron) supply have been suggested to play a central role in explaining past glacial or interglacial changes in CO2 concentration and earth temperature. It was considered that N2 fixation on a regional scale would change global nitrogen availability and the biological carbon pump on the timescale of ocean circulation. The direct link between N2 fixation and carbon export proposed here for the WTSP, a hotspot of N2 fixation, allows for a much closer coupling between N2 fixation and the biological carbon pump, which may in turn require us to consider changes at shorter timescales such as that associated with climate change.
All data and metadata are available at the French INSU/CNRS LEFE CYBER database (scientific coordinator: Hervé Claustre; data manager, webmaster: Catherine Schmechtig) at the following web address: http://www.obs-vlfr.fr/proof/php/outpace/outpace.php, INSU/CNRS LEFE CYBER (2017).
The authors declare that they have no conflict of interest.
This article is part of the special issue “Interactions between planktonic organisms and biogeochemical cycles across trophic and N2 fixation gradients in the western tropical South Pacific Ocean: a multidisciplinary approach (OUTPACE experiment)”. It is not associated with a conference.
This is a contribution of the OUTPACE (Oligotrophy to the UlTra-oligotrophy PACific Experiment) project (https://outpace.mio.univ-amu.fr/, last access: 8 May 2018) funded by the French research national agency (ANR-14-CE01-0007-01), the LEFE-CYBER program (CNRS-INSU), the GOPS program (IRD), and the CNES (BC T23, ZBC 4500048836). The OUTPACE cruise (https://doi.org/10.17600/15000900) was managed by the MIO (OSU Institut Pytheas, AMU) from Marseille (France) and received funding from European FEDER fund under project 1166-39417. The authors thank Nicolas Metzl for constructive comments on the manuscript and the SNAPO-CO2 (Service National d'Analyse des paramètres Océaniques du CO2-LOCEAN – Paris). The authors also thank the crew of the R/V L'Atalante for outstanding shipboard operation. Gilles Rougier and Marc Picheral are warmly thanked for their efficient help in CTD rosette management and data processing, as is Catherine Schmechtig for the LEFE-CYBER database management. The satellite-derived data of sea surface temperature and Chl a concentration and current have been provided by CLS in the framework of the CNES funding; we warmly thank Marie Isabelle Pujol and Guillaume Taburet for their support in providing these data. Aurelia Lozingot is acknowledged for the administrative work.
We acknowledge NOAA, and in particular Rick Lumpkin, for providing the
Surface Velocity Program drifter. The Argo data were collected
and made freely available by the international Argo project and the national
programs that contribute to it (http://www.argo.ucsd.edu,
http://argo.jcommops.org, last access: 8 May 2018). Argo is a pilot
program of the Global Ocean Observing System. Argo DOI
(https://doi.org/10.17882/42182). All data and metadata are available at the following
web address: http://www.obs-vlfr.fr/proof/php/outpace/outpace.php (last
access: 8 May 2018).
Edited by: Emilio
Marañón
Reviewed by: Fanny Monteiro and two anonymous
referees
Al-Mutairi, H. and Landry, M. R.: Active export of carbon and nitrogen at station ALOHA by diel migrant zooplankton, Deep-Sea Res. Pt. II, 48, 2083–2103, https://doi.org/10.1016/S0967-0645(00)00174-0, 2001.
Aminot, A. and Kérouel, R.: Dosage automatique des nutriments dans les eaux marines : méthodes en flux continu, Ed. Ifremer, Méthodes d'analyse en milieu marin, 188 pp., 2007.
Antia, A. N.: Solubilization of particles in sediment traps: revising the stoichiometry of mixed layer export, Biogeosciences, 2, 189–204, https://doi.org/10.5194/bg-2-189-2005, 2005.
Banse, K.: Reflections about chance in my career, and on the top-down regulated world, Annu. Rev. Mar. Sci., 5, 2.1–2.19, 2013.
Bates, N. R., Best, M. H. P., Neely, K., Garley, R., Dickson, A. G., and Johnson, R. J.: Detecting anthropogenic carbon dioxide uptake and ocean acidification in the North Atlantic Ocean, Biogeosciences, 9, 2509–2522, https://doi.org/10.5194/bg-9-2509-2012, 2012.
Berthelot, H., Moutin, T., L'Helguen, S., Leblanc, K., Hélias, S., Grosso, O., Leblond, N., Charrière, B., and Bonnet, S.: Dinitrogen fixation and dissolved organic nitrogen fueled primary production and particulate export during the VAHINE mesocosm experiment (New Caledonia lagoon), Biogeosciences, 12, 4099–4112, https://doi.org/10.5194/bg-12-4099-2015, 2015.
Bianchi, D., Stock, C., Galbraith, E. D., and Sarmiento, J. L.: Diel vertical migration: Ecological controls and impacts on the biological pump in a one dimensional ocean model, Global Biogeochem. Cy., 27, 478–491, https://doi.org/10.1002/gbc.20031, 2013.
Blain, S., Bonnet, S., and Guieu, C.: Dissolved iron distribution in the tropical and sub tropical South Eastern Pacific, Biogeosciences, 5, 269–280, https://doi.org/10.5194/bg-5-269-2008, 2008.
Bonnet, S., Caffin, M., Berthelot, H., and Moutin, T.: Hot spot of N2 fixation in the western tropical South Pacific pleads for a spatial decoupling between N2 fixation and denitrification, P. Natl. Acad. Sci. USA, 114, E2800–E2801, https://doi.org/10.1073/pnas.1619514114, 2017.
Bonnet S., Caffin, M., Berthelot, H., Grosso, O., Guieu, C., and Foster, R.: Contribution of dissolved and particulate fractions to the Hot Spot of N2 fixation in the Western Tropical South Pacific Ocean (OUTPACE cruise), Biogeosciences Discuss., in preparation, 2018.
Böttjer, D., Dore, J. E., Karl, D. M., Letelier, R. M., Mahaffey, C., Wilson, S. T., Zehr, J., and Church, M. J.: Temporal variability of nitrogen fixation and particulate nitrogen export at Station ALOHA, Limnol. Oceanogr., 62, 200–216, 2017.
Bouffard, D. and Boegman, L.: A diapycnal diffusivity model for stratified environmental flows, Dynam. Atmos. Oceans, 61, 14—34, 2013.
Bouruet-Aubertot, P., Cuypers, Y., Doglioli, A., Caffin, M., Yohia, C., de Verneil, A., Petrenko, A., Lefèvre, D., Le Goff, H., Rougier, G., Picheral, M., and Moutin, T.: Longitudinal contrast in Turbulence along a ∼ 19∘ S section in the Pacific and its consequences on biogeochemical fluxes, Biogeosciences Discuss., https://doi.org/10.5194/bg-2018-170, in review, 2018.
Boutin, J., Quilfen, Y., Merlivat, L., and Piolle, J. F.: Global average of air-sea CO2 transfer velocity from QuikSCAT scatterometer wind speeds, J. Geophys. Res., 114, C04007, https://doi.org/10.1029/2007JC004168, 2009.
Buesseler, K. O., Antia, A. N., Chen, M., Fowler, S. W., Gardner, W. D., Gustafsson, O., Harada, K., Michaels, A. F., van der Loeff, M. R., Sarin, M., Steinberg, D. K., and Trull, T.: An assessment of the use of sediment traps for estimating upper ocean particle fluxes, J. Mar. Res., 65, 345–416, 2007.
Brandes, J. A. and Devol, A. H.: A global marine fixed nitrogen isotopic budget: Implications for Holocene nitrogen cycling, Global Biogeochem. Cy., 16, 67.61–67.14, https://doi.org/10.1029/2001GB001856, 2002.
Broecker, W. S. and Henderson, G. M.: The sequence of events surrounding Termination II and their implications for the cause of glacial-interglacial CO2 changes, Paleoceanogr. Paleoclimatol, 13, 352–364, 1998.
Burd, A. B., Buchan, A., Church, M., Landry, M., McDonnell, A., Passow, U., Steinberg, D., and Benway, H.: Towards a transformative understanding of the biology of the ocean's biological pump: Priorities for future research, Report of the NSF Biology of the Biological Pump Workshop, 19–20 February (Hyatt Place New Orleans, New Orleans, LA) 6 pp., https://doi.org/10.1575/1912/8263, 2016.
Caffin, M., Moutin, T., Foster, R. A., Bouruet-Aubertot, P., Doglioli, A. M., Berthelot, H., Guieu, C., Grosso, O., Helias-Nunige, S., Leblond, N., Gimenez, A., Petrenko, A. A., de Verneil, A., and Bonnet, S.: N2 fixation as a dominant new N source in the western tropical South Pacific Ocean (OUTPACE cruise), Biogeosciences, 15, 2565–2585, https://doi.org/10.5194/bg-15-2565-2018, 2018.
Campbell, L., Carpenter, E. J., Montoya, J. P., Kustka, A. B., and Capone, D. G.: Picoplankton community structure within and outside a Trichodesmium bloom in the southwestern Pacific Ocean, Vie Milieu, 55, 185–195, 2005.
Carlson, C. A.: Production and removal processes, in: Biogeochemistry of Marine Dissolved Organic Matter, edited by: Hansell, D. A. and Carlson, C. A., 91–151, Academic, San Diego, Calif., https://doi.org/10.1016/B978-012323841-2/50006-3, 2002.
Capone, D. G. and Knapp, A. N.: Oceanography – A marine nitrogen cycle fix?, Nature, 445, 159–160, 2007.
Cauwet, G.: HTCO method for dissolved organic carbon analysis in seawater: influence of catalyst on blank estimation, Mar. Chem., 47, 55–64, 1994.
Cauwet, G.: Determination of dissolved organic carbon (DOC) and nitrogen (DON) by high temperature combustion, in: Methods of seawater analysis, edited by: Grashoff, K., Kremling, K., and Ehrhard, M., 3rd Ed., Wiley-VCH, Weinheim, 407–420, 1999.
Codispoti, L. A.: An oceanic fixed nitrogen sink exceeding 400 Tg N a−1 vs the concept of homeostasis in the fixed-nitrogen inventory, Biogeosciences, 4, 233–253, https://doi.org/10.5194/bg-4-233-2007, 2007.
Codispoti, L. A., Brandes, J. A., Christensen, J. P., Devol, A. H., Naqvi, S. W. A., Paerl, H. W., and Yoshinari, T.: The oceanic fixed nitrogen and nitrous oxide budgets: Moving targets as we enter the anthropocene?, Sci. Mar., 65, 85–105, 2001.
Copin-Montégut, G. and Avril, B.: Vertical distribution and temporal variation of dissolved organic carbon in the North-Western Mediterranean Sea, Deep-Sea Res., 40, 1963–1972, 1993.
de Boyer Montégut, C., Madec, G., Fischer, A. S., Lazar, A., and Iudicone, D.: Mixed layer depth over the global ocean: an examination of profile data and a profile-based climatology, J. Geophys. Res., 109, C12003, https://doi.org/10.1029/2004JC002378, 2004.
Dekaezemacker, J., Bonnet, S., Grosso, O., Moutin, T., Bressac, M., and Capone, D. G.: Evidence of active dinitrogen fixation in surface waters of the eastern tropical South Pacific during El Nino and La Nina events and evaluation of its potential nutrient controls, Global Biogeochem. Cy., 27, 768–779, https://doi.org/10.1002/gbc.20063, 2013.
Deutsch, C. and Weber, T.: Nutrient Ratios as a Tracer and Driver of Ocean Biogeochemistry, Annu. Rev. Mar. Sci., 41, 4–113, 2012.
Deutsch, C., Gruber, N., Key, R., and Sarmiento, J. L.: Denitrification and N2 fixation in the Pacific Ocean, Global Biogeochem. Cy., 15, https://doi.org/10.1029/2000GB001291, 2001.
Deutsch, C., Sarmiento J. L., Sigman D. M., Grüber N., and Dunne J. P.: Spatial coupling of nitrogen inputs and losses in the ocean, Nature, 445, 163–167, 2007.
de Verneil, A., Rousselet, L., Doglioli, A. M., Petrenko, A. A., Maes, C., Bouruet-Aubertot, P., and Moutin, T.: OUTPACE long duration stations: physical variability, context of biogeochemical sampling, and evaluation of sampling strategy, Biogeosciences, 15, 2125–2147, https://doi.org/10.5194/bg-15-2125-2018, 2018.
Dickson, A. G.: An exact definition of total alkalinity and a procedure for the estimation of alkalinity and total inorganic carbon from titration data, Deep-Sea Res., 28A, 609–623, 1981.
DOE: Handbook of methods for the analysis of the various parameters of the carbon dioxide system in sea water; version 2, edited by: Dickson, A. G. and Goyet, C., ORNL/CDIAC-74, 1994.
Dore, J. E., Lukas, R., Sadler, D. W., and Karl, D. M.: Climate-driven changes to the atmospheric CO2 sink in the subtropical North Pacific Ocean, Nature, 424, 754-757, https://doi.org/10.1038/nature01885, 2003.
Duce, R. and Tindale, N.: Atmospheric transport of iron and its deposition in the ocean, Limnol. Oceanogr., 36, 1715–1726, 1991.
Duhamel, S., Zeman, F., and Moutin, T.: A dual-labeling method for the simultaneous measurement of dissolved inorganic carbon and phosphate uptake by marine planktonic species, Limnol. Oceanogr.-Meth., 4, 416–425, 2006.
Dupouy, C., Neveux, J., Subramaniam, A., Mulholland, M. R., Montoya, J. P., Campbell, L., Carpenter, E. J., and Capone, D. G.: Satellite captures Trichodesmium blooms in the southwestern tropical Pacific, EOS, 81, 13–16, 2000.
Dupouy, C., Benielli-Gary, D., Neveux, J., Dandonneau, Y., and Westberry, T. K.: An algorithm for detecting Trichodesmium surface blooms in the South Western Tropical Pacific, Biogeosciences, 8, 3631–3647, https://doi.org/10.5194/bg-8-3631-2011, 2011.
Edmond, J. M.: High precision determination of totration alkalinity and the total carbone dioxide contentof seawater by potentiometric titration, Deep Sea Res., 17, 737–750, 1970.
Dutkiewicz, S., Ward, B. A., Monteiro, F., and Follows, M. J.: Interconnection of nitrogen fixers and iron in the Pacific Ocean: Theory and numerical simulations, Global Biogeochem. Cy., 26, GB1012, https://doi.org/10.1029/2011GB004039, 2012.
Falkowski, P. G.: Evolution of the nitrogen cycle and its influence on the biological sequestration of CO2 in the ocean, Nature, 387, 272–275, 1997.
Falkowski, P. G., Ziemann, D., Kolber, Z., and Bienfang, P. K.: Role of eddy pumping in enhancing primary production in the ocean, Nature, 352, p. 55, 1991.
Falkowski, P. G., Barber, R. T., and Smetacek, V.: Biogeochemical Controls and Feedbacks on Ocean Primary Production, Science, 281, 200–206, 1998.
Fitzsimmons, J. N., Boyle, E. A., and Jenkins, W. J.: Distal transport of dissolved hydrothermal iron in the deep South Pacific Ocean, P. Natl. Acad. Sci. USA, 25, 16654–16661, https://doi.org/10.1073/pnas.1418778111, 2014.
Fumenia, A., Moutin, T., Bonnet, S., Benavides, M., Petrenko, A., Helias Nunige, S., and Maes, C.: Excess nitrogen as a marker of intense dinitrogen fixation in the Western Tropical South Pacific Ocean: impact on the thermocline waters of the South Pacific, Biogeosciences Discuss., https://doi.org/10.5194/bg-2017-557, in review, 2018.
Ganachaud, A., Cravatte, S., Sprintall, J., Germineaud, C., Marion Alberty, M., Jeandel, C., Eldin, G., Metzl, N., Bonnet, S., Benavides, M., Heimburger, L.-E., Lefèvre, J., Michael, S., Resing, J., Quéroué, F., Sarthou, G., Rodier, Berthelot, H., Baurand, F., Grelet, J., Hasegawa, T., Kessler, W., Kilepak, M., Lacan, F., Privat, E., Send, U., Van Beek, P., Souhaut, S., and Sonke, J. E.: The Solomon Sea: its circulation, chemistry, geochemistry and biology explored during two oceanographic cruises, Elem. Sci. Anth., 5, 33, https://doi.org/10.1525/elementa.221, 2017.
Garcia, H. E. and Gordon, L. I.: Oxygen solubility in seawater: Better fitting equations, Limnol. Oceanogr., 37, 1307–1312, https://doi.org/10.4319/lo.1992.37.6.1307, 1992.
Gattuso, J.-P. and Lavigne, H.: Technical Note: Approaches and software tools to investigate the impact of ocean acidification, Biogeosciences, 6, 2121–2133, https://doi.org/10.5194/bg-6-2121-2009, 2009.
Gimenez, A., Baklouti, M., Bonnet, S., and Moutin, T.: Biogeochemical fluxes and fate of diazotroph-derived nitrogen in the food web after a phosphate enrichment: modeling of the VAHINE mesocosms experiment, Biogeosciences, 13, 5103–5120, https://doi.org/10.5194/bg-13-5103-2016, 2016.
Gimenez, A., Baklouti, M., and Moutin, T.: Diazotrophy as the main driver of planktonic production and biogeochemical C, N, P cycles in the Western Tropical South Pacific Ocean: results from a 1DV biogeochemical-physical coupled model, Biogeosciences Discuss., https://doi.org/10.5194/bg-2018-162, in review, 2018.
Grüber, N.: The dynamics of the marine nitrogen cycle and its influence on atmospheric CO2, in: The ocean carbon cycle and climate, edited by: Follows, M. and Oguz, T., Kluwer Academic, Dordrecht, 2004.
Grüber, N.: Elusive marine nitrogen fixation, P. Natl. Acad. Sci. USA, 113, 4246–4248, 2016.
Grüber, N. and Sarmiento, J. L.: Global patterns of marine nitrogen fixation and denitrification, Global Biogeochem. Cy., 11, 235–266, 1997.
Guieu, C., Bonnet, S., Petrenko, A. A., Menkes, C., Chavagnac, V., Desboeufs, K., Maes, C., and Moutin, T.: Iron from a submarine source impacts the productive layer of the Western Tropical South Pacific (WTSP), Nature Sci. Rep., in revision, 2018.
Hansell, D. A. and Carlson, C. A.: Localized refractory dissolved organic carbon sinks in the deep ocean, Global Biogeochem. Cy., 27, 705–710, https://doi.org/10.1002/gbc.20067, 2013.
Holmes, R. M., Aminot, A., Kérouel, R., Hooker, B. A., and Peterson, B. J.: A simple and precise method for measuring ammonium in marine and freshwater ecosystems, Can. J. Fish. Aquat. Sci., 56, 1801–1808, 1999.
Jickells, T. D., Buitenhuis, E., Altieri, K., Baker, A. R., Capone, D. G., Duce, R. A., Dentener, F., Fennel, K., Kanakidou, M., LaRoche, J., Lee, K., Liss, P., Middelburg, J. J., Moore, J. K., Okin, G., Oschlies, A., Sarin, M., Seitzinger, S., Sharples, J., Singh, A., Suntharalingam, P., Uematsu, M., and Zamora, L. M.: A reevaluation of the magnitude and impacts of anthropogenic atmospheric nitrogen inputs on the ocean, Global Biogeochem. Cy., 31, 289–305, https://doi.org/10.1002/2016GB005586, 2017.
Kana, T. M., Darkangelo, C., Hunt, M. D., Oldham, J. B., Bennett, G. E., and Cornwell, J. C.: Membrane Inlet Mass Spectrometer for Rapid High-Precision Determination of N2, O2, and Ar in Environmental Water Samples, Anal. Chem., 66, 4166–4170, https://doi.org/10.1021/ac00095a009, 1994.
Karl, D. M.: Microbially mediated transformations of phosphorus in the sea: new views of an old cycle, Annu. Rev. Mar. Sci., 6, 279–337, 2014.
Karl, D. M., Christian, J. R., Dore, J. E., Hebel, D. V., Letelier, R. M., Tupas, L. M., and Winn, C. D.: Seasonal and interannual variability in primary production and particle flux at station ALOHA, Deep-Sea Res. Pt. II, 43, 539–568, 1996.
Karl, D. M., Letelier, R. M, Tupas, L. M., Dore, J. E., Christian, J. R., and Hebel, D. V.: The role of nitrogen fixation in biogeochemical cycling in the subtropical North Pacific Ocean, Nature, 388, 533–538, 1997.
Karl, D. M., Church, M. J., Dore, J. E., Letelier, R. M., and Mahaffey, C.: Predictable and efficient carbon sequestration in the North Pacific Ocean supported by symbiotic nitrogen fixation, P. Natl. Acad. Sci. USA, 109, 1842–1849, https://doi.org/10.1073/pnas.1120312109, 2012.
Kim, D., Jeong, D. J., Kim, T. W., Noh, J. H., Kim, H. J., Choi, D. H., Kim, E., and Jeon, D.: The reduction in the biomass of cyanobacterial N2 fixer and the biological pump in the Northwestern Pacific Ocean, Nature Sci. Rep., 7, 41810, https://doi.org/10.1038/srep41810, 2017.
Knapp, A. N., Fawcett, S. E., Martínez-Garcia, A., Leblond, N., Moutin, T., and Bonnet, S.: Nitrogen isotopic evidence for a shift from nitrate- to diazotroph-fueled export production in the VAHINE mesocosm experiments, Biogeosciences, 13, 4645–4657, https://doi.org/10.5194/bg-13-4645-2016, 2016.
Knapp, A. N., McCabe, K. M., Grosso, O., Leblond, N., Moutin, T., and Bonnet, S.: Distribution and rates of nitrogen fixation in the western tropical South Pacific Ocean constrained by nitrogen isotope budgets, Biogeosciences, 15, 2619–2628, https://doi.org/10.5194/bg-15-2619-2018, 2018.
Lachkar, Z., Lévy, M., and Smith, S.: Intensification and deepening of the Arabian Sea oxygen minimum zone in response to increase in Indian monsoon wind intensity, Biogeosciences, 15, 159–186, https://doi.org/10.5194/bg-15-159-2018, 2018.
Landing, W. M. and Bruland, K. W.: The contrasting biogeochemistry of iron and manganese in the Pacific Ocean, Geochim. Cosmochim. Ac., 51, 29–43, 1987.
Landolfi, A., Dietze, H., Koeve, W., and Oschlies, A.: Overlooked runaway feedback in the marine nitrogen cycle: the vicious cycle, Biogeosciences, 10, 1351–1363, https://doi.org/10.5194/bg-10-1351-2013, 2013.
Landry, M. R., Selph, K. E., Taylor, A. G., Décima, M., Balch, W. M., and Bidigare, R. R.: Phytoplankton growth, grazing and production balances in the HNLC equatorial Pacific, Deep-Sea Res. Pt. II, 58, 524–535, 2011.
Langdon, C.: Determination of Dissolved Oxygen in Seawater by Winkler Titration Using the Amperometric Technique, in: The GO-SHIP Repeat Hydrography Manual: A Collection of Expert Reports and Guidelines, edited by: Hood, E. M., Sabine, C. L., and Sloyan, B. M., IOCCP Report Number 14, ICPO Publication Series Number 134, available at: http://www.go-ship.org/HydroMan.html (last access: 8 May 2018), 2010.
Law, C. S., Woodward, E. M. S., Ellwood, M. J., Marriner, A., Bury, S. J., and Safi, K. A.: Response of surface nutrient inventories and nitrogen fixation to a tropical cyclone in the southwest Pacific, Limnol. Oceanogr., 56, 1372–1385, 2011.
Lévy, M., Ferrari, R., Franks, P. J. S., Martin, A. P., and Rivière, P.: Bringing physics to life at the submesoscale, Geophys. Res. Lett., 39, L14602, https://doi.org/10.1029/2012GL052756, 2012.
Levy, M., Jahn, O., Dutkiewicz, S., Follows, M. J., and d'Ovidio, F.: The dynamical landscape of marine phytoplankton diversity, Royal. Soc. Interface, 12, 20150481, https://doi.org/10.1098/rsif.2015.0481, 2015.
Liss, P. S. and Merlivat, L.: Air-Sea Gas Exchange Rates: Introduction and Synthesis, in: The Role of Air-Sea Exchange in Geochemical Cycling, edited by: P., Buat-Ménard, NATO ASI Series (Series C: Mathematical and Physical Sciences), vol. 185, Springer, Dordrecht, https://doi.org/10.1007/978-94-009-4738-2_5, 1986.
Lueker, T. J., Dickson, A., and Keeling, C. D.: Ocean pCO2 calculated from dissolved inorganic carbon, alkalinity, and equations for K1 and K2: validation based on laboratory measurements of CO2 in gas and seawater at equilibrium, Mar. Chem., 70, 105–119, 2000.
Mahaffey, C., Michaels, A. F., and Capone, D. G.: The conundrum of marine N2 fixation, Am. J. Sci., 305, 546–595, 2005.
Marañón, E., Cermeno, P., and Perez, V.: Continuity in the photosynthetic production of dissolved organic carbon from eutrophic to oligotrophic waters, Mar. Ecol.-Prog. Ser., 299, 7–17, 2005.
Marty, J. C. and Chiavérini, J.: Seasonal and interannual variations in phytoplankton production at DYFAMED time-series station, northwestern Mediterranean Sea, Deep-Sea Res. Pt. II, 49, 2017–2030, 2002.
McDougall, T. J. and Barker, P. M.: Getting started with TEOS-10 and the Gibbs Seawater (GSW) Oceanographic Toolbox, 28 pp., SCOR/IAPSO WG127, 2011.
McElroy, M. B.: Marine biological controls on atmospheric CO2 and climate, Nature, 302, 328–329, 1983.
McMahon, K. W., McCarthy, M. D., Sherwood, O. A., Larsen, T., and Guilderson, T. P.: Millennial-scale plankton regime shifts in the subtropical North Pacific Ocean, Science, 350, 1530–1533, 2015.
Merlivat, L., Gonzalez Davila, M., Caniaux, G., Boutin, J., and Reverdin, G.: Mesoscale and diel to monthly variability of CO2 and carbon fluxes at the ocean surface in the northeastern Atlantic, J. Geophys. Res., 114, C03010, https://doi.org/10.1029/2007JC004657, 2009.
Michaels, A. F., Karl, D. M., Capone, D. G.: Element stoichiometry, new production and nitrogen fixation, Oceanography, 14, 68–77, 2001.
Millero, F. J.: The marine inorganic carbon cycle, Chem. Rev., 107, 308–341, 2007.
Minas, H. J., Minas, M., and Packard, T. T.: Productivity in upwelling areas deduced from hydrographic and chemical fields, Limnol. Oceanogr., 31, 1182–1206, 1986.
Moisander, P. H., Zhang, R., Boyle, E. A., Hewson, I., Montoya, J. P., and Zehr, J. P.: Analogous nutrient limitations in unicellular diazotrophs and Prochlorococcus in the South Pacific Ocean, ISME J., 6, 733–744, 2012.
Monteiro, F. M., Dutkiewicz, S., and Follows, M. J.: Biogeographical controls on the marine nitrogen fixers, Global Biogeochem. Cy., 25, GB2003, https://doi.org/10.1029/2010GB003902, 2011.
Montoya, J. P., Voss, M., Kahler, P., and Capone, D. G.: A Simple, High-Precision, High-Sensitivity Tracer Assay for N2 Fixation, Appl. Environ. Microb., 62, 986–993, 1996.
Moore, C. M., Mills, M. M. M., Arrigo, K. R., Berman-Frank, I., Bopp, L., Boyd, P. W., Galbraith, E. D., Geider, R. J., Guieu, C., Jaccard, S. L., Jickells, T. D., La Roche, J., Lenton, T. M., Mahowald, N. M., Maranon, E., Marinov, I., Moore, J. K., Nakatsuka, T., Oschlies, A., Saito, M. A., Thingstad, T. F., Tsuda, A., and Ulloa, O.: Processes and patterns of oceanic nutrient limitation, Nat. Geosci., 6, 701–710, 2013.
Moutin, T. and Raimbault, P.: Primary production, carbon export and nutrients availability in western and eastern Mediterranean Sea in early summer 1996 (MINOS cruise), J. Marine Syst., 33–34, 273–288, https://doi.org/10.1016/S0924-7963(02)00062-3, 2002.
Moutin, T., Raimbault, P., and Poggiale, J. C.: Production primaire dans les eaux de surface de la Méditerranée occidentale: Calcul de la production journalière, C. R. Acad. Sci. Paris, Sciences de la vie, 322, 651–659, 1999.
Moutin, T., Thingstad, T. F., Van Wambeke, F., Marie, D., Slawyk, G., Raimbault, P., and Claustre, H.: Does competition for nano-molar phosphate supply explain the predominance of the cyanobacterium Synechococcus?, Limnol. Oceanogr., 47, 1562–1567, 2002.
Moutin, T., Van Den Broeck, N., Beker, B., Dupouy, C., Rimmelin, P., and LeBouteiller, A.: Phosphate availability controls Trichodesmium spp. biomass in the SW Pacific ocean, Mar. Ecol.-Prog. Ser., 297, 15–21, 2005.
Moutin, T., Karl, D. M., Duhamel, S., Rimmelin, P., Raimbault, P., Van Mooy, B. A. S., and Claustre, H.: Phosphate availability and the ultimate control of new nitrogen input by nitrogen fixation in the tropical Pacific Ocean, Biogeosciences, 5, 95–109, https://doi.org/10.5194/bg-5-95-2008, 2008.
Moutin, T., Van Wambeke, F., and Prieur, L.: Introduction to the Biogeochemistry from the Oligotrophic to the Ultraoligotrophic Mediterranean (BOUM) experiment, Biogeosciences, 9, 3817–3825, https://doi.org/10.5194/bg-9-3817-2012, 2012.
Moutin, T., Doglioli, A. M., de Verneil, A., and Bonnet, S.: Preface: The Oligotrophy to the UlTra-oligotrophy PACific Experiment (OUTPACE cruise, 18 February to 3 April 2015), Biogeosciences, 14, 3207–3220, https://doi.org/10.5194/bg-14-3207-2017, 2017a.
Moutin, T., Bonnet, S., Richards, K., Capone, D. G., Marañón, E., and Mémery, L. (Eds.): Interactions between planktonic organisms and biogeochemical cycles across trophic and N2 fixation gradients in the western tropical South Pacific Ocean: a multidisciplinary approach (OUTPACE experiment), Biogeosciences, https://www.biogeosciences.net/special_issue894.html, 2017b.
NOAA ESRL Global Monitoring Division: Atmospheric Carbon Dioxide Dry Air Mole Fractions from quasi-continuous measurements at American Samoa, edited by: Thoning, K. W., Kitzis, D. R., and Crotwell, A., National Oceanic and Atmospheric Administration (NOAA), Earth System Research Laboratory (ESRL), Global Monitoring Division (GMD): Boulder, Colorado, USA, Version 2014-08 at: https://doi.org/10.7289/V51834DB, 2014.
Oschlies, A. and Garcon, V.: Eddy-induced enhancement of primary production in a model of the North Atlantic Ocean, Nature, 394, 266–269, 1998.
Oudot, C., Gerard, R., Morin, P., and Gningue, I.: Precise shipboard determination of dissolved-oxygen (Winkler Procedure) with a commercial system, Limnol. Oceanogr., 33, 146–150, 1988.
Owens, W. B. and Millard Jr., R. C.: A new algorithm for CTD oxygen calibration, J. Phys. Oceanogr., 15, 621–631, 1985.
Pujo-Pay, M. and Raimbault, P.: Improvement of the wet-oxidation procedure for simultaneous determination of particulate organic nitrogen and phosphorus collected on filters, Mar. Ecol.-Prog. Ser., 105, 203–207, 1994.
Pujo-Pay, M., Conan, P., Oriol, L., Cornet-Barthaux, V., Falco, C., Ghiglione, J.-F., Goyet, C., Moutin, T., and Prieur, L.: Integrated survey of elemental stoichiometry (C, N, P) from the western to eastern Mediterranean Sea, Biogeosciences, 8, 883–899, https://doi.org/10.5194/bg-8-883-2011, 2011.
Raven, J. A.: The iron and molybdenum use efficiencies of plant growth with different energy, carbon and nitrogen source, New Phytol., 109, 279–287, 1988.
Redfield, A. C.: On the proportions of organic derivatives in sea water and their relation to the composition of plankton, in: James Johnstone Memorial Volume, edited by: Daniel, R. J., University Press, 176–192, 1934.
Rousselet, L., de Verneil, A., Doglioli, A. M., Petrenko, A. A., Duhamel, S., Maes, C., and Blanke, B.: Large- to submesoscale surface circulation and its implications on biogeochemical/biological horizontal distributions during the OUTPACE cruise (southwest Pacific), Biogeosciences, 15, 2411–2431, https://doi.org/10.5194/bg-15-2411-2018, 2018.
Sarmiento, J. L. and Gruber, N.: Ocean Biogeochemical Dynamics, Princeton University Press, Princeton, 503 pp., 2006.
Sharp, J. H.: Improved analysis for “particulate” organic carbon and nitrogen from seawater, Limnol. Oceanogr., 19, 984–989, 1974.
Smeti, H., Pagano, M., Menkès, C., Lebourges Dhaussy, A., Hunt, B. P. V., Allain, V., Rodier, M., de Boissieu, F., Kestenare, E., and Sammari, C.: Spatial and temporal variability of zooplankton off New Caledonia (Southwestern Pacific) from acoustics and net measurements, J. Geophys. Res.-Oceans, 120, 2676–2700, 2015.
Straub, M., Sigman, D. M., Ren, H., Martínez-García, A., Meckler, A. N., Hain, M. P., and Haug, G. H.: Changes in North Atlantic nitrogen fixation controlled by ocean circulation, Nature, 501, 7466, https://doi.org/10.1038/nature12397, 2013.
Stukel, M. R., Aluwihare, L. I., Barbeau, K. A., Chekalyuk, A. M., Goericke, R., Miller, A. J., Ohman, M. D., Ruacho, A., Song, H., Stephens, B., and Landry, M. R.: Mesoscale ocean fronts enhance carbon export due to gravitational sinking and subduction, P. Natl. Acad. Sci. USA, 114, 1252–1257, https://doi.org/10.1073/pnas.1609435114, 2017.
Sugimura, Y. and Suzuki, Y.: A high-temperature catalytic oxidation method for the determination of non-volatile dissolved organic carbon in seawater by direct injection of a liquid sample, Mar. Chem., 24, 105–131, 1988.
Tagliabue, A., Bopp, L., Dutay, J. C., Bowie, A. R., Chever, F., Jean-Baptiste, P., Bucciarelli, E., Lannuzel, D., Remenyi, T., Sarthou, G., Aumont, O., Gehlen, M., and Jeandel, C.: Hydrothermal iron contribution to oceanic dissolved iron inventory, Nat. Geosci., 3, 252–256, https://doi.org/10.1038/ngeo818, 2010.
Tagliabue, A., Bowie, A. R., Boyd, P. W., Buck, K. N., Johnson, K. S., and Saito, M. A.: The integral role of iron in ocean biogeochemistry, Nature, 543, 51–59, https://doi.org/10.1038/nature21058, 2017.
Takahashi, T., Olafsson, J., Goddard, J., Chipman, D. W., and Sutherland, S. C.: Seasonal variation of CO2 and nutrients in the high-latitude surface oceans: a comparative study, Global Biogeochem. Cy., 7, 843–878, 1993.
Takahashi, T., Sutherland, S. C., Chipman, D. W., Goddard, J. G., Cheng Ho, Newberger, T., Sweeney, C., and Munro, D. R.: Climatological Distributions of pH, pCO2, Total CO2, Alkalinity, and CaCO3 Saturation in the Global Surface Ocean, and Temporal Changes at Selected Locations, Mar. Chem., https://doi.org/10.1016/j.jmarchem.2014.06.004, 2014.
Taylor, B. W., Keep, C. F., Hall, Jr., R. O., Koch, B. J., Tronstad, L. M., Flecker, A. S., and Ulseth, A. J.: Improving the fluorometric ammonium method: matrix effects, background fluorescence, and standard additions, J. N. Am. Benthol. Soc., 26, 167–177, 2007.
Thingstad, T. F., Skjoldal, E. F., and Bohne, R. A.: Phosphorus cycling and algal–bacterial competition in Sandsfjord, western Norway, Mar. Ecol.-Prog. Ser., 99, 239–259, 1993.
Tyrell, T.: The relative influences of nitrogen and phosphorus on oceanic primary production, Nature, 400, 525–531, 1999.
Valdés, V., Carlotti, F., Escribano, R., Donoso, K., Pagano, M., Molina, V., and Fernandez, C.: Nitrogen and phosphorus recycling mediated by copepods in Western Tropical South Pacific, Biogeosciences Discuss., https://doi.org/10.5194/bg-2017-563, in review, 2018.
Van Den Broeck, N., Moutin, T., Rodier, M., and Le Bouteiller, A.: Seasonal variations of phosphate availability in the SW Pacific Ocean near New Caledonia, Mar. Ecol.-Prog. Ser., 268, 1–12, 2004.
Van Wambeke, F., Christaki, U., Giannakourou, A., Moutin, T., and Souvemerzoglou, K.: Longitudinal and vertical trends of bacterial limitation by phosphorus and carbon in the Mediterranean Sea, Microbiol. Ecol., 43, 119–133, 2002.
Van Wambeke, F., Gimenez, A., Duhamel, S., Dupouy, C., Lefevre, D., Pujo-Pay, M., and Moutin, T.: Dynamics and controls of heterotrophic prokaryotic production in the western tropical South Pacific Ocean: links with diazotrophic and photosynthetic activity, Biogeosciences, 15, 2669–2689, https://doi.org/10.5194/bg-15-2669-2018, 2018.
Volk, T. and Hoffert, M. I.: The carbon cycle and atmospheric CO2: natural variations Archean to present, Chapman conference papers, 1984, edited by: Sundquist, E. T. and Broecker, W. S., American Geophysical Union, Geophysical Monograph 32, 99–110, 1985.
Wagener, T., Guieu, C., Losno, R., Bonnet, S., and Mahowald, N. M.: Revisiting atmospheric dust export to the Southern Hemisphere ocean: Biogeochemical implications, Global Biogeochem. Cy., 22, 1–13, https://doi.org/10.1029/2007GB002984, 2008.
Weber, T. and Deutsch, C.: Local versus basin-scale limitation of marine nitrogen fixation, P. Natl. Acad. Sci. USA, 111, 8741–8746, 2014.
Wells, M. L., Vallis, G. K., and Silver, E. A.: Tectonic processes in Papua New Guinea and past productivity in the eastern equatorial Pacific Ocean, Nature, 398, 601–604, 1999.
Weiss, R. F. and Price, B. A.: Nitrous oxide solubility in water and seawater, Mar. Chem., 8, 347–359, 1980.
Winkler, L. W.: Die Bestimmung des im Wasser gelosten Sauerstoffes, Ber. Dtsch. Chem. Ges., 21, 2843–2853, 1888.
Wu, J., Sunda, W., Boyle, E. A., and Karl, D. M.: Phosphate depletion in the western North Atlantic Ocean, Science, 289, 759–762, 2000.
Xie, X. H., Cuypers, Y., Bouruet-Aubertot, P., Ferron, B., Pichon, A., Lourenço, A., and Cortes, N.: Large-amplitude internal tides, solitary waves, and turbulence in the central Bay of Biscay, Geophys. Res. Lett., 40, 2748–2754, 2013.
Yoshikawa, C., Makabe, A., Shiozaki, T., Toyoda, S., Yoshida, O., Furuya, K., and Yoshida, N.: Nitrogen isotope ratios of nitrate and N* anomalies in the subtropical South Pacific, Geochem. Geophy. Geosy., 16, 1439–1448, https://doi.org/10.1002/2014GC005678, 2015.
Zhang, X. and Dam, H. G.: Downward export of carbon by die1 migrant mesozooplankton in the central equatorial Pacific, Deep-Sea Res. Pt. II, 44, 2191–2202, 1998.