the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Reviews and syntheses: Revisiting the boron systematics of aragonite and their application to coral calcification
Thomas M. DeCarlo
Michael Holcomb
Malcolm T. McCulloch
The isotopic and elemental systematics of boron in aragonitic coral skeletons have recently been developed as a proxy for the carbonate chemistry of the coral extracellular calcifying fluid. With knowledge of the boron isotopic fractionation in seawater and the B∕Ca partition coefficient (KD) between aragonite and seawater, measurements of coral skeleton δ11B and B∕Ca can potentially constrain the full carbonate system. Two sets of abiogenic aragonite precipitation experiments designed to quantify KD have recently made possible the application of this proxy system. However, while different KD formulations have been proposed, there has not yet been a comprehensive analysis that considers both experimental datasets and explores the implications for interpreting coral skeletons. Here, we evaluate four potential KD formulations: three previously presented in the literature and one newly developed. We assess how well each formulation reconstructs the known fluid carbonate chemistry from the abiogenic experiments, and we evaluate the implications for deriving the carbonate chemistry of coral calcifying fluid. Three of the KD formulations performed similarly when applied to abiogenic aragonites precipitated from seawater and to coral skeletons. Critically, we find that some uncertainty remains in understanding the mechanism of boron elemental partitioning between aragonite and seawater, and addressing this question should be a target of additional abiogenic precipitation experiments. Despite this, boron systematics can already be applied to quantify the coral calcifying fluid carbonate system, although uncertainties associated with the proxy system should be carefully considered for each application. Finally, we present a user-friendly computer code that calculates coral calcifying fluid carbonate chemistry, including propagation of uncertainties, given inputs of boron systematics measured in coral skeleton.
Please read the corrigendum first before continuing.
-
Notice on corrigendum
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
-
Article
(6153 KB)
- Corrigendum
-
Supplement
(71 KB)
-
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(6153 KB) - Corrigendum
-
Supplement
(71 KB) - BibTeX
- EndNote
Quantifying the carbonate chemistry of the fluid from which corals accrete their skeletons is essential for understanding the mechanisms of skeletal growth and the sensitivity of skeletal composition to environmental variability. It is generally thought that corals precipitate aragonite (CaCO3) crystals within an extracellular fluid-filled space between the living polyp and the skeleton (Barnes, 1970). Evidence from skeletal geochemistry and fluorescent dye experiments suggests that while seawater is the initial source of the calcifying fluid (McConnaughey, 1989; Adkins et al., 2003; Cohen and McConnaughey, 2003; Gagnon et al., 2012; Tambutté et al., 2012), the carbonate chemistry of the calcifying fluid is subject to substantial modifications (i.e., pH and dissolved inorganic carbon, or DIC) that enhance the rapid nucleation and growth of aragonite crystals (Al-Horani et al., 2003; Venn et al., 2011). Because the isolation and small size of the calcifying fluid makes it difficult to sample directly, a variety of techniques have been employed to characterize its composition. These include microelectrodes inserted into tissue incisions or through the mouth (Al-Horani et al., 2003; Ries, 2011; Cai et al., 2016), pH-sensitive dyes (Venn et al., 2011, 2013; Holcomb et al., 2014; Comeau et al., 2017b), Raman spectroscopy (DeCarlo et al., 2017), and a variety of skeletal-based geochemical proxies (Rollion-Bard et al., 2010, 2011; Inoue et al., 2011; Trotter et al., 2011; McCulloch et al., 2012b; Allison et al., 2014; Holcomb et al., 2014; DeCarlo et al., 2015). Although microelectrodes and pH-sensitive dyes are arguably the most direct methods, their utilities are limited by difficulties of applying them to corals living in their natural environment or developing seasonally resolved time series. Geochemical proxies, although indirect, can be readily applied to the skeletons of corals living in both laboratory and natural environments, and to skeletons accreted years or even centuries ago.
In recent years, boron systematics (including δ11B and B∕Ca) have become one of the most commonly applied proxies for the carbonate chemistry of coral calcifying fluid (Hönisch et al., 2004; Trotter et al., 2011; McCulloch et al., 2012b, a, 2017; Allison et al., 2014; DeCarlo et al., 2016; Stewart et al., 2016; Comeau et al., 2017a; Wu et al., 2017; D'Olivo and McCulloch, 2017; Kubota et al., 2017; Ross et al., 2017; Schoepf et al., 2017). The sensitivity of boron isotopes to seawater pH arises from the borate versus boric acid speciation being pH dependent and the isotopic fractionation between these species being constant (Klochko et al., 2006). Since the δ11B composition of aragonite precipitating from seawater reflects that of the borate species (Klochko et al., 2006; Trotter et al., 2011; Noireaux et al., 2015), the δ11B composition of the skeletal carbonate records the pH of the calcifying fluid. Furthermore, the B∕Ca ratio depends inversely on the concentration of carbonate ion () if borate substitutes for carbonate ion in the aragonite lattice (Holcomb et al., 2016).
Use of combined boron isotopic (δ11B) and elemental (B∕Ca) systematics has several advantages relative to other geochemical proxies. For example, while stable carbon and oxygen isotopes are sensitive to carbonate chemistry, they are complicated by kinetic effects, strong sensitivities to the photosynthetic activity of coral symbionts, and variable compositions in seawater, which together have precluded their utility as acceptable carbonate system proxies (Adkins et al., 2003; Cohen and McConnaughey, 2003; Schoepf et al., 2014). The U∕Ca ratio of aragonite is also sensitive to , but the amount of U in coral skeleton relative to its concentration in seawater suggests that [U]cf is depleted substantially, complicating its utility as a direct cf proxy (DeCarlo et al., 2015). Conversely, the B∕Ca and δ11B compositions of seawater are homogeneous (Foster et al., 2010; Lee et al., 2010) and likely not modified substantially by photosynthetic activity (Hönisch et al., 2004). Further, incorporation into the skeleton is less important for B∕Ca than U∕Ca because the partition coefficient between B and is at least 2 orders of magnitude smaller than that of U ∕ (DeCarlo et al., 2015; Mavromatis et al., 2015; Holcomb et al., 2016), meaning that [B]cf is depleted much less than [U]cf as skeletal aragonite precipitates. While a low partition coefficient causes Rayleigh fractionation for elements in a closed system (e.g., coral [Mg] ∕ [Ca]cf) (Gaetani and Cohen, 2006), cf is elevated relative to seawater and is modified by CO2 diffusion and pH up-regulation (i.e., it is not in a closed system) (Adkins et al., 2003; Cai et al., 2016), meaning that [B] ∕ is likely not changed substantially due to skeletal aragonite precipitation. Therefore, boron-based proxies are thought to be largely dependent on carbonate chemistry alone (Trotter et al., 2011; McCulloch et al., 2017). Finally, the combination of two carbonate system proxies (pH and ) derived from boron systematics allows for computation of the full carbonate system (Zeebe and Wolf-Gladrow, 2001).
Abiogenic laboratory experiments provide the underlying quantitative foundation necessary to apply these proxies to aragonitic coral skeletons. Klochko et al. (2006) determined the fractionation factor (αB3−B4) between boric acid and borate in seawater, which allows δ11B of carbonates to be used as a pH proxy when combined with knowledge of pKB (Dickson, 1990) and seawater δ11B (Foster et al., 2010). Although there is potential for B isotopic fractionation between aragonite and seawater (Balan et al., 2018), the veracity of the δ11B proxy has been largely confirmed by comparison with direct in situ measurements using either pH microelectrodes or confocal microscopy of pH-sensitive dyes in the calcifying fluid (Ries, 2011; Venn et al., 2011; Holcomb et al., 2014; Cai et al., 2016). Additionally, results from two sets of abiogenic precipitation experiments can be used to constrain the partitioning of B∕Ca between fluid and aragonite (Mavromatis et al., 2015; Holcomb et al., 2016). Thus, while all the information theoretically required to constrain the full seawater carbonate system from boron systematics is now available, a variety of different approaches have been presented, especially regarding the interpretation of B∕Ca partitioning (Mavromatis et al., 2015; Holcomb et al., 2016; Allison, 2017; McCulloch et al., 2017). Here, we assess the abiogenic partitioning data (Mavromatis et al., 2015; Holcomb et al., 2016), and the subsequent fitting of those data (Allison, 2017; McCulloch et al., 2017). We consider which mechanisms of B incorporation and sensitivities of B∕Ca partitioning are plausible, and the implications for interpreting coral skeletons. Our focus is on the combined application of δ11B and B∕Ca because it is only when the two are used in tandem that it is possible to calculate the full calcifying fluid carbonate system. Finally, we present a user-friendly computer code to calculate coral calcifying fluid carbonate chemistry from measurements of δ11B and B∕Ca. The code also propagates known uncertainties for deriving calcifying fluid cf and DICcf, and allows for evaluating the effects of using different constants and partition coefficient formulations.
The main discrepancy among various applications of boron systematics to coral skeletons relates to the partition coefficient of boron between aragonite and seawater. Given the variety of possible exchange reactions and partition coefficients that have been proposed (Allen and Hönisch, 2012; Mavromatis et al., 2015; Holcomb et al., 2016; Allison, 2017; McCulloch et al., 2017), we begin with a brief review of how partition coefficients are derived. In general, the substitution of minor elements into a solid is described by an exchange reaction such that
For example, the substitution of Sr2+ for Ca2+ in aragonite follows (Gaetani and Cohen, 2006)
Element distribution described by this exchange is quantified through a partition coefficient, expressed as the concentration ratio of products over reactants:
Equation (3) is typically rearranged as
The case of Sr2+ substituting for Ca2+ is straightforward in that the exchange reaction (Eq. 2) is charge balanced. Boron is more complicated because it is commonly thought that the singly charged B(OH) is incorporated into aragonite in place of the doubly charged (Mavromatis et al., 2015; Noireaux et al., 2015). There are at least two possible exchange reactions for B(OH) to substitute for that maintain charge balance:
following Holcomb et al. (2016), or
following McCulloch et al. (2017). The KD for Eq. (5) is
and for Eq. (6) is
where aragonite is assumed equal to [Ca2+]aragonite, and Eqs. (7) and (8) differ by whether or not the square root of is used. Since Eq. (6) includes H+ in the products, this reaction implies that the KD may be pH dependent (McCulloch et al., 2017). Incorporation of B into aragonite may also involve adsorption of B(OH) onto crystal surfaces, incorporation at defect sites, or local charge balance by Na+ (Balan et al., 2018).
Conversely, Allison et al. (2014) and Allison (2017) considered exchange reactions in which borate substitutes for bicarbonate (HCO), with the partition coefficient
This approach resolves the issue of charge balance and would account for reacting with H+, thus removing the pH dependence expected from Eq. (8). However, Eq. (9) implies that aragonite forms via the reaction
rather than
Whether aragonite precipitates via Eqs. (10) or (11) is testable because the rate of the net forward reaction should depend on the concentrations of the reactants. Burton and Walter (1987) demonstrated that the rate of aragonite precipitation increases as a function of ΩAr (where ΩAr = [Ca2+] ∕ Ksp) and temperature, although they did not explicitly consider the relationship between and precipitation rate. Holcomb et al. (2016) reported bulk precipitation rates for aragonites precipitated from seawater with various and , with independence between these two variables achieved by manipulating pH and DIC. While the bulk precipitation rates were not normalized to surface area as in Burton and Walter (1987), the experimental vessels used by Holcomb et al. (2016) were of consistent dimensions and material. Thus, the bulk precipitation rate data of Holcomb et al. (2016) should be comparable among their experiments, allowing us to evaluate between the reactions of Eqs. (10) and (11). The aragonite precipitation rates reported by Holcomb et al. (2016) at 25 ∘C are significantly correlated with both (r2 = 0.56, p<0.01) and ΩAr (r2 = 0.62, p<0.01) (Fig. 1a, b). Experiments conducted at 20, 33, and 40 ∘C are consistent with this trend (Fig. 1a, b), and with previous observations that precipitation rate increases with temperature (Burton and Walter, 1987), although we do not attempt to quantify temperature effects on the order of the reaction (as performed by Burton and Walter, 1987) since only two experiments were conducted at each temperature other than 25 ∘C. Conversely, there are no significant correlations between aragonite precipitation rate at 25 ∘C and either (r2 = 0.00, p=0.95) or [Ca2+] (r2=0.01, p=0.54) as would be expected based on Eq. (10). Other possibilities include precipitation reactions involving both and HCO, or total DIC (Allison et al., 2014; Allison, 2017). However, there are no significant correlations between precipitation rate and either + (r2 = 0.01, p=0.59) or DIC (r2=0.01, p=0.59) (Fig. 1e, f). Together, these data lead us to conclude that aragonite precipitates from seawater via Eq. (11). Therefore, since B∕Ca partition coefficients expressed with do not have a chemical reaction basis, we do not consider them further. Rather, we consider only the B∕Ca partition coefficients that are based on borate substituting for (Eqs. 7–8).
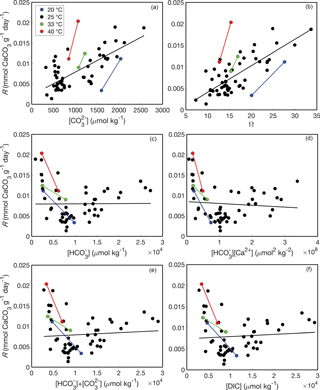
Figure 1Aragonite precipitation rates as functions of fluid chemistry based on data from Holcomb et al. (2016). Each point represents a separate abiogenic aragonite precipitation experiment conducted at 20 ∘C (blue), 25 ∘C (black), 33 ∘C (green), and 40 ∘C (red). Bulk aragonite precipitation rates (R) are plotted against mean fluid (a), ΩAr (b), (c), [Ca2+] (d), + (e), and DIC (f). Solid lines show regression fits at each temperature (note that there are only two experiments at each temperature other than 25 ∘C, and thus line fits for these temperatures should be interpreted with caution).
The second source of discrepancies between various applications of boron systematics to coral skeletons is the dependence of the KD on fluid chemistry. Holcomb et al. (2016) fit the KD as either a function of or ΩAr, McCulloch et al. (2017) refit the Holcomb et al. (2016) data as a function of [H+], and Allison (2017) fit data from both Mavromatis et al. (2015) and Holcomb et al. (2016) as a function of ΩAr.
At the outset, it is important to recognize that there are two key differences between the abiogenic experiments of Mavromatis et al. (2015) and Holcomb et al. (2016). Firstly, Mavromatis et al. (2015) precipitated aragonite from NaCl solutions, whereas Holcomb et al. (2016) used filtered seawater. Secondly, and ΩAr are lower in the experiments of Mavromatis et al. (2015) relative to Holcomb et al. (2016). Potentially as result of one or both of these differences, Mavromatis et al. (2015) found much lower KD values than Holcomb et al. (2016). Here, we consider four possible KD dependencies based on these two experimental datasets (Fig. 2).
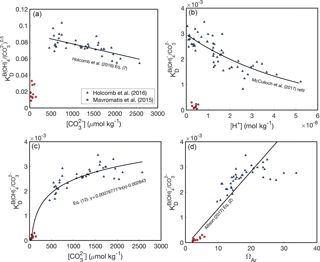
Figure 2B∕Ca KD formulations. Abiogenic B∕Ca partitioning data from Mavromatis et al. (2015) (red circles) and Holcomb et al. (2016) (blue triangles) fit as functions of fluid chemistry: (a, c) (Holcomb et al., 2016), [H+] (b) (McCulloch et al., 2017), and ΩAr (d) (Allison, 2017). Note that KD in (a) is defined with Eq. (7) and in (b–d) is defined with Eq. (8). We use only the Mavromatis et al. (2015) with [B] < 1000 µmol kg−1 due to the apparent effect of [B] on KD (Holcomb et al., 2016).
The first two formulations assume that there are substantial compositional effects on B∕Ca partitioning, and thus the offsets in KD between Mavromatis et al. (2015) and Holcomb et al. (2016) arise due to the use of NaCl versus seawater solutions, respectively (Fig. 2a, b). If this is correct, the Holcomb et al. (2016) data are more appropriate for application to corals based on evidence that they precipitate their skeletons from seawater-based solutions (McConnaughey, 1989; Cohen and McConnaughey, 2003; Gagnon et al., 2012; Tambutté et al., 2012). Holcomb et al. (2016) precipitated their aragonites from seawater solutions modified with [Ca2+] and [Mg2+] ranging between 6 and 20 and 48 and 98 mmol kg−1, respectively, without any apparent effects on the B∕Ca KD. While this suggests that the KD is not highly sensitive to seawater elemental chemistry, it is still possible that there are subtle compositional effects that have little influence on KD in modified seawater, but become apparent in the NaCl solutions used by Mavromatis et al. (2015). Assuming some compositional effects do exist, we are left with the two plausible KD expressions (Eqs. 7–8), and the previously presented dependencies on either (Holcomb et al., 2016) or [H+] McCulloch et al. (2017).
Alternatively, it is possible that there are negligible effects from using NaCl or seawater solutions and, therefore, the data from both Mavromatis et al. (2015) and Holcomb et al. (2016) should be fit by a single, continuous function. There are again two plausible formulations: KD increases as a function of or ΩAr (Fig. 2c, d). Allison (2017) proposed a linear fit between KD and ΩAr that includes both the Mavromatis et al. (2015) and Holcomb et al. (2016) data. From a practical standpoint, however, this latter approach is problematic in that it requires an independent proxy for [Ca2+] (see Sect. 8) and the linear fit effectively precludes its use for deriving coral calcifying fluid chemistry (see Sect. 4). In an attempt to avoid these issues, we introduce a logarithmic relationship between KD and , which fits both the Mavromatis et al. (2015) and Holcomb et al. (2016) data (Fig. 2c):
where parentheses indicate 95 % confidence, KD is defined by Eq. (8), and is in units of micromoles per kilogram. Mechanistically, the increase in KD with or ΩAr (or precipitation rate) is consistent with the surface entrapment model proposed by Watson (2004). In this model, minor element impurities, such as B, are incorporated in the near-surface layer of a growing crystal. Slower-growing crystals allow these impurities to diffuse out of the near-surface region into the fluid, whereas faster-growing crystals bury the near-surface impurities into the bulk crystal. The sensitivity of KD to or ΩAr is also consistent with a surface kinetic model (DePaolo, 2011), in which trace element partitioning depends on the net rate of precipitation relative to dissolution. Thus, both the surface entrapment and kinetic models offer potential explanations as to why the low-ΩAr experiments of Mavromatis et al. (2015) produced lower KD than the higher-ΩAr experiments of Holcomb et al. (2016).
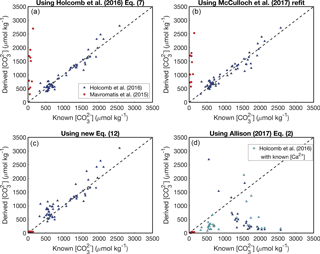
Figure 3Reconstructing experimental fluid using the KD formulations presented in Fig. 2. Symbols are the same as Fig. 2. In panel (d), negative solutions have been excluded (see Appendix). Calculations using the Allison (2017) KD formulation have been performed with both assuming seawater [Ca2+] (blue) and using the [Ca2+] reported from the experiments (cyan).
We conducted a simple test to evaluate the utility of the four KD dependencies considered above. For each KD formulation, we used the reported aragonite B∕Ca, fluid [B(OH)], and pH data of Mavromatis et al. (2015) and Holcomb et al. (2016) to calculate the fluid , and then we compared the predicted to the concentrations measured during the experiments (Fig. 3) (see also Ross et al., 2017, for a similar analysis). The basis for this approach is to assess how well the experimental fluid can be reconstructed using boron systematics alone. When boron systematics are applied to coral skeletons, is predicted from only B∕Ca and δ11B. However, since δ11B was not reported by Holcomb et al. (2016), we instead use the measured pH for the McCulloch et al. (2017) KD formulation. Additionally, since [B] was manipulated in some experiments, we use reported fluid [B(OH)] instead of calculating it from pH as is performed in applications to corals (Allison et al., 2014; McCulloch et al., 2017). Nevertheless, since pH (and thus seawater [B(OH)]) is readily calculated from δ11B, our approach is suitable for evaluating the utility of each KD formulation for reconstructing with B∕Ca.
Since three of the KD formulations (Holcomb et al., 2016, Allison, 2017, and our new Eq. 12) themselves depend on , we solved for as follows. An initial guess of was used to calculate an initial KD, and this KD was used to solve for by rearranging Eq. (7) to
and Eq. (8) to
where Eq. (14) is used for Allison (2017) and our new Eq. (12), and Eq. (13) is used for Holcomb et al. (2016). We then calculated the residual between the calculated (Eqs. 13–14) and initially estimated . Finally, we iteratively adjusted the initial estimate for each data point until it equaled the derived from Eqs. (13)–(14).
Both the Holcomb et al. (2016) fit (their Eq. 7) and the McCulloch et al. (2017) refit perform similarly, effectively reconstructing the fluid of the Holcomb et al. (2016) experimental data (root mean square error, RMSE = 151 and 163 µmol kg−1, respectively), but performing poorly for the Mavromatis et al. (2015) data (RMSE = 1370 and 1385 µmol kg−1, respectively) (Fig. 3a, b). This is not surprising because these KD dependencies are offset from the Mavromatis et al. (2015) data (Fig. 2a, b). Our new logarithmic equation performs well for both datasets (RMSE = 42 and 204 µmol kg−1 for Mavromatis et al. (2015) and Holcomb et al. (2016), respectively). The Allison (2017) formulation (assuming [Ca2+] of 10 µmol kg−1) performs well for the Mavromatis et al. (2015) data (RMSE = 51 µmol kg−1), but creates a trend opposite that expected for the Holcomb et al. (2016) data (RMSE = 1375 µmol kg−1) (Fig. 3d). Using the reported [Ca2+] and Ksp from the Holcomb et al. (2016) experiments in the Allison (2017) formulation improves the results slightly and generates more positive solutions, but the RMSE is still 950 µmol kg−1.
An alternative way to understand these patterns is to investigate the relationship between and the ratio of fluid [B(OH)] to solid B∕Ca (Fig. 4). Following Eqs. (13)–(14), should be positively related to , and this behavior is clearly evident in the abiogenic aragonites of Holcomb et al. (2016) (blue triangles in Fig. 4). The KD formulations of Holcomb et al. (2016), McCulloch et al. (2017), and our new Eq. (12) all closely track the abiogenic data, especially for < 2000 µmol kg−1. Conversely, the Allison (2017) fit (assuming [Ca2+] of 10 mmol kg−1) produces the opposite trend and is invalid or negative below a of ∼ 0.44 mol kg−1 (see Appendix for derivation of an analytical solution).
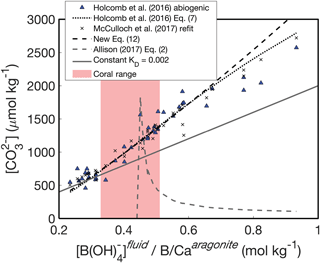
Figure 4Experimental fluid as a function of . The KD formulations of Holcomb et al. (2016) (dotted black line), McCulloch et al. (2017) (black crosses), and Eq. (12) (dashed black line) all capture the trend of increasing with increasing that is apparent in the abiogenic data (blue triangles). A constant KD (solid grey line) underestimates the slope between and . The pink shaded region shows the range of derived for Porites corals by McCulloch et al. (2017).
The behavior of the KD formulations can be understood by inspecting the residuals between initial estimates and those derived from Eqs. (13)–(14) (Fig. 5). The Holcomb et al. (2016) KD formulation generates unique solutions (i.e., where the residual equals zero) that increase with (Fig. 5a), which is the ideal behavior. Our new Eq. (12) also produces increasing solutions with increasing (Fig. 5b); however, a major issue of this formulation is that there may be two solutions for each . Finally, although the Allison (2017) KD formulation produces unique solutions, they increase with decreasing (Fig. 5c), opposite to that expected (Fig. 4).
The reason for the poor behavior of the Allison (2017) formulation is the linear fit between KD and ΩAr with an intercept near the origin. When using this formulation to predict from boron systematics alone, we must assume [Ca2+] is approximately equal to seawater (∼10 mmol kg−1), meaning that ΩAr is directly related to . Since the intercept in the Allison (2017) KD formulation is close to the origin, any change in results in an almost proportional change in KD. It can be seen why this is problematic by inspecting how is derived from Eq. (14). The is derived from pH (or δ11B) and measured B∕Ca, so this ratio remains constant while we find the appropriate KD that minimizes the residual , as in Fig. 5. Therefore, Eq. (14) is effectively reduced to being a function of KD multiplied by a constant. However, since KD changes almost directly proportionally to according to Allison (2017), it is difficult to find a that explains different values. Although Allison (2017) recognized the difficulty of explaining the range of B∕Ca observed in corals (see their Fig. 8g), the implication of applying this KD formulation to predict was not discussed. Our analysis suggests that this KD formulation is poorly suited for accurately reconstructing fluid from boron systematics (Figs. 3d, 4).
Another approach presented by Allison (2017) is to use a constant KD. We selected a KD value of 0.02 as an example that fits the abiogenic data near the low- range of the data (Fig. 4). While a constant KD performs better than the linear fit to ΩAr, it underestimates the slope of the relationship between and (Fig. 4). This is not surprising because the abiogenic data clearly show the KD does not remain constant as changes (Fig. 2). Since using a constant KD will underestimate variability in cf when applied to corals, we do not recommend this approach.
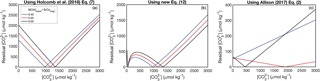
Figure 5Predicting from the KD formulations which themselves depend on : Holcomb et al. (2016) (a), Eq. (12) (b), and Allison (2017) (c). Each panel shows the residual between a guess of used to calculate KD and that calculated from Eqs. (13)–(14), plotted against the guess. The final is derived by finding where the residual is minimized for a particular (three of which are plotted as examples in red, blue, and black).
The ability of boron systematics to predict two independent carbonate chemistry parameters allows for calculation of the full carbonate system. This has prompted several recent applications deriving the carbonate chemistry of coral calcifying fluids (Allison et al., 2014; Comeau et al., 2017a; D'Olivo and McCulloch, 2017; Kubota et al., 2017; McCulloch et al., 2017; Ross et al., 2017; Schoepf et al., 2017). Here, we investigate the differences in derived coral calcifying fluid that arise from the choice of KD formulation. We use the paired δ11B and B∕Ca data of the “Davies 2” coral from McCulloch et al. (2017) as an example.
Derived cf shows similar seasonality when using the KD formulations of Holcomb et al. (2016), McCulloch et al. (2017), or our new Eq. (12) (Fig. 6). Regardless of which of these three KD formulations are used, cf is highest in summer and lowest in winter over a multiyear time series. This is consistent with other reports of B∕Ca seasonality in coral skeletons (Sinclair, 2005; D'Olivo and McCulloch, 2017; McCulloch et al., 2017; Ross et al., 2017), and with an independent approach based on Rayleigh modeling of minor elements in coral skeleton (Gaetani and Cohen, 2006; Gaetani et al., 2011). The primary difference among the derived values is that the KD formulations from Holcomb et al. (2016) and our Eq. (12) produce seasonal cycles with ∼ 50 % greater amplitude relative to the McCulloch et al. (2017) KD formulation. The absolute values of derived cf is approximately equal for all three formulations at the summertime maxima, but are lower during winter when using the KD formulations from Holcomb et al. (2016) or our Eq. (12), relative to McCulloch et al. (2017). Conversely, using the Allison (2017) KD formulation produces the opposite seasonal pattern with amplitude several times greater than the other KD formulations. This large discrepancy is not surprising given the behavior of the Allison (2017) KD formulation when retrospectively applied to the fluid composition of abiogenic aragonites (Fig. 3).
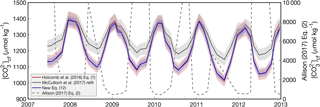
Figure 6Application of the four KD formulations for the “Davies 2” Porites coral data from McCulloch et al. (2017). Derived cf is plotted over multiple years using the KD formulations of Holcomb et al. (2016) (black), McCulloch et al. (2017) (red), Eq. (12) (blue), and Allison (2017) (dashed grey line). Shading represents 1 standard deviation of the systematic errors due to uncertainty in each KD formulation. Note that (1) the Holcomb et al. (2016) and the Eq. (12) lines plot nearly on top of each other, and (2) cf derived from the Allison (2017) KD formulation corresponds to the right y axis.
We present here a user-friendly computer code for deriving cf and DICcf from boron systematics (Supplement). The function is provided in both MATLAB and R formats, and it calculates cf and DICcf given inputs of δ11B, B∕Ca, temperature, salinity, and water depth. It allows easy toggling between what we consider the three plausible KD formulations (Holcomb et al., 2016, McCulloch et al., 2017, and our new Eq. 12). Furthermore, the code permits a choice of [B]sw functions since Allison et al. (2014) and Allison (2017) used the relation between salinity and [B]sw from Uppstrom (1974), whereas D'Olivo and McCulloch (2017) and McCulloch et al. (2017) used that of Lee et al. (2010). The carbonate dissociation constants can also be toggled between Dickson and Millero (1987) and Lueker et al. (2000). The code follows the calculations of CO2SYS (Lewis et al., 1998) for converting between pH scales and accounting for pressure effects on equilibrium constants, and uses the δ11Bsw of Foster et al. (2010) and the αB3−B4 of Klochko et al. (2006).
Perhaps most importantly, the code propagates known uncertainties into the derivation of cf and DICcf. These uncertainties are estimated using a Monte Carlo scheme, in which random errors (assuming Gaussian distributions) are added to parameters while repeating the calculations many times. The non-systematic uncertainty of derived values depends on the measurement precisions of δ11B, B∕Ca, temperature, and salinity. These will depend on the instruments and protocols used, and for δ11B and B∕Ca should be estimated by each laboratory, for example by repeated measurements of an external consistency standard. The systemic errors of derived values depend on the uncertainties of the various KD formulations, uncertainties associated with δ11Bsw (Foster et al., 2010), [B]sw (Lee et al., 2010), αB3−B4 (Klochko et al., 2006), and pKB (Dickson, 1990), and if known, any uncertainties in the accuracy of δ11B, B∕Ca, temperature, and salinity measurements.
With our code, the parameter space of cf derived from δ11B and B∕Ca, and the differences among KD formulations, can be readily visualized (Fig. 7). This enables future applications of boron systematics to coral skeletons to consider how the choice of KD formulation affects the particular question being investigated. We also apply the code to calculate carbonate system parameters using published δ11B and B∕Ca datasets (Fig. 8). Coral δ11B is tightly related to pHcf, varying only slightly with changes in seawater temperature and salinity (Fig. 8b). Likewise, B∕Ca is primarily a function of cf, but also depends in part on borate concentration, and hence on pHcf (Fig. 8c). For this reason, it is difficult to directly interpret coral B∕Ca, and instead we recommend pairing δ11B and B∕Ca to calculate the full calcifying fluid carbonate chemistry.
Interestingly, this analysis shows that coral calcifying fluid cf and DIC are consistently positively correlated across studies (Fig. 8f), whereas the sign of correlations between pH and both cf and DIC varies (Fig. 8d–e). Assuming cf is the carbonate system parameter most important for aragonite precipitation, these patterns may suggest that elevating DICcf is critical to the coral calcification process, although up-regulating pH is still important for shifting the carbonate system to favor over HCO. In addition, the large changes in pH, DIC, and that occur within the calcifying fluid relative to natural variability in the open ocean likely preclude the utility of boron systematics for reconstructing seawater carbonate chemistry, reinforcing previous conclusions made for both corals and foraminifera (Yu et al., 2010; Rae et al., 2011; Rollion-Bard et al., 2011). Rather, the boron systematics of coral skeletons are primarily useful for investigating calcifying fluid dynamics and understanding coral biomineralization.
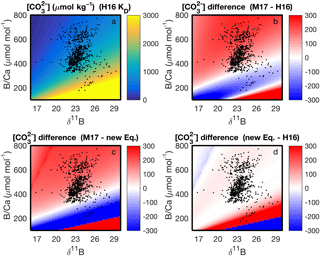
Figure 7Application of our computer code to visualizing the parameter space of (µmol kg−1) derived from B∕Ca and δ11B at 25 ∘C and salinity 35. The upper left panel shows absolute derived with the KD of Holcomb et al. (2016) (“H16”), whereas the other panels show the differences in among the KD formulations of H16, McCulloch et al. (2017) (“M17”), and our new Eq. (12). The black dots show coral data from the literature (see Fig. 8 legend below). Note that the actual derived for the coral data will also depend on variations of the in situ temperature and salinity, which are not accounted for in the plots.
In contrast to boron systemics, which consistently show elevated DICcf, microelectrode measurements of cf and pHcf imply that DICcf is depleted (Cai et al., 2016), relative to that of seawater (typically ). The reason for this discrepancy is not yet clear, and resolving it should be a high priority because whether DICcf is greater than or less than seawater implies different calcification strategies. Reducing DICcf may be an efficient strategy to increase pHcf because the reduced buffering capacity means that less energy is required to elevate pH via proton pumping (Cai et al., 2016). Alternatively, increasing DICcf means that a higher ΩAr is achieved for a given pHcf. Deciphering between these possibilities has key implications for whether calcification is limited by DICcf (or CO2 diffusion into the calcifying fluid) or by ΩAr. Two independent approaches to quantifying calcifying fluid carbonate chemistry are consistent with the high DICcf scenario. First, coral U∕Ca ratios imply that DICcf is between 2600 and 6100 µmol kg−1 (DeCarlo et al., 2015), which is a similar range to that derived from boron systematics (Fig. 8). Second, boron systematics-derived is consistent with a combination of Raman-spectroscopy-derived ΩAr and trace element ratios (Mg / Ca and Sr / Ca) (DeCarlo et al., 2017). Nevertheless, since low DICcf has been derived from microelectrodes in several species (Cai et al., 2016), studies combining multiple approaches (i.e., geochemistry and microelectrodes) on the same specimens will be essential for resolving the DICcf discrepancy.
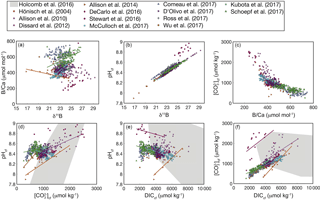
Figure 8Correlations among coral calcifying fluid carbonate system parameters based on published boron systematics datasets: (a) B∕Ca and δ11B, (b) pHcf and δ11B, (c) cf and B∕Ca, (d) pH and cf, (e) pHcf and DICcf, and (f) cf and DICcf. Colors show different studies, and lines are plotted for significant (p<0.05) correlations using all the data within each study. The grey area shows the convex hull of the parameter space covered in the abiogenic experiments of Holcomb et al. (2016). Calculations are performed using the Holcomb et al. (2016) KD formulation.
Despite the availability of abiogenic B∕Ca partitioning data from two experiments (Mavromatis et al., 2015; Holcomb et al., 2016), and several attempts to fit the data (Holcomb et al., 2016; Allison, 2017; McCulloch et al., 2017), it is important to recognize that uncertainties still remain, in particular an understanding of the controlling factors, and thus the appropriate KD formulation to apply. From a mechanistic viewpoint, the key fundamental question that remains is whether the abiogenic data of Mavromatis et al. (2015) and Holcomb et al. (2016) are directly comparable and thus should be fit with a continuous function (e.g., Eq. 12), or if they are incomparable because Mavromatis et al. (2015) used NaCl solutions and Holcomb et al. (2016) used seawater. If they are comparable, then our new Eq. (12) or a similar fit to both datasets is the most appropriate KD formulation. Calcite precipitation studies provide some support for the hypothesis that crystal growth rate or ΩAr influences B∕Ca partitioning (Ruiz-Agudo et al., 2012; Uchikawa et al., 2015, 2017), but it is not yet known if these results can be extended to aragonite precipitation from seawater. Alternatively, if the solution chemistry makes the two experiments incomparable, the Holcomb et al. (2016) KD data are most likely the more suitable choice for corals because the experiments were conducted with seawater at ΩAr comparable to that of coral calcifying fluids (DeCarlo et al., 2017), and they can be fit as a function of either or [H+]. However, it is important to recognize that the parameter space of CO2 system parameters covered in the Holcomb et al. (2016) experiments includes some, but not all, of the published coral data (Fig. 8). Further, since we are unable to conclusively distinguish whether the two abiogenic datasets are directly comparable, all three KD formulations may be considered equally valid until proven otherwise. Additional abiogenic experiments aimed at this question will clearly be useful in refining the boron systematics proxies.
From a practical standpoint, the KD formulations of Holcomb et al. (2016) and McCulloch et al. (2017) may be the most appropriate. Both produce unique solutions of that increase with , and they effectively reconstruct fluid using the abiogenic aragonites precipitated from seawater. While our Eq. (12) produces cf estimates that are nearly identical under most δ11B and B∕Ca combinations to those derived using the Holcomb et al. (2016) KD formulation (Fig. 7), Eq. (12) can have nonunique solutions, which could complicate interpretations of cf in some cases.
A final consideration is that two of the KD formulations (Holcomb et al. (2016) and our new Eq. 12) are fit to . Fitting Eq. (12) to a wider range of helps to account for the different solution chemistries and associated growth rates of the two abiogenic precipitation studies (Mavromatis et al., 2015; Holcomb et al., 2016), but ΩAr or crystal growth rate may be the true controlling factor (Watson, 2004; van der Weijden and van der Weijden, 2014). However, Holcomb et al. (2016) did not find a temperature dependence of B∕Ca partitioning, as would be expected if precipitation rate influenced KD. While growth rate is likely related to (Burton and Walter, 1987), the two could decouple with changes in temperature or if coral calcifying fluid [Ca2+]cf departs from seawater levels. Recent evidence combining Raman spectroscopy with boron systematics suggests [Ca2+]cf is within ∼ 25 % of seawater (DeCarlo et al., 2017; DeCarlo et al., 2018) but this has yet to be tested on a range of coral species and locations. Thus, future abiogenic experiments designed to test under what conditions or crystal growth rates control B∕Ca partitioning, as well as development of proxies for [Ca2+]cf, may improve the accuracy of deriving calcifying fluid carbonate chemistry from boron systematics.
Recent abiogenic aragonite precipitation experiments have made possible the application of boron systematics to quantifying the full carbonate system of coral calcifying fluid. However, a number of approaches to doing so have been utilized (Allison et al., 2014; Allison, 2017; D'Olivo and McCulloch, 2017; McCulloch et al., 2017), without a comprehensive analysis of which KD formulations are plausible (i.e., can reproduce the experimental fluid chemistry) or the implications for interpreting coral skeletons. We evaluated four potential B∕Ca KD formulations involving B(OH) substituting for in the aragonite lattice. Our analysis suggests that there are at least three plausible KD formulations (Holcomb et al., 2016, McCulloch et al., 2017, and our new Eq. 12) that can be used to determine the KD and its dependence on fluid chemistry. Despite the differences in plausible approaches, we show that all three produce similar patterns in derived coral calcifying fluid carbonate chemistry. Nevertheless, subtle differences in derived carbonate chemistry remain among the approaches, and addressing these differences should be the target of future abiogenic aragonite precipitation experiments. Finally, we present a code that computes coral calcifying fluid carbonate chemistry from boron systematics and allows for comparison among different KD formulations.
Codes are available in the Supplement.
In the main text, we used numerical solutions to predict based on Eq. (14). Here, we show an analytical solution to Eq. (14) for the Allison (2017) KD formulation. Allison (2017) fit KD to ΩAr with a linear regression in the form:
where
with concentrations in units of moles per kilogram and where Ksp is the solubility product. Inserting Eq. (A2) into Eq. (A1) yields
and then inserting Eq. (A3) into Eq. (14) of the main text yields
where is in units of moles per kilogram. We must now solve Eq. (A4) for . First, expand the right side of the equation:
Multiply both sides by Ksp:
Collect all the terms on the left side of the equation:
Factor out :
Solve for :
In seawater at 25 ∘C and salinity 34, [Ca2+] is approximately 0.01 mol kg−1 and Ksp is (Riley and Tongudai, 1967; Lewis et al., 1998). According to Allison (2017), a is and b is . Inserting these values in Eq. (A9) yields
The denominator equals zero (i.e., the solution is undefined) when = = 0.44. If , then the denominator is positive, and since the numerator is always negative, this means that the predicted will be negative. Predicted will be highest when the denominator is a small negative number, which occurs when is slightly greater than 0.44. As increases ≫ 0.44, the absolute value of the denominator increases more than that of the numerator because the coefficient attached to is raised to the −6 power in the denominator and to the −11 power in the numerator. The implication is that predicted will decrease as increases beyond 0.44. This is the same conclusion reached in the main text, and is the opposite trend to that observed in the abiogenic aragonites (Fig. 4).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-15-2819-2018-supplement.
The authors declare that they have no conflict of interest.
The authors thank Glenn Gaetani for valuable comments. This study was funded
by an ARC Laureate Fellowship (FL120100049) awarded to Malcolm T. McCulloch, and the ARC
Centre of Excellence for Coral Reef Studies (CE140100020).
Edited by: Markus Kienast
Reviewed by: two anonymous referees
Adkins, J. F., Boyle, E. A., Curry, W. B., and Lutringer, A.: Stable isotopes in deep-sea corals and a new mechanism for “vital effects”, Geochim. Cosmochim. Ac., 67, 1129–1143, 2003. a, b, c
Al-Horani, F. A., Al-Moghrabi, S. M., and De Beer, D.: The mechanism of calcification and its relation to photosynthesis and respiration in the scleractinian coral Galaxea fascicularis, Mar. Biol., 142, 419–426, https://doi.org/10.1007/s00227-002-0981-8, 2003. a, b
Allen, K. A. and Hönisch, B.: The planktic foraminiferal B∕Ca proxy for seawater carbonate chemistry: A critical evaluation, Earth Planet. Sc. Lett., 345, 203–211, 2012. a
Allison, N.: Reconstructing coral calcification fluid dissolved inorganic carbon chemistry from skeletal boron: An exploration of potential controls on coral aragonite B∕Ca, Heliyon, 3, e00387, https://doi.org/10.1016/j.heliyon.2017.e00387, 2017. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, aa, ab, ac, ad
Allison, N., Cohen, I., Finch, A. A., Erez, J., and Tudhope, A. W.: Corals concentrate dissolved inorganic carbon to facilitate calcification, Nat. Commun., 5, 5741, https://doi.org/10.1038/ncomms6741, 2014. a, b, c, d, e, f, g, h
Balan, E., Noireaux, J., Mavromatis, V., Saldi, G. D., Montouillout, V., Blanchard, M., Pietrucci, F., Gervais, C., Rustad, J. R., Schott, J., and Gaillardet, J.: Theoretical isotopic fractionation between structural boron in carbonates and aqueous boric acid and borate ion, Geochim. Cosmochim. Ac., 222, 117–129, https://doi.org/10.1016/j.gca.2017.10.017, 2018. a, b
Barnes, D. J.: Coral skeletons: an explanation of their growth and structure, Science, 170, 1305–1308, https://doi.org/10.1126/science.170.3964.1305, 1970. a
Burton, E. A. and Walter, L. M.: Relative precipitation rates of aragonite and Mg calcite from seawater: Temperature or carbonate ion control?, Geology, 15, 111–114, 1987. a, b, c, d
Cai, W.-J., Ma, Y., Hopkinson, B. M., Grottoli, A. G., Warner, M. E., Ding, Q., Hu, X., Yuan, X., Schoepf, V., Xu, H., Han, C., Melman, T. F., Hoadley, K. D., Pettay, D. T., Matsui, Y., Baumann, J. H., Levas, S., Ying, Y., and Wang, Y.: Microelectrode characterization of coral daytime interior pH and carbonate chemistry, Nat. Commun., 7, 11144, https://doi.org/10.1038/ncomms11144, 2016. a, b, c, d, e, f
Cohen, A. L. and McConnaughey, T. A.: Geochemical Perspectives on Coral Mineralization, Rev. Mineral. Geochem., 54, 151–187, https://doi.org/10.2113/0540151, 2003. a, b, c
Comeau, S., Cornwall, C. E., and McCulloch, M. T.: Decoupling between the response of coral calcifying fluid pH and calcification to ocean acidification, Sci. Rep., 7, 7573, https://doi.org/10.1038/s41598-017-08003-z, 2017a.
Comeau, S., Tambutté, E., Carpenter, R. C., Edmunds, P. J., Evensen, N. R., Allemand, D., Ferrier-Pagès, C., Tambutté, S., and Venn, A. A.: Coral calcifying fluid pH is modulated by seawater carbonate chemistry not solely seawater pH, P. Roy. Soc. Lond. B. Bio., 284, 20161669, https://doi.org/10.1098/rspb.2016.1669, 2017b.
DeCarlo, T. M., Gaetani, G. A., Holcomb, M., and Cohen, A. L.: Experimental determination of factors controlling U∕Ca of aragonite precipitated from seawater: implications for interpreting coral skeleton, Geochim. Cosmochim. Ac., 162, 151–165, https://doi.org/10.1016/j.gca.2015.04.016, 2015. a, b, c, d
DeCarlo, T. M., Gaetani, G. A., Cohen, A. L., Foster, G. L., Alpert, A. E., and Stewart, J.: Coral Sr-U Thermometry, Paleoceanography, 31, 626–638, https://doi.org/10.1002/2015PA002908, 2016. a
DeCarlo, T. M., D'Olivo, J. P., Foster, T., Holcomb, M., Becker, T., and McCulloch, M. T.: Coral calcifying fluid aragonite saturation states derived from Raman spectroscopy, Biogeosciences, 14, 5253–5269, https://doi.org/10.5194/bg-14-5253-2017, 2017. a, b, c, d
DeCarlo, T. M., Comeau, S., Cornwall, C. E., and McCulloch, M. T.: Coral resistance to ocean acidification linked to increased calcium at the site of calcification, Proc. R. Soc. B, 285, 20180564, https://doi.org/10.1098/rspb.2018.0564, 2018.
DePaolo, D. J.: Surface kinetic model for isotopic and trace element fractionation during precipitation of calcite from aqueous solutions, Geochim. Cosmochim. Ac., 75, 1039–1056, https://doi.org/10.1016/J.GCA.2010.11.020, 2011. a
Dickson, A. G.: Standard potential of the reaction: AgCl (s)+ 1/2H2 (g)= Ag (s)+ HCl (aq), and the standard acidity constant of the ion HSO4- in synthetic sea water from 273.15 to 318.15 K, J. Chem. Thermodyn., 22, 113–127, 1990. a, b
Dickson, A. G. and Millero, F. J.: A comparison of the equilibrium constants for the dissociation of carbonic acid in seawater media, Deep-Sea Res., 34, 1733–1743, https://doi.org/10.1016/0198-0149(87)90021-5, 1987. a
D'Olivo, J. P. and McCulloch, M. T.: Response of coral calcification and calcifying fluid composition to thermally induced bleaching stress, Sci. Rep., 7, 2207, https://doi.org/10.1038/s41598-017-02306-x, 2017. a, b, c, d, e
Foster, G. L., Pogge von Strandmann, P. A. E., and Rae, J. W. B.: Boron and magnesium isotopic composition of seawater, Geochem. Geophys. Geosys., 11, Q08015, https://doi.org/10.1029/2010GC003201, 2010. a, b, c, d
Gaetani, G. A. and Cohen, A. L.: Element partitioning during precipitation of aragonite from seawater: A framework for understanding paleoproxies, Geochim. Cosmochim. Ac., 70, 4617–4634, https://doi.org/10.1016/j.gca.2006.07.008, 2006. a, b, c
Gaetani, G. A., Cohen, A. L., Wang, Z., and Crusius, J.: Rayleigh-Based, Multi-Element Coral Thermometry: a Biomineralization Approach to Developing Climate Proxies, Geochim. Cosmochim. Ac., 75, 1920–1932, https://doi.org/10.1016/j.gca.2011.01.010, 2011. a
Gagnon, A. C., Adkins, J. F., and Erez, J.: Seawater transport during coral biomineralization, Earth Planet. Sc. Lett., 329, 150–161, 2012. a, b
Holcomb, M., Venn, A. A., Tambutté, E., Tambutté, S., Allemand, D., Trotter, J., and McCulloch, M.: Coral calcifying fluid pH dictates response to ocean acidification, Sci. Rep., 4, 5207, https://doi.org/10.1038/srep05207, 2014. a, b, c
Holcomb, M., DeCarlo, T., Gaetani, G., and McCulloch, M.: Factors affecting B∕Ca ratios in synthetic aragonite, Chem. Geol., 437, 67–76, https://doi.org/10.1016/j.chemgeo.2016.05.007, 2016. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, aa, ab, ac, ad, ae, af, ag, ah, ai, aj, ak, al, am, an, ao, ap, aq, ar, as, at, au, av, aw, ax, ay, az, ba, bb, bc, bd, be, bf, bg, bh, bi, bj, bk, bl, bm
Hönisch, B., Hemming, N. G., Grottoli, A. G., Amat, A., Hanson, G. N., and Bijma, J.: Assessing scleractinian corals as recorders for paleo-pH: Empirical calibration and vital effects, Geochim. Cosmochim. Ac., 68, 3675–3685, 2004. a, b
Inoue, M., Suwa, R., Suzuki, A., Sakai, K., and Kawahata, H.: Effects of seawater pH on growth and skeletal U∕Ca ratios of Acropora digitifera coral polyps, Geophys. Res. Lett., 38, L12809, https://doi.org/10.1029/2011GL047786, 2011. a
Klochko, K., Kaufman, A. J., Yao, W., Byrne, R. H., and Tossell, J. A.: Experimental measurement of boron isotope fractionation in seawater, Earth Planet. Sci. Lett., 248, 276–285, https://doi.org/10.1016/j.epsl.2006.05.034, 2006. a, b, c, d, e
Kubota, K., Yokoyama, Y., Ishikawa, T., Suzuki, A., and Ishii, M.: Rapid decline in pH of coral calcification fluid due to incorporation of anthropogenic CO2, Sci. Rep., 7, 7694, https://doi.org/10.1038/s41598-017-07680-0, 2017. a, b
Lee, K., Kim, T.-W., Byrne, R., Millero, F., Feely, R., and Liu, Y.-M.: The universal ratio of boron to chlorinity for the North Pacific and North Atlantic oceans, Geochim. Cosmochim. Ac., 74, 1801–1811, https://doi.org/10.1016/J.GCA.2009.12.027, 2010. a, b, c
Lewis, E., Wallace, D., and Allison, L. J.: Program developed for CO2 system calculations, Tech. rep., Brookhaven Natl. Lab., Dep. of Appl. Sci., Upton, New York, 1998. a, b
Lueker, T. J., Dickson, A. G., and Keeling, C. D.: Ocean pCO calculated from dissolved inorganic carbon, Mar. Chem., 70, 105–119, 2000. a
Mavromatis, V., Montouillout, V., Noireaux, J., Gaillardet, J., and Schott, J.: Characterization of boron incorporation and speciation in calcite and aragonite from co-precipitation experiments under controlled pH, temperature and precipitation rate, Geochim. Cosmochim. Ac., 150, 299–313, https://doi.org/10.1016/j.gca.2014.10.024, 2015. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, aa, ab
McConnaughey, T.: 13C and 18O isotopic disequilibrium in biological carbonates: I. Patterns, Geochim. Cosmochim. Ac., 53, 151–162, https://doi.org/10.1016/0016-7037(89)90282-2, 1989. a, b
McCulloch, M., Trotter, J., Montagna, P., Falter, J., Dunbar, R., Freiwald, A., Försterra, G., López Correa, M., Maier, C., and Rüggeberg, A.: Resilience of cold-water scleractinian corals to ocean acidification: Boron isotopic systematics of pH and saturation state up-regulation, Geochim. Cosmochim. Ac., 87, 21–34, 2012a. a
McCulloch, M. T., Falter, J., Trotter, J., and Montagna, P.: Coral resilience to ocean acidification and global warming through pH up-regulation, Nat. Clim. Change, 2, 623–627, 2012b. a, b
McCulloch, M. T., D'Olivo Cordero, J. P., Falter, J., Holcomb, M., and Trotter, J. A.: Coral calcification in a changing World: the interactive dynamics of pH and DIC up-regulation, Nat. Commun., 8, 15686, https://doi.org/10.1038/ncomms15686, 2017. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, aa, ab, ac, ad, ae
Noireaux, J., Mavromatis, V., Gaillardet, J., Schott, J., Montouillout, V., Louvat, P., Rollion-Bard, C., and Neuville, D.: Crystallographic control on the boron isotope paleo-pH proxy, Earth Planet. Sci. Lett., 430, 398–407, https://doi.org/10.1016/j.epsl.2015.07.063, 2015. a, b
Rae, J. W., Foster, G. L., Schmidt, D. N., and Elliott, T.: Boron isotopes and B∕Ca in benthic foraminifera: Proxies for the deep ocean carbonate system, Earth Planet. Sci. Lett., 302, 403–413, https://doi.org/10.1016/J.EPSL.2010.12.034, 2011. a
Ries, J. B.: A physicochemical framework for interpreting the biological calcification response to CO2-induced ocean acidification, Geochim. Cosmochim. Ac., 75, 4053–4064, 2011. a, b
Riley, J. P. and Tongudai, M.: The major cation/chlorinity ratios in sea water, Chem. Geol., 2, 263–269, 1967. a
Rollion-Bard, C., Blamart, D., Cuif, J. P., and Dauphin, Y.: In situ measurements of oxygen isotopic composition in deep-sea coral, Lophelia pertusa: Re-examination of the current geochemical models of biomineralization, Geochim. Cosmochim. Ac., 74, 1338–1349, 2010. a
Rollion-Bard, C., Blamart, D., Trebosc, J., Tricot, G., Mussi, A., and Cuif, J. P.: Boron isotopes as pH proxy: A new look at boron speciation in deep-sea corals using 11B MAS NMR and EELS, Geochim. Cosmochim. Ac., 75, 1003–1012, 2011. a, b
Ross, C. L., Falter, J. L., and McCulloch, M. T.: Active modulation of the calcifying fluid carbonate chemistry (δ11B, B∕Ca) and seasonally invariant coral calcification at sub-tropical limits, Sci. Rep., 7, 13830, https://doi.org/10.1038/s41598-017-14066-9, 2017. a, b, c, d
Ruiz-Agudo, E., Putnis, C., Kowacz, M., Ortega-Huertas, M., and Putnis, A.: Boron incorporation into calcite during growth: Implications for the use of boron in carbonates as a pH proxy, Earth Planet. Sci. Lett., 345–348, 9–17, https://doi.org/10.1016/j.epsl.2012.06.032, 2012. a
Schoepf, V., Levas, S. J., Rodrigues, L. J., McBride, M. O., Aschaffenburg, M. D., Matsui, Y., Warner, M. E., Hughes, A. D., and Grottoli, A. G.: Kinetic and metabolic isotope effects in coral skeletal carbon isotopes: A re-evaluation using experimental coral bleaching as a case study, Geochim. Cosmochim. Ac., 146, 164–178, https://doi.org/10.1016/j.gca.2014.09.033, 2014. a
Schoepf, V., Jury, C. P., Toonen, R. J., and McCulloch, M. T.: Coral calcification mechanisms facilitate adaptive responses to ocean acidification., P. Roy. Soc. Lond. B. Bio., 284, 20172117, https://doi.org/10.1098/rspb.2017.2117, 2017. a, b
Sinclair, D. J.: Correlated trace element “vital effects” in tropical corals: a new geochemical tool for probing biomineralization, Geochim. Cosmochim. Ac., 69, 3265–3284, 2005. a
Stewart, J. A., Anagnostou, E., and Foster, G. L.: An improved boron isotope pH proxy calibration for the deep-sea coral Desmophyllum dianthus through sub-sampling of fibrous aragonite, Chem. Geol., 447, 148–160, https://doi.org/10.1016/j.chemgeo.2016.10.029, 2016. a
Tambutté, E., Tambutté, S., Segonds, N., Zoccola, D., Venn, A., Erez, J., and Allemand, D.: Calcein labelling and electrophysiology: insights on coral tissue permeability and calcification, P. Roy. Soc. Lond. B. Bio., 279, 19–27, https://doi.org/10.1098/rspb.2011.0733, 2012. a, b
Trotter, J., Montagna, P., McCulloch, M., Silenzi, S., Reynaud, S., Mortimer, G., Martin, S., Ferrier-Pagès, C., Gattuso, J. P., and Rodolfo-Metalpa, R.: Quantifying the pH “vital effect” in the temperate zooxanthellate coral Cladocora caespitosa: Validation of the boron seawater pH proxy, Earth Planet. Sci. Lett., 303, 163–173, 2011. a, b, c, d
Uchikawa, J., Penman, D. E., Zachos, J. C., and Zeebe, R. E.: Experimental evidence for kinetic effects on B∕Ca in synthetic calcite: Implications for potential B(OH)4− and B(OH)3 incorporation, Geochim. Cosmochim. Ac., 150, 171–191, https://doi.org/10.1016/j.gca.2014.11.022, 2015. a
Uchikawa, J., Harper, D. T., Penman, D. E., Zachos, J. C., and Zeebe, R. E.: Influence of solution chemistry on the boron content in inorganic calcite grown in artificial seawater, Geochim. Cosmochim. Ac., 218, 291–307, https://doi.org/10.1016/j.gca.2017.09.016, 2017. a
Uppstrom, L.: The boron/chlorinity ratio of deep-sea water from the Pacific Ocean, Deep Sea Research and Oceanographic Abstracts, 21, 161–162, 1974. a
van der Weijden, C. and van der Weijden, R.: Calcite growth: Rate dependence on saturation, on ratios of dissolved calcium and (bi)carbonate and on their complexes, J. Cryst. Growth, 394, 137–144, https://doi.org/10.1016/J.JCRYSGRO.2014.02.042, 2014. a
Venn, A., Tambutte, E., Holcomb, M., Allemand, D., and Tambutte, S.: Live tissue imaging shows reef corals elevate pH under their calcifying tissue relative to seawater, PLoS One, 6, e20013, https://doi.org/10.1371/journal.pone.0020013, 2011. a, b, c
Venn, A. A., Tambutté, E., Holcomb, M., Laurent, J., Allemand, D., and Tambutté, S.: Impact of seawater acidification on pH at the tissue-skeleton interface and calcification in reef corals., P. Natl. Acad. Sci. USA, 110, 1634–1639, https://doi.org/10.1073/pnas.1216153110, 2013. a
Watson, E. B.: A conceptual model for near-surface kinetic controls on the trace-element and stable isotope composition of abiogenic calcite crystals, Geochim. Cosmochim. Ac., 68, 1473–1488, 2004. a, b
Wu, H. C., Dissard, D., Le Cornec, F., Thil, F., Tribollet, A., Moya, A., and Douville, E.: Primary Life Stage Boron Isotope and Trace Elements Incorporation in Aposymbiotic Acropora millepora Coral under Ocean Acidification and Warming, Frontiers Mar. Sci., 4, 129, https://doi.org/10.3389/fmars.2017.00129, 2017. a
Yu, J., Foster, G. L., Elderfield, H., Broecker, W. S., and Clark, E.: An evaluation of benthic foraminiferal B∕Ca and δ11B for deep ocean carbonate ion and pH reconstructions, Earth Planet. Sci. Lett., 293, 114–120, https://doi.org/10.1016/J.EPSL.2010.02.029, 2010. a
Zeebe, R. E. and Wolf-Gladrow, D. A.: CO2 in seawater: equilibrium, kinetics, isotopes, vol. 65, Elsevier Science Limited, Amsterdam, 2001. a
- Abstract
- Introduction
- Partitioning of B∕Ca between aragonite and seawater
- Fitting the experimental B∕Ca partitioning data
- Back-application of partition coefficient formulations to abiogenic datasets
- Application to deriving coral calcifying fluid carbonate chemistry
- A computer code for applying boron systematics to coral skeletons
- Relationships among coral calcifying fluid carbonate chemistry parameters
- Which KD formulation to use?
- Conclusions
- Code availability
- Appendix A
- Competing interests
- Acknowledgements
- References
- Supplement
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(6153 KB) - Full-text XML
- Corrigendum
-
Supplement
(71 KB) - BibTeX
- EndNote
- Abstract
- Introduction
- Partitioning of B∕Ca between aragonite and seawater
- Fitting the experimental B∕Ca partitioning data
- Back-application of partition coefficient formulations to abiogenic datasets
- Application to deriving coral calcifying fluid carbonate chemistry
- A computer code for applying boron systematics to coral skeletons
- Relationships among coral calcifying fluid carbonate chemistry parameters
- Which KD formulation to use?
- Conclusions
- Code availability
- Appendix A
- Competing interests
- Acknowledgements
- References
- Supplement





