the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
Catchment tracers reveal discharge, recharge and sources of groundwater-borne pollutants in a novel lake modelling approach
Emil Kristensen
Mikkel Madsen-Østerbye
Philippe Massicotte
Ole Pedersen
Stiig Markager
Theis Kragh
Groundwater-borne contaminants such as nutrients, dissolved organic carbon (DOC), coloured dissolved organic matter (CDOM) and pesticides can have an impact the biological quality of lakes. The sources of pollutants can, however, be difficult to identify due to high heterogeneity in groundwater flow patterns. This study presents a novel approach for fast hydrological surveys of small groundwater-fed lakes using multiple groundwater-borne tracers. Water samples were collected from the lake and temporary groundwater wells, installed every 50 m within a distance of 5–45 m to the shore, were analysed for tracer concentrations of CDOM, DOC, total dissolved nitrogen (TDN, groundwater only), total nitrogen (TN, lake only), total dissolved phosphorus (TDP, groundwater only), total phosphorus (TP, lake only), δ18O ∕ δ16O isotope ratios and fluorescent dissolved organic matter (FDOM) components derived from parallel factor analysis (PARAFAC). The isolation of groundwater recharge areas was based on δ18O measurements and areas with a high groundwater recharge rate were identified using a microbially influenced FDOM component. Groundwater discharge sites and the fractions of water delivered from the individual sites were isolated with the Community Assembly via Trait Selection model (CATS). The CATS model utilized tracer measurements of TDP, TDN, DOC and CDOM from the groundwater samples and related these to the tracer measurements of TN, TP, DOC and CDOM in the lake. A direct comparison between the lake and the inflowing groundwater was possible as degradation rates of the tracers in the lake were taken into account and related to a range of water retention times (WRTs) of the lake (0.25–3.5 years in 0.25-year increments). These estimations showed that WRTs above 2 years required a higher tracer concentration of inflowing water than found in any of the groundwater wells around the lake. From the estimations of inflowing tracer concentration, the CATS model isolated groundwater discharge sites located mainly in the eastern part of the lake with a single site in the southern part. Observations from the eastern part of the lake revealed an impermeable clay layer that promotes discharge during heavy precipitation events, which would otherwise be difficult to identify using traditional hydrological methods. In comparison to the lake concentrations, high tracer concentrations in the southern part showed that only a smaller fraction of water could originate from this area, thereby confirming the model results. A Euclidean cluster analysis of δ18O isotopes identified recharge sites corresponding to areas adjacent to drainage channels, and a cluster analysis of the microbially influenced FDOM component C4 further identified five sites that showed a tendency towards high groundwater recharge rate. In conclusion, it was found that this methodology can be applied to smaller lakes within a short time frame, providing useful information regarding the WRT of the lake and more importantly the groundwater recharge and discharge sites around the lake. Thus, it is a tool for specific management of the catchment.
- Article
(3565 KB) -
Supplement
(488 KB) - BibTeX
- EndNote
Most lakes are connected to the groundwater, which to some degree defines their chemical and biological characteristics (Lewandowski et al., 2015). Particularly in smaller lakes and ponds, the groundwater contributes nutrients, dissolved organic carbon (DOC), coloured dissolved organic matter (CDOM) or other contaminants, which can have a negative impact on the biological quality of the lakes (for nitrogen and phosphorous, see review by Lewandowski et al., 2015). These inputs often result in unfavourable light conditions for submerged macrophytes due to either increased phytoplankton biomass (Smith, 2003) or increased light absorption from high CDOM concentrations. The negative impacts of the contaminants make the identification of pollutant sources an important management issue for lakes, which, however, is complicated for groundwater due to temporal and spatial differences in discharge and associated pollutant concentrations (e.g. Meinikmann et al., 2013). In addition, the lake hydrology itself may be important, particularly in small water bodies. For example, low or fluctuating water level can have a large influence on the biodiversity of the lake (Chow-Fraser et al., 1998). This illustrates the need for approaches to quickly identify discharge (i.e. groundwater exfiltrating to the lake) and recharge (i.e. lake water infiltrating to the groundwater) areas on the lake scale and thereby provide the necessary tools for an effective management strategy for ponds and small lakes.
Groundwater discharge and recharge are traditionally identified and quantified by measurements of the hydraulic head through the installation of piezometers around the lake and of the hydraulic conductivity in the sediments (Rosenberry et al., 2015). This method is often combined with the use of seepage meters, which quantify the water entering or leaving through the lake bottom (Lee and Cherry, 1979). However, this method is challenged by the heterogeneous nature of groundwater seepage related to the specific hydraulic conductivity of the lake bed sediments (Cherkauer and Nader, 1989; Kishel and Gerla, 2002; Rosenberry, 2005). Furthermore, these methods are also time-consuming as they have to be carried out several times throughout the season. The heterogeneity and annual variability in groundwater seepage call for a robust, easier and faster method to determine groundwater inputs and influences.
Various conservative tracers have been used to achieve estimates of groundwater flow and water retention times (WRTs) in lakes. These tracers are divided into three main categories: (1) environmental tracers (naturally derived tracers from the atmosphere or catchment that are transported to the system), (2) historical tracers (anthropogenic tracers such as 3H or 36Cl from nuclear testing) or (3) applied tracers (tracers added to the system such as Br, Cl or fluorescent dyes) (Stets et al., 2010). Precipitation-derived environmental tracers, such as the isotope δ18O (reported in the Vienna-standard mean ocean water (SMOW), where and R is the δ18O ∕ δ16O ratio (Turner et al., 1987)), have been used to trace the interaction between groundwater and surface water. As evaporation occurs in the surface water it becomes enriched with δ18O, producing a unique lake δ18O∕δ16O ratio, which can be traced in the areas with groundwater recharge (Krabbenhoft et al., 1990). The isotopic composition can also be related to evaporation lines (from the local evaporation line describing the δ18O and δ2H relationship) to estimate WRT (Gibson et al., 2002). Overall, these tracers provide information on flow patterns in the terrain or WRT, but they do not provide information regarding discharge in specific areas or the concentrations of the previously mentioned pollutants in the discharging water. We propose a different approach utilizing both conservative and non-conservative tracers such as dissolved carbon and nutrients, which are partly transferred to the percolating groundwater on its way to the lake (Kidmose et al., 2011) and have a direct influence on the lake's biological structure.
Some non-conservative tracers such as fluorescent dissolved organic matter (FDOM), which can be determined using parallel factor analysis (PARAFAC), have been used to trace DOM in aquatic environments (He et al., 2014; Massicotte and Frenette, 2011; Stedmon et al., 2003; Stedmon and Markager, 2005b; Walker et al., 2009). PARAFAC analysis is a modelling tool that can separate multiple FDOM samples (emission and excitation matrices) into specific fluorescent components (Stedmon et al., 2003). The fluorescent components can be biologically produced proteins derived from bacteria or molecules from the degradation of terrestrial organic material. These components have previously been found visually using a single excitation emission matrix and the observed fluorescent peaks (Coble, 1996). The differentiation between the fluorescent components are both a strength and a weakness as we can isolate many different components, but all of them can differ in both degradation and production rate in the lake and groundwater. Furthermore, these FDOM components have not yet been investigated as tracers in groundwater-fed lakes, as they, just as the rest of the non-conservative biological tracers, are volatile.
This is observed as a change in tracer concentrations (often a decrease) after the groundwater is discharged to the lake. The speed at which the change in concentration occurs is typically related to seasonal variations (e.g. temperature, mixing of the water column and UV radiation) and the WRT of the lake, e.g. the amount of time the tracer has been in the lake. The removal and degradation rates have been examined in many instances, e.g. for phosphorus (Larsen and Mercier, 1976; Vollenweider, 1975), nitrate (Harrison et al., 2009; Jensen et al., 1995), CDOM and DOC (Madsen-Østerbye et al., 2018). In a modelling approach, these rates are important as they provide information about the change in tracer concentration from the time when the tracer entered the lake. From this, it is possible to back-calculate the mixed inflow concentration of specific tracers when they were discharged to the lake. These estimations are crucial when working with non-conservative tracers, as they enable a direct comparison between the tracer concentration found in the catchment and the estimated lake concentration before degradation took place, which originates from the mixed inflow of groundwater.
As the concentrations of both conservative and non-conservative tracers in a groundwater-fed lake correspond to the mixed concentrations of discharging groundwater, taking degradation and atmospheric deposition into account, it is possible to utilize the Community Assembly via Trait Selection (CATS) approach. This model has been used to predict the relative abundances of a set of species from measures of community-aggregated trait values (average leaf area, root length, etc.) for all plant species at a site (Shipley, 2009; Shipley et al., 2006, 2011). The CATS model has three main parameters: (1) it models the probabilities that (2) maximize the entropy, which (3) is based on a set of constraints (Laliberté et al., 2014; Shipley et al., 2011). In reality, the model (1) predicts the relative abundances of species at a location from their (3) average trait values by (2) minimizing the number of species that explain the mean trait values. Maximum entropy (2) is the maximizing of “new knowledge gained” related to plant communities. This means moving from “all species have the same relative abundances” to “a few species have a high relative abundance”. When applying the model to the lake–groundwater interaction, we use the measured tracer concentrations at groundwater well sites around the lake as the individual plant species and the estimated mixed lake concentration before degradation took place as the community-aggregated trait values.
Determining groundwater movement using both conservative and non-conservative tracers found around the lake shore overcomes some fundamental shortcomings related to traditional sampling. Firstly, we often measure tracers, which do not have a direct impact on the lake ecosystem and therefore do not provide meaningful information regarding the inflow of nutrients or CDOM. Furthermore, the sampling is only performed in a few places throughout the catchment, which does not necessarily provide all the information on the groundwater flow patterns or to which degree water enters the lake and where. To overcome this, we measured conservative and relevant non-conservative tracers in and around a small lake with the aim of developing a novel approach to identify groundwater discharge and recharge areas on a high spatial scale. Thus areas that deliver pollutants to the lake, in which groundwater recharge happens and where recharge occurs with an increased flow rate, were pinpointed. The latter can spark further investigations into the lake WRT. Information regarding the WRT of the lake is especially useful when investigating how the concentrations of pollutants in the lake will develop after future restoration attempts. In the present study, the eight following tracers were measured: FDOM, CDOM, DOC, total dissolved phosphorus (TDP), total dissolved nitrogen (TDN), total phosphorus (TP), total nitrogen (TN) and δ18O ∕ δ16O isotope ratios. For these tracers, we tested (1) if groundwater discharge sites and pollutant sources can be estimated with the CATS model based on tracer concentrations, (2) whether conservative and non-conservative tracers can be used to detect groundwater recharge areas as well as provide insights into which areas possess a high groundwater recharge rate and (3) if catchment-derived tracer concentrations can be used to estimate a range of WRTs, which can be used with the CATS model.

Figure 1(a) Aerial photo of Lake Tvorup Hul showing groundwater well sampling sites (numbers). Orange numbers denote groundwater recharge sites, red numbers show sites with a high degree of recharge, white numbers represent possible groundwater discharge sites and light blue shows model-isolated discharge sites. Positions a, b and c show the three sampling sites in the lake. Missing samples in the northeastern part are due to an absence of groundwater in the area. The adjacent drainage channels north and west of the lake are marked with white lines. (b) Inverse-distance-weighted (IDW) contour map of fluorescence component C4. The blue-green colour corresponds to lake concentrations; darker blue indicates increased concentrations and lighter blue denotes decreased concentrations throughout the catchment. Areas with low differences between fluorescence in the lake and in the catchment are seen north of the lake and indicate parts with a fast groundwater recharge.
A small groundwater-fed lake in the sandy northwestern part of Denmark was chosen for this study (Tvorup Hul, area: 4 ha, mean depth: 2.4 m, 56∘91′ N, 8∘46′ E, UTM Zone 32). Coniferous forest and heathland dominate the catchment, although some agricultural activities are found in the eastern part of the catchment (Fig. 1a). Various isoetids including the rare nationally threatened species Isoetes echinospora and Subularia aquatica inhabited the lake until some decades ago when brownification increased significantly (based on Rebsdorf, 1981, and the present study), probably due to increasing soil pH (Ekström et al., 2011). This led to a restoration attempt in 1992; a channel was established to bypass the stream going through the lake, thus making the lake fed by groundwater. CDOM, DOC and the hydrologic conditions in the lake have since been investigated in several projects (Madsen-Østerbye et al., 2018; Solvang, 2016). This has resulted in extensive background data as well as estimations of WRTs between 0.4 and 3.3 years based on water table heights, hydraulic conductivity and seepage meter samplings (Solvang, 2016, and preliminary work Peter Engesgaard, personal communications, 2017).
2.1 Sampling and laboratory analysis
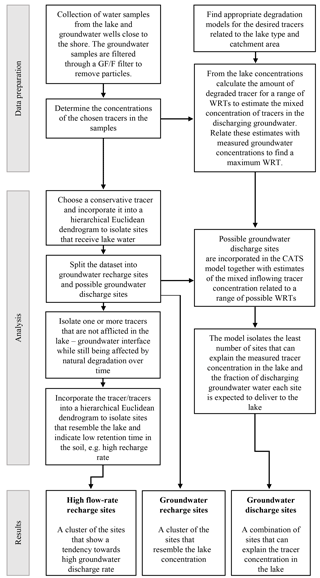
A total of 30 groundwater samples were taken every 50 m around the lake within a distance of 5–45 m to the shore in temporary groundwater wells at 1.25 m depth in February 2016. The data preparation, analysis and results are visualized in Fig. 2. The water in the wells was replaced three times before transferring the sample water to an acid-rinsed container. The samples were filtered through pre-combusted 0.7 µm nominal pore size Whatman GF/F filters the same day and kept cool and dark in hermetically sealed acid-rinsed BOD flasks until examination. Unfiltered samples were also collected from the lake.
DOC concentrations were measured using a total organic carbon analyser (Shimadzu, Japan) in accordance with Kragh and Søndergaard (2004). The CDOM absorbance was measured on a spectrophotometer (UV-1800, Shimadzu, Japan) between 240 and 750 nm in 1 nm intervals in a 1 cm quartz glass cuvette and expressed as the absorbance at 340 nm (ACDOM (340) cm−1). The samples were analysed for δ18O and δ16O isotopes at the Department of Geosciences and Natural Resource Management (University of Copenhagen) using mass spectrometry in accordance with Appelo and Postma (2005). δ18O is presented in the standard δ notation V-SMOW as δ18O ‰ (Vienna Standard Mean Ocean Water) (Turner et al., 1987). TDP and TDN were determined for groundwater samples while TN and TP were determined for lake water, as inflowing nutrients become incorporated into aquatic organisms. Nutrients were measured by transferring 5 mL sample water and 5 mL potassium persulfate reagent to acid-rinsed autoclave vials before autoclaving for 45 min. Then 2.5 mL of borate buffer was added after cooling and analysed in an autoanalyser (AA3HRAutoAnalyzer, SEAL, USA) together with blanks and internal standard row.
2.2 PARAFAC modelling
The fluorescent properties of DOM samples were investigated using PARAFAC. The FDOM samples were initially diluted 2–12 times to account for self-quenching, also referred to as inner filter effect, which occurs with high CDOM absorbance in the sample (Kothawala et al., 2013). Sample and blank fluorescence were measured using a spectrofluorometer (Cary Eclipse, Agilent Technologies, USA) by excitations between 240 and 450 nm, in 5 nm steps, while scanning the emissions from 300 to 600 nm in 2 nm increments. Prior to PARAFAC analysis, fluorescence data were processed in R (3.3.1) (R Core team, 2017) using the eemR (0.1.3) package. Blank values were subtracted following the documentation provided in the eemR package to remove Raman and Rayleigh scattering (Bahram et al., 2006; Lakowicz, 2006; Zepp et al., 2004). The data were then Raman normalized by dividing the florescent intensities by the integral of the Raman peak of the blank sample (Lawaetz and Stedmon, 2009) and lastly corrected for the inner filter effect (Kothawala et al., 2013) before being exported to MATLAB (2015b). In MATLAB, the fluorescence data were combined with a larger dataset (>1000 fluorescent samples from Massicotte and Frenette (2011) originating from a range of diverse aquatic systems) in order to increase the diversity of FDOM components. This allows for the detection of components insufficiently represented in the collected samples (Fellman et al., 2009; Stedmon and Bro, 2008; Stedmon and Markager, 2005a). The drEEM package was used to perform the PARAFAC modelling following the same procedure as described in Murphy et al. (2013). A split-half analysis, in which the dataset is split into two parts and compared multiple times, was used to test the results found in the PARAFAC model. A contour map showing the measured FDOM concentrations in groundwater was plotted in ArcMap (ArcMap 10.4.1, ESRI, USA) using the inverse-distance-weighted (IDW) function with barriers fitted around the lake and drainage channels.
2.3 Groundwater recharge and areas with a high groundwater recharge rate
A hierarchical Euclidean cluster of δ18O ‰ was employed to determine groundwater recharge areas using the Stat base package in R. δ18O ‰ was chosen as it is both conservative and biologically inert. Groundwater well sites that formed a cluster together with the lake samples were considered as being groundwater recharge sites, e.g. water originating from the lake, and were excluded for the later estimations of groundwater discharge sites. The groundwater recharge sites were further investigated using a range of non-conservative tracers influenced by biological degradation. We found that some of the tracer concentrations changed when moving from the lake to the groundwater. For example, CDOM showed a decrease in concentration when entering the groundwater, which is properly due to pH changes in the soil. An inspection of the results revealed that a protein-based fluorescent component met our criteria of being (1) non-conservative, (2) not afflicted by the lake–groundwater interface and (3) not too easily degraded or produced in high amounts, which could create false positive groundwater recharge sites. The PARAFAC component was related to the lake concentration with a hierarchical Euclidean cluster dendrogram, and the sites that clustered together with the lake samples indicated a high groundwater recharge rate.
2.4 Non-conservative tracer degradation and lake WRT
Lake WRT was found using traditional hydrological methods combined with non-conservative tracer concentrations, which were related to their degradation rates to form a proxy for the maximum WRT. Previous hydrological models suggested that the lake had a WRT between 0.4 and 3.3 years. To further narrow this range, we estimated WRT by relating the concentrations found in the lake to their respective degradation rates related to increasing WRT, e.g. by adding the estimated removed tracer since the groundwater entered the lake to the measured concentration in the lake. This enabled us to narrow the span of the WRT based on the estimated mixed inflowing tracer concentration related to the actual catchment concentrations. For example, if the estimated inflow concentration of a tracer is 100 µmol L−1 at a WRT of 2 years, and the highest catchment tracer concentration is 50 µmol L−1, then the catchment does not support a WRT of 2 years. In this instance, we estimated lake tracer concentrations of TN, TP, CDOM and DOC for WRTs from 0.25 to 3.5 years in 0.25-year increments following Eq. (1):
where MIC is the mixed inflow concentration, trlake is the tracer concentration found in the lake and ret (frac) is the retention fraction of the tracer at a known WRT. Retention models used in this study were based on the lake type as well as the geographical location of our lake. As there is not one model that can provide removal rates across all lakes, we encourage the readers to find models related to their specific lake type. Thus, phosphorus equilibrium concentration in this study was found using Eq. (2) modified from Larsen and Mercier (1976), which describes phosphor retention in lakes with low productivity:
where retP (frac) is the retention fraction of phosphorus and WRT is the water retention time in the lake. Similarly, nitrate inflow concentrations were estimated using a modified Danish nitrate removal model derived from Jensen et al. (1995) describing retention for shallow lakes with a short WRT (0–6 years) Eq. (3):
where retN (frac) is the retention fraction of nitrate and WRT is the water retention time in the lake. The corresponding retention fractions removed at different WRTs were related to the lake concentrations to estimate what the mixed inflow concentration must have been to produce the present lake concentration. The combined summer UV radiation and bacterial degradation rates of DOC and CDOM in groundwater from the dominating catchment vegetation type of the lake (Madsen-Østerbye et al., 2018) were extrapolated to the rest of the year. This was performed by relating the degradation rates to the mean monthly UV index (DMI, 2015) while assuming a linear relationship between the UV index and degradation rates. Thus we were able to estimate the specific removal of DOC and CDOM on a monthly basis related to the concentration measured in the lake at the time of sampling following Eq. (4):
where trlake is the lake concentration in the specific month, trlakepm is the lake tracer concentration in the previous month, mff is the monthly flushing fraction (), degra (frac) is the degradation fraction in the present month related to UV radiation and trinflow is the inflowing tracer concentration. Equation (4) was solved for trinflow and calculated using the same WRTs as the nitrate and phosphorus models.
2.5 The CATS model
Since the concentrations of both conservative and non-conservative tracers in a groundwater-fed lake correspond to the mixed concentrations of discharging groundwater, while taking degradation and atmospheric deposition into account, it is possible to utilize the CATS model. In the present study, the concentrations of non-conservative tracers (DOC, CDOM, TDP and TDN) at groundwater well sites around the lake acted as the individual plant species at a site and the equilibrium tracer concentrations derived from Eq. (1) (DOC, CDOM, TP and TN) acted as the community-aggregated trait values. When choosing tracers, it is important that there is differentiation between the concentrations measured at the sites. This means that a higher number of tracers and higher uncorrelated concentration differences between the sites result in a more secure determination of groundwater discharge sites. All tracers were investigated as a combined package, e.g. a single site is described by all the tracers mentioned above, and was run using the maxent function in the FD (functional diversity) package in R to compute the CATS model (Laliberté et al., 2014). Further information on the calculations can be found in the supplementary material for the FD package (Laliberté et al., 2014). From this, the model predicts the minimum number of groundwater well sites along the lake shore, which explains the measured concentrations in the recipient lake by maximizing the sites' relative contribution. The model also computes lambda values from the least-squares regression measuring which tracers are most influential on the relative fractions of water originating from the groundwater well sites. Consequently, lambda values quantify how much the relative contribution from the sites change when one tracer is changed a unit while the rest of the tracers are kept constant.
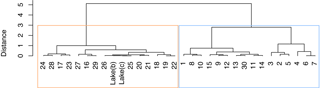
Figure 3Euclidean hierarchical clustering of the δ18O ‰ showing two clusters. The first cluster, marked with orange, groups with lake samples and is therefore regarded as a recharge site. The other cluster, marked with light blue, is possible groundwater discharge sites to the lake. The y axis denotes the linear distance between the δ18O ‰ samples fed to the model. The third lake sample was lost during preparation.
3.1 Groundwater recharge
Recharge areas were identified with a Euclidean hierarchical cluster dendrogram of δ18O ‰. The cluster revealed two main groups marked with orange and light blue in Fig. 3. The first group (orange) shows the groundwater well sites, ranging from sites 18 to 29, which clustered together with lake samples. The samples in this orange cluster share a clear resemblance with lake δ18O ‰ measurements and were therefore considered as groundwater recharge sites. The recharge sites were located in the north and western part of the lake and are marked with orange in Fig. 1a.
3.2 Fluorescent DOM
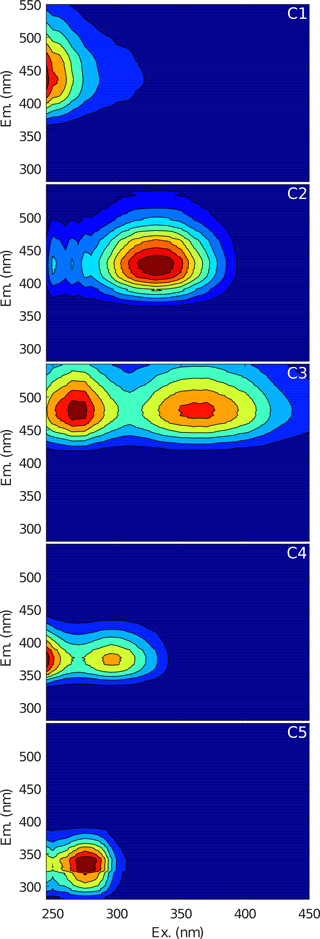
PARAFAC and split-half analysis modelling identified five distinct fluorescent DOM components (C1–C5, explained variance 96.79 %). The spectral properties of the five fluorophores (components) identified by the PARAFAC analysis (Fig. 4) revealed that the DOM pool had both terrestrial and microbial influence. Component C1 was similar to previously found components from terrestrial humic-like material (Stedmon et al., 2003). The component absorbs in the UV-C region, which is absorbed by the ozone layer and atmosphere (Diffey, 2002), and is for this reason expected to be mainly photo-resistant (Ishii and Boyer, 2012). Component C2 has been reported to be both marine and terrestrial humic-like (Coble, 1996; Murphy et al., 2006) and seems to be degraded by visible light and produced by microbial degradation in equal amounts (Stedmon and Markager, 2005b). Component C3 was also believed to be of terrestrial humic-like origin and was similar to the fluorescent peak C described by Coble (1996). The component absorbs in the UV-A region and is susceptible to both microbial and photochemical degradation (Stedmon et al., 2007; Stedmon and Markager, 2005a). Component C3 may be an intermediate product or produced biologically since changes in the concentration have been observed in the open oceans and in sea ice that has no apparent connection to the terrestrial environment (Ishii and Boyer, 2012). Component C4 is similar to component 5 found in Stedmon et al. (2003) and is believed to be a combination of fluorescent labile materials named peak N and T, which are produced biologically associated with DOM degradation (Coble, 1996; Stedmon and Markager, 2005b). Component C5 is linked to free tryptophan, which is a product of microbial activity (Determann et al., 1998). This component has been found to decrease during dark incubations and UV exposure (Stedmon et al., 2007), but component C5 is also associated with the degradation of DOM (Stedmon and Markager, 2005b) and autochthonous production (Murphy et al., 2008).
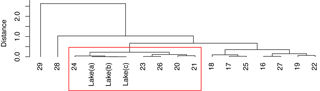
Figure 5Euclidean hierarchical clustering of fluorescent component C4 from recharging groundwater sites. The fluorescence found at sites 20, 21, 23, 24 and 26 clusters together with lake fluorescence (marked red). This indicates that these sites have a high degree of groundwater recharge. Groundwater well site 24 seems to be especially important in this regard.
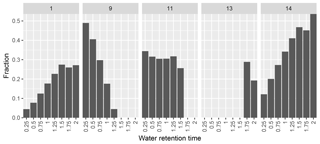
Figure 6Results derived from the CATS model shown in a bar plot in which the groundwater well sites (their numbering) are seen on the top x axis and the fractions of groundwater discharge estimated to derive from the sites are shown on the y axis (only the sites that deliver more than 0.1 % water to the lake are shown). The bottom x axis denotes the different water retention times used in this model. Three to four sites generally explain the estimated concentrations in the lake.
The highest fluorescence concentrations were found in the groundwater while the lake water fluorescence concentrations were generally lower (Table S1). Component C1 had the highest fluorescence with a value of 7.8 Raman's units (R.U.) in the lake and a maximum fluorescence of 47.1 at groundwater well site 7. Component C5 had the lowest fluorescence in the lake (0.27 ) and a maximum fluorescence of 2.9 at groundwater well site number 8. Component C5 also varied much between groundwater samples with the lowest value of 0.1 or 28 times lower than the maximum concentration. Components C1, C2 and C3 had low lake-like concentrations in recharge areas (orange sites in Fig. 1a). Concentrations of C4 were generally higher in groundwater around the lake than in the lake (1.1–1.5 vs. 1.1 visualized in Fig. 1b). Component C4 was chosen as a proxy for groundwater recharge as the concentration of the C4 component increase with biological activity and there were no apparent concentration changes in the lake–groundwater interface. The cluster diagram of component C4 showed that especially site 24 grouped with lake samples, but sites 20, 21, 23 and 26 also showed high comparability with the lake (Fig. 5), which can also be observed from the IDW map of component C4 around the lake (Fig. 1b).
3.3 Groundwater discharge areas and lake WRT
Tracer concentrations of the lake narrowed down the possible WRT. Equilibrium tracer concentrations of DOC, CDOM, TDP and TDN (found using Eqs. 1–4) for WRTs between 0.25 and 3.5 years in 0.25-year increments revealed that concentrations of TDN in the catchment are not high enough to support WRT values over 2 years based on the nitrogen retention model used. Thus, catchment tracer data revealed a possible WRT between 0 and 2 years.
Groundwater discharge areas were found employing the CATS model on nutrient concentrations and DOM fractions estimated using Eq. (1). related to WRTs between 0.25 and 2 years. The estimated phosphorus concentrations ranged from 46 to 80 µg PL−1 (Eqs. 1 and 2) while nitrate concentrations ranged from 1113 to 2417 µg NL−1 (Eqs. 1 and 3). CDOM and DOC degradation rates were related to the UV index and varied from 0.64 % in December to 28 % per month in June for DOC and between 0.46 and 20 % for ACDOM (340) in the same months and were significantly different from each other (P<0.001). Thus, estimated mixed inflow concentrations of CDOM ranged from ACDOM(340)=0.43 to 1.04 cm−1 while DOC ranged from 1205 to 3160 µmol L−1 for a WRT between 0.25 and 2 years (Eqs. 1 and 4). The CATS model isolated the minimum number of sites that explained the estimated lake concentrations. The model identified sites 1, 9, 11, 13 and 14 as the groundwater discharge sites delivering more than 0.1 % of the water throughout the different WRTs (Fig. 6). Changes in site distribution and fractions of discharging water were observed between the different WRTs, but in general, groundwater from 3–4 sites explains the estimated concentrations in the lake (Fig. 6). Site number 14 delivers more water with a higher WRT (to a maximum of 54 % of the total discharge). Site 1 peaks at a WRT of 1.25, providing 27 % of the water to the lake. Site number 9 delivers less water with increasing WRT, but 49 % at the lowest WRT of 0.25 years. Site number 11 delivers 26 to 34 % of the water to the lake until a WRT above 1.5 years is reached, at which site 13 explains the concentration in the lake better and provides 29 and 19 % of the water to the lake. Overall, 73 to 96 % of the water is estimated to arrive from the eastern part of the lake, while site number 1 (in the southern part) is estimated to deliver 4 to 27 % of the water. Lambda values, explaining which tracers are the most important when predicting the fractions of water originating from groundwater well sites, showed that CDOM was the most important tracer when determining which sites delivered water to the lake with a mean lambda value for all WRTs of 24.2 vs. 0.1–5.9 for the other tracers.
The combination of biological and hydrological methods in a novel approach provided a better estimate of the WRT, an identification of groundwater recharge and discharge areas, and the fractions of water coming from each site. Based on the model results and earlier hydrological studies, we will discuss the main questions from the introduction (1) if groundwater discharge sites and pollutant sources can be estimated with the CATS model based on tracer concentrations, (2) whether conservative and non-conservative tracers can be used to detect groundwater recharge areas as well as provide insights into which areas have a high groundwater recharge rate and (3) if catchment-derived tracer concentrations can be used to estimate a range of the WRTs, which can be used with the CATS model. Furthermore, we will discuss which of the tracers work and which could possibly work with refined methods, as well as how these findings could benefit lake restoration programmes.
4.1 Determination of groundwater recharge areas
Groundwater recharge sites were identified along the northern and western part of Tvorup Hul with a hierarchical cluster analysis of the conservative δ18O tracer. The exact same areas are also the ones with adjacent drainage channels (Fig. 1a), which facilitate the areas as recharge sites. While δ18O ‰ worked well as a general groundwater recharge estimator, it does not indicate which sites deliver more water. An indication of this can be found when examining the non-conservative tracers such as the fluorescent components.
Sites resembling the fluorescence found in the lake will indicate a high groundwater recharge rate, while a difference in concentration between lake and groundwater sites will indicate a lower groundwater recharge rate where there is sufficient time for a significant modification of the components representing the DOM pool of the lake. The fluorescent component C4 has previously been found to increase with biological activity (Coble, 1996), which is why we used it as a proxy to estimate the sites with a high groundwater recharge rate. The hierarchical Euclidean cluster dendrogram of component C4 showed that sites in the northern part of the lake formed a group (sites 24, 20, 21, 23 and 26) (Fig. 5 and visually in Fig. 1b). This information can be of importance related to placement of seepage meters, which will result in better estimations of the groundwater discharge and recharge and as such the modelled WRT of the lake. In other words, it might be advantageous to carry out groundwater sampling first to estimate sites with high discharge rates, then estimate WRT, utilizing these sites and finally model groundwater discharge areas by using the improved and narrowed WRT range.
CDOM generally showed much lower absorbance at groundwater recharge sites than in the lake, making it less suitable for estimating recharge areas. The decrease in absorption is possibly due to low soil pH, causing flocculation of CDOM in the soil matrix (Ekström et al., 2011). The same was observed with fluorescence of component C1, which had lower intensities in recharge areas, indicating that component C1 is linked to CDOM. While component C1 was not particularly useful for estimating groundwater recharge, it could be useful to estimate discharge sites. To utilize the component for discharge estimates there is a need for an assessment of the degradation rate. While it has been shown that component C1 is largely photo-resistant, as it does not absorb the UV-A radiation areas and is largely resistant to microbial degradation processes (Ishii and Boyer, 2012), no reliable rates for the degradation have been found. In this study, we found that only sites number 9 and number 11 hold concentrations lower than the lake (Table S1), indicating that most groundwater discharge would originate from these sites if little to no degradation takes place.
4.2 Determination of groundwater discharge areas
Neither δ18O nor previous seepage meter samplings have achieved a similar understanding of groundwater recharge areas in Tvorup Hul as compared to the present approach. While the δ18O ‰ provides a way of separating groundwater and surface water, using it to determine groundwater discharge sites is simply not possible due to the homological distribution seen in groundwater (Krabbenhoft et al., 1990). Previous seepage meter samplings provided scattered and momentary estimations of discharge sites, indicating that groundwater entered the lake from the southern bank (Solvang, 2016). This does not correspond to tracer concentrations found in the southern area, which show very high CDOM absorbance at 340 nm (ACDOM(340)=1.3–3.1 cm−1) and DOC concentrations (3114–10 467 µmol L−1) in relation to the lake (ACDOM(340)=0.4 cm−1∕DOC 1058 µmol L−1). This hints that the lake is influenced by groundwater discharge from other areas as well. The lowest DOC concentrations in the southern area were several times higher than those from the equilibrium estimation, suggesting a WRT above 6 years, which is well beyond previous estimates of WRT. Samples from the eastern shore had lower concentrations all around, proposing that water from this area influences the lake water. Thus, if the water actually originated from the southern area, the lake would need to have a prolonged WRT, resulting in increased removal of tracers from the lake. This requirement conflicts with the remaining tracers, for which especially TDN sets an upper limit of 2 years to the WRT.
The CATS model used in this study shows that while a fraction of groundwater enters the lake from the southern bank, most of the water originates from the eastern shore (Fig. 1a). Seepage meter measurements from the eastern shore showed both discharging and recharging of groundwater (Solvang, 2016). The same was observed for δ18O ‰ samples from the eastern part of the lake, which were lower than in the groundwater from the southern shore, indicating an influence of newly precipitated water or influence from the lake. Sampling in the northeastern and eastern part of the lake revealed an area with little groundwater and a clay deposit layer that possibly reduces infiltration to deeper groundwater layers. As a result, precipitations could enter the lake as surface and subsurface run-off water originating from the hills to the east and the plateau in the northeastern corner (Fig. 1a), resulting in short bursts of discharging water. The multi-tracer approach enables the determination of discharge areas much more precisely and on a temporal scale related to the WRT of the lake (in this instance the previous 3 to 24 months). Consequently, the model is able to track uncommon events such as heavy precipitation events in which a large amount of water is discharged to the lake during a short period. These events are often difficult to track as seepage meters need to be deployed in this exact period as well as in the right places.
4.3 Tracer influences
Most tracers used in this study are less conservative compared to δ18O and can therefore change both in the lake water and in the catchment soils. This entails an understanding of processes and rates that influence the concentrations. The temporal variability in nitrate concentrations in groundwater are related to the flow rate rather than seasonal changes (Kennedy et al., 2009). The same was observed for phosphorus, where particularly dry periods followed by heavy rain increased the phosphorus concentration measured in groundwater-fed springs (Kilroy and Coxon, 2005). Thus, in the case of northern Europe, sampling during late winter might be the best solution because soils are saturated at this time of year (Sand-Jensen and Lindegaard, 2004). Previously polluted areas, e.g. from wastewater infiltration, with increased concentrations of DOC and nutrients are likely to be in a state of imbalance, resulting in a reduction in concentrations over time (Repert et al., 2006). For this reason, in these areas, it is important to conduct temporal sampling following decreases in concentrations and to relate the samples to lake concentrations during sampling. Lake inter-annual DOC and CDOM changes were generally low in our study with an annual ACDOM(340)=0.41 cm−1 ± SD 0.05, corresponding to what is observed in larger water bodies where WRT integrates inflowing DOC and CDOM (Winterdahl et al., 2014). Inter-annual DOC and CDOM variations in groundwater from the lake catchment (Fig. S1) showed the same tendency as described for nutrients, and this suggests that sampling should be performed at multiple times or in a period without drought or high rainfall. On a broader scale, the variation in DOC is known to be related to hydrology (Erlandsson et al., 2008), mean air temperature (Winterdahl et al., 2014) and the recovery from acid deposition (Evans et al., 2006; Monteith et al., 2007). Sampling from wet areas with standing surface water resulted in high concentrations of most tracers (Table S1). Consequently, these areas should be avoided, seeing that they provide no information regarding the discharge of groundwater. The removal of CDOM and DOC also changes on an annual basis in lakes and is related to bacterial degradation, photodegradation, sources and mixing of the water column. A sensitivity analysis of the results was conducted by running the CATS model with a ±10 % change in tracer concentrations. The results showed that sites generally remained unchanged with only smaller deviations in percent-wise distribution in discharge up to a WRT of 1.25 years (Fig. S2). Above this point, there are some differences in sites, which change between sites number 11 and number 13. In conclusion, even when changing multiple parameters in the model, the same five groundwater wells are identified, explaining the measured lake concentrations. Future investigations into variation in tracers in groundwater and degradation rates in lakes will likely strengthen this model.
The processes that influence changes in FDOM are still being investigated (Ishii and Boyer, 2012). Tracing FDOM has been conducted in both rivers and open waters (Baker, 2001, 2002; Stedmon and Markager, 2005a), but only a few studies have been conducted in groundwater. These studies have focused on changes in FDOM from deep groundwater wells (Lapworth et al., 2008) or tracing FDOM using samples that are collected very far apart (Chen et al., 2010). Specific fluorescence intensity of components showed large differences among sites in this study, up to a factor of 28, between groundwater well sites, with the lowest at site 11 and highest at site 8, around the relatively small lake. These findings illustrate the problem when applying FDOM as a tracer over large distances in groundwater. In addition to bio- and photodegradation of fluorescent components, absorption changes have also been observed in relation to Fe(III) concentrations (Klapper et al., 2002). This might change the concentrations of FDOM components as they travel from anoxic groundwater with reduced iron into the oxic lake water. Overall, PARAFAC components have the potential to work as groundwater tracers, but there is a need for a better understanding of the processes that cause changes in fluorescence characteristics of DOM and hence concentrations of FDOM components both in the lake and in the lake–groundwater interface.
4.4 Potential lake management influence
The determination of discharge sites can result in direct management related to specific problematic areas. The model used in this study showed that water entering the lake primarily originated from the catchment to the east of the lake. If water from this part were diverted around the lake, there would be a reduction in CDOM absorbance of 61–89 % based on calculations relating percent-wise discharge, its concentrations and WRTs from 0.25 to 2 years in 0.25-year increments. Conversely, diverting water around the lake at site number 1 would only result in a lowered inflowing CDOM absorbance of 11–39 %. Moreover, in both cases, there would be an increase in photobleaching of present CDOM in the lake caused by the increased WRT. Furthermore, huge reductions would occur for TP and TN, with a decrease of 82–96 % if diverting water from the eastern shore, in contrast to the southern shore with a modelled decrease of 4–18 % in TP and TN. In the future, hydrology is likely to be the main driver of variability in DOM (Erlandsson et al., 2008) with an estimated increase in CDOM by a factor of 4 in lakes with short WRT (Weyhenmeyer et al., 2016). This makes it critical to establish a modelling tool that is capable of pinpointing sites delivering pollutants to lakes and provide us with the ability to take action and reduce the impact on the ecological state of lakes.
The present method and modelling tool can improve estimates of recharge and discharge areas as well as WRT in smaller lakes on a temporal scale. The model provides accurate estimates of discharge fractions, related to field measurements, and can be used for precise management of problematic pollution areas. The hierarchical clustering can be used to estimate groundwater recharge sites, which can be incorporated as a guideline for a better estimation of WRT in lakes. Furthermore, the use of multiple tracers strengthens the model and keeps a certain degree of freedom in regard to the choice of tracers related to laboratory capabilities.
The underlying data can be accessed in the Supplement (Table S1).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-15-1203-2018-supplement.
The authors declare that they have no conflict of interest.
We are grateful to Naturstyrelsen (the Department for Nature and
Conservation) for access to the study area in Nationalpark Thy. The study was
partly supported by a grant to the Centre for Lake Restoration, a Villum Kann
Rasmussen Centre of Excellence. Peter Engesgaard and Ingeborg Solvang are
acknowledged for their comments on the paper and for supplying data on
oxygen isotopes.
Edited by: Florian
Wittmann
Reviewed by: two anonymous referees
Appelo, C. A. and Postma, D.: Geochemistry, Groundwater and Pollution, Balkema, 2005.
Bahram, M., Bro, R., Stedmon, C., and Afkhami, A.: Handling of Rayleigh and Raman scatter for PARAFAC modeling of fluorescence data using interpolation, J. Chemometr., 20, 99–105, https://doi.org/10.1002/cem.978, 2006.
Baker, A.: Fluorescence excitation - Emission matrix characterization of some sewage-impacted rivers, Environ. Sci. Technol., 35, 948–953, https://doi.org/10.1021/es000177t, 2001.
Baker, A.: Spectrophotometric discrimination of river dissolved organic matter, Hydrol. Process., 16, 3203–3213, https://doi.org/10.1002/hyp.1097, 2002.
Chen, M., Price, R. M., Yamashita, Y., and Jaffé, R.: Comparative study of dissolved organic matter from groundwater and surface water in the Florida coastal Everglades using multi-dimensional spectrofluorometry combined with multivariate statistics, Appl. Geochem., 25, 872–880, https://doi.org/10.1016/j.apgeochem.2010.03.005, 2010.
Cherkauer, D. S. and Nader, D. C.: Distribution of groundwater seepage to large surface-water bodies: the effect of hydraulic heterogeneities, J. Hydrol., 109, 151–165, https://doi.org/10.1016/0022-1694(89)90012-7, 1989.
Chow-Fraser, P., Lougheed, V., Le Thiec, V., Crosbie, B., Simser, L., and Lord, J.: Long-term response of the biotic community to fluctuating water levels and changes in water quality in Cootes Paradise Marsh, a degraded coastal wetland of Lake Ontario, Wetl. Ecol. Manag., 6, 19–42, https://doi.org/10.1023/A:1008491520668, 1998.
Coble, P. G.: Characterization of marine and terrestrial DOM in seawater using excitation-emission matrix spectroscopy, Mar. Chem., 51, 325–346, https://doi.org/10.1016/0304-4203(95)00062-3, 1996.
Determann, S., Lobbes, J. M., Reuter, R., and Rullkötter, J.: Ultraviolet fluorescence excitation and emission spectroscopy of marine algae and bacteria, Mar. Chem., 62, 137–156, https://doi.org/10.1016/S0304-4203(98)00026-7, 1998.
Diffey, B. L.: Sources and measurement of ultraviolet radiation, Methods, 28, 4–13, https://doi.org/10.1016/S1046-2023(02)00204-9, 2002.
DMI: UV-dose: DMI, available at: http://www.dmi.dk/vejr/sundhedsvejr/uv-indeks/uv-dose/ (last access: 12 May 2016), 2015.
Ekström, S. M., Kritzberg, E. S., Kleja, D. B., Larsson, N., Nilsson, P. A., Graneli, W., and Bergkvist, B.: Effect of acid deposition on quantity and quality of dissolved organic matter in soil water, Environ. Sci. Technol., 45, 4733–4739, https://doi.org/10.1021/es104126f, 2011.
Erlandsson, M., Buffam, I., Fölster, J., Laudon, H., Temnerud, J., Weyhenmeyer, G. A., and Bishop, K.: Thirty-five years of synchrony in the organic matter concentrations of Swedish rivers explained by variation in flow and sulphate, Glob. Change Biol., 14, 1191–1198, https://doi.org/10.1111/j.1365-2486.2008.01551.x, 2008.
Evans, C. D., Chapman, P. J., Clark, J. M., Monteith, D. T., and Cresser, M. S.: Alternative explanations for rising dissolved organic carbon export from organic soils, Glob. Change Biol., 12, 2044–2053, https://doi.org/10.1111/j.1365-2486.2006.01241.x, 2006.
Fellman, J. B., Miller, M. P., Cory, R. M., D'Amore, D. V., and White, D.: Characterizing dissolved organic matter using PARAFAC modeling of fluorescence spectroscopy: a comparison of two models, Environ. Sci. Technol., 43, 6228–6234, https://doi.org/10.1021/es900143g, 2009.
Gibson, J. J., Prepas, E. E., and McEachern, P.: Quantitative comparison of lake throughflow, residency, and catchment runoff using stable isotopes: modelling and results from a regional survey of Boreal lakes, J. Hydrol., 262, 128–144, https://doi.org/10.1016/S0022-1694(02)00022-7, 2002.
Harrison, J. A., Maranger, R. J., Alexander, R. B., Giblin, A. E., Jacinthe, P. A., Mayorga, E., Seitzinger, S. P., Sobota, D. J., and Wollheim, W. M.: The regional and global significance of nitrogen removal in lakes and reservoirs, Biogeochemistry, 93, 143–157, https://doi.org/10.1007/s10533-008-9272-x, 2009.
He, X. S., Xi, B. D., Gao, R. T., Wang, L., Ma, Y., Cui, D. Y., and Tan, W. B.: Using fluorescence spectroscopy coupled with chemometric analysis to investigate the origin, composition, and dynamics of dissolved organic matter in leachate-polluted groundwater, Environ. Sci. Pollut. R., 22, 8499–8506, https://doi.org/10.1007/s11356-014-4029-7, 2014.
Ishii, S. K. L. and Boyer, T. H.: Behavior of reoccurring parafac components in fluorescent dissolved organic matter in natural and engineered systems: a critical review, Environ. Sci. Technol., 46, 2006–2017, https://doi.org/10.1021/es2043504, 2012.
Jensen, J. P., Lauridsen, T. L., Søndergaard, M., Jeppesen, E., Agerbo, E., and Sortkjær, L.: Ferske Vandområder – Søer, Vandmiljøplanens overvågningsprogram 1995, 96, 1995.
Kennedy, C. D., Genereux, D. P., Corbett, D. R., and Mitasova, H.: Spatial and temporal dynamics of coupled groundwater and nitrogen fluxes through a streambed in an agricultural watershed, Water Resour. Res., 45, W09401, https://doi.org/10.1029/2008WR007397, 2009.
Kidmose, J., Engesgaard, P., Nilsson, B., Laier, T., and Looms, M. C.: Spatial distribution of seepage at a flow-through lake: Lake Hampen, Western Denmark, Vadose Zone J., 10, 110–124, https://doi.org/10.2136/vzj2010.0017, 2011.
Kilroy, G. and Coxon, C.: Temporal variability of phosphorus fractions in Irish karst springs, Environ. Geol., 47, 421–430, https://doi.org/10.1007/s00254-004-1171-4, 2005.
Kishel, H. F. and Gerla, P. J.: Characteristics of preferential flow and groundwater discharge to Shingobee Lake, Minnesota, USA, Hydrol. Process., 16, 1921–1934, https://doi.org/10.1002/hyp.363, 2002.
Klapper, L., McKnight, D. M., Fulton, J. R., Blunt-Harris, E. L., Nevin, K. P., Lovley, D. R., and Hatcher, P. G.: Fulvic acid oxidation state detection using fluorescence spectroscopy, Environ. Sci. Technol., 36, 3170–3175, https://doi.org/10.1021/es0109702, 2002.
Kothawala, D. N., Murphy, K. R., Stedmon, C. A., Weyhenmeyer, G. A., and Tranvik, L. J.: Inner filter correction of dissolved organic matter fluorescence, Limnol. Oceanogr.-Meth., 11, 616–630, https://doi.org/10.4319/lom.2013.11.616, 2013.
Krabbenhoft, D. P., Bowser, C. J., Anderson, M. P., and Valley, J. W.: Estimating groundwater exchange with lakes: 1. The stable isotope mass balance method, Water Resour. Res., 26, 2445–2453, https://doi.org/10.1029/WR026i010p02445, 1990.
Kragh, T. and Søndergaard, M.: Production and bioavailability of autochthonous dissolved organic carbon: effects of mesozooplankton, Aquat. Microb. Ecol., 36, 61–72, https://doi.org/10.3354/ame036061, 2004.
Lakowicz, J. R.: Principles of Fluorescence Spectroscopy, edited by: Lakowicz, J. R., Springer US, Boston, MA, 2006.
Laliberté, E., Legendre, P., and Shipley, B.: Measuring functional diversity from multiple traits, and other tools for functional ecology, available at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.494.7392&rep=rep1&type=pdf (last access: 6 April 2017), 2014.
Lapworth, D. J., Gooddy, D. C., Butcher, A. S., and Morris, B. L.: Tracing groundwater flow and sources of organic carbon in sandstone aquifers using fluorescence properties of dissolved organic matter (DOM), Appl. Geochem., 23, 3384–3390, https://doi.org/10.1016/j.apgeochem.2008.07.011, 2008.
Larsen, D. P. and Mercier, H. T.: Phosphorus retention capacity of lakes, J. Fish. Res. Board Can., 33, 1742–1750, https://doi.org/10.1139/f76-221, 1976.
Lawaetz, A. J. and Stedmon, C. A.: Fluorescence intensity calibration using the Raman scatter peak of water, Appl. Spectrosc., 63, 936–940, https://doi.org/10.1366/000370209788964548, 2009.
Lee, D. R. and Cherry, J. A.: A field exercise on groundwater flow using seepage meters and mini-piezometers, J. Geol. Educ., 27, 6–10, https://doi.org/10.5408/0022-1368-27.1.6, 1979.
Lewandowski, J., Meinikmann, K., Nützmann, G., and Rosenberry, D. O.: Groundwater – the disregarded component in lake water and nutrient budgets. Part 2: Effects of groundwater on nutrients, Hydrol. Process., 29, 2922–2955, https://doi.org/10.1002/hyp.10384, 2015.
Madsen-Østerbye, M., Kragh, T., Pedersen, O., and Sand-Jensen, K.: Coupled photochemical and microbial decomposition of dissolved organic carbon in humic Lake Tvorup and groundwater inflows, Ecol. Eng., under review, 2018.
Massicotte, P. and Frenette, J. J.: Spatial connectivity in a large river system: resolving the sources and fate of dissolved organic matter, Ecol. Appl., 21, 2600–2617, https://doi.org/10.1890/10-1475.1, 2011.
Meinikmann, K., Lewandowski, J., and Nützmann, G.: Lacustrine groundwater discharge: combined determination of volumes and spatial patterns, J. Hydrol., 502, 202–211, https://doi.org/10.1016/j.jhydrol.2013.08.021, 2013.
Monteith, D. T., Stoddard, J. L., Evans, C. D., de Wit, H. A., Forsius, M., Høgåsen, T., Wilander, A., Skjelkvåle, B. L., Jeffries, D. S., Vuorenmaa, J., Keller, B., Kopácek, J., and Vesely, J.: Dissolved organic carbon trends resulting from changes in atmospheric deposition chemistry, Nature, 450, 537–540, https://doi.org/10.1038/nature06316, 2007.
Murphy, K. R., Ruiz, G. M., Dunsmuir, W. T. M., and Waite, T. D.: Optimized parameters for fluorescence-based verification of ballast water exchange by ships, Environ. Sci. Technol., 40, 2357–2362, https://doi.org/10.1021/es0519381, 2006.
Murphy, K. R., Stedmon, C. A., Waite, T. D., and Ruiz, G. M.: Distinguishing between terrestrial and autochthonous organic matter sources in marine environments using fluorescence spectroscopy, Mar. Chem., 108, 40–58, https://doi.org/10.1016/j.marchem.2007.10.003, 2008.
Murphy, K. R., Stedmon, C. A., Graeber, D., and Bro, R.: Fluorescence spectroscopy and multi-way techniques, PARAFAC, Anal. Methods-UK, 5, 6557, https://doi.org/10.1039/c3ay41160e, 2013.
R Core team: R: A Language and Environment for Statistical Computing, R Found. Stat. Comput., Vienna, Austria, available at: https://www.r-project.org/ (last access: 2 December 2017), 2017.
Rebsdorf, A.: Miljøprojekter 38; Forsuringstruede danske søer – Rapport over undersøgelser af den kemiske status i nogle forsuringstruede danske Lobeliasøer i relation til sur nedbør, Miljøstyrelsen, 1981.
Repert, D. A., Barber, L. B., Hess, K. M., Keefe, S. H., Kent, D. B., Leblanc, D. R., and Smith, R. L.: Long-term natural attenuation of carbon and nitrogen within a groundwater plume after removal of the treated wastewater source, Environ. Sci. Technol., 40, 1154–1162, https://doi.org/10.1021/es051442j, 2006.
Rosenberry, D. O.: Integrating seepage heterogeneity with the use of ganged seepage meters, Limnol. Oceanogr.-Meth., 3, 131–142, https://doi.org/10.4319/lom.2005.3.131, 2005.
Rosenberry, D. O., Lewandowski, J., Meinikmann, K., and Nützmann, G.: Groundwater – the disregarded component in lake water and nutrient budgets. Part 1: Effects of groundwater on hydrology, Hydrol. Process., 29, 2895–2921, https://doi.org/10.1002/hyp.10403, 2015.
Sand-Jensen, K. and Lindegaard, C.: Ferksvandsbiologi, Gyldendal, 2004.
Shipley, B.: From Plant Traits to Vegetation Structure: Chance and Selection in the Assembly of Ecological Communities, Cambridge University Press, https://doi.org/10.1017/CBO9780511806971, 2009.
Shipley, B., Vile, D., and Garnier, E.: From plant traits to plant communities: a statistical mechanistic approach to biodiversity, Science, 314, 812–814, https://doi.org/10.1126/science.1131344, 2006.
Shipley, B., Laughlin, D. C., Sonnier, G., and Otfinowski, R.: A strong test of a maximum entropy model of trait-based community assembly, Ecology, 92, 507–517, https://doi.org/10.1890/10-0394.1, 2011.
Smith, V.: Eutrophication of freshwater and coastal marine ecosystems a global problem, Environ. Sci. Pollut. R., 10, 126–139, https://doi.org/10.1065/espr2002.12.142, 2003.
Solvang, I. S.: Groundwater and Surface Water Interaction in Thy National Park, Master thesis, University of Copenhagen, 2016.
Stedmon, C. A. and Bro, R.: Characterizing dissolved organic matter fluorescence with parallel factor analysis: a tutorial, Limnol. Oceanogr., 6, 572–579, https://doi.org/10.4319/lom.2008.6.572, 2008.
Stedmon, C. A. and Markager, S.: Resolving the variability of dissolved organic matter fluorescence in a temperate estuary and its catchment using PARAFAC analysis, Limnol. Oceanogr., 50, 686–697, https://doi.org/10.4319/lo.2005.50.2.0686, 2005a.
Stedmon, C. A. and Markager, S.: Tracing the production and degradation of autochthonous fractions of dissolved organic matter using fluorescence analysis, Limnol. Oceanogr., 50, 1415–1426, https://doi.org/10.4319/lo.2005.50.5.1415, 2005b.
Stedmon, C. A., Markager, S., and Bro, R.: Tracing dissolved organic matter in aquatic environments using a new approach to fluorescence spectroscopy, Mar. Chem., 82, 239–254, https://doi.org/10.1016/S0304-4203(03)00072-0, 2003.
Stedmon, C. A., Markager, S., Tranvik, L., Kronberg, L., Slätis, T., and Martinsen, W.: Photochemical production of ammonium and transformation of dissolved organic matter in the Baltic Sea, Mar. Chem., 104, 227–240, https://doi.org/10.1016/j.marchem.2006.11.005, 2007.
Stets, E. G., Winter, T. C., Rosenberry, D. O., and Striegl, R. G.: Quantification of surface water and groundwater flows to open- and closed-basin lakes in a headwaters watershed using a descriptive oxygen stable isotope model, Water Resour. Res., 46, W03515, https://doi.org/10.1029/2009WR007793, 2010.
Turner, J. V., Arad, A., and Johnston, C. D.: Environmental isotope hydrology of salinized experimental catchments, J. Hydrol., 94, 89–107, https://doi.org/10.1016/0022-1694(87)90034-5, 1987.
Vollenweider, R. A.: Input-output models, Schweiz. Z. Hydrol., 37, 53–84, https://doi.org/10.1007/BF02505178, 1975.
Walker, S. A., Amon, R. M. W., Stedmon, C., Duan, S., and Louchouarn, P.: The use of PARAFAC modeling to trace terrestrial dissolved organic matter and fingerprint water masses in coastal Canadian Arctic surface waters, J. Geophys. Res.-Biogeo., 114, G00F06, https://doi.org/10.1029/2009JG000990, 2009.
Weyhenmeyer, G. A., Müller, R. A., Norman, M., and Tranvik, L. J.: Sensitivity of freshwaters to browning in response to future climate change, Climatic Change, 134, 225–239, https://doi.org/10.1007/s10584-015-1514-z, 2016.
Winterdahl, M., Erlandsson, M., Futter, M. N., Weyhenmeyer, G. A., and Bishop, K.: Intra-annual variability of organic carbon concentrations in running waters: drivers along a climatic gradient, Global Biogeochem. Cy., 28, 451–464, https://doi.org/10.1002/2013GB004770, 2014.
Zepp, R. G., Sheldon, W. M., and Moran, M. A.: Dissolved organic fluorophores in southeastern US coastal waters: correction method for eliminating Rayleigh and Raman scattering peaks in excitation-emission matrices, Mar. Chem., 89, 15–36, https://doi.org/10.1016/j.marchem.2004.02.006, 2004.